Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 апреля 2021 года; проверки требуют 3 правки.

Разложение ускорения 



Центростреми́тельное (норма́льное) ускоре́ние — составляющая ускорения тела, характеризующая быстроту изменения направления вектора скорости (вторая составляющая, тангенциальное ускорение, характеризует изменение модуля скорости). Направлено к центру кривизны траектории, с чем и связан термин.
Обозначается символом, выбранным для ускорения, с добавлением значка «нормальное»: 

Пример движения с ненулевым центростремительным ускорением — движение по окружности (в таком случае 
В классической механике нормальное ускорение вызывается компонентами сил, направленными ортогонально вектору скорости. Например, движение космического объекта на орбите характеризуется центростремительным ускорением, вызванным гравитацией. Составляющая суммы сил, обусловливающая наличие нормального ускорения, называется центростремительной силой. Связанное понятие для неинерциальных систем отсчёта — центробежная сила.
Осестремительное ускорение, рассматриваемое в случаях вращения тела вокруг оси, в проекции на плоскость, перпендикулярную оси, предстаёт как центростремительное.
Общая формула[править | править код]
Нормальное ускорение 
или (с использованием соотношения 
,
где 


Выражения могут быть переписаны в векторном виде:
.
Здесь 
Эти формулы применимы как к частной ситуации равномерного движения (



Вывод формулы[править | править код]
Для разложения ускорения на тангенциальное и нормальное можно продифференцировать по времени вектор скорости, представленный в виде 

.
Здесь первое слагаемое — тангенциальное ускорение, а второе — нормальное ускорение. Через 






Равенство 














О радиусе кривизны[править | править код]
Вычисление радиуса кривизны и координат центра кривизны траектории является математической задачей (см. Кривизна). Если кривая задана уравнением 


,
а положение центра кривизны — по формулам[2]
.
Единичный вектор нормали в таком случае составит (

.
Если известна зависимость радиус-вектора материальной точки от времени 
,
где 


Мотивация, замечания[править | править код]
То, что разложение вектора ускорения на компоненты — одну вдоль касательной к траектории (тангенциальное ускорение) и другую ортогональную ей (нормальное ускорение) — может быть удобным и полезным, довольно очевидно само по себе. При движении с постоянной по модулю скоростью тангенциальная составляющая становится равной нулю, то есть в этом важном частном случае остается только нормальная составляющая. Кроме того, каждая из этих составляющих имеет ярко выраженные собственные свойства и структуру, и нормальное ускорение содержит в структуре своей формулы достаточно важное и нетривиальное геометрическое наполнение. Крайне важен также частный случай движения по окружности.
Абсолютная величина тангенциального ускорения зависит только от путевого ускорения, совпадая с его абсолютной величиной, в отличие от абсолютной величины нормального ускорения, которая от путевого ускорения не зависит, зато зависит от путевой скорости.
История понятия[править | править код]
Первым правильные формулы для центростремительного ускорения (или центробежной силы) получил, по-видимому, Гюйгенс. Практически с этого времени рассмотрение центростремительного ускорения входит в обычную технику решения механических задач.
Несколько позже эти формулы сыграли существенную роль в открытии закона всемирного тяготения (формула центростремительного ускорения использовалась для получения закона зависимости гравитационной силы от расстояния до источника гравитации, исходя из выведенного из наблюдений третьего закона Кеплера).
К XIX веку рассмотрение центростремительного ускорения становится уже совершенно рутинным как для чистой науки, так и для инженерных приложений.
См. также[править | править код]
- Тангенциальное ускорение
- Кривизна кривой
- Центробежная сила
Примечания[править | править код]
- ↑ Как видно из формулы, при движении с постоянной путевой скоростью — тангенциальное ускорение попросту равно нулю.
- ↑ 1 2 Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. М., «Высш. школа», c. 368-370.
Сергей Сергеевич Соев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Ускорение точки, движущейся по окружности
Полное ускорение точки, движущейся по окружности, складывается из двух составляющих:
- тангенциального ускорения, направленного по касательной к данной окружности;
- центростремительного ускорения, направленного по радиусу от точки к центру окружности.
Замечание 1
Тангенциальное ускорение отражает изменение величины скорости движения, центростремительное, называемое также нормальным и обозначаемое обычно как $a_n$, – измерение направления вектора скорости.
Центростремительное ускорение
Формула для расчета центростремительного ускорения:
$a_n = frac{v^2}{R}$,
где $v$ – мгновенная скорость, $R$ – радиус кривизны траектории.
Выразив мгновенную скорость из угловой как
$v = omega cdot R$
и подставив в формулу, найдем центростремительное ускорение как
$a_n = frac{(omega cdot R)^2}{R} = omega^2 cdot R$
Основы теории о центростремительном ускорении заложил голландский физик Христиан Гюйгенс (1629 — 1695 гг.). В своем сочинении “Маятниковые часы” он не только изложил инженерные расчеты, необходимые для изготовления хронометров, но и сформулировал физические законы циклического движения. В частности, Гюйгенс открыл зависимость периодичности колебаний маятника от длины подвеса, описал явление изохронности ввел понятие центробежной силы и центростремительного ускорения. Это дало толчок не только прикладной механике, но и развитию теории о движении небесных тел, повлиявшей, в частности, на научные взгляды Исаака Ньютона.
Особенностью кругового движения является то, что даже если точка движется по окружности со скоростью неизменной величины (тангенциальное ускорение равно нулю), ее суммарное ускорение не равно нулю, поскольку направление вектора скорости всё время меняется. В этом заключается физический смысл центростремительного ускорения.
«Формула центростремительного ускорения в физике» 👇
Геометрически центростремительное ускорение можно выразить следующим образом. Рассмотрим окружность, по которой движется точка.
Рисунок 1. Центростремительное ускорение. Автор24 — интернет-биржа студенческих работ
Выберем в качестве ее начального положения верхнюю точку. При этом вектор мгновенной скорости $vec{v_1}$ будет направлен горизонтально. Когда точка пройдет некоторую дугу, вектор мгновенной скорости $vec{v_2}$ окажется наклоненным к первому под углом $varphi$, который равен пройденному угловому расстоянию. Таким образом, центростремительный вектор окажется основанием равнобедренного треугольника с углом при вершине $varphi$ и стороной $bar{v_A} = bar{v_B}$. Обозначим длину основания этого треугольника как $Delta v$. Подобный треугольник со стороной $R$ мы видим внутри окружности. Его вершина соответствует ее центру. Приняв, что при достаточно малом $varphi$ длины дуги и хорды между точками $A$ и $B$ приблизительно совпадают, найдем из подобия треугольников, что
$frac{R}{v cdot Delta t} approx frac{v}{Delta v}$,
где $v cdot Delta t$ – путь, пройденный точкой по дуге, почти совпадающей с хордой.
Формулу можно преобразовать следующим образом:
$frac{Delta v}{Delta t} approx frac{v^2}{R}$
Учитывая малое пройденное угловое расстояние (при $Delta t$ стремящемся к нулю), можно считать вектор $vec{Delta v}$ направленным к центру окружности. Следовательно,
$vec{a_n} = frac{Delta vec{v}}{Delta t}; Delta t to 0; a_n = frac{v^2}{R}$
Замечание 2
Хорошим способом представить себе центростремительное ускорение является конкретный пример. Центростремительное ускорение Земли, вращающейся вокруг своей оси, составляет $0,03 м/с^2$. Это значит, что в его отсутствие почва “уходила бы у нас из под ног” со скоростью 3 см/с.
Пример 1
Велосипедист едет по дороге со скоростью 10 м/с. Какое центростремительное ускорение точки обода колеса, если его радиус 35 см?
Подставим в формулу центростремительного ускорения числовые значения:
$a_n = frac{{10}^2}{0,35} = 285 m/c^2$
Ответ: 285 метров в секунду.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Физика > Центростремительное ускорение
Центростремительное ускорение – постоянное изменение скорости, необходимое для подержания объектом кругового движения.
Задача обучения
- Разобрать центростремительное ускорение с позиции скорости вращения.
Основные пункты
- Чтобы объект смог поддерживать круговое движение, ему необходимо все время менять направление.
- Скорость выступает вектором, поэтому перемены в направлении влияют на нее.
- Перемена скорости – ускорение, а перемена за счет кругового движения – центростремительное ускорение.
- Его можно рассчитать при помощи линейного квадрата скорости, деленного на радиус круга.
Термины
- Ускорение – количество, на которое увеличивается скорость.
- Круговое движение – перемещение по кругу.
- Скорость – векторная величина, отображающая темп перемены положения во времени и направлении.
Обзор
Любая перемена скорости руководствуется ускорением. Перемены в величине скорости определяются нашим интуитивным и каждодневным применением термина «ускорение». Но скорость выступает вектором, поэтому обладает направлением. Выходит, что любое изменение направления перемещения должно учитывать ускорение.
Равномерное круговое движение – перемещение по кругу со стабильной скоростью. Если она стабильна, значит нет смысла думать об ускорении. Но во время прохождения по кругу направление изменяется все время. Поэтому можно говорить о присутствии ускорения. Это соответствует ситуации с американскими горками, где на резких поворотах кажется, что скорость вырастает.
Расчет центростремительного ускорения
Давайте определим, как выглядит формула для центростремительного ускорения движения тела по окружности. Для этого нужно располагать скоростью объекта и радиусом круга. Поможет уравнение:
ac = v/r
Здесь v – линейная скорость объекта, а r – радиус круга.
Также центростремительное ускорение можно найти как:
аc = ω2r
Омега выступает скоростью вращения и задается как .

Когда тело перемещается по кругу, направление вектора скорости меняется все время
Что такое центростремительное ускорение
Определение
Центростремительным ускорением называется ускорение тела при движении тела по окружности.
Данная величина характеризует, насколько быстро изменяется направление линейной скорости объекта при его движении по окружности.
Обозначается центростремительное ускорение латинской буквой a, так как это векторная величина, обычно ее обозначение условно выглядит так: (vec a)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Единицами измерения в международной системе СИ является м/с2.
Силы центростремительная и центробежная, в чем отличия
Определение
На любое тело, передвигающееся по круговой траектории, воздействует постоянная сила, которая направлена к центру окружности, описывающей траекторию движения. Эта сила получила название центростремительной.
Определение
Центробежная сила представляет собой силу инерции. По третьему закону Исаака Ньютона, на каждое действие приходится равное ему по силе, но противоположное по направлению противодействие. И центробежная сила является той самой силой, которая противоположна центростремительной силе.
Сходства центростремительной и центробежной силы:
- Они являются инерциальными.
- Возникают всегда при движении тела.
- Появляются только парами и всегда уравновешивают друг друга.
Их различия заключаются в следующем:
- Центростремительная сила всегда направлена к центру окружности, в то время как центробежная сила противоположна центростремительной по направлению.
- Слово «центростремительная» с латинского языка переводится как «искать центр», а «центробежная» — «бежать от центра».
Куда направлен вектор центростремительного ускорения
При передвижении точки по окружности ее скорость направлена по касательной к окружности, а ускорение — по радиусу к центру окружности. Т.е. центростремительное ускорение всегда перпендикулярно скорости.
Вывод формулы центростремительного ускорения
Как найти через угловую и линейную скорость
Центростремительное ускорение, при условии равномерного движения по окружности, можно вычислить с помощью линейной скорости движения.
Центростремительное ускорение можно вычислить через угловую скорость.
Определение
Угловой скоростью (omega) называется физическая величина, численно равная отношению угла поворота (varphi) к тому интервалу времени (t), за который этот поворот произошел:
(omega =fracvarphi t)
Измеряется величина в рад/с.
Зависимость ускорения от скорости математически выглядит так:
(a=omega^2times R)
Расчет центростремительного ускорения через радиус
Центростремительное ускорение, теория и онлайн калькуляторы
Центростремительное ускорение
Центростремительное ускорение при равномерном движении по окружности
Пусть материальная точка равномерно движется по окружности. Тогда модуль ее скорости не изменяется ($v=const$). Но это не значит, что ускорение материальной точки равно нулю. Вектор скорости направлен по касательной к траектории движения точки. При перемещении по окружности скорость изменяет свое направление постоянно. Значит, точка движется с ускорением.
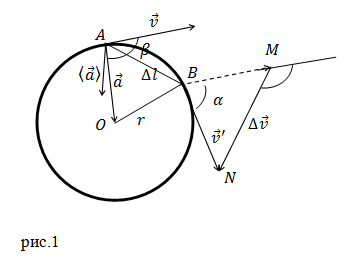
Рассмотрим точки A и B принадлежащие траектории движения рассматриваемого тела. Вектор изменения скорости для этих точек равен:
[Delta overline{v}={overline{v}}’-overline{v}left(1right).]
Если время движения, между точками A и B мало, то дуга AB мало отличается от хорды AB. Треугольники AOB и BMN подобны, следовательно:
[frac{Delta v}{v}=frac{Delta l}{r}=alpha left(2right).]
Модуль среднего ускорения найдем как:
[leftlangle arightrangle =frac{Delta v}{Delta t}=frac{vDelta l}{rDelta t}left(3right).]
Величину мгновенного ускорения можно получить, перейдя к пределу при $Delta tto 0 $ от $leftlangle arightrangle $:
[a={mathop{lim }_{Delta tto 0} leftlangle arightrangle }={mathop{lim }_{Delta tto 0} frac{vDelta l}{rDelta t}=frac{v}{r} }mathop{{rm lim}}_{Delta tto 0}frac{Delta l}{Delta t}=frac{v}{r}v=frac{v^2}{r}left(4right).]
Вектор среднего ускорения составляет с вектором скорости угол равный:
[beta =frac{pi +alpha }{2}left(5right).]
При $Delta tto 0 $ угол $alpha to 0.$ Получается, что вектор мгновенного ускорения составляет с вектором скорости угол $frac{pi }{2}$.
Мы получили, что материальная точка, равномерно движущаяся по окружности, имеет ускорение, направленное к центру траектории движения (перпендикулярное вектору скорости), его модуль равен скорости в квадрате, деленной на радиус окружности.
Такое ускорение называют центростремительным или нормальным, обозначают его обычно ${overline{a}}_n$.
[a_n=frac{v^2}{r}={omega }^2r left(6right),]
где $omega $ – угловая скорость движения материальной точки ($v=omega cdot r$).
Определение центростремительного ускорения
Определение
И так, центростремительное ускорение (в общем случае) – это составляющая полного ускорения материальной точки, которая характеризует,
как быстро изменяется направление вектора скорости при криволинейном перемещении.
Другой компонентой полного ускорения является тангенциальное ускорение, оно отвечает за изменение величины скорости.
Центростремительное ускорение равно:
[{overline{a}}_n=frac{v^2}{r^2}overline{r }left(7right),]
где $e_r=frac{overline{r }}{r}$ – единичный вектор, направленный от центра кривизны траектории к рассматриваемой точке.
Впервые верные формулы для центростремительного ускорения были получены Х. Гюйгенсом.
Единицей измерения центростремительного ускорения в Международной системе единиц является метр, деленный на секунду в квадрате:
[left[a_nright]=frac{м}{с^2}.]
Примеры задач с решением
Пример 1
Задание. Диск вращается вокруг неподвижной оси. Закон изменения угла поворота радиуса диска задает уравнение: $varphi =5t^2+7 (рад)$. Чему равно центростремительное ускорение точки A диска, которая находится на расстоянии $r=$0,5 м от оси вращения к окончанию четвертой секунды от начала вращения?
Решение. Сделаем рисунок.
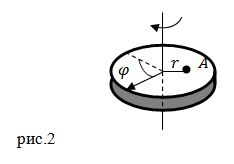
Модуль центростремительного ускорения равен:
[a_n=frac{v^2}{r}={omega }^2rleft(1.1right).]
Угловую скорость вращения точки найдем как:
[omega =frac{dvarphi }{dt} (1.2)]
уравнение изменения угла поворота в зависимости о времени:
[omega =frac{dleft(5t^2+7right)}{dt}=10t left(1.3right).]
В конце четвертой секунды угловая скорость равна:
[omega left(t=4right)=10cdot 4=40 left(frac{рад}{с}right).]
Используя выражение (1.1) найдем величину центростремительного ускорения:
[a_n={(40)}^2cdot 0,5=800 left(frac{м}{с^2}right).]
Ответ. $a_n=800frac{м}{с^2}$.
Пример 2
Задание. Движение материальной точки задается при помощи уравнения: $overline{r}left(tright)=0,5 (overline{i}{cos left(omega tright)+overline{j}{sin (omega t) } })$, где $omega =2 frac{рад}{с}$. Какова величина нормального ускорения точки?
Решение. За основу решения задачи примем определение центростремительного ускорения в виде:
[a_n=frac{v^2}{R}left(2.1right).]
Из условий задачи видно, что траекторией движения точки является окружность. В параметрическом виде уравнение: $overline{r}left(tright)=0,5 (overline{i}{cos left(omega tright)+overline{j}{sin (omega t) } })$, где $omega =2 frac{рад}{с}$ можно представить как:
[left{ begin{array}{c}
x=0,5{cos left(2tright);; } \
y=0,5{sin left(2tright). } end{array}
right.]
Радиус траектории можно найти как:
[R=sqrt{x^2+y^2}=sqrt{{(0,5{cos (2t) })}^2+{(0,5{sin (2t)) }}^2}=sqrt{{left(0,5right)}^2(c{os}^2left(2tright)+{sin}^2(2t))}=0,5.]
Компоненты скорости равны:
[v_x=frac{dx}{dt}=-0,5cdot 2{sin left(2tright) }left(2.2right).]
[v_y=frac{dy}{dt}=0,5cdot 2{cos left(2tright) }left(2.3right).]
Получим модуль скорости:
[v=sqrt{v^2_x+v^2_y}=sqrt{{{sin}^2 left(2tright)+{cos}^2(2t) }}=1 left(frac{м}{с}right)(2.4).]
Подставим величину скорости и радиус окружности в выражение (2.2), имеем:
[a_n=frac{1^2}{0,5}=2left(frac{м}{с^2}right).]
Ответ. $a_n=2frac{м}{с^2}$.
Читать дальше: сила тяги.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!


