Как найти разность двух смешанных чисел правило

Как найти разность двух смешанных чисел правило

В данной статье рассмотрим правила, согласно которым выполняется действие вычитания смешанных чисел. Разберем конкретные примеры и некоторые нюансы при их решении. Изучим вычитание обыкновенной дроби и натурального числа из смешанного числа, а также – вычитание смешанного числа из дроби и натурального числа. Рассматривать вычитание мы будем при условии вычитания из большего числа меньшее.

Вычитание смешанных чисел

Пусть в качестве исходных данных даны два смешанных числа: abc и def , необходимо выполнить вычитание данных смешанных чисел.

Нам известно, что любое смешанное число возможно представить, как сумму его целой и дробной части, тогда получим:

abc-def=a+bc-d+ef

Свойства действий сложения и вычитания дают возможность выполнить вычисление полученного выражения различными способами. Опираясь на значения дробных частей смешанных чисел

abc и def , необходимо придерживаться следующих схем вычисления:

  • если дробная часть уменьшаемого больше, чем дробная часть вычитаемого:

bc>ef, то вычитание оптимально будет произвести так:

abc-def=(a-d)+bc-ef

Пример 1

Произвести вычитание смешанных чисел: 356-249 .

Решение

Сравним дробные части смешанных чисел, т.е. 56 и 49 . Чтобы определить, какая из дробей больше, приведем их к общему наименьшем знаменателю или наименьшему общему кратному: НОК (6, 9) = 18. При этом дополнительным множителем для дроби 56 станет 18 : 6 = 3; а для дроби 49 – 18 : 9 = 2, поэтому : 56=5·36·3=1518 и 49=4·29·2=818 .

Оценим полученный результат: 1518>818, что означает 56>49. Т.е. дробная часть уменьшаемого больше дробной части вычитаемого, и тогда действие вычитания производится путем раздельного вычитания целых и дробных частей заданных смешанных чисел:

3-2=156-49=1518-818=15-818=718

Т.е.: (3-2)+56-49=1+718=1718

Ответ: 356-249=1718

  • если дробные части заданных смешанных чисел равны: bc=ef , а, соответственно разность их равна нулю, то результатом вычитания таких смешанных чисел будет разность их целых частей:

abc-def=(a-d)+bc-ef=a-d+0=a-d

Пример 2

Произвести вычитание смешанных чисел 15710 и 2710 .

Решение

Мы видим, что дробные части заданных чисел равны, т.е. их разность есть нуль. Таким образом, действие вычитания заданных чисел сводится к нахождению разности их целых частей: 15710-2710=15+710-2+710=15-2+710-710=15-2+0=13

Ответ: 15710-2710=13

  • если дробная часть уменьшаемого меньше дробной части вычитаемого: bc<ef , то действие вычитания оптимально произвести так:

abc-def=a-d-ef+bc

Пример 3

Произвести вычитание смешанных чисел: 2625-81415 .

Решение

Проведем сравнение дробных частей заданных чисел, определив для начала наименьший общий знаменатель: НОК (5, 15) = 15, тогда 25=2·35·3=615 .

Следовательно: 615<1415, т.е. дробная часть уменьшаемого меньше дробной части вычитаемого. Таким образом, находить разность заданных смешанных чисел будем так: 2625-81415=26615-81415=26+615-8+1415==26-8-1415+615=18-1415+615

Для начала вычтем дробь из натурального числа (в скобках): 18-1415=(17+1)-1415=17+1+1415=17+11+1415==17+1515-1415=17+115

Тогда 18-1415+615=17+115+615=17+115+615==17+715=17715

Ответ: 2625-81415=17715 .

Вычитание обыкновенной дроби из смешанного числа

Схема вычитания правильной дроби из смешанного числа такая же, как при действии вычитания смешанных чисел.

Пример 4

Найти разницу: 356-415

Решение:

Приведем дробные части заданных чисел к единому наименьшему общему кратному: НОК (6, 15) = 30, тогда 65=5·56·5=2530 и 415=4·215·2=830 .

Таким образом, 56>415 .

В итоге вычитание возможно произвести так: 356-415=3+56-415=3+56-415=3+2530-830=3+1730=31730

Ответ: 356-415=31730

Пример 5

Произвести действие вычитания: 127-37

Решение

Дробные части исходных чисел имеют одинаковый знаменатель, что дает возможность их легко сравнить. Понятно, что 27 меньше, чем 37.

Тогда находить разницу будем так:

127-37=1+27-37=1-37+27=11-37+27==77-37+27=47+27=67

Ответ: 127-37=67.

Добавим еще одну, в общем очевидную деталь вычислений: если дробная часть смешанного числа равна вычитаемой дроби, то итогом вычисления будет число, равное целой части уменьшаемого смешанного числа. К примеру:

16311-311=16+311-311=16+311-311=16+0=16

Чтобы вычесть неправильную дробь из смешанного числа, необходимо выделить целую часть из неправильной дроби, а затем производить вычисление.

Пример 6

Вычислить значение разности: 7512-199 .

Решение: вычитаемая дробь является неправильной, выделим из нее целую часть и получим: 199=219

Приведем к общему знаменателю дробные части заданных чисел и согласно указанным выше схемам произведем вычитание смешанных чисел:

7512-219=7+512-2+19=7-2+512-19==5+1536-436=5+1136=51136

Ответ: 7512-199=51136 .

Вычитание натурального числа из смешанного

Определение 1

Для совершения действия вычитания натурального числа из смешанного, необходимо вычесть заданное натуральное число из целой части смешанного числа, а дробную часть оставить без изменений: abc-n=a-n+bc

Пример 7

Необходимо вычесть из смешанного числа 1511528 натуральное число 44.

Решение: 1511528-44=151+1528-44=151-44+1528=107+1528=1071528

Ответ: 1511528-44=1071528

Вычитание смешанного числа из обыкновенной дроби

Очевидно, что любое заданное смешанное число будет больше единицы. Уменьшаемая дробь должна быть больше вычитаемого, тогда эта дробь – неправильная. Необходимо выделить целую часть из неправильной дроби, и далее выполнение действия вычитания смешанного числа из обыкновенной дроби сведется к вычитанию смешанных чисел.

Пример 8

Необходимо выполнить вычитание: 749-612

Решение 

В первую очередь выделим целую часть неправильной уменьшаемой дроби: 749=829 , тогда заданный пример примет вид: 749-612=829-612

Найдем наименьший общий знаменатель: НОК (9, 2) = 18.

Получим: 29=2·29·2=418 и 12=1·92·9=918.

Тогда:

829-612=8418-6918=8+418-6+918=8-6-918+418==2-918+418=1+1-918+418=1+1-918+418==1+1-918+418=1+918+418=1+918+418==1+9+418=1+1318=11318

Ответ: 749-612=11318

Вычитание смешанного числа из натурального

Чтобы произвести действие вычитания смешанного числа из натурального, сначала от натурального числа отнимаем целую часть смешанного, после чего из полученного результата вычитаем дробную часть:

n-abc=n-a+bc=n-a-bc

Пример 9

Необходимо вычесть из натурального числа 18 смешанное число.

Решение

18-535=18-5+35=18-5-35=13-35=12+1-35==12+1-35=12+11-35=12+55-35=12+5-35==12+25=1225

Ответ: 18-535=1225

Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник
  1. Главная
  2. Справочники
  3. Справочник по математике 5-9 класс
  4. Обыкновенные дроби
  5. Смешанное число

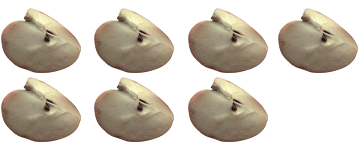
Пусть у нас есть 7 яблок:

Нам необходимо разделить их поровну между тремя детьми. Как это возможно сделать?

1 способ:

Можно каждое яблоко разделить на три доли, то есть мы получим по 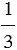 яблока, и дать всем детям долю от каждого яблока. Тогда каждый ребенок получит семь таких долей, значит, один ребенок получит  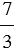яблока:

2 способ:

Так как у нас семь яблок, то мы можем каждому ребенку дать по два целых яблока, а седьмое поделить между ними поровну, то есть по 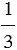яблока каждому:

В этом случае каждый ребенок получит по яблока.

Такую сумму, как  , принято записывать так: 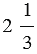. Число 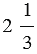читают: “две целых одна третья”. Число 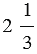называют смешанным числом. В нем  число 2 называют целой частью, а число 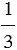– его дробной частью, при этом дробная часть смешанного числа – это всегда правильная дробь.

Вернемся к задаче, которую мы рассматривали. В обоих случаях дети получили одинаковые части яблок, то есть мы можем сказать, что: .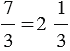

Данное равенство показывает, что неправильную дробь 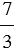можно записать в виде смешанного числа 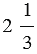. Говорят, что из неправильной дроби 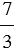выделена целая часть. При этом из любой неправильной дроби, числитель которой нацело не делится на знаменатель, можно выделить целую часть, то есть записать ее в виде смешанного числа. При этом, если числитель делится нацело на знаменатель, то эта дробь равна натуральному числу.

Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части.

Пример 1: Выделим целую часть из неправильной дроби .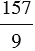

Для этого разделим 157 на 9 с остатком, имеем: 157: 9 = 17 (ост. 4)

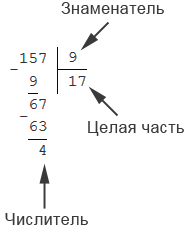
То есть получили, что неполное частное равно 17, а остаток – 4. Значит, .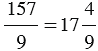

Мы выделили целую часть неправильной дроби, или по-другому, представили неправильную дробь в виде смешанного числа. На практике часто приходится выполнять обратное, то есть смешанное число представлять в виде неправильной дроби.

Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.

Пример 2: Преобразуем в смешанную дробь число :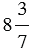

.

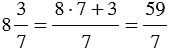Стоит отметить, что переместительное и сочетательное свойство сложения натуральных чисел выполняются и для смешанных чисел. На их основе мы можем записать:

Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.

Пример 3:  Найдем сумму чисел 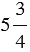и :

Обратите внимание, что число 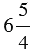не является смешанным, так как дробь 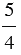является неправильной.

Со смешанными числами можно также проводить операцию вычитания. При этом, если дробная часть уменьшаемого больше или равна дробной части вычитаемого, то можно воспользоваться следующим правилом.

Чтобы найти разность двух смешанных чисел, надо из целой и дробной частей уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

Пример 4: Найдем разность чисел 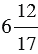и :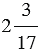

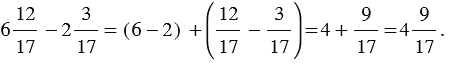
В случае, если дробная часть уменьшаемого меньше дробной части вычитаемого, данное правило использовать нельзя, но уменьшаемое можно преобразовать так, чтобы данное правило было применимо.

Пример 5: Найдем разность чисел 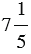и :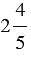

Мы видим, что дробная часть уменьшаемого меньше дробной части вычитаемого, выполним преобразование уменьшаемого:

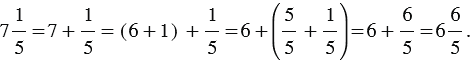
Тогда имеем:

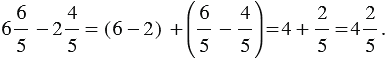
Советуем посмотреть:

Доли. Обыкновенные дроби

Сравнение дробей

Делители и кратные

Признаки делимости на 10, на 5 и на 2

Четные и нечетные числа

Признаки делимости на 9 и на 3

Простые и составные числа

Разложение на простые множители

Наибольший общий делитель

Наименьшее общее кратное

Деление и дроби

Сложение и вычитание дробей с одинаковыми знаменателями

Сложение и вычитание смешанных чисел

Основное свойство дроби

Решето Эратосфена

Приведение дробей к общему знаменателю

Сравнение, сложение и вычитание дробей с разными знаменателями

Умножение обыкновенных дробей

Деление обыкновенных дробей

Обыкновенные дроби


Правило встречается в следующих упражнениях:

5 класс

Задание 1085,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1117,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1127,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1155,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1161,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1738,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1820,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 803,
Мерзляк, Полонский, Якир, Учебник

Номер 807,
Мерзляк, Полонский, Якир, Учебник

Номер 1139,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 293,
Мерзляк, Полонский, Якир, Учебник

Номер 378,
Мерзляк, Полонский, Якир, Учебник

Номер 451,
Мерзляк, Полонский, Якир, Учебник

Номер 534,
Мерзляк, Полонский, Якир, Учебник

Номер 948,
Мерзляк, Полонский, Якир, Учебник

Номер 1100,
Мерзляк, Полонский, Якир, Учебник

Номер 1116,
Мерзляк, Полонский, Якир, Учебник

Задание 644,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1517,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 5,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1

7 класс

Номер 125,
Мерзляк, Полонский, Якир, Учебник

Номер 480,
Мерзляк, Полонский, Якир, Учебник

Номер 481,
Мерзляк, Полонский, Якир, Учебник

Номер 496,
Мерзляк, Полонский, Якир, Учебник

Номер 530,
Мерзляк, Полонский, Якир, Учебник

Номер 573,
Мерзляк, Полонский, Якир, Учебник

Номер 976,
Мерзляк, Полонский, Якир, Учебник

Номер 1055,
Мерзляк, Полонский, Якир, Учебник

Номер 1149,
Мерзляк, Полонский, Якир, Учебник

Номер 1215,
Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 46,
Мерзляк, Полонский, Якир, Учебник

Номер 138,
Мерзляк, Полонский, Якир, Учебник

Номер 139,
Мерзляк, Полонский, Якир, Учебник

Номер 193,
Мерзляк, Полонский, Якир, Учебник

Номер 212,
Мерзляк, Полонский, Якир, Учебник

Номер 254,
Мерзляк, Полонский, Якир, Учебник

Номер 277,
Мерзляк, Полонский, Якир, Учебник

Номер 282,
Мерзляк, Полонский, Якир, Учебник

Номер 380,
Мерзляк, Полонский, Якир, Учебник

Номер 499,
Мерзляк, Полонский, Якир, Учебник

Источник

Вычитание смешанных чисел

  • Калькулятор вычитания смешанных чисел

Чтобы вычесть смешанное число из другого смешанного числа, нужно отдельно вычесть целую часть из целой, а дробную из дробной и полученные результаты сложить.

Вычислим разность     и   :

вычитание смешанных чисел

Вычитание смешанных чисел можно записывать в более краткой форме, без промежуточных вычислений:

Если целые или дробные части уменьшаемого и вычитаемого окажутся равными, то в результате целая или дробная части соответственно будут равны нулю:

Если уменьшаемое равно вычитаемому, то разность равна нулю:

Если дробные части уменьшаемого и вычитаемого имеют разные знаменатели, то сначала их нужно привести к общему знаменателю, а потом выполнить вычитание:

вычитание смешанных чисел с разными знаменателями

Если дробная часть уменьшаемого меньше дробной части вычитаемого, то из целой части уменьшаемого нужно взять одну единицу, представить её в виде дроби и прибавить к дробной части, после этого из дробной части уменьшаемого можно вычесть дробную часть вычитаемого:

вычитание смешанных дробей с разными знаменателями

Чтобы из натурального числа вычесть смешанное число, у натурального числа нужно взять одну единицу и представить её в виде дроби:

вычитание смешанного числа из натурального

Чтобы вычесть натуральное число из смешанного числа, нужно натуральное число вычесть из целой части смешанного числа, оставив дробную часть без изменений:

При вычитании обыкновенной дроби из смешанного числа, дробь вычитается из дробной части смешанного числа. Если дробь больше, чем дробная часть смешанного числа, то из целой части нужно взять одну единицу, представить её в виде дроби и прибавить к дробной части, после этого можно выполнить вычитание:

Также, смешанные числа можно записать в виде неправильных дробей и выполнить вычитание, а в конце (если требуется по условию задания) записать результат в виде смешанного числа:

вычитание неправильных дробей

Калькулятор вычитания смешанных чисел

Данный калькулятор поможет вам выполнить вычитание смешанных чисел. Просто введите уменьшаемое и вычитаемое и нажмите кнопку Вычислить. Данный калькулятор позволяет также выполнять вычитание: натурального числа и дроби, смешанного числа и дроби, натурального и смешанного числа, натуральных чисел.

Источник

Сегодня на уроке мы научимся складывать и вычитать
смешанные числа.

На прошлом уроке мы с вами уяснили, что сумму
натурального числа и правильной дроби принято записывать без знака «+». Такую
сумму называют смешанным числом. Натуральное число называют целой
частью смешанного числа, а дробь – дробной частью смешанного числа. То есть

При сложении смешанных чисел пользуются переместительным
и сочетательным свойствами сложения.

Пример

Найти сумму чисел  и
.

В записи в тетрадях не стоит расписывать, как вы
считаете достаточно написать:

Таким образом, чтобы сложить смешанные числа,
нужно сложить по отдельности их целые и дробные части и записать сумму
полученных чисел.

Иногда при сложении смешанных чисел в их дробной
части может получиться неправильная дробь. В этом случае из неё выделяют
целую часть, и добавляют её к уже имеющейся дробной части.

Пример

Найти сумму чисел  и
.

Таким образом, если при сложении дробных
частей получилась неправильная дробь, то выделяют целую часть этой дроби и
добавляют к уже имеющейся целой части.

Задача

На столе лежало 2  яблока. Принесли ещё 1  яблока. Сколько яблок лежит на столе?

Решение

Посмотрите, что получилось: складывали смешанные
числа, а ответ выражен натуральным или можно ещё сказать целым числом.

При вычитании смешанных чисел пользуются свойством
вычитания числа из суммы и свойством вычитания суммы из числа.

Пример

Найти разность дробей  и
.

В тетрадях пишут короче:

Таким образом, чтобы найти разность смешанных
чисел, нужно найти отдельно разность целых частей и отдельно разность дробных
частей.

Есть в примерах на вычитание и «особые» случаи.

Например

Вычтем из дроби  дробь
.

Запомните! Не начинайте выполнять вычитание, пока
не убедитесь, что из числителя первой дроби можно вычесть числитель второй
дроби.

Иногда в примерах нужно вычесть из натурального
числа смешанную дробь.

Например

Найдём значение выражения .

Итоги

Чтобы сложить смешанные числа, нужно сложить по
отдельности их целые и дробные части и записать сумму полученных чисел.

Если при сложении дробных частей получилась
неправильная дробь, выделить целую часть из этой дроби и прибавить её к
полученной целой части.

Чтобы найти разность смешанных чисел, нужно найти
отдельно разность целых частей и отдельно разность дробных частей.

Если дробная часть уменьшаемого меньше дробной части
вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую
часть.

Источник
  • Ответы к учебнику для 5 класса. А. Г. Мерзляк
  • Переход на главную страницу сайта

Вопросы к параграфу

1. В виде какого числа можно представить сумму натурального числа и правильной дроби?

В виде смешанного числа.

2. Как в записи смешанного числа называют натуральное число? Правильную дробь?

  • Натуральное число называют целой частью смешанного числа.
  • Правильную дробь называют дробной частью смешанного числа.

3. Какой дробью является дробная часть смешанного числа?

Правильной дробью.

4. В каком случае неправильная дробь равна натуральному числу?

Неправильная дробь равна натуральному числу в том случае, если числитель нацело делится на знаменатель.

5. Как неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число?

Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

6. Как смешанное число преобразовать в неправильную дробь?

Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а её знаменатель записать в знаменатель дробной части смешанного числа.

7. Сформулируйте правило сложения двух смешанных чисел.

Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.

8. Как найти разность двух смешанных чисел?

Чтобы найти разность двух смешанных чисел, надо из целой и дробной части уменьшаемого вычесть целую и дробную части вычитаемого.

Решаем устно

1. Сравните значения выражений:

1)

frac{7}{11}  +  frac{10}{11}    >   frac{23}{11}  —  frac{8}{11}

frac{7+10}{11}    >   frac{23-8}{11}

frac{17}{11}   >   frac{15}{11}

2)

frac{19}{27} +  frac{13}{27}  —  frac{10}{27}    >   frac{16}{27}  — frac{7}{27} +  frac{14}{27}

frac{19+13-10}{27}   >  frac{16-7+14}{27}

frac{22}{27}  >  frac{13}{27}

3)

frac{9}{16} +  frac{4}{3}   >   frac{23}{11}   —    frac{2}{3}

frac{9+8}{16}   >  frac{4-2}{3}

frac{17}{16}  >  frac{2}{3}

4)

frac{30}{51} +  frac{16}{51}  +  frac{4}{51}  <   frac{7}{9}  +  frac{2}{9}

frac{30+16+4}{51}   < frac{7+2}{9}

frac{50}{51}  <   frac{9}{9}

2. Ответом к каким из следующих задач является число frac{5}{6} ?

1) Сколько килограммов конфет получил каждый из шести отрядов, между которыми поделили поровну 5 кг конфет?

5 : 6 = frac{5}{6} ( кг) — получил каждый из шести отрядов.

2) С какой скоростью шёл пешеход, если за 6 ч он прошёл 5 км?

5 : 6 = frac{5}{6} (км/ч) — скорость пешехода.

3) Из 6 м ткани сшили пять фартуков. Сколько метров ткани пошло на один фартук?

6 : 5 = frac{6}{5}  ( м) — пошло на 1 фартук.

4) Решите уравнение 6x = 5.

6х = 5

х = frac{5}{6}.

Ответ: frac{5}{6} является ответом к задаче № 1, №2 и №4.

3. Решите уравнение:

1)

frac{y}{6}  = 3

y : 6 = 3

y = 3 • 6

y = 18

2)

frac{6}{y}  = 3

6 : y = 3

y = 6 : 3

y = 2

3)

3y = 6

y = 6 : 3

y = 2

4)

6y = 3

y = 3 : 6

y = frac{3}{6}

4. Назовите все пары правильных дробей со знаменателем 9, сумма которых равна frac{7}{9}.

frac{1}{9}  +  frac{6}{9}  =  frac{7}{9}  и  frac{6}{9}  +  frac{1}{9}  =  frac{7}{9}

frac{2}{9} +  frac{5}{9}  =  frac{7}{9}   и  frac{5}{9}  +  frac{2}{9}  =  frac{7}{9}

frac{3}{9} +  frac{4}{9}  =  frac{7}{9}   и  frac{4}{9}  +  frac{3}{9}  =  frac{7}{9}

5. На обед Пончик съел 42 вареника, из которых  frac{4}{7}  составляли вареники с творогом, frac{1}{7} — вареники с картофелем, а остальные — вареники с вишней. Сколько вареников с вишней съел Пончик?

1) frac{4}{7}  +  frac{1}{7}  = frac{5}{7} ( вареников) — с творогом и с картофелем.

2) 42 : 7 • 5 = 6 • 5 = 30 (шт) — вареники с творогом и картофелем.

3) 42 — 30 = 12 (шт) — вареники с вишней.

Ответ: 12 шт.

Упражнения

769. Преобразуйте неправильную дробь в смешанное число:

1) frac{9}{4}  =  frac{8+1}{4} = frac{8}{4}  +  frac{1}{4} = 2frac{1}{4}

2) frac{16}{7}  =  frac{14+2}{7}  =  frac{14}{7}  +  frac{2}{7}  = 2frac{2}{7}

3) frac{29}{8}  =  frac{24+5}{8}  =  frac{24}{8}  +  frac{5}{8}  =  3frac{5}{8}

4) frac{55}{9}  =  frac{54+1}{9}  =  frac{54}{9}  +  frac{1}{9}  =  6frac{1}{9}

5) frac{83}{24}  =  frac{72+11}{24}  =  frac{72}{24}  +  frac{11}{24}  =  3frac{11}{24}

6) frac{96}{19}  =  frac{95+1}{19}  =  frac{95}{19}  +  frac{1}{19}  =  5frac{1}{19}

770. Преобразуйте неправильную дробь в смешанное число:

1) frac{13}{5}  =  frac{10+3}{5}  =  frac{10}{5}  +  frac{3}{5}  =  2frac{3}{5}

2) frac{18}{11}  =  frac{11+7}{11}  =  frac{11}{11}  +  frac{7}{11}  =  1frac{7}{11}

3) frac{37}{12}  =  frac{36+1}{12}  =  frac{36}{12}  +  frac{1}{12}  =  3frac{1}{12}

4) frac{68}{23}  =  frac{46+22}{23}  =  frac{46}{23}  +  frac{22}{23}  =  2frac{22}{23}

5) frac{79}{12}  =  frac{72+7}{12}  =  frac{72}{12}  +  frac{7}{12}  =  6frac{7}{12}

6) frac{83}{18}  =  frac{72+11}{18}  =  frac{72}{18}  +  frac{11}{18}  =  4frac{11}{18}

771. Запишите частное в виде дроби и выделите из полученной дроби целую и дробную части:

1) 10 : 6 =  frac{10}{6}  =  frac{6+4}{6}  =  1frac{4}{6}

2) 18 : 5 =  frac{18}{5}  = frac{15+3}{5}  =  3frac{3}{5}

3) 23 : 11 =  frac{23}{11}  =  frac{22+1}{11}  =  2frac{1}{11}

4) 19 : 6 = frac{19}{6}  =  frac{18+1}{6}  = 3frac{1}{6}

5) 425 : 50 =  frac{425}{50}  =  frac{400+25}{50}  =  8frac{25}{50}

6) 55 : 6 =  frac{55}{6}  =  frac{54+1}{6}  =  9frac{1}{6}

772. Запишите частное в виде дроби и выделите из полученной дроби целую и дробную части:

1) 7 : 2 =  frac{7}{2}  =  frac{6+1}{2}  =  3frac{1}{2}

2) 9 : 4 =  frac{9}{4}  =  frac{8+1}{4}  =  2frac{1}{4}

3) 25 : 8 =  frac{25}{8}  =  frac{24+1}{8}  =  3frac{1}{8}

4) 110 : 20 =  frac{110}{20}  =  frac{100+10}{20}  =  5frac{10}{20}

5) 327 : 10 =  frac{327}{10}  =  frac{320+7}{10}  =  32frac{7}{10}

6) 812 : 81 =  frac{812}{81}  =  frac{810+2}{81}  =  10frac{2}{81}

773. Запишите число в виде неправильной дроби:

1) 2frac{4}{7}  =  frac{2cdot 7+4}{7}  =  frac{14+4}{7}  =  frac{18}{7}

2) 3frac{5}{12}  =  frac{3cdot 12+5}{12}  =  frac{36+5}{12}  =  frac{41}{12}

3) 4frac{7}{20}  =  frac{4cdot 20+7}{20}  =  frac{80+7}{20}  =  frac{87}{20}

4) 6frac{11}{24}  =  frac{6cdot24+11}{24} = frac{144+11}{24}  =  frac{155}{24}

5) 7frac{23}{100}  =  frac{7cdot 100+23}{100}  =  frac{700+23}{100}  =  frac{723}{100}

6) 10frac{16}{27}  =  frac{10cdot 27+16}{27}  =  frac{270+16}{27}  =  frac{286}{27}

774. Запишите число в виде неправильной дроби:

1) 4frac{3}{4}  =  frac{4cdot 4+3}{4}  =  frac{16+3}{4}  =  frac{19}{4}

2) 9frac{6}{11}  =  frac{9cdot 11+6}{11}  =  frac{99+6}{11}  =  frac{105}{11}

3) 3frac{9}{17}  =  frac{3cdot 17+9}{17}  =  frac{51+9}{17}  =  frac{60}{17}

4) 12frac{5}{6}  =  frac{12cdot 6+5}{6}  =  frac{72+5}{6}  =  frac{77}{6}

5) 13frac{49}{100}  =  frac{13cdot 100+49}{100}  =  frac{1300+49}{100}  =  frac{1349}{100}

6) 8frac{3}{16}  =  frac{8cdot 16+3}{16}  =  frac{128+3}{16}  =  frac{131}{16}

775. Выполните действия:

1) 8 +  frac{4}{21}  =  8frac{4}{21}

2) 5frac{16}{19}  +  3frac{5}{19}  =  (5+3) + left ( frac{16}{19}+frac{5}{19} right ) = 8+frac{21}{19}  = 8+frac{19+2}{19}  = 8+1frac{2}{19}  = 9frac{2}{19}

3) 7frac{7}{16}-3frac{3}{16} = left ( 7-3 right )+left ( frac{7}{16}-frac{3}{16} right ) = 4+frac{7-3}{16}  = 4+frac{4}{16}  =  4frac{4}{16}

4) 10frac{12}{17}+5frac{4}{17}-3frac{3}{17}  =  left ( 10+5-3 right )+left ( frac{12}{17}+frac{4}{17}-frac{3}{17} right ) = 12+frac{12+4-3}{17}  = 12+frac{13}{17}  =  12frac{13}{17}

776. Выполните действия:

1) frac{14}{93}+5 =  5frac{14}{93}

2) 6frac{17}{41}+7frac{19}{41}  = left ( 6+7 right )+left ( frac{17}{41}+frac{19}{41} right ) = 13+frac{17+19}{41}  =  13+frac{36}{41}  =  13frac{36}{41}

3) 24frac{9}{38}-17frac{5}{38}  = left ( 24-17 right )+left ( frac{9}{38}-frac{5}{38} right ) = 7+frac{9-5}{38}  = 7+frac{4}{38}  =  7frac{4}{38}

4) 15frac{7}{10}-2frac{4}{10}+6frac{1}{10}  = left ( 15-2+6 right )+left ( frac{7}{10}-frac{4}{10}+frac{1}{10} right ) = 19+frac{7-4+1}{10}  =  19+frac{4}{10}  =  19frac{4}{10}

777. Вычислите:

1) 6frac{4}{9}+3frac{5}{9}=left ( 6+3 right )+left ( frac{4}{9}+frac{5}{9} right )=9+frac{4+5}{9}=9+frac{9}{9}=9+1=10

2) 10frac{11}{19}+5frac{14}{19}  =  left ( 10+5 right )+left ( frac{11}{19}+frac{14}{19} right )  =  15+frac{11+14}{19}  =  15+frac{25}{19}  =  15+frac{19+6}{19}  =  15+1frac{6}{19}  =  16frac{6}{19}

3) 2frac{3}{13}+2frac{11}{13}  =  left ( 2+2 right )+left ( frac{3}{13}+frac{11}{13} right )  =  4+frac{3+11}{13}  =  4+frac{14}{13}  =  4+frac{13+1}{13}  =  4+1frac{1}{13}  = 5frac{1}{13}

4) 1frac{5}{8}+3frac{7}{8}  =  left ( 1+3 right )+left ( frac{5}{8}+frac{7}{8} right )  =  4+frac{5+7}{8}  =  4+frac{12}{8}  =  4+frac{8+4}{8}  =  4+1frac{4}{8}  =  5frac{4}{8}

5) 1-frac{3}{11}  =  frac{11}{11}-frac{3}{11}  =  frac{11-3}{11}  =  frac{8}{11}

6) 1-frac{13}{40}  =  frac{40}{40} - frac{13}{40}  =  frac{40-13}{40}  =  frac{27}{40}

7) 4-1frac{4}{7}  =  3frac{7}{7}-1frac{4}{7}  =  left ( 3-1 right )+left ( frac{7}{7}-frac{4}{7} right )  =  2+frac{3}{7}  =  2frac{3}{7}

8) 10-9frac{3}{10}  =  9frac{10}{10}-9frac{3}{10}  =  left ( 9-9 right )+left ( frac{10}{10}-frac{3}{10} right )  =  0+frac{10-3}{10}  =  frac{7}{10}

9) 5frac{2}{7}-2frac{5}{7}  =  4frac{1cdot 7+2}{7}-2frac{5}{7}  =  4frac{9}{7}-2frac{5}{7}  =  left ( 4-2 right )+left ( frac{9}{7}-frac{5}{7} right )  =  2+frac{4}{7}  = 2frac{4}{7}

10) 14frac{6}{20}-8frac{12}{20} = 13frac{1cdot 20+6}{20}-8frac{12}{20}  =  13frac{26}{20}-8frac{12}{20}  =  left ( 13-8 right )+left ( frac{26}{20}-frac{12}{20} right )  =  5+frac{26-12}{20}  =  5+frac{14}{20}  =  5frac{14}{20}

11) 8frac{3}{14}-5frac{9}{14}  =  7frac{1cdot 14+3}{14}-5frac{9}{14}  = 7frac{17}{14}-5frac{9}{14}  =  left ( 7-5 right )+left ( frac{17}{14}-frac{9}{14} right )  =  2+frac{17-9}{14}  =  2+frac{8}{14}  =  2frac{8}{14}

12) 7frac{10}{21}-4frac{16}{21}  =  6frac{1cdot 21+10}{21}-4frac{16}{21}  =  6frac{31}{21}-4frac{16}{21}  =  left ( 6-4 right )+left ( frac{31}{21}-frac{16}{21} right )  =  2+frac{31-16}{21}  =  2+frac{15}{21}  =  2frac{15}{21}

13) 14frac{8}{31}-6frac{8}{31}  =  left ( 14-6 right )+left ( frac{8}{31}-frac{8}{31} right )  =  8+0  =  8

14) left ( 12frac{5}{22}+7frac{17}{22} right )-left ( 13frac{7}{23}-9frac{15}{23} right )  =  left ( left ( 12+7 right )+left ( frac{5}{22}+frac{17}{22} right ) right )-left ( 12frac{23cdot 1+7}{23}-9frac{15}{23} right )  =  left ( 19+frac{22}{22} right )-left ( left ( 12-9 right )+left ( frac{30}{23}-frac{15}{23} right ) right )  =  20-left ( 3+frac{15}{23} right )  =  20-3frac{15}{23}  =  19frac{23}{23}-3frac{15}{23}  =  left ( 19-3 right )+left ( frac{23}{23}-frac{15}{23} right )  =  16+frac{8}{23}  =  16frac{8}{23}

778. Вычислите:

1) 7frac{14}{15}+2frac{1}{15}  =  left ( 7+2 right )+left ( frac{14}{15}+frac{1}{15} right )  =  9+frac{15}{15}  =  10

2) 9frac{24}{27}+12frac{13}{27}  =  left ( 9+12 right )+left ( frac{24}{27}+frac{13}{27} right )  = 21+frac{37}{27}  = 21+frac{27+10}{27}  =  21+1frac{10}{27}  =  22frac{10}{27}

3) 1-frac{12}{19}  =  frac{19}{19}-frac{12}{19}  =  frac{7}{19}

4) 8-3frac{6}{15}  =  7frac{15}{15}-3frac{6}{15}  =  left ( 7-3 right )+left ( frac{15}{15}-frac{6}{15} right )  =  4+frac{9}{15}  =  4frac{9}{15}

5) 12-11frac{6}{11}  =  11frac{11}{11}-11frac{6}{11}  =  left ( 11-11 right )+left ( frac{11}{11}-frac{6}{11} right )  =  0+frac{5}{11}  =  frac{5}{11}

6) 16frac{3}{13}-6frac{8}{13}  =  15frac{1cdot 13+3}{13}-6frac{8}{13}  = 15frac{16}{13}-6frac{8}{13}  =  left ( 15-6 right )+left ( frac{16}{13}-frac{8}{13} right )  =  9+frac{8}{13}  =  9frac{8}{13}

7) 13frac{4}{9}-2frac{8}{9}  =  12frac{1cdot 9+4}{9}-2frac{8}{9}  = 12frac{13}{9}-2frac{8}{9}  =  left ( 12-2 right )+left ( frac{13}{9}-frac{8}{9} right )  =  10+frac{5}{9}  =  10frac{5}{9}

8) 10frac{7}{16}-4frac{12}{16}  =  9frac{1cdot 16+7}{16}-4frac{12}{16}  = 9frac{23}{16}-4frac{12}{16}  =  left ( 9-4 right )+left ( frac{23}{16}-frac{12}{16} right )  =  5+frac{11}{16}  =  5frac{11}{16}

9) 29frac{49}{53}-8frac{49}{53}  =  left ( 29-8 right )+left ( frac{49}{53}-frac{49}{53} right )  =  21+0  =  21

10) left ( 20frac{16}{25}+13frac{9}{25} right )-left ( 23frac{4}{14} +7frac{13}{14}right )  =  left ( left ( 20+13 right )+left ( frac{16}{25}+frac{9}{25} right ) right )-left ( left ( 23+7 right )+left ( frac{4}{14}+frac{13}{14} right ) right )  =  left ( 33+frac{25}{25} right )-left ( 30+frac{17}{14} right )  =  34-left ( 30+frac{14+3}{14} right )  =  34-left ( 30+1frac{3}{14} right )  =  34-31frac{3}{14}  =  33frac{14}{14}-31frac{3}{14}  =  left ( 33-31 right )+left ( frac{14}{14}-frac{3}{14} right )  =  2+frac{11}{14}  = 2frac{11}{14}

779. Решите уравнение:

1)

x+4frac{4}{19}=6frac{2}{19}

x=6frac{2}{19}-4frac{4}{19}

x=5frac{21}{19}-4frac{4}{19}

x=left ( 5-4 right )+left ( frac{21}{19}-frac{4}{19} right )

x=1frac{17}{19}

2)

25-x=8frac{3}{14}

x=25-8frac{3}{14}

x=24frac{14}{14}-8frac{3}{14}

x=left ( 24-8 right )+left ( frac{14}{14}-frac{3}{14} right )

x=16frac{11}{14}

3)

32-x=9frac{18}{35}

x=32-9frac{18}{35}

x=31frac{35}{35}-9frac{18}{35}

x=left ( 31-9 right )+left ( frac{35}{35}-frac{18}{35} right )

x=22frac{17}{35}

780. Решите уравнение:

1)

4frac{5}{7}-left ( x-6frac{3}{7} right )=2frac{6}{7}

x-6frac{3}{7}=4frac{5}{7}-2frac{6}{7}

x-6frac{3}{7}=3frac{12}{7}-2frac{6}{7}

x-6frac{3}{7}=left ( 3-2 right )+left ( frac{12}{7}-frac{6}{7} right )

x-6frac{3}{7}=1frac{6}{7}

x=1frac{6}{7}+6frac{3}{7}

x=7frac{9}{7}

x=8frac{2}{7}

2)

19frac{28}{34}-left ( m+2frac{29}{34} right )=12frac{15}{34}

m+2frac{29}{34}=19frac{28}{34}-12frac{15}{34}

m+2frac{29}{34}=left ( 19-12 right )+left ( frac{28}{34}-frac{15}{34} right )

m+2frac{29}{34}=7frac{13}{34}

m=7frac{13}{34}-2frac{29}{34}

m=6frac{47}{34}-2frac{29}{34}

m=4frac{18}{34}

781. Решите уравнение:

1)

7frac{7}{30}-left ( 5frac{11}{30}-y right )=3frac{19}{30}

5frac{11}{30}-y=7frac{7}{30}-3frac{19}{30}

5frac{11}{30}-y=6frac{37}{30}-3frac{19}{30}

5frac{11}{30}-y=3frac{18}{30}

y=5frac{11}{30}-3frac{18}{30}

y=4frac{41}{30}-3frac{18}{30}

y=1frac{23}{30}

2)

left ( x-1frac{9}{17} right )+2frac{14}{17}=5frac{5}{17}

x-1frac{9}{17}=5frac{5}{17}-2frac{14}{17}

x-1frac{9}{17}=4frac{22}{17}-2frac{14}{17}

x-1frac{9}{17}=2frac{8}{17}

x=2frac{8}{17}+1frac{9}{17}

x=3frac{17}{17}

x=4

782. Степан, Иван и Андрей съели арбуз. Степан съел frac{2}{9} арбуза, Иван — frac{4}{9} . Какую часть арбуза съел Андрей?

Мерзляк 5 класс - § 29. Смешанные числа

1) frac{2}{9}  +  frac{4}{9}  =  frac{6}{9}  (часть) — арбуза съели Степан и Иван.

2) 1-frac{6}{9}=frac{9}{9}-frac{6}{9}=frac{3}{9} (часть) — арбуза съел Андрей.

Ответ:  frac{3}{9}  часть арбуза.

783. Мария, Ирина, Елена и Ольга съели торт. Мария съела frac{3}{16} торта, Ирина — frac{5}{16} , Елена — frac{2}{16}. Какую часть торта съела Ольга?

Мерзляк 5 класс - § 29. Смешанные числа

1) frac{3}{16}  +  frac{5}{16}  +  frac{2}{16}  =  frac{3+5+2}{16}  =  frac{10}{16}  (часть) — торта съели Мария, Ирина и Елена.

2) 1-frac{10}{16}=frac{16}{16}-frac{10}{16}=frac{6}{16} (часть) — торта съела Ольга.

Ответ: frac{6}{16} часть торта.

784. Три тракториста вспахали вместе поле. Бригадир записал, что один из них вспахал frac{5}{13} поля, второй — frac{4}{13}, а третий — frac{6}{13}. Не ошибся ли бригадир.

Мерзляк 5 класс - § 29. Смешанные числа

1) frac{5}{13}  +  frac{4}{13}  +  frac{6}{13}  =  frac{5+4+6}{13}  =  frac{15}{13}  =  1frac{2}{13} (части) — поля вспахано по записям бригадира.

2) 1frac{2}{13} >  1 , значит бригадир ошибся, так как трактористы не могли вспахать больше, чем всё поле, равное 1.

Ответ: Бригадир ошибся.

785. Фермер решил выделить под морковь frac{3}{20} огорода, под свёклу — frac{4}{20}, под лук — frac{6}{20}, под горох — frac{2}{20}, под картофель — frac{7}{20}. Сможет ли он реализовать свой план?

Мерзляк 5 класс - § 29. Смешанные числа

1) frac{3}{20}  +  frac{4}{20}  +  frac{6}{20}  +  frac{2}{20}  +  frac{7}{20}  =  frac{3+4+6+2+7}{20}  =  frac{22}{20} (части) — решил выделить фермер.

2) frac{22}{20}  >  1 , значит не сможет реализовать свой план.

Ответ: нет, не сможет.

786. 1) Какое наибольшее натуральное число удовлетворяет неравенству:

а) n<frac{123}{30}

frac{123}{30}=frac{4cdot 30+3}{30}=4frac{3}{30}

n< 4frac{3}{30} , наибольшее натуральное число, при котором неравенство верно — 4.

Ответ: n = 4.

б) n<frac{198}{15} 

frac{198}{15}=frac{13cdot 15+3}{15}=13frac{3}{15}

n< 13frac{3}{15} , наибольшее натуральное число, при котором неравенство верно — 13.

Ответ: n = 13.

2) Какое наименьшее натуральное число удовлетворяет неравенству:

а) m>frac{13}{5} 

frac{13}{5}=frac{2cdot 5+3}{5}=2frac{3}{5}

m> 2frac{3}{5} , наименьшее натуральное число, при котором неравенство верно — 3.

Ответ: m = 3.

б) frac{275}{10}<m 

frac{275}{10}=frac{27cdot 10+5}{10}=27frac{3}{5}

27frac{3}{5}< m, наименьшее натуральное число, при котором неравенство верно — 28.

Ответ: m = 28.

787. 1) Какое наибольшее натуральное число удовлетворяет неравенству:

а) n<frac{206}{13} 

frac{206}{13}=frac{15cdot 13+11}{13}=15frac{11}{13}

n< 15frac{11}{13} , наибольшее натуральное число, при котором неравенство верно — 15.

Ответ: n = 15.

б) frac{324}{16}>n 

frac{324}{16}=frac{20cdot 16+4}{16}=20frac{4}{16}

20frac{4}{16}> n, наибольшее натуральное число, при котором неравенство верно — 20.

Ответ: n = 20.

2) Какое наименьшее натуральное число удовлетворяет неравенству:

а) m>frac{34}{6}

frac{34}{6}=frac{5cdot 6+4}{6}=5frac{4}{6}

m> 5frac{4}{6} , наименьшее натуральное число, при котором неравенство верно — 6.

Ответ: m = 6.

б) frac{421}{16}<m

frac{421}{16}=frac{26cdot 16+5}{16}=26frac{5}{16}

26frac{5}{16}< m, наименьшее натуральное число, при котором неравенство верно — 27.

Ответ: m = 27.

788. Найдите все натуральные значения х, при которых верно неравенство:

1)

2frac{1}{3}< frac{x}{3}< 3frac{2}{3}

frac{7}{3}< frac{x}{3}< frac{11}{3}

Неравенство верно при х = 8, 9 и 10.

2)

1frac{5}{12}< frac{17}{x}< 2frac{1}{8}

frac{17}{12}< frac{17}{x}< frac{17}{8}

Неравенство верно при х = 9, 10 и 11.

789. Найдите все натуральные значения х, при которых верно неравенство:

1)

3frac{11}{15}< frac{x}{15}< 4

frac{56}{15}< frac{x}{15}< frac{60}{15}

Неравенство верно при х = 57, 58 и 59.

2)

3frac{1}{8}< frac{25}{x}< 8frac{1}{3}

frac{25}{8}< frac{25}{x}< frac{25}{3}

Неравенство верно при х =4, 5, 6 и 7.

790. При каких натуральных значениях a является верным неравенство, левая часть которого — неправильная дробь:

1)

frac{20}{a}< 2

Неравенство будет верным при а = 11, 12, 13, 14, 15, 16, 17, 18, 19 и 20.

2) 

frac{4}{a}> a

Неравенство будет верным при а = 1.

791. При каких натуральных значениях a является верным неравенство frac{10}{a}> a, левая часть которого — неправильная дробь?

Неравенство будет верным при а = 1, 2 и 3.

Упражнения для повторения

792. Одна из сторон треугольника в 2 раза меньше второй и на 7 см меньше третьей. Найдите стороны треугольника, если его периметр равен 39 см.

Мерзляк 5 класс - § 29. Смешанные числа

Пусть длина первой стороны треугольника — х см. Тогда длина второй стороны — 2х см, а длина третьей стороны — (х + 7) см. Мы знаем, что периметр треугольника равен 39 см.

Составим уравнение:

х + 2х + (х + 7) = 39
(х + 2х + х) + 7 = 39
4х + 7 = 39
4х = 39 — 7
4х = 32
х = 32 : 4
х = 8 (см) — длина первой стороны треугольника.

2х = 2 • 8 = 16 (см) — длина второй стороны треугольника.

х + 7 = 8 + 7 = 15 (см) — длина третьей стороны треугольника.

Ответ: 8 см, 16 см и 15 см.

793. Общая площадь трёх крупнейших волжских водохранилищ Куйбышевского, Рыбинского и Волгоградского составляет 14 197 км². Площадь Волгоградского водохранилища на 1 463 км² меньше площади Рыбинского водохранилища и на 3 383 км² меньше площади Куйбышевского водохранилища. Найдите площадь каждого водохранилища.

Мерзляк 5 класс - § 29. Смешанные числа

Пусть х км² — площадь Волгоградского водохранилища. Тогда площадь Рыбинского водохранилища (х + 1 463) км², а площадь Куйбышевского водохранилища — (х + 3 383) км². Мы знаем, что общая площадь трёх водохранилищ 14 197 км².

Составим уравнение:

Мерзляк 5 класс - § 29. Смешанные числа

х + (х + 1 463) + (х + 3 383) = 14 197
(х + х + х) + (1 463 + 3 383) = 14 197
3х + 4 846 = 14 197
3х = 14 197 — 4 846
3х = 9 351
х = 9 351 : 3
х = 3 117 (км²) — площадь Волгоградского водохранилища.

х + 1 463 = 3 117 + 1 463 = 4 580 (км²) — площадь Рыбинского водохранилища.

х + 3 383 = 3 117 + 3 383 = 6 500 (км²) — площадь Куйбышевского водохранилища.

Ответ: Волгоградское — 3 117 км², Рыбинское — 4 580 км², Куйбышевское — 6 500 км².

794. Пакет кефира стоит 68 р. У Кати есть 200 р. Какое наибольшее количество пакетов кефира она может купить? Сколько денег останется у Кати?

200 = 68 • 2 + 64 

Значит Катя сможет купить 2 пакета молока и у неё ещё останется 64 рубля.

Ответ: 2 пакета молока, 64 рубля.

795. По дороге в одном направлении идут два пешехода. В 12 ч 54 мин расстояние между ними было 540 м. Скорость пешехода, который идёт впереди, равна 25 м/мин, что составляет  frac{5}{8} скорости пешехода, который идёт сзади. В котором часу второй пешеход догонит первого?

Мерзляк 5 класс - § 29. Смешанные числа

1) 25 : 5 • 8 = 5 • 8 = 40 (м/мин) — скорость движения второго пешехода.

2) 40 — 25 = 15 (м/мин) — скорость сближения пешеходов.

3) 540 : 15 = 36 (мин) — потребуется второму пешеходу, чтобы догнать первого.

4) 12 ч 54 мин + 36 мин = 12 ч 90 мин = 13 ч 30 мин — время, в которое второй пешеход догонит первого.

Ответ: в 13 часов 30 минут.

Задача от мудрой совы

796. Ученики Фёдоров, Сидоров и Петров входили в сборную школы по шахматам. Имена этих учеников были Фёдор, Сидор и Пётр. Известно, что фамилия Фёдора не Петров, волосы у Сидора рыжего цвета и учится он в 6 классе; Петров учится в 7 классе, а волосы у Фёдорова чёрного цвета. Укажите фамилию и имя каждого мальчика.

Мерзляк 5 класс - § 29. Смешанные числа

Занесём в таблицу данные, которые нам известны:

  • «фамилия Фёдорова не Петров»
  • «волосы Сидора рыжего цвета»
  • «Сидор учится в 6 классе».

Теперь начнём рассуждать:

  • «Петров учится в 7 классе» — мы уже знаем, что «фамилия Фёдорова не Петров», значит Петровым может быть только Пётр
  • «волосы Фёдорова чёрного цвета» — по условию у Сидора волосы рыжие, значит чёрные волосы у Фёдора, а его фамилия — Фёдоров.
  • оставшийся мальчик Сидор носит фамилию Сидоров.

Ответ: Фёдор Фёдоров, Сидор Сидоров и Пётр Петров.

  • Ответы к учебнику для 5 класса. А. Г. Мерзляк
  • Переход на главную страницу сайта
Источник

Добавить комментарий