Как найти производную если степень в степени

Содержание:

• 1-ый способ
• 2-ой способ
• 3-ий способ

Рассмотрим способы нахождения ее производной.

1-ый способ

Применяя формулу:

$$left(u(x)^{v(x)}right)^{prime}=v(x) cdot u(x)^{v(x)-1} cdot u^{prime}(x)+u(x)^{v(x)} cdot ln u(x) cdot v^{prime}(x)$$

То есть вначале производная берется как от степенной функции, а потом как от показательной.

$$left(u(x)^{v(x)}right)^{prime}=u(x)^{v(x)} cdot ln u(x) cdot v^{prime}(x)+v(x) cdot u(x)^{v(x)-1} cdot u^{prime}(x)$$

2-ой способ

С помощью логарифмического дифференцирования:

$$begin{array}{c}
y(x)=u(x)^{v(x)} \
ln y(x)=ln u(x)^{v(x)} \
ln y(x)=v(x) cdot ln u(x) \
(ln y(x))^{prime}=(v(x) cdot ln u(x))^{prime} \
frac{y^{prime}(x)}{y(x)}=v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime} Rightarrow \
Rightarrow y^{prime}(x)=y(x)left[v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime}right]= \
=u(x)^{v(x)}left[v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime}right]
end{array}$$

3-ий способ

Представим функцию $y(x)=u(x)^{v(x)}$ в следующем виде
(используются свойства логарифмов):

$$y(x)=u(x)^{v(x)}=e^{ln u(x)^{w(x)}}=e^{v(x) ln u(x)}$$

Тогда

$$begin{array}{c}
y^{prime}(x)=left(e^{v(x) ln u(x)}right)^{prime}=e^{v(x) ln u(x)} cdot(v(x) ln u(x))^{prime}= \
=e^{v(x) ln u(x)} cdotleft[v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime}right]= \
=u(x)^{v(x)} cdotleft[v^{prime}(x) cdot ln u(x)+v(x) cdot(ln u(x))^{prime}right]
end{array}$$

Читать дальше: основные теоремы дифференциального исчисления.

Найдем производную функции f(x)=ax,a>0,a≠0f(x)=a^x, a>0, a ne 0 и приведем некоторые ее свойства и практические примеры использования.

Производная функции f(x)=a в степени x

Как известно, производной функции f(x)f(x), определенной в точке x0x_0 и в некотором интервале, содержащем x0x_0, называют предел следующего вида:

f′(x0)=dfdx∣x=x0=lim⁡Δx→0f(x0+Δx)−f(x0)Δxf^{‘}(x_0)=dfrac{df}{dx}Bigr|_{x=x_0}=limlimits_{Delta x to 0}dfrac{ f(x_0+ Delta x)-f(x_0 )}{ Delta x}

если только такой предел существует.

Таким образом, для вычисления производной функции f(x)f(x) необходимо последовательно:

1. Записать выражение для приращения функции:

Δf(x0)=f(x0+Δx)−f(x0)Delta f(x_0 )=f(x_0+Delta x)-f(x_0 )

1. Упростить, по возможности, дробь

Δf(x0)Δx=f(x0+Δx)−f(x0)Δxdfrac {Delta f(x_0)}{Delta x}=dfrac {f(x_0+Delta x)-f(x_0)}{Delta x}

1. Вычислить предел дроби при Δx→0Delta x to 0 и записать полученное выражение для производной.

Применим этот алгоритм к вычислению производной показательной функции:

• Записываем приращение функции:

Δf(x0)=f(x0+Δx)−f(x0)=ax0+Δx−ax0=ax0(aΔx−1)Delta f(x_0)= f(x_0+Delta x)-f(x_0)= a^{x_0+Delta x}-a^{x_0}=a^{x_0} (a^{Delta x}-1)

• Получаем дробь:

Δf(x0)Δx=ax0aΔx−1Δxdfrac {Delta f(x_0)}{Delta x}= a^{x_0} dfrac {a^{Delta x}-1}{Delta x}

• Вычисляем производную:

f′(x0)=lim⁡Δx→0ax0aΔx−1Δx=ax0lim⁡Δx→0aΔx−1Δxf'(x_0 )= limlimits_{Delta x to 0} {a^{x_0} dfrac {a^{Delta x}-1}{Delta x}}= a^{x_0}limlimits_{Delta x to 0} {dfrac {a^{Delta x}-1}{Delta x}}

Используем далее представление показательной функции с помощью экспоненты:

ax=eln⁡a⋅xa^x=e^{ln {a} cdot x}

Тогда:

f′(x0)=ax0lim⁡Δx→0eln⁡a⋅Δx−1Δx=ln⁡a⋅ax0lim⁡t→0et−1tf'(x_0 )= a^{x_0}limlimits_{Delta x to 0} {dfrac {e^{ln {a} cdot Delta x}-1}{Delta x}}= ln {a} cdot a^{x_0}limlimits_{t to 0} {dfrac {e^{t}-1} {t}}

где t=ln⁡a⋅Δxt = ln {a} cdot Delta {x}

Для преобразования ete^{t} используем представление числа e≈2,71828e approx 2,71828 (числа Непера или числа Эйлера) в виде предела:

e=lim⁡n→∞(1+1n)ne=limlimits_{ntoinfty} Bigl( {1+dfrac {1}{n}} Bigr) ^n

Следовательно:

et=lim⁡n→∞(1+tn)ne^{t} =limlimits_{ntoinfty} Bigl( {1+dfrac {t}{n}} Bigr) ^n

Используем для выражения под знаком предела бином Ньютона:

(1+tn)n=1+Cn1tn+Cn2(tn)2+…+Cnn(tn)nBigl( {1+dfrac {t}{n}} Bigr) ^n=1+C_n^1 dfrac{t}{n}+ C_n^2 Bigl( {dfrac{t}{n}}Bigr)^2+ ldots + C_n^n Bigl( {dfrac{t}{n}}Bigr)^n

Тогда:

f′(x0)=ln⁡a⋅ax0lim⁡t→0lim⁡n→∞(1+Cn1tn+Cn2(tn)2+…+Cnn(tn)n)−1t=ln⁡a⋅ax0lim⁡t→0(lim⁡n→∞Cn1tn+Cn2(tn)2+…+Cnn(tn)nt)=ln⁡a⋅ax0lim⁡t→0lim⁡n→∞(Cn11n+Cn2t2−1n2+…+Cnntn−1nn)=ln⁡a⋅ax0lim⁡n→∞lim⁡t→0(n1n+Cn2t2−1n2+…+Cnntn−1nn)=ln⁡a⋅ax0(1+lim⁡n→∞lim⁡t→0(Cn2t2−1n2+…+Cnntn−1nn))f'(x_0 )= ln {a} cdot a^{x_0}limlimits_{t to 0}dfrac {limlimits_{ntoinfty} Bigl( {1+C_n^1 dfrac{t}{n}+ C_n^2 Bigl( {dfrac{t}{n}}Bigr)^2+ ldots + C_n^n Bigl( {dfrac{t}{n}}Bigr)^n }Bigr)-1}{t} = ln {a} cdot a^{x_0}limlimits_{t to 0}Bigl( limlimits_{ntoinfty} dfrac {C_n^1 dfrac{t}{n}+ C_n^2 Bigl( {dfrac{t}{n}}Bigr)^2+ ldots + C_n^n Bigl( {dfrac{t}{n}}Bigr)^n }{t}Bigr)= ln {a} cdot a^{x_0}limlimits_{t to 0} limlimits_{ntoinfty} Bigl( {C_n^1 dfrac{1}{n}+ C_n^2 dfrac{t^{2-1} }{n^2}+ ldots + C_n^n dfrac{t^{n-1} }{n^n}}Bigr)= ln {a} cdot a^{x_0}limlimits_{ ntoinfty } limlimits_{t to 0} Bigl( {n dfrac{1}{n}+ C_n^2 dfrac{t^{2-1} }{n^2}+ ldots + C_n^n dfrac{t^{n-1} }{n^n}}Bigr)=ln {a} cdot a^{x_0} Bigl( 1+ limlimits_{ ntoinfty } limlimits_{t to 0} Bigl( { C_n^2 dfrac{t^{2-1} }{n^2}+ ldots + C_n^n dfrac{t^{n-1} }{n^n}}Bigr) Bigr)

Учитывая, что:

lim⁡t→0(Cn2t2−1n2+…+Cnntn−1nn)=0limlimits_{t to 0} Bigl( { C_n^2 dfrac{t^{2-1} }{n^2}+ ldots + C_n^n dfrac{t^{n-1} }{n^n}}Bigr)=0

получаем:

f′(x0)=ln⁡a⋅ax0(1+0)f'(x_0 )= ln {a} cdot a^{x_0}(1+0)

Таким образом:

f′(x)=(ax)′=axln⁡af'(x)= (a^{x})^{‘}= a^{x} ln {a}

Как и следовало ожидать, при a=ea=e производная экспоненциальной функции f(x)=exf(x)=e^x равна этой же функции:

(ex)′=exln⁡e=ex(e^x )’=e^x ln {e}=e^x

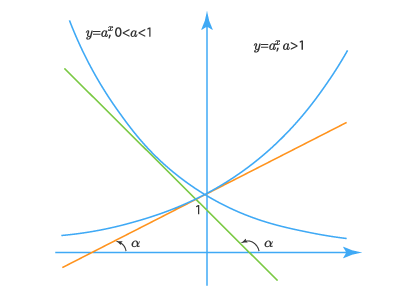
Некоторые свойства и практические примеры

• Угол наклона αalpha касательной к графику функции y=axy=a^x в точке x=x0x=x_0 определяется соотношением:

tg⁡α=y′(x0)=axln⁡atg alpha =y^{‘} (x_0 )= a^{x} ln {a}

Здесь угол αalpha это угол между касательной и осью OxOx отсчитываемый от положительного направления OxOx против часовой стрелки.

Производная функции f(x)=axf(x)=a^x в точке x0=0x_0=0 равна:

f′(x0)=(ax)x0=0′=a0ln⁡a=ln⁡af’ (x_0 )=(a^x )_{x_0=0}’=a^0 ln {a}=ln {a}

• Производная сложной функции

y=ag(x)y=a^{g(x)}

согласно правил дифференцирования, равна:

y′=g′(x)ag(x)ln⁡ay’=g'(x) a^{g(x)} ln {a}

• Производная сложной функции

y=u(v),y=u(v), где v=axv=a^x

равна:

y′=uv′⋅v′=uv′⋅axln⁡ay’=u’_v cdot v’=u’_v cdot a^x ln {a}

Пример 1

Зная производную экспоненты и используя правило для дифференцирования сложной функции, найти производную показательной функции.

Решение

Воспользуемся формулой для производной экспоненты:

(ex)′=ex(e^x )’=e^x

Тогда:

(eg(x))′=g′(x)eg(x)(e^{g(x)})’=g'(x)e^{g(x)}

Полагая:

g(x)=xln⁡ag(x)= x ln {a}

находим:

(exln⁡a)′=(xln⁡a)′exln⁡a=ln⁡a⋅exln⁡a(e^{x ln {a}})’=(x ln {a} )’ e^{x ln {a}}= ln {a} cdot e^{x ln {a}}

Учитывая, что

exln⁡a=axe^{x ln {a}}=a^{x}

получаем:

(ax)′=axln⁡a(a^x )’=a^x ln {a}

Как и следовало ожидать, результат совпадает с полученным ранее.

Пример 2

Найти производную функции

f(x)=23×2−2xf(x)=2^{3x^2-2x}

Решение

f′(x)=(23×2−2x)′=(3×2−2x)′⋅23×2−2xln⁡2=(6x−2)⋅23×2−2xln⁡2f'(x)= Bigl( 2^{3x^2-2x} Bigr)’=(3x^2-2x)’ cdot 2^{3x^2-2x} ln {2}=(6x-2) cdot 2^{3x^2-2x} ln {2}

Пример 3

Найти производную функции

f(x)=sin⁡x2xf(x)= sin {x^{2x}}

Решение

Полагаем x2x=vx^{2x}=v

Тогда

f′(x)=(sin⁡v)v′⋅v′=cos⁡v⋅(x2x)′=cos⁡(x2x)⋅(e2xln⁡x)′=cos⁡(x2x)⋅(2xln⁡x)′⋅e2xln⁡x=e2xln⁡xcos⁡(x2x)⋅(2ln⁡x+2)=x2xcos⁡(x2x)⋅(2ln⁡x+2)f'(x) = (sin v)_v’ cdot v’ = cos v cdot (x^{2x} )’=cos (x^{2x}) cdot (e^{2x ln {x}})’= cos (x^{2x}) cdot (2x ln {x})’ cdot e^{2x ln {x}}= e^{2x ln {x}} cos (x^{2x}) cdot (2 ln {x}+2) = x^{2x}cos (x^{2x}) cdot (2 ln {x}+2)

Производная степенно-показательной функции

Определение

Степенно-показательной
функцией (или показательно-степенной,
илифункцией
в степени функция)
называется функция вида 

Рассмотрим
способы нахождения ее производной.

1-ый
способ

Применяя
формулу:

То
есть вначале производная берется как
от степенной функции, а потом как от
показательной.

Замечание

Порядок
следования слагаемых неважен: можно
вначале взять производную от показательной
функции, а затем как от степенной, так
как от перестановки слагаемых сумма не
меняется:

2-ой
способ

С
помощью логарифмического
дифференцирования:

3-ий
способ

Представим
функцию в
следующем виде (используютсясвойства
логарифмов):

Тогда

1. Дифференцирование
   неявной функции одной и двух переменных.

Если
независимая переменная и
функциясвязаны
уравнением вида,
которое не разрешено относительно,
то функцияназываетсянеявной
функцией переменной .

Всякую
явно заданную функцию можно
записать в неявном виде.
Обратно сделать не всегда возможно.

Несмотря
на то, что уравнение не
разрешимо относительно,
оказывается возможным найти производную
отпо.
В этом случае необходимопродифференцировать обе
части заданного уравнения, рассматривая
функцию как
функцию от,
а затем из полученного уравнения найти
производную.

1. Полное
   приращение и полный дифференциал
   функции двух переменных. Необходимое
   условие дифференцируемости.

1. Экстремум
   функции 2-х переменных. Необходимое
   условие. Достаточное условие.

2. Градиент
   скалярного поля. Свойства. Уравнение
   касательной плоскости и нормали к
   поверхности.

3. Производная
   по направлению и ее физический смысл.
   Формула для вычисления.

Как считать производную степенной функции

3 февраля 2015

Этим видео я начинаю длинную серию уроков, посвященную производным. Этот урок состоит из нескольких частей.

В первую очередь, я расскажу вам, что вообще такое производные и как их считать, но не мудреным академическим языком, а так, как я сам это понимаю и как объясняю своим ученикам. Во-вторых, мы рассмотрим простейшее правило для решения задач, в которых будем искать производные суммы, производные разности и производные степенной функции.

Мы рассмотрим более сложные комбинированные примеры, из которых вы, в частности, узнаете, что подобные задачи, содержащие корни и даже дроби, могут быть решены при использовании формулы производной степенной функции. Кроме того, конечно, будет множество задач и примеров решений самого разного уровня сложности.

Вообще, изначально я собирался записать коротенький 5-минутный ролик, но сами видите, что из этого получилось. Поэтому хватит лирики — приступаем к делу.

Что такое производная?

Итак, начнем издалека. Много лет назад, когда деревья были зеленее, а жизнь была веселее, математики задумались вот над чем: рассмотрим простую функцию, заданную своим графиком, назовем ее $y=fleft( x right)$. Разумеется, график существует не сам по себе, поэтому нужно провести оси $x$, а также ось $y$. А теперь давайте выберем любую точку на этом графике, абсолютно любую. Абсциссу назовем ${{x}_{1}}$, ордината, как не трудно догадаться, будет $fleft( {{x}_{1}} right)$.

Рассмотрим на том же графике еще одну точку. Не важно, какую, главное, чтобы она отличалась от первоначальной. У нее, опять же, есть абсцисса, назовем ее ${{x}_{2}}$, а также ордината — $fleft( {{x}_{2}} right)$.

Итак, мы получили две точки: у них разные абсциссы и, следовательно, разные значения функции, хотя последнее — необязательно. А вот что действительно важно, так это что, что из курса планиметрии нам известно: через две точки можно провести прямую и, причем, только одну. Вот давайте ее и проведем.

А теперь проведем через самую первую из них прямую, параллельную оси абсцисс. Получим прямоугольный треугольник. Давайте его обозначим $ABC$, прямой угол $C$. У этого треугольника возникает одно очень интересное свойство: дело в том, что угол$alpha $, на самом деле, равен углу, под которым пересекается прямая $AB$ с продолжением оси абсцисс. Судите сами:

1. прямая $AC$параллельна оси $Ox$ по построению,
2. прямая $AB$ пересекает $AC$ под $alpha $,
3. следовательно, $AB$ пересекает $Ox$под тем же самым $alpha $.

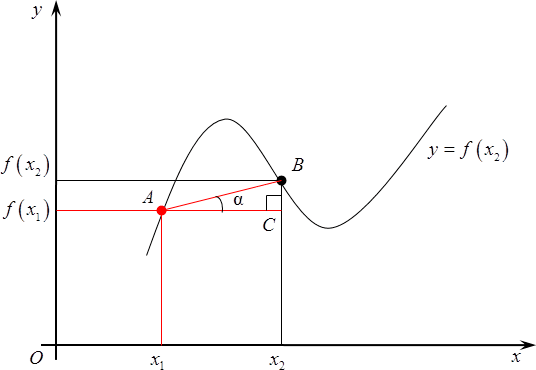
Что мы можем сказать об $text{ }!!alpha!!text{ }$? Ничего конкретного, разве что в треугольнике $ABC$отношение катета $BC$ к катету $AC$ равно тангенсу этого самого угла. Так и запишем:

[tg=frac{BC}{AC}]

Разумеется, $AC$ в данном случае легко считается:

[AC={{x}_{2}}-{{x}_{1}}]

Точно также и $BC$:

[BC=fleft( {{x}_{2}} right)-fleft( {{x}_{1}} right)]

Другими словами, мы можем записать следующее:

[operatorname{tg}text{ }!!alpha!!text{ }=frac{fleft( {{x}_{2}} right)-fleft( {{x}_{1}} right)}{{{x}_{2}}-{{x}_{1}}}]

Теперь, когда мы все это выяснили, давайте вернемся к нашему графику и рассмотрим новую точку $B$. Сотрем старые значения и возьмем и возьмем $B$ где-нибудь поближе к ${{x}_{1}}$. Вновь обозначим ее абсциссу за ${{x}_{2}}$, а ординату — $fleft( {{x}_{2}} right)$.

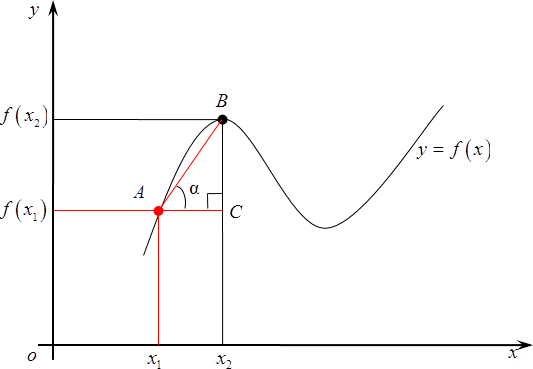
Вновь рассмотрим наш маленький треугольник $ABC$и $text{ }!!alpha!!text{ }$ внутри него. Совершенно очевидно, что это будет уже совсем другой угол, тангенс будет также другим потому, что длины отрезков $AC$ и $BC$ существенно изменились, а формула для тангенса угла нисколько не поменялась — это по-прежнему соотношение между изменением функции и изменением аргумента.

Наконец, продолжаем двигать $B$ все ближе к изначальной точке $A$, в результате треугольник еще уменьшится, а прямая, содержащая отрезок $AB$, все больше будет походить на касательную к графику функции.

 

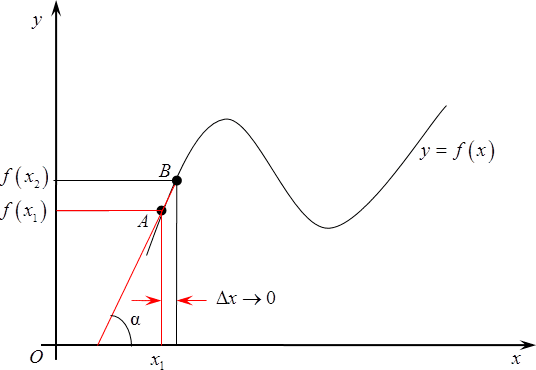
В итоге, если продолжать сближение точек, т. е., уменьшать расстояние до нуля, то прямая $AB$, действительно, превратится в касательную к графику в данной точке, а $text{ }!!alpha!!text{ }$превратится из обычного элемента треугольника в угол между касательной к графику и положительным направлением оси $Ox$.

И вот тут мы плавно переходим к определению$f$, а именно, производной функции в точке ${{x}_{1}}$ называется тангенс угла $alpha $ между касательной к графику в точке ${{x}_{1}}$ и положительным направлением оси $Ox$:

[{f}’left( {{x}_{1}} right)=operatorname{tg}text{ }!!alpha!!text{ }]

Возвращаясь к нашему графику, следует отметить, что в качестве ${{x}_{1}}$ можно выбрать любую точку на графике. Например, с тем же успехом мы могли снять штрих в точке, показанной на рисунке. 

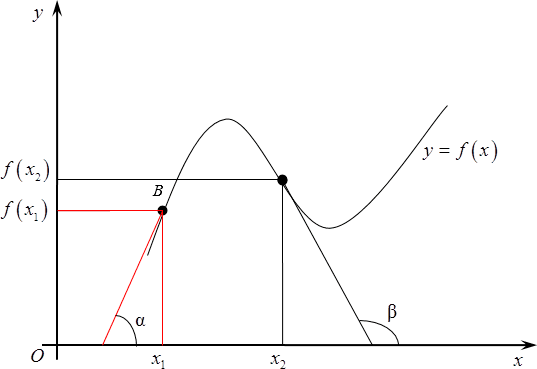
Угол между касательной и положительным направлением оси назовем $beta $. Соответственно, $f$ в ${{x}_{2}}$ будет равна тангенсу этого угла $beta $.

[{f}’left( {{x}_{2}} right)=tgtext{ }!!beta!!text{ }]

В каждой точке графика будет своя касательная, а, следовательно, свое значение функции. В каждом из этих случаев помимо точки, в которой мы ищем производную разности или суммы, или производную степенной функции, необходимо взять другую точку, находящуюся на некотором расстоянии от нее, а затем устремить эту точку к исходной и, разумеется, выяснить, как в процессе такого движения будет меняться тангенс угла наклона.

Производная степенной функции

К сожалению, подобное определение нас совершено не устраивает. Все эти формулы, картинки, углы не дают нам ни малейшего представления о том, как считать реальную производную в реальных задачах. Поэтому давайте немного отвлечемся от формального определения и рассмотрим более действенные формулы и приемы, с помощью которых уже можно решать настоящие задачи.

Начнем с самых простых конструкций, а именно, функций вида $y={{x}^{n}}$, т.е. степенных функций. В этом случае мы можем записать следующее: ${y}’=ncdot {{x}^{n-1}}$. Другими словами, степень, которая стояла в показателе, показывается в множителе спереди, а сам показатель уменьшается на единицу. Например:

[begin{align}& y={{x}^{2}} \& {y}’=2cdot {{x}^{2-1}}=2x \end{align}]

А вот другой вариант:

[begin{align}& y={{x}^{1}} \& {y}’={{left( x right)}^{prime }}=1cdot {{x}^{0}}=1cdot 1=1 \& {{left( x right)}^{prime }}=1 \end{align}]

Пользуясь этими простыми правилами, давайте попробуем снять штрих следующих примеров:

[fleft( x right)={{x}^{6}}]

Итак, мы получаем:

[{{left( {{x}^{6}} right)}^{prime }}=6cdot {{x}^{5}}=6{{x}^{5}}]

Теперь решим второе выражение:

[begin{align}& fleft( x right)={{x}^{100}} \& {{left( {{x}^{100}} right)}^{prime }}=100cdot {{x}^{99}}=100{{x}^{99}} \end{align}]

Разумеется, это были очень простые задачи. Однако реальные задачи более сложные и они не ограничиваются одними лишь степенями функции.

Итак, правило № 1 – если функция представлена в виде других двух, то производная этой суммы равна сумме производных:

[{{left( f+g right)}^{prime }}={f}’+{g}’]

Аналогично, производная разности двух функций равна разности производных:

[{{left( f-g right)}^{prime }}={f}’-{g}’]

Пример:

[{{left( {{x}^{2}}+x right)}^{prime }}={{left( {{x}^{2}} right)}^{prime }}+{{left( x right)}^{prime }}=2x+1]

Кроме того, есть еще одно важное правило: если перед некоторой $f$ стоит константа $c$, на которую эта функция умножается, то $f$ всей этой конструкции считается так:

[{{left( ccdot f right)}^{prime }}=ccdot {f}’]

Пример:

[{{left( 3{{x}^{3}} right)}^{prime }}=3{{left( {{x}^{3}} right)}^{prime }}=3cdot 3{{x}^{2}}=9{{x}^{2}}]

Наконец, еще одно очень важное правило: в задачах часто встречается отдельное слагаемое, которое вообще не содержит $x$. Например, мы можем наблюдать это в наших сегодняшних выражениях. Производная константы, т. е., числа, никак не зависящего от $x$, всегда равна нулю, причем совершенно неважно, чему равна константа $c$:

[{{left( c right)}^{prime }}=0]

Пример решения:

[{{left( 1001 right)}^{prime }}={{left( frac{1}{1000} right)}^{prime }}=0]

Еще раз ключевые моменты:

1. Производная суммы двух функций всегда равна сумме производных: ${{left( f+g right)}^{prime }}={f}’+{g}’$;
2. По аналогичным причинам производная разности двух функций равна разности двух производных: ${{left( f-g right)}^{prime }}={f}’-{g}’$;
3. Если у функции присутствует множитель константа, то эту константу можно выносить за знак производной: ${{left( ccdot f right)}^{prime }}=ccdot {f}’$;
4. Если вся функция представляет собой константу, то ее производная всегда ноль: ${{left( c right)}^{prime }}=0$.

Давайте посмотрим, как все это работает на реальных примерах. Итак:

[y={{x}^{5}}-3{{x}^{2}}+7]

Записываем:

[begin{align}& {{left( {{x}^{5}}-3{{x}^{2}}+7 right)}^{prime }}={{left( {{x}^{5}} right)}^{prime }}-{{left( 3{{x}^{2}} right)}^{prime }}+{7}’= \& =5{{x}^{4}}-3{{left( {{x}^{2}} right)}^{prime }}+0=5{{x}^{4}}-6x \end{align}]

В этом примере мы видим и производную суммы, и производную разности. Итого, производная равна $5{{x}^{4}}-6x$.

Переходим ко второй функции:

[fleft( x right)=3{{x}^{2}}-2x+2]

Записываем решение:

[begin{align}& {{left( 3{{x}^{2}}-2x+2 right)}^{prime }}={{left( 3{{x}^{2}} right)}^{prime }}-{{left( 2x right)}^{prime }}+{2}’= \& =3{{left( {{x}^{2}} right)}^{prime }}-2{x}’+0=3cdot 2x-2cdot 1=6x-2 \end{align}]

Вот мы и нашли ответ.

Переходим к третьей функции — она уже посерьезней:

[y=2{{x}^{3}}-3{{x}^{2}}+frac{1}{2}x-5]

Решаем:

[begin{align}& {{left( 2{{x}^{3}}-3{{x}^{2}}+frac{1}{2}x-5 right)}^{prime }}={{left( 2{{x}^{3}} right)}^{prime }}-{{left( 3{{x}^{2}} right)}^{prime }}+{{left( frac{1}{2}x right)}^{prime }}-{5}’= \& =2{{left( {{x}^{3}} right)}^{prime }}-3{{left( {{x}^{2}} right)}^{prime }}+frac{1}{2}cdot {x}’=2cdot 3{{x}^{2}}-3cdot 2x+frac{1}{2}cdot 1=6{{x}^{2}}-6x+frac{1}{2} \end{align}]

Ответ мы нашли.

Переходим к последнему выражению — самому сложному и самому длинному:

[y=6{{x}^{7}}-14{{x}^{3}}+4x+5,{{x}_{0}}=-1]

Итак, считаем:

[begin{align}& {{left( 6{{x}^{7}}-14{{x}^{3}}+4x+5 right)}^{prime }}={{left( 6{{x}^{7}} right)}^{prime }}-{{left( 14{{x}^{3}} right)}^{prime }}+{{left( 4x right)}^{prime }}+{5}’= \& =6cdot 7cdot {{x}^{6}}-14cdot 3{{x}^{2}}+4cdot 1+0=42{{x}^{6}}-42{{x}^{2}}+4 \end{align}]

Но на этом решение не заканчивается, потому что нас просят не просто снять штрих, а посчитать ее значение в конкретной точке, поэтому подставляем в выражение −1 вместо $x$:

[{y}’left( -1 right)=42cdot 1-42cdot 1+4=4]

Идем далее и переходим к еще более сложным и интересным примерам. Дело в том, что формула решения степенной производной ${{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}$ имеет еще более широкую область применения, чем обычно принято считать. С ее помощью можно решать примеры с дробями, корнями и т. д. Именно этим мы сейчас и займемся.

Для начала еще раз запишем формулу, которая поможет нам найти производную степенной функции:

[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]

А теперь внимание: до сих пор мы рассматривали в качестве $n$ лишь натуральные числа, однако ничего не мешаем рассмотреть дроби и даже отрицательные числа. Например, мы можем записать следующее:

[begin{align}& sqrt{x}={{x}^{frac{1}{2}}} \& {{left( sqrt{x} right)}^{prime }}={{left( {{x}^{frac{1}{2}}} right)}^{prime }}=frac{1}{2}cdot {{x}^{-frac{1}{2}}}=frac{1}{2}cdot frac{1}{sqrt{x}}=frac{1}{2sqrt{x}} \end{align}]

Ничего сложного, поэтому посмотрим, как эта формула поможет нам при решении более сложных задач. Итак, пример:

[y=sqrt{x}+sqrt[3]{x}+sqrt[4]{x}]

Записываем решение:

[begin{align}& left( sqrt{x}+sqrt[3]{x}+sqrt[4]{x} right)={{left( sqrt{x} right)}^{prime }}+{{left( sqrt[3]{x} right)}^{prime }}+{{left( sqrt[4]{x} right)}^{prime }} \& {{left( sqrt{x} right)}^{prime }}=frac{1}{2sqrt{x}} \& {{left( sqrt[3]{x} right)}^{prime }}={{left( {{x}^{frac{1}{3}}} right)}^{prime }}=frac{1}{3}cdot {{x}^{-frac{2}{3}}}=frac{1}{3}cdot frac{1}{sqrt[3]{{{x}^{2}}}} \& {{left( sqrt[4]{x} right)}^{prime }}={{left( {{x}^{frac{1}{4}}} right)}^{prime }}=frac{1}{4}{{x}^{-frac{3}{4}}}=frac{1}{4}cdot frac{1}{sqrt[4]{{{x}^{3}}}} \end{align}]

Возвращаемся к нашему примеру и записываем:

[{y}’=frac{1}{2sqrt{x}}+frac{1}{3sqrt[3]{{{x}^{2}}}}+frac{1}{4sqrt[4]{{{x}^{3}}}}]

Вот такое сложное решение.

Переходим ко второму примеру — здесь всего два слагаемых, но каждое из них содержит как классическую степень, так и корни.

[y={{x}^{3}}sqrt[3]{{{x}^{2}}}+{{x}^{7}}sqrt[3]{x}]

Сейчас мы узнаем, как найти производную степенной функции, которая, кроме того, содержит и корень:

[begin{align}& {{left( {{x}^{3}}sqrt[3]{{{x}^{2}}}+{{x}^{7}}sqrt[3]{x} right)}^{prime }}={{left( {{x}^{3}}cdot sqrt[3]{{{x}^{2}}} right)}^{prime }}={{left( {{x}^{3}}cdot {{x}^{frac{2}{3}}} right)}^{prime }}= \& ={{left( {{x}^{3+frac{2}{3}}} right)}^{prime }}={{left( {{x}^{frac{11}{3}}} right)}^{prime }}=frac{11}{3}cdot {{x}^{frac{8}{3}}}=frac{11}{3}cdot {{x}^{2frac{2}{3}}}=frac{11}{3}cdot {{x}^{2}}cdot sqrt[3]{{{x}^{2}}} \& {{left( {{x}^{7}}cdot sqrt[3]{x} right)}^{prime }}={{left( {{x}^{7}}cdot {{x}^{frac{1}{3}}} right)}^{prime }}={{left( {{x}^{7frac{1}{3}}} right)}^{prime }}=7frac{1}{3}cdot {{x}^{6frac{1}{3}}}=frac{22}{3}cdot {{x}^{6}}cdot sqrt[3]{x} \end{align}]

Оба слагаемых посчитаны, осталось записать окончательный ответ:

[{y}’=frac{11}{3}cdot {{x}^{2}}cdot sqrt[3]{{{x}^{2}}}+frac{22}{3}cdot {{x}^{6}}cdot sqrt[3]{x}]

Мы нашли ответ.

Производная дроби через степенную функцию

Но и на этом возможности формулы для решения производной степенной функции не заканчиваются. Дело в том, что с ее помощью можно считать не только примеры с корнями, но также и с дробями. Это как раз та редкая возможность, которая значительно упрощает решение таких примеров, но при этом зачастую игнорируется не только учениками, но и учителями.

Итак, сейчас мы попытаемся совместить сразу две формулы. С одной стороны, классическая производная степенной функции

[{{left( {{x}^{n}} right)}^{prime }}=ncdot {{x}^{n-1}}]

С другой стороны мы знаем, что выражение вида $frac{1}{{{x}^{n}}}$ представимо в виде ${{x}^{-n}}$. Следовательно,

[left( frac{1}{{{x}^{n}}} right)’={{left( {{x}^{-n}} right)}^{prime }}=-ncdot {{x}^{-n-1}}=-frac{n}{{{x}^{n+1}}}]

Пример:

[{{left( frac{1}{x} right)}^{prime }}=left( {{x}^{-1}} right)=-1cdot {{x}^{-2}}=-frac{1}{{{x}^{2}}}]

Таким образом, производные простых дробей, где в числителе стоит константа, а в знаменателе — степень, также считаются с помощью классической формулы. Посмотрим, как это работает на практике.

Итак, первая функция:

[fleft( x right)=frac{1}{{{x}^{2}}}]

Считаем:

[{{left( frac{1}{{{x}^{2}}} right)}^{prime }}={{left( {{x}^{-2}} right)}^{prime }}=-2cdot {{x}^{-3}}=-frac{2}{{{x}^{3}}}]

Первый пример решен, переходим ко второму:

[y=frac{7}{4{{x}^{4}}}-frac{2}{3{{x}^{3}}}+frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}}]

Решаем:

[begin{align}& {{left( frac{7}{4{{x}^{4}}}-frac{2}{3{{x}^{3}}}+frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}} right)}^{prime }}= \& ={{left( frac{7}{4{{x}^{4}}} right)}^{prime }}-{{left( frac{2}{3{{x}^{3}}} right)}^{prime }}+{{left( 2{{x}^{3}} right)}^{prime }}-{{left( 3{{x}^{4}} right)}^{prime }} \& {{left( frac{7}{4{{x}^{4}}} right)}^{prime }}=frac{7}{4}{{left( frac{1}{{{x}^{4}}} right)}^{prime }}=frac{7}{4}cdot {{left( {{x}^{-4}} right)}^{prime }}=frac{7}{4}cdot left( -4 right)cdot {{x}^{-5}}=frac{-7}{{{x}^{5}}} \& {{left( frac{2}{3{{x}^{3}}} right)}^{prime }}=frac{2}{3}cdot {{left( frac{1}{{{x}^{3}}} right)}^{prime }}=frac{2}{3}cdot {{left( {{x}^{-3}} right)}^{prime }}=frac{2}{3}cdot left( -3 right)cdot {{x}^{-4}}=frac{-2}{{{x}^{4}}} \& {{left( frac{5}{2}{{x}^{2}} right)}^{prime }}=frac{5}{2}cdot 2x=5x \& {{left( 2{{x}^{3}} right)}^{prime }}=2cdot 3{{x}^{2}}=6{{x}^{2}} \& {{left( 3{{x}^{4}} right)}^{prime }}=3cdot 4{{x}^{3}}=12{{x}^{3}} \end{align}]…

Теперь собираем все эти слагаемые в единую формулу:

[{y}’=-frac{7}{{{x}^{5}}}+frac{2}{{{x}^{4}}}+5x+6{{x}^{2}}-12{{x}^{3}}]

Мы получили ответ.

Однако прежде чем двигаться дальше, хотел бы обратить ваше внимание на форму записи самих исходных выражений: в первом выражении мы записали $fleft( x right)=…$, во втором: $y=…$ Многие ученики теряются, когда видят разные формы записи. Чем отличаются $fleft( x right)$ и $y$? На самом деле, ничем. Это просто разные записи с одним и тем же смыслом. Просто когда мы говорим $fleft( x right)$, то речь идет, прежде всего, о функции, а когда речь идет об $y$, то чаще всего подразумевается график функции. В остальном же это одно и то же, т. е., производная в обоих случаях считается одинаково.

Сложные задачи с производными

В заключение хотелось бы рассмотреть пару сложных комбинированных задач, в которых используется сразу все то, что мы сегодня рассмотрели. В них нас ждут и корни, и дроби, и суммы. Однако сложными эти примеры будут лишь в рамках сегодняшнего видеоурока, потому что по-настоящему сложные функции производных будут ждать вас впереди.

Итак, заключительная часть сегодняшнего видеоурока, состоящая из двух комбинированных задач. Начнем с первой из них:

[y={{x}^{3}}-frac{1}{{{x}^{3}}}+sqrt[3]{x}]

Считаем:

[begin{align}& {{left( {{x}^{3}}-frac{1}{{{x}^{3}}}+sqrt[3]{x} right)}^{prime }}={{left( {{x}^{3}} right)}^{prime }}-{{left( frac{1}{{{x}^{3}}} right)}^{prime }}+left( sqrt[3]{x} right) \& {{left( {{x}^{3}} right)}^{prime }}=3{{x}^{2}} \& {{left( frac{1}{{{x}^{3}}} right)}^{prime }}={{left( {{x}^{-3}} right)}^{prime }}=-3cdot {{x}^{-4}}=-frac{3}{{{x}^{4}}} \& {{left( sqrt[3]{x} right)}^{prime }}={{left( {{x}^{frac{1}{3}}} right)}^{prime }}=frac{1}{3}cdot frac{1}{{{x}^{frac{2}{3}}}}=frac{1}{3sqrt[3]{{{x}^{2}}}} \end{align}]

Производная функции равна:

[{y}’=3{{x}^{2}}-frac{3}{{{x}^{4}}}+frac{1}{3sqrt[3]{{{x}^{2}}}}]

Первый пример решен. Рассмотрим вторую задачу:

[y=-frac{2}{{{x}^{4}}}+sqrt[4]{x}+frac{4}{xsqrt[4]{{{x}^{3}}}}]

Во втором примере действуем аналогично:

[{{left( -frac{2}{{{x}^{4}}}+sqrt[4]{x}+frac{4}{xsqrt[4]{{{x}^{3}}}} right)}^{prime }}={{left( -frac{2}{{{x}^{4}}} right)}^{prime }}+{{left( sqrt[4]{x} right)}^{prime }}+{{left( frac{4}{xcdot sqrt[4]{{{x}^{3}}}} right)}^{prime }}]

Посчитаем каждое слагаемое отдельно:

[begin{align}& {{left( -frac{2}{{{x}^{4}}} right)}^{prime }}=-2cdot {{left( {{x}^{-4}} right)}^{prime }}=-2cdot left( -4 right)cdot {{x}^{-5}}=frac{8}{{{x}^{5}}} \& {{left( sqrt[4]{x} right)}^{prime }}={{left( {{x}^{frac{1}{4}}} right)}^{prime }}=frac{1}{4}cdot {{x}^{-frac{3}{4}}}=frac{1}{4cdot {{x}^{frac{3}{4}}}}=frac{1}{4sqrt[4]{{{x}^{3}}}} \& {{left( frac{4}{xcdot sqrt[4]{{{x}^{3}}}} right)}^{prime }}={{left( frac{4}{xcdot {{x}^{frac{3}{4}}}} right)}^{prime }}={{left( frac{4}{{{x}^{1frac{3}{4}}}} right)}^{prime }}=4cdot {{left( {{x}^{-1frac{3}{4}}} right)}^{prime }}= \& =4cdot left( -1frac{3}{4} right)cdot {{x}^{-2frac{3}{4}}}=4cdot left( -frac{7}{4} right)cdot frac{1}{{{x}^{2frac{3}{4}}}}=frac{-7}{{{x}^{2}}cdot {{x}^{frac{3}{4}}}}=-frac{7}{{{x}^{2}}cdot sqrt[4]{{{x}^{3}}}} \end{align}]

Все слагаемые посчитаны. Теперь возвращаемся к исходной формуле и складываем вместе все три слагаемых. Получаем, что окончательный ответ будет таким:

[{y}’=frac{8}{{{x}^{5}}}+frac{1}{4sqrt[4]{{{x}^{3}}}}-frac{7}{{{x}^{2}}cdot sqrt[4]{{{x}^{3}}}}]

И на этом все. Это был первый наш урок. В следующих уроках мы рассмотрим более сложные конструкции, а также выясним, зачем вообще нужны производные. 

Смотрите также:

1. Производная произведения и частного
2. Правила вычисления производных
3. Теорема Виета
4. Преобразование уравнений
5. Тест по методу интервалов для строгих неравенств
6. Тест по задачам B14: средний уровень, 2 вариант

Содержание:

1. Производная степенной функции
2. Производная показательной функции
3. Степенная функция и ее производные

Теорема:

Пусть и – дифференцируемые в точке функции. Тогда функция называемая показательно-степенной, имеет производную

Доказательство:

Логарифмируем и полученное равенство дифференцируем Умножаем обе части равенства на и, имея ввиду получаем:

Это и есть равенство , которое называется формулой Бернулли. Смысл формулы заключается в следующем: производная показательно-степенной функции есть сумма результатов дифференцирования как функции чисто показательной и чисто степенной.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Пример 1:

Найти .

Решение:

 

Производная степенной функции

Пусть. Найти . Закрепим и найдем соответствующее значение функции . Придадим аргументу приращение и найдем новое значение функции

Тогда и Положив и вспомнив “замечательный предел” имеем

или

Возможно вам будут полезны данные страницы:

Примеры:

1. Если ,то
2. Если ,то
3. Если ,то

Рекомендуется отдельно запомнить производную квадратного корня. Именно, пусть . Тогда по общей формуле или

т. е. производная квадратного корня равна единице, деленной на два таких же корня.

Наиболее распространенными экспоненциальными и логарифмическими функциями в курсе исчисления являются естественная экспоненциальная функция и естественная логарифмическая функция

В этом случае, в отличие от случая экспоненциальной функции, мы действительно можем найти производную от общей функции логарифма.

Производная показательной функции

Пусть (эта функция, как уже говорилось, называется показательной; не следует путать ее со степеннбй функцией ). Чтобы найти производную этой функции, проводим обычные преобразованияоткуда

Составим отношение

Устремим к нулю. Тогда, вспоминая “замечательный предел” (гл. И, § 1, п° 10) мы получаем Следовательно,

Интересен частный случай выведенной формулы, когда . Именно, а так как , то

Задача:

Пусть и. Предположим, что существуют производные и , которые нам известны. Найти производную .

Решение:

Закрепим аргумент , тогда и соответственно будут иметь значения и . Придадим аргументу приращение , тогда получит приращение , а это, в свою очередь, вызывает появление приращения .

Интересующая нас производная есть предел отношения при Но это отношение можно переписать и так:

Что касается второго множителя то по самому определению производной ясно, что при он стремится к

Что касается первого сомножителя ,то хочется думать, что по аналогичным соображениям он будет стремиться к Однако это непосредственно не очевидно. В самом деле, ведь а у нас дано не ,а . Тем не менее небольшое рас-

суждение позволяет преодолеть возникшее затруднение. Именно, ведь— функция аргумента имеющая производную .

Значит, эта функция непрерывна. Но тогда бесконечно малому приращению аргумента отвечает бесконечно малое же приращение . Стало быть, при будет и , а тогда Поскольку предел произведения равен произведению пределов, имеем при , откуда окончательно Таким образом, производная сложной функции по независимой переменной равна ее производной по промежуточной переменной, умноженной на производную промежуточной переменной по независимой.

Замечание. Правило цепочки станет совершенно наглядным, если мы вспомним, что есть скорость изменения относительно . Действительно, если у меняется вдвое быстрее, а меняется втрое быстрее , то

В то же время ясно, что у меняется в шесть раз быстрее т. е. . Стало быть,

Степенная функция и ее производные

Определение:

Функция, заданная формулой называется степенной с показателем .

Если , то степенная функция определена при , так как . При целых формулой степенная функцияопределена и для . При четных функция четная, а при нечетных – функция нечетная. Поэтому исследование степенной функции достаточно провести на промежутке .

Для любого из области определения производная степенной функции находится так:

Действительно, так как При степенная функция убывает на промежутке , так как при (рис. 5).

Рисунок 5 – График степенной функции при Пристепенная функция возрастает , так как при (рис.6).

Рисунок 6 – График степенной функции при При степенная функция и при и . Поэтому точка нуль присоединяется к промежутку возрастания, то есть при степенная функция возрастает на промежутке .

Рисунок 7 – График степенной функции при Производной степенной функции является

При общий вид первообразных степенной функции имеет вид:

При первообразной функции является

Пример 2:

Первообразная для степенной функции определяется по формуле .Таким образом первообразная для функции будет равна

Пример 3:

Найдите первообразную для функции Первообразная для функции будет равна 3. Вычислите интеграл Интеграл вычислим по формуле неопределенного интеграла степенной функции По правилам интегрирования определенного интеграла получим:

Пример 4:

Вычислите интеграл

Пример 5:

Вычислите площадь фигуры, ограниченной линиями