- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Площадь
- Площадь параллелограмма
Назовем одну из сторон параллелограмма основанием, а перпендикуляр, проведенный из любой точки противоположной стороны к прямой, содержащей основание, – высотой параллелограмма.
Теорема
Площадь параллелограмма равна произведению его основания на высоту
Доказательство
Дано: ABCD – параллелограмм, S – площадь ABCD, ВН и СК – высоты
Доказать: S = AD  BH
BH
Доказательство:
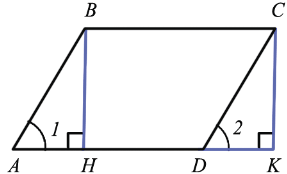
Докажем, что площадь прямоугольника НВСК также равна S. Рассмотрим трапецию АВСК: с одной стороны, она составлена из параллелограмма ABCD и треугольника DCK. Но с другой стороны, она составлена из прямоугольника НВСК и треугольника АВН. Но  DCK =
DCK =  АВН (по гипотенузе (АВ = CD, т.к. они противоположные стороны параллелограмма) и острому углу(углы 1 и 2 как соответственные углы при пересечении параллельных прямых АВ и CD секущей AD)), а равные фигуры имеют равные площади, поэтому их площади равны.
АВН (по гипотенузе (АВ = CD, т.к. они противоположные стороны параллелограмма) и острому углу(углы 1 и 2 как соответственные углы при пересечении параллельных прямых АВ и CD секущей AD)), а равные фигуры имеют равные площади, поэтому их площади равны.
 площадь параллелограмма ABCD и прямоугольника НВСК также равны, т.е. площадь прямоугольника НВСК равна S. По теореме площадь прямоугольника равна произведению его смежных сторон, т.е. S = BC
площадь параллелограмма ABCD и прямоугольника НВСК также равны, т.е. площадь прямоугольника НВСК равна S. По теореме площадь прямоугольника равна произведению его смежных сторон, т.е. S = BC  BH, а так как BC = AD, то S = AD
BH, а так как BC = AD, то S = AD  BH. Теорема доказана
BH. Теорема доказана
Советуем посмотреть:
Понятие площади многоугольника
Площадь квадрата
Площадь прямоугольника
Площадь треугольника
Площадь трапеции
Теорема Пифагора
Теорема, обратная теореме Пифагора
Формула Герона
Площадь
Правило встречается в следующих упражнениях:
7 класс
Задание 459,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 460,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 502,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 510*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 526,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 603,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 832,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 841,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1021,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1241,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Преподаватель который помогает студентам и школьникам в учёбе.
Площадь параллелограмма – определение и вычисление с примерами решения
Теорема (о площади параллелограмма). Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
Доказательство:
Пусть 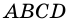
1) Проведем высоту 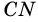 к прямой, содержащей сторону
к прямой, содержащей сторону 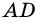 параллелограмма.
параллелограмма.
2) 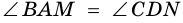 (как соответственные углы при параллельных прямых
(как соответственные углы при параллельных прямых 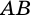 и
и 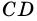 и секущей
и секущей 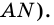 Поэтому
Поэтому 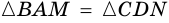 (по гипотенузе и острому углу).
(по гипотенузе и острому углу).
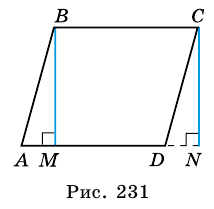
3) Параллелограмм 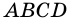 состоит из трапеции
состоит из трапеции 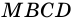 и треугольника
и треугольника 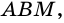 а прямоугольник
а прямоугольник 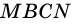 – из трапеции
– из трапеции 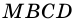 и треугольника
и треугольника 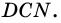 Так как треугольники
Так как треугольники 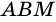 и
и 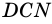 равны, то равны и их площади, а потому равными будут площади параллелограмма
равны, то равны и их площади, а потому равными будут площади параллелограмма 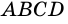 и прямоугольника
и прямоугольника 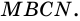
4) 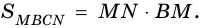 Но
Но 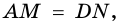 и поэтому
и поэтому 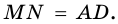 Следовательно,
Следовательно, 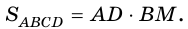
Заметим, что если основание высоты 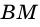 – точка
– точка 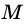 -совпадает с точкой
-совпадает с точкой 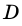 или лежит на продолжении стороны
или лежит на продолжении стороны 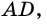 то доказательство теоремы будет аналогичным.
то доказательство теоремы будет аналогичным.
В общем виде формулу площади 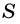 параллелограмма можно записать так:
параллелограмма можно записать так:
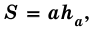
где 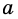 – сторона параллелограмма,
– сторона параллелограмма, 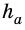 – высота, к ней проведенная.
– высота, к ней проведенная.
Пример:
Докажите, что высоты ромба, проведенные из одной вершины, равны.
Доказательство:
Пусть 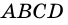 – данный ромб,
– данный ромб, 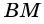 и
и 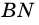 – его высоты (рис. 232).
– его высоты (рис. 232).
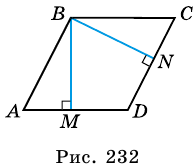
Ромб является параллелограммом, поэтому 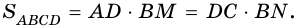 Но
Но 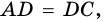 а значит
а значит 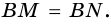
Пример:
Периметр параллелограмма равен 36 см, а его высоты – 4 см и 5 см. Найдите площадь параллелограмма.
Решение:
1) Пусть 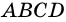 – данный параллелограмм,
– данный параллелограмм, 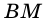 и
и 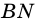 – его высоты (рис. 232),
– его высоты (рис. 232), 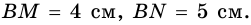
2) 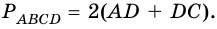 По условию
По условию 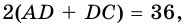 поэтому
поэтому 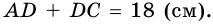
3) Пусть 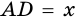 см, тогда
см, тогда 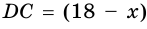 см.
см.
4) Так как по формуле площади параллелограмма 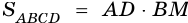 или
или 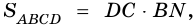 имеем уравнение:
имеем уравнение: 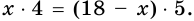 То есть
То есть 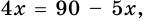 откуда
откуда 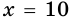 (см).
(см).
5) Тогда 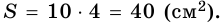
Ответ. 40 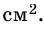
Площадь параллелограмма
С помощью формулы площади прямоугольника можно доказать формулу площади произвольного параллелограмма.
Теорема (формула площади параллелограмма)
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне:
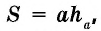
где 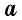 — сторона параллелограмма,
— сторона параллелограмма, 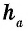 — проведенная к ней высота.
— проведенная к ней высота.
Доказательство:
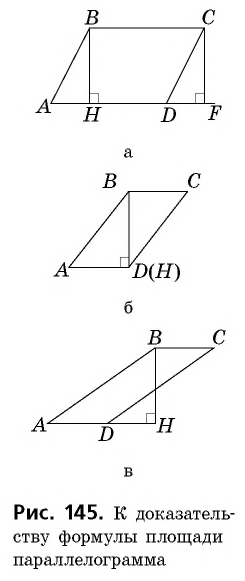
Пусть 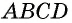 — данный параллелограмм, не являющийся прямоугольником (рис. 145, а). Проведем его высоты
— данный параллелограмм, не являющийся прямоугольником (рис. 145, а). Проведем его высоты 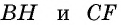 и докажем, что
и докажем, что 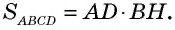 Четырехугольник
Четырехугольник 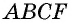 является прямоугольной трапецией, площадь которой можно вычислить двумя способами — как сумму площадей параллелограмма
является прямоугольной трапецией, площадь которой можно вычислить двумя способами — как сумму площадей параллелограмма 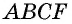 и треугольника
и треугольника 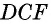 или как сумму площадей прямоугольника
или как сумму площадей прямоугольника 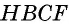 и треугольника
и треугольника 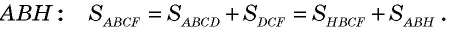 Треугольники
Треугольники 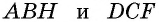 равны по гипотенузе и катету
равны по гипотенузе и катету 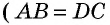 как противолежащие стороны параллелограмма,
как противолежащие стороны параллелограмма, 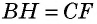 как расстояния между параллельными прямыми). Следовательно, эти треугольники имеют равные площади. Тогда площади параллелограмма
как расстояния между параллельными прямыми). Следовательно, эти треугольники имеют равные площади. Тогда площади параллелограмма 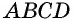 и прямоугольника
и прямоугольника 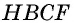 также равны, т.е.
также равны, т.е. 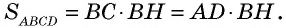 Случаи, когда точка
Случаи, когда точка 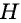 не является внутренней точкой отрезка
не является внутренней точкой отрезка  (рис. 145, б, в), рассмотрите самостоятельно.
(рис. 145, б, в), рассмотрите самостоятельно.
Пример:
Площадь параллелограмма равна  а длины его высот — 3 см и 4 см. Найдите периметр параллелограмма.
а длины его высот — 3 см и 4 см. Найдите периметр параллелограмма.
Решение:
Пусть дан параллелограмм с площадью 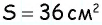 и высотами
и высотами 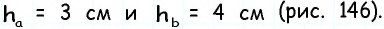 (рис. 146).
(рис. 146).
Поскольку 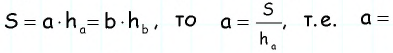
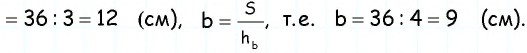
Следовательно, периметр параллелограмма равен 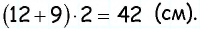
Ответ: 42 см.
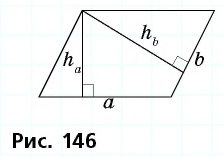
Решая приведенную задачу, можно заметить интересную закономерность: чем больше сторона параллелограмма, тем меньше проведенная к ней высота.
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
- Трапеция и ее свойства
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Четырехугольники и окружность
- Параллелограмм, его свойства и признаки
Вывод
формулы площади параллелограмма сводится
к построению прямоугольника, равного
данному параллелограмму по площади.
Примем одну сторону параллелограмма
за основание, а перпендикуляр, проведенный
из любой точки противолежащей стороны
на прямую, содержащую основание будем
называть высотой параллелограмма. Тогда
площадь параллелограмма будет равна
произведению его основания на высоту.
[4, c.
254]
Теорема.
Площадь
параллелограмма равна произведению
его основания на высоту.
Доказательство.
Рассмотрим параллелограмм
 с площадью
с площадью .
.
Примем сторону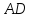 за
за
основание и проведем высоты и
и (рисунок 2.3.1). Требуется доказать, что
(рисунок 2.3.1). Требуется доказать, что .
.

Рисунок
2.3.1
Докажем
сначала, что площадь прямоугольника
 также равна
также равна .
.
Трапеция составлена из параллелограмма
составлена из параллелограмма и треугольника
и треугольника .
.
С другой стороны, она составлена из
прямоугольника НВСК и треугольника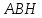 .
.
Но прямоугольные треугольники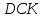 и
и
равны
по гипотенузе и острому углу (их
гипотенузы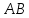 и
и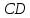 равны как противоположные стороны
равны как противоположные стороны
параллелограмма, а углы 1 и 2 равны как
соответственные углы при пересечении
параллельных прямых и
и секущей
секущей ),
),
поэтому их площади равны. Следовательно,
площади параллелограмма и прямоугольника
и прямоугольника также равны, то есть площадь прямоугольника
также равны, то есть площадь прямоугольника равна
равна .
.
По теореме о площади прямоугольника,
но так как ,
,
то .
.
Теорема
доказана.
Пример
2.3.1.
В
ромб со стороной
 и острым углом
и острым углом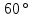
вписана окружность. Определить площадь
четырёхугольника, вершинами которого
являются точки касания окружности со
сторонами ромба.[5, c.
150]
Решение:
Радиус
вписанной в ромб
 окружности (рисунок 2.3.2)
окружности (рисунок 2.3.2) ,
,
поскольку
 Четырёхугольник
Четырёхугольник является прямоугольником, так как его
является прямоугольником, так как его
углы опираются на диаметр окружности.
Его площадь ,
,
где (катет, лежащий против угла
(катет, лежащий против угла ),
),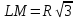 .
.
Рисунок
2.3.2
Итак,

Ответ:

Пример
2.3.2.
Дан
ромб
 ,
,
диагонали которого равны 3 см и 4 см. Из
вершины тупого угла
 проведены высоты
проведены высоты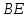 и
и Вычислить площадь четырёхугольника
Вычислить площадь четырёхугольника
Решение:
Площадь
ромба
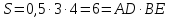
(рисунок 2.3.3).

Рисунок
2.3.3
Далее,
из
 находим
находим (см) и, следовательно,
(см) и, следовательно, (см). Тогда из
(см). Тогда из получим:
получим:
 (см).
(см).
Итак,

Ответ:

Пример
2.3.3.
Площадь
четырёхугольника равна
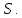
Найти площадь параллелограмма, стороны
которого равны и параллельны диагоналям
четырёхугольника.
Решение:
Так
как
 и
и (рисунок 2.3.4), то
(рисунок 2.3.4), то – параллелограмм и, значит,
– параллелограмм и, значит, .
.

Рисунок
2.3.4
Аналогично
получаем
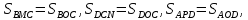 откуда следует, что
откуда следует, что .
.
Ответ:
 .
.
2.4 Площадь треугольника
Существует
несколько формул для вычисления площади
треугольника. Рассмотрим те, что изучаются
в школе.
Первая
формула вытекает из формулы площади
параллелограмма и предлагается учащимся
в виде теоремы. [4, c.
254]
Теорема.
Площадь треугольника равна половине
произведения его основания на высоту.
Доказательство.
Пусть
 – площадь треугольника
– площадь треугольника .
.
Примем сторону за основание треугольника и проведем
за основание треугольника и проведем
высоту .
.
Докажем что:
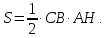

Рисунок
2.4.1
Достроим
треугольник
 до параллелограмма
до параллелограмма так, как показано на рисунке. Треугольники
так, как показано на рисунке. Треугольники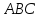 и
и равны по трем сторонам (
равны по трем сторонам ( – их общая сторона,
– их общая сторона,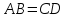 и
и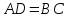 как противоположные стороны параллелограма
как противоположные стороны параллелограма ),
),
поэтому их площади равны. Следовательно,
площадь S треугольника АВС равна половине
площади параллелограмма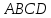 ,
,
т.е.
Теорема
доказана.
Важно
обратить внимание учащихся на два
следствия, вытекающих из данной теоремы.
А именно:
-
площадь
прямоугольного треугольника равна
половине произведения его катетов. -
если
высоты двух треугольников равны, то их
площади относятся как основания.
Эти
два следствия играют важную роль в
решении разного рода задач. С опорой на
данную доказывается еще одна теорема,
имеющая широкое применение при решении
задач.
Теорема.
Если
угол одного треугольника равен углу
другого треугольника, то их площади
относятся как произведения сторон,
заключающих равные углы.
Доказательство.
Пусть
 и
и – площади треугольников
– площади треугольников и
и ,
,
у которых углы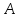 и
и равны.
равны.

Рисунок
2.4.2
Докажем,
что:
 .
.
Наложим
треугольник
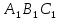 .
.
на треугольник так, чтобы вершина
так, чтобы вершина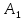 совместилась с вершиной
совместилась с вершиной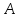 ,
,
а стороны и
и наложились соответственно на лучи
наложились соответственно на лучи и
и .
.

Рисунок
2.4.3
Треугольники
 и
и имеют общую высоту
имеют общую высоту ,
,
поэтому ,
, .
.
Треугольники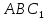 и
и также имеют общую высоту –
также имеют общую высоту – ,
,
поэтому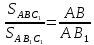 ,
, .
.
Перемножая полученные равенства, получим .
.
Теорема
доказана.
Вторая
формула. Площадь
треугольника равна половине произведения
двух его сторон на синус угла между
ними.
Существует несколько способов
доказательства этой формулы, и я
воспользуюсь одним из них.
Доказательство.
Из
геометрии известна теорема о том, что
площадь треугольника равна половине
произведения основания на высоту,
опущенную на это основание:
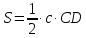 .
.
В
случае остроугольного треугольника

 .
.
В случае тупого угла
 .
.
Ho ,
,
а поэтому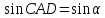 .
.
Итак, в обоих случаях .
.
Подставив вместо в геометрической формуле площади
в геометрической формуле площади
треугольника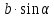 ,
,
получим тригонометрическую формулу
площади треугольника:

Теорема
доказана.
Третья
формула
для площади треугольника – формула
Герона
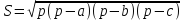 ,
,
названа так в честь древнегреческого
ученого Герона Александрийского, жившего
в первом веке нашей эры. Эта формула
позволяет находить площадь треугольника,
зная его стороны. Она удобна тем, что
позволяет не делать никаких дополнительных
построений и не измерять углов. Ее вывод
основывается на второй из рассмотренных
нами формул площади треугольника и
теореме косинусов:
и
 .
.
Далее
мы должны из второй формулы (теоремы
косинусов) выразить через
 сначала
сначала ,
,
а затем и и подставить в формулу для площади.
и подставить в формулу для площади.
Прежде
чем перейти к реализации этого плана,
заметим, что
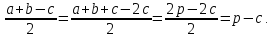
Точно
так же имеем:

Теперь
выразим косинус через
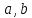 и
и :
:

Так
как любой угол в треугольнике больше
 и меньше
и меньше ,
,
то . Значит,
. Значит, .
.
Теперь
отдельно преобразуем каждый из
сомножителей в подкоренном выражении.
Имеем:


Значит,

Подставляя
это выражение в формулу для площади,
получаем:
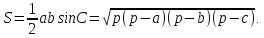
Тема
«Площадь треугольника» имеет большое
значение в школьном курсе математики.
Треугольник – простейшая из геометрических
фигур. Он является «структурным элементом»
школьной геометрии. Подавляющее
большинство геометрических задач
сводятся к решению треугольников. Не
исключение и задача о нахождении площади
правильного и произвольного
n-угольника.[6,c.238]
Пример
2.4.1.
Чему
равна площадь равнобедренного
треугольника, если его основание
 ,
,
а боковая сторона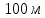 ?
?
Решение:
 –равнобедренный,
–равнобедренный,
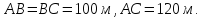

Рисунок
2.4.4
Проведём

по свойству равнобедренного треугольника
 –
–
медиана и высота. Тогда
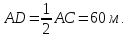
В
 по
по
теореме Пифагора:
 Находим
Находим
площадь треугольника:

Ответ:

Пример
2.4.2.
В
прямоугольном треугольнике биссектриса
острого угла делит противоположный
катет на отрезки длиной 4 и 5 см. Определить
площадь треугольника.[7, c.
78]
Решение:

Пусть
 (рисунок 2.4.5). Тогда
(рисунок 2.4.5). Тогда и
и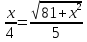 (посколькуBD
(посколькуBD
–
биссектриса). Отсюда имеем
 ,
,
то есть .
.
Значит,

Рисунок
2.4.5
Ответ:
Пример
2.4.3.
Найти
площадь равнобедренного треугольника,
если его основание равно
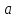 ,
,
а длина высоты, проведённой к основанию,
равна длине отрезка, соединяющего
середины основания и боковой стороны.
Решение:
По
условию,

–
средняя линия
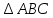 (рисунок 2.4.6). Так как
(рисунок 2.4.6). Так как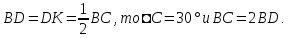 В
В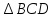 имеем:
имеем:
 или
или
 ,
,
откуда Следовательно,
Следовательно,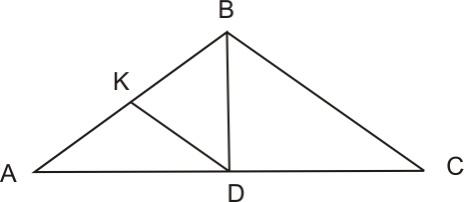
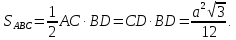
Рисунок
2.4.6
Ответ:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Урок 10. Площадь параллелограмма
Выведем формулу для вычисления площади параллелограмма.
Докажем, что площадь параллелограмма равна произведению его основания на высоту.
Одну из сторон параллелограмма будем условно называть основанием. Перпендикуляр, проведенный из любой точки противоположной стороны к прямой, содержащей основание, назовем высотой параллелограмма.
Дано:
ABCD – параллелограмм с площадью S.
AD – основание, BH и CE – высоты.
Доказать:
S = AD ∙ BH
Доказательство:
SABCE = SABCD + SCDE или SABCE = SBCEH + SABH
Треугольники CDE и ABH равны по гипотенузе и острому углу, значит
SCDE = SABH, следовательно SABCD = SBCEH
S = BC ∙ BH = AD ∙ BH
В общем виде формула для вычисления площади параллелограмма имеет вид Sпараллелограмма = ah
Ромб также является параллелограммом, поэтому площадь ромба также можно найти, перемножив основание на высоту, проведенную к этому основанию.
SABCD = BC ∙ AK = ah
-
1
-
2
Как найти площадь параллелограмма, треугольника, трапеции
Любовь Петровна Гаврилюк
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Площадь параллелограмма
Теорема 1
Площадь параллелограмма определяется как произведение длины его стороны, на высоту, проведенную к ней.
Математически это можно записать следующим образом
[S=ah]
где $a$ сторона параллелограмма, $h$ – высота, проведенная к этой стороне.
Доказательство.
Пусть нам дан параллелограмм $ABCD$, у которого $AD=BC=a$. Проведем высоты $DF$ и $AE$ (рис. 1).
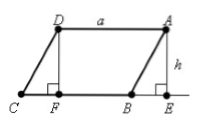
Рисунок 1.
Очевидно, что фигура $FDAE$ — прямоугольник.
[angle BAE={90}^0-angle A, ] [angle CDF=angle D-{90}^0={180}^0-angle A-{90}^0={90}^0-angle A=angle BAE]
Следовательно, так как $CD=AB, DF=AE=h$, по $I$ признаку равенства треугольников $triangle BAE=triangle CDF$. Тогда
[S_{FDAE}=S_{ABCD}-S_{CDF}+S_{BAE}=S_{ABCD}-S_{CDF}+S_{CDF}=S_{ABCD}]
Значит по теореме о площади прямоугольника:
[S_{ABCD}=S_{FDAE}=ah]
Теорема доказана.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Теорема 2
Площадь параллелограмма определяется как произведение длины его смежных сторон, на синус угла между этими сторонами.
Математически это можно записать следующим образом
[S=absinalpha ]
где $a, b$ стороны параллелограмма, $alpha $ — угол между ними.
Доказательство.
Пусть нам дан параллелограмм $ABCD$, у которого $BC=a, CD=b, angle C=alpha $. Проведем высоту $DF=h$ (рис. 2).
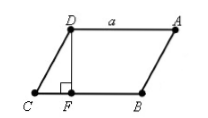
Рисунок 2.
По определению синуса, получим
[sinalpha =frac{DF}{CD}=frac{h}{b}]
Следовательно
[h=bsinalpha ]
Значит, по теореме $1$:
[S=ah=absinalpha ]
Теорема доказана.
Площадь треугольника
Теорема 3
Площадь треугольника определяется как половина произведения длины его стороны, на высоту, проведенную к ней.
Математически это можно записать следующим образом
[S=frac{1}{2}ah]
где $a$ сторона треугольника, $h$ – высота, проведенная к этой стороне.
Доказательство.
Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).
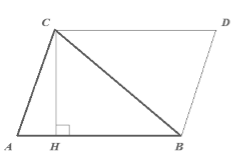
Рисунок 3.
Очевидно, что по $I$ признаку равенства треугольников $triangle ACB=triangle CDB$. Тогда
[S_{ABC}=frac{1}{2}S_{ABCD}]
Значит по теореме $1$:
[S_{ABC}=frac{1}{2}ah]
Теорема доказана.
«Как найти площадь параллелограмма, треугольника, трапеции» 👇
Теорема 4
Площадь треугольника определяется как половина произведения длины его смежных сторон, на синус угла между этими сторонами.
Математически это можно записать следующим образом
[S=frac{1}{2}absinalpha ]
где $a, b$ стороны треугольника, $alpha $ — угол между ними.
Доказательство.
Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).
Очевидно, что по $I$ признаку равенства треугольников $triangle ACB=triangle CDB$. Тогда
[S_{ABC}=frac{1}{2}S_{ABCD}]
Значит по теореме $1$:
[S_{ABC}=frac{1}{2}absinalpha ]
Теорема доказана.
Площадь трапеции
Теорема 5
Площадь трапеции определяется как половина произведения суммы длин его оснований, на его высоту.
Математически это можно записать следующим образом
[S=frac{1}{2}(a+b)h]
Доказательство.
Пусть нам дана трапеция $ABCK$, где $AK=a, BC=b$. Проведем в ней высоты $BM=h$ и $KP=h$, а также диагональ $BK$ (рис. 4).
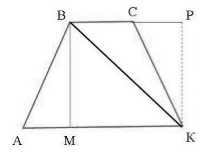
Рисунок 4.
[S_{ABCK}=S_{ABK}+S_{BCK}]
По теореме $3$, получим
[S_{ABK}=frac{1}{2}AKcdot BM=frac{1}{2}ah, S_{BCK}=frac{1}{2}BCcdot KP=frac{1}{2}bh]
Тогда
[S_{ABCK}=frac{1}{2}ah+frac{1}{2}bh=frac{1}{2}(a+b)h]
Теорема доказана.
Пример задачи
Пример 1
Найти площадь равностороннего треугольника, если длина его стороны равняется $a.$
Решение.
Так как треугольник равносторонний, то все его углы равняются ${60}^0$.
Тогда, по теореме $4$, имеем
[S=frac{1}{2}acdot acdot sin{60}^0=frac{a^2sqrt{3}}{4}]
Ответ: $frac{a^2sqrt{3}}{4}$.
Заметим, что результат этой задачи можно применять при нахождении площади любого равностороннего треугольника с данной стороной.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 19.05.2023

