Как найти стороны прямоугольного треугольника
Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
следовательно: c = √ a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √ 5² – 4² = √ 25 – 16 = √ 9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
Как с помощью тангенса найти сторону треугольника. Теорема Пифагора, чтобы найти катет прямоугольного треугольника
В жизни нам часто придется сталкиваться с математическими задачами: в школе, в университете, а затем помогая своему ребенку с выполнением домашнего задания. Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.
Что такое прямоугольный треугольник
Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник – это геометрическая фигура из трех отрезков, которые соединяют точки, не лежащие на одной прямой, и один из углов этой фигуры равен 90 градусам. Стороны, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла – гипотенузой.
Находим катет прямоугольного треугольника
Существует несколько способов, позволяющих узнать длину катета. Хотелось бы рассмотреть бы их подробнее.
Теорема Пифагора, чтобы найти катет прямоугольного треугольника
Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора. Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².
Пример. Гипотенуза равна 5 см, а катет – 3 см. Преобразовываем формулу: c²=a²+b² → a²=c²-b². Далее решаем: a²=5²-3²; a²=25-9; a²=16; a=√16; a=4 (см).


Тригонометрические соотношения, чтобы найти катет прямоугольного треугольника
Также можно найти неизвестный катет, если известны любая другая сторона и любой острый угол прямоугольного треугольника. Есть четыре варианта нахождения катета при помощи тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу. Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.


Найти катет прямоугольного треугольника при помощи синуса
Синус угла (sin) – это отношение противолежащего катета к гипотенузе. Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.
Пример. Гипотенуза равна 10 см, угол А равен 30 градусов. По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).


Найти катет прямоугольного треугольника при помощи косинуса
Косинус угла (cos) – это отношение прилежащего катета к гипотенузе. Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза. Преобразуем формулу и получим: b=cos*c.
Пример. Угол А равен 60 градусов, гипотенуза равна 10 см. По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).


Найти катет прямоугольного треугольника при помощи тангенса
Тангенс угла (tg) – это отношение противолежащего катета к прилежащему. Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b.
Пример. Угол А равен 45 градусов, гипотенуза равна 10 см. По таблице вычисляем тангенс угла А, он равен Решаем: a=tg∠A*b; a=1*10; a=10 (см).


Найти катет прямоугольного треугольника при помощи котангенса
Котангенс угла (ctg) – это отношение прилежащего катета к противолежащему. Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.
Пример. Угол А равен 30 градусов, противолежащий катет равен 5 см. По таблице тангенс угла А равен √3. Вычисляем: b=ctg∠A*a; b=√3*5; b=5√3 (см).


Итак, теперь вы знаете, как находить катет в прямоугольном треугольнике. Как видите, это не так уж и сложно, главное – запомнить формулы.
Сторону треугольника дозволено обнаружить не только по периметру и площади, но и по заданной стороне и углам. Для этого применяются тригонометрические функции – синус и косинус . Задачи с их применением встречаются в школьном курсе геометрии, а также в вузовском курсе аналитической геометрии и линейной алгебры.
Инструкция
1. Если знаменита одна из сторон треугольника и угол между ней и иной его стороной, воспользуйтесь тригонометрическими функциями – синус ом и косинус ом. Представьте себе прямоугольный треугольник НBC , у которого угол? равен 60 градусам. Треугольник НBC показан на рисунке. От того что синус , как знаменито, представляет собой отношение противолежащего катета к гипотенузе, а косинус – отношение прилежащего катета к гипотенузе, для решения поставленной задачи воспользуйтесь дальнейшим соотношением между этими параметрами:sin ?=НB/BCСоответственно, если вы хотите узнать катет прямоугольного треугольника, выразите его через гипотенузу дальнейшим образом:НB=BC*sin ?
2. Если в условии задачи, напротив, дан катет треугольника, обнаружьте его гипотенузу, руководствуясь дальнейшим соотношением между заданными величинами:BC=НB/sin ?По аналогии обнаружьте стороны треугольника и с применением косинус а, изменив предыдущее выражение дальнейшим образом:cos ?=НC/BC
3. В элементарной математике существует представление теоремы синус ов. Руководствуясь фактами, которые описывает данная теорема, также дозволено обнаружить стороны треугольника. Помимо этого, она разрешает обнаружить стороны треугольника, вписанного в окружность, если знаменит вестим радиус последней. Для этого воспользуйтесь соотношением, указанным ниже:a/sin ?=b/sin b=c/sin y=2RЭта теорема применима в том случае, когда знамениты две стороны и угол треугольника, либо дан один из углов треугольника и радиус описанной вокруг него окружности.
4. Помимо теоремы синус ов, существует и аналогичная ей по сути теорема косинус ов, которая, как и предыдущая, также применима к треугольникам всех 3 разновидностей: прямоугольному, остроугольному и тупоугольному. Руководствуясь фактами, которые доказывают эта теорема, дозволено находить неведомые величины, применяя следующие соотношения между ними:c^2=a^2+b^2-2ab*cos ?
Геометрическая фигура, состоящая из трёх точек, не принадлежащих одной прямой называемых вершинами, и трёх попарно соединяющих их отрезков, называемых сторонами, именуется треугольником. Существует уйма задач на нахождение сторон и углов треугольника по ограниченному числу начальных данных, одна из таких задач – нахождение стороны треугольника по одной из его сторон и двум углам .

Инструкция
1. Пускай построен треугольник?ABC и знамениты – сторона BC и углы?? и. Знаменито, что сумма углов всякого треугольника равна 180?, следственно в треугольнике?ABC угол?? будет равен?? = 180? – (?? + ??).Обнаружить стороны AC и AB дозволено применяя теорему синусов, которая гласитAB/sin?? = BC/sin?? = AC/sin?? = 2 * R, где R – радиус описанной около треугольника?ABC окружности,тогда получаемR = BC/sin. AB = 2 * R * sin. AC = 2 * R * sin. Теорему синусов дозволено использовать при всяких данных 2-х углах и стороне.

2. Стороны заданно треугольника дозволено обнаружить, вычислив его площадь по формулеS = 2 * R? * sin?? * sin?? * sin. где R вычисляется по формулеR = BC/sin. R – радиус описанной около треугольника?ABC отсюдаТогда сторону AB дозволено обнаружить, вычислив высоту, опущенную на неёh = BC * sin. отсель по формуле S = 1/2 * h * AB имеемAB = 2 * S/hАналогичным образом дозволено вычислить сторону AC.

3. Если в качестве углов даны внешние углы треугольника?? и. то обнаружить внутренние углы дозволено с поддержкой соответствующих соотношений?? = 180? – . = 180? – . = 180? – (?? + ??).Дальше действуем подобно первым двум пунктам.

Постижение треугольников ведется математиками на протяжении нескольких тысячелетий. Наука о треугольниках – тригонометрия – использует особые величины: синус и косинус.

Прямоугольный треугольник
Изначально синус и косинус появились из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было подмечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается неизменно идентичным.Именно так и были введены представления синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы могут использоваться не только в прямоугольных треугольниках. Дабы обнаружить значение тупого либо острого угла, стороны всякого треугольника, довольно применить теорему косинусов и синусов.Теорема косинусов достаточно примитивна: «Квадрат стороны треугольника равен сумме квадратов 2-х других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними». Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему зачастую расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Производные
Производная – математический инструмент, показывающий, как стремительно меняется функция касательно метаморфозы ее довода. Производные применяются в алгебре, геометрии, экономике и физике, ряде технических дисциплин. При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса. Производной синуса является косинус, а косинуса – синус, но со знаком «минус».
Применение в математике
Особенно зачастую синусы и косинусы применяются при решении прямоугольных треугольников и задач, связанных с ними. Удобство синусов и косинусов обнаружило свое отражение и в технике. Углы и стороны было примитивно оценивать по теоремам косинусов и синусов, разбивая трудные фигуры и объекты на «примитивные» треугольники. Инженеры и архитекторы, зачастую имеющие дело с расчетами соотношения сторон и градусных мер, тратили много времени и усилий для вычисления косинусов и синусов не табличных углов. Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов различных углов. В советское время некоторые преподаватели принуждали своих подопечных учить страницы таблиц Брадиса назубок.
Площадь треугольника равна половине произведения его сторон на синус угла между ними.
Рассмотрим произвольный треугольник ABC. Пусть в нем сторона BC = a, сторона CA = b и S – площадь этого треугольника. Необходимо доказать, что S = (1/2)*a*b*sin(C) .
Для начала введем прямоугольную систему координат и поместим начало координат в точку С. Расположим нашу систему координат так, чтобы точка B лежала на положительном направлении оси Сх, а точка А имела бы положительную ординату.
Если все выполнить правильно, то должен получится следующий рисунок.
Площадь данного треугольника можно вычислить по следующей формуле: S = (1/2)*a*h , где h – это высота треугольника. В нашем случае высота треугольника h равна ординате точки А, то есть h = b*sin(C).
Учитывая полученные результат, формулу площади треугольника можно переписать следующим образом: S = (1/2)*a*b*sin(C). Что и требовалось доказать.
Решение задач
Задача 1. Найти площадь треугольника ABC, если а) AB = 6*√8 см, АС = 4 см, угол А = 60 градусов б) BC = 3 см, AB = 18*√2 см, угол B= 45 градусов в) AC = 14 см, CB = 7 см, угол C= 48 градусов.
По доказанной выше теореме площадь S треугольника ABC равна:
а) S = ((1/2) *6*√8*4*sin(60˚)) = 12*√6 см^2.
б) S = (1/2)*BC*BA*sin(B)=((1/2)* 3*18*√2 *(√2/2)) = 27 см^2.
в) S = (1/2)*CA*CB*sin(C) = ½*14*7*sin48˚ см^2.
Значение синуса угла считаем на калькуляторе либо используем значения из таблицы значений тригонометрических углов. Ответ:
в) приблизительно 36.41 см^2.
Задача 2. Площадь треугольника ABC равна 60 см^2. Найдите сторону AB, если AC = 15 см, угол А = 30˚.
Положим S – площадь треугольника ABC. По теореме о площади треугольника имеем:
Подставим в неё имеющиеся у нас значения:
60 = (1/2)*AB*15*sin30˚ = (1/2)*15*(1/2)*AB=(15/4)*AB.
Отсюда выражаем длину стороны AB: AB = (60*4)/15 = 16.
Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Игры с линейкой и карандашом
Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону – гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.
Найти синус для угла больше 90°
Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.

Вычисление синуса по другим тригонометрическим функциям
Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.

Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.

Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс – функция, обратная тангенсу относительно числа 1. Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.

Как находить синус по трём сторонам треугольника
Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.

Ну, а синус можно далее рассчитать по косинусу согласно формулам выше.
Если в задаче даны длины двух сторон треугольника и угол между ними, то можно применить формулу площади треугольника через синус.

Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По синус угла в 30° равен 0.5
Площадь треугольника будет равна 3 кв. см.
Также могут быть и другие условия. Если дана длина одной стороны и углы, то для начала нужно вычислить недостающий угол. Т.к. сумма всех углов треугольника равняется 180°, то: 
Площадь будет равна половине квадрата стороны, умноженной на дробь. В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:

Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол: 
Подставляем данные в формулу
Получаем, что площадь треугольника равняется 3,87 кв. см.
II. Площадь треугольника через косинус
Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти не известные стороны, а уже потом использовать .
По теореме косинусов квадрат неизвестной стороны треугольника равняется сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла, находящегося между ними.
Из теоремы выводим формулы для поиска длины неизвестной стороны:

Зная как найти недостающую сторону, имея две стороны и угол между ними можно легко посчитать площадь. Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.
Пример расчета формулы площади треугольника через косинус
Дан треугольник с известными сторонами a = 3, b = 4, и углом γ= 45°. Для начала найдем недостающую сторону с . По косинус 45°=0,7. Для этого подставим данные в уравнение, выведенное из теоремы косинусов.
Теперь используя формулу, найдем
Понравилось?
Нажмите на кнопку, если статья Вам понравилась, это поможет нам развивать проект. Спасибо!
Треугольник. Расчет сторон прямоугольного треугольника через тригонометрические функции.
Проанализируем прямоугольный треугольник ABC в котором обозначим катеты как а, b и гипотенузу как с соответственно.
Вполне логично сделать вывод, будут верны следующие равенства:
Значит катет прямоугольного треугольника допускается представить как произведение гипотенузы и синуса угла, противолежащего этому катету, либо и косинуса угла, прилежащего к нему.
На основе этих соотношений так же можно определить гипотенузу прямоугольного треугольника:
Иначе говоря, гипотенуза будет частным от деления катета либо на синус противолежащего к нему угла, либо на косинус прилежащего к катету угла.
Значит, катет прямоугольного треугольника допускается представить как произведением другого катета на тангенс угла, противолежащего первому катету, либо на котангенс угла, прилежащего к первому катету.
[spoiler title=”источники:”]
http://school10-mgn.ru/kak-s-pomoshchyu-tangensa-naiti-storonu-treugolnika-teorema-pifagora.html
http://www.calc.ru/Treugolnik-Raschet-Storon-Pryamougolnogo-Treugolnika-Cherez-.html
[/spoiler]
Содержание:
Пусть в прямоугольном треугольнике гипотенуза равна с, один из острых углов равен 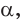
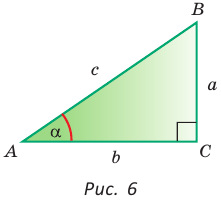
Определения синуса, косинуса, тангенса и котангенса острого угла
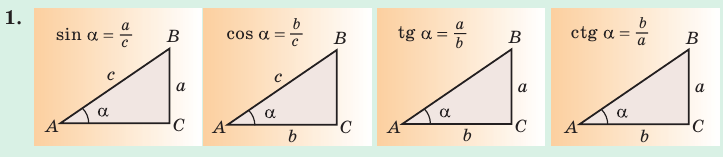
Определение. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
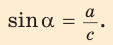
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
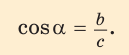
Определение. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:
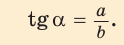
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:
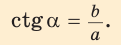
Пример:
Угол К в  равен 90° (рис. 7).
равен 90° (рис. 7).
Тогда:
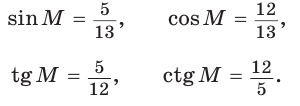
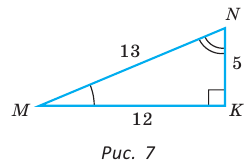
Для угла N катет МК — противолежащий, а катет NK — прилежащий (см. рис. 7, с. 11). Поэтому согласно определениям получаем:
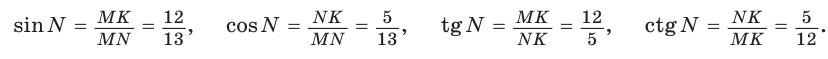
Можно заметить, что синус острого угла а прямоугольного треугольника и косинус другого острого угла этого треугольника, содержащего 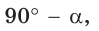 равны, т. е.
равны, т. е. 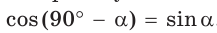 . Так же
. Так же 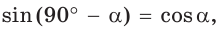
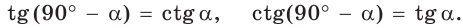 Например,
Например, 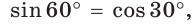
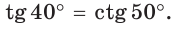
А теперь выполните Тест 1 и Тест 2.
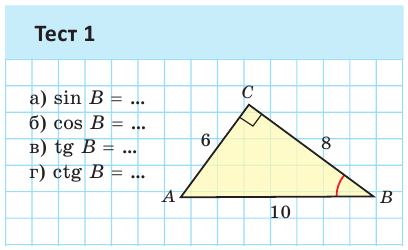
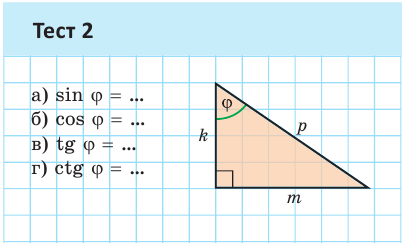
Значение синуса острого угла, а также косинуса, тангенса и котангенса зависит только от величины угла и не зависит от размеров и расположения прямоугольного треугольника с указанным острым углом.
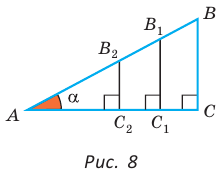
Это следует из того, что прямоугольные треугольники с равным острым углом подобны, а у подобных треугольников соответствующие стороны пропорциональны. Так, в  (рис. 8)
(рис. 8) 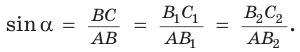
Значения синуса, косинуса, тангенса и котангенса углов 30°, 45°, 60°
Рассмотрим прямоугольный треугольник АВС, у которого 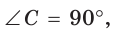
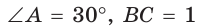 (рис. 9). Так как катет, лежащий против угла в 30°, равен половине гипотенузы, то АВ = 2. По теореме Пифагора
(рис. 9). Так как катет, лежащий против угла в 30°, равен половине гипотенузы, то АВ = 2. По теореме Пифагора
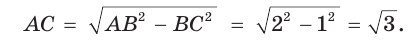 Тогда:
Тогда:
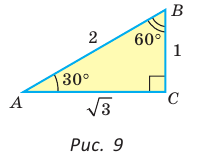
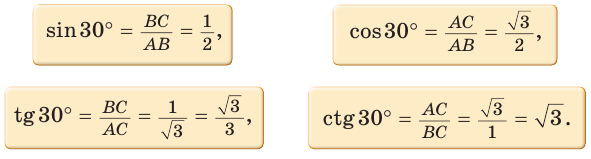
Так как  (см. рис. 9), то
(см. рис. 9), то

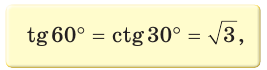
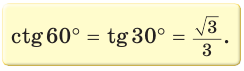
Рассмотрим равнобедренный прямоугольный треугольник АВС, у которого 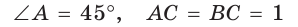 (рис. 10). По теореме Пифагора
(рис. 10). По теореме Пифагора
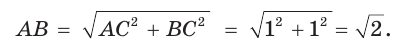
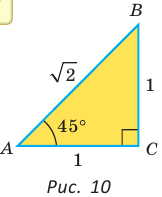
Тогда:
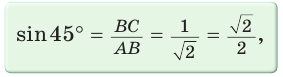
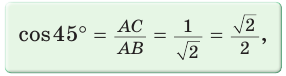
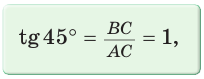
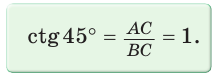
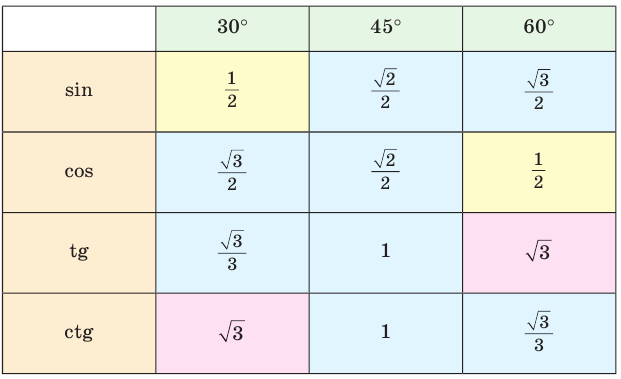
Составим таблицу значений синусов, косинусов, тангенсов и котангенсов для углов 30°, 45° и 60°.
Нахождение значений тригонометрических функций
Значения синуса, косинуса, тангенса и котангенса данного угла можно приближенно находить при помощи специальных тригонометрических таблиц* либо калькулятора.
Например, с помощью калькулятора, компьютера или мобильного телефона (смартфона) находим: sin45° = 0,707106… . Приближенное значение тригонометрических функций при решении задач будем брать с округлением до четырех знаков после запятой: sin45° = 0,7071.
Итак, точное значение sin 45° равно 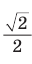 . а приближенное — 0,7071.
. а приближенное — 0,7071.
Таблицы и калькулятор также позволяют находить величину острого угла по значению синуса, косинуса или тангенса. Например, найдем острый угол, синус которого равен 0,4175. Выбрав на компьютере вид калькулятора «инженерный», далее «градусы», нужно ввести последовательно  . На экране появится ответ: 24,676… . Округлим его до десятых долей градуса и получим 24,7°. Учитывая, что 1° содержит 60 угловых минут, получим: 0,7° = 0,7 • 60′ = 42′. Искомый угол, синус которого 0,4175, приближенно равен 24°42′.
. На экране появится ответ: 24,676… . Округлим его до десятых долей градуса и получим 24,7°. Учитывая, что 1° содержит 60 угловых минут, получим: 0,7° = 0,7 • 60′ = 42′. Искомый угол, синус которого 0,4175, приближенно равен 24°42′.
А теперь выполните Тест 3.

Тригонометрические функции острого угла
Синус, косинус, тангенс и котангенс являются функциями угла, так как каждому острому углу 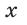 соответствует единственное значение синуса, косинуса, тангенса и котангенса. Они называются тригонометрическими функциями и записываются так:
соответствует единственное значение синуса, косинуса, тангенса и котангенса. Они называются тригонометрическими функциями и записываются так: 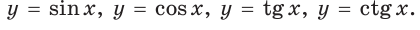
Поскольку в прямоугольном треугольнике катет меньше гипотенузы, то для острого угла 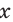 справедливо:
справедливо: 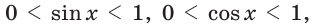 следовательно синус и косинус острого угла положительны и меньше 1.
следовательно синус и косинус острого угла положительны и меньше 1.
Тангенс и котангенс острого угла могут принимать любое положительное значение. Например, tg85° ~ 11,4.
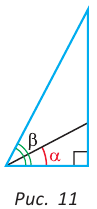
С увеличением острого угла синус и тангенс возрастают, а косинус и котангенс убывают (рис. 11), то есть если 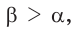 то
то
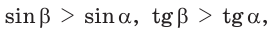 но
но 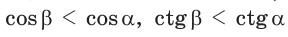 (cm. c. 28, задачу 2*). Это гарантирует, что синус (косинус, тангенс и котангенс) острого угла определяют этот угол однозначно.
(cm. c. 28, задачу 2*). Это гарантирует, что синус (косинус, тангенс и котангенс) острого угла определяют этот угол однозначно.
Пример №1
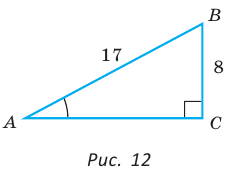
В прямоугольном треугольнике АВС, где 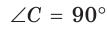 , катет ВС равен 8 см, гипотенуза АВ равна 17 см. Найти косинус угла А (рис. 12).
, катет ВС равен 8 см, гипотенуза АВ равна 17 см. Найти косинус угла А (рис. 12).
Решение:
По теореме Пифагора найдем катет 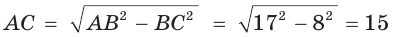 (см). Косинус острого угла прямоугольного треугольника равен от ношению прилежащего катета к гипотенузе. Тогда
(см). Косинус острого угла прямоугольного треугольника равен от ношению прилежащего катета к гипотенузе. Тогда 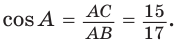
Ответ: 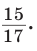
Пример №2
Гипотенуза АВ прямоугольного треугольника АВС равна 20 см, 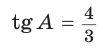 (рис. 13). Найти площадь треугольника.
(рис. 13). Найти площадь треугольника.
Решение:
Так как 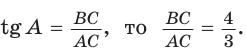 Обозначим
Обозначим 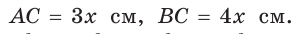 По теореме Пифагора
По теореме Пифагора 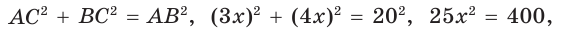
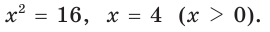 Тогда
Тогда 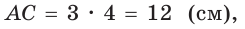 ВС = 4 • 4 = 16(см),
ВС = 4 • 4 = 16(см), 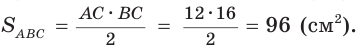
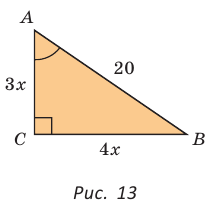
Ответ: 96 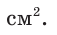
Пример №3
При помощи циркуля и линейки построить угол, синус которого равен 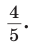
Решение:
Идея решения. Построим прямоугольный треугольник с катетом, равным 4 единицы, и гипотенузой, равной 5 единиц. Синус угла, противолежащего указанному катету, будет равен 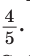
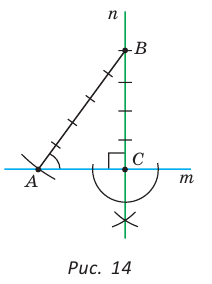
Построение. 1) Строим прямой угол С (рис. 14), для чего проводим произвольную прямую 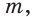 отмечаем на ней точку С и строим прямую
отмечаем на ней точку С и строим прямую 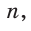 проходящую через точку С перпендикулярно прямой
проходящую через точку С перпендикулярно прямой 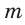 (вспомните по рисунку алгоритм построения). 2) На прямой
(вспомните по рисунку алгоритм построения). 2) На прямой 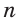 от точки С откладываем последовательно четыре равных отрезка. Получаем отрезок ВС, который содержит 4 единицы. 3) Строим окружность с центром в точке В радиусом, равным пяти единицам. В пересечении этой окружности и прямой
от точки С откладываем последовательно четыре равных отрезка. Получаем отрезок ВС, который содержит 4 единицы. 3) Строим окружность с центром в точке В радиусом, равным пяти единицам. В пересечении этой окружности и прямой 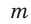 получаем точку А.
получаем точку А.
Угол ВАС — искомый.
Доказательство:
Из 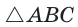 находим
находим 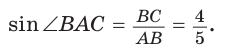
Алгоритм решения прямоугольного треугольника
Под решением прямоугольного треугольника понимают нахождение его неизвестных сторон и углов по некоторым элементам, определяющим этот треугольник. Рассмотрим три задачи:
- нахождение катета по гипотенузе и острому углу;
- нахождение катета по другому катету и острому углу;
- нахождение гипотенузы по катету и острому углу.
Пример №4
Гипотенуза прямоугольного треугольника равна 6, острый угол равен 32° (рис. 23). Найти катет, прилежащий к данному углу. Ответ округлить до 0,1.
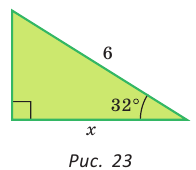
Решение:
Примем длину искомого катета за 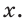
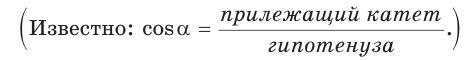
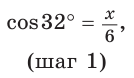


Ответ: 5,1.
Пример №5
Катет прямоугольного треугольника равен 2,5, а прилежащий к нему угол равен 68° (рис. 24). Найти другой катет. Ответ округлить до 0,1.
Решение:
Примем длину неизвестного катета за 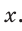
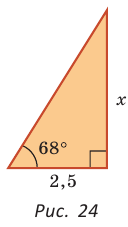
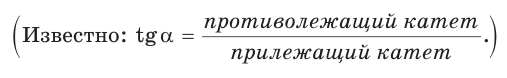
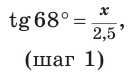
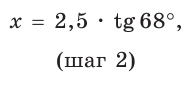

Ответ: 6,2.
Пример №6
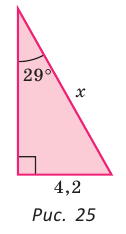
Катет прямоугольного треугольника равен 4,2, противолежащий ему угол равен 29° (рис. 25). Найти гипотенузу треугольника. Ответ округлить до 0,1.
Решение:
Примем длину гипотенузы за 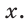
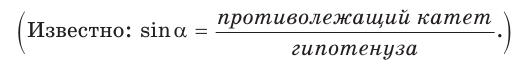
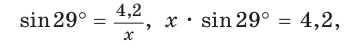
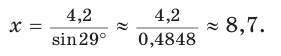
Ответ: 8,7.
Правила решения прямоугольного треугольника
Преобразуем формулы синуса, косинуса, тангенса и котангенса и запишем результаты для треугольника на рисунке 26:
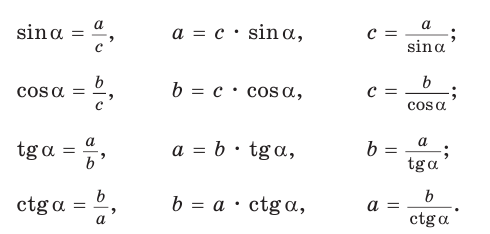
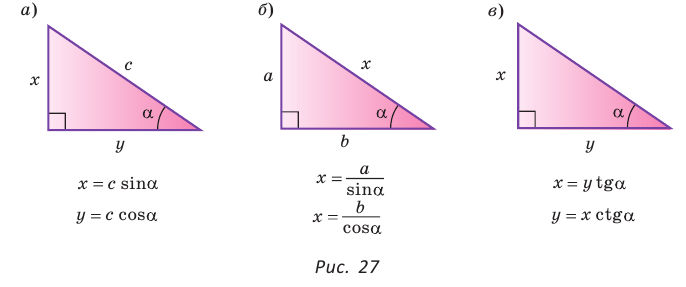
Удобно пользоваться следующими правилами:
- Катет равен гипотенузе, умноженной на синус противолежащего или на косинус прилежащего угла (рис. 27, а).
- Гипотенуза равна катету, деленному на синус противолежащего или на косинус прилежащего угла (рис. 27, б).
- Катет равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к первому катету угла (рис. 27, в).
Пример №7
В 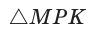 известно:
известно: 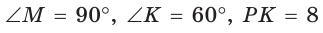 (рис. 28).
(рис. 28).
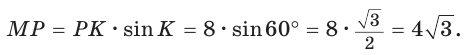
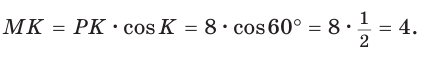
Полезно запомнить!
Если в прямоугольном треугольнике с углом 30° (или 60°) дан меньший катет а, то больший
катет 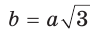 (рис. 29, а). А если дан больший катет
(рис. 29, а). А если дан больший катет 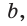 то меньший катет
то меньший катет 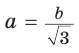 (рис. 29, б).
(рис. 29, б).
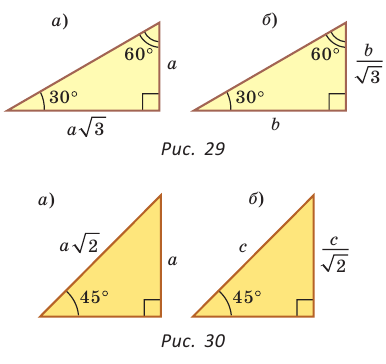
Если в прямоугольном треугольнике с углом 45° дан катет а,
то гипотенуза 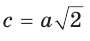 (рис. 30, а), а если дана гипотенуза с, то катет
(рис. 30, а), а если дана гипотенуза с, то катет 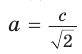 (рис. 30, б).
(рис. 30, б).
Пример №8
В прямоугольном треугольнике АВС известно: 
 — высота, проведенная к гипотенузе (рис. 31). Найти проекцию НВ катета ВС на гипотенузу.
— высота, проведенная к гипотенузе (рис. 31). Найти проекцию НВ катета ВС на гипотенузу.
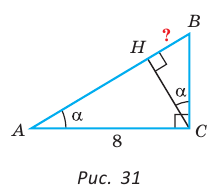
Решение:
Заметим, что  так как эти углы дополняют
так как эти углы дополняют  Из
Из 
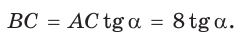 Из
Из 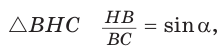
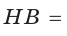
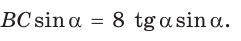
Ответ: 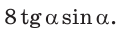
Пример №9
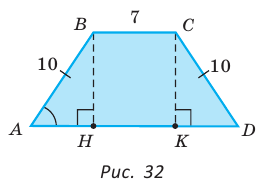
В равнобедренной трапеции ABCD меньшее основание ВС равно 7, боковая сторона АВ равна 10, sinA = 0,8. Найти площадь трапеции.
Решение:
Площадь трапеции находится по формуле 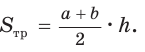 Найдем большее основание и высоту трапеции. Проведем в трапеции высоты ВН и СК (рис. 32). Так как НВСК — прямоугольник (все углы — прямые), то НК = ВС = 7. Из равенства прямоугольных треугольников АНВ и DKC (по катету и гипотенузе) АН = KD. Из прямоугольного треугольника АНВ находим:
Найдем большее основание и высоту трапеции. Проведем в трапеции высоты ВН и СК (рис. 32). Так как НВСК — прямоугольник (все углы — прямые), то НК = ВС = 7. Из равенства прямоугольных треугольников АНВ и DKC (по катету и гипотенузе) АН = KD. Из прямоугольного треугольника АНВ находим: 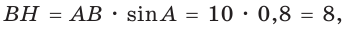 откуда АН = 6 (пифагорова тройка 6, 8, 10). Тогда
откуда АН = 6 (пифагорова тройка 6, 8, 10). Тогда 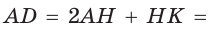
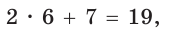
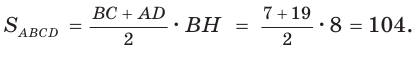
Ответ: 104.
Тригонометрические формулы
Используя формулы 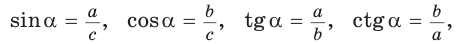 где
где 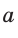 и
и 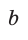 — катеты, с — гипотенуза прямоугольного треугольника, можно получить формулы, связывающие значения тригонометрических функций острого угла.
— катеты, с — гипотенуза прямоугольного треугольника, можно получить формулы, связывающие значения тригонометрических функций острого угла.
1. Основное тригонометрическое тождество
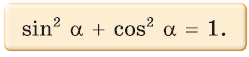
Доказательство:
По теореме Пифагора 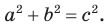
Тогда 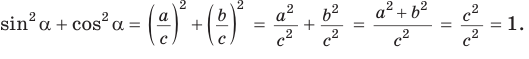
Следствие:
Так как синус и косинус острого угла а положительны, то
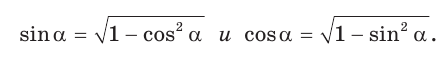
2. Выражение тангенса и котангенса через синус и косинус
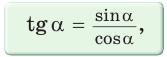
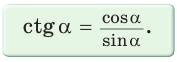
Доказательство:
a)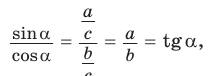 б)
б)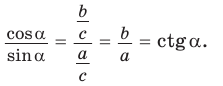
Следствие:
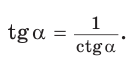
Проверим справедливость основного тригонометрического тождества.
Верно ли, например, что 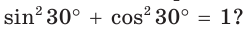 Да, это верно, так как
Да, это верно, так как 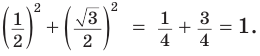
3. Основная задача
Дано: 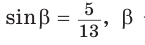 — острый угол.
— острый угол.
Найти: 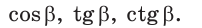
Решение:
Способ 1. Используем основное тригонометрическое тождество: 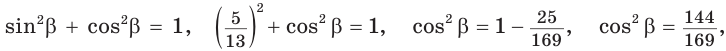
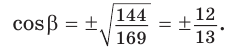 Так как косинус острого угла больше нуля, то
Так как косинус острого угла больше нуля, то 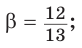 откуда
откуда 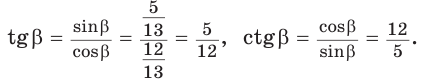
Способ 2. Изобразим прямоугольный треугольник с катетом 5 и гипотенузой 13 (рис. 41). Синус угла, противолежащего данному катету, равен 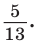 Поэтому этот угол равен
Поэтому этот угол равен 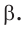 По теореме Пифагора другой катет равен
По теореме Пифагора другой катет равен 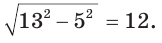 Тогда
Тогда 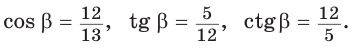
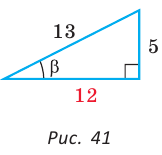
Способ 3. Пусть катет, противолежащий углу 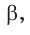 равен 5х, тогда гипотенуза равна
равен 5х, тогда гипотенуза равна 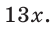 По теореме Пифагора прилежащий катет равен
По теореме Пифагора прилежащий катет равен 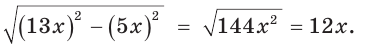 Отсюда
Отсюда 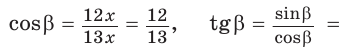
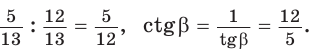
Ответ: 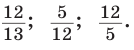
Пример №10
В параллелограмме ABCD (рис. 42) сторона ВС = 50 см, высота ВК = 30 см, 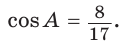 . Найти периметр параллелограмма.
. Найти периметр параллелограмма.
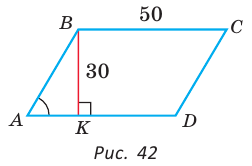
Решение:
Из треугольника АВК находим: 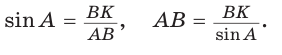 Из основного тригонометрического тождества следует:
Из основного тригонометрического тождества следует: 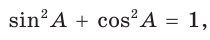
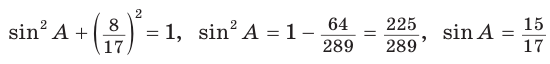 (так как угол А — острый, то sinA > 0). Тогда
(так как угол А — острый, то sinA > 0). Тогда 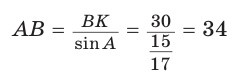 (см )
(см ) 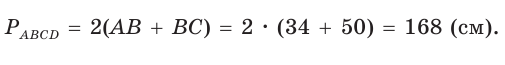
Ответ: 168 см.
Пример №11
Доказать, что при увеличении угла от 0° до 90°:
а) синус угла увеличивается от 0 до 1, а косинус — уменьшается от 1 до 0;
б) тангенс угла увеличивается от О до бесконечности.
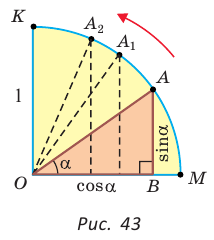
Решение:
а) Рассмотрим прямоугольные треугольники с гипотенузой, равной 1. Для этого опишем радиусом ОМ, равным 1, четверть окружности — дугу МК (рис. 43). Пусть  Опустим из точки А перпендикуляр АВ на ОМ. Тогда
Опустим из точки А перпендикуляр АВ на ОМ. Тогда 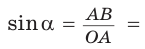
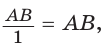
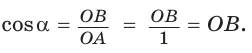 При повороте радиуса ОМ вокруг центра О против часовой стрелки, начиная от ОМ и заканчивая ОК, угол
При повороте радиуса ОМ вокруг центра О против часовой стрелки, начиная от ОМ и заканчивая ОК, угол 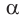 будет увеличиваться от 0° до 90° (образуя указанные на чертеже углы:
будет увеличиваться от 0° до 90° (образуя указанные на чертеже углы: 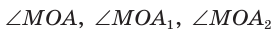 и т. д.). Величина катета АВ, противолежащего углу
и т. д.). Величина катета АВ, противолежащего углу 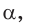 будет увеличиваться от 0 до 1. А величина катета ОВ, наоборот, будет уменьшаться от 1 до 0. Таким образом, при увеличении угла от 0° до 90° его синус увеличивается от 0 до 1, а косинус уменьшается от 1 до 0.
будет увеличиваться от 0 до 1. А величина катета ОВ, наоборот, будет уменьшаться от 1 до 0. Таким образом, при увеличении угла от 0° до 90° его синус увеличивается от 0 до 1, а косинус уменьшается от 1 до 0.
Из формулы 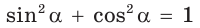 также следует (учитывая положительность синуса и косинуса острого угла), что с увеличением синуса от 0 до 1 косинус уменьшается от 1 до 0.
также следует (учитывая положительность синуса и косинуса острого угла), что с увеличением синуса от 0 до 1 косинус уменьшается от 1 до 0.
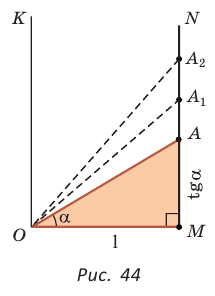
б) Для определения изменения тангенса угла удобно рассматривать треугольники, у которых прилежащий катет не изменяется и остается равным 1, а противолежащий катет изменяется. Рассмотрим прямоугольный треугольник АОМ, у которого отрезок ОМ = 1, 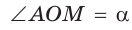 (рис. 44). По определению
(рис. 44). По определению 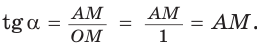 Угол
Угол 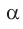 станем изменять, перемещая точку А по прямой MN, начиная от точки М и проходя через точки
станем изменять, перемещая точку А по прямой MN, начиная от точки М и проходя через точки 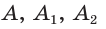 и т. д. При этом угол
и т. д. При этом угол 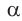 и его тангенс начнут возрастать. Таким образом, когда угол
и его тангенс начнут возрастать. Таким образом, когда угол 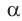 при движении точки А вверх будет стремиться к углу КОМ, равному 90°, то тангенс этого угла будет неограниченно возрастать.
при движении точки А вверх будет стремиться к углу КОМ, равному 90°, то тангенс этого угла будет неограниченно возрастать.
К такому же выводу можно прийти, рассматривая формулу 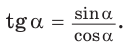 При увеличении угла
При увеличении угла  от 0° до 90° числитель дроби будет увеличиваться от 0 до 1, а знаменатель — уменьшаться от 1 до 0, значит, вся дробь будет увеличиваться от 0 до бесконечности. Таким образом, при увеличении угла от 0° до 90° его тангенс увеличивается от 0 до бесконечности.
от 0° до 90° числитель дроби будет увеличиваться от 0 до 1, а знаменатель — уменьшаться от 1 до 0, значит, вся дробь будет увеличиваться от 0 до бесконечности. Таким образом, при увеличении угла от 0° до 90° его тангенс увеличивается от 0 до бесконечности.
Пример №12
В основании прямоугольного параллелепипеда  лежит квадрат, диагональ которого
лежит квадрат, диагональ которого 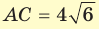 см. Диагональ
см. Диагональ 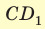 боковой грани составляет с ребром основания
боковой грани составляет с ребром основания 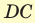 угол
угол  (рис. 46). Найдите объем параллелепипеда.
(рис. 46). Найдите объем параллелепипеда.
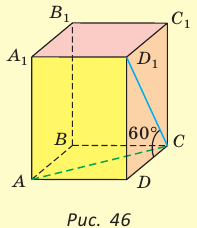
Решение:
Объем прямоугольного параллелепипеда находится по формуле 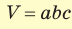 , где а, b и с — его измерения. Так как ABCD — квадрат, то
, где а, b и с — его измерения. Так как ABCD — квадрат, то 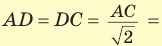
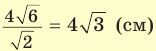 . Из прямоугольного треугольника
. Из прямоугольного треугольника 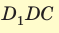 находим
находим 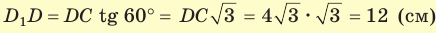 . Искомый объем
. Искомый объем 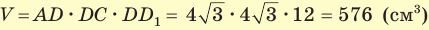 .
.
Ответ: 576 см3.
Синус, косинус, тангенс и котангенс тупого угла
1. Определение значений 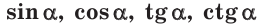 для любого угла а от 0° до 180°
для любого угла а от 0° до 180°
Ранее мы дали определения синуса, косинуса, тангенса и котангенса острого угла через отношение сторон прямоугольного треугольника. Сделаем теперь это для углов от 0° до 180°.
Рассмотрим полуокружность с центром в начале координат и радиусом, равным 1 (рис. 48). От положительной полуоси  против часовой стрелки отложим острый угол
против часовой стрелки отложим острый угол 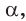 сторона которого пересекает полуокружность в точке
сторона которого пересекает полуокружность в точке 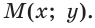 . Из прямоугольного треугольника OMN, где ОМ = 1, ON = х, MN = у, получаем:
. Из прямоугольного треугольника OMN, где ОМ = 1, ON = х, MN = у, получаем: 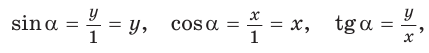
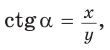 то есть синус, косинус,
то есть синус, косинус,
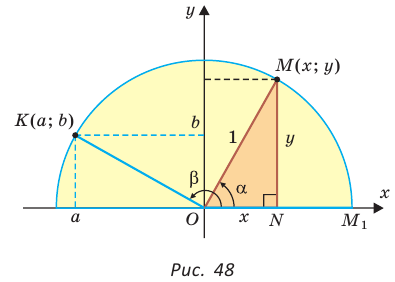
тангенс и котангенс острого угла а выражаются через координаты  точки
точки  Точно так же определяются значения
Точно так же определяются значения  и
и 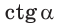 для любого угла а из промежутка
для любого угла а из промежутка 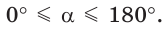 Таким образом, синусом угла а называется ордината
Таким образом, синусом угла а называется ордината 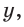 косинусом — абсцисса
косинусом — абсцисса 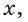 тангенсом — отношение ординаты к абсциссе
тангенсом — отношение ординаты к абсциссе 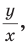 а котангенсом — отношение абсциссы к ординате
а котангенсом — отношение абсциссы к ординате 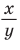 точки М единичной полуокружности.
точки М единичной полуокружности.
Например, для тупого 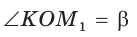 (рис. 48), где
(рис. 48), где 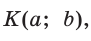 получим:
получим:
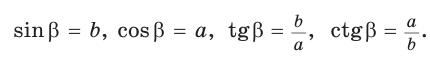
Для любого положения точки  на единичной полуокружности верно равенство
на единичной полуокружности верно равенство  (докажите самостоятельно). Поэтому для углов
(докажите самостоятельно). Поэтому для углов 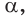 где
где  верно основное тригонометрическое тождество
верно основное тригонометрическое тождество 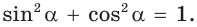
Также верны тождества: 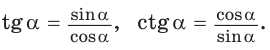
Нахождение синуса, косинуса, тангенса и котангенса тупых углов
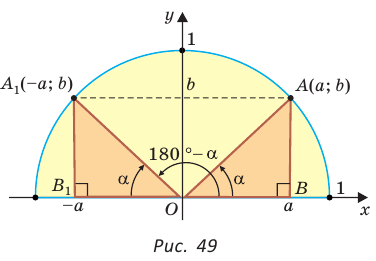
Пусть  откуда
откуда 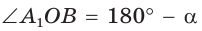 (рис. 49). Так как
(рис. 49). Так как 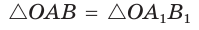 по гипотенузе и острому углу, то
по гипотенузе и острому углу, то 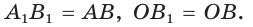 Точки
Точки 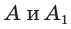 имеют координаты:
имеют координаты: 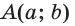 и
и 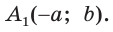 Тогда
Тогда 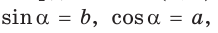
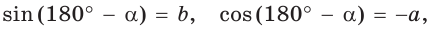 то есть для углов от 0° до 180° справедливы равенства:
то есть для углов от 0° до 180° справедливы равенства:
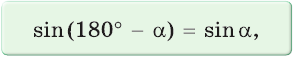
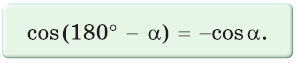
Можно пользоваться следующим правилом:
Синус тупого угла равен синусу смежного с ним острого угла.
Косинус тупого угла равен косинусу смежного с ним острого угла, взятому со знаком «минус».
Пример 1. 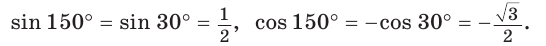
Разделив почленно равенство 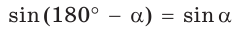 на равенство
на равенство 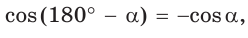 а затем наоборот, получим равенства:
а затем наоборот, получим равенства:
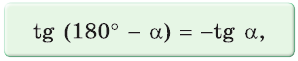
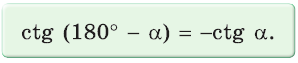
Можно пользоваться следующим правилом:
Тангенс (котангенс) тупого угла равен тангенсу (котангенсу) смежного с ним острого угла, взятому со знаком «минус».
Пример 2. 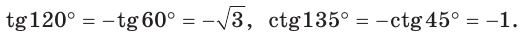
Указанные формулы и правила позволяют находить значения тригонометрических функций тупого угла через значения тригонометрических функций острого угла, который дополняет данный тупой угол до 180°: синусы углов, дополняющих друг друга до 180°, равны между собой, а косинусы, тангенсы и котангенсы — противоположны. Так как синус, косинус, тангенс и котангенс острого угла положительные, то синус тупого угла положительный, а косинус, тангенс и котангенс — отрицательные.
Значения тригонометрических функций для углов 0°, 90°, 180°
Если луч ОМ совпадет с лучом  (рис. 50), то будем считать, что
(рис. 50), то будем считать, что 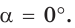 Тогда:
Тогда:
а) 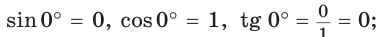 значение
значение 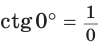 не определено, так как деление на нуль невозможно;
не определено, так как деление на нуль невозможно;
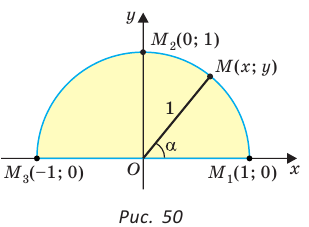
б) 
 значение
значение  не определено, так как деление на нуль невозможно; в)
не определено, так как деление на нуль невозможно; в) 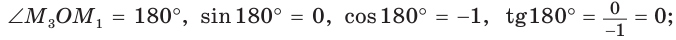 значение
значение 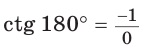 не определено, так как деление на нуль невозможно.
не определено, так как деление на нуль невозможно.
Поскольку проекции радиуса, равного 1, на оси координат меньше либо равны 1, то для углов 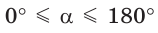 справедливы неравенства:
справедливы неравенства: 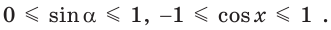
Пример №13
Найти 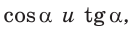 если
если 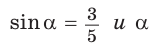 – тупой угол.
– тупой угол.
Решение:
Способ 1. Так как 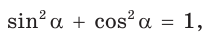 то
то 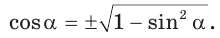 Поскольку угол
Поскольку угол 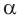 — тупой, то его косинус отрицательный. Поэтому
— тупой, то его косинус отрицательный. Поэтому 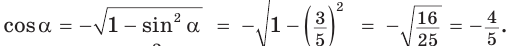 Тогда
Тогда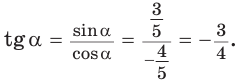
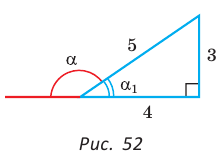
Способ 2. Синус острого угла 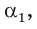 смежного с данным тупым углом
смежного с данным тупым углом 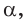 равен также
равен также 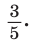 Построим прямоугольный треугольник со сторонами 3, 4 и 5 (рис. 52). В нем
Построим прямоугольный треугольник со сторонами 3, 4 и 5 (рис. 52). В нем 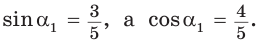 Так как косинусы смежных углов противоположны, то
Так как косинусы смежных углов противоположны, то 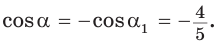 . Аналогично,
. Аналогично, 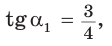
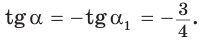
Ответ: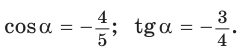
Формулы площади треугольника и площади параллелограмма
Тригонометрические функции позволяют получить формулы для вычисления площади треугольника и площади параллелограмма. Сформулируем их в виде двух теорем.
Теорема. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними, т. е. 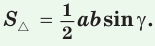
Доказательство:
Пусть в треугольнике  — острый,
— острый,  — высота (рис. 56, а).
— высота (рис. 56, а).
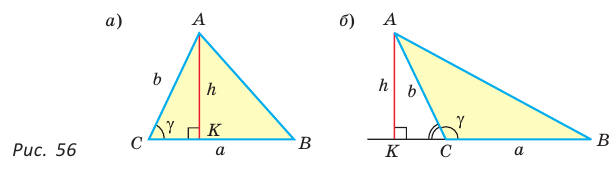
Из прямоугольного треугольника 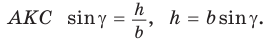 Тогда
Тогда 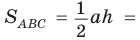
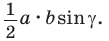
Если угол  тупой (рис. 56,
тупой (рис. 56, 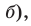 то
то 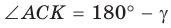 — острый. Из прямоугольного треугольника АКС следует, что
— острый. Из прямоугольного треугольника АКС следует, что 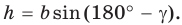 Так как
Так как 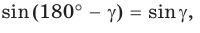 то
то 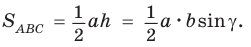
Если 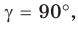 то
то 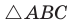 — прямоугольный с катетами
— прямоугольный с катетами 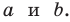 Учитывая, что
Учитывая, что  получим:
получим: 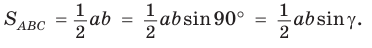
Теорема доказана.
Теорема. Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними, т. е. 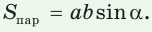
Используя рисунок 57, докажите эту теорему самостоятельно.
Замечание. Если 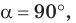 то параллелограмм является прямоугольником. Его площадь
то параллелограмм является прямоугольником. Его площадь 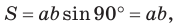 так как
так как  Таким образом, формула площади прямоугольника
Таким образом, формула площади прямоугольника 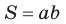 — частный случай формулы площади параллелограмма
— частный случай формулы площади параллелограмма 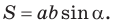

Известно, что слово «синус» в переводе с латинского имеет множество значений: изгиб, дуга, пазуха, бухта, впадина, залив, хорда, забота и нежная любовь. При помощи Интернета выясните:
а) какое из значений подходит к математическому понятию «синуса»;
б) какие из значений относятся к медицине и почему насморк врачи иногда называют синуситом.
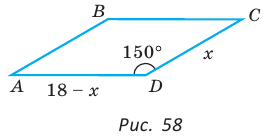
Пример №14
Дан параллелограмм ABCD, площадь которого 40 см2, а периметр 36 см. Найти стороны параллелограмма, если его угол D равен 150° (рис. 58).
Решение:
Полупериметр параллелограмма равен 18 см. Если 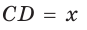 см, то
см, то 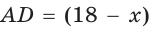 см.
см.
Тогда
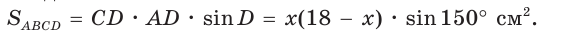
Так как 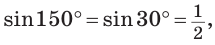 то
то 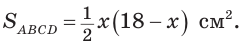
По условию 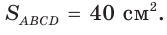 Составим и решим уравнение:
Составим и решим уравнение: 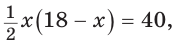
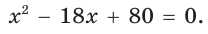 По теореме Виета (обратной)
По теореме Виета (обратной) 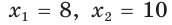 — корни.
— корни.
Если CD = 8 см, то AD = 10 см, если CD = 10 см, то AD = 8 см.
Ответ: 8 см, 10 см.
Пример №15
Доказать, что площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними, т.е. 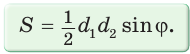
Доказательство:
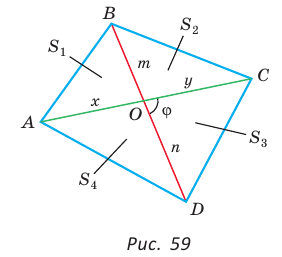
Пусть диагонали 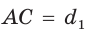 и
и 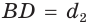 четырехугольника ABCD (рис. 59) пересекаются в точке О,
четырехугольника ABCD (рис. 59) пересекаются в точке О, 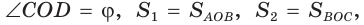
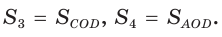 Докажем, что
Докажем, что 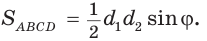
Обозначим 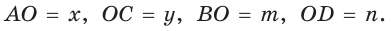 Заметим, что
Заметим, что 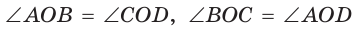 как вертикальные,
как вертикальные, 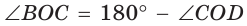 по свойству смежных углов. Поэтому
по свойству смежных углов. Поэтому 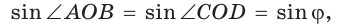
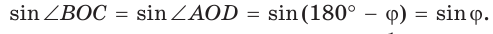 По формуле площади треугольника
По формуле площади треугольника 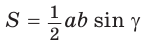 у получим:
у получим:
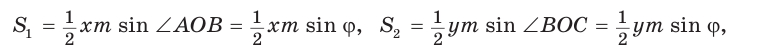
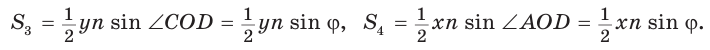
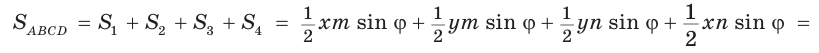
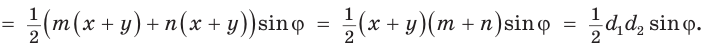
Утверждение доказано
Среднее пропорциональное (среднее геометрическое) в прямоугольном треугольнике
Если для положительных чисел 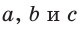 выполняется пропорция
выполняется пропорция 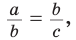 то число
то число 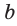 называется средним пропорциональным чисел а и с (между числами а и с). Из указанной пропорции
называется средним пропорциональным чисел а и с (между числами а и с). Из указанной пропорции 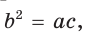 откуда
откуда 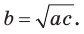 В такой форме записи число
В такой форме записи число 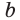 еще называют средним геометрическим чисел а и с.
еще называют средним геометрическим чисел а и с.
Пример №16
Число 4 является средним пропорциональным, или средним геометрическим чисел 2 и 8, так как = 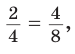 или
или 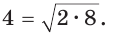
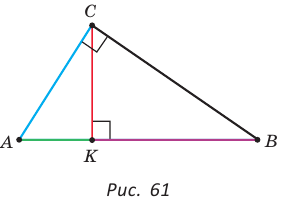
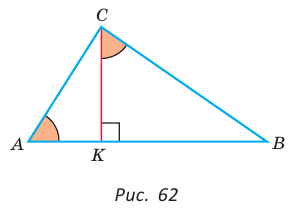
В прямоугольном треугольнике АВС, где 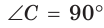 , проведем высоту СК (рис. 61). Отрезок АК является проекцией катета АС на гипотенузу, а отрезок ВК — проекцией катета ВС на гипотенузу. Катеты, гипотенуза, высота и проекции катетов на гипотенузу связаны отношениями, которые мы сформулируем в виде следующей теоремы.
, проведем высоту СК (рис. 61). Отрезок АК является проекцией катета АС на гипотенузу, а отрезок ВК — проекцией катета ВС на гипотенузу. Катеты, гипотенуза, высота и проекции катетов на гипотенузу связаны отношениями, которые мы сформулируем в виде следующей теоремы.
Теорема (о среднем пропорциональном в прямоугольном треугольнике).
а) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу, т. е. 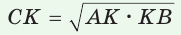 (см. рис. 61).
(см. рис. 61).
б) Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу, т. е. 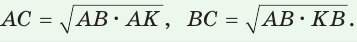
Доказательство:
а)3аметим, что если 
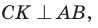 то
то 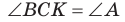 (эти углы дополняют
(эти углы дополняют 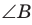 до 90°) (рис. 62). Из
до 90°) (рис. 62). Из 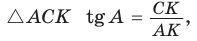 из
из 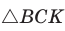
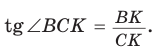 Отсюда
Отсюда 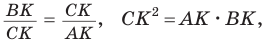
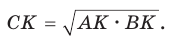
б) Из 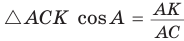 , из
, из 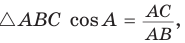 откуда
откуда 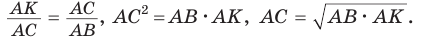
Аналогично доказывается, что 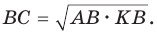 Теорема доказана.
Теорема доказана.
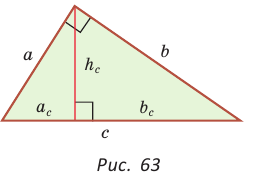
Обозначив катеты 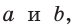 гипотенузу с, высоту
гипотенузу с, высоту 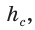 проекции катетов на гипотенузу
проекции катетов на гипотенузу 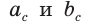 (рис. 63), получим следующие формулы:
(рис. 63), получим следующие формулы:
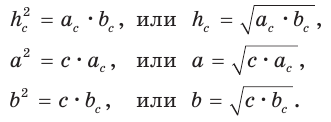
Пример №17
Найти площадь прямоугольного треугольника, если проекции катетов на гипотенузу равны 2 см и 8 см.
Решение:
Пусть СН — высота прямоугольного треугольника АВС 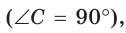 АН = 2 см — проекция катета АС на гипотенузу, НВ = 8 см —
АН = 2 см — проекция катета АС на гипотенузу, НВ = 8 см —
проекция катета СВ на гипотенузу (рис. 64). Так как высота СН есть среднее геометрическое между проекциями катетов на гипотенузу, то 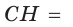
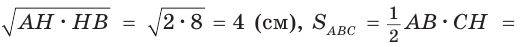
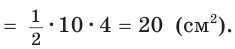
Ответ: 20 см2.
Пример №18
В прямоугольном треугольнике АВС из вершины прямого угла С проведена высота 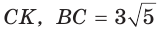 см, АК = 12 см (рис. 65). Найти гипотенузу АВ.
см, АК = 12 см (рис. 65). Найти гипотенузу АВ.
Решение:
Пусть 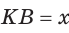 см, тогда
см, тогда 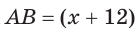 см.
см.
Катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу. Поэтому 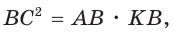 т. е.
т. е. 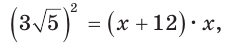
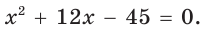 По теореме Виета (обратной)
По теореме Виета (обратной) 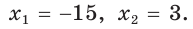 По смыслу задачи
По смыслу задачи 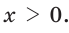 Значит, КВ = 3 см, АВ = 15 см.
Значит, КВ = 3 см, АВ = 15 см.
Ответ: 15 см.
Пример №19
При помощи циркуля и линейки построить отрезок, равный среднему геометрическому отрезков т и п .
Решение:
Пусть даны отрезки т и п . Необходимо построить отрезок 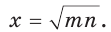
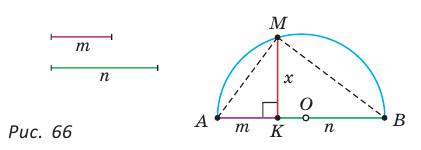
Построение.
1) На произвольной прямой откладываем данные отрезки: 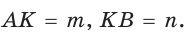
2) На отрезке АВ как на диаметре строим полуокружность, для чего находим середину О отрезка АВ, откуда ОА — радиус данной окружности.
3) Из точки К восстанавливаем перпендикуляр к прямой АВ до пересечения с полуокружностью в точке М (рис. 66).
Отрезок 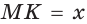 — среднее пропорциональное отрезков
— среднее пропорциональное отрезков 
Доказательство:
 — прямой как вписанный угол, опирающийся на диаметр. В прямоугольном треугольнике АМВ высота МК является средним пропорциональным проекций катетов AM и МВ на гипотенузу
— прямой как вписанный угол, опирающийся на диаметр. В прямоугольном треугольнике АМВ высота МК является средним пропорциональным проекций катетов AM и МВ на гипотенузу 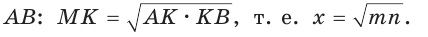
Повторение*
В 8-м классе мы доказали следующую теорему:
Теорема (о касательной и секущей). Если из одной точки к окружности проведены касательная и секущая, то квадрат отрезка касательной, соединяющего данную точку и точку касания, равен произведению отрезков се кущей, соединяющих данную точку и точки пересечения секущей с окружностью, т. е. 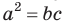 (рис. 70).
(рис. 70).
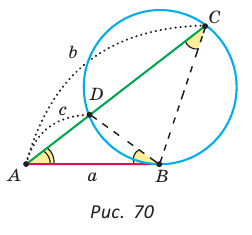
Как видим, отрезок 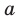 является средним пропорциональным между отрезками
является средним пропорциональным между отрезками 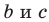 секущей. Глядя на рисунок 70, вспомните идею доказательства теоремы.
секущей. Глядя на рисунок 70, вспомните идею доказательства теоремы.
Теорема о площадях треугольников с общим (равным) углом
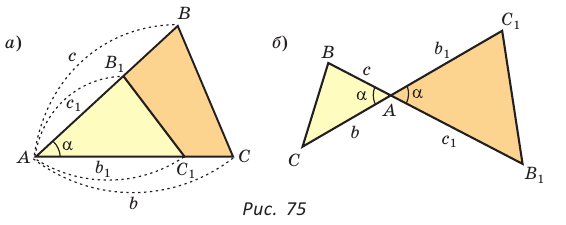
Площади треугольников, имеющих общий угол (или равный угол), относятся как произведения сторон, заключающих этот угол (рис. 75),
т.е. 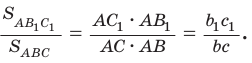
Доказательство:
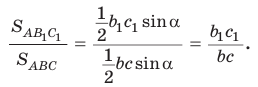
Следствие: Верно:
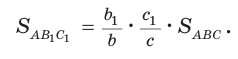
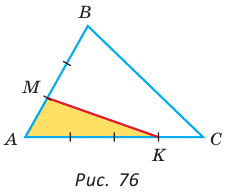
Пример №20
Площадь треугольника АВС равна 16, АК : КС = 3 :1 , AM : МВ = 1 :2 (рис. 76). Найти 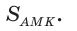
Решение:
Способ 1. По следствию из теоремы о площадях треугольников с общим углом получаем:
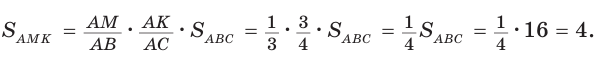
Способ 2. 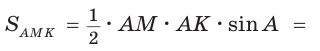
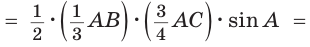
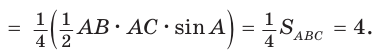
Ответ: 4.
Теорема Менелая
Если дан треугольник АВС и прямая 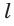 пересекает стороны ВС, АВ и продолжение стороны АС в точках
пересекает стороны ВС, АВ и продолжение стороны АС в точках 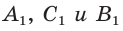 соответственно (рис. 79), то
соответственно (рис. 79), то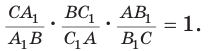
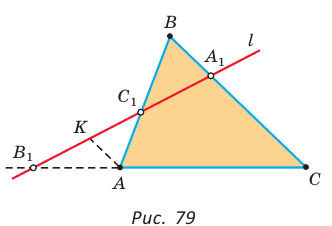
Доказательство:
Проведем отрезок 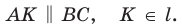 Так как
Так как 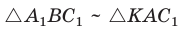 и
и  (по двум углам), то
(по двум углам), то 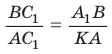 и
и 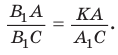 Перемножив почленно указанные пропорции, получим
Перемножив почленно указанные пропорции, получим
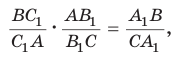 откуда
откуда 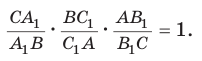
Замечание. При составлении произведения трех отношений теоремы Менелая можно начинать с любой из шести точек (трех вершин треугольника и трех точек пересечения прямой  с прямыми, содержащими стороны треугольника) и двигаться по контуру либо по часовой, либо против часовой стрелки. При этом вершины треугольника и точки пересечения должны чередоваться.
с прямыми, содержащими стороны треугольника) и двигаться по контуру либо по часовой, либо против часовой стрелки. При этом вершины треугольника и точки пересечения должны чередоваться.
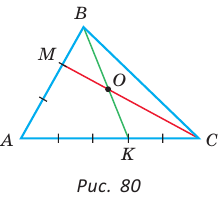
Пример №21
В треугольнике АВС на сторонах АВ и АС взяты соответственно точки М и К, такие, что AM : МВ = 2 :1 , АК : КС = 3 :2 . Отрезки СМ и ВК пересекаются в точке О. Найти ВО : ОК.
Решение:
Способ 1 (теорема Менелая). Рассмотрим 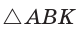 (рис. 80). Прямая
(рис. 80). Прямая 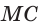 пересекает две его стороны АВ и ВК соответственно в точках М и О и продолжение третьей стороны АК в точке С. По теореме Менелая
пересекает две его стороны АВ и ВК соответственно в точках М и О и продолжение третьей стороны АК в точке С. По теореме Менелая 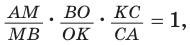 откуда
откуда 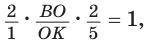
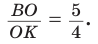
Способ 2 (теорема Фалеса обобщенная). Проведем 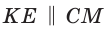 (рис. 81). По теореме Фалеса
(рис. 81). По теореме Фалеса 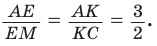 Тогда АЕ — три части, ЕМ — две части, AM — пять частей, откуда
Тогда АЕ — три части, ЕМ — две части, AM — пять частей, откуда 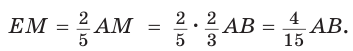
Но 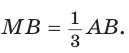 Отсюда
Отсюда 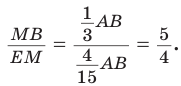 Для
Для 
по теореме Фалеса 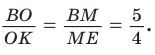
Ответ: 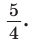
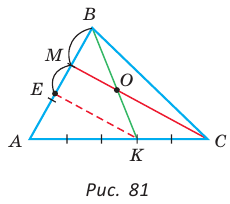
Пример №22
Дан равнобедренный треугольник АВС (АВ = ВС), площадь которого равна 80. Точка К делит высоту ВН в отношении 1 : 3, считая от основания. Прямая АК пересекает сторону ВС в точке М. Найти площадь четырехугольника НКМС (рис. 82).
Решение:
1) 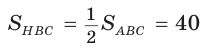 (ВН — высота и медиана треугольника АВС).
(ВН — высота и медиана треугольника АВС).
2) Применим теорему Менелая к треугольнику НВС.
Прямая AM пересекает его стороны ВН и ВС соответственно в точках К и М и продолжение стороны НС в точке  Тогда
Тогда 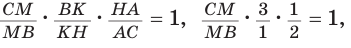
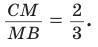 Откуда
Откуда 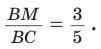
3) 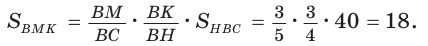
4) 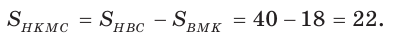
Ответ: 22.
Неравенство Коши
Среднее арифметическое двух неотрицательных чисел больше либо равно их среднему геометрическому, т. е.
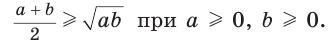
Например, 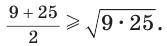 Действительно,
Действительно, 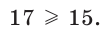
Алгебраическое доказательство указанного неравенства таково. Рассмотрим разность левой и правой частей неравенства 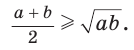 Получим:
Получим: 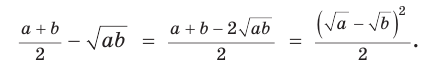 Так как
Так как 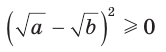 при всех допустимых
при всех допустимых  , то
, то 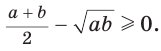 Следовательно, неравенство
Следовательно, неравенство 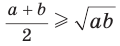 верно.
верно.
Неравенство 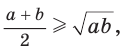 где
где 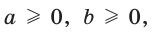 называется неравенством Коши по имени известного французского математика и часто используется при решении олимпиадных задач.
называется неравенством Коши по имени известного французского математика и часто используется при решении олимпиадных задач.
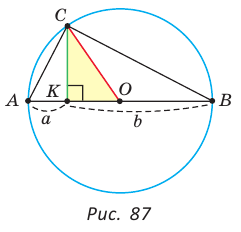
Приведем геометрическое доказательство указанного неравенства. Изобразим окружность с диаметром АВ и центром в точке О (рис. 87). На диаметре возьмем точку К (для определенности левее центра О). Пусть  Из точки К восстановим перпендикуляр КС, где точка С принадлежит окружности. Проведем радиус ОС. Так как вписанный угол, опирающийся на диаметр, прямой, то
Из точки К восстановим перпендикуляр КС, где точка С принадлежит окружности. Проведем радиус ОС. Так как вписанный угол, опирающийся на диаметр, прямой, то  прямоугольный, СК — его высота, проведенная к гипотенузе. По теореме о среднем пропорциональном в прямоугольном треугольнике
прямоугольный, СК — его высота, проведенная к гипотенузе. По теореме о среднем пропорциональном в прямоугольном треугольнике 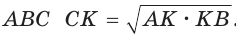 . Но радиус ОС равен половине диаметра АВ, т. е.
. Но радиус ОС равен половине диаметра АВ, т. е. 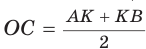 . В
. В 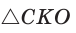 катет меньше гипотенузы, т. е.
катет меньше гипотенузы, т. е. 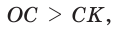 так как катет меньше гипотенузы. Отсюда
так как катет меньше гипотенузы. Отсюда 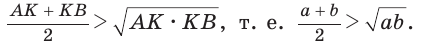
Равенство левой и правой частей неравенства достигается, когда точка К совпадает с точкой О и 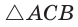 становится равнобедренным и прямоугольным. Поэтому справедливо неравенство
становится равнобедренным и прямоугольным. Поэтому справедливо неравенство 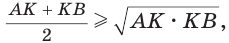 т. е
т. е 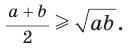
ЗАПОМИНАЕМ
2. Значения тригонометрических функций углов 30 45°, 60°:
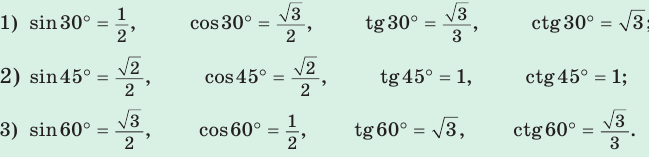
3. Тригонометрические формулы (тождества):
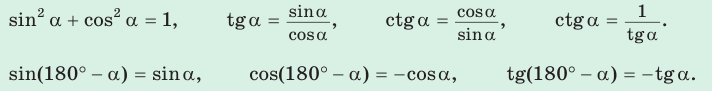
Примеры: 
4. Формулы площади треугольника и параллелограмма:

5. Среднее пропорциональное в прямоугольном треугольнике:
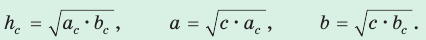
- Сумма углов треугольника
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Угол – определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
Содержание
- – Как найти катет при помощи косинуса?
- – Как найти гипотенузу если известны катеты?
- – Как найти катет если два угла по 45?
- – Как найти гипотенузу если известен катет и его проекция?
- – Как найти катет в прямоугольном треугольнике по теореме Пифагора?
- – Чему равен синус числа Пи?
Катет прямоугольного треугольника равен его гипотенузе, умноженной на синус противолежащего или на косинус прилежащего к этому катету угла.
Как найти катет при помощи косинуса?
Найти катет прямоугольного треугольника при помощи косинуса
Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза.
Как найти гипотенузу если известны катеты?
Если известна длина обоих катетов, то ее размер вычисляется по теореме Пифагора: сумма квадратов двух катетов равняется квадрату гипотенузы.
Как найти катет если два угла по 45?
Тогда по формуле Пифагора: а²+b²=c² имеем 2а²=с², отсюда а=с/√2 или а=с√2/2. Ответ: против угла 45° лежит катет, равный другому катету или равный гипотенузе, деленной на √2.
Как найти гипотенузу если известен катет и его проекция?
Если длина гипотенузы неизвестна, а даны лишь длины обоих катетов (А и В), то в вычислении длины нужной проекции (Ас) можно задействовать теорему Пифагора. Выразите в соответствии с ней длину гипотенузы через длины катетов √(А²+В²) и подставьте полученное выражение в формулу из предыдущего шага: Ас = А²/√(А²+В²).
Как найти катет в прямоугольном треугольнике по теореме Пифагора?
Катет — одна из двух сторон, образующих прямой угол. Формула Теоремы Пифагора выглядит так: a2 + b2 = c2, где a, b — катеты, с — гипотенуза.
Чему равен синус числа Пи?
Синус пи. таким образом, синус пи – это тоже самое, что синус 180 градусов и он равен нулю. 2. Косинус пи.
Интересные материалы:
Сколько будет стоить закрасить царапину?
Сколько будет светить солнце?
Сколько бугатти в мире?
Сколько было ледниковых периодов?
Сколько было выпущено газ 24?
Сколько было высадок на луну?
Сколько часов держит энергетик?
Сколько часов до луны?
Сколько часов ехать 1500 км?
Сколько часов God of War?
Теорема косинусов
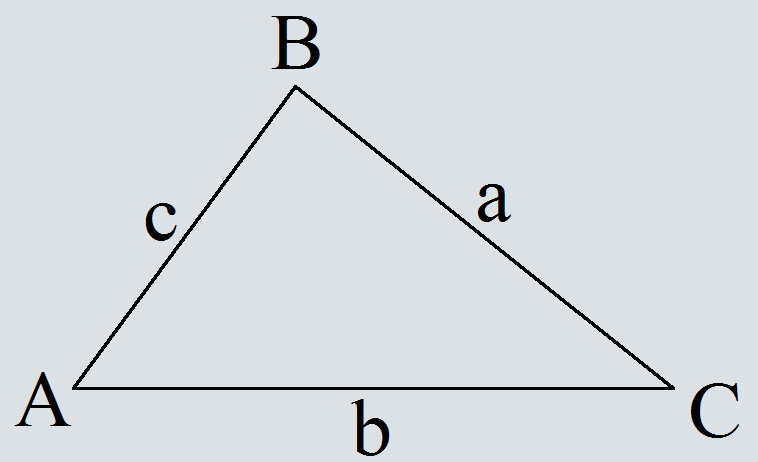
Определение теоремы косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
a2=b2+c2-2*b*c*cos(A)
b2=a2+c2-2*a*c*cos(B)
c2=a2+b2-2*a*b*cos(C)
Расчёт стороны по теореме косинусов
Введите сторону
Введите сторону
Введите угол
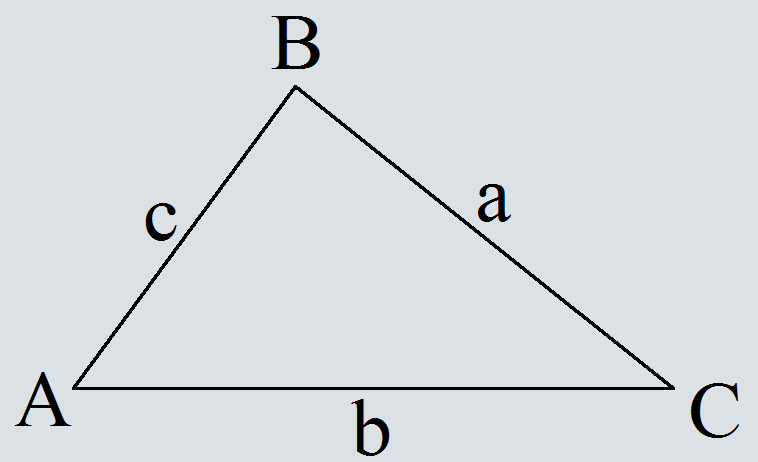
Формула расчёта стороны по теореме косинусов
Где a, b и c – стороны треугольника,
A – угол между сторонами b и c
Расчёт углов треугольника по теореме косинусов
Введите сторону a
a =
Введите сторону b
b =
Введите сторону c
c =
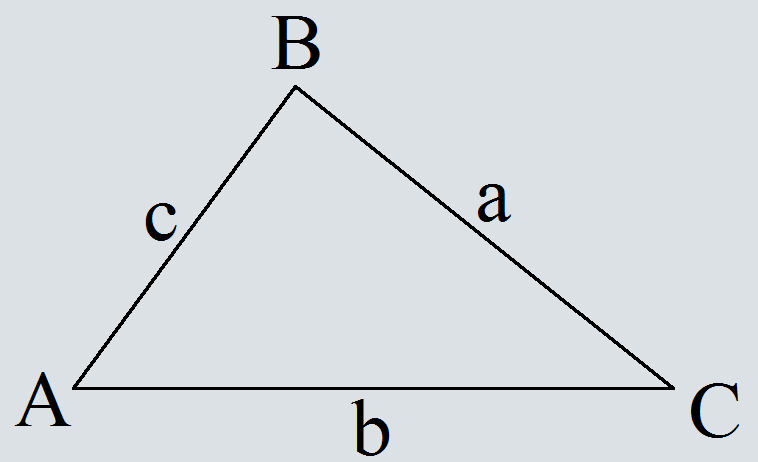
Формулы расчёта углов по теореме косинусов
Где a, b и c – стороны треугольника,
A, B и C – углы треугольника
Доказательство теоремы косинусов
Дано
Треугольник со сторонами a, b и c.

Доказать
a2=b2+c2-2*b*c*cos(α)
Доказательство
Из вершины B проведём высоту h
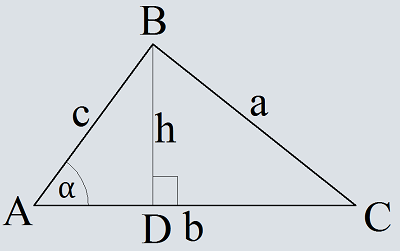
Сравним и упростим
Теорема доказана
Это смотря какие данные нам даны для решения.
Например есть теорема Пифагора:
по ней, если катеты a и b, а гипотенуза c, то:
a²+b²=c²
Отсюда можно найти катет, зная длину гипотенузы и второго катета:
a²=c²-b²
a=√(c²-b²)
Также находим и b:
b=√(c²-a²)
Ещё можно найти катет через тригонометрические функции, то есть зная угол через синусы, косинусы, тангенсы, котангенсы и т.д.
Если представить треугольник как вписанный в круг, то зная угол и размер гипотенузы можно найти катеты.
В рассматриваемом треугольнике, вписанном в круг, гипотенуза будет радиусом круга и приравнивается к 1 (к единице). А катеты – это синус и косинус, они меньше единицы.
Допустим зная угол α можно вычислить sin(α) и cos(α).
Синус соответствует вертикальному катету, а косинус горизонтальному.
Теперь, чтобы найти длины этих катетов, нужно перевести их из коэффициентов, которые меньше единицы, в реальные длины. Для этого их нужно домножить на длину гипотенузы:
Если:
Y – вертикальный катет, а X – горизонтальный катет (см. картинку) a Z – гипотенуза, то:
Y=Z*sin(α)
X=Z*cos(α)
Можно найти катет и зная лишь длину второго катета, а также угол.
Допустим знаем Y и угол α.
Тогда запросто находим гипотенузу, выражая её из предыдущей формулы:
Z=sin(α)/Y
А затем уже находим второй катет: X=Z*cos(α)
Если же наоборот знаем только X катет (горизонтальный, относительно приведённого рисунка), то находим гипотенузу так:
Z=X/cos(α)
А затем уже находим катет Y: Y=Z*sin(α)


