Решение.
Для решения задачи необходимы: μ0 = 4∙π⋅10-7 Гн/м − магнитная постоянная.
Рассмотрим четыре участка, АВ, ВС, СД, ДА.
Направление вектора магнитной индукции на каждом участке определим по правилу буравчика. В точке О результирующий вектор магнитной индукции направлен от нас. Применим принцип суперпозиции.
[ begin{align}
& vec{B}={{{vec{B}}}_{AB}}+{{{vec{B}}}_{BC}}+{{{vec{B}}}_{CD}}+{{{vec{B}}}_{DA}}, \
& Ox: B={{B}_{AB}}+{{B}_{BC}}+{{B}_{CD}}+{{B}_{DA}} (1). \
end{align}
]
Определим модуль вектора магнитной индукции на участке АВ.
Индукция магнитного поля в произвольной точке О, созданного отрезком проводника с током конечной длины, определим используя закон Био – Савара – Лапласа.
[ begin{align}
& dB=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot sin alpha dalpha , B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot intlimits_{{{alpha }_{1}}}^{{{alpha }_{2}}}{sin alpha dalpha ,} \
& B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot (cos {{alpha }_{1}}-cos {{alpha }_{2}}) (3). \
end{align} ]
Где: R – расстояние от т. О до проводника; – α1 и α2 углы, образованные радиус-вектором, проведенном в т. О соответственно из начала и конца проводника, с направлением тока.
Определим модуль вектора магнитной индукции на каждом участке.
α2 = 3∙π/4, α1 = π/ 4.
[ begin{align}
& B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot (cos frac{pi }{4}-cos frac{3cdot pi }{4}) , B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot (frac{sqrt{2}}{2}+frac{sqrt{2}}{2}) , \
& {{B}_{BC}}={{B}_{DA}}={{B}_{CD}}={{B}_{AB}}=frac{sqrt{2}cdot {{mu }_{0}}cdot I}{4cdot pi cdot R} (5),R=frac{d}{2} (6), \
& B=4cdot frac{sqrt{2}cdot {{mu }_{0}}cdot I}{2cdot pi cdot d}, B=2cdot frac{sqrt{2}cdot {{mu }_{0}}cdot I}{pi cdot d} (7). \
& B=frac{2cdot sqrt{2}cdot 4cdot pi cdot {{10}^{-7}}cdot 5}{pi cdot 0,15}=37,6cdot {{10}^{-6}}. \
end{align}
]
Ответ 9,43 мкТ получается если бы квадрат был изготовлен из проволоки длиной 15 см.
Ответ: В = 37,6∙10-6 Тл.
Нужна помощь в написании работы?
По квадратной рамке течёт ток 4 А. Напряжённость магнитного поля в центре рамки 4,5 А/м. Определить периметр рамки.
Дано: I = 4 A, H = 4,5 А/м.
Найти: р.
Решение. Пусть а – длина стороны квадратной рамки. Тогда напряжённость Н1
магнитного поля, создаваемого в центре квадрата током I, протекающим по одной стороне квадратной рамки определяется по формуле:
![]() , (1)
, (1)
где r = ![]() – кратчайшее расстояние от стороны квадрата до его центра, a1 = a2= = 45° углы между стороной квадрата и линиями, соединяющими концы стороны с центром квадрата. Таким образом, можно записать формулу (1) в более простом виде:
– кратчайшее расстояние от стороны квадрата до его центра, a1 = a2= = 45° углы между стороной квадрата и линиями, соединяющими концы стороны с центром квадрата. Таким образом, можно записать формулу (1) в более простом виде:
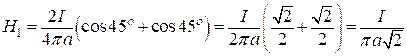 . (2)
. (2)
Согласно принципу суперпозиции суммарная напряжённость Н магнитного поля, создаваемого четырьмя сторонами квадрата равна 4Н1. Следовательно,
![]() , (3)
, (3)
откуда ![]() .
.
Так как периметр квадрата р = 4а, то
![]() ;
;
![]() = 3,2 м.
= 3,2 м.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
Получить выполненную работу или консультацию специалиста по вашему
учебному проекту
Узнать стоимость
2018-05-14 ![]()
Квадратная рамка с током $I = 0,90 А$ расположена в одной плоскости с длинным прямым проводником, по которому течет ток $I_{0} = 5,0 А$. Сторона рамки $a = 8,0 см$. Проходящая через середины противоположных сторон ось рамки параллельна проводу и отстоит от него на расстояние, которое в $eta = 1,5$ раза больше стороны рамки. Найти:
а) амперову силу, действующую на рамку;
б) механическую работу, которую нужно совершить для поворота рамки вокруг ее оси на $180^{ circ}$, если токи поддерживают неизменными.
Решение:

(а) Как видно из условия, силы Ампера на сторонах (2) и (4) равны по величине, но противоположны по направлению. Следовательно, чистая эффективная сила на рамке является результатом сил, испытываемых сторонами (1) и (3).
Теперь сила Ампера на (1),
$F_{1} = frac{ mu_{0} }{2 pi} frac{ii_{0} }{ left ( eta – frac{1}{2} right ) }$
и на (3),
$F_{3} = frac{ mu_{0} }{2 pi} frac{i_{0}i }{ left ( eta + frac{1}{2} right ) }$
Итак, результирующая сила на рамке $= F_{1} – F_{3}$, (поскольку они противоположны).
$= frac{2 mu_{0} ii_{0} }{ pi (4 eta^{2} – 1 ) } = 0,40 мкН$.
(б) Выполненная работа при повороте рамки на некоторый угол $A = int id Phi = i ( Phi_{кон} – Phi_{нач} )$, где $Phi_{кон}$ – поток через рамку в конечном положении, а $Phi_{нач}$ – в исходное положение.
Итак, $| Phi_{кон} | = | Phi_{нач} | = Phi$ и $Phi_{нач} = – Phi_{кон}$
значит, $Delta Phi = 2 Phi$ и $A = i2 Phi$
Следовательно, $A = 2i int vec{B} cdot d vec{S} = 2i int_{a left ( eta – frac{1}{2} right ) }^{ a left ( eta + frac{1}{2} right ) } frac{ mu_{0} }{2 pi} frac{i_{0}a }{r} dr = frac{ mu_{0}ii_{0} a }{ pi} ln left ( frac{2 eta + 1}{2 eta – 1} right )$
 Готовое решение: Заказ №8367
Готовое решение: Заказ №8367
 Тип работы: Задача
Тип работы: Задача
 Статус: Выполнен (Зачтена преподавателем ВУЗа)
Статус: Выполнен (Зачтена преподавателем ВУЗа)
 Предмет: Физика
Предмет: Физика
 Дата выполнения: 18.08.2020
Дата выполнения: 18.08.2020
 Цена: 227 руб.
Цена: 227 руб.
Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
По квадратной рамке со стороной 0,2 м течёт ток, который создаёт в центре рамки магнитное поле напряжённостью 4,5 А/м. Определить силу тока в рамке.
Решение.
Для нахождения магнитной индукции, создаваемой в центре рамки каждой стороной, воспользуемся формулой для индукции от проводника конечных размеров: , где Гн/м – магнитная постоянная; − сила тока в проводнике; − расстояние от точки, для которой определяется магнитная индукция, до проводника; − угол между направлением тока в проводнике и вектором, проведённым из точки проводника

Закон Био-Савара-Лапласа в магнитостатике – примерно то же самое, что и закон Кулона в электростатике. С помощью этого закона определяется индукция магнитного поля, созданного постоянным электрическим током. В сегодняшней статье разберем несколько примеров решения задач по магнитостатике на применение закона Био-Савара-Лапласа.
Присоединяйтесь к нам в телеграме, чтобы вовремя получать полезную рассылку и актуальные новости. А еще, не пропустите приятные скидки и акции на нашем втором канале.
Закон Био-Савара-Лапласа: решение задач
В нашем блоге есть материалы, которые помогут справиться с задачами по разным темам:
- Общая памятка по решению физических задач.
- Более 40 формул по физике.
Задача на закон Био-Савара-Лапласа №1
Условие
Прямой провод согнут в виде квадрата со стороной а=8 см. Какой силы ток надо пропустить по проводнику, чтобы напряженность магнитного поля в точке пересечения диагоналей была 20 А/м?
Решение
Согласно принципу суперпозиции напряженность магнитного поля в точке пересечения диагоналей квадрата будет равна сумме напряженностей, которые создают стороны. Поскольку стороны одинаковые, то:
H=4H1=4B1μ0
Будем использовать формулу для магнитной индукции поля, создаваемого отрезком прямого провода с током (выводится из закона Био-Савара-Лапласа):
Тогда для напряженности в точке пересечения диагоналей получим:
Отсюда можем выразить ток:
I=πaH4cosα=3,14×0,08×204cos45=1,78 А
Ответ: 1,78 А.
Задача на закон Био-Савара-Лапласа №2
Условие
Используя закон Био-Савара-Лапласа, определите магнитную индукцию в вакууме B поля в центре кругового проводника радиусом 10 см, если сила тока в проводнике равна 5 A.
Решение
Модуль магнитной индукции в центре кругового тока вычисляется по формуле:
B=μ0μI2rμ=1 – магнитная проницаемость для вакуумаμ0=1,25×10-6 Гнм – магнитная постоянная
Вычислим индукцию:
В=1,25×10-6×1×52×0,1=3,1×10-5 Тл
Ответ: 0,31 мкТл.
Задача на закон Био-Савара-Лапласа №3
Условие
Используя закон Био-Савара-Лапласа выведите формулу для индукуии из предыдущей задачи.
Решение
Пусть ток идет по тонкому проводу в форме окружности, имеющей радиус R.
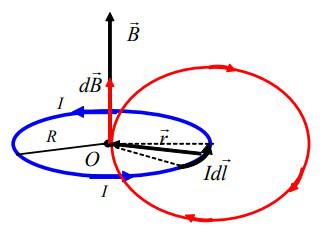
Разобъем провод на бесконечно малые элементы dl. Каждый такой элемент создает в центре окружности индукцию dB, направленную вдоль положительной нормали к контуру. По закону Био-Савара-Лапласа:
B=μ04πIdlsinαr2
Угол альфа между векторами r и Idl равен 90 градусам, а r=R. Тогда, можно записать:
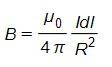
Интегрируя это выражение по контуру, получим:
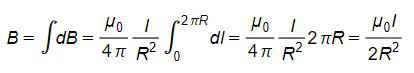
Ответ: см. выше.
Задача на закон Био-Савара-Лапласа №4
Условие
По квадратной рамке со стороной a=0,2 м течет ток 4 А. Определить напряженность и индукцию магнитного поля в центре рамки.
Решение
Будем рассматривать каждую из четырех сторон рамки, как отдельный проводник, создающий в ее центре магнитную индукцию. Направление векторно-магнитной индукции определяется по правилу правого винта: все векторы направлены в одну сторону, перпендикулярно рамке.
Найдем индукцию, создаваемую одной стороной рамки:
B1=μμ0I4πr(cosα1-cosα2)
r=a2α1=45°α2=135°В1=μμ0I2πa(cos45-cos135)
По принципу суперпозиции, запишем формулу для общей индукции в центре рамки и вычислим:
B=4B1=2μμ0Iπa(cos45-cos135)B=1×1,25×10-6×42×3,14×0,2(0,707+0,707)=22,6×10-6 Тл
Ответ: 22,6 мкТл.
Задача на закон Био-Савара-Лапласа №5
Условие
Проводник согнут в виде правильного треугольника со стороной а=20 см. Какой ток протекает по периметру треугольника, если в его центре напряженность поля равна Н = 71,64 А/м?
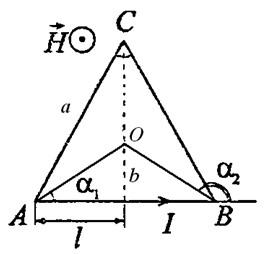
Решение
Условно разбиваем проводник на три проводника, каждый из которых создает магнитное поле. По закону Био – Савара – Лапласа элемент контура dl, по которому течет ток I, создает в некоторой точке А пространства магнитное поле напряженностью:
dH0=Isinα4πr2dl
r – расстояние от точки А до элемента тока dl, α – угол между радиус-вектором и элементом тока dl. Напряженность магнитного поля в точке О будет равна:
Н0=∫-∞+∞Isinα4πr2dl
Учтем, что:
l=b×ctgαdl=-bdαsin2αr=bsinα
Теперь выражение для напряженности можно переписать в следующем виде:
H0=-I4πb∫α1α2sinαdα=I4πbcosα1-cosα2b=a2tgαH0=I2π×a×tgαcosα1-cosα2
Из рисунка видно, что угол α1 равен 30 градусам, а угол α2 = 150. Очевидно, что результирующая напряженность:
Н=3Н0
Н=3I2π×a×tg30cos30-cos150
Отсюда найдем ток:
I=2πH×a×tg303(cos30-cos150)=2×3,14×71,64×0,2×0,5773(0,866+0,866)=10А
Ответ: 10 А.
Вопросы на закон Био-Савара-Лапласа
Вопрос 1. Сформулируйте закон Био-Савара-Лапласа
Ответ. Закон Био-Савара-Лапласа гласит:
Магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока.
B⇀=∑B⇀ii
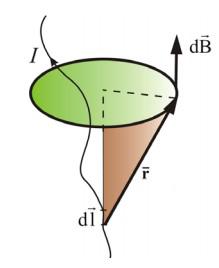
Элементарный участок dl с током I создает магнитную индукцию:
B=μ04πIdlsinαr2
Здесь альфа — угол между радиусом-вектором и направлением тока в проводнике.
Вопрос 2. Что такое магнитная индукция?
Ответ. Магнитная индукция — векторная физическая величина, силовая характеристика магнитного поля. Определяет, с какой силой поле действует на заряд, движущийся в нем.
Вопрос 3. Сформулируйте теорему о циркуляции магнитной индукции.
Ответ. Циркуляция вектора магнитной индукции по произвольному замкнутому контуру, охватывающему токи, прямо пропорциональна алгебраической сумме токов, пронизывающих этот контур:
∮Вdl=μ0∑iIi
Вопрос 4. Как определяется направление вектора магнитной индукции?
Ответ. Направление вектора магнитной индукции определяется по правилу буравчика (правого винта):
Направление вращения головки винта дает направление вектора магнитной индукции, поступательное движение винта соответствует направлению тока в элементе.
Вопрос 5. Что такое напряженность магнитного поля?
Ответ. Напряженность — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M. Связана с индукцией формулой:
H⇀=B⇀μ0
Нужна помощь в решении задач и выполнении других заданий? Профессиональный сервис для учащихся всегда к вашим услугам.
