Основные формулы термодинамики и молекулярной физики, которые вам пригодятся. Еще один отличный день для практических занятий по физике. Сегодня мы соберем вместе формулы, которые чаще всего используются при решении задач в термодинамике и молекулярной физике.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Итак, поехали. Попытаемся изложить законы и формулы термодинамики кратко.
Идеальный газ
Идеальный газ – это идеализация, как и материальная точка. Молекулы такого газа являются материальными точками, а соударения молекул – абсолютно упругие. Взаимодействием же молекул на расстоянии пренебрегаем. В задачах по термодинамике реальные газы часто принимаются за идеальные. Так гораздо легче жить, и не нужно иметь дела с массой новых членов в уравнениях.
Итак, что происходит с молекулами идеального газа? Да, они движутся! И резонно спросить, с какой скоростью? Конечно, помимо скорости молекул нас интересует еще и общее состояние нашего газа. Какое давление P он оказывает на стенки сосуда, какой объем V занимает, какая у него температура T.
Для того, чтобы узнать все это, есть уравнение состояния идеального газа, или уравнение Клапейрона-Менделеева
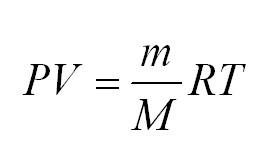
Здесь m – масса газа, M – его молекулярная масса (находим по таблице Менделеева), R – универсальная газовая постоянная, равная 8,3144598(48) Дж/(моль*кг).
Универсальная газовая постоянная может быть выражена через другие константы (постоянная Больцмана и число Авогадро)
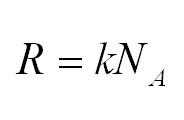
Массу, в свою очередь, можно вычислить, как произведение плотности и объема.
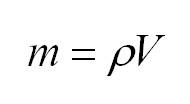
Основное уравнение молекулярно-кинетической теории (МКТ)
Как мы уже говорили, молекулы газа движутся, причем, чем выше температура – тем быстрее. Существует связь между давлением газа и средней кинетической энергией E его частиц. Эта связь называется основным уравнением молекулярно-кинетической теории и имеет вид:
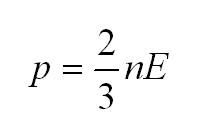
Здесь n – концентрация молекул (отношение их количества к объему), E – средняя кинетическая энергия. Найти их, а также среднюю квадратичную скорость молекул можно, соответственно, по формулам:
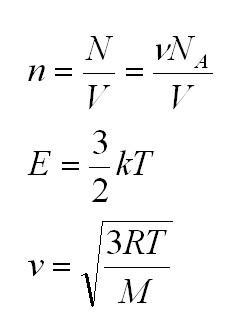
Подставим энергию в первое уравнение, и получим еще один вид основного уравнения МКТ
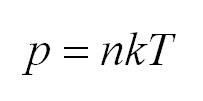
Первое начало термодинамики. Формулы для изопроцессов
Напомним Вам, что первый закон термодинамики гласит: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа U и на совершение газом работы A. Формула первого закона термодинамики записывается так:
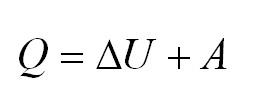
Как известно, с газом что-то происходит, мы можем сжать его, можем нагреть. В данном случае нас интересуют такие процессы, которые протекают при одном постоянном параметре. Рассмотрим, как выглядит первое начало термодинамики в каждом из них.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Изотермический процесс протекает при постоянной температуре. Тут работает закон Бойля-Мариотта: в изотермическом процессе давление газа обратно пропорционально его объёму. В изотермическом процессе:
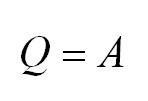
Изохорный процесс протекает при постоянном объеме. Для этого процесса характерен закон Шарля: При постоянном объеме давление прямо пропорционально температуре. В изохорном процессе все тепло, подведенное к газу, идет на изменение его внутренней энергии.
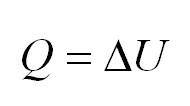
Изобарный процесс идет при постоянном давлении. Закон Гей-Люссака гласит, что при постоянном давлении газа его объём прямо пропорционален температуре. При изобарном процессе тепло идет как на изменение внутренней энергии, так и на совершение газом работы.
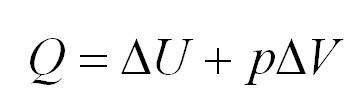
Адиабатный процесс. Адиабатный процесс – это такой процесс, который проходит без теплообмена с окружающей средой. Это значит, что формула первого закона термодинамики для адиабатного процесса выглядит так:
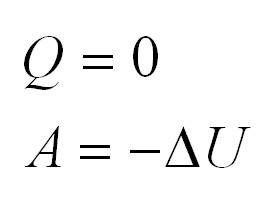
Внутренняя энергия одноатомного и двухатомного идеального газа
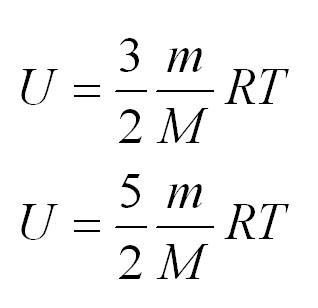
Теплоемкость
Удельная теплоемкость равна количеству теплоты, которое необходимо для нагревания одного килограмма вещества на один градус Цельсия.
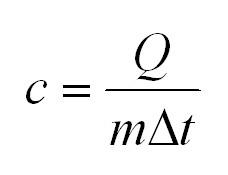
Помимо удельной теплоемкости, есть молярная теплоемкость (количество теплоты, необходимое для нагревания одного моля вещества на один градус) при постоянном объеме, и молярная теплоемкость при постоянном давлении. В формулах ниже, i – число степеней свободы молекул газа. Для одноатомного газа i=3, для двухатомного – 5.
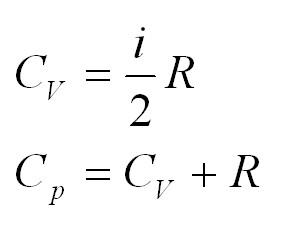
Тепловые машины. Формула КПД в термодинамике
Тепловая машина, в простейшем случае, состоит из нагревателя, холодильника и рабочего тела. Нагреватель сообщает тепло рабочему телу, оно совершает работу, затем охлаждается холодильником, и все повторяется вновь. Типичным примером тепловой машины является двигатель внутреннего сгорания.
Коэффициент полезного действия тепловой машины вычисляется по формуле
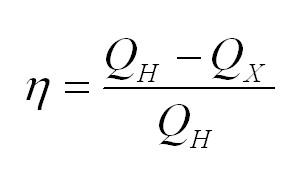
Вот мы и собрали основные формулы термодинамики, которые пригодятся в решении задач. Конечно, это не все все формулы из темы термодинамика, но их знание действительно может сослужить хорошую службу. А если возникнут вопросы – помните о студенческом сервисе, специалисты которого готовы в любой момент прийти на выручку.
Модель идеального газа считается самой простейшей относительно основных положений МКТ. Кинетическая модель идеального газа молекул говорит о том, что при взаимодействии между собой, шарики рассматриваются в качестве идеально упругих. Суммарный объем всех молекул достаточно мал по сравнению с объемом сосуда, в котором находится данный газ. Модель необходима для описания его поведения при различных давлениях и температурах.
Цель молекулярно-кинетической теории – установка связи между макроскопическими и макроскопическими параметрами.
После соударения молекул между собой и стенками сосуда происходит изменение направления движения и времени между интервалами столкновений. Модель идеального газа основывается на законах механики Ньютона, то тесть столкновения соответствуют закону упругого удара.
Чтобы определить давление газа на стенку сосуда, учитывается модель идеального газа. Исходя из этого, происходит возникновение сил, которые подчиняются 3 закону Ньютона. Отсюда получим, что проекция скорости υx перпендикулярна относительно стенки, а знак меняется на противоположный. Проекция υy параллельна и постоянна. Это показано на рисунке 3.2.1.
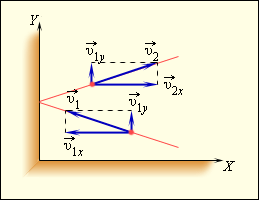
Рисунок 3.2.1. Упругое столкновение молекулы со стенкой.
Отсюда следует, что изменение импульса можно записать в виде 2m0υx с массой молекулы, равной m0. Необходимо выделить площадь S, как показано на рисунке 3.2.2. По прошествии времени Δt с S поверхностью столкнутся молекулы с проекциями скорости υx, которая направлена в сторону стены, и основанием цилиндра S с высотой υxΔt.
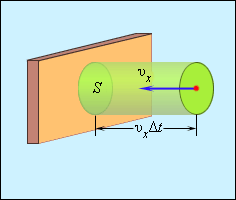
Рисунок 3.2.2. Определение числа столкновений молекул с поверхностью S.
Если за единицу объема брать сосуд с n-ым количеством молекул, тогда их число в объеме цилиндра нужно обозначить, как nSυxΔt. Очевидно, что происходит столкновение только половины имеющихся молекул. Тогда количество ударов о S за время Δt равняется 12nSvx∆t.
При столкновении происходит изменение импульса 2m0υx. Тогда формула nm0vx2S∆t говорит о полном его изменении за определенный промежуток времени. Исходя из закона механики, изменение импульса всех молекул записывается как FΔt. Силой F обозначается средняя сила, которая действует на молекулы. Но 3 закон Ньютона говорит о том, что аналогичная сила по модулю оказывает действие на поверхность S. Данное утверждение можно зафиксировать F∆t=nm0vx2S∆t.
Далее для упрощения следует разделить равенство на выражение SΔt. Формула примет вид p=FS=nm0vx2 со значением р, обозначаемым в качестве давления газа на стенку сосуда.
Все молекулы, находящиеся в сосуде на единицу объема, имеют разные проекции скоростей на ось Ох. При столкновениях прослеживалось статистическое их распределение по скоростям, причем с разными направлениями векторов их скоростей.
Распределением Максвелла называют распределение молекул газа по модулю скоростей.
Еще в 1860 г Дж. Максвелл вывел закон распределения молекул газа по скоростям, основываясь на основных положениях молекулярно-кинетической теории молекулы. Рисунок 3.2.3. наглядно показывает распределения молекул по скоростям с помощью кривых. На оси Ох располагается модуль скорости, а на Оу – количество молекул, находящихся на интервале от υ до υ+Δυ. На рисунке 3.2.3. данное значение выделено в виде столбика.
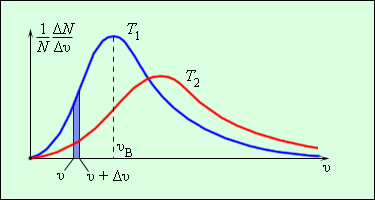
Рисунок 3.2.3. Распределение молекул по скоростям. T2>T1.
Характерные параметры распределения Максвелла – это вероятная скорость υв,которая соответствует кривой распределения, и среднеквадратичная скорость υкв=υ2→, где υ2→обозначающие среднее значение квадрата скорости.
Если растет температура, тогда максимум кривой будет смещен в сторону больших скоростей, то есть υв и υкв увеличатся.
Распределение Максвелла
Для записи формулы давления газа необходимо предположить, что все молекулы разделены на n1, n2, n3 группы с проекциями υx1, υx2, υx3. Иначе говоря, записываем ∑ini=n. Можно зафиксировать, как nim0vxi2. Тогда суммарное давление примет вид p=m0∑inivxi2.
Данная сумма является суммой квадратов проекций υx всех n молекул на единичном объеме газа. При делении выражения на n получим среднее значение квадратичной скорости проекции υx. Запишем в виде 1n∑niυxi2=vx2→i.
Другая интерпретация формулы давления газа p=nm0vx2→. Все направления векторов различные, потому среднее значение квадратов проекций на координатные оси равняется vx2→=vy2→=vz2→=13v2→.
Формула для среднего давления газа на стенку сосуда обозначим, как p=p→=13nm0v2→=23nm0v2→2=23nEk→.
Из уравнения видна связь между р и m0 и количеством молекул n, средней квадратичной скоростью v2→ и средней кинетической энергией Ek→ молекул. Такое уравнение получило название уравнения молекулярно-кинетической уравнения теории газов.
Отсюда следует, что давление газа – это две трети средней кинетической энергии, которое имеется в единице объема. Основное уравнение молекулярно-кинетической теории газов или строения вещества содержит произведение количества молекул n на Ek→. Предположительно сосуд имеет газ неизменного объема V, тогда n=NV=const (N – число молекул в сосуде). Изменение давления происходит пропорционально изменению кинетической энергии.
Физика. Температура
Температура связана с понятием теплового равновесия. При контакте тела обмениваются энергией, которая передается и получает название количества теплоты.
Тепловым равновесием называют состояние системы тел, которые находятся в тепловом контакте с теплопередачей и с постоянными макроскопическими параметрами.
Температура – физический параметр, который находится в тепловом равновесии. Введение понятия температуры идет из нулевого закона термодинамики.
Температура измеряется с помощью термометра. Для его создания выбирается термометрическое вещество и величину, которая его характеризует. Разные конструкции подразумевают отличия в их свойствах.
Каждый термометр должен быть откалиброван. Использование природных систем с неизменной температурой необходимо для хорошего теплообмена. Температура плавления льда равняется 0 градусов Цельсия, а точка кипения воды – 100 градусов. Одно маленькое деление из шкалы равняется 1 градусу. Существует обозначение замерзания воды по Фаренгейту, то есть 32 °F. Получаем, что формула примет вид TF=95TC+32 или TC=59(TF-32).
На рисунке 3.2.4. изображен газовый термометр, который чаще всего заполняют разряженным гелием, воздухом с неизменным объемом, обозначаемым V = const, и давлением р. Из опыта видно, что возрастание давления идет с повышением температуры по Цельсию.

Рисунок 3.2.4. Газовый термометр с постоянным объемом.
Температура кипения газов при давлении
Чтобы произвести калибровку газового термометра, следует выполнить измерение состояния молекул при 0 и 100 градусах. Для этого мы наносим точки p0 и p100 на график, после чего проводим прямую линию, как изображено на рисунке 3.2.5. Получившийся калибровочный график способен определить температуру с разными значениями давления. При низких температурах возможно нахождение ее «гипотетической». Из опыта видно, что на свойства газа не влияет температура в-273,15 °С. При понижении температур газ переходит в жидкое или твердое состояние, поэтому получение охлажденного газа невозможно.
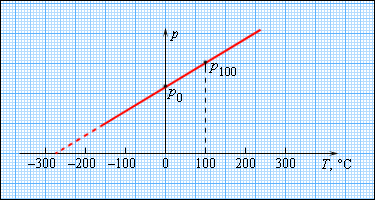
Рисунок 3.2.5. Зависимость давления газа от температуры при V = const.
В 1848 году У. Кельвин предлагает использовать точку нулевого давления газа для составления шкалы. Отличие от измерений температуры в Цельсиях в том, что нулевая точка сдвинута на TК =TС+273,15.
По системе СИ температура измеряется по Кельвину и обозначается К. Тогда комнатная температура запишется TС=20 °С, а по Кельвину – TК=293,15 К.
Температура кипения газов. Шкала Кельвина
Температурная шкала Кельвина считается абсолютной. Она наиболее приемлема для обозначения физических теорий.
Шкала Кельвина может быть не привязана двумя фиксированными точками, а именно: точка плавления льда и кипения воды с нормальным атмосферным давлением.
Нулевое давление называется абсолютным нулем температуры.
Шкала Кельвина имеет точку, в которой лед, вода и пар будут находиться в тепловом равновесии. Для калибровки других термометров применяют газовые, так как для практики они не подходят в виду своих больших размеров. Отсюда следует, что давление разреженного газа в сосуде постоянного объема V изменяется прямо пропорционально его абсолютной температуре, то есть p~T. Из опыта видно, что неизменный объем V и температура давления T прямо пропорциональны количеству вещества в сосуде к его объему: p~υV=NNAV=nNA~n, где N принимает обозначение числа молекул в сосуде, а NА – постоянная Авогадро, n=NV – концентрации молекул.
После объединения соотношений получим, что запись примет вид p=nkT, где k считается универсальной постоянной величиной для всех газов, иначе говоря, постоянная Больцмана. Этот ученый являлся одним из создателей опытного обоснования основных положений молекулярно-кинетической теории. Ее обозначение в системе СИ k=1,38ċ10–23 Дж/К.
При сравнении соотношения p=nkT с уравнением МКТ газов, получим EK→.
Средняя кинетическая энергия беспорядочного движения молекул газа прямо пропорциональна абсолютной температуре.
Температура является мерой для кинетической энергии молекул, которая не зависит от ее величины. Броуновская частица из жидкости и газа обладает аналогичной средней кинетической энергией, как и другая отдельная молекула. Это суждение верно для разномассовых молекул, находящихся в одном сосуде. Состояние равновесия говорит о том, что на них действуют одинаковые средние кинетические энергии, которые определяются температурой смеси. Запись давления смеси газов запишется как сумма парциальных давлений каждого из них: p=p1+p2+p3+…=(n1+n2+n3+ …)kT.
Отсюда видно, что n1, n2, n3,… является концентрацией молекул газов в смеси. Выражение относят к молекулярно-кинетической теории, установленной Дальтоном: давление в смеси химически невзаимодействующих газов равняется сумме их парциальных давлений.
Температура – термодинамическая макроскопическая характеристика, которая играет важную роль практически во всех физических процессах. В данной статье сосредоточим свое внимание на освещении вопросов, что такое абсолютная температура газа идеального и как ее можно вычислить.
Абсолютная шкала температур
Для начала познакомимся со шкалой, которая используется в физике для описания температуры. Она называется абсолютной или шкалой Кельвина. Впервые ее ввел в использование английский физик лорд Кельвин в 1848 году. При этом ученый основывался на завоевавшей популярность шкале Цельсия.

Абсолютная температура так называется потому, что она имеет нижний предел – 0 кельвин, при котором считается “замороженным” любой вид движения (на самом деле при 0 К существуют так называемые нулевые колебания). Верхнего предела у этой шкалы нет.
С градусами Цельсия C абсолютная шкала T связана следующим простым равенством:
T = C + 273,15.
В отличие от других температурных шкал, например, от шкалы Фаренгейта, кельвин имеет точно такой же масштаб, что и градус Цельсия. Последнее означает, что для перевода в абсолютную любой температуры по Цельсию достаточно добавить к ней число 273,15. Так, по шкале Кельвина вода замерзает при 273,15 К, а кипит при 373,15 К.

Краткое понятие о газе идеальном
Поскольку далее будет рассмотрена формула для определения абсолютной температуры газа идеального, то будет полезным познакомиться с этим понятием поближе. Под идеальным понимают такой газ, молекулы которого практически не взаимодействуют друг с другом, обладают большой кинетической энергией по сравнению с потенциальной, и расстояния между которыми значительно превышают их собственные размеры.
Все реальные газы проявляют поведение идеальных при небольших давлениях и высоких температурах. Примерами могут служить благородные газы, воздух, метан и другие. В то же время пар H2O даже при низких давлениях сильно отличается от идеального газа, поскольку в нем всегда присутствуют значительные водородные связи между полярными молекулами воды.
Температура абсолютная идеального газа
Существует два подхода к определению температуры в газах. Рассмотрим каждый из них.
Первый подход заключается в привлечении положений молекулярно-кинетической теории (МКТ) и физического смысла самой температуры T. Последний заключается в кинетической энергии частиц газа. Чем больше эта энергия, тем выше температура, причем зависимость является прямо пропорциональной. Используя формулу из механики для энергии кинетической и постоянную Больцмана kB можно записать следующее равенство МКТ:
m*v2/2 = 3/2*kB*T.
Где m – масса движущейся поступательно частицы. Выражая из этого равенства величину T, получаем формулу:
T = m*v2/(3*kB).
Чем меньше масса частицы и чем больше ее скорость, тем выше абсолютная температура.
Второй подход в определении величины T заключается в использовании универсального уравнения Клапейрона-Менделеева. Это уравнение было записано в XIX веке Эмилем Клапейроном (впоследствии модифицировано Д. И. Менделеевым) как результат обобщения открытых экспериментально в XVII-XIX веках газовых законов (Шарля, Гей-Люссака, Бойля-Мариотта, Авогадро). Математически универсальное уравнение записывается так:
P*V = n*R*T.
Как видно, оно связывает три основных термодинамических величины системы: давление P, объем V и температуру абсолютную T. Две другие величины, присутствующие в уравнении, – это n – количество вещества и R – газовая постоянная.
Не представляет особого труда получить формулу для температуры из Клапейрона-Менделеева закона:
T = P*V/(n*R).
В закрытой системе (n = const) температура газа прямо пропорциональна произведению объема на давление.
Пример задачи
Воздух, которым мы дышим, является смесью газов идеальных. Известно, что молярная масса воздуха составляет 29 г/моль. Необходимо определить температуру воздуха, если средняя скорость его молекул составляет 530 м/с.
Очевидно, что решение этой задачи можно получить, если воспользоваться следующим выражением:
T = m*v2/(3*kB).
Массу одной молекулы m воздуха можно получить, если поделить величину M на число Авогадро NA. Произведение же числа NA на константу Больцмана kB – это не что иное, как газовая постоянная R, которая равна 8,314 Дж/(К*моль). Учитывая эти рассуждения, получаем рабочую формулу:
T = M*v2/(3*R ) = 0,029*6002/(3*8,314) = 326,60 К.

В градусах Цельсия найденной температуре соответствует значение 53,45 oC. На нашей планете такие температуры характерны для жарких песчаных пустынь в полдень.
Физическая дисциплина «Термодинамика», имеющая дословный перевод с греческого как θέρμη — «тепло», δύναμις — «сила», занимается изучением общих характеристик макросистем и обращения энергии внутри них. Эту науку относят к феноменологическому типу, хотя опирается она на факты, полученные опытным путем.
Термодинамическая система, рассматриваемая в данном ракурсе, имеет конкретные характеристики, не применимые к единичным атомам и молекулам. К ним относят температуру, энергию, объем, концентрацию растворов, давление.
Определение таких параметров происходит по формулам термодинамики.
Основные формулы термодинамики
Особенностью термодинамики является то, что ее постулаты не касаются взаимодействия отдельных единиц (атомов, молекул), как в молекулярной физике. Предметом изучения предстают общие взаимопревращения энергии, образование теплоты, теплопередача и совершение работы.
Исходя из этого, выделяют основные формулы термодинамики, к которым относятся:
- Уравнение Менделеева-Клайперона: (PV=(m/M)*RT). Его смысл — в изменениях трех входящих величин, которые направлены на характеристику состояния идеального газа.
- Количество вещества, обозначаемое буквой (ν). (nu=N/NA=m/mu)
Величина, выражающая, сколько одинаковых структурных компонентов (единиц) находится в веществе.
- Закон Дальтона: давление смеси газов на стенку сосуда равно сумме давлений каждого входящего в смесь элемента: (p=p1+p2+…pn.)
- Главное уравнение МКТ (молекулярно-кинетической теории): (p=2n/3<varepsilon>n=N/V). Выражает математическое соотношение таких параметров, как давление газа и микропараметров: массы молекул, их скорости движения, концентрации.
- Средняя кинетическая энергия поступательного движения молекулы газа. Для обозначения применяется (E_k), выражается через формулу: (E_k=E_{моля}/NA=3/2ast RT/NA). Ее мерой является абсолютная температура идеального газа, поскольку потенциальная энергия (вследствие взаимодействия молекул друг с другом) равна нулю. Зная, что R/NA=k, получается формула: (E_k=3/2ast kT).
- Давление идеального газа прямо пропорционально концентрации и его температуре: (P=nkT.)
- Скорость молекул определяется по формулам:
(V=surd(2kT/m_o)=surd(2RT/mu)) — наиболее вероятная;
(<V>=surd(8kT/pi m_o)=surd(8RT/pimu)) — среднеарифметическая;
(<Vкв>surd(3kT/m_o)=surd(3RT/mu)) — средняя квадратичная. - Сумма кинетических энергий всех молекул определяет внутреннюю энергию всего идеального газа. Математически выражение выглядит так: (U=i/2ast(m/mu)ast RT.)
- Формула для определения работы, которую совершает идеальный газ при расширении:( A=P(V_2-V_1).)
- Формула первого закона термодинамики: (Q=Delta U+A.)
- Для определения удельной теплоемкости вещества применяется математическое выражение: (С=Delta Q/mdT.)
- Кроме удельной теплоемкости, существует понятие молярной теплоемкости. Для ее определения применяется формула: (C=cmu). Для изохорного процесса правильная формула принимает вид: (C_v=1/2ast R), для изобарного: (C_p=((i+2)/2)ast R).
Первое начало термодинамики
Согласно первому закону термодинамики, (Q) (количество внутренней теплоты), которое получил газ извне, расходуется на совершение работы (А) и изменение внутренней энергии (U). Формула закона: (Q=Delta U+A).
На практике газ может быть нагрет либо охлажден. Однако в данном случае рассматривается изотермический процесс, в котором один из характеризующих параметров остается неизменным.
Если процесс изотермичен, в химии включается закон Бойля-Мариота. В нем говорится, что давление газа соотносится к изначальному объему, при стабильной температуре, обратно пропорционально.
(Q=A)
Когда процесс происходит при неизменном объеме, говорят об изохорности. Здесь вступает в действие закон Шарля. В обозначенных условиях то тепло, которое поступило к газу, расходуется на изменение внутренней энергии. Другими словами, (P) пропорционально (T).
(Q=Delta U)
Протекание процессов в идеальном газе при неизменном давлении носит характер изобарного. Здесь действует закон Гей-Люссака, который выражается уравнением:
(Q=Delta U=pDelta V)
Полная формулировка закона гласит: полученное тепло при изобарном процессе расходуется на совершение работы газом, а также изменяет его внутреннюю энергию.
Часть процессов происходят изолированно от внешней среды. Газ не получает дополнительной энергии. Такая ситуация носит название адиабатной и математически записывается: (Q=0). Работа (А) в таком случае выражается: (A=-Delta U.)
Уравнение идеального газа в термодинамике
Молекулы идеального газа постоянно движутся. От того насколько велика скорость их движения, зависит общее состояние газа, а также величина его воздействия, например, на стенки сосуда. Поэтому одним из основных уравнений термодинамики является Клайперона-Менделеева:
(PV=(m/M)ast RT)
В уравнении (m) — единица массы газа, (M) — его молекулярная масса, (R) — универсальная величина, называемая газовой постоянной. Ее значение = 8,3144598. Измеряется в Дж/(моль*кг).
В основе термодинамики лежат и другие газовые постоянные, например, число Авогадро, постоянная Больцмана. Таким образом, (R=kNA.)
Из уравнения Клайперона-Менделеева можно также вычислить массу. Она будет равна произведению плотности на объем: (m=rho V).
Основное уравнение молекулярно-кинетической теории (МКТ)
Решение части задач зависит от знания особенностей взаимосвязи между давлением газа и характеристикой кинетической энергии его молекул. Математическое выражение такой зависимости носит название основного уравнения МКТ:
(p=2/3ast nE)
В данном выражении кинетическая энергия обозначена буквой (Е), а концентрация молекул — (n). Каждую из этих величин физики можно найти исходя из соответствующих формул, после чего уравнение для молекулярно-кинетической теории (МКТ) приобретает вид:
(p=nkT)
Формула теплоемкости и главная формула КПД в термодинамике
Когда теплообмен проявляется передачей телу определенного количества теплоты, его энергия, как и температура, меняются.
То количество теплоты, обозначаемое (Q), которое понадобится для того, чтобы 1 кг определенного вещества нагреется на 1 К, носит определение теплоемкости вещества и обозначается с.
Математическое выражение относительно переданного количества теплоты выглядит формулой:
(Q=cm(t_2-t_1)=cmDelta t)
Измеряется величина в Дж/(кг∙К).
При t2⟩t1, количество теплоты со знаком плюс, следовательно, вещество нагревается. Если наоборот, то Q — со знаком минус, и вещество остывает.
В физике, характеризуя свойства вещества, говорят о его теплоемкости. Это имеет значение, например, при выборе стройматериалов или сырья для изготовления нагревательных приборов. Теплоемкость равна произведению массы на удельную теплоемкость данного тела:
(C=cm)
Учитывая, что в величине теплоемкости уже отражена масса, то сокращенная формула для определения (Q) выглядит так:
(Q=C(t_2-t_1))
С другой стороны, то количество теплоты, которое отдает источник, можно высчитать по формуле:
(Q=Pt.)
В выражении буквой (P) обозначается мощность нагревателя, а (t) — время их контакта.
Конструкция, состоящая из нагревателя, тела-реципиента теплоты и охладителя, носит название тепловой машины. В качестве примера рассматривается двигатель внутреннего сгорания. Как и любой механизм, она имеет такую характеристику, как КПД — коэффициент полезного действия. Для его расчета применяется формула:
(eta=(Q_н-Q_x)/Q_н)
Внутренняя энергия одноатомного и двухатомного идеального газа
Характерной особенностью идеального газа является отсутствие у его составляющих частей потенциальной энергии. Вся внутренняя энергия — это сумма кинетических энергий всех молекул. Она является величиной, прямо пропорциональной температуре идеального газа:
(mw2/2=alpha T)
В этом уравнении:
(alpha T=3Rmu/2Nmu)
Исходя из приведенных формул, величина кинетической энергии поступательного движения идеального газа должна определяться исходя из выражения:
(mv2/2=(3Rmu/2Nmu)ast T)
Поступательное движение характеризуется тремя степенями свободы. На каждую из них приходится одна треть общей кинетической энергии.
Двух- и более атомные молекулы газа характеризуются степенями свободы, касающимися вращательного движения.
Если обозначить число молекул в одном киломоле за (Nμ), то внутренняя энергия идеального газа будет измеряться по формуле:
(Umu=1/2(Rmu Ti))
В формуле (i) — число степеней свобод.
Если газ одноатомный, (i=3), двуатомный — 5, трех- и более — 6.
Задачи на термодинамику характеризуют распространенные физические процессы, поэтому часть включаются в программы экзаменов. Если для их решения не хватает времени, можно обратиться за помощью в Феникс.Хелп. На профильном сайте вам помогут справиться с любой, даже запутанной задачей, экономя ваши время и силы.
Термодинами́ческая температу́ра (англ. thermodynamic temperature, нем. thermodynamische Temperatur), или абсолю́тная температу́ра (англ. absolute temperature, нем. absolute Temperatur) является единственной функцией состояния термодинамической системы, которая характеризует направление самопроизвольного теплообмена между телами (системами)[1][2].
Термодинамическая температура обозначается буквой 
Молекулярно-кинетическая теория, со своей стороны, связывает абсолютную температуру со средней кинетической энергией поступательного движения молекул идеального газа в условиях термодинамического равновесия:
где 



История[править | править код]
Измерение температуры прошло долгий и трудный путь в своём развитии. Так как температура не может быть измерена непосредственно, то для её измерения использовали свойства термометрических тел, которые находились в функциональной зависимости от температуры. На этой основе были разработаны различные температурные шкалы, которые получили название эмпирических, а измеренная с их помощью температура называется эмпирической. Существенными недостатками эмпирических шкал являются отсутствие их непрерывности и несовпадение значений температур для разных термометрических тел: как между реперными точками, так и за их пределами. Отсутствие непрерывности эмпирических шкал связано с отсутствием в природе вещества, которое способно сохранять свои свойства во всём диапазоне возможных температур. В 1848 году Томсон (лорд Кельвин) предложил выбрать градус температурной шкалы таким образом, чтобы в её пределах эффективность идеальной тепловой машины была одинаковой. В дальнейшем, в 1854 году он предложил использовать обратную функцию Карно для построения термодинамической шкалы, не зависящей от свойств термометрических тел. Однако, практическая реализация этой идеи оказалась невозможной. В начале XIX века в поисках «абсолютного» прибора для измерения температуры снова вернулись к идее идеального газового термометра, основанного на законах идеальных газов Гей-Люссака и Шарля. Газовый термометр в течение долгого времени был единственным способом воспроизведения абсолютной температуры. Новые направления в воспроизведении абсолютной температурной шкалы основаны на использовании уравнения Стефана ─ Больцмана в бесконтактной термометрии и уравнения Гарри (Харри) Найквиста ─ в контактной.[3]
Физические основы построения термодинамической шкалы температур[править | править код]
1. Термодинамическая шкала температур принципиально может быть построена на основании теоремы Карно, которая утверждает, что коэффициент полезного действия идеального теплового двигателя не зависит от природы рабочего тела и конструкции двигателя, и зависит только от температур нагревателя и холодильника.
где 


Из приведённого выше уравнения следует соотношение:
Это соотношение может быть использовано для построения абсолютной термодинамической температуры. Если один из изотермических процессов цикла Карно 


2. Абсолютная температурная шкала может быть построена, если использовать в качестве термометрического тела идеальный газ. В самом деле, из уравнения Клапейрона вытекает соотношение
Если измерять давление газа, близкого по свойствам к идеальному, находящегося в герметичном сосуде постоянного объёма, то таким способом можно установить температурную шкалу, которая носит название идеально-газовой. Преимущество этой шкалы состоит в том, что давление идеального газа при 
3. В различных учебниках по термодинамике приводятся доказательства того, что температура, измеренная по идеально-газовой шкале, совпадает с термодинамической температурой. Следует, однако, оговориться: несмотря на то, что численно термодинамическая и идеально-газовая шкалы абсолютно идентичны, с качественной точки зрения между ними есть принципиальная разница. Только термодинамическая шкала является абсолютно независимой от свойств термометрического вещества.
4. Как уже было указано, точное воспроизведение термодинамической шкалы, а также идеально-газовой, сопряжено с серьёзными трудностями. В первом случае необходимо тщательно измерять количество теплоты, которая подводится и отводится в изотермических процессах идеального теплового двигателя. Такого рода измерения неточны. Воспроизведение термодинамической (идеально-газовой) температурной шкалы в диапазоне от 10 до 1337 K возможно с помощью газового термометра. При более высоких температурах заметно проявляется диффузия реального газа сквозь стенки резервуара, а при температурах в несколько тысяч градусов многоатомные газы распадаются на атомы. При ещё больших температурах реальные газы ионизируются и превращаются в плазму, которая не подчиняется уравнению Клапейрона. Наиболее низкая температура, которая может быть измерена газовым термометром, заполненным гелием при низком давлении равна 1 K. Для измерения температур за пределами возможностей газовых термометров используют специальные методы измерения. Подробнее см. Термометрия.
Примечания[править | править код]
- ↑ Белоконь Н. И. Основные принципы термодинамики, 1968, с. 10, 55.
- ↑ Кириллин В. А. Техническая термодинамика, 1983, с. 5.
- ↑ Різак В., Різак І., Рудавський Е. Кріогенна фізика і техніка, 2006, с. 174—175.
- ↑ Різак В., Різак І., Рудавський Е. Кріогенна фізика і техніка, 2006, с. 17—18.
Литература[править | править код]
- Украинская советская энциклопедия: в 12 томах = Українська радянська енциклопедія (укр.) / За ред. М. Бажана. — 2-ге вид. — К.: Гол. редакція УРЕ, 1974—1985.
- Малая горная энциклопедия. В 3 т. = Мала гірнича енциклопедія / (На укр. яз.). Под ред. В. С. Белецкого. — Донецк: Донбасс, 2004. — ISBN 966-7804-14-3.
- Белоконь Н. И. Термодинамика. — М.: Госэнергоиздат, 1954. — 417 с.
- Белоконь Н. И. Основные принципы термодинамики. — М.: Недра, 1968. — 112 с.
- Кириллин В. А. Техническая термодинамика. — М.: Энергоатомиздат, 1983. — 414 с.
- Вукалович М. П., Новиков И. И. Техническая термодинамика. — М.: Энергия, 1968. — 497 с.
- Сивухин Д. В. Общий курс физики. Т. II. Термодинамика и молекулярная физика. — М.: Физматлит, 2005. — 544 с. — ISBN 5-9221-0601-5.
- Базаров И. П. Термодинамика. — М.: Высшая школа, 1991. — 376 с. — ISBN 5-06-000626-3.
- Різак В., Різак І., Рудавський Е. Кріогенна фізика і техніка. — К.: Наукова думка, 2006. — 512 с. — ISBN 966-00-480-X.




