С 2022 года в первую часть ЕГЭ было добавлено задание по теме “Графики функций” Для решения задачи нужно сначала составить формулу, задающую функцию, а затем с её помощью вычислить ответ
Начнём с линейной функции, которая изучается в школьном курсе математики с 6 класса.
Линейная функция – функция вида у=кх+в, график линейной функции – прямая.
Для построения прямой (графика линейной функции) достаточно двух точек — потому что через две несовпадающие точки всегда можно провести прямую, причем единственную.
Простое задание:
На рисунке изображён график линейной функции. Напишите формулу, которая задаёт эту линейную функцию
График функции проходит через точку (0;-2), лежащую на оси Оу, значит в=-2 и уравнение прямой у=кх – 2. Осталось найти к (угловой коэффициент)
1 способ: График функции проходит через точку (5; 2), подставляем у-2, х=5 в уравнение у=кх – 2, получаем 2=к*5-2, откуда к=0,8
Таким образом, искомая формула у=0,8х-2
2 способ(для 11 класса), смотрите второе фото в галерее:
построим прямоугольный треугольник так, чтобы гипотенуза лежала на графике (на прямой), а вершины треугольника совпадали с “узлами” клеток.
Угловой коэффициент к равен tq a (тангенсу угла наклона а), а тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. Считаем по клеточкам и получаем 4/5=0,8
Ответ тот же!
Как вы понимаете, на ЕГЭ это всего лишь половина задания.
Задание 509198 с сайта Решу ЕГЭ (на сайте нет решения этого задания)
На рисунке даны графики двух линейных функций. Найдите абсциссу точки пересечения графиков
Чтобы найти точку пересечения, надо знать формулы, которыми задаётся каждая линейная функция
Начнём с синего графика. Он проходит через точку (0;1), значит в уравнении у=кх+в, в=1, осталось найти к (два способа нахождения в галерее
Итак, линейная функция, график которой построен синим цветом, задаётся формулой: у= х+1
теперь займёмся красным графиком. Здесь не видно точки пересечения с осью Оу, поэтому коэффициент в быстро не найти. Начнём с углового коэффициента, к=3/2=1,5, теперь найдём в, например возьмём точку (-2;4)
4=1,5*(-2)+в, откуда в=7, то есть линейная функция, график которой построен красным цветом, задаётся формулой: у=1,5х+7
Коэффииенты к и в можно найти и другим способом:
Это первая половина задания. Во второй находим абсциссу точки пересечения (значение х)
х+1=1,5х+7
-0,5х=7-1
х=-12
Ответ: -12
Остались вопросы? Задавайте!
построить график линейной функции:
a)
y=13x+1,x∈−6;3
; b)
y=13x+1,x∈−6;3
.
Составим таблицу значений функции:
| (x) | (-6) | (3) |
| (y) | (-1) | (2) |
Построим на координатной плоскости (xOy) точки ((-6;-1)) и ((3;2)) и
проведём через них прямую.
Далее выделим отрезок, соединяющий построенные точки.
Этот отрезок и есть график линейной функции
y=13x+1,x∈−6;3
.
Точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены тёмными кружочками.

b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)).
Поэтому точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены светлыми кружочками.

По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.
В случае
a)
y=13x+1,x∈−6;3
, имеем:
yнаиб
(= 2) и
yнаим
(= -1);
b)
y=13x+1,x∈−6;3
, концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.

Материал используется на уроке алгебры в 7 классе при изучении линейной функции.
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Слайд 1
2 урок . По графику научить определять заданную функцию. Тема «Линейная функция и её график».
Слайд 2
На рисунке представлен график функции у = kx + b. Записать формулу линейной функции, соответствующей данному графику. Так как ордината точки пересечения графика функции с осью Оy равна 1, следовательно, b=1. у = kx + 1 Выбираем на графике произвольную точку и определяем её координаты: если x = 2, то у = 2 . Подставим в нашу формулу и получим уравнение относительно k. 2 = 2k+1 2k=1 k = 0.5 Записываем формулу линейной функции: у = 0,5х + 1.
По теме: методические разработки, презентации и конспекты
- Мне нравится
Прежде чем перейти к изучению функции «y = kx»
внимательно изучите урок
«Что такое функция в математике»
и
«Как решать задачи на функцию».
Важно!

Функцию вида «y = kx + b» называют линейной функцией.
Буквенные множители «k» и «b»
называют
числовыми коэффициентами.
Вместо «k» и «b»
могут стоять любые числа (положительные, отрицательные или дроби).
Другими словами, можно сказать, что «y = kx + b» — это семейство всевозможных функций, где вместо
«k» и «b» стоят числа.
Примеры функций типа «y = kx + b».
- y = 5x + 3
- y = −x + 1
- y = x − 2
- y = 0,5x
Давайте определим для каждой функций выше, чему равны числовые коэффициенты
«k» и
«b».
| Функция | Коэффициент «k» | Коэффициент «b» | ||||
|---|---|---|---|---|---|---|
| y = 5x + 3 | k = 5 | b = 3 | ||||
| y = −x + 1 | k = −1 | b = 1 | ||||
y =
x − 2 |
k =
|
b = −2 | ||||
| y = 0,5x | k = 0,5 | b = 0 |
Обратите особое внимание на функцию «y = 0,5x»
в таблице. Часто совершают ошибку при поиске в ней числового коэффициента «b».
Рассматривая
функцию «y = 0,5x», неверно утверждать, что числового коэффициента
«b» в функции нет.
Числовый коэффициент «b» присутствет в функции типа «y = kx + b» всегда.
В функции «y = 0,5x»
числовый коэффициент «b» равен нулю.
Как построить график линейной функции
«y = kx + b»
Запомните!
![]()
Графиком линейной функции «y = kx + b» является прямая.
Так как графиком функции «y = kx + b»
является прямая линия, функцию называют линейной функцией.
Из геометрии вспомним аксиому (утверждение, которое не требует доказательств),
что через любые две точки можно провести прямую и притом только одну.
Исходя из аксиомы выше следует, что
чтобы построить график функции вида
«у = kx + b» нам достаточно будет найти всего
две точки.
Для примера построим график функции «y = −2x + 1».
Найдем значение функции «y» для двух произвольных значений «x».
Подставим, например, вместо «x» числа «0» и «1».
Важно!

Выбирая произвольные числовые значения вместо «x», лучше брать числа
«0» и «1».
С этими числами легко выполнять расчеты.
| x | Расчет «y = −2x + 1» |
|---|---|
| 0 | y(0) = −2 · 0 + 1 = 1 |
| 1 | y(1) = −2 · 1 + 1 = −2 + 1 = −1 |
Полученные значения «x» и «y» — это координаты точек графика функции.
Запишем полученные координаты точек «y = −2x + 1» в таблицу.
| Точка |
Координата по оси «Оx» (абсцисса) |
Координата по оси «Оy» (ордината) |
|---|---|---|
| (·)A | 0 | 1 |
| (·)B | 1 | −1 |
Отметим полученные точки на системе координат.
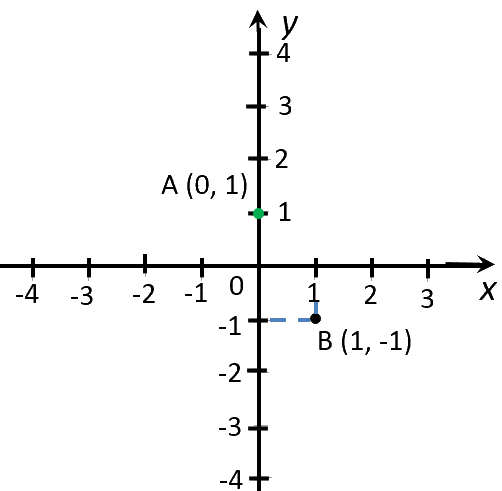
Теперь проведем прямую через отмеченные точки. Эта прямая будет
являться графиком функции «y = −2x + 1».
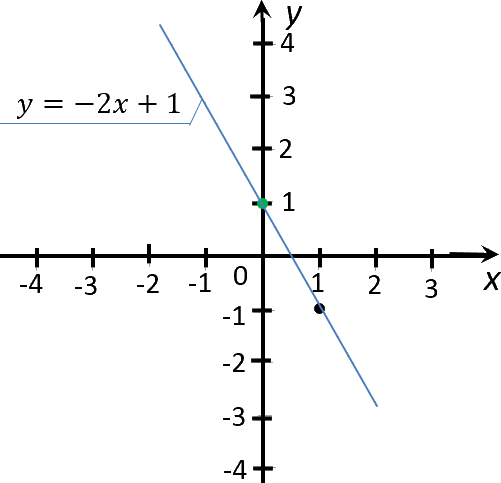
Как решать задачи на
линейную функцию «y = kx + b»
Рассмотрим задачу.
Построить график функции «y = 2x + 3». Найти по графику:
- значение «y» соответствующее значению «x» равному −1; 2; 3; 5;
- значение «x», если значение «y» равно
1; 4; 0; −1.
Вначале построим график функции «y = 2x + 3».
Используем правила, по которым мы строили график функции выше.
Для построения графика функции «y = 2x + 3» достаточно найти всего две точки.
Выберем два произвольных числовых значения для «x». Для удобства расчетов выберем числа
«0» и «1».
Выполним расчеты и запишем их результаты в таблицу.
| Точка |
Координата по оси «Оx» |
Координата по оси «Оy» |
|---|---|---|
| (·)A | 0 | y(0) = 2 · 0 + 3 = 3 |
| (·)B | 1 | y(1) = 2 ·1 + 3 = 5 |
Отметим полученные точки на прямоугольной системе координат.
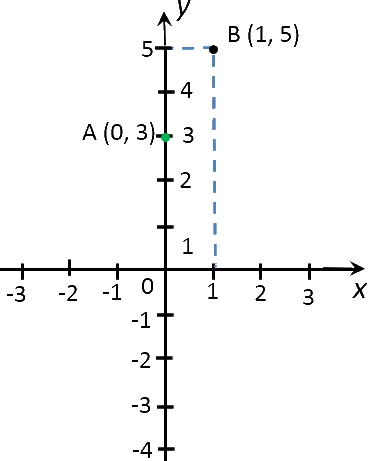
Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции
«y = 2x + 3».
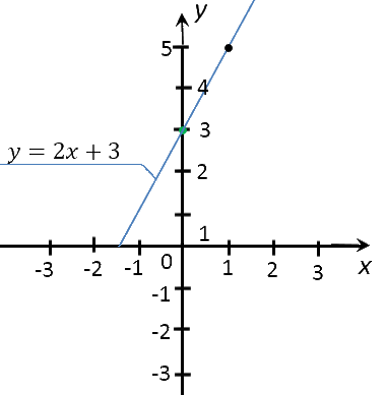
Теперь работаем с построенным графиком функции «y = 2x + 3».
Требуется найти значение «y»,
соответствующее значению «x»,
которое равно −1; 2; 3; 5.
Тему
«Как получить координаты точки функции» с графика функции
мы уже подробно рассматривали в уроке
«Как решать задачи на функцию».
В этому уроке для решения задачи выше вспомним только основные моменты.
Запомните!
![]()
Чтобы найти значение «y» по известному значению «x» на графике
функции необходимо:
- провести перпендикуляр от оси «Ox»
(ось абсцисс)
из заданного числового значения «x»
до пересечения
с графиком функции; - из полученной точки пересечения перпендикуляра и графика функции провести еще один перпендикуляр к оси
«Oy»
(ось ординат); - полученное числовое значение на оси «Oy» и будет искомым значением.
По правилам выше найдем на построенном ранее графике функции «y = 2x + 3»
необходимые значения функции «y» для
«x» равным −1; 2; 3; 5.
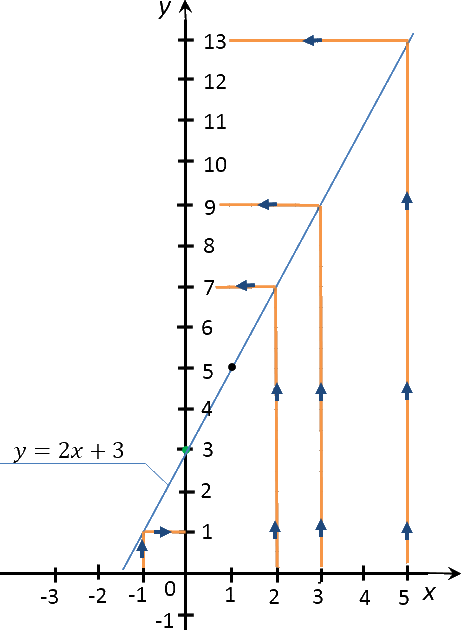
Запишем полученные результаты в таблицу.
| Заданное значение «x» | Полученное с графика значение «y» |
|---|---|
| −1 | 1 |
| 2 | 7 |
| 3 | 9 |
| 5 | 13 |
Переходим ко второму заданию задачи. Требуется найти значение «x»,
если значение «y» равно 1; 4; 0; −1.
Выполним те же действия, что и при решении предыдущего задания.
Разница будет лишь в том, что изначально мы будем проводить перпендикуляры от оси
«Oy».
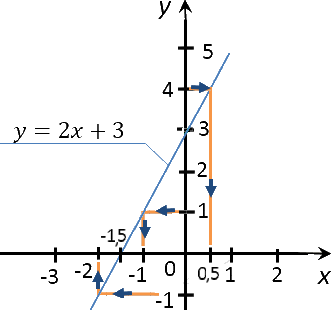
Запишем полученные результаты в таблицу.
| Заданное значение «y» | Полученное с графика значение «x» |
|---|---|
| −1 | −2 |
| 0 | −1,5 |
| 1 | −1 |
| 4 | 0,5 |
Как проверить, проходит ли график через точку
Рассмотрим другое задание.
Не выполняя построения графика функции
«y = 2x −
», выяснить, проходит ли график
через точки с координатами (0;
− ) и (1; −2).
Запомните!
![]()
Чтобы проверить принадлежность точки графику функции нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси
«Ox» вместо
«x», а координату по оси
«Oy» вместо «y») и выполнить арифметические расчеты.
- Если получится верное равенство, значит, точка принадлежит графику функции.
- Если получится неверное равенство, значит, точка
не принадлежит графику функции.
Подставим в функцию
«y = 2x −
»
координаты точки (0;
− ).
− = 2 · 0
−
− =
−
(верно)
Это означает, что график функции «y = 2x −
» проходит через точку с координатами (0;
− ).
Проверим точку с координатами (1; −2).
Также подставим координаты
в функцию «y = 2x −
».
−2 = 2 · 1 −
−2 = 2 −
−2 = 1 −
−2 = 1 (неверно)
Это означает, что график функции «y = 2x −
» не проходит через точку с координатами (1; −2).
Как найти точки пересечения графика с осями
Рассмотрим задачу.
Найти координаты точек пересечения графика функции «y = −1,5x + 3» с осями координат.
Для начала построим график функции «y = −1,5x + 3» и на графике отметим точки пересечения
с осями.
Для построения графика функции найдем координаты двух точек
функции
«y = −1,5x + 3».
Выберем два произвольных числовых значения для «x» и рассчитаем значение
«y» по формуле
функции. Например, для x = 0 и
x = 1.
| Точка |
Координата по оси «Оx» |
Координата по оси «Оy» |
|---|---|---|
| (·)A | 0 | y(0) = −1,5 · 0 + 3 = 3 |
| (·)B | 1 | y(1) = −1,5 · 1 + 3 = 1,5 |
Отметим полученные точки на системе координат и проведем через них прямую.
Тем самым мы построим график функции «y = −1,5x + 3».
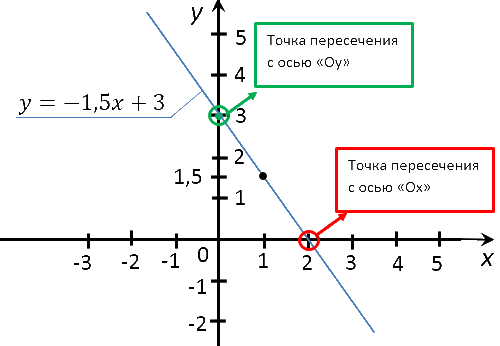
Теперь найдем координаты точек пересечения графика функции с осями по формуле функции.
Запомните!
![]()
Чтобы найти координаты точки пересечения графика функции
с осью
«Oy»
(осью ординат)
нужно:
- приравнять координату точки по оси
«Ox» к нулю
(x = 0); - подставить вместо «x» в формулу функции ноль и найти значение
«y»; - записать полученные координаты точки пересечения с осью
«Oy».
Подставим вместо «x» в формулу функции «y = −1,5x + 3» число ноль.
y(0) = −1,5 · 0 + 3 = 3
(0; 3) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Oy».
Запомните!
![]()
Чтобы найти координаты точки пересечения графика функции
с осью
«Ox»
(осью абсцисс)
нужно:
- приравнять координату точки по оси
«Oy» к нулю
(y = 0); - подставить вместо «y» в формулу функции ноль и найти значение
«x»; - записать полученные координаты точки пересечения с осью
«Oy».
Подставим вместо «y» в формулу функции «y = −1,5x + 3» число ноль.
0 = −1,5x + 3
1,5x = 3 | :(1,5)
x = 3 : 1,5
x = 2
(2; 0) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Ox».
Чтобы было проще запомнить, какую координату точки нужно приравнивать к нулю, запомните
«правило противоположности».
Важно!

Если нужно найти координаты точки пересечения графика с осью
«Ox», то приравниваем
«y» к нулю.
И наооборот. Если нужно найти координаты точки пересечениа графика с осью
«Oy»,
то приравниваем «x» к нулю.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
19 мая 2023 в 9:06
Михаил Лысенко

Профиль
Благодарили: 0
Сообщений: 1

Михаил Лысенко
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
19 мая 2023 в 13:04
Ответ для Михаил Лысенко
Борис Гуров

Профиль
Благодарили: 1
Сообщений: 28

Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Добрый день!
Это квадратичная функция. Они разобраны в другом уроке
0
Спасибо
Ответить
