2016-12-18 ![]()
Кольцо радиуса $R$, по которому циркулирует ток $I$, поместили в однородное магнитное поле с индукцией $B$, перпендикулярное плоскости кольца. С какой силой растянуто кольцо? Действием на кольцо магнитного поля, создаваемого током кольца, пренебречь.
Решение:

Запишем закон Ньютона (условие равновесия) для малого элемента кольца длиной $l$, опирающегося на угол $2 alpha$:
$vec{T}_{1} + vec{T}_{2} + vec{F}_{A} = 0$, (1)
где $T_{1} = T_{2} = T$ — сила, с которой растянуто кольцо,
$F_{A} = BIl$ (2)
сила Ампера, действующая на элемент кольца $l$, по которому течет ток $I$ (учтено, что угол между вектором $B$ и направлением тока $I$ равен $90^{ circ}$).
Проецируя (1) на ось $x$:
$2T sin alpha = F_{A}$
и учитывая, что $l = R 2 alpha$ и для малых $alpha sin alpha approx alpha$, получаем:
$T = BIR$.
Примечание.
При рассмотренном в данной задаче взаимном расположении кольца с током и индукции магнитного поля $B$, кольцо находится в состоянии устойчивого равновесия. При изменении направления вектора $B$ или изменении направления тока в кольце равновесие кольца становится неустойчивым: кольцо уже не растягивается магнитным полем, а сжимается.
Другой вариант решения задачи основан на использовании закона Ньютона (условия равновесия) полукольца.

Разобьем полукольцо на малые фрагменты $l_{i}$. Силу $vec{F}$ действующую на полукольцо со стороны магнитного поля, представим в виде
$vec{F} = sum vec{F}_{i}$, (3)
где $F_{i} = BIl_{i}$. Спроецируем (3) на ось $x$:
$F = sum F_{ix} = sum BIl_{i} sin alpha_{i} = BI sum l_{i} sin alpha_{i} = BI sum l_{0i} = BI2R$. (3x)
Условие равновесия полукольца
$2T = F$. (4)
Из (3x, 4) находим $T = BIR$.
Задачи, тесты
Е. Г.
Петрова,
гимназия № 2, г. Раменское, Московская обл.
Общий метод решения задач из разных разделов
Любой учитель, долгое время работающий в профильном классе, в конце концов приходит к двум выводам:
• невозможно разобрать на уроках все интересные задачи из методической копилки учителя, тем более что их всё больше и больше. Значит, нужно осваивать на примере ключевых задач общие методы и приёмы решения, обучая ребят не количеством, а качеством подобранных задач;
Статья подготовлена при поддержке компании «Maxceiling». Если Вы решили приобрести качественные и надежные натяжные потолки, то оптимальным решением станет обратиться в компанию «Maxceiling». Перейдя по ссылке: «натяжные потолки Балашиха», вы сможете, не отходя от экрана монитора, оставить заявку на установку натяжных потолков. Более подробную информацию о ценах и акциях действующих на данный момент вы сможете найти на сайте www.Maxceiling.Ru.
• ребёнок не может долго помнить приём решения, если его не повторять время от времени. И вот тут оказывается очень продуктивным подбирать задачи, имеющие тот же алгоритм, или приём решения, что и в предыдущей теме, даже если темы не связаны. Тогда ученика не пугает бесконечное количество задач.
Необходимо отметить, что если предлагаемый метод не будет закреплён в следующих темах, то, как бы хорошо он ни был усвоен, большинство учащихся его забывает. Неоднократное возвращение к знакомому методу происходит иногда очень неожиданно. Приводим пример решения известной задачи в теме «Механика» и использование этого алгоритма в других, казалось бы, не связанных темах.
Тема «Механика»
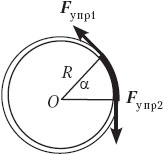
• Из резинового жгута длиной L и массой m изготовлено кольцо. Это кольцо вращается с угловой скоростью ω в горизонтальной плоскости вокруг вертикальной оси, проходящей через его центр. Определите силу натяжения, возникающую в кольце.
Метод решения этой задачи специфичен потому, что каждый элемент жгута при вращении имеет своё направление центростремительного ускорения, а значит, сила, действующая на каждый элемент, меняет своё направление от элемента к элементу. К тому же ученики помнят, что закон Гука применяется при упругих растяжениях прямолинейного стержня. Поэтому метод заключается в разбиении кольца на бесконечное количество малых элементов, которые практически прямолинейны в силу малости их размеров, и применении второго закона Ньютона отдельно для каждого элемента:
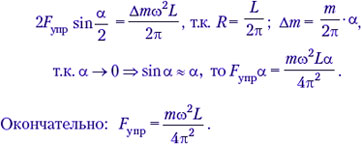
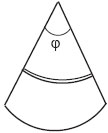
• Кольцо массой m изготовлено из проволоки, которая обрывается при силе натяжения Т0. Кольцо помещают на идеально гладкий конус. При каком минимальном плоском угле конуса φ кольцо не разорвётся?
При решении этой задачи необходимо рассмотреть условие покоя малого элемента на гладкой наклонной плоскости, но алгоритм решения аналогичен.
Рассмотрим условие покоя малого элемента кольца:
Ni + mig + Tупр.рез = 0.
Силу результирующего натяжения Tупр.рез находим, как в предыдущей задаче:

• Жёсткость резинового жгута длиной L и массой m равна k. Кольцо, изготовленное из жгута, вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через центр кольца. Оцените, при какой угловой скорости вращения кольца ω радиус его будет равен R.
Решение аналогично предыдущей, однако требуется вспомнить закон Гука
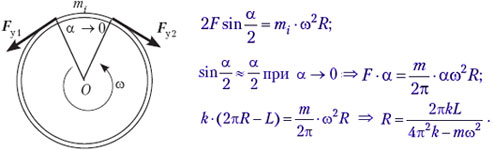
Тема «Электростатика»
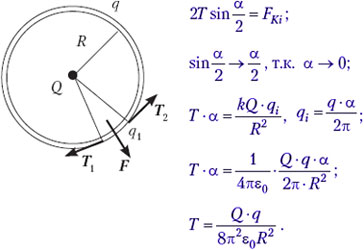
• Тонкое проволочное кольцо радиусом R несёт электрический заряд q. В центре кольца расположен одноимённый с q заряд Q, причём Q ≫ q. Определите силу Т, растягивающую кольцо.
Решение. Условие равновесия элемента кольца:
Тема «Электромагнетизм»
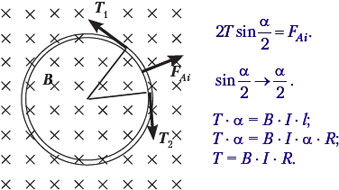
• Тонкое металлическое кольцо радиусом R помещается в однородное магнитное поле индукцией В так, что плоскость кольца перпендикулярна линиям магнитного поля. Определите силу упругости Т, возникающую внутри кольца при пропускании по нему тока силой I.
Тема «Механические колебания»
• Тонкое кольцо радиуса R совершает осесимметричные колебания. Определите период колебаний Т кольца. Кольцо изготовлено из материала плотностью ρ, имеющего модуль упругости Е.
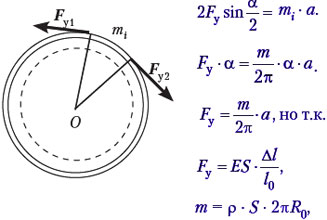
R – R0 = х – смещение элемента кольца вдоль радиуса при колебании относительно положения равновесия, причём ax < 0 при х = 0, то:
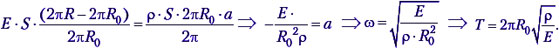
Тема «Движение в вязкой среде»
• Тело массой m, имеющее начальную скорость υ0, попадает в вязкую среду, сила сопротивления движению тела которой пропорциональна его скорости: F = αυ, где α – известный коэффициент. Определите путь, пройденный телом до остановки.
Для решения этой задачи на движение тела под действием переменной силы требуется освоение особой методики: пользоваться законами равноускоренного движения для определения пройденного пути нельзя. Алгоритм решения вновь сводится к тому, чтобы разбить всё время движения на бесконечно малые интервалы времени и рассмотреть движение отдельно на каждом таком интервале.
Для кинематических величин используем определение мгновенной скорости и мгновенного ускорения:
Fмгн = mамгн; –αυмгн = mамгн.
Но поскольку 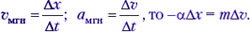
Просуммировав эти уравнения по всем интервалам времени, получаем: αs = mυ0. И окончательно: 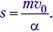
Тема «Электромагнитная индукция»
• По горизонтальным параллельным рельсам, расстояние между которыми равно d, может скользить без трения перемычка массой m. Рельсы соединены резистором сопротивлением R и помещены в вертикальное однородное магнитное поле индукцией В. Перемычке сообщают скорость υ0. Найдите путь s, пройденный перемычкой до остановки.
Cитуация аналогична рассмотренным. Зная, что изменение магнитного потока через замкнутый контур приведёт к возникновению индукционного тока, а значит, к возникновению силы Ампера, действующей на перемычку, запишем: 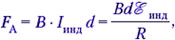 но
но 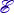 инд = В · υ · d, поэтому окончательно получаем
инд = В · υ · d, поэтому окончательно получаем 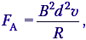 т.е. опять движение тела под действием силы, зависящей от скорости, – переменной силы, как и в предыдущей задаче. Учитываем, что сила Ампера направлена, в соответствии с правилом Ленца, против направления движения перемычки, и применяем приём для расчёта тормозного пути из предыдущей задачи:
т.е. опять движение тела под действием силы, зависящей от скорости, – переменной силы, как и в предыдущей задаче. Учитываем, что сила Ампера направлена, в соответствии с правилом Ленца, против направления движения перемычки, и применяем приём для расчёта тормозного пути из предыдущей задачи: 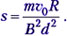
Тема «Движение заряженной частицы в магнитном поле»
• Вязкая жидкость помещена в однородное магнитное поле индукцией В. Частица массой m и зарядом q влетает в жидкость со скоростью υ0 перпендикулярно вектору В. Вязкая среда действует на частицу с силой сопротивления, пропорциональной скорости частицы υ: Fсопр = –kυ. Определите модуль перемещения частицы от момента попадания в среду до полной остановки.
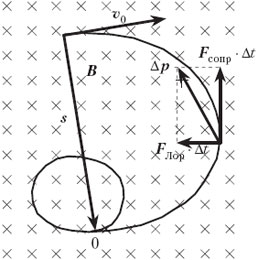
В этой задаче на частицу действуют даже две переменные силы, пропорциональные скорости: сила сопротивления Fсопр и сила Лоренца FЛор, причём эти силы взаимно перпендикулярны. Метод решения задачи тот же.
Fсопр = –kυ ⇒ Fсопр⇅ υ;
FЛор = qυ × B ⇒ FЛор ⊥ υ ⇒ FЛор ⊥Fсопр.
Рассмотрим элемент движения частицы (векторное сложение):
(Fсопр + FЛор)Δti = Δpi ⇒ –kυΔti + qυΔti × B = Δpi.
Подобный треугольник векторов образуют соответствующие векторы в течение всего времени движения частицы, поэтому, суммируя эти равенства, получим для перемещения s в точку остановки:
–ks + qs × B = – mυ0.
По теореме Пифагора, для векторного треугольника k2s2 + q2s2B2 = m2υ02. Отсюда находим модуль перемещения:
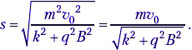
Таких «перекрёстных» задач, решать которые можно одним и тем же методом, можно найти немало, и это помогает учителю. В статье использовались тексты задач, предложенных на конкурсных испытаниях при поступлении в МГТУ им. Н.Э.Баумана и МФТИ.
UptoLike
- « Задача 417
- Задача 419 »
40
Тонкое проводящее кольцо с током (I = 40) А помещено в однородное магнитное поле ((B = 80) мТл). Плоскость кольца перпендикулярна линиям магнитной индукции. Радиус (R) кольца равен 20 см. Найти силу (F), растягивающую кольцо.

- « Задача 417
- Задача 419 »
ОПРЕДЕЛЕНИЯ
- расстояние или прямая от центра окружности или сферы к любой точке окружности или поверхности сферы
- мера действия на данное материальное тело со стороны других тел или полей
- скалярная характериска электрического тока i; равна отношению заряда Δq, переносимого через поперечное сечение проводника за время Δt, i = Δq/Δt
- основная характеристика магнитного поля (B) средняя суммарная напряженность микроскопических магнитных полей, созданных отдельными электронами и другими элементарными частицами
- поле, в любой точке которого сила действия на магнитную стрелку одинакова по модулю и направлению
Дополнительные материалы
Для данной задачи нет дополнительных материалов
Похожие задачи







Растяжение кругового кольца
Растягивание круговое кольцо Когда равномерно распределенные радиальные силы действуют вокруг тонкого круглого кольца(рис. 28), они вызывают равномерное удлинение ring. To определив натяжение P кольца, представим, что кольцо разрезано с горизонтальным диаметральным сечением (рис.28, Б), а верхняя часть считается свободным телом.
- Если ^означает равномерную нагрузку на единицу длины оси кольца, а r-радиус оси, то сила, действующая на элемент кольца, вырезается на 2 соседних участках(p, где Лф-центральный угол, соответствующий элементу. Воздействуя на одну половину кольца, которая принимает сумму вертикальных составляющих всех сил, получаем следующее уравнение равновесия О Откуда? Р = qр. (13)
Растягивающее напряжение кольца получается путем деления силы р на площадь поперечного сечения кольца*). В практических применениях, часто необходимо определить напряжение на растяжение вращая кольца. С этим. Рис.28.
Случай q представляет собой центробежную силу на единицу длины кольца и определяется из уравнения
Людмила Фирмаль
Где Q-вес единицы длины кольца, g-радиус оси, а v-скорость движения точки кольца по радиусу. ковер-это ускорение силы тяжести. Подставляя это выражение вместо q в уравнение (13), оно выглядит следующим образом: p_W. е 9. Соответствующее растягивающее напряжение П с г в ’ Видно, что напряжение пропорционально плотности материала V. 2) и Квадрат окружной скорости.
Если стальное кольцо и скорость v = 30 м / с, то это напряжение составит 72 кг / cm2.So, в том же материале, для разных скоростей vx, если vt выражается в метрах в секунду, напряжение составит 0,08 oj кг / см2. * ) Для тонких колец уместно предположить, что напряжение равномерно распределено по всему поперечному сечению кольца(см. Часть II). а) для тонких колец скорость на оси может быть такой же, как и окружная скорость.
- 1.Определите максимальное растягивающее напряжение стенки пресс-цилиндра, показанное на рисунке. Если внутренний диаметр составляет 25 см, а толщина стенки-2,5 СМ5. Решение. Максимальное гидростатическое давление p в цилиндре получается из следующего уравнения: СТ 25 * П — = 40 ООО кг、 Где Р = 81,5 кг / см2.Разрезаем базовое кольцо от цилиндра до оси цилиндра, которая имеет ширину 1 см, и применяем формулу (13). в этом случае c = p = » = 81,5 кг! См и г-12,5 см、 Рисунок 29. Р 81.5-12.5. а-у= — 2-57Г — = 407″5 k * 1 cmg、
2.Поскольку медная трубка прочно прикреплена к стальной трубе при высокой температуре (рис. 29), давление между трубками при этой температуре отсутствует. Определите напряжение, возникающее в меди и стали при охлаждении трубы до комнатной температуры t (t, наружный диаметр стальной трубы (I, толщина стальной трубы LS, толщина медной трубы Im
Решение. должный к разнице в коэффициентах линейного расширения am и ac, охлаждать создает давление между наружной пробкой и внутренней трубкой. когда x-давление на 1 см2, растягивающее напряжение медной трубки составляет °м 2LM * Сжимающее усилие стальной трубы Х(1 ′ Потому что давление х определяется из условия, что относительное укорочение при охлаждении обеих труб одинаковое、 °И (- <0> — 2vs ( ’ — / ‘ ) + 21dG ’ Откуда? HL к, АА.) 2л». +£с
Аналогичным образом можно рассчитать напряжение стальной трубы. 3, Каким будет дополнительное напряжение трубки при воздействии внутреннего гидростатического давления Р » 6,6 кг / см?В этом случае внутренняя 20. Диаметр (1X = 10cm. Ls= 0,3 см и Am = d-0,3 см(см. рис. 29). Решение. Если отрезать основное кольцо шириной 1 см от трубки, то максимальное натяжение кольца будет следующим: Р = 33 кг.
В связи с тем, что относительное окружное удлинение меди и стали одинаково, напряжение пропорционально модулю упругости. То есть, напряжение тока меди будет усилием steel. At в то же время 20. Таким образом, сила Р равномерно распределяется на 2 металла, а растягивающее напряжение меди, вызванное гидростатическим давлением, составляет = 2?G = — 2ÏG= 3° ’ 3 Kg1SMK 2-ю-0,3 Напряжение в стали os-am= 55 кг / СМГ.
4.Составное кольцо состоит из внутреннего медного кольца и наружного стального кольца. Внутренний диаметр стального кольца в 6 раз меньше наружного диаметра медного кольца. Поэтому, система собрана после подогревать стальное кольцо. Во время охлаждения стальное кольцо оказывает давление на медное кольцо(давление из-за усадки).
Поперечное сечение обоих колец прямоугольное, радиальные размеры Ls и Am, а размерность в направлении, перпендикулярном плоскости кольца, равна 1. Размеры LS и Lm можно считать небольшими по сравнению с диаметром d, который является контактной поверхностью 2 колец. Решение. пусть x-равномерно распределенное давление на 1 см2 контактной поверхности кольца.
Напряжение сжатия меди и напряжение растяжения стали определяются из уравнения х <1 ху 0, «- 2л „°с-2 л, “ (с) М. При уменьшении наружного диаметра медного кольца КА°М А И-2л Кен- Увеличение внутреннего диаметра стального кольца А, эйс, ХС? — EU 2HP£S ’
Неизвестное давление x выводится из уравнения Т (*+о: И- Откуда? Где мы находим напряжение из уравнения (a) б //£е £ б £ с Су » — тг = с д д сме. 1 + Я£м + * * * £» а. по вращению кольца с постоянной скоростью N оборотов в минуту определите напряжение, возникающее в составном кольце предыдущей задачи Решение. Поскольку медь плотнее стали и имеет более низкий модуль упругости, вращение медного кольца создает давление в стальном кольце (x = 1 см *контактной поверхности между 2 кольцами).
Тогда соответствующее напряжение определяется из уравнения (а)предыдущего problem. In кроме этих напряжений, необходимо учитывать напряжения, возникающие от центробежных сил. Через усы утяжелите единицу объема стали и меди, используя формулу (15)、 -я нет.) «Нет■» Добавляя эти напряжения к напряжению от давления x, заметим, что относительное удлинение объема кольца одинаково, получим следующее уравнение для определения x:
Таким образом, вы можете вычислить x для каждого конкретного случая
Людмила Фирмаль
Зная x, вы можете найти полное напряжение меди и стали без каких-либо проблем. 6.Допустимые напряжения[st)= 200 кг / см2 и * fM-8,8 г / см1 определяют предельную скорость движения медного кольца. Ответ, v = 48,3 м / с.
7.Определите напряжение меди при комнатной температуре(см. Задание 2) Для рис. 29)/ / / 0 = 55°C, am-ac-40-10 ″ Ls = Lm. •Ответ. am = 156,2 кг / см2. 8.In Задача 5, если начальное напряжение при сборке в одном кольце равно A0, Li = hc,£c = 2£m при сжатии, определить число оборотов n>min ®, при котором напряжение в медном кольце равно нулю.
Решение. Скорость вращения N определяется из уравнения 9.Найдите напряжение составного кольца в задаче 4.Настройки 6 = * 0.003 см, d = 10 см, hc = hK и — = r — = 2.Температура М. Кольцо после сборки увеличивается на 10°C. am= 165 * 10″ 7 и ac = 125 * 10 ″ 7. Ответ. am-as = 200 кг / см .Величина изменения напряжения составляет 27 кг / см2. 10.In Задача 5, найти напряжения в Стали и меди при l = 3000 об / мин, d = 60 см, Ls =£m = 1,2 см, mf = 7,8 г / см и M = 8. 8 г! См.*
Смотрите также:
Предмет сопротивление материалов: сопромат

Меню
- Главная
- Заказ решений
- Готовые решения
- Статьи
- Новости
- Авторы
Есть идеи?
Решения Чертовасайт решений Чертова А.Г. Воробьева А.А.
Поиск
Глава5. Электромагнетизм (§ 21-27) >> §22 Сила, действующая на проводник с током в магнитном поле >> задача – 22.5
Условие:
По тонкому проводу в виде кольца радиусом R=20 см течет ток I=100 А. Перпендикулярно плоскости кольца возбуждено однородное магнитное поле с индукцией В=20 мТл. Найти силу F, растягивающую кольцо.
При клике на картинку откроется ее увеличенная версия в новой вкладке.
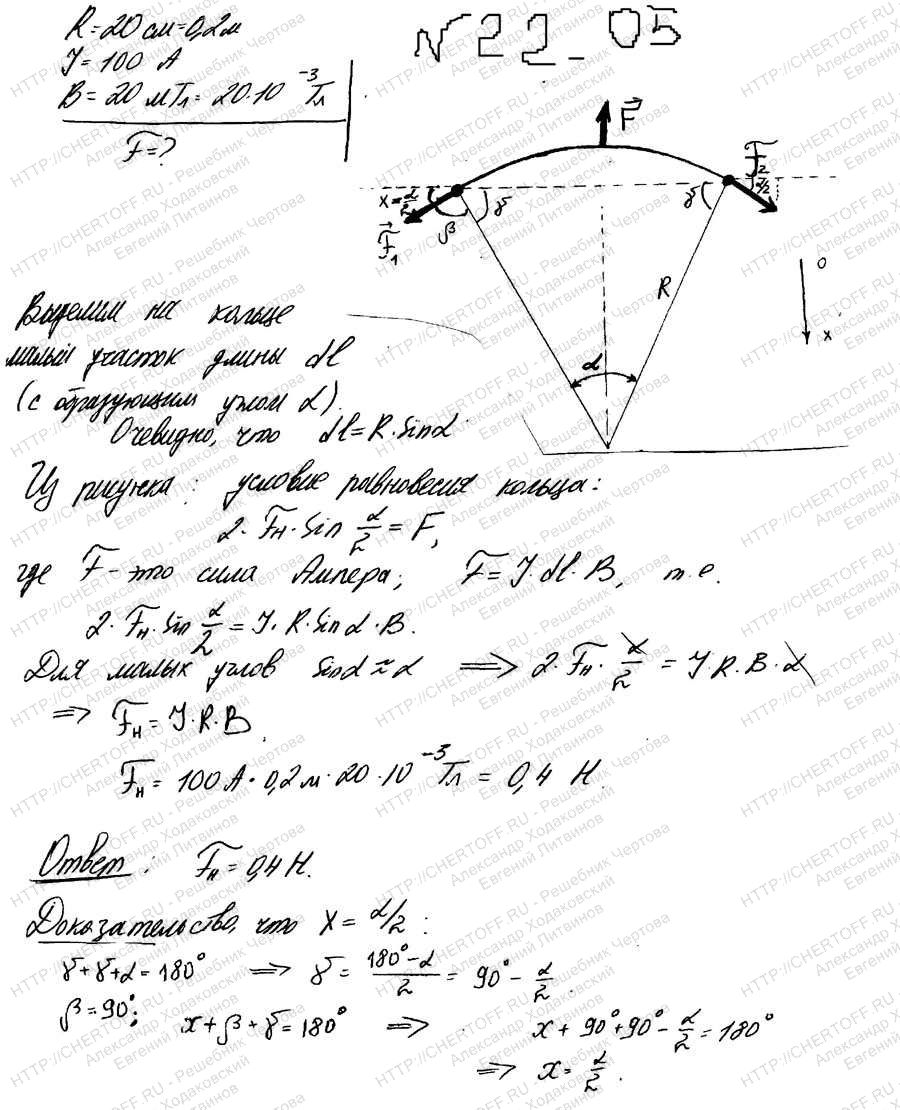
Не забываем поделиться записью!
Последние статьи
- Подходы к решению задач по физике
- Что такое физика и какие задачи и вопросы она решает?
- Общие рекомендации по решению статистических задач
- Он-лаин или офф-лаин обучение? Что выбрать?
- Изучение геометрии в восьмом классе без хлопот становится реальностью
Наши партнеры

© 2012 Решения Чертова | Авторы Bandit & AJ Акции | Sitemap | FAQ&ask
![]()
