Синусом угла в прямоугольном треугольнике называют отношение противолежащего катета к гипотенузе.
Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.
Для простоты запоминания можно дать такое определение: синус угла — это отношение дальнего от рассматриваемого угла катета к гипотенузе.
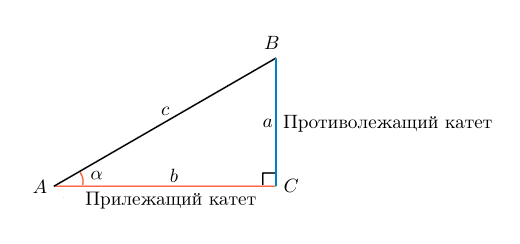
В случае с рисунком, описанным выше: sinα=acsinalpha=frac{a}{c}
В треугольнике, один из углов которого равен 90 градусам, известен катет при угле αalpha и равен он 3 см3text{ см}. Также дано произведение длин катетов и равно 12 см212text{ см}^2. Найдите синус угла αalpha.
Решение
Сначала нужно найти длину неизвестного нам катета. Для этого воспользуемся данным нам произведением. Обозначим неизвестный катет за xx. Тогда, по условию задачи:
3⋅x=123cdot x=12
x=123=4x=frac{12}{3}=4
a=x=4a=x=4
По теореме Пифагора найдем гипотенузу:
a2+b2=c2a^2+b^2=c^2
42+32=c24^2+3^2=c^2
25=c225=c^2
c=5c=5
sinα=ac=45=0.8sinalpha=frac{a}{c}=frac{4}{5}=0.8
Ответ
0.80.8
Вычислите синус 45 градусов.
Решение
Для этого воспользуемся тригонометрической таблицей углов. Находим, что:
sin45∘=π4=0.785sin 45^circ=frac{pi}{4}=0.785
Ответ
0.7850.785
Если в задаче известен косинус угла и нужно найти его синус, то наличие известных длин катетов и гипотенузы не обязательны. Достаточно просто воспользоваться основным тригонометрическим тождеством, которое имеет следующий вид:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
αalpha — любой угол.
Квадрат косинуса угла в треугольнике равен 0.8. Найдите синус данного угла.
Решение
Воспользуемся основным тригонометрическим тождеством:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
sin2α+0.8=1sin^2alpha+0.8=1
sin2α=0.2sin^2alpha=0.2
sinα=0.2sinalpha=sqrt{0.2}
sinα≈0.447sinalphaapprox0.447
Ответ
0.4470.447
Испытываете проблемы с вычислением синуса? Оформите задачу по математике на заказ у наших экспертов!
Тест по теме «Вычисление синуса»
Перевести косинус в синус и обратно
Перевести косинус в синус (cos в sin) и обратно
Перевести:
Значение cos(x):
Угол, градусы:
Значение sin(x):
Популярные сообщения из этого блога
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн – косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о “Использование сердечного индекса Руфье в медико-спортивном контроле”. Проба Руфье – представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор – онлайн tg φ: cos φ: ± Поделиться в соц сетях:
Уведомление
Cookie
Калькулятор приведения тригонометрических функций
Калькулятор выполняет приведение к тригонометрическим функциям выражений, содержащих такие функции как: синус, косинус, тангенс, котангенс, секанс, косеканс. Помимо выражения тригонометрических функций через другие, калькулятор также выполнит тригонометрические преобразования, через тригонометрические тождества.
Тригонометрические функции записываются как:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс cot(x), секанс sec(x), косеканс csc(x).
Примеры: sin(5π/6), cos(π/3), sin(2π-t), tan(π + t), x-sin(π/5)+cos(π/3), sin(x)^2 + cos(x)^2 и т.д.
Найти синус через косинус, тангенс, котангенс, секанс, косеканс угла
Онлайн калькулятор тригонометрических функций предназначен для того, чтобы быстро найти ответ на задачу, в которой нужно рассчитать, чему равен синус, косинус, тангенс онлайн.
Здесь также выполняется расчет котангенса, секанса, косеканса, версинуса, коверсинуса, гаверсинуса, экссеканса и экскосеканса. Единицы измерения – градусы, минуты, секунды. Ответ вычисляется после нажатия на кнопку “Решить”.
Пример задачи. Используем онлайн калькулятор синуса, косинуса, тангенса для того, чтобы найти синус и тангенс, зная косинус угла А в виде дроби Cos A = 1/3. В поле “тригонометрическая функция” указывается “cos”, “числитель” — число “1”, “знаменатель” — число “3”.
Решение синусов и тангенсов:
По таблице “Косинусы” находим значение угла A с градусами и минутами = 70,528779° = 70°32′.
Так как Sin2 + Cos2 = 1, то, используя тригонометрический калькулятор синусов онлайн:
1) значение синуса Sin A = √1 – (1/3)2 = √9/9 – 1/9 = √(9 – 1)/9 = √8/9 = 2,828427 / 3 = 0,942809;
2) значение тангенса tg A = Sin A / Cos A = (2,828427 / 3) • (3/1) = 8,485281/3 = 2,828427.
Пример задачи. Найти синус, тангенс через косинус угла А = Cos A = -0,5 с помощью онлайн калькулятора синусов, косинусов, тангенсов, котангенсов. В поле “тригонометрическая функция” указывается “cos”, “числитель” — число “- 0,5”.
Решение синусов и тангенсов:
По таблице “Косинусы” находим угол A в градусах = 120° = 120°0′.
Используем формулу основного тригонометрического тождества
Sin2 + Cos2 = 1. Далее требуется вычислить синус.
1) значение синуса Sin A = √1 – (-0,5)2 = √1 – 0,25 = √0,75 = 0,866025;
2) значение тангенса tg A = Sin A / Cos A = 0,866025 / -0,5 = -1,732051.
Пример задачи.
Используем калькулятор синусов и косинусов градусов, минут, секунд онлайн, чтобы найти значение синуса, косинуса, тангенса, котангенса угла A = 12°34’56” = 12 градусов 34 минуты 56 секунд.
Решение:
A = 12°34’56” = 12,582222°
Синус угла sin 12°34’56” = 0,2178404227.
Косинус угла cos 12°34’56” = 0,9759844015.
Тангенс угла tg 12°34’56” = sin 12°34’56” / cos 12°34’56” = 0,2232007218.
Котангенс угла ctg 12°34’56” = cos 12°34’56” / sin 12°34’56” = 4,4802722491.
Секанс sec 12°34’56” = 1 / cos 12°34’56” = 1,0246065402.
Косеканс cosec 12°34’56” = 1 / sin 12°34’56” = 4,5905162484.
Версинус versin 12°34’56” = 1 – cos 12°34’56” = 0,0240155994.
Коверсинус coversin 12°34’56” = 1 – sin 12°34’56” = 0,7821595773.
Гаверсинус haversin 12°34’56” = 0,0240155994 / 2 = 0,0120077997.
Экссеканс exsec 12°34’56” = 1,0246065402 – 1 = 0,0246065402.
Экскосеканс excsc 12°34’56” = 4,5905162484 – 1 = 3,5905162484.
Дано:
ΔABC – прямоугольный треугольник,
гипотенуза AB = c,
катет BC = a,
катет AC = b,
Таблица значений синуса угла
В геометрии синус угла A – отношение противолежащего катета “a” к гипотенузе “c”.
Математическая формула синуса. sin A = a/c

Синус угла 0 градусов: sin 0° = sin 0 = 0
Синус угла 30 градусов: sin 30° = sin (π/6) = 1/2
Синус угла 45 градусов: sin 45° = sin (π/4) = √2/2
Синус угла 60 градусов: sin 60° = sin (π/3) = √3/2
Синус угла 90 градусов: sin 90° = sin (π/2) = 1
Синус угла 180 градусов: sin 180° = 0
Таблица косинуса угла
Косинус угла A – отношение прилежащего катета “b” к гипотенузе “c”.
Формула косинуса. cos A = b/c
Косинус угла 0 градусов: cos 0° = cos 0 = 1
Косинус угла 30 градусов: cos 30° = cos (π/6) = √3/2
Косинус угла 45 градусов: cos 45° = cos (π/4) = √2/2
Косинус угла 60 градусов: cos 60° = cos (π/3) = 1/2
Косинус угла 90 градусов: cos 90° = cos (π/2) = 0
Косинус угла 180 градусов: cos 180° = –1
Таблица тангенса угла
В тригонометрии тангенс угла A – отношение противолежащего катета “a” к прилежащему катету “b”.
Геометрическая формула тангенса. tg A = a/b
Тангенс угла 0 градусов: tg 0° = tg 0 = 0
Тангенс угла 30 градусов: tg 30° = tg (π/6) = √3/3
Тангенс угла 45 градусов: tg 45° = tg (π/4) = 1
Тангенс угла 60 градусов: tg 60° = tg (π/3) = √3
Тангенс угла 90 градусов: tg 90° = tg (π/2) = не определяется
Тангенс угла 180 градусов: tg 180° = 0
Котангенс угла
Котангенс угла A – отношение длины прилежащего катета “b” к противолежащему катету “a”.
Формула котангенса. ctg A = b/a
Секанс
Секанс угла A равен отношению гипотенузы “c” к длине прилежащего катета “b”.
Формула секанса. sec A = c/b
Косеканс
Косеканс угла A – отношение гипотенузы “c” к противолежащему катету “a”.
Формула косеканса. cosec A = c/a
Версинус
Формула версинуса. versin A = 1 — cos A.
Коверсинус
Коверсинус рассчитывается как coversin A = 1 — sin A.
Гаверсинус
Формула гаверсинуса. haversin A = (versin A)/2.
Экссеканс
Экссеканс вычисляется по формуле: exsec A = sec A — 1.
Экскосеканс
Формула экскосеканса. excsc A = cosec A — 1.
Для решения задачи следует воспользоваться основным тригонометрическим тождеством: сумма квадратов синуса и косинуса одного и того же угла равна 1.
Отсюда синус угла равен плюс минус корню квадратному из разности 1 и квадрата косинуса угла.

Какой знак перед корнем квадратным брать зависит от того, где находится угол, косинус которого известен.
Если в условии задачи значение косинуса больше нуля (равенство нулю рассмотрено, как частный случай, ниже, хотя применимы рассуждения и для нуля), то угол находится либо в 1-й, либо в 4-й четверти.
Для определенности в условии задачи обычно дается ограничение для угла.
Если указано, что 0< a< 90 (1 четверть), то значение синуса тоже следует брать со знаком плюс.
Если же 270< a< 360 (4 четверть), то значение синуса следует брать со знаком минус.
Если значение косинуса угла меньше нуля, то это означает, что угол может находиться во 2-й или 3-й четверти.
1) 90< a< 180 (2 четверть).
Тогда синус угла будет положительным и равняется корню квадратному из разности 1 и квадрата косинуса угла.
2) 180< a< 270 (3 четверть).
В этом случае синус угла будет отрицательным и равняется тому же значению, что и в первом случае, только со знаком минус.
Частные случаи: Если cos a = 0, то sina=1; если cos a = 1, то sina=0; cos a = -1, то sina=0. Эти значения также легко находятся из основного тригонометрического тождества.
Приведем примеры.
Пример 1. Найти синус угла, если cos a = -0,8. 180<a<270 (в градусах)
Решение. Находим разность 1 и квадрата значения cos a, т.е. квадрата (-0,8).
-0,8 возводим в квадрат, получим (-0,8)*(-0,8) = 0, 64. Подставим его в искомую разность:
1-0,64=0,36
Получили квадрат значения синуса. Для нахождения значения самого синуса, извлечем корень квадратный из 0,36 и возьмем его со знаком + и со знаком – (см. картинку). Получим 0,6 или -0,6.
Так как по условию угол находится в 3 четверти, то искомое значение синуса будет отрицательным. Значит выбираем -0,6.
Ответ: sina=-0,6.
Рассмотрим для краткости изложения этот же пример для случая, когда угол находится во второй четверти:
Пример 2. Найти синус угла, если cos a = -0,8. 90<a<180 (в градусах)
Решение будет точно таким же, как для примера 1.
Изменится лишь выбор ответа. Рассуждения будут следующими:
Так как по условию угол находится во 2 четверти, то искомое значение синуса будет положительным. Значит выбираем 0,6.
Ответ: sina=0,6.
