Как выразить длину через формулу периода колебаний математического маятника?
Георгий Пилипенко
Профи
(544),
на голосовании
7 лет назад
Голосование за лучший ответ
Вика Лапина
Ученик
(135)
7 лет назад
задай вопрос мне по этому поводу твоему http://vk.com/id175795693
П.А.Н.
Мудрец
(13212)
7 лет назад
Из этого (см. внизу)?
L = (T^2 * g) / (4 * pi^2)
Георгий ПилипенкоПрофи (544)
7 лет назад
Thanks
Георгий ПилипенкоПрофи (544)
7 лет назад
мне уже не надо)
Похожие вопросы
1
![]()
габбас
[215K]
4 года назад
Если известен период колебаний математического маятника, то длину маятника можно подсчитать по известной формуле периода математического маятника Т=2*пи*корень квадратный из( L/g), где g=9,8 м/с2 – ускорение свободного падения на Земле (приблизительно). Оттуда длина маятника L = (Т^2*g)/(4*пи^2) = (1*9,8)/(4*3,14*3,14) = 9,8/39,48 = 0,248 м или примерно 25 см.
Ответ: 25 см.
автор вопроса выбрал этот ответ лучшим
комментировать
в избранное
ссылка
отблагодарить
Задания
Версия для печати и копирования в MS Word
Тип 12 № 311544 

i
Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле где
— длина нити (в метрах). Пользуясь данной формулой, найдите длину нити маятника, период колебаний которого составляет 7 с.
Спрятать решение
Решение.
Выразим длину маятника:
Подставляя, получаем:
Ответ: 12,25.
Аналоги к заданию № 46: 311544 337952 338064 … Все
Источник: ГИА-2012. Математика. Контрольная работа.(1 вар)
Спрятать решение
·
Прототип задания
·
Помощь
Физика 9 класс
Анонимный вопрос
1 июня 2018 · 8,0 K
ОтветитьУточнить
Ирина С.6,1 K
Книги, звери и еда – это хобби навсегда. · 19 янв 2019
Формула для расчета периода математического маятника:
T=2*π*sqrt(l/g), где l-длина математического маятника, g-ускорение свободного падения. Из нее можно получить формулу для l:
l=(T^2*g)/(4*π^2)=(4^2*10)/(4*3.14^2)=4.06 м.
7,9 K
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Как найти длину через период колебаний

- Как найти период и частоту колебаний
- Как найти резонансную частоту
- Как измерить частоту
При решении задач на нахождение периода и частоты колебаний, а также длины волны используйте следующие физические и математические константы:
— скорость света в вакууме: c=299792458 м/с (некоторые исследователи, в частности, креационисты, считают, что в прошлом данная физическая константа могла иметь другую величину);
— скорость звука в воздухе при атмосферном давлении и нуле градусов по Цельсию: Fзв=331 м/с;
— число «пи» (до пятидесятого знака): π=3,14159265358979323846264338327950288419716939937510 (безразмерная величина).
Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.
Для маятника это максимальное расстояние, на которое удаляется шарик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.

Амплитуда колебаний измеряется в единицах длины — метрах, сантиметрах и т. д. На графике колебаний амплитуда определяется как максимальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).

Период колебаний.
Период колебаний — это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.
Другими словами, период колебаний (Т) — это время, за которое совершается одно полное колебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.

За полный период колебаний, таким образом, тело проходит путь, равный четырем амплитудам. Период колебаний измеряется в единицах времени — секундах, минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).

Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющейся величины точно повторяются через определенный промежуток времени, т. е. для гармонических колебаний. Однако это понятие применяется также и для случаев приблизительно повторяющихся величин, например, для затухающих колебаний.
Частота колебаний.
Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.
Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:
 .
.
В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:
 .
.
Циклическая частота — это число колебаний, совершаемых за 2π секунд.
Повторяющиеся движения или процессы, которые воспроизводят все состояния предыдущего цикла являются периодическими. Одной из характеристик периодических процессов или колебаний является период.
Период колебаний — Это время за которое периодический процесс проходит полностью один цикл.
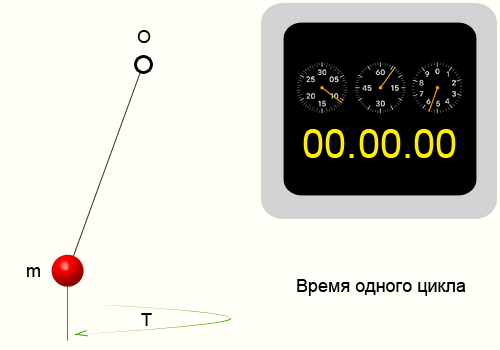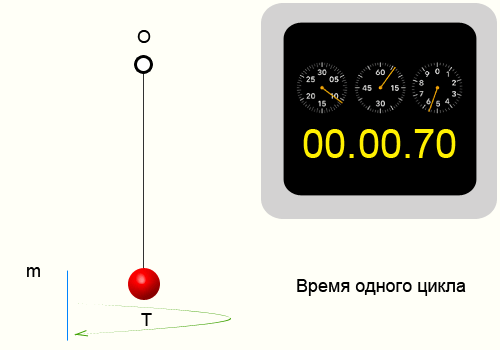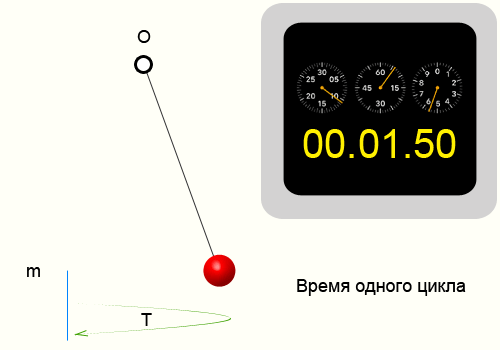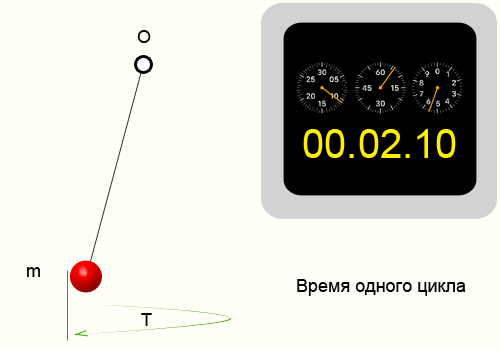
Для того чтобы найти период колебаний, необходимо взять определенный временной интервал и подсчитать количество циклов, после чего воспользоваться формулой:
| ∆t | определенный временной интервал, | секунд |
|---|---|---|
| N | количество циклов, | шт. |
| f | частота колебаний (число циклов в одну секунду), | Герц |
Пример определения периода колебаний
Например возьмем кусочек пластилина и подвесим его на нитке. Отведем нитку от положения равновесия и отпустим. На сотовом телефоне в момент отпускания запустим секундомер. Отсчитаем 10 циклов, т.е. нить 10 раз вернется в ту же точку из которой мы ее отпустили. Секундомер показал 14.35 секунд, соответственно приблизительный период колебаний нити 1.435 секунд.
