Загрузить PDF
Загрузить PDF
Во время химических реакций происходит поглощение или выделение тепла в окружающую среду. Такой теплообмен между химической реакцией и окружающей средой называется энтальпией, или H. Однако измерить энтальпию напрямую невозможно, поэтому принято рассчитывать изменение температуры окружающей среды (обозначаемое ∆H). ∆H показывает, что в ходе химической реакции происходит выделение тепла в окружающую среду (экзотермическая реакция) или поглощение тепла (эндотермическая реакция). Рассчитывается энтальпия так: ∆H = m x s x ∆T, где m — масса реагентов, s — теплоемкость продукта реакции, ∆T — изменение температуры в результате реакции.
-

1
Определите реагенты и продукты реакции. Любая химическая реакция имеет реагенты и продукты реакции. Продукт реакции создается в результате взаимодействия реагентов. Другими словами реагенты — это ингредиенты в рецепте, а продукт реакции — это готовое блюдо. Чтобы найти ∆H реакции, необходимо знать реагенты и продукты реакции.
- Например, необходимо найти энтальпию реакции образования воды из водорода и кислорода: 2H2 (водород) + O2 (кислород) → 2H2O (вода). В этой реакции H2 и O2 – реагенты, а H2O — продукт реакции.
-

2
Определите общую массу реагентов. Далее необходимо подсчитать массу реагентов. Если вы не можете взвесить их, то подсчитайте молекулярную массу, чтобы найти фактическую. Молекулярная масса — это постоянная, которую можно найти в периодической таблице Менделеева или в других таблицах молекул и соединений. Умножьте массу каждого реагента на число молей.
- В нашем примере реагенты водород и кислород имеют молекулярные массы 2 г и 32 г соответственно. Поскольку мы используем 2 моль водорода (коэффициент в химической реакции перед водородом H2) и 1 моль кислорода (отсутствие коэффициента перед O2 обозначает 1 моль), то общая масса реагентов рассчитывается следующим образом:
2 × (2 г) + 1 × (32 г) = 4 г + 32 г = 36 г
- В нашем примере реагенты водород и кислород имеют молекулярные массы 2 г и 32 г соответственно. Поскольку мы используем 2 моль водорода (коэффициент в химической реакции перед водородом H2) и 1 моль кислорода (отсутствие коэффициента перед O2 обозначает 1 моль), то общая масса реагентов рассчитывается следующим образом:
-

3
Определите теплоемкость продукта. Далее определите теплоемкость продукта реакции. Каждая молекула имеет определенную величину теплоемкости, которая является постоянной. Найдите эту постоянную в таблицах учебника по химии. Существует несколько единиц измерения теплоемкости; в наших расчетах мы будем использовать Дж/г°C.
- Обратите внимание на то, что при наличии нескольких продуктов реакции вам потребуется рассчитать теплоемкость каждого, а затем сложить их, чтоб получить энтальпию всей реакции.
- В нашем примере, продукт реакции — вода, которая имеет теплоемкость 4,2 Дж/г°C.
-

4
Найдите изменение температуры. Теперь мы найдем ∆T — разницу температур до и после реакции. Из начальной температуры (T1) вычтите конечную температуру (T2). Чаще всего в задачах по химии используется шкала Кельвина (К) (хотя по шкале Цельсия (°С) получится тот же результат).
- В нашем примере давайте предположим, что начальная температура реакции была 185 K, а после реакции стала 95 K, значит, ∆T вычисляется так:
∆T = T2 – T1 = 95 K – 185 K = -90 K
- В нашем примере давайте предположим, что начальная температура реакции была 185 K, а после реакции стала 95 K, значит, ∆T вычисляется так:
-

5
Найдите энтальпию по формуле ∆H = m x s x ∆T. Если известна m — масса реагентов, s — теплоемкость продукта реакции и ∆T — изменение температуры, то можно подсчитать энтальпию реакции. Подставьте значения в формулу ∆H = m x s x ∆T и получите энтальпию. Результат вычисляется в Джоулях (Дж).
- В нашем примере энтальпия вычисляется так:
∆H = (36 г) × (4,2 ДжK – 1 г – 1) × (-90 K) = -13608 Дж
- В нашем примере энтальпия вычисляется так:
-

6
Определите, выделяется или поглощается энергия в ходе рассматриваемой реакции. Одна из самых распространенных причин, по которой требуется вычислить ∆H на практике, — узнать, будет ли реакция экзотермической (выделение тепла и снижение собственной энергии) или эндотермической (поглощение тепла из окружающей среды и повышение собственной энергии). Если значение ∆H положительное, значит, реакция эндотермическая. Если отрицательное, значит, реакция экзотермическая. Чем больше абсолютное значение ∆H, тем больше энергии выделяется или поглощается. Будьте осторожны, если собираетесь проводить практический опыт: во время реакций с высоким значением энтальпии может произойти большое высвобождение энергии, и если оно протекает быстро, то может привести ко взрыву.
- В нашем примере конечный результат получился равным -13608 Дж. Перед значением энтальпии отрицательный знак, а это означает, что реакция экзотермическая. Горячие газы (в виде пара) H2 и O2 должны выделить некоторое количество тепла, чтобы образовать молекулу воды, то есть реакция образования H2O является экзотермической.
Реклама
-

1
Подсчитайте энергию связей для оценки энтальпии. Почти все химические реакции приводят к разрыву одних связей и образованию других. Энергия в результате реакции не возникает ниоткуда и не разрушается: это та энергия, которая требуется для разрыва или образования этих связей. Поэтому изменение энтальпии всей реакции можно довольно точно оценить путем суммирования энергии этих связей.
- Например, рассмотрим реакцию: H2 + F2 → 2HF. В этом случае, энергия для разрыва связи в молекуле H2 составляет 436 кДж/моль, а энергия для разрыва F2 составляет 158 кДж/моль.[1]
Наконец, энергия необходимая для образования связи в молекуле HF из H и F = -568 кДж/моль.[2]
Умножаем последнее значение на 2, так как в ходе реакции получаем 2 моль HF: 2 × -568 = -1136 кДж/моль. Складываем значения:
436 + 158 + (-1136) = -542 кДж/моль.
- Например, рассмотрим реакцию: H2 + F2 → 2HF. В этом случае, энергия для разрыва связи в молекуле H2 составляет 436 кДж/моль, а энергия для разрыва F2 составляет 158 кДж/моль.[1]
-

2
Используйте энтальпию образования для оценки энтальпии. Энтальпия образования позволяет рассчитать ∆H через вычисление реакций образования реагентов и продуктов. Если известна энтальпия образования продуктов реакции и реагентов, то вы можете оценить энтальпию в целом путем сложения, как и в случае энергии, рассмотренном выше.
- Например, рассмотрим следующую реакцию: C2H5OH + 3O2 → 2CO2 + 3H2O. Мы знаем, что энтальпия образования рассчитывается:[3]
C2H5OH → 2C + 3H2 + 0,5O2 = 228 кДж/моль
2C + 2O2 → 2CO2 = -394 × 2 = -788 кДж/моль
3H2 + 1.5 O2 → 3H2O = -286 × 3 = -858 кДж/моль
Теперь необходимо сложить значения образованных веществ, полученные выше, для определения энтальпии реакции: C2H5OH + 3O2 → 2CO2 + 3H2O,
228 + -788 + -858 = -1418 кДж/моль.
- Например, рассмотрим следующую реакцию: C2H5OH + 3O2 → 2CO2 + 3H2O. Мы знаем, что энтальпия образования рассчитывается:[3]
-

3
Не забывайте о знаках перед значениями энтальпии. При вычислении энтальпии образования формулу для определения энтальпии реакции продукта вы переворачиваете, и знак энтальпии должен поменяться. Другими словами, если вы переворачиваете формулу, то знак энтальпии должен смениться на противоположный.
- В примере обратите внимание на то, что реакция образования для продукта C2H5OH записана наоборот. C2H5OH → 2C + 3H2 + 0,5O2 то есть C2H5OH распадается, а не синтезируется. Поэтому знак перед энтальпией в такой реакции положительный, 228 кДж/моль, хотя энтальпия образования C2H5OH составляет -228 кДж/моль.
Реклама
-

1
Возьмите чистую емкость и налейте туда воды. Увидеть принципы энтальпии в действии нетрудно — достаточно провести простой опыт. Необходимо, чтобы на результат эксперимента не повлияли посторонние загрязнители, так что емкость нужно вымыть и простерилизовать. Ученые для измерения энтальпии используют специальный закрытые контейнеры — калориметры, но вам вполне подойдет стеклянный стакан или колба. Заполните емкость чистой водопроводной водой комнатной температуры. Желательно проводить эксперимент в прохладном помещении.
- Для эксперимента желательно использовать небольшую емкость. Мы будем рассматривать энтальпию реакции воды с «Алка-Зельтцер», поэтому, чем меньше воды используется, тем более очевидным будет изменение температуры.
-

2
Поместите термометр в емкость. Возьмите термометр и опустите его в емкость с водой так, чтобы граница прочтения температуры была ниже уровня воды. Снимите показания термометра — это будет начальная температура, T1.
- Предположим, что температуры воды 10 °C. Мы будем использовать это значение для демонстрации принципов энтальпии.
-

3
Добавьте в емкость одну таблетку «Алка-Зельтцер». Готовы начать опыт? Бросьте в воду одну таблетку «Алка-Зельтцер». Она сразу начнет пузыриться и шипеть. Это происходит из-за реакции между бикарбонатом (HCO3–) и лимонной кислотой (H+). В результате образуются вода и углекислый газ по формуле: 3HCO3− + 3H+ → 3H2O + 3CO2.
-

4
Измерьте конечную температуру. Наблюдайте за ходом реакции: таблетка «Алка-Зельтцер» будет постепенно растворяться. Когда она растворится полностью, измерьте температуру еще раз. Вода должна стать немного холоднее. Если температура воды напротив стала выше начальной, значит, эксперименту помешали какие-то внешние факторы (например, слишком теплое помещение, где проводился эксперимент).
- Предположим, что температура составляет теперь 8 °C.
-

5
Подсчитаем энтальпию реакции. Когда таблетка «Алка-Зельтцер» вступает в реакцию с водой, образуются вода и углекислый газ (те самые шипучие пузырьки) и происходит снижение температуры (это тот результат, который должен получиться, если опыт прошел успешно). Можно сделать вывод, что данная химическая реакция является эндотермической, то есть она сопровождается поглощением энергии из окружающей среды — в данном случае из воды. В результате температура воды снижается.
- В нашем эксперименте температура воды снизилась на два градуса. Это согласуется с теорией: реакция растворения «Алка-Зельтцер» в воде эндотермическая и сопровождается небольшим поглощением энергии.
Реклама
Советы
- В подсчетах используется шкала Кельвина (K) — это температурная шкала, аналогическая шкале Цельсия, и часто применяемая в химии и физике. Чтобы перевести значение градусов Цельсия в кельвины, необходимо добавить или вычесть 273 градуса: K = °C + 273.
Реклама
Об этой статье
Эту страницу просматривали 115 749 раз.
Была ли эта статья полезной?
| Энтальпия | |
|---|---|
 |
|
| Размерность |
 |
| Единицы измерения | |
| СИ | Дж |
| СГС | эрг |
| Примечания | |
| Внесистемные единицы: калория, британская тепловая единица |
Энтальпи́я (от др.-греч. ενθαλπω — «нагреваю», также теплова́я фу́нкция[1][2], теплова́я фу́нкция Гиббса[3], теплосодержа́ние[1][3] и изобарно-изоэнтропийный потенциал[4]) — функция состояния 



(Определение энтальпии)
Из уравнения для дифференциала внутренней энергии[9][10]:
(Дифференциал внутренней энергии)
где 

(Дифференциал энтальпии)
которое является полным дифференциалом функции 
Понятие энтальпии существенно дополняет математический аппарат термодинамики[⇨] и гидродинамики[⇨].
Важно, что в изобарном процессе при постоянном 
равное сумме изменения внутренней энергии 


Отношение малого количества теплоты, 

Это экспериментально измеримая величина, и из её измерений находят температурную зависимость энтальпии[⇨].
Энтальпия — экстенсивная величина: для составной системы она равна сумме энтальпий её независимых частей. Как и внутренняя энергия, энтальпия определяется с точностью до произвольного постоянного слагаемого.


Первое упоминание об использовании термина «энтальпия» в его современном значении[21]
История вопроса[править | править код]
Понятие энтальпии было введено и развито Дж. В. Гиббсом[22][23][24] в 1875 году в классической работе «О равновесии гетерогенных веществ». Для обозначения этого понятия Гиббс использовал термин «тепловая функция при постоянном давлении»[25][26].
Автором термина «энтальпия» в его современном значении считают Х. Камерлинг-Оннеса. Впервые о его авторстве упоминает работа 1909 года[27][28] в связи с обсуждением сохранения энтальпии в эффекте Джоуля — Томсона[⇨], хотя в печатных публикациях самого Камерлинг-Оннеса это слово не встречается[29]. Что же касается буквенного обозначения 

Энтальпия как термодинамический потенциал[править | править код]
Поскольку внутренняя энергия является термодинамическим потенциалом относительно энтропии и объёма[30],
определение энтальпии можно рассматривать как преобразование Лежандра для перехода от потенциала относительно переменных 


Из выражения для дифференциала энтальпии получаются ещё два уравнения состояния, непосредственно выражающие температуру и объём через энтальпию и давление[32]:
Если известна энтальпия, другие термодинамические потенциалы — внутренняя энергия 


Из равных друг другу смешанных производных энтальпии выводятся две термодинамические производные, связанные третьим соотношением Максвелла[33]:
Через вторые производные энтальпии выражаются ещё две термодинамические производные:
Первая из этих производных характеризует теплоёмкость при постоянном давлении 
Метод якобианов позволяет получить тождества, аналогичные соотношениям Бриджмена, для выражения любых термодинамических производных через приведённые производные энтальпии.
Зависимость энтальпии от числа частиц[править | править код]
Для состоящей из одинаковых частиц открытой системы число частиц 
где 






Схема контрольного объёма. За малый интервал времени 
В англоязычной литературе, особенно технической, понятие открытой системы обычно отождествляют с понятием «контрольного объёма» (англ. control volume)[39], который ограничен воображаемой неподвижной контрольной[40] поверхностью, проницаемой для вещества, но оставляющей неизменной заключённый в ней объём. В то же время закрытую систему называют «контрольной массой» (англ. control mass). Последнее название подчеркивает постоянство массы (





Энергия контрольного объёма)
Если в системе присутствуют несколько различных веществ характеризующихся массами 

Удельная энтальпия[править | править код]
| Удельная энтальпия | |
|---|---|
 |
|
| Размерность |
 |
| Единицы измерения | |
| СИ | Дж/кг |
| СГС | эрг/г |
| Примечания | |
| Внесистемные единицы: кал/г, кал/кг |
| Молярная (мольная) энтальпия | |
|---|---|
 |
|
| Размерность |
 |
| Единицы измерения | |
| СИ |
Дж/моль ( кг/моль) кг/моль) |
| СГС |
эрг/моль ( 1 г/моль) 1 г/моль) |
| Примечания | |
| Внесистемная единица: кал/моль |
| Плотность энтальпии | |
|---|---|
 |
|
| Размерность |
 |
| Единицы измерения | |
| СИ | Дж/м3 |
| СГС | эрг/см3 |
Вместо экстенсивной величины энтальпии часто используют её отношение 

Соотношение для полного дифференциала удельной энтальпии можно получить, разделив уравнение для дифференциала энтальпии на 
(Дифференциал удельной энтальпии)
Удельную энтальпию можно представлять графически в виде 


Вводят также молярную (мольную) энтальпию 



Плотности внутренней энергии и энтальпии (на единицу объёма) вводят как отношение этих величин к объёму. Отдельные обозначения для этих величин здесь не вводятся, их можно выразить через удельные величины и массовую плотность:
Деление уравнения для дифференциала энергии контрольного объёма на величину контрольного объёма даёт соотношение[47]:
(Дифференциал плотности энергии)
Плотность энергии и энтальпии идеального газа[править | править код]
Для идеального газа с постоянной теплоёмкостью плотность внутренней энергии и энтальпии простым образом выражается через давление[48]:
где 


Энтальпия сложных термодинамических систем[править | править код]
Для термодинамических систем сложного типа, в которых термодинамическая работа[50] не сводится к работе внешних сил давления 
где 






Обобщенная энтальпии сохраняет смысл эквивалента теплоты для изобарного процесса[54][55], если не только давление, но и все остальные обобщённые силы поддерживаются постоянными: 
Энтальпия образования[править | править код]
Для приложений к химии в общем случае открытых систем для полного дифференциала энтальпии получаем:
Выражение для 
где 


Подставив это выражение в соотношение (***), получаем дифференциальную версию фундаментального уравнения Гиббса для энтальпии:
Все химические реакции сопровождаются выделением (экзотермические) или поглощением (эндотермические) тепла. Одно из приложений энтальпии основано на том, что множество химических процессов в реальных или лабораторных условиях реализуются именно при постоянном (атмосферном) давлении. Поэтому мерой теплового эффекта реакции служит изменение энтальпии ΔН в ходе химической реакции, в результате которой исходные вещества исчезают и образуются продукты реакции. В случае экзотермических реакций система теряет тепло и ΔН — величина отрицательная. В случае эндотермических реакций система поглощает тепло и ΔН — величина положительная. В частности, энтальпия образования — это количество теплоты, которое поглощается (если энтальпия образования положительна) или выделяется (если энтальпия образования отрицательна) при образовании сложного вещества из простых веществ.
Значение энтальпии образования и другие термодинамические свойства веществ приведены в справочниках[58][59].
Зависимость энтальпии от температуры[править | править код]
Во многих приложениях (но только не в качестве термодинамического потенциала!) энтальпию системы удобно представлять в виде функции 




Температурная производная энтропии выражается через (измеримую) теплоёмкость при постоянном давлении 


Для идеального газа в силу закона Гей-Люссака
(Энтальпия идеального газа)
где 


Для реальных систем изменение энтальпии при изменении температуры в изобарическом процессе практически удобно рассчитывать, если известна теплоёмкость при постоянном давлении 


Поскольку разности энтальпий продуктов химической реакции и исходных веществ определяет тепловой эффект химической реакции[⇨], разность теплоёмкостей продуктов реакции и исходных веществ определяет зависимость теплового эффекта реакции от температуры (термохимический закон Кирхгофа).
Сохранение энтальпии в эффекте Джоуля — Томсона[править | править код]
Рис. 2 — Сохранение энтальпии в эффекте Джоуля — Томсона. Изменение энергии газа в ходе этого процесса равно работе: 

Сохранение энтальпии в процессе Джоуля — Томсона привлекается для количественного описания эффекта. Схема процесса представлена на рисунке 2. Левый поршень, вытесняя газ под давлением 








Из уравнения для дифференциала энтальпии выводится выражение для коэффициента Джоуля — Томсона 

![{displaystyle C_{P}mathrm {d} T+left[V-Tleft({frac {partial V}{partial T}}right)_{P}right]mathrm {d} P=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10e30be2110fa951c716fb887b72bb50a0fe82b4)
а выражение для дифференциала энтальпии в переменных 
В процессе Джоуля — Томсона давление всегда убывает, следовательно, энтропия возрастает.
Полная энергия и полная энтальпия[править | править код]
| Полная энтальпия (удельная) (энтальпия торможения) |
|
|---|---|
 |
|
| Размерность |
 |
| Единицы измерения | |
| СИ | Дж/кг |
| СГС | эрг/г |
| Примечания | |
| Зависит от выбора системы отсчёта |
Для движущихся тел помимо внутренней энергии, включающей кинетическую энергию теплового движения составляющих тело частиц (измеренную в системе координат, в которой тело как целое покоится), вводят также его полную энергию в системе координат, относительно которой тело движется со скоростью 

(Дифференциал полной энергии)
где 



Обобщение дифференциала плотности энергии для полной энергии принимает вид[47]:
(Дифференциал плотности полной энергии)
Релятивистская энтальпия[править | править код]
| Полная энтальпия (инвариантная релятивистская) |
|
|---|---|
 |
|
| Размерность |
 |
| Единицы измерения | |
| СИ | Дж |
| СГС | эрг |
| Примечания | |
| Лоренц-инвариант |
| Полная энтальпия (релятивистская) |
|
|---|---|
 |
|
| Размерность |
 |
| Единицы измерения | |
| СИ | Дж |
| СГС | эрг |
| Примечания | |
Образует 4-вектор вместе с импульсом  |
Если скорость тела 


Релятивистская полная энергия 




В неподвижной системе отсчета энтальпия и импульс движущегося тела[68][67]
образуют 4-вектор, а инвариантная энтальпии в движущейся с телом системы отсчёта даётся инвариантной функцией этого 4-вектора:
Именно полная энтальпия (а не энергия) релятивистского тела оказывается аналогом энергии релятивистской частицы. Давление 

является следствием Лоренцева сокращения. Уравнение релятивистской термодинамики даётся выражением[68]:
Оно позволяет решить любой вопрос термодинамики движущихся систем, если известна функция 


Энтальпия в гидродинамике[править | править код]
| Механика сплошных сред |
|---|
 |
| Сплошная среда |
|
Классическая механика Закон сохранения массы · Закон сохранения импульса |
|
Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость |
|
Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение |
|
Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука |
| См. также: Портал:Физика |
Энтальпия играет большую роль в гидродинамике, науке о движениях жидкостей и газов (в гидродинамике газы тоже называют жидкостями). Течения идеальной жидкости (то есть без вязкости и теплопроводности) описываются следующими уравнениями в частных производных[69]:
(Уравнение непрерывности)
(Уравнение Эйлера)
где 








(Уравнение Эйлера, выраженное через энтальпию)
Такое представление обладает значительными преимуществами, поскольку в силу «адабатичности» течения идеальной жидкости, задаваемого уравнением сохранения энтропии:
член в уравнении Эйлера, связанный с градиентом энтропии, во многих случаях не даёт вклада в рассчитываемые эффекты.
Поток энергии[править | править код]
Выражение для дифференциала плотности полной энергии позволяет получить скорость изменения последней[47]:
Интеграл Бернулли[править | править код]
Из приведённых здесь термодинамических соотношений для энтальпии следует простой вывод интеграла Бернулли и в наиболее общей его форме. Закон утверждает, что вдоль линии тока для стационарного течения идеальной жидкости[70] сохраняется следующая величина:
где 



Вывод закона Бернулли из уравнения Эйлера и термодинамических соотношений
1. В уравнении Эйлера для стационарного (


2. Скалярное произведение этого уравнения на единичный вектор 
так как произведение градиента на единичный вектор даёт производную по направлению 
3. Выражение для Дифференциала удельной энтальпии даёт:
так что
В стационарном течении идеальной жидкости все частицы, движущиеся вдоль данной линии тока, имеют одинаковую энтропию[71] (
См. также[править | править код]
- Тепловой эффект химической реакции
- Удельная теплота плавления
Комментарии[править | править код]
- ↑ В России определение энтальпии
как суммы
закреплено действующими стандартами[7][8].
- ↑ Это соотношение носит название дифференциальной формы фундаментального уравнения Гиббса для энтальпии закрытой термодеформационной системы[12][13][14].
- ↑ Энтальпию, заданную в виде функции её естественных независимых переменных, называют интегральной формой фундаментального уравнения Гиббса[15][16][17] для энтальпии закрытой термодеформационной системы[12][18][19].
- ↑ В термодинамике при написании частных производных внизу справа указывают переменные, который при вычислении производной считают постоянным. Причина в том, что в термодинамике для одной и той же функции используют различные наборы независимых переменных, которые, во избежание неопределённости, приходится перечислять.
- ↑ Число частиц в закрытой системе тоже может быть переменным, например числе фотонов равновесного излучения в полости с абсолютно чёрными стенками[34].
- ↑ Использование масс независимых компонентов, а не масс составляющих систему веществ, позволяет учитывать химические превращения в системе без явного рассмотрения протекающих в ней химических реакций (см. статью Химическая термодинамика).
- ↑ Энергия
включает в себя энергию химической связи и вносит значительный вклад в энтальпию образования[⇨] газообразных сложных веществ
Примечания[править | править код]
- ↑ 1 2 3 Энтальпия // Большая российская энциклопедия. Том 35. Москва, 2017, стр. 396.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, §14. Тепловая функция.
- ↑ 1 2 3 Зубарев Д. Н., Энтальпия, 1992.
- ↑ Горшков В. И., Кузнецов И. А., Основы физической химии, 2009, с. 111.
- ↑ Enthalpy, H // IUPAC Gold Book.
- ↑ Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин, 1984, с. 13.
- ↑ §113-04-21. Энтальпия (Н)//ГОСТ IEC 60050-113-2015 (2015). Дата обращения: 1 декабря 2018.
- ↑ §54. Энтальпия(теплосодержание)//ГОСТ Р 57700.4-2017 (2017). Дата обращения: 1 декабря 2018.
- ↑ Зубарев Д. Н., Термодинамика, 1992.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (12.3).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (16.3).
- ↑ 1 2 Белов Г. В., Термодинамика, ч. 1, 2017, с. 155.
- ↑ Степановских Е. И. и др., Химическая термодинамика в вопросах и ответах, 2014, с. 37.
- ↑ Мечковский Л. А., Блохин А. В., Химическая термодинамика, ч. 1, 2012, с. 124.
- ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 312.
- ↑ Воронин Г. Ф., Основы термодинамики, 1987, с. 76.
- ↑ Мюнстер А., Химическая термодинамика, 2002, с. 90—91.
- ↑ Белов Г. В., Термодинамика, ч. 2, 2016, с. 23.
- ↑ Зарубин Д. П., Физическая химия, 2017, с. 45.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, с. 67.
- ↑ Dalton, 1909.
- ↑ Гиббс Дж. В., Термодинамические работы, 1950, Примечание 3, с. 448.
- ↑ 1 2 Howard, 2002, с. 697.
- ↑ Ахметов Б. В. и др. Физическая и коллоидная химия, 1986, с. 64.
- ↑ Гиббс Дж. В., Термодинамика. Статистическая механика, 1982, с. 96, 510.
- ↑ Henderson, Douglas; Eyring, Henry; Jost, Wilhelm. Physical Chemistry: An Advanced Treatise (неопр.). — Academic Press, 1967. — С. 29.
- ↑ Dalton, 1909, с. 863.
- ↑ Laidler (англ.) (рус.; Keith. The World of Physical Chemistry (англ.). — Oxford University Press, 1995. — P. 110.
- ↑ Van Ness, 2003, с. 486.
- ↑ Зубарев Д. Н., Потенциал термодинамический, 1994, с. 89.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, §45. Термодинамические функции.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (14.4).
- ↑ Беляев Н. М., Термодинамика, 1987, с. 126.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, §63. Чёрное излучение.
- ↑ 1 2 Зубарев Д. Н., Термодинамика, 1992.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнения (24.5–7).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (15.7).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (24.11).
- ↑ Automotive Encyclopedia, 2015, §1.1.2.2. Open dynamic system, с. 27.
- ↑ Белов Г. В., Термодинамика, ч. 1, 2017, с. 11.
- ↑ Automotive Encyclopedia, 2015, Уравнение (15), с. 28.
- ↑ Мюнстер А., Химическая термодинамика, 2002, с. 103.
- ↑ Кубо Р., Термодинамика, 1970, с. 24—25.
- ↑ Поль Р. В., Механика, акустика и учение о теплоте, 2013, с. 446.
- ↑ Поль Р. В., Механика, акустика и учение о теплоте, 2013, с. 449–451.
- ↑ Quantities, Units and Symbols in Physical Chemistry (англ.). IUPAC (2015). Дата обращения: 7 декабря 2018. Архивировано из оригинала 11 февраля 2014 года.
- ↑ 1 2 3 Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2015, §6. Поток энергии.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнения (42.5), (43.2) и (43.4).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, §63.
- ↑ Зубарев Д. Н., Работа в термодинамике, 1994.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, §12.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (45.21).
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (45.25).
- ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 121.
- ↑ Базаров И. П., Термодинамика, 2010, с. 113.
- ↑ Артемов А. В., Физическая химия, 2013, с. 23.
- ↑ Ипполитов Е. Г. и др., Физическая химия, 2005, с. 35.
- ↑ Search for Species Data by Chemical Formula (англ.). Дата обращения: 3 декабря 2018.
- ↑ Термодинамические свойства. Дата обращения: 3 декабря 2018.
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (43.4).
- ↑ Пригожин И., Дефэй Р., Химическая термодинамика, 2009, с. 51.
- ↑ Алабовский А. Н., Недужий И. А., Техническая термодинамика и теплопередача, 1990, с. 25—26.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (19.3).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (18.1).
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (46.1).
- ↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (18.2).
- ↑ 1 2 3 4 Зубарев Д. Н., Релятивистская термодинамика, 1994.
- ↑ 1 2 3 Каллен Г., Горвиц Дж., Релятивистская термодинамика, 1972.
- ↑ 1 2 Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2015, Уравнение (2.4).
- ↑ Вишневецкий С. Л., Бернулли уравнение, 1988, с. 187.
- ↑ Седов Л. И. Механика сплошной среды, 1970, Глава VII. §2. Функция давления.
Литература[править | править код]
- Алабовский А. Н., Недужий И. А. Техническая термодинамика и теплопередача. — 3-е изд., пераб. и доп. — Киев: Выща школа, 1990. — 256 с. — ISBN 5-11-001997-5.
- Ансельм А. И. Основы статистической физики и термодинамики. — 2-е изд., стереотип. — СПб.: Лань, 2007. — 427 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-0756-9.
- Артемов А. В. Физическая химия. — М.: Академия, 2013. — 288 с. — (Бакалавриат). — ISBN 978-5-7695-9550-9.
- Ахметов Б. В., Новиченко Ю. П., Чапурин В. И. Физическая и коллоидная химия. — Л.: Химия, 1986. — 320 с.
- Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
- Белов Г. В. Термодинамика. Часть 1. — 2-е изд., испр. и доп. — М.: Юрайт, 2017. — 265 с. — (Бакалавр. Академический курс). — ISBN 978-5-534-02731-0.
- Белов Г. В. Термодинамика. Часть 2. — М.: Юрайт, 2016. — 249 с. — (Бакалавриат). — ISBN 978-5-9916-7252-8.
- Беляев Н. М. Термодинамика. — Киев: Вища школа, 1987. — 344 с.
- Болгарский А. В., Мухачев Г. А., Щукин В. К. Термодинамика и теплопередача. — 2-е изд., перераб. и доп. — М.: Высшая школа, 1975. — 496 с.
- Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М.: Инфра-М, 2017. — 868 с. — (Высшее образование: Бакалавриат). — ISBN 978-5-16-104227-4.
- Буданов В. В., Максимов А. И. Химическая термодинамика / Под ред. О. И. Койфмана. — 3-е изд., стер. — СПб.: Лань, 2017. — 320 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-2271-5.
- Вишневецкий С. Л. Бернулли уравнение // Физическая энциклопедия. — Большая Российская энциклопедия, 1988. — Т. 5: Стробоскопические приборы — Яркость. — С. 187.
- Воронин Г. Ф. Основы термодинамики. — М.: Изд-во Моск. ун-та, 1987. — 192 с.
- Гамбург Ю. Д. Химическая термодинамика. — М.: Лаборатория знаний, 2016. — 237 с. — (Учебник для высшей школы). — ISBN 978-5-906828-74-3.
- Герасимов Я. И., Древинг В. П., Еремин Е. Н. и др. Курс физической химии / Под общ. ред. Я. И. Герасимова. — 2-е изд., испр. — М.: Химия, 1970. — Т. 1. — 592 с.
- Гиббс Дж. В. Термодинамические работы / Пер. с англ. под ред. проф. В. К. Семенченко. — М. — Л.: Гостехиздат, 1950. — 492 с. — (Классики естествознания).
- Гиббс Дж. В. Термодинамика. Статистическая механика / Отв. ред. Д. Н. Зубарев. — М.: Наука, 1982. — 584 с. — (Классики науки).
- Горшков В. И., Кузнецов И. А. Основы физической химии. — 3-е изд. — М.: Бином. Лаборатория знаний, 2009. — 408 с. — ISBN 978-5-94774-375-3.
- Еремин В. В., Каргов С. И., Успенская И. А. и др. Основы физической химии. Теория и задачи. — М.: Экзамен, 2005. — 481 с. — (Классический университетский учебник). — ISBN 5-472-00834-4.
- Зарубин Д. П. Физическая химия. — М.: Инфра-М, 2017. — 474 с.
- Зубарев, Д. Н. Потенциал термодинамический // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 89—91. — 704 с. — ISBN 5-85270-087-8.
- Зубарев, Д. Н. Работа в термодинамике // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 193. — 704 с. — ISBN 5-85270-087-8.
- Зубарев, Д. Н. Релятивистская термодинамика // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 333—334. — 704 с. — ISBN 5-85270-087-8.
- Зубарев Д. Н. Термодинамика // Физическая энциклопедия / Ред.А. М. Прохоров. — М.: Большая Советская Энциклопедия, 1992. — Т. 5. — С. 83—87.
- Зубарев Д. Н. Энтальпия // Физическая энциклопедия / Ред. А. М. Прохоров. — М.: Большая Советская Энциклопедия, 1992. — Т. 5. — С. 616.
- Ипполитов Е. Г., Артемов А. В., Батраков В.В. Физическая химия / Под ред. Е. Г. Ипполитова. — М.: Академия, 2005. — 448 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-1456-6.
- Каллен Г., Горвиц Дж. Релятивистская термодинамика // Успехи Физических Наук : журнал. — 1972. — Т. 107, вып. 7. — С. 489—502. — doi:10.3367/UFNr.0107.197207g.0489.
- Колесников И. М., Винокуров В. А. Термодинамика физико-химических процессов. — 2-е, перераб. и доп. — М.: Нефть и газ, 2005. — 480 с. — ISBN 5-7246-0351-9.
- Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
- Ландау Л. Д., Лифшиц Е. М. Гидродинамика. — Издание 6-е, исправленное. — М.: Физматлит, 2015. — 728 с. — («Теоретическая физика», том VI). — ISBN 978-5-9221-1625-1.
- Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 5-е. — М.: Физматлит, 2002. — 616 с. — («Теоретическая физика», том V). — ISBN 5-9221-0054-8.
- Мечковский Л. А., Блохин А. В. Химическая термодинамика. В двух частях. Часть 1. Феноменологическая термодинамика. Основные понятия, фазовые равновесия. — Минск: Издательство БГУ, 2012. — 141 с. — ISBN 978-985-518-635-0.
- Мюнстер А. Химическая термодинамика / Пер. с нем. под. ред. чл.-корр. АН СССР Я. И. Герасимова. — 2-е изд., стереотип. — М.: УРСС, 2002. — 296 с. — ISBN 5-354-00217-6.
- Новиков И. И. Термодинамика. — 2-е изд., испр. — СПб.: Лань, 2009. — 592 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-0987-7.
- Поль Р. В. Механика, акустика и учение о теплоте. — Рипол Классик, 2013. — 490 с. — ISBN 5458431251, 9785458431255.
- Пригожин И., Дефэй Р. Химическая термодинамика / Пер. с англ. под ред. В. А. Михайлова. — 2-е изд.. — М.: Бином. Лаборатория знаний, 2009. — 533 с. — (Классика и современность. Естествознание). — ISBN 978-5-9963-0201-7.
- Савельев И. В. Курс общей физики. — М.: КноРус, 2012. — Т. 1. Механика. Молекулярная физика и термодинамика. — 528 с. — ISBN 9785406025888.
- Свиридов В. В., Свиридов А. В. Физическая химия. — СПб.: Лань, 2016. — 597 с. — ISBN 978-5-8114-2262-3.
- Седов Л. И. Механика сплошной среды. — М.: Наука, 1970. — Т. 2. — 568 с.
- Сивухин Д. В. Общий курс физики. — Издание 5-е, исправленное. — М.: Физматлит, 2005. — Т. II. Термодинамика и молекулярная физика. — 544 с. — ISBN 5-9221-0601-5.
- Степановских Е. И., Брусницына Л. А., Маскаева Л. Н. Химическая термодинамика в вопросах и ответах. — Екатеринбург: Уральский издательско-полиграфический центр, 2014. — 221 с. — ISBN 978-5-4430-0061-9.
- Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп. — М.: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0.
- Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин / Отв. ред. И. И. Новиков. — АН СССР. Комитет научно-технической терминологии. Сборник определений. Вып. 103. — М.: Наука, 1984. — 40 с.
- Хаазе Р. Термодинамика необратимых процессов / Пер. с нем. под ред. А. В. Лыкова. — М.: Мир, 1967. — 544 с.
- Хачкурузов Г. А. Основы общей и химической термодинамики. — М.: Высшая школа, 1979. — 268 с.
- Dalton J. P. Researches on the Joule-Kelvin effect, especially at low temperatures. I. Calculations for hydrogen // KNAW Proceedings. — 1909. — Т. 11. — С. 863—873.
- Howard Irmgard K. H Is for Enthalpy, Thanks to Heike Kamerlingh Onnes and Alfred W. Porter (англ.) // Journal of Chemical Education : журнал. — 2002. — Vol. 79, iss. 6. — P. 697—698. — ISSN 0021-9584. — doi:10.1021/ed079p697.
- Van Ness Hendrick C. H Is for Enthalpy (англ.) // Journal of Chemical Education : журнал. — 2003. — Vol. 80, iss. 5. — P. 486. — ISSN 0021-9584. — doi:10.1021/ed080p486.1.
- Part 1 : Engines — Fundamentals // Encyclopedia of Automitive Engineering / Editors-in-Chief : David Crolla, David E. Foster, Toshio Kobayashi, Nicolas Vaughan. — John Wiley & Sons, 2015. — Т. 1. — 607 с. — ISBN 978-0-470-97402-5.
Что такое энтальпия?
Энтальпия – это количество тепла, которое термодинамическая система выделяет или поглощает из окружающей среды, когда она находится под постоянным давлением, термодинамическая система означает любой объект.
В физике и химии энтальпия – это термодинамическая величина, единицей измерения которой является Джоуль (Дж) и она обозначается буквой H.
Формула для расчета энтальпии:
H = E + PV
Где:
- H – энтальпия, E – энергия термодинамической системы, P – давление термодинамической системы, V – объем.
В этой формуле произведение давления, умноженного на объем (PV), равно механической работе, которая применяется к системе.
Следовательно, энтальпия равна энергии термодинамической системы плюс механическая работа, приложенная к ней.
Однако энтальпия системы может быть измерена только в тот момент, когда происходит изменение энергии. Изменение, представленное знаком Δ, дает новую формулу:
∆H = ∆E + P∆V
Это означает, что изменение энтальпии (∆H) равно изменению энергии (∆E) плюс механическая работа, приложенная к системе (P∆V).
Энтальпия происходит от греческого enthálpō , что означает добавление или добавление тепла. Термин был впервые придуман голландским физиком Хайке Камерлинг Оннесом, лауреатом Нобелевской премии по физике в 1913 году.
Типы энтальпии
Существует несколько типов энтальпии в зависимости от веществ и процессов. Когда процесс включает в себя выделение энергии, это экзотермическая реакция, в то время как захват энергии означает, что это эндотермическая реакция.
На основании вышеизложенного энтальпии подразделяются на:
Формирование энтальпии
Это энергия, которая требуется, чтобы сформировать моль вещества из элементов, которые его составляют. Напомним, что моль является единицей измерения вещества, эквивалентной 6,023х10 23 атомам или молекулам.
Примером энтальпии образования является объединение кислорода (O) и водорода (H) с образованием воды (H 2 O), изменение энергии или энтальпии которой (ΔH) составляет -285820 кДж / моль.
Энтальпия реакции
Это энергия, которая выделяет химическую реакцию под постоянным давлением.
Примером энтальпии реакции является образование метана (CH4) из объединения углерода (C) и водорода (H):
C + 2H 2 → CH 4
Смотрите также Химическая реакция.
Энтальпия раствора
Относится к количеству тепла, выделяемого или поглощаемого веществом при растворении в водном растворе.
Примером энтальпии растворения является то, что происходит при растворении серной кислоты (H 2 SO 4) в воде (H 2 O). Количество энергии, выделяемой кислотой, настолько велико, что это раствор, который необходимо использовать с определенными мерами безопасности.
Нейтрализующая энтальпия
Это энергия, которая улавливается или выделяется, когда кислота и основание смешиваются, нейтрализуя друг друга.
Пример энтальпии нейтрализации – это когда мы смешиваем уксусную кислоту (CH₃COOH) с бикарбонатом (NaHCOH).
Смотрите также Кислоты и основания.
Энтальпия горения
Это энергия, выделяемая, когда один моль органического вещества реагирует с кислородом в воздухе и выделяет углекислый газ (CO 2).
Примером энтальпии горения является та, которая генерируется пропаном (C 3 H 8), который выделяет энергию, которая используется в качестве бытового топлива:
C 3 H 8 + 5 O 2 → 3CO 2 + 4H 2 O
Выпуски 2,044 x 10 3 кДж / моль
Изменение энтальпии (ΔH) = -2,044×10 ^ 3 кДж / моль
Смотрите также Горение.
Энтальпия разложения
Это количество тепла или энергии, которое выделяется, когда один моль вещества распадается на более простые элементы.
Примером энтальпии разложения является случай, когда перекись водорода или перекись водорода разлагается с образованием воды и кислорода:
2H 2 O 2 → 2H 2 O + O 2
Выпущено 96,5 кДж / моль
Изменение энтальпии (ΔH) = 96,5 кДж / моль
Энтальпия растворения
Это относится к количеству тепла или энергии, которые вещество захватывает или выделяет, когда в раствор добавляется больше воды.
Примером энтальпии растворения является добавление порошкообразного моющего средства в воду.
Смотрите также Химический раствор.
Изменение фазы энтальпии
Это относится к обмену энергией, который происходит, когда элемент меняет состояние (твердое, жидкое или газообразное). В этом смысле мы имеем:
- Энтальпия плавления: изменение энтальпии при переходе от твердого тела к жидкости. Энтальпия сублимации: изменение энтальпии при переходе от твердого тела к газу. Энтальпия испарения: переход от жидкости к газу.
Примером энтальпии изменения фазы является то, что происходит в круговороте воды, поскольку при переходе из жидкого состояния в газообразное или твердое состояние (или любое из его возможных сочетаний) вода выделяет или поглощает энергию. В этом случае изменение энергии при переходе воды из жидкости в газ при 100 ° С равно 40,66 кДж / моль.
Смотрите также:
- Эндотермическая реакция. Экзотермическая реакция.
Для чего нужна энтальпия?
Энтальпия используется для точного измерения изменений энергии, возникающих в системе, при приеме или выделении энергии в окружающую среду.
Энтальпия – это сложное понятие термодинамики, которое обычно не используется в повседневной жизни, поскольку мы не рассчитываем энергию, необходимую, например, для нагрева воды для чая. Тем не менее, можно понять, как это работает с повседневным примером.
Когда мы кипятим воду, ее температура постепенно повышается, пока не достигнет точки кипения (100 ° C). В данном случае речь идет об отрицательной энтальпии, поскольку термодинамическая система должна была брать энергию из окружающей среды, чтобы повысить ее температуру.
С другой стороны, когда мы даем той же воде немного остыть после кипячения, ее температура начинает постепенно снижаться без необходимости внешнего вмешательства. В этом случае это положительная энтальпия, поскольку энергия выделяется в окружающую среду.
Энтальпия и энтропия
Энтропия – это физическая величина, которая измеряет количество энергии в системе, которая недоступна. Вычисляя эту величину, можно узнать степень беспорядка или хаоса в структуре системы.
Соотношение между энтальпией и энтропией определяется равновесием системы. При меньшей энтальпии (обмене энергией) система стремится к равновесию; но в то же время энтропия возрастает, поскольку в системе существует большая вероятность хаоса.
Со своей стороны, минимальная энтропия подразумевает более низкий уровень хаоса и, следовательно, обмен энергией (энтальпия) будет больше.
Энтальпия
Внутренняя энергия.
Химическая
система может состоять из
различных частиц: молекул, атомов или
ионов. Каждая из частиц
обладает энергией, которая обусловлена
ее поступательными
и вращательными движениями, колебаниями
атомов и атомных
групп в молекулах, силами притяжения и
отталкивания,
действующими как внутри частиц, так и
между ними,
внутриядерными взаимодействиями и т.
д. (показать
рисунок).
Суммарный запас энергии системы,
складывающийся из сильно различающихся
энергий отдельных частиц, называют
внутренней
энергией системы.
Ее обозначают буквой U.
Внутренняя энергия –функция
состояния системы,
т. е. ее характеристика, в отличие от
физических условий существования
системы, которые называют
параметрами.
К числу
параметров системы относятся температура
Т, давление р и объем V,
Определить экспериментально
абсолютное значение внутренней энергии
невозможно. Однако можно измерить
изменение внутренней энергии:
ΔU=Uкон–Uнач

Первое начало
термодинамики. В
соответствии с первым началом
термодинамики — законом
сохранения энергии —
теплота Q,
подводимая к системе, расходуется на
изменение внутренней энергии ΔU
и на совершение работы А:
Q
= ΔU +
А
Работа, выполняемая
химической системой, часто приводит к
ее расширению. Если система не совершает
других видов работы, например,
электрическую или магнитную, то работу
расширения можно
рассчитать, пользуясь уравнением
A
= pΔV
Если в системе
происходит химическая реакция, не
вызывающая
изменения объема, т. е. если ΔV=
0, то и работа,
выполняемая такой системой, тоже
равна нулю. В этом случае вся поглощенная
системой теплота расходуется на
увеличение внутренней
энергии системы:
Q
= ΔU
Часто без изменения
или с пренебрежимо малым изменением
объема протекают реакции в системах,
состоящих из твердых или
жидких компонентов.
Энтальпия.
Гораздо чаще реакции проходят при
постоянном
давлении. Таковы все реакции, осуществляемые
экспериментаторами
в открытой лабораторной посуде, и все
природные процессы,
происходящие на поверхности Земли. В
ходе всех этих
реакций давление не меняется. Оно равно
атмосферному давлению
(101,3 кПа). В процессах, происходящих при
постоянном
давлении, подводимая к системе теплота
расходуется не только на увеличение
внутренней энергии, но и на совершение
работы А
= рΔV,
в результате
которой увеличивается объем системы:
Q
= ΔU
+ рΔV
Изменение объема
ΔV
равно разности конечного и начального
объемов системы:
ΔV=Vкон–Vнач
Подставив в уравнение
для Q
выражения для разностей ΔU
и ΔV
получаем
Q
= Uкон–Uнач
+p(Vкон–Vнач)
или
Q
= (Uкон+
pVкон)
–(Uнач
+ pVнач)
В уравнении в скобках
приведены конечное и начальное значения
еще одной (наряду с внутренней энергией)
функции состояния
системы — энтальпии,
которую
обозначают буквой
H:
H=
U
+ pV.
Q
= Hкон–Hнач=
ΔH (5.7)
Величину ΔH
называют изменением энтальпии в процессе
или тепловым эффектом процесса, но часто
используют сокращенные
названия: теплота или энтальпия процесса.
Термохимия.
Раздел химической термодинамики,
изучающий
тепловые эффекты химических процессов,
называют термохимией.
Тепловой эффект процесса — количество
теплоты выделенной или поглощенной в
результате этого процесса.
Так как для создания
и высокого, и низкого давления требуются
огромные затраты энергии, подавляющее
большинство химических
реакций в природе, в промышленности и
в лабораториях происходит при
постоянном давлении, равном атмосферному.
По этой причине чаще всего рассматривают
тепловые эффекты при постоянном
давлении. Их обозначают буквой Qр.
В соответствии с уравнением (5.7) тепловой
эффект процесса, происходящего при
постоянном давлении, равен изменению
энтальпии системы.
Если энтальпия
реагентов больше, чем энтальпия продуктов
реакции, то реакция сопровождается
выделением теплоты, т. е. является
экзотермической. В ходе экзотермической
реакции энтальпия
системы уменьшается, что соответствует
отрицательному
значению ΔH
(рис. 5.2, а).
Наоборот, если энтальпия реагентов
меньше энтальпии продуктов, то реакция
происходит с поглощением теплоты, т. е.
является
эндотермической. В ходе эндотермической
реакции энтальпия
системы увеличивается, поэтому ΔH
имеет положительное
значение (рис. 5.2, б).

Термохимические
уравнения. Химическое
уравнение, в котором
наряду с формулами реагентов, продуктов
реакции и их
стехиометрическими коэффициентами
указан тепловой эффект, называют
термохимическим
уравнением. В
термохимических
уравнениях справа от формул веществ в
скобках указывают агрегатное
состояние: (г) — газообразное, (ж) —
жидкое, (т) — твердое, (к) —
кристаллическое, (р) — растворенное.
Для сравнения ΔH
различных реакций их необходимо
приводить к
одинаковым условиям. Как правило,
тепловой эффект реакций
приводится для стандартных
условий: давления
101,3 кПа (1 атм) и
любой фиксированной температуры.
Величины ΔH
в этих условиях называют стандартными
и обозначают
ΔHoT.
Верхний индекс o
говорит о том, что тепловой эффект
приводится для
стандартного давления, а нижний индекс
характеризует
фиксированную температуру. Например,
запи ΔHo400
= 22 кДж обозначает, что тепловой эффект
какой-то реакции,
осуществляемой при нормальном атмосферном
давлении и
температуре 400 К, равен 22 кДж. Чаще всего
приводят значения ΔHoT
для 298,15 К (25 °С) и вместо ΔHo
298,15 пишут просто ΔHo.
Следует отметить,
что числовое значение теплового эффекта
реакции зависит
от формы записи термохимического
уравнения.
Например, уравнение реакции синтеза
фтороводорода можно
записать с дробными стехиометрическими
коэффициентами у химических формул
водорода и фтора:
1/2 Н2(г)
+ 1/2 F2(г)
= НF(г);
ΔHo
= -270,7 кДж
Такая форма записи
говорит о том, что превращение 0,5 моль
газообразного
водорода и 0,5 моль газообразного фтора
в 1 моль газообразного
фтороводорода при давлении 101,3 кПа и
температуре
25 °С сопровождается выделением 270,7 кДж
теплоты. (О том,
что реакция происходит с выделением
теплоты, т. е. является экзотермической,
свидетельствует отрицательное значение
ΔHo)
Если это же уравнение записать с
целочисленными коэффициентами, то
числовое значение теплового эффекта
будет в два
раза больше, так как в два раза увеличиваются
количества реагентов и продуктов
реакции:
Н2(г)
+ F2(г)
= 2 НF(г);
ΔHo
=-541,4 кДж
В обоих случаях при
образовании 1 моль газообразного
фтороводорода
выделяется 270,7 кДж теплоты.
Стандартная
молярная энтальпия образования.
Абсолютное
значение энтальпии вычислить невозможно,
можно рассчитать только относительные
значения в сравнении с ее значениями
в стандартном
состоянии. Стандартное
состояние в химической термодинамике
выбирают таким, чтобы было удобно
проводить
необходимые в каждом конкретном случае
расчеты, поэтому
определение стандартного состояния
может изменяться в зависимости от
поставленной задачи. Для процесса
образования
сложного вещества из простых веществ
в качестве стандартного
выбрано наиболее устойчивое состояние
при стандартных
условиях, т. е. при давлении 101,3 кПа и
заданной температуре.
В справочниках чаще всего приводят
стандартную молярную
энтальпию образования при температуре
298,15 К, которую
обозначают как ΔHoобр,
298
или ΔHof,
298.
В этих обозначениях
верхний индекс ° — символ стандартного
состояния, нижние
индексы: обр. и / — сокращения соответственно
от русского слова образование и
английского formation,
число 298 означает температуру
298,15 К (его часто опускают).
Стандартная
молярная энтальпия образования – –
изменение энтальпии
при образовании 1 моль данного вешества
в стандартном
состоянии из простых вешеств, также
находящихся в
стандартном состоянии.
Стандартные энтальпии
образования простых веществ в
стандартных условиях принимают равными
нулю. Если химический
элемент в стандартных условиях образует
несколько простых веществ (аллотропных
модификаций), то в качестве стандартного
состояния выбирают наиболее устойчивое
из них. Например,
для углерода стандартным состоянием
считается графит,
а для серы — ромбическая форма. В таких
случаях в скобках после химической
формулы простого вещества указывают
название наиболее устойчивой аллотропной
модификации: С(графит), S(ромб).
Стандартные
молярные энтальпии фазовых переходов.
Энтальпия
изменяется не только в результате
химических реакций, но и при фазовых
переходах: превращении одной аллотропной
модификации в другую, плавлении и
затвердевании, испарении и конденсации,
сублимации и десублимации. Сублимация
(возгонка) —
переход твердого вещества непосредственно
в газообразное,
минуя плавление. Десублимация
— обратный
процесс. Температура, при которой
происходит фазовое превращение,
называется температурой
перехода. Приводимые
в справочниках
стандартные
молярные энтальпии фазовых переходов
представляют
собой изменения энтальпии в результате
фазового перехода 1 моль вещества,
находящегося в стандартном
состоянии при температуре перехода и
нормальном атмосферном давлении.
Для взаимно обратных процессов, например
испарения и конденсации, молярные
энтальпии равны по абсолютной
величине, но обратны по знаку, поэтому
в справочниках
приводят значения только одной из этих
величин. Например, приводимая в
справочниках молярная энтальпия
испарения воды ΔHoисп
= 40,66 кДж/моль. Это означает, что для
превращения 1
моль жидкой воды в водяной пар при
температуре кипения
398,15 К (100 °С) и давлении 101,3 кПа нужно
затратить 40,66 кДж теплоты.
Положительное значение ΔHo
пл свидетельствует
о том, что этот процесс эндотермический.
В результате
обратного, экзотермического процесса
конденсации 1 моль воды
выделяет 40,66 кДж теплоты. Следовательно,
ΔHo
конд = =
-40,66 кДж/моль.
Стандартные
молярные энтальпии сгорания. Определить
экспериментально теплоты образования
подавляющего большинства
органических веществ не удается, так
как невозможно получить их прямым
синтезом из простых веществ. Поэтому
в термохимических расчетах для
органических соединений используют
найденные опытным путем теплоты сгорания
этих веществ в
кислороде. Стандартная
молярная энтальпия сгорания —
изменение энтальпии при полном сгорании
1 моль вещества в
его стандартном состоянии при стандартных
условиях. Для веществ, состоящих
только из атомов углерода, водорода
и кислорода, полное сгорание означает
их превращение в СО2
и Н20.
Продукты окисления других элементов
определяют в каждом конкретном
эксперименте.
Определяя
экспериментально теплоты сгорания
пищевых продуктов и кормов для
сельскохозяйственных животных,
устанавливают их энергетическую
ценность. При этом тепловой эффект
реакции относят не к количеству вещества
в молях, а к его
массе в граммах. Например, энергетическая
ценность 100 г
сахара равна 1680 кДж. В диетологии и в
науке о кормлении
сельскохозяйственных животных
энергетическую ценность
продуктов и кормов называют калорийностью
и измеряют в
ккал/г (1 ккал = 4,184 кДж).
Закон Гесса.
Тепловые эффекты многих реакций не
могут быть определены экспериментально,
например, для многих веществ
невозможно опытным путем определить
энтальпию образования, потому что
далеко не все сложные вещества можно
получить
прямым синтезом из простых веществ. В
таких случаях прибегают
к термохимическим расчетам, в основе
которых лежит
закон, установленный в 1840 г. российским
ученым Г. И.
Гессом.
Тепловой эффект
химической реакции зависит только от
начального и конечного состояний
системы и не зависит от пути перехода.
Это означает, что
если из данных реагентов данные продукты
могут быть получены с помощью двух
или нескольких различных
последовательностей реакций, то сумма
тепловых эффектов
для каждой из этих последовательностей
будет одной и той же. Примером
является получение диоксида углерода
из графита, которое
можно осуществить двумя путями.
Первый путь: прямое
окисление графита кислородом до С02:
С(графит) + О2(г)
= СО2(г);
ΔHo
= -393,5 кДж
Второй путь: окисление
графита сначала до СО, а затем окисление
СО до СО2:
С(графит) +1/2
О2(г)
– СО2(г);
ΔHo1
= -110,5 кДж
СО(г) + 1/2
О2(г)
= СО2(г);
ΔHo2
= -283,0 кДж
В соответствии с законом Гесса
ΔHo=
ΔHo1+
ΔHo2
в чем нетрудно убедиться, найдя сумму
ΔHo1+
ΔHo2=
-110,5 + (-283,0) = -393,5 кДж,
Из закона Гесса
следует, что тепловой эффект реакции
можно вычислить,
если из суммы стандартных молярных
энтальпий
образования продуктов реакции вычесть
сумму стандартных молярных энтальпий
образования реагентов:
ΔHoреакции
= Σ[ΔHof,298(продукты)]
– Σ
[ΔHof,298
(реагенты)].
При суммировании
каждое значение ΔHof,298
нужно умножать
на стехиометрический
коэффициент, стоящий в термохимическом
уравнении перед формулой соответствующего
вещества. Например,
для реакции горения фосфина
4РН3(г)
+ 8О2(г)
= Р4О10(т)
+ 6Н2О(ж)
изменение
энтальпии равно:
ΔHo
реакции
= ΔHof
(Р4010)
+ 6 ΔHof
(Н20)
– [4 ΔHof
(РН3)
+ 8 ΔHof
(02)];
ΔHo
реакции=
-2984,00 + 6(-285,83) – [4 • 5,40 + 8 – 0] =
– -4720,58 кДж.
Тепловой эффект
реакций с участием органических веществ,
для которых известны стандартные
молярные теплоты сгорания, в
соответствии с законом Гесса можно
вычислить, если из суммы стандартных
молярных энтальпий сгорания реагентов
вычесть сумму
стандартных молярных энтальпий сгорания
продуктов (суммирование следует
осуществлять с учетом стехиометрических
коэффициентов, как
и в расчетах с использованием ΔHof,298).
Тепловые эффекты
реакций обычно слабо зависят от
температуры, поэтому для их достаточно
точной оценки, как правило,
можно пользоваться значениями стандартных
молярных энтальпий
образования и сгорания для температуры
298,15 К. Для более
строгих расчетов с учетом зависимости
молярных энтальпий
от температуры и давления предназначены
специальные
термодинамические справочники,
позволяющие вычислять ΔH
при других
параметрах.
Энтропия
Причины
самопроизвольного протекания
реакций. Среди
самопроизвольных реакций известны как
экзотермические (ΔHреакции
< 0), так и эндотермические (ΔHреакции
> 0) реакции. Следовательно,
изменение энтальпии нельзя считать
единственной причиной
самопроизвольного протекания реакций.
Очевидно, что есть, по меньшей мере,
еще одна характеристика системы,
изменение которой оказывает влияние
на направление протекания
процесса, наряду с ΔHреакции.
Эта функция состояния системы
называется энтропией
и обозначается
буквой S.
Она была введена
немецким физиком Р. Клаузиусом в 1865 г.
Качественное
представление о содержании понятия
энтропии
можно получить из анализа такого
эксперимента. Пусть два чистых газа,
например кислород и азот, первоначально
имеют одинаковые
давление и температуру и содержатся в
сосудах, соединенных
трубкой с закрытым краном, как это
показано на рис..
Если кран открыть, то газы приходят в
соприкосновение и самопроизвольно
смешиваются вплоть до достижения
равновесных концентраций. Процесс
смешения не сопровождается
никакими тепловыми эффектами и после
достижения равновесных концентраций
самопроизвольного разделения газов
никогда не происходит.
Совершенно ясно, что смесь кислорода и
азота — их взаимный
газовый раствор — является одновременно
и более устойчивой, и более сложной
системой, чем исходные чистые газы.
Интуитивные
представления и точный теоретический
анализ дают
одинаковый итог рассмотрения эксперимента
по смешению газов: смесь, взаимный
раствор газов, представляет собой более
вероятное состояние, чем исходное
состояние системы из двух чистых
газов.
Анализируя опыт со смешением газов,
можно сделать вывод: системы
способны самопроизвольно изменяться
при отсутствии
энергетических стимулов, если они могут
перейти в
состояние, характеризуемое большей
вероятностью


Рис. 5.3. Самопроизвольное
смешение двух газов: а
— кран закрыт; б
— кран открыт
Термодинамическая
вероятность. Чтобы
уяснить смысл понятия
вероятность
состояния, рассмотрим
пример с игрой в
кости. Эта игра состоит в том, что два
игрока бросают два кубика,
на каждой грани которых проставлены
очки от 1 до 6. Каждый из игроков перед
бросанием называет сумму очков, которая,
по его мнению, выпадет на верхних гранях
двух костей. Если
сумма действительно равна названной,
игрок выигрывает ставку. Сумма очков
может равняться 2, 3, …, 12. Вопрос о
вероятности
состояния в этой игре можно поставить
так: какая сумма
имеет наибольшую вероятность реализации?
Легко видеть, что вероятность выпадения
суммы 7 вшестеро выше выпадения сумм 2
и 12. Действительно, суммы 2 и 12 могут
выпасть каждая единственным образом 1
+ 1 или 6 + 6, а
сумма 7 может выпасть следующими шестью
способами: 3 + 4; 4
+ 3; 2+ 5; 5+ 2; 1 + 6; 6 + 1.
Таким образом, в
качестве меры вероятности состояния
системы
можно избрать число способов, которыми
это состояние
может реализоваться.
Чтобы представить себе, как велико число
способов реализации
состояния с заданной суммой энергий
молекул (макросостояния),
рассмотрим пример, когда каждая из трех
молекул А, В и С может иметь одну из трех
различающихся между собой энергий:
Е1,
Е2
или Е3.
Энергии Е1,
Е2
и Е3
, которыми
могут обладать
молекулы, называют энергетическими
уровнями. Каждый
из способов распределения молекул по
уровням называют
Таблица 5.1. Способы распределения трех
молекул:
А, В и С по трем
различным энергетическим уровням; E1,
Е2
и Е3
-
Номер микросостояния
Молекулы с энергией
Е,
Е2
Е3
1
А
В
С
2
В
С
А
3
С
А
В
4
с
В
А
5
А
С
В
6
В
А
С
микросостоянием.
Все возможные
способы распределения трех молекул
по трем энергетическим уровням
представлены в таблице,
из которой видно, что число способов
реализации макросостояния
с энергией Е1
+ Е2
+ Е3
равно шести.
Если же N молекул распределяются по k
уровням таким образом,
чтобы на уровне с энергией Е1
было N1
молекул, на уровне
Е2
было N2
молекул и т. д.:
Энергетический уровень Е1
Е2 Е3
… Еi
… Еk
Число молекул на
уровне N1
N2
N3
… Ni
… Nk
то число микросостояний, отвечающих
макросостоянию с энергией,
равной сумме энергий N
частиц,
распределенных по k
уровням, будет равно
w=N!/(N1!
•N2!•N3!…Ni!…Nk!) (5.9)
Символом N!
(факториал)
обозначают произведение всех целых
чисел от 1 до N,
т. е. N! = 1
• 2 • 3 • … • N.
В рассмотренном
выше примере с распределением трех
молекул по
трем энергетическим уровням на каждом
энергетическом
уровне было по одной молекуле, т.е.
N1
= N2
= N3
= 1,
а общее число молекул
N
= 3, следовательно, число микросостояний
w=3!/(1!
•1!
•1!)
Число микросостояний,
отвечаюшее данному макросостоянию,
называют
термодинамической вероятностью этого
макроскопического состояния.
Согласно уравнению
(5.9), числовые значения w
тем больше,
чем больше общее
число частиц N
= N1+N2+N3
+ … +Ni+
… +Nk
и чем больше число энергетических
уровней k.
Для больших множеств частиц вероятности
их термодинамических
состояний — всегда гигантские числа.
Их крайне неудобно
вычислять и измерять, поэтому вместо
термодинамических вероятностей
применяют математически равноценные
им величины
энтропии, которые пропорциональны
натуральным логарифмам
w.
В расчете на 1 моль частиц энтропия S
определяется через термодинамическую
вероятность макросостояния вещества
при помощи уравнения
Больцмана—Планка:
S=Rlnw. (5.10)
где R
— универсальная
газовая постоянная.
Энтропия. В
соответствии с уравнением (5.10) энтропия
— мера вероятности данного
состояния, т. е. числа способов,
которыми это
состояние может реализоваться.
Энтропия возрастает
вместе со сложностью порядка, с помощью
которого реализуется макросостояние.
Но чем сложнее порядок,
тем труднее его воспринимают, тем чаще
его называют неупорядоченностью
или беспорядком. Поэтому часто говорят,
что энтропия
— мера
неупорядоченности, хаотичности системы.
Так же как внутренняя
энергия и энтальпия, энтропия -функция
состояния вещества. Она зависит от
температуры, давления, фазового
состояния вещества.
Второе начало термодинамики. Существует
несколько эквивалентных
формулировок этого фундаментального
положения всей науки в целом. Одна
из них звучит следующим образом:
при любых
самопроизвольно протекающих процессах
в изолированной
системе ее энтропия не может убывать.
Для необратимых
процессов в изолированных системах
изменение
энтропии ΔS
> 0, для обратимых процессов ΔS
= 0. Обратимым в термодинамике
называют такой процесс, после которого
система и ее окружение могут вернуться
в начальное состояние таким
образом, чтобы во всех участвующих в
процессе телах не осталось никаких
изменений. Обратимый процесс обязательно
должен быть равновесным, т. е. проходить
настолько медленно и осторожно,
чтобы на каждом этапе превращения
успевало возникать состояние,
бесконечно близкое к равновесному.
Все реальные процессы необратимы, лишь
небольшое число из
них можно приближенно рассматривать
как обратимые. Таким образом, в
результате реальных процессов энтропия
изолированной системы всегда
увеличивается.
Третье начало
термодинамики.
Это
фундаментальное положение термодинамики,
которое не является следствием первого
и второго начал термодинамики:
при абсолютном
нуле температуры энтропия кристалла,
имеющего
полностью упорядоченную структуру,
равна нулю при любых
значениях параметров состояния.
Эта формулировка
третьего начала термодинамики была
предложена М,
Планком в 1911 г. Она означает, что для
любого вещества
можно на основе экспериментальных
данных определить абсолютные значения
энтропии, поскольку за точку отсчета
принято ее нулевое значение.
Энтропию 1 моль
вещества в его стандартном состоянии
при давлении
101,15 кПа и фиксированной температуре
называют стандартной
молярной энтропией.
Стандартную энтропию
обозначают символом SoT.
Она измеряется
в Дж/(моль·К). В справочниках чаще всего
приводят числовые
значения стандартной энтропии при
температуре 298,15
К (25 °С) и обозначают ее символом S°
без нижнего индекса.
Изменение энтропии
при фазовых переходах. На
рис. 5.4 показана
зависимость энтропии металлического
свинца от температуры.
Из этого рисунка
видно, что с повышением температуры
энтропия увеличивается. Она быстро
растет в кристаллическом свинце за
счет усиления колебаний атомов в решетке.
При достижении температуры плавления
происходит скачкообразное увеличение
энтропии на
величину ΔS
ПЛ в результате
фазового перехода, сопровождающегося
резким возрастанием
хаотичности системы.
В твердой фазе атомы свинца
располагались упорядочение
в узлах кристаллической
решетки. В жидкости
же такого строгого порядка,
распространяющегося на весь
объем фазы, уже нет, хотя
еще сохраняется так называемый
ближний порядок вблизи
каждого из атомов. Повышение
температуры жид
Кого свинца не
вызывает такого быстрого роста энтропии,
который наблюдается в кристаллическом
состоянии. Однако при достижении
температуры кипения происходит огромное
увеличение
энтропии на величину δs
исп,
потому что из жидкого состояния,
в котором подвижность атомов свинца
была ограничена их
достаточно плотным взаимным расположением,
свинец переходит
в
газообразное
состояние, где атомы находятся друг от
друга на расстояниях, значительно
превышающих их собственные
размеры, и могут свободно совершать
любые хаотичные перемещения,
образуя совершенно неупорядоченную
систему. Энтропия паров свинца с
повышением температуры возрастает
незначительно.
Аналогичные
изменения энтропии с ростом температуры
и
в результате фазовых переходов наблюдаются
и у других веществ.
Наименьшие числовые значения энтропии
характерны для
твердых кристаллических веществ. Причем
они больше у веществ со сложной структурой
молекул, в которых возможны
колебательные и вращательные движения
одних частей молекул относительно
других. Особенно высоки числовые значения
энтропии для газов.
Изменение энтропии
в химических реакциях. Расчет
изменения
энтропии системы в результате химической
реакции осуществляют аналогично
расчету теплового эффекта реакции,
используя уравнение
ΔSoреакции
= Σ[ΔSo
(продукты)] –
Σ
[ΔSo
(реагенты)].
где Σ[ΔSo
(продукты)] –
сумма энтропии продуктов реакции; Σ
[ΔSo
(реагенты)]—
сумма энтропии реагентов. При суммировании
нужно учитывать стехиометрические
коэффициенты перед формулами
реагентов и продуктов.
Как найти энтальпию реакции
3 методика:Вычисление энтальпииПодсчет энтальпииЭкспериментальный подсчет энтальпии
Некоторые химические реакции могут поглощать или выделять тепло окружающей среды. Такой теплообмен между химической реакцией и окружающей средой, называется энтальпией, или H. Однако, нельзя точно измерить энтальпию, поэтому принято рассчитывать изменение температуры окружающей среды (обозначаемое ∆H). ∆H показывает, что в ходе химической реакции происходит выделение тепла в окружающую среду (экзотермическая реакция) или поглощение тепла (эндотермическая реакция). Рассчитывается энтальпия так: ∆H = m x s x ∆T, где m – это масса реагентов, s – это теплоемкость, ∆T – это разница температуры.
Шаги
Метод 1 из 3: Вычисление энтальпии
-

1
Найдите реагенты и продукты реакции. Любая химическая реакция имеет реагенты и продукты реакции. Продукт реакции создается в результате взаимодействия реагентов. Другими словами реагенты – это ингредиенты в рецепте, а продукт реакции – это готовое блюдо. Чтобы найти ∆H реакции, необходимо найти реагенты и продукты реакции..- Например, необходимо найти энтальпию реакции образования воды из водорода и кислорода: 2H2 (Водород) + O2 (Кислород) → 2H2O (Вода). В этой реакции H2 и O2 – это реагенты, а H2O – это продукт реакции.
-

2
Определите общую массу реагентов. Далее необходимо подсчитать массу реагентов. Если вы не можете взвесить их, то подсчитайте молекулярную массу, чтобы найти фактическую. Молекулярная масса – это постоянная, которую можно найти в периодической таблице Менделеева или в других таблицах молекул и соединений. Умножьте массу каждого реагента на число молей.- В нашем примере, реагенты, водород и кислород, имеют молекулярные массы 2 г и 32 г соответственно. Поскольку мы используем 2 моль водорода (коэффициент в химической реакции перед водородом H2) и 1 моль кислорода (отсутствие коэффициента перед O2 обозначает 1 моль), то общая масса реагентов рассчитывается следующим образом:
2 × (2г) + 1 × (32г) = 4г + 32г = 36г
- В нашем примере, реагенты, водород и кислород, имеют молекулярные массы 2 г и 32 г соответственно. Поскольку мы используем 2 моль водорода (коэффициент в химической реакции перед водородом H2) и 1 моль кислорода (отсутствие коэффициента перед O2 обозначает 1 моль), то общая масса реагентов рассчитывается следующим образом:
-

3
Определите теплоемкость продукта. Далее определите теплоемкость продукта реакции. Каждая молекула имеет определенную величину теплоемкости, которая является постоянной. Найдите эту постоянную в таблицах учебника по химии. Существует несколько единиц измерения теплоемкости. Для расчета нам потребуется Дж/г°C.- Обратите внимание на то, что при наличии нескольких продуктов реакции, вам потребуется рассчитать теплоемкость каждого, а затем сложить их, чтоб получить энтальпию всей реакции.
- В нашем примере, продукт реакции – вода, которая имеет теплоемкость 4,2 Дж/г°C.
-

4
Найдите разницу температуры. Теперь мы найдем ∆T – изменение температуры до и после реакции. Из начальной температуры (T1) вычтите конечную температуру (T2). Чаще всего используется шкала Кельвина (К) для определения температуры (хотя по шкале Цельсия (°С) получится тот же результат).- В нашем примере давайте предположим, что начальная температура реакции была 185K, а после реакции стала 95K, значит, ∆T вычисляется так:
∆T = T2 – T1 = 95K – 185K = -90K
- В нашем примере давайте предположим, что начальная температура реакции была 185K, а после реакции стала 95K, значит, ∆T вычисляется так:
-

5
Найдите энтальпию по формуле ∆H = m x s x ∆T. Если известна m – масса реагентов, s – теплоемкость продукта реакции и ∆T – изменение температуры, то можно подсчитать энтальпию реакции. Подставьте значения в формулу ∆H = m x s x ∆T и получите энтальпию. Результат вычисляется в Джоулях (Дж).- В нашем примере энтальпия вычисляется так:
∆H = (36г) × (4.2 ДжK-1 г-1) × (-90K ) = -13,608 Дж
- В нашем примере энтальпия вычисляется так:
-

6
Определение выделения или поглощения энергии. Наиболее важная характеристика энтальпии ∆H – это определение будет реакция экзотермической (выделение тепла и снижение собственной энергии) или эндотермической (поглощение тепла из окружающей среды и повышение собственной энергии). Если знак перед значением ∆H положительный, значит реакция эндотермическая. Если знак отрицательный, значит реакция экзотермическая. Остерегайтесь больших значений энтальпии, потому что это может означать большой и быстрый выброс энергии, что может привести к взрыву.- В нашем примере, конечный результат получился равным -13 608 Дж. Перед значением энтальпии отрицательный знак, а это означает, что реакция экзотермическая. Горячие газы (в виде пара) H2 и O2 должны выделить некоторое количество тепла, чтобы образовать молекулу воды, то есть реакция образования H2O является экзотермической.
Метод 2 из 3: Подсчет энтальпии
-

1
Подсчитайте энергию связей для оценки энтальпии. Почти все химические реакции приводят к разрыву одних связей и образованию новых. Так по разрыву или образованию химических связей можно оценить изменение энтальпии всей реакции при помощи суммирования энергии этих связей.- Например, рассмотрим реакцию: H2 + F2 → 2HF. В этом случае, энергия для разрыва связи в молекуле H2 составляет 436 кДж/моль, а энергия для разрыва F2 составляет 158 кДж/моль.[1] Наконец, энергия необходимая для образования связи в молекуле HF из H и F = -568 кДж/моль.[2] Умножаем последнее значение на 2, т.к. получаем в ходе реакции 2 моль HF, т.е. 2 × -568 = -1136 кДж/моль. Складываем значения:
436 + 158 + -1136 = -542 кДж/моль.
- Например, рассмотрим реакцию: H2 + F2 → 2HF. В этом случае, энергия для разрыва связи в молекуле H2 составляет 436 кДж/моль, а энергия для разрыва F2 составляет 158 кДж/моль.[1] Наконец, энергия необходимая для образования связи в молекуле HF из H и F = -568 кДж/моль.[2] Умножаем последнее значение на 2, т.к. получаем в ходе реакции 2 моль HF, т.е. 2 × -568 = -1136 кДж/моль. Складываем значения:
-

2
Используйте энтальпию образования для оценки энтальпии. Энтальпия образования позволяет рассчитать ∆H через вычисление реакций образования реагентов и продуктов. Если известна энтальпия образования продуктов реакции и реагентов, то вы можете рассчитать энтальпию образования по следующему примеру.- Например, рассмотрим следующую реакцию: C2H5OH + 3O2 → 2CO2 + 3H2O. Мы знаем, что энтальпия образования рассчитывается:[3]
C2H5OH → 2C + 3H2 + 0.5O2 = 228 кДж/моль
2C + 2O2 → 2CO2 = -394 × 2 = -788 кДж/моль
3H2 + 1.5 O2 → 3H2O = -286 × 3 = -858 кДж/моль
Теперь необходимо сложить значения образованных веществ, полученные выше, для определения энтальпии реакции: C2H5OH + 3O2 → 2CO2 + 3H2O,
228 + -788 + -858 = -1418 кДж/моль.
- Например, рассмотрим следующую реакцию: C2H5OH + 3O2 → 2CO2 + 3H2O. Мы знаем, что энтальпия образования рассчитывается:[3]
-

3
Не забывайте про знаки перед значениями энтальпии. При вычислении энтальпии образования, формулу для определения энтальпии реакции продукта вы переворачиваете, то знак энтальпии должен поменяться. Другими словами, если вы переворачиваете формулу, то знак энтальпии должен смениться на противоположный.- В примере, обратите внимание на то, что реакция образования для продукта C2H5OH записана наоборот. C2H5OH → 2C + 3H2 + 0.5O2 т.е. C2H5OH распадается, а не синтезируется. Поэтому знак перед энтальпией в такой реакции положительный: 228 кДЖмоль, хотя энтальпия образования C2H5OH составляет -228 кДжмоль.
Метод 3 из 3: Экспериментальный подсчет энтальпии
-

1
Возьмите чистую емкость и налейте туда воды. Давайте посмотрим принципы энтальпии экспериментально. Убедитесь, что используемые предметы не содержат загрязнителей и очистителей. Ученые используют специальный закрытые контейнеры – калориметры, для измерения энтальпии, но также можно использовать стеклянный стакан или колбу. Заполните его чистой водопроводной водой. Желательно проводить эксперимент в холодном помещении.- Для эксперимента желательно использовать небольшой контейнер. Мы будем рассматривать энтальпию реакции с Алька-Зельцер, поэтому, чем меньше воды используется, тем более очевидным будет изменение температуры.
-

2
Поместите термометр в контейнер. Поместите в контейнер термометр так, чтобы граница прочтения температуры была ниже уровня воды. Начальная температура теперь известна – T1.- Предположим, что температуры воды 10°C. Через несколько шагов мы поймем на практике, что такое энтальпия и как это работает.
-

3
Добавьте одну таблетку Алька-Зельцер в контейнер. Готовы? Кидайте одну таблетку Алька-Зельцер в воду, которая сразу начнет пузыриться и шипеть. Это происходит из-за реакции между бикарбонатом (HCO3-) и лимонной кислотой (H+). В результате образуется вода и углекислый газ по формуле: 3HCO3− + 3H+ → 3H2O + 3CO2. -

4
Измерьте конечную температуру. Таблетка Алька-Зельцер должна полностью раствориться. Измерьте температуру еще раз. Температура должна быть немного ниже. Если температура воды сейчас выше начальной температуры, значит, эксперименту помешали какие-то внешние факторы (например, слишком теплое помещение, где проводился эксперимент).- Предположим, что измеренная второй раз температура составляет 8°C.
-

5
Подсчитаем энтальпию реакции. В ходе эксперимента должно наблюдаться снижение температуры воды после растворения таблетки Алька-Зельцер. Можно сделать вывод, что данная реакция является эндотермической, т.е. химическая реакция сопровождается поглощением энергии окружающей среды. Кроме того в результате реакции образуется газ, который также поглощает энергию окружающей среды. Все это приводит к снижению температуры воды.- В нашем эксперименте температура воды упала на 2 градуса. Это доказывает, что реакция растворения Алька-Зельцер в воде эндотермическая.
Советы
- В подсчетах используется шкала Кельвина (K) – это температурная шкала аналогическая Цельсию. Чтобы перевести значение Цельсия в Кельвина, необходимо добавить или вычесть 273 градуса: K = °C + 273.










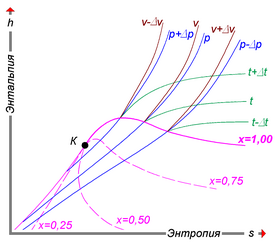









![{displaystyle quad mathrm {d} H=C_{P}mathrm {d} T+left[V-Tleft({frac {partial V}{partial T}}right)_{P}right]mathrm {d} P.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db8b72626dbc316bfcff5dcbb2aae49c93912304)













