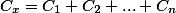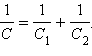1 мФ = 0,001 Ф. 1 мкФ = 0,000001 = 10⁻⁶ Ф. 1 нФ = 0,000000001 = 10⁻⁹ Ф. 1 пФ = 0,000000000001 = 10⁻¹² Ф.
В соответствии со вторым правилом Кирхгофа, падения напряжения V₁, V₂ and V₃ на каждом из конденсаторов в группе из трех соединенных последовательно конденсаторов в общем случае различные и общая разность потенциалов V равна их сумме:

По определению емкости и с учетом того, что заряд Q группы последовательно соединенных конденсаторов является общим для всех конденсаторов, эквивалентная емкость Ceq всех трех конденсаторов, соединенных последовательно, определяется как

или

Для группы из n соединенных последовательно конденсаторов эквивалентная емкость Ceq равна величине, обратной сумме величин, обратных емкостям отдельных конденсаторов:

или

Эта формула для Ceq и используется для расчетов в этом калькуляторе. Например, общая емкость соединенных последовательно трех конденсаторов емкостью 10, 15 and 20 мкФ будет равна 4,62 мкФ:

Если конденсаторов только два, то их общая емкость определяется по формуле

или

Если имеется n соединенных последовательно конденсаторов с емкостью C, их эквивалентная емкость равна

Отметим, что для расчета общей емкости нескольких соединенных последовательно конденсаторов используется та же формула, что и для расчета общего сопротивления параллельно соединенных резисторов.
Отметим также, что общая емкость группы из любого количества последовательно соединенных конденсаторов всегда будет меньше, чем емкость самого маленького конденсатора, а добавление конденсаторов в группу всегда приводит к уменьшению емкости.

Конденсаторы на печатной плате
Отдельного упоминания заслуживает падение напряжения на каждом конденсаторе в группе последовательно соединенных конденсаторов. Если все конденсаторы в группе имеют одинаковую номинальную емкость, падение напряжения на них скорее всего будет разным, так как конденсаторы в реальности будут иметь разную емкость и разный ток утечки. На конденсаторе с наименьшей емкостью будет наибольшее падение напряжения и, таким образом, он будет самым слабым звеном этой цепи.

Выравнивающие резисторы уменьшают разброс напряжений на отдельных конденсаторах
Для получения более равномерного распределения напряжений параллельно конденсаторам включают выравнивающие резисторы. Эти резисторы работают как делители напряжения, уменьшающие разброс напряжений на отдельных конденсаторах. Но даже с этими резисторами все равно для последовательного включения следует выбирать конденсаторы с большим запасом по рабочему напряжению.
Если несколько конденсаторов соединены параллельно, разность потенциалов V на группе конденсаторов равна разности потенциалов соединительных проводов группы. Общий заряд Q разделяется между конденсаторами и если их емкости различны, то заряды на отдельных конденсаторах Q₁, Q₂ and Q₃ тоже будут различными. Общий заряд определяется как

Конденсаторы, соединенные параллельно

По определению емкости, эквивалентная емкость группы конденсаторов равна

отсюда

или

Для группы n включенных параллельно конденсаторов

То есть, если несколько конденсаторов включены параллельно, их эквивалентная емкость определяется путем сложения емкостей всех конденсаторов в группе.
Возможно, вы заметили, что конденсаторы ведут себя противоположно резисторам: если резисторы соединены последовательно, их общее сопротивление всегда будет выше сопротивлений отдельных резисторов, а в случае конденсаторов всё происходит с точностью до наоборот.

Конденсаторы на печатной плате
Эквивалентная ёмкость конденсаторов
| Номиналы ёмкостей конденсаторов, разделенные запятыми |
| Эквивалентная ёмкость конденсаторов при последовательном соединении |
| Альтернативное отображение |
| Эквивалентная ёмкость конденсаторов при паралельном соединении |
| Альтернативное отображение |
Последовательное соединение
Написав бот, расчета размерностей Система единиц измерения онлайн теперь начнем осваивать такую многогранную и сложную область как электротехника.
И первое, что нам пригодится, это расчет эквивалентных характеристик основных электрических элементов( ёмкость, индуктивность, сопротивление).
Хотелось бы напомнить, что ёмкости некоторых типовых конструкций мы уже умеем рассчитывать Ёмкость конденсатора онлайн
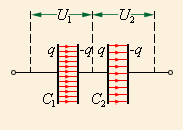
Сами по себе формулы очень просты, но нюанс состоит в том, как нам точно посчитать ёмкость двух последовательно соединенных конденсаторов если один из конденсаторов имеет ёмкость 10 пФ, а второй 250нФ. Размерность показывает что они различаются в 1000 раз. Можно конечно все перевести в абсолютные значения, но это при большом количестве конденсаторов способствует возникновению ошибок.
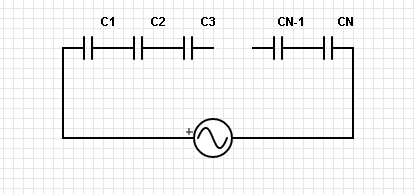
Итак, последовательное соединение конденсаторов имеет следующий вид
И формула расчета эквивалентной ёмкости выглядит так
Паралельное СОЕДИНЕНИЕ
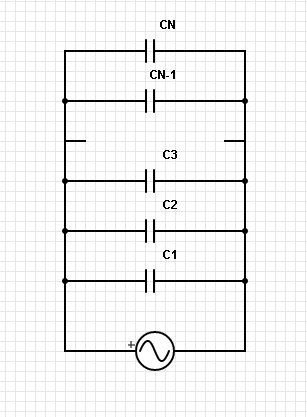
Последовательное соединение нескольних конденсаторов выглядит так, как показано на рисунке
А формула становится до безобразия простой и наглядной
Синтаксис
Он очень прост
calc_e список емкостей с размерностями через запятую.
В ответе мы получим эквививалентное значение ёмкости при последовательном и паралельных соединениях.
Важное замечание: размерности нужно писать на русском языке. Для пользователей сайта, не знающих русский язык, можем по запросу добавить обработку англоязычных наименований приставок и размерностей. Это не сложно.
Примеры
Рассчитать ёмкость трех конденсаторов следующих номиналов: 10 пФ, 0.2нФ и 344мФ
В запросе так и пишем calc_e 10пФ,0.2нФ,344мФ
Ответ не заставит себя долго ждать и выглядит вот так
| Эквивалентная ёмкость конденсаторов при паралельном соединении |
|
9.5238095235459пикофарад |
| Альтернативное отображение |
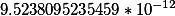 |
| Эквивалентная ёмкость конденсаторов при последовательном соединении |
|
344.00000021милифарад |
| Альтернативное отображение |
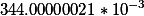 |
Удачи в расчетах!
Содержание
- 1 Как рассчитывается электрическая ёмкость конденсаторов?
- 2 Как определить емкость конденсатора формула?
- 3 Как можно увеличить общую емкость конденсаторов?
- 4 Что происходит при последовательном соединении конденсаторов?
- 5 Как рассчитать емкость конденсатора при последовательном соединении?
- 6 Сколько в одном фараде Микрофарад?
- 7 Как определить емкость плоского конденсатора?
- 8 Как найти заряд q?
- 9 Как работать с конденсатором?
- 10 Какие физические величины сохраняются при последовательном соединении конденсаторов?
- 11 Чему равна общая емкость батареи конденсаторов?
- 12 Что произойдет с электрической емкостью конденсаторов Если они соединены последовательно?
- 13 В каком случае используют параллельное соединение конденсаторов?
Как рассчитывается электрическая ёмкость конденсаторов?
Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2 . Емкость рассчитывается по формуле: C=4πεε0R1R2R2−R1 C = 4 π ε ε 0 R 1 R 2 R 2 — R 1 , где R1 и R2 являются радиусами обкладок.
Как определить емкость конденсатора формула?
Емкость конденсатора с диэлектриком из воздуха можно подсчитать по формуле C=S/(4∙π∙d)∙1,11, пФ, где S – площадь одной обкладки, см2; d – расстояние между обкладками, см; C – емкость конденсатора, пФ. Емкость конденсатора, состоящего из n пластин (рис. 3), равна: C=(n-1)∙ S/(4∙π∙d)∙1,11, пФ.
Как можно увеличить общую емкость конденсаторов?
Для увеличения ёмкости конденсаторы соединяются параллельно. Для увеличения сопротивления резисторы соединяются последовательно. Вода через трубу с двумя валенками течёт хуже, чем через трубу с одним валенком.
Что происходит при последовательном соединении конденсаторов?
При последовательном соединении конденсаторов уменьшается общая емкость и увеличивается общее напряжение конденсаторов. А общее напряжение будет равняться сумме напряжений всех конденсаторов. Например: мы имеем три конденсатора по 30 мкФ x 100 В каждый.
Как рассчитать емкость конденсатора при последовательном соединении?
Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов.
Сколько в одном фараде Микрофарад?
Так как 1 фарад — очень большая емкость, поэтому используются меньшие значения, такие как: микрофарад (мкФ), равный одной миллионной фарада; нанофарад (нФ), равный одной миллиардной; пикофарад (пФ), равный одной триллионной фарада. В системе СГСЭ основной единицей емкости является сантиметр (см).
Как определить емкость плоского конденсатора?
Ёмкость плоского конденсатора находиться по формуле: Где ε0=8,854187817·10 −12 Ф/м — электрическая постоянная, ε — диэлектрическая проницаемость диэлектрика расположенного между обкладками конденсатора, S — площадь обкладки конденсатора, d — расстояние между обкладками.
Как найти заряд q?
Формула нахождения заряда
В соответствии с ней, нужно перемножить силу тока на время его прохождения по проводнику. Количество заряда можно узнать через формулу +-ne, где n служит целым числом, а е равно значению = -1,6*10^-19 Кулон. Обратите внимание!
Как работать с конденсатором?
Принцип работы конденсатора: его заряд и разряд
В момент подключения к источнику постоянного тока через конденсатор начинает протекать ток заряда. Он убывает по мере зарядки конденсатора и в итоге падает до величины тока саморазряда, определяющегося проводимостью материала диэлектрика.
Какие физические величины сохраняются при последовательном соединении конденсаторов?
Последовательное соединение конденсаторов
заряды одинаковы, складываются величины, обратные емкости.
Чему равна общая емкость батареи конденсаторов?
Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Что произойдет с электрической емкостью конденсаторов Если они соединены последовательно?
Вследствие того что через все последовательно соединенные конденсаторы течет одинаковый ток, количество накопленого электрического заряда для каждого конденсатора будет одинаковым, независимо от его емкости. … Это означает, что в режиме постоянного тока конденсатор С2 электрически изолирован от общей цепи.
В каком случае используют параллельное соединение конденсаторов?
Токи через конденсаторы группы протекают разные: через конденсатор с большей емкостью потечет больший ток. На практике параллельное соединение применяется для получения емкости нужной величины, когда она выходит за границы диапазона, выпускаемого промышленностью, или не укладываются в стандартный ряд емкостей.
ПРАКТИЧАСКАЯ
РАБОТА №1
«Расчет
эквивалентной емкости при смешанном
соединении конденсаторов, а также
распределения зарядов и напряжений»
На
рисунке 1 дана схема соединения
конденсаторов. Значение емкостей
конденсаторов и значение одного из
напряжений или зарядов для своего
варианта взять из таблицы 1.
Вычислить
эквивалентную емкость батареи
конденсаторов; напряжение сети, напряжение
на каждом конденсаторе; общий заряд и
заряд на каждом конденсаторе; энергию,
накопленную батареей, а также потенциал
заданной точки.
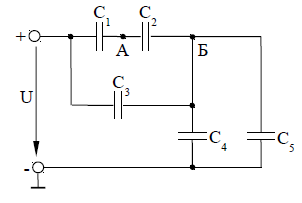
Рисунок
1
Таблица
1
|
№ вар. |
Емкость |
Напряжение, заряд |
Точка, |
||||
|
С1 |
С2 |
С3 |
С4 |
С5 |
|||
|
1 |
120 |
280 |
16 |
80 |
70 |
U=20 |
Б |
|
2 |
600 |
200 |
150 |
400 |
200 |
Q3=72∙10-4 |
Б |
|
3 |
24 |
12 |
2 |
16 |
14 |
U5=25 |
А |
|
4 |
30 |
20 |
12 |
20 |
16 |
Q4=4∙10-4 |
Б |
|
5 |
10 |
15 |
24 |
6 |
9 |
U1=15 |
А |
|
6 |
12 |
6 |
5 |
9 |
9 |
Q2=282∙10-6 |
А |
|
7 |
30 |
15 |
10 |
65 |
15 |
Q5=6∙10-4 |
А |
|
8 |
18 |
9 |
12 |
15 |
21 |
U2=84 |
Б |
|
9 |
140 |
60 |
6 |
30 |
18 |
U3=50 |
А |
|
10 |
150 |
50 |
37,5 |
30 |
20 |
Q1=3∙10-4 |
Б |
|
11 |
200 |
300 |
40 |
160 |
100 |
U=40 |
Б |
|
12 |
540 |
150 |
90 |
380 |
120 |
Q3=54∙10-4 |
А |
|
13 |
46 |
26 |
8 |
34 |
28 |
U5=45 |
Б |
|
14 |
60 |
45 |
25 |
40 |
30 |
Q4=8∙10-4 |
А |
|
15 |
30 |
25 |
46 |
20 |
18 |
U1=30 |
Б |
|
16 |
25 |
15 |
10 |
20 |
15 |
Q2=564∙10-6 |
Б |
|
17 |
60 |
30 |
45 |
120 |
25 |
Q5=15∙10-4 |
Б |
|
18 |
36 |
18 |
24 |
30 |
44 |
U2=160 |
А |
|
19 |
300 |
140 |
12 |
50 |
38 |
U3=100 |
Б |
|
20 |
280 |
100 |
70 |
65 |
45 |
Q1=6∙10-4 |
А |
|
21 |
60 |
150 |
9 |
40 |
25 |
U=10 |
Б |
|
22 |
300 |
100 |
70 |
200 |
90 |
Q3=36∙10-4 |
А |
|
23 |
14 |
6 |
4 |
8 |
10 |
U5=15 |
А |
|
24 |
90 |
60 |
25 |
40 |
26 |
Q4=12∙10-4 |
Б |
|
25 |
6 |
8 |
12 |
4 |
12 |
U1=7 |
А |
|
26 |
46 |
18 |
15 |
27 |
18 |
Q2=846∙10-6 |
Б |
|
27 |
90 |
45 |
30 |
190 |
65 |
Q5=18∙10-4 |
А |
|
28 |
560 |
35 |
25 |
45 |
20 |
U2=320 |
А |
|
29 |
400 |
240 |
15 |
35 |
100 |
U3=150 |
А |
|
30 |
390 |
150 |
200 |
90 |
180 |
Q1=9∙10-4 |
Б |
ПРИМЕР
На
рисунке 2 приведена схема соединения
конденсаторов. Определить эквивалентную
емкость
Сэкв
батареи
конденсаторов, общий заряд Q, напряжение
сети U, напряжение и заряд на каждом
конденсаторе, если дано: C1=24
мкФ; С2=С3=8
мкФ; С4=12
мкФ; С5=6
мкФ; напряжение на пятом конденсаторе
U5=30
В.

Рисунок
2
Дано:
C1=24
мкФ;
С2=С3=8
мкФ;
С4=12
мкФ;
С5=6
мкФ;
U5=30
В
Определить:
U, Q, Сэкв,
U1,
U2,
U3,
U4,
Q1.
Решение:
1.
Общая емкость последовательно соединенных
конденсаторов С4
и
С5:
![]()
2.
Общая емкость параллельно соединенных
конденсаторов С3
иС4,5:
![]()
3.
Общая емкость последовательно соединенных
конденсаторов С1,
С2
и
С3,4,5,
которая и является
эквивалентной
емкостью батареи конденсаторов:
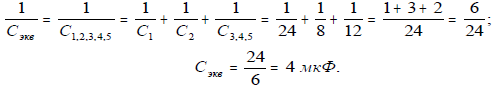
4.
По заданному напряжению U5
и
емкости конденсатора С5
определяем
заряд, накапливаемый
этим
конденсатором:
![]()
5.
Заряд конденсатора С4
Q4=Q5=Q4,5=180・10-6
Кл,
т. к. конденсаторы С4
и
С5
соединены
последовательно.
6.
Напряжение на четвертом конденсаторе:
![]()
7.
Напряжение на третьем конденсаторе:
![]()
8.
Заряд конденсатора С3:
![]()
9.
Общий заряд батареи и заряды конденсаторов
С1
и
С2:
![]()
10.
Напряжение на первом и втором конденсаторах:
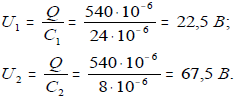
11.
Напряжение сети (напряжение последовательно
соединенных конденсаторов С1,
С2,
С3,4,5):
![]()
12.
Энергия электрического поля батареи:
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Методика расчёта электрических цепей с конденсаторами.
Краткие теоретические сведения:
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
|
В системе СИ единица электроемкости называется фарад (Ф):
|
|
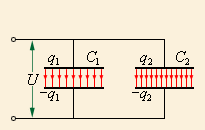
Конденсаторы могут соединяться между собой, образуя батареи конденсаторов. При параллельном соединении конденсаторов (рис. 1.) напряжения на конденсаторах одинаковы: U1 = U2 = U, а заряды равны q1 = С1U и q2 = C2U. Такую систему можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q1 + q2при напряжении между обкладками равном U. Отсюда следует
|
Таким образом, при параллельном соединении электроемкости складываются.
|
|
При последовательном соединении (рис.2.) одинаковыми оказываются заряды обоих конденсаторов: q1 = q2 = q, а напряжения на них 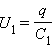
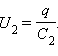 Такую систему можно рассматривать как единый конденсатор, заряженный зарядом q при напряжении между обкладками U = U1 + U2. Следовательно,
Такую систему можно рассматривать как единый конденсатор, заряженный зарядом q при напряжении между обкладками U = U1 + U2. Следовательно,
|
При последовательном соединении конденсаторов складываются обратные величины емкостей.
Пример расчёта:На рисунке 2 приведена схема соединения конденсаторов. Определить эквивалентнуюемкостьСэкв батареи конденсаторов, общий заряд Q, напряжение сети U, напряжение и заряд на каждом конденсаторе, если дано: C1=24 мкФ; С2=С3=8 мкФ; С4=12 мкФ; С5=6 мкФ; напряжение на пятом конденсаторе U5=30 В.
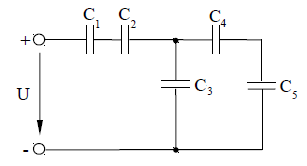
Рисунок 3
Дано: C1=24 мкФ; С2=С3=8 мкФ; С4=12 мкФ; С5=6 мкФ; U5=30 ВОпределить: U, Q, Сэкв, U1, U2, U3, U4, Q1.
Решение: 1. Общая емкость последовательно соединенных конденсаторов С4 и С5:
![]()
2. Общая емкость параллельно соединенных конденсаторов С3 иС4,5:
![]()
3. Общая емкость последовательно соединенных конденсаторов С1, С2 и С3,4,5, которая и является эквивалентной емкостью батареи конденсаторов:
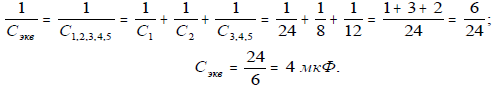
4. По заданному напряжению U5 и емкости конденсатора С5 определяем заряд, накапливаемый этим конденсатором:
![]()
5. Заряд конденсатора С4 Q4=Q5=Q4,5=180・10-6 Кл, т. к. конденсаторы С4 и С5 соединены последовательно. 6. Напряжение на четвертом конденсаторе:
![]()
7. Напряжение на третьем конденсаторе:
![]()
8. Заряд конденсатора С3:
![]()
9. Общий заряд батареи и заряды конденсаторов С1 и С2:
![]()
10. Напряжение на первом и втором конденсаторах:
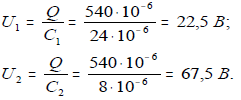
11. Напряжение сети (напряжение последовательно соединенных конденсаторов С1, С2, С3,4,5):
![]()
12. Энергия электрического поля батареи:
![]()
Выполнить задание:
На рисунке 4 дана схема соединения конденсаторов. Значение емкостей конденсаторов и значение одного из напряжений или зарядов для своего варианта взять из таблицы 1.Вычислить эквивалентную емкость батареи конденсаторов; напряжение сети, напряжение на каждом конденсаторе; общий заряд и заряд на каждом конденсаторе; энергию, накопленную батареей, а также потенциал заданной точки.
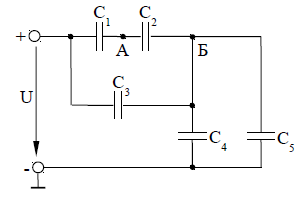
Рисунок 4.
Таблица 1
|
№ вар. |
Емкость конденсатора, мкФ |
Напряжение, заряд |
Точка, потенциал которой следует вычислить |
||||
|
С1 |
С2 |
С3 |
С4 |
С5 |
|||
|
1 |
120 |
280 |
16 |
80 |
70 |
U=20 В |
Б |
|
2 |
600 |
200 |
150 |
400 |
200 |
Q3=72∙10-4 Кл |
Б |
|
3 |
24 |
12 |
2 |
16 |
14 |
U5=25 В |
А |
|
4 |
30 |
20 |
12 |
20 |
16 |
Q4=4∙10-4 Кл |
Б |
|
5 |
10 |
15 |
24 |
6 |
9 |
U1=15 В |
А |
|
6 |
12 |
6 |
5 |
9 |
9 |
Q2=282∙10-6Кл |
А |
|
7 |
30 |
15 |
10 |
65 |
15 |
Q5=6∙10-4 Кл |
А |
|
8 |
18 |
9 |
12 |
15 |
21 |
U2=84 В |
Б |
|
9 |
140 |
60 |
6 |
30 |
18 |
U3=50 В |
А |
|
10 |
150 |
50 |
37,5 |
30 |
20 |
Q1=3∙10-4 Кл |
Б |
Ответить на контрольные вопросы:
1.От чего зависит ёмкость конденсатора ?
2.Как изменится ёмкость батареи конденсаторов, если вместо последовательного соединения их соединили параллельно?
3.Изменится ли ёмкость воздушного конденсатора, если раздвинуть пластины так, чтобы расстояние между ними увеличилось с 5 до 14 мм?