До сих пор
предполагалось, что заряды и их поля
находятся в вакууме. В последующих
параграфах мы рассмотрим, какое влияние
на электрическое поле и на взаимодействие
электрических зарядов оказывает
вещественная среда – проводники и
диэлектрики.
Электрический
диполь
это система, состоящая из двух одинаковых
по значению, но разных по знаку точечных
заряда (+q,-
q),
расстояние ℓ между которыми (плечо
диполя) значительно меньше расстояния
до рассматриваемых точек поля (рис.12.16).
 Основной
Основной
характеристикой диполя является его
электрический, или дипольный момент.
Дипольный
момент
–это вектор, направленный по оси диполя
(прямой, проходящей через оба заряда)
от отрицательного заряда к положительному
и равный произведению заряда │q│
на плечо ℓ.
![]() (12.35)
(12.35)
Единица электрического
момента диполя – кулон-метр (Кл۰м).
Е сли
сли
диполь поместить в однородное
электростатическое поле напряжён-ностью
Е (рис.12.17), то на каждый из его зарядов
действует сила: на положительныйF+
= +qE,
на отрицательный F–
= – qE.
Эти силы равны по модулю, но противоположны
по направлению. Они образуют пару сил,
плечо которой ℓsinα,
и создают момент пары сил М. Вектор
![]() направлен перпендикулярно векторам
направлен перпендикулярно векторам![]() и
и![]() (см.рис. – на нас). Модуль
(см.рис. – на нас). Модуль![]() определяется соотношениемM=qEℓsinα,
определяется соотношениемM=qEℓsinα,
где α
– угол между векторами
![]() и
и![]() .
.
M=qEℓsinα=рЕsinα
или в векторной
форме
![]() (12.36)
(12.36)
Таким образом, на
диполь в однородном электрическом поле
действует вращающий момент, зависящий
от электрического момента, ориентации
диполя в поле и напряжённость поля.
В однородном поле
момент пары сил стремится повернуть
диполь так, чтобы векторы
![]() и
и![]() и были параллельны.
и были параллельны.
§ 12.6 Поле диполя
Определим
напряжённость электростатического
поля в точке, лежащей посередине на оси
диполя (рис.12.18).
Напряжённость
![]() поля в точке О равна векторной сумме
поля в точке О равна векторной сумме
напряжённостей![]() и
и![]() ,
,
создаваемых положительным и отрицательным
зарядом в отдельности.
![]()
Н а
а
оси диполя между зарядами -q
и +q
векторы напряжённости
![]() и
и![]() направлены в одну сторону, поэтому
направлены в одну сторону, поэтому
результирующая напряжённость по модулю
равна их сумме.
![]()
Если же находить
напряжённость поле в точке А, лежащей
на продолжении оси диполя (рис.12.18),
то векторы
![]() и
и![]() будут направлены в разные стороны и
будут направлены в разные стороны и
результирующая напряжённость по модулю
равна их разности:
![]()
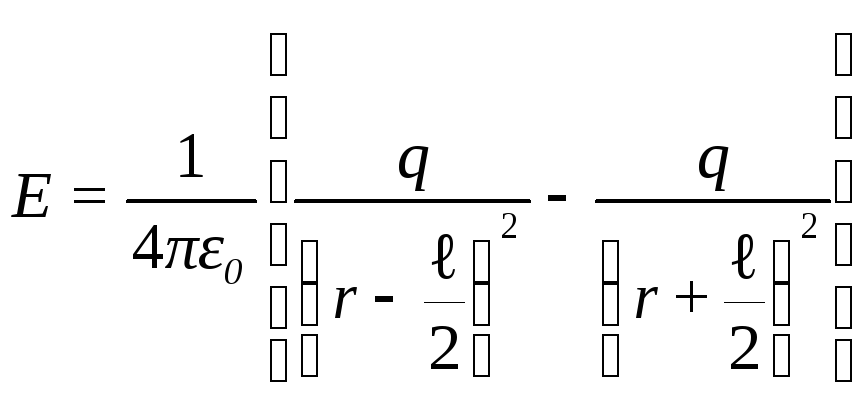
Или

(r
– расстояние между средней точкой диполя
и точкой, лежащей на оси диполя, в которой
определяется напряжённость поля).
Пренебрегая в
знаменателе величиной
![]() ,
,
так какr
>>ℓ получим
![]() или
или
![]() (12.37)
(12.37)
(р- электрический
момент диполя).
 Напряжённость
Напряжённость
поля в
точке С, лежащей на перпендикуляре,
восстановленном из средней точки диполя
(рис.12.19).
Так как расстояние от зарядов +q
и – q
до точки В одинаковое r1
= r2
, то
![]()
Вектор результирующей
напряжённости в точке В по модулю равен
![]()
Из рисунка видно,
что
![]() ,
,
тогда

Так как r
>>ℓ, то можно приближённо считать r1
≈ r,
тогда формула для расчёта напряжённости
в точке, лежащей на перпендикуляре,
остановленном из средней точки диполя,
имеет вид
![]() (12.38)
(12.38)
Напряжённость
поля диполя в произвольной точке
определяется по формуле
![]() (12.39)
(12.39)
(р- электрический
момент диполя, r
– расстояние от центра диполя до точки,
в которой определяется напряжённость
поля, α
– угол между радиус-вектором r
и плечом диполя ℓ).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тогда векторная величина, равная:
[overrightarrow{p_e}=qoverrightarrow{l }left(1right),]
называется моментом диполя (электрическим моментом диполя). В формуле (1) $q$ — абсолютное значение каждого из зарядов диполя.
Электрическое поле диполя складывается из напряжённостей зарядов, которые составляют диполь. Так как плечо диполя мало, поэтому можно считать, что оно много меньше, чем расстояние до точек, в которых рассчитывается напряженность поля. Найдем потенциал диполя. В точке А (рис.1) формула для потенциала будет иметь вид:
[{varphi }_A=frac{q}{4pi {varepsilon }_0varepsilon }left(frac{1}{r_+}-frac{1}{r_-}right)left(2right).]
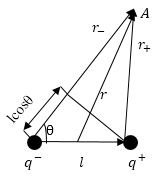
Рис. 1
Так как $lll r$, можно считать, что:
[r_–r_+approx lcostheta , r_-cdot r_+approx r^2left(3right).]
При этом местоположение точки A можно характеризовать вектором$overrightarrow{ r}$ с началом в любой точке диполя, ввиду малых геометрических размеров диполя. В таком случае формулу (2) можно записать в виде:
[varphi left(rright)=frac{1}{4pi {varepsilon }_0varepsilon }frac{overrightarrow{p_e}cdot overrightarrow{r}}{r^3}left(4right),]
где $qlcostheta =frac{overrightarrow{p_e}cdot overrightarrow{r}}{r}.$ Зная связь напряженности поля и потенциала:
[overrightarrow{E}=-gradvarphi (5)]
запишем формулу для напряженности поля диполя, которая будет иметь вид:
[overrightarrow{E}=frac{1}{4pi {varepsilon }_0varepsilon }left(frac{3left({overrightarrow{p}}_ecdot overrightarrow{r}right)overrightarrow{r}}{r^5}-frac{overrightarrow{p_e}}{r^3}right)left(6right).]
Согласно формуле (6) напряженность поля диполя убывает быстрее, чем напряженность кулоновского поля одиночного заряда, пропорционально третьей степени расстояния. Силовые линии электростатического поля около диполя изображены на рис. 2.
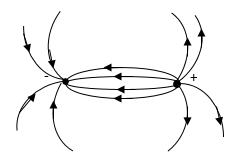
Рис. 2
Модуль вектора сопряженности
Если сферическую систему координат разместить так, чтобы ее центр совпал с серединой плеча диполя, а полярная ось была параллельна $overrightarrow{p_e}$ (рис.3), то составляющие вектора напряженности будут иметь вид:
[E_r=frac{1}{2pi {varepsilon }_0varepsilon }frac{p_ecos vartheta}{r^3},E_vartheta=frac{1}{4pi {varepsilon }_0varepsilon }frac{p_esin vartheta}{r^3},E_{varphi }=0. left(7right).]
В таком случае модуль вектора напряженности равен:
[E=frac{1}{4pi {varepsilon }_0varepsilon }frac{p_e}{r^3}sqrt{3{cos}^2vartheta+1}left(8right).]
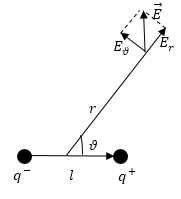
Рис. 3
Вычисление момента сил
В однородном поле сила, которая действует на диполь со стороны поля ($overrightarrow{F}$), равна нулю, так как к зарядам приложены одинаковые по модулю и противоположные по направлению силы:
[overrightarrow{F}={overrightarrow{F}}_++{overrightarrow{F}}_-=0left(9right),]
где ${overrightarrow{F}}_+$- сила, действующая на положительный заряд диполя, ${overrightarrow{F}}$ – сила, действующая на отрицательный заряд диполя.
Момент этих сил равен:
[overrightarrow{M}=overrightarrow{p_e}times overrightarrow{E}left(10right).]
Момент сил $overrightarrow{M}$ стремится повернуть ось диполя в направлении поля $overrightarrow{E}.$ Существует два положения равновесия диполя: диполь параллелен полю (устойчивое положение) и антипараллелен (неустойчивое положение).
Если поле не однородно, то сила (сумма сил действующих на положительный и отрицательный заряд) не равна нулю.$ overrightarrow{F}={overrightarrow{F}}_++{overrightarrow{F}}_-ne 0$. В этом случае сила равна:
[overrightarrow{F}=qleft({overrightarrow{E}}_+-{overrightarrow{E}}_-right)left(11right).]
В том случае, если мы имеем дело с точечным диполем (плечо диполя очень мало), то сила, действующая на диполь, может быть записана как:
[overrightarrow{F}=p_{ex}frac{partial overrightarrow{E}}{?x}+p_{ey}frac{partial overrightarrow{E}}{partial y}+p_{ez}frac{partial overrightarrow{E}}{partial z}left(12right).]
или, что то же самое, но короче:
[overrightarrow{F}=left(overrightarrow{p}overrightarrow{nabla }right)overrightarrow{E}left(13right).]
|
Электрическим диполем называется система двух одинаковых по величине разноименных точечных зарядов + q и – q, расстояние между которыми значительно меньше расстояния до тех точек, в которых определяется поле системы. Прямая, проходящая через оба заряда, называется осью диполя. Вектор, направленный по оси диполя от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя 
рис 7.1 Представление о диполях часто позволяет с известным приближением описать взаимодействие молекул различных веществ. Модель дипольного строения вещества лежит в основе теории диэлектриков. Вектор
совпадающий по направлению с плечом диполя и равный произведению заряда |q| на плечо 
рис 7.2 Пользуясь рисунком 7.2, произведем расчет поля диполя. Будем исследовать поле диполя в вакууме. Согласно принципа суперпозиции потенциал поля в данной точке наблюдения равен:
В этом случае можно положить, что
и предыдущую формулу можно переписать так:
|
Зная зависимость потенциала от координат, можно определить напряженность поля по формулам (6.1). Для этой цели будем пользоваться полярными координатами r и  с полярной осью, совпадающей с моментом диполя. Составляющая напряженности поля
с полярной осью, совпадающей с моментом диполя. Составляющая напряженности поля ![]() (проекция напряженности на r) равна:
(проекция напряженности на r) равна:
| (7.3) |
Составляющая, перпендикулярная к r, равна:
| (7.4) |
Полная напряженность в точке наблюдения равна:
| (7.5) |
| (7.6) |
| (7.7) |
Эти формулы определяют напряженность и потенциал поля для точек, лежащих на линии момента диполя.
Если ![]() или
или ![]() , то
, то
| (7.8) |
| (7.9) |
Эти формулы определяют напряженность и потенциал поля по линии, перпендикулярной к моменту диполя. Сравнивая (7.6) и (7.8), видим, что в обоих случаях напряженность обратно пропорциональна кубу расстояния от диполя.
Теперь рассмотрим поведение диполя во внешнем электрическом поле (рис. 7.3). Если диполь поместить в однородное электрическое поле, образующие диполь заряды + q и – q окажутся под действием равных по величине, но противоположных по направлению сил ![]() (F = F1 = F2 = qE).
(F = F1 = F2 = qE).

рис 7.3
Эти силы образуют пару, плечо которой равно d = l sin![]() ,т.е. зависит от ориентации диполя относительно поля. Модуль каждой из сил, действующих на диполь:
,т.е. зависит от ориентации диполя относительно поля. Модуль каждой из сил, действующих на диполь:
| (7.10) |
(p – электрический момент диполя). Формула (7.10) может быть записана в векторном виде:
| (7.11) |
Момент сил (7.11) стремится повернуть диполь так, чтобы его электрический момент ![]() установился по направлению поля.
установился по направлению поля.
Найдем потенциальную энергию, которой обладает диполь во внешнем электрическом поле. Согласно формуле (5.7) эта энергия равна
| (7.12) |

рис 7.4
![]()
Подставив это значение в формулу (7.12), получим, что
| (7.13) |
В этой формуле ![]() есть угол между векторами
есть угол между векторами ![]() и
и ![]() ,поэтому ее можно написать в виде
,поэтому ее можно написать в виде
| (7.14) |
Заметим, что это выражение не учитывает энергию взаимодействия зарядов +q и – q, образующих диполь.
Мы получили формулу (7.14), считая для простоты поле однородным. Однако эта формула справедлива и для неоднородного поля.
Рассмотрим диполь, находящийся в неоднородном поле, обладающем симметрией относительно оси х. Пусть центр диполя лежит на этой оси, причем электрический момент диполя образует с осью угол ,отличный от pi/2 (рис.7.5).

рис 7.5
В этом случае силы, действующие на заряды диполя, не одинаковы по величине. Поэтому, кроме вращательного момента, на диполь будет действовать сила, стремящаяся переместить его в направлении оси х. Чтобы получить значение этой силы, воспользуемся формулой, которая показывает связь силы с потенциальной энергией: ![]() . Согласно этой формуле
. Согласно этой формуле
![]()
В соответствии с (7.14):
W (x, y, z) = – p E (x, y, z) cos ![]()
(ориентацию диполя относительно вектора ![]() считаем неизменной:
считаем неизменной: ![]() = const).
= const).
Для точек оси x производные E по y и z равны нулю. Соответственно ![]() .Таким образом, отлична от нуля лишь компонента силы
.Таким образом, отлична от нуля лишь компонента силы ![]() . Она равна
. Она равна
| (7.15) |
Электрический диполь в физике
Содержание:
- Что такое электрический диполь
- Электрический дипольный момент
-
Поведение электрического диполя в электрических полях
- Поведение электрического диполя в однородном поле
- Поведение электрического диполя в неоднородном поле
- Эксперименты с электрическим диполем
- Единицы измерения электрического диполя
- Задачи на вычисление электрического диполя
Что такое электрический диполь
Для полного понимания того, как работают и ведут себя диэлектрики в электрическом поле на уровне атомов или молекул веществ, необходимо дать объяснение тому, каким образом реагирует электрически нейтральная система на внешнее электрическое поле. Самой простой вариант реакции, когда зарядов вообще нет, не будет рассмотрен нами. Все понимают, что в диэлектриках находятся заряды электричества. Они располагаются в атомном составе молекул, а также в ионах решетки кристаллов, в других элементах.
Из-за этого стоит взять во внимание и проанализировать систему, которая будет проста по своему строению, но интересна для исследования. Это система электрически нейтральна, в ней находятся два одинаковых по своему размеру заряда, но они по знаку создают оппозицию. Так, в системе появляются заряды +q и -q. Они располагаются друг от друга на дистанции l. Подобная система носит название электрического диполя.
Электрический диполь — комплекс в физике, который состоит из двух одинаковых по размеру, но оппозиционно настроенных по знаку точечных зарядов, которые располагаются друг от друга на дистанции l.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
На рисунке ниже доступно показано, как располагаются заряды в системе:
Источник: online.mephi.ru
А вот так будет выглядеть в рамках электрического поля сети напряженности поля электричества электрического диполя:
Источник: online.mephi.ru
Вот таким образом будет выглядеть поверхность, которая образована однопотенциальными точками электрического диполя:
Источник: online.mephi.ru
Таким образом выглядит то, как выглядят данные явления вместе:
Источник: online.mephi.ru
Электрический дипольный момент
Момент электрического диполя — самая значимая характерная черта электрического диполя в целом. Для того чтобы узнать формулу расчета момента электрического диполя необходимо добавить в систему вектор l, который будет иметь направление от негативно-заряженной точки -q в положительную по заряду точку +q.
В таком случае вектор под буквой p, который и воплощает в себе момент электрического диполя будет высчитываться по данной формуле: ([overrightarrow{p}=qtimes{overrightarrow{l}}]).
Поведение электрического диполя в электрических полях
Поведение электрического диполя в однородном поле
Посмотрите на то, как будет себя вести прочный электрический диполь во внешнем электрическом поле. Прочным диполем называют диполь, у которого расстояние l остается неизменным.
Такие силы будут воздействовать на поле:
Источник: online.mephi.ru
Примечание 1
Допустим, что ориентация момента электрического диполя будет создавать угол ([alpha])с вектором E. Так, можно увидеть, что на дипольный заряд со знаком + воздействуют силы, которые равны по своей ориентации на вектор E. Данная сила равняется ([F_{1}=+qE]).
На дипольный заряд со знаком – воздействуют силы, которые имеют противоположную ориентацию. Данная сила равняется ([F_{2}=-qE]).
Момент вращения данной совокупности сил будет равняться ([M=Flsinalpha=qElsinalpha]).
Из-за того, что ql=p, тогда ([M=pEsinalpha]). Если брать формулы векторов, то будет верна данная формула:([overrightarrow{M}=left[overrightarrow{p}timesoverrightarrow{E}right]]. )
Необходимо помнить, что ([overrightarrow{c}=left[overrightarrow{a}timesoverrightarrow{b}right]])обозначает умножение a-вектора на b-вектор. Получается, что если момент электрического диполя не будет изменяться в молекуле (то есть, ([p=const])), момент механики, который воздействует на молекулу, будет соотноситься с показателем уровня напряженности внешнего поля электричества. Он также будет находиться в зависимости от угла, который образуется между вектором p и вектором E. На электрический диполь будут действовать моменты различных сил, он будет вертеться и совершать определенную работу. Она будет выражаться в данной формуле: ([delta{A}=Mdalpha=pEsinalpha{d}alpha]).
Работа будет делать больше уровень показателей скрытой энергии диполя. Из-за этого можно вывести формулу потенциальной энергии электрического диполя в рамках поля электричества: ([delta{П}=pEsinalpha{d}alpha]) . Из данной формулы показатель П будет вычисляться таким образом: ([П=-pEcosalpha{d}alpha+const]). Еще можно его посчитать по такой формуле:([П=-pEcosalpha{d}alpha=-(overrightarrow{p}timesoverrightarrow{E})]) , но при условии, что const будет равен нулю.
Примечание 2
На изображении понятно, что внешнее поле электричества хочет развернуть электрический диполь так, чтобы были равны по ориентации вектор момента электричества p и вектор E. При таком раскладе ([alpha=0]), что значит, что показатель M также будет равняться нулю. Но если смотреть на это по-другому, то в случае ([alpha=0]) возможная дипольная энергия в рамках внешнего электрического поля будет иметь небольшую величину ([П_{min}=-pE]). Это соотносится с позицией стабильного баланса со стороны поля.
Если в случае смещения диполя от данной позиции в очередной раз появляется момент механики, который способствует тому, чтобы электрический диполь встал в такое положение, которое занимал изначально. Нестабильным называется положение баланса, при котором момент электрического диполя ориентирован против электрического поля (то есть ([alpha=pi]) , M=0).
Возможная энергия поля в данном варианте будет предельной по своей величине: ([П_{max}=+pE]). В случае незаметных колебаний от данной позиции силы, которые появляются в поле, не способствуют возвращению электрического диполя в исходное положение. Наоборот, они делают все, чтобы отклонение стало больше.
На рисунке ниже дан пример эксперимента, который показывает, как появляется момент сил электричества, что воздействуют на диэлектрик в рамках поля электричества. Так, на длинный образец диэлектрика, который располагается под определенным углом к линиям силы поля электричества, воздействует момент сил. Именно он пытается повернуть данный образец в длину электрического поля. Диэлектрик, который подвешивают за половину его длины в рамках не имеющего объема конденсатора, поворачивается перпендикулярно пластинкам конденсатора после того, как на них направляется большое напряжение от машины, которая генерирует электричество. Создание момента вращения обуславливается взаимным влиянием палочки, которая стала поляризованной, на поле электричества конденсатора.
Источник: online.mephi.ru
Поведение электрического диполя в неоднородном поле
Если поместить электрический диполь в неоднородное электрическое поле, то на него будет воздействовать сила равнодействия ([F_{равн}]), которая будет желать двинуть диполь. Опишем только частный вариант подобной ситуации.
Сделаем направление оси x по электрическому полю E. Допустим, что электрический диполь под воздействием электрического поля совершил какое-то движение по линии силы, поэтому негативный заряд располагается в точке, координатой которой является x. Положительный по знаку заряд будет находиться в точке, координатой которой является x+l. Предположим, что значение напряженности электрического поля находится в зависимости от x-координаты. В таком случае сила, которая будет равно действовать на все (то есть ([F_{равн}])), будет равняться:
Пример 1
([F_{равн}=F_{1}+F_{2}=qE(x+l)-qE(x)=qfrac{delta{E}}{delta{x}}l=pfrac{delta{E}}{delta{x}}]). Подобные итоговые значения могут быть выведены из подобного отношения: ([F_{x}=-frac{delta{П}}{delta{x}}]). В данном случае можно вычислить показатели П по формулам, что были даны выше. В случае увеличения E по мере возрастания x, получится следующее отношение: ([frac{delta{E}}{delta{x}}>0]). Тогда и проекция ([F_{x}]) равнодействующих на поле сил будет иметь знак +.
Получается, что данная сила будет желать того, чтобы направить электрический диполь в место, в котором уровень напряженности электрического поля будет максимально большим. Именно так можно объяснить очень популярный фокус, при котором бумажные куски без заряда (то есть нейтральны) будут тянуться к расческе, которая имеет электрический заряд. Если бы кусочки бумаги находились в рамках плоского конденсатора, а электрическое поле было однородным, то никакого движения с их стороны не произошло бы.
Эксперименты с электрическим диполем
Посмотрим на некоторое количество экспериментов, которые показывают, как появляются силы, что воздействуют на диэлектрик, который размещают в поле электричества без однородности. На рисунке ниже вы можете видеть, как диэлектрик втягивается в промежуток между обшивкой плоского конденсатора. В поле электричества и статики без однородности на диэлектрик влияют силы, которые способны втянуть его в место, где поле наиболее активное.
Источник: online.mephi.ru
Также можно показать похожий результат на примере абсолютно прозрачного сосуда. Внутрь данного сосуда кладут плоский конденсатор. В него также наливают немного диэлектрика, но в жидком виде. Подобным диэлектриком является керосиновая жидкость. Похожую конструкцию вы можете увидеть на рисунке ниже.
Конденсатор соединяют с источником питания, который имеет высокие показатели вольтажа. Это может быть машина, которая производит электричество. Когда она будет приведена в состояние работы, то в нижней части конденсатора, в месте, где действует неоднородность электрического поля, на керосиновую жидкость будет влиять сила, которая неизбежно втянет его в промежуток между данными пластинками. Из-за этого этого количество керосиновой жидкости в самом конденсаторе будет немного выше, чем с наружной части. После того как будет выключено электрическое поле, керосиновый уровень между данными пластинками упадет до объемов, которые есть в сосуде.
Источник: online.mephi.ru
В существующих в жизни веществах очень редко можно встретить электрические диполи, которые создаются исключительно при помощи двух электрических зарядов. Очень часто ученые рассматривают строение диполей, который образованы от большого количества зарядов. То есть, ученые исследуют очень сложные по структуре системы. Стоит отметить, что термин электрического момента диполя можно использовать как в системах с двумя зарядами, так и в системах с большим количеством зарядов. В такой ситуации момент электрического диполя будет рассчитываться таким образом: ([overrightarrow{p}=sum_i{q_{i}}overrightarrow{r_{i}}]).
В данной формуле ([q_{i}])является значением заряда с условным номером i
и ([overrightarrow{r_{i}}]) является вектором-радиусом, который задает расположение данного заряда.
Если зарядов будет два, то есть ([q_{1}=+q] и [q_{2}=-q]), нужно использовать следующую формулу: ([overrightarrow{p}=q(overrightarrow{r_{1}}-overrightarrow{r_{2}})=qoverrightarrow{l}])
Примечание 3
Представим, что система с заряда электричества станет абсолютно нейтральной. В рамках данной системы будут находиться заряды со знаком +. Все их значения и расположения будут обозначены специальным значком +. Знак – указывает на значения с негативным зарядом, а также на местоположение данных зарядов и их векторов. В таком случае возможно записать отношение ([overrightarrow{p}=q(overrightarrow{r_{1}}-overrightarrow{r_{2}})=qoverrightarrow{l}]) в качестве выражения ([overrightarrow{p}=sum_i{q_{i}}overrightarrow{r_i^+}-sum_k{q_{k}}overrightarrow{r_k^-}]. )
В данной формуле в первой части суммировать все значения нужно, потому что у них есть знак + в обозначении. Во второй части необходимо суммировать все значения, потому что у них есть знак – в обозначении.
Нейтральность в плане электрического заряда системы показывает на то, что все заряды со знаком + равны всем зарядом со знаком -. То есть, ([q=sum_i{q_{i^+}}=sum_k{q_k^-}]).
Рассмотрим термин центр разных зарядов, то есть тех, кто имеет знак + и тех, кто имеет знак -.( [overrightarrow{R^{+}}=frac{sum_i{q_i^+}}{overrightarrow{r_i^+}}{sum_i{q_i^+}}] и [overrightarrow{R^{-}}=frac{sum_i{q_k^-}}{overrightarrow{r_k^-}}{sum_k{q_k^-}}])
Формулы, которые приведены выше, схожи по своей сути с выражениями для массового центра в рамках раздела механика в физике. Из-за этого они и носят название центров зарядов со знаком + и знаком -.
Можно при учете всех этих данных и выражения ([overrightarrow{p}=sum_i{q_{i}}overrightarrow{r_i^+}-sum_k{q_{k}}overrightarrow{r_k^-}]) можно записать момент электрического диполя системы зарядов в качестве следующего отношения: ([overrightarrow{p}=q(overrightarrow{R^{+}}-overrightarrow{R^{-}})=qoverrightarrow{l}]) . В данной формуле используется вектор l, который был проведен из центра зарядов со знаком – в центр с зарядами со знаком +. Сущность всех этих экспериментов в том, чтобы показать, что на каждую нейтральную со стороны электричества систему зарядов можно наложить равный ей электрический диполь.
Единицы измерения электрического диполя
В Системе единиц измерения электрический момент электрического диполя не обладает специальным наименованием. Принято его обозначать в качестве ([Клtimes{м}]). Также его можно изменить в дебаях.
Задачи на вычисление электрического диполя
Задача 1
Задача 1
Электрический диполь с моментом (p=1[пКлtimes{м}]) ритмично колеблется со скоростью вращения в ([omega=10^{4}] [frac{рад}{с}]) по отношению к оси, которая перпендикулярна дипольному плечу и проходит по центру диполя. Нужно рассчитать, каково значение усредненной вероятной энергии П с зарядом Q=1нКл, который находится на дистанции в r=2 сантиметра от дипольного центра, лежит во вращательной плоскости за временной промежуток, который равен:
- полупериоду (то есть периоду от ([t_{1}]=0 до [t_{2}=frac{T}{2}]));
- во все ([tgg{T}]).
При этом в изначальном положении нужно принять, что П равно нулю.
Решение задачи:
Потенциальная энергия диполя вычисляется по формуле: ([П=pEcosalpha]). В процессе вращения электрического диполя вокруг собственной оси будут такие значения: ([cosalpha=sin{omega{t}}Rightarrow{П=pEsinomega{t}}]). В данной формуле ([E=frac{Q}{4pi}E_{0}r^{2}]) является формулой напряженности поля электричества. Получается, что ([П=frac{pQsinomega{t}}{4pi{E_{0}}r^{2}}]). ([langle{П}rangle=frac{Qp}{4pi{E_{0}}r^{2}}langlesinomega{t}rangle])будет средней величиной потенциальной энергии диполя. В данной формуле ([omega=frac{2pi}{T}], [T=frac{2pi}{omega}]. [T=frac{2pi}{omega}=frac{2pi}{10^{4}}=6,28times10^{4}c])
Усредненная величина за половину периода будет такой: ([langle{sinomega{t}}rangle=frac{pi}{2}Rightarrowlangle{П}rangle=frac{Qp}{4pi{E_{0}r^{2}}}timesfrac{pi}{2}=frac{Qp}{8pi{E_{0}r^{2}}}]. )
Получается: ([langle{П}rangle=frac{-10^{-9}times10^{-12}}{8,85times10^{-12}times(0,02)^{2}}=14,3times10^{9}]Дж=14,3кДж.)
При условии ([tgg{T}]): ([langlesin{omega{t}}ranglerightarrow0Rightarrowlangle{П}rangle=0])
Ответ: ([langle{П}rangle=0] и [langle{П}rangle=14,3кДж])
Задача 2
Электрический диполь с моментом (p=200 [пКлtimes{м}]) располагается в электрической поле без однородности. Уровень неоднородности электрического поля выражается в значении ([frac{delta{E}}{delta{x}}=1frac{МВ}{м^{2}}]) , которая взята с ориентацией на дипольную ось. Нужно найти силу, которая воздействует на электрический диполь с данной ориентацией.
Решение:
Сила, которая воздействует на диполь будет вычисляться таким образом: ([F=pfrac{delta{E}}{delta{x}}cosalpha]. [cosalpha=cos0^{circ}=1]), потому что электрический диполь располагается в относительной свободе в рамках электрического поля. ([Rightarrow{F}=pfrac{delta{E}}{delta{x}}Rightarrow{F}=200times10^{-12}times10^{6}=200times10^{-6}]Н=0,2мН.)
Ответ: F=0,2мН.
Задача 3
Необходимо рассчитать момент электрического диполя p в случае, когда заряд данного диполя равняется Q=10 нКл, а плечо равняется l=0,5 см.
Решение:
([P=mid{Q}mid{l}]=[P=10^{-8}times5times10^{-3}=5times10^{-11}] [Клtimes{м}]. )
Задача 4
Электрический диполь с моментом в (p=20 [нКлtimes{м}]) располагается в однородном поле электричества напряженностью (E=50 [frac{кВ}{м}]) . Вектор момента диполя равен углу ([alpha=60^{circ}]). Нужно узнать, какое значение потенциальной энергии диполя П.
В качестве потенциальной исходной энергии принимается энергия, которая равна положению электрического диполя при перпендикулярности вектора момента диполя и линий электрического поля.
Потенциальная энергия равна П=0, в случае ([alpha=90^{circ}]. [delta{П}=-Fdelta{x}] ) является формулой возможной энергии. В ней ([F=pfrac{delta{E}}{delta{x}}cosalpha]) является силой, которая воздействует на диагональ. ([П=int{-pfrac{delta{E}}{delta{x}}}cosalpha{delta{x}}=-pEcosalpha]. [П=20times10^{-9}times50times10^{3}timescos60^{circ}=-500times10^{-6}]Дж=-500мкДж. )
Ответ: П=-500мкДж.

