Найдите большую диагональ призмы. Объясните как решать
Ученик
(45),
на голосовании
9 лет назад
Голосование за лучший ответ
rafael ahmetov
Высший разум
(122431)
9 лет назад
Большая диагональ призмы является диагональю прямоугольника, (скажем так, стоящего вертикально) , высота которого равна боковому ребру (2), а длина – большой диагонали ромба. Поскольку острый угол ромба равен 60 градусам, то малая диагональ разбивает ромб на два равносторонних треугольника. Тогда большая диагональ ромба равна удвоенной высоте треугольника со стороной 2, т. е 2*√(3). Тогда, по теореме Пифагора, большая диагональ призмы равна √((2*√(3))^2+2^2)=4.
Призма является геометрической объемной фигурой, характеристики и свойства которой изучают в старших классах школ. Как правило, при ее изучении рассматривают такие величины, как объем и площадь поверхности. В данной же статье раскроем несколько иной вопрос: приведем методику определения длины диагоналей призмы на примере четырехугольной фигуры.
Какая фигура называется призмой?
В геометрии дается следующее определение призме: это объемная фигура, ограниченная двумя многоугольными одинаковыми сторонами, которые параллельны друг другу, и некоторым числом параллелограммов. Рисунок ниже показывает пример призмы, соответствующий данному определению.
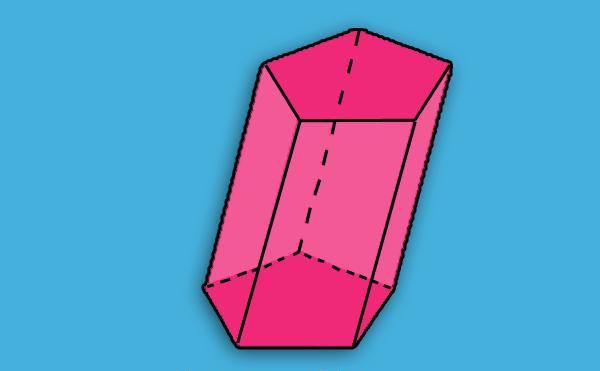
Мы видим, что два красных пятиугольника равны друг другу и находятся в двух параллельных плоскостях. Пять розовых параллелограммов соединяют эти пятиугольники в цельный объект – призму. Два пятиугольника называются основаниями фигуры, а ее параллелограммы – это боковые грани.
Призмы бывают прямые и наклонные, которые также называют прямоугольными и косоугольными. Разница между ними заключается в углах между основанием и боковыми гранями. Для прямоугольной призмы все эти углы равны 90o.
По количеству сторон или вершин многоугольника в основании говорят о призмах треугольных, пятиугольных, четырехугольных и так далее. Причем если этот многоугольник является правильным, а сама призма прямой, то такую фигуру называют правильной.
Приведенная на предыдущем рисунке призма является пятиугольной наклонной. Ниже же изображена пятиугольная прямая призма, которая является правильной.
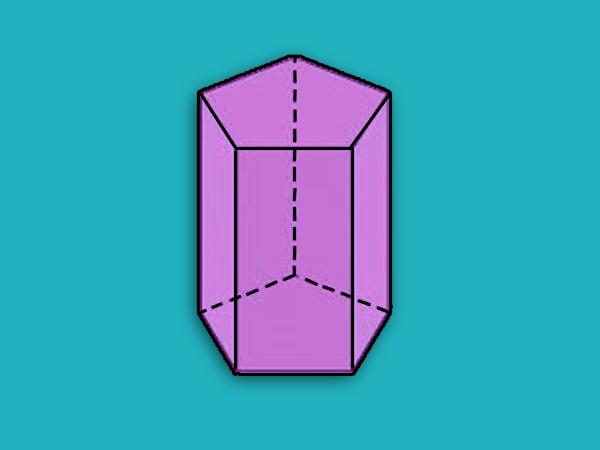
Все вычисления, включая методику определения диагоналей призмы, удобно выполнять именно для правильных фигур.
Какие элементы характеризуют призму?
Элементами фигуры называют составные части, которые ее образуют. Конкретно для призмы можно выделить три главных типа элементов:
- вершины;
- грани или стороны;
- ребра.
Гранями считаются основания и боковые плоскости, представляющие параллелограммы в общем случае. В призме всегда каждая сторона относится к одному из двух типов: либо это многоугольник, либо параллелограмм.
Ребра призмы – это те отрезки, которые ограничивают каждую сторону фигуры. Как и грани, ребра также бывают двух типов: принадлежащие основанию и боковой поверхности или относящиеся только к боковой поверхности. Первых всегда в два раза больше, чем вторых, независимо от вида призмы.
Вершины – это точки пересечения трех ребер призмы, два из которых лежат в плоскости основания, а третье – принадлежит двум боковым граням. Все вершины призмы находятся в плоскостях оснований фигуры.
Числа описанных элементов связаны в единое равенство, имеющее следующий вид:
Р = В + С – 2.
Здесь Р – количество ребер, В – вершин, С – сторон. Это равенство называется теоремой Эйлера для полиэдра.
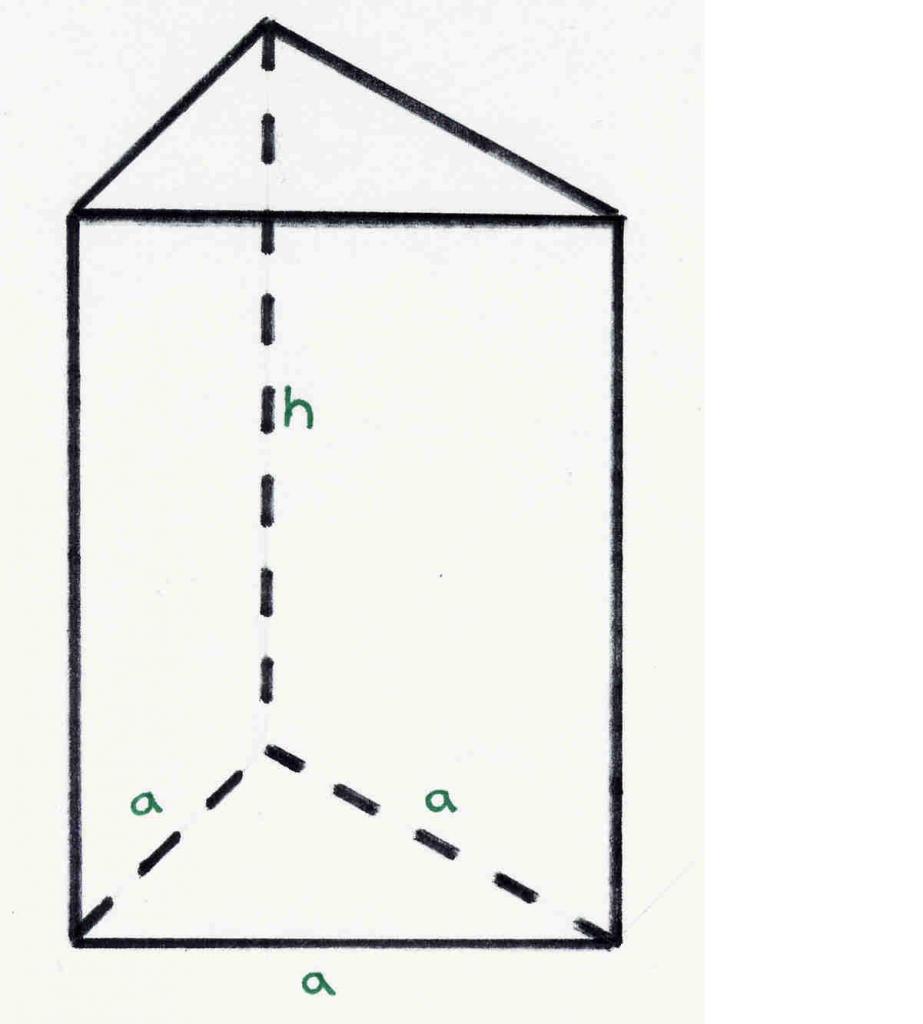
На рисунке показана треугольная правильная призма. Каждый может посчитать, что она имеет 6 вершин, 5 сторон и 9 ребер. Эти цифры согласуются с теоремой Эйлера.
Диагонали призмы
После таких свойств, как объем и площадь поверхности, в задачах по геометрии часто встречается информация о длине той или иной диагонали рассматриваемой фигуры, которая либо дана, либо ее нужно найти по другим известным параметрам. Рассмотрим, какие бывают диагонали у призмы.
Все диагонали можно разделить на два типа:
- Лежащие в плоскости граней. Они соединяют несоседние вершины либо многоугольника в основании призмы, либо параллелограмма боковой поверхности. Значение длин таких диагоналей определяется, исходя из знания длин соответствующих ребер и углов между ними. Для определения диагоналей параллелограммов всегда используются свойства треугольников.
- Лежащие внутри объема призмы. Эти диагонали соединяют неоднотипные вершины двух оснований. Эти диагонали оказываются полностью внутри фигуры. Их длины рассчитать несколько сложнее, чем для предыдущего типа. Методика расчета предполагает учет длин ребер и основания, и параллелограммов. Для прямых и правильных призм расчет является относительно простым, поскольку он осуществляется с использованием теоремы Пифагора и свойств тригонометрических функций.
Далее приведем примеры вычисления различных диагоналей.
Диагонали сторон четырехугольной прямой призмы
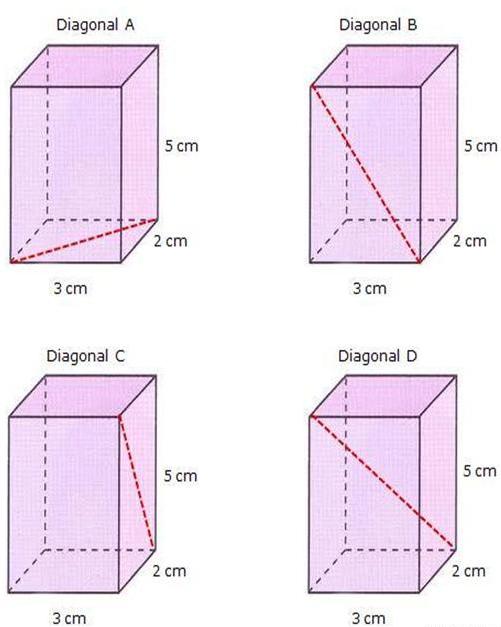
На рисунке выше изображены четыре одинаковые прямые призмы, и даны параметры их ребер. На призмах Diagonal A, Diagonal B и Diagonal C штриховой красной линией изображены диагонали трех разных граней. Поскольку призма является прямой с высотой 5 см, а ее основание представлено прямоугольником со сторонами 3 см и 2 см, то отыскать отмеченные диагонали не представляет никакого труда. Для этого необходимо воспользоваться теоремой Пифагора.
Длина диагонали основания призмы (Diagonal A) равна:
DA = √(32+22) = √13 ≈ 3,606 см.
Для боковой грани призмы диагональ равна (см. Diagonal B):
DB = √(32+52) = √34 ≈ 5,831 см.
Наконец, длина еще одной боковой диагонали равна (см. Diagonal C):
DС = √(22+52) = √29 ≈ 5,385 см.
Длина внутренней диагонали
Теперь рассчитаем длину диагонали четырехугольной призмы, которая изображена на предыдущем рисунке (Diagonal D). Сделать это не так сложно, если заметить, что она является гипотенузой треугольника, в котором катетами будут высота призмы (5 см) и диагональ DA , изображенная на рисунке вверху слева (Diagonal A). Тогда получаем:
DD = √(DA2+52) = √(2 2+32+52) = √38 ≈ 6,164 см.
Правильная призма четырехугольная
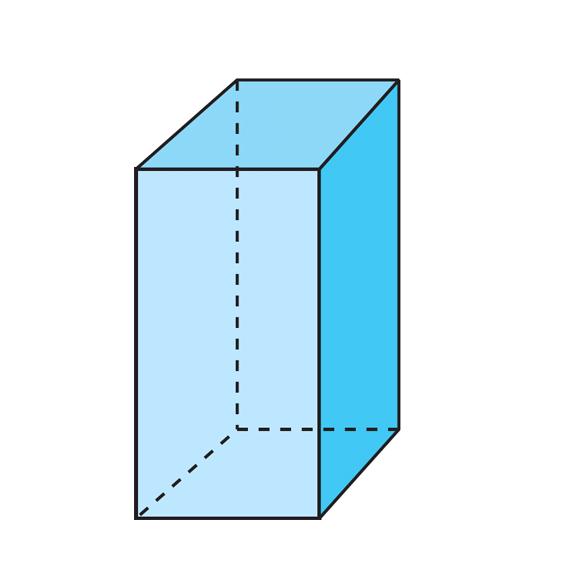
Диагональ правильной призмы, основанием которой является квадрат, рассчитывается аналогичным образом, как и в приведенном выше примере. Соответствующая формула имеет вид:
D = √(2*a2+c2).
Где a и c – длины стороны основания и бокового ребра, соответственно.
Заметим, что при вычислениях мы использовали только теорему Пифагора. Для определения длин диагоналей правильных призм с большим числом вершин (пятиугольные, шестиугольные и так далее) уже необходимо применять тригонометрические функции.

в основании прямой призмы лежит ромб со строной 6 см и углом 60°.Меньшая диагональ призмы наклонена к основанию под углом 45°.Найдите длину большей диагонали

Светило науки – 320 ответов – 9151 помощь
Обозначим призму АВСДА1В1С1Д1. Угол ВСД=60. Меньшая диагональ В1Д, угол ВДВ1=45. Треугольник ВСД равносторонний (ВС=ВД, угол С=60), следовательно ВД=ВС=ДС=6.В треугольнике ВДВ1 угол ВДВ1=45, поскольку он прямоугольный то и угол ДВ1В=45.Следовательно высота призмы Н=ВВ1=ВД=6. Обозначим точку пересечения диагоналей О. ОС=ВС*cos 30= 6*(корень из 3/2)=3 корня из 3. Длина большей диагонали АС1= корень из(АС квадрат +СС1 квадрат)=корень из (36*3+36)=12.
ngersediou
Вопрос по геометрии:
В правильной шестиугольной призме сторона основания равна 7 а меньшая диагональ-24.Вычислить длину большей диагонали призмы
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
udine690
использовано: свойства правильного шестиугольника ( сторона равна радиусу описанной окружности, угол равен 120 градусов), теорема косинусов, значение косинуса 120 градусов, теорема Пифагора

Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Как найти диагональ правильной призмы
Нахождение диагонали правильной призмы часто используется как промежуточный этап при решении более сложных задач. Общая формула легко выводится при рассмотрении двух прямоугольных треугольников.
Инструкция
Для нахождения диагонали правильной призмы вам необходимо разобраться всего в нескольких определениях.
Призмой называется многогранник, имеющий в качестве оснований два равных многоугольника (треугольника, четырехугольника и т.д.), лежащих в параллельных плоскостях, а в качестве боковых граней – параллелограммы.
Прямой призмой называется призма, у которой боковые грани-прямоугольники.
Правильной призмой называется прямая призма, основания которой являются правильными многоугольниками (равносторонний треугольник, квадрат, и т.д.)
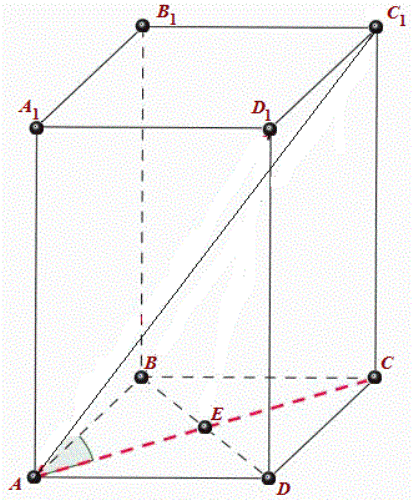
АВСDА1В1С1D1 – Правильная четырехугольная призма.
АА1В1В – боковая грань правильной четырехугольной призмы.
Все четыре боковых грани данной призмы равны.
АВСD и А1В1С1D1 -основания призмы (квадраты, лежащие в параллельных плоскостях).
Диагональю многогранника называется отрезок, соединяющий две его не смежные вершины, т.е вершины, которые не принадлежат одной грани.
Из рисунка видно, что точка А и точка С 1 не принадлежат одной грани и следовательно отрезок АС1 – диагональ данной призмы.
Для того чтобы найти диагональ, призмы надо рассмотреть треугольник АСС1. Этот треугольник прямоугольный. Диагональ призмы АС1 в рассматриваемом треугольнике будет являться гипотенузой, а отрезки АС и СС1 катетами. Из теоремы Пифагора (в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов) следует, что:
АС12 = АС2 + СС12 (1);
Далее следует рассмотреть треугольник АСD. Треугольник АСD тоже прямоугольный (т.к. основание призмы – квадрат). Для удобства можно обозначить сторону основания буквой а. Таким образом по теореме Пифагора:
АС2 = а2 +а2, АС = √2а (2);
Если обозначить высоту призмы буквой h и подставить выражение (2) в выражение (1), получится:
АС12 = 2а2+h2, АС1 = √(2a^2+h^2 ), где а – сторона основания, h – высота.
Данная формула справедлива для любой правильной призмы.
Источники:
- диагональная призма
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
