Пусть
интегрируема и ограничена на
и
![]()
,
![]()
— соответственно, верхняя и нижняя
грани
на отрезке
.
Тогда, существует такое число
![]()
,
что:
![]()
и

.
Число

называется средним значением функции
![]()
на отрезке
.
Примеры:
4.1. Вычислить
среднее значение функции
![]()
на отрезке
![]()
.
По формуле
среднего значения функции на интервале,
получаем

.◄
4.2. Вычислить
среднее значение функции
![]()
на отрезке
![]()
.
По формуле
среднего значения функции на интервале,
получаем

.◄
4.3. Вычислить
среднее значение функции
![]()
на отрезке
![]()
.
По формуле
среднего значения функции на интервале,
получаем

.◄
5. Несобственные интегралы
5. 1. Интегралы с бесконечными пределами
Если
непрерывна на интервале
![]()
,
то интеграл

называется
несобственным интегралом от
.
Если предел существует и конечен,
интеграл называется сходящимся, если
нет, то расходящимся. Если
![]()
при
![]()
,
то при
![]()
интеграл сходится, при
![]()
интеграл расходится.
Отметим важные
примеры несобственных интегралов:

– интеграл Пуассона,
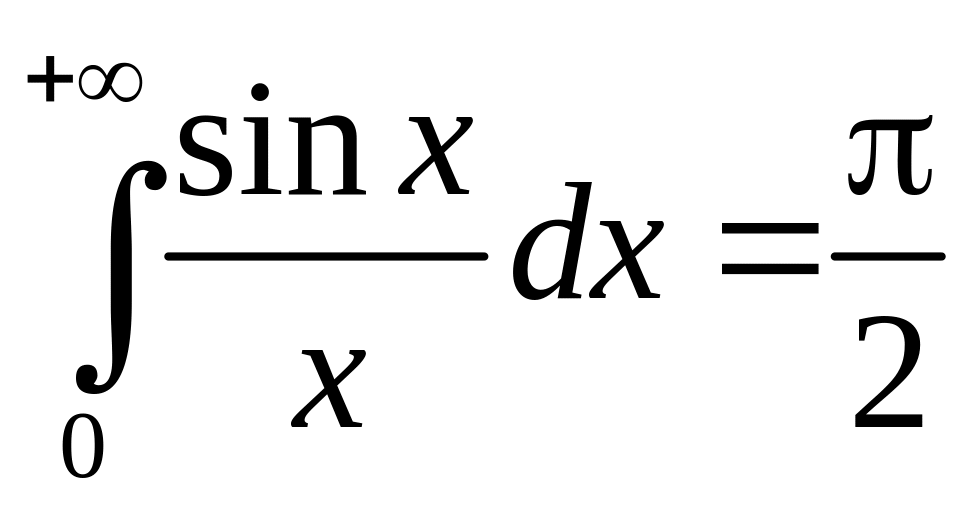
– интеграл Дирихле,
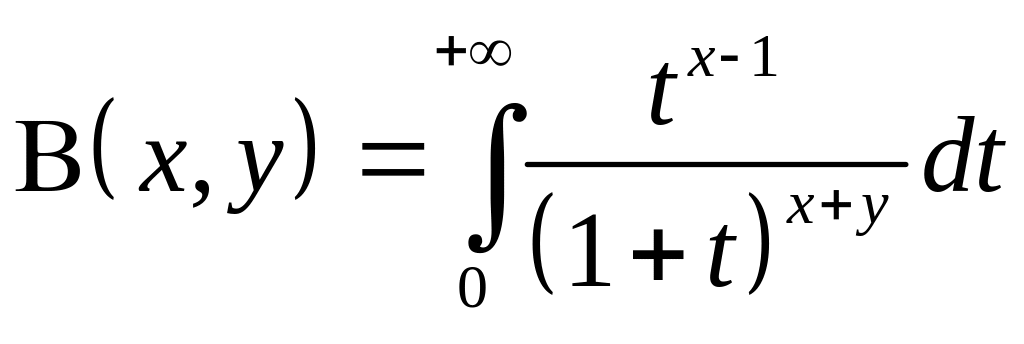
– Бета-функция
(эйлеров интеграл 1 рода),

– Гамма-функция
(эйлеров интеграл 2 рода).
Примеры:
5.1.1. Вычислить
интеграл
![]()
Найдём

.
Предел существует
и конечен. Значит, интеграл сходится. ◄
5.1.2. Вычислить
интеграл

Найдём

.
Предел не существует.
Несобственный интеграл расходится. ◄
5.1.3. Вычислить
интеграл
.
Подынтегральная
функция чётная, поэтому

.
Вычислим интеграл:

.
Получили

.
Интеграл сходится. ◄
5.1.4. Доказать
расходимость интеграла
.
Так как при
![]()
,

,
то вычисляя
интеграл
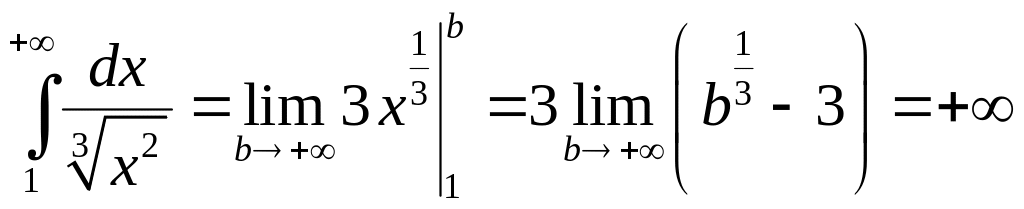
.
Этот интеграл
расходится. Следовательно, по признаку
сравнения исходный интеграл
тоже расходится.
5.2. Интегралы от функций с бесконечными разрывами
Если
непрерывна на
![]()
и неограниченна в любой окрестности
точки
![]()
,
то интеграл

называется
несобственным интегралом от
.
Если предел существует и конечен,
интеграл называется сходящимся, если
нет, то расходящимся. Если
![]()
![]()
при
![]()
,
то при
![]()
интеграл сходится, при
![]()
интеграл расходится.
Примеры:
5.2.1. Исследовать
на сходимость интеграл
.
Так как
подынтегральная функция
![]()
терпит
разрыв в точке
![]()
,
то получим:
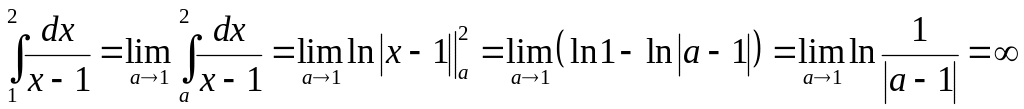
Конечного предела
не существует, значит, интеграл расходится.
◄
5.2.2.
Исследовать на сходимость интеграл
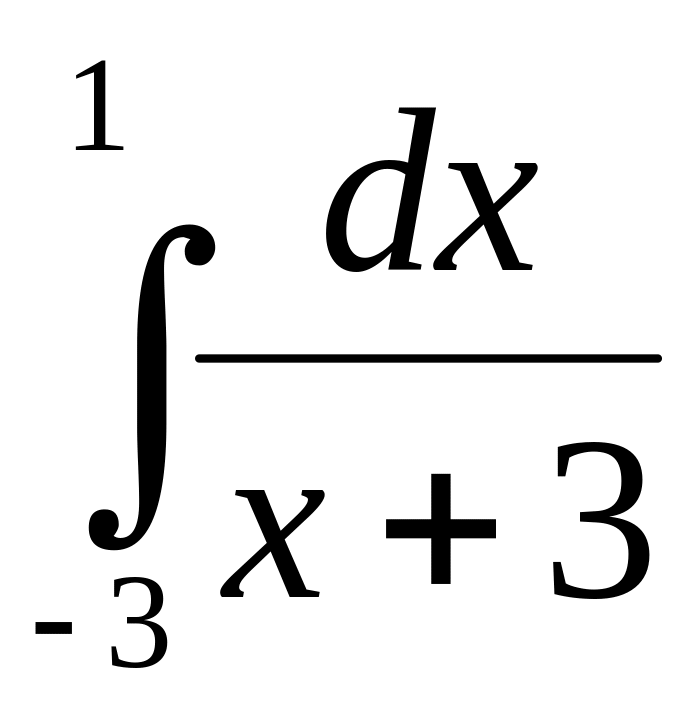
Так как
подынтегральная функция
![]()
терпит
разрыв в точке
![]()
,
то получим:

.
Конечный предел
равен бесконечности. Значит, интеграл
расходится. ◄
5.2.3. Исследовать
на сходимость интеграл

Так как
подынтегральная функция
![]()
терпит
разрыв в точке![]()
,
получим:

.
Применим
интегрирование по частям. Пусть
![]()
Тогда
![]()
.
И первоначальный
интеграл примет вид:

.
Предел конечен.
Поэтому интеграл сходится.
◄
5.2.4. Исследовать
на сходимость интеграл
Имеем

.
Предел бесконечен.
Следовательно, интеграл расходится.
◄
6. Геометрические и физические приложения определенного интеграла
6.1. Вычисление площади криволинейной трапеции
Площадь плоской
области
![]()
стандартной относительно оси
![]()
,
ограниченной прямыми
![]()
и
![]()
и кривыми
![]()
,
![]()
такими, что для любых
![]()
выполнено
![]()
(т.е.![]()
)
вычисляется

.
Аналогично площадь
плоской области стандартной относительно
оси
![]()
,
ограниченной прямыми
![]()
и
![]()
и кривыми
![]()
,
![]()
такими, что для любых
![]()
выполнено
![]()
(т.е.![]()
)
вычисляется

.
Если область
ограничена непрерывной замкнутой
кривой, заданной параметрически
![]()
,
то её площадь можно
вычислить по одной из трёх формул

,

,

.
Какую из них удобнее
применять, зависит от конкретного вида
функций
![]()
и
![]()
.
Площадь области
:
![]()
,
называемой
криволинейным сектором, ограниченной
графиком
![]()
и двумя лучами, составляющими с полярной
осью углы
![]()
и
![]()
имеет площадь

.
Примеры:
6.1.1.
Вычислить площадь области, ограниченной
линиями:
![]()
и
![]()
.
Изобразим фигуру
в декартовой системе координат:
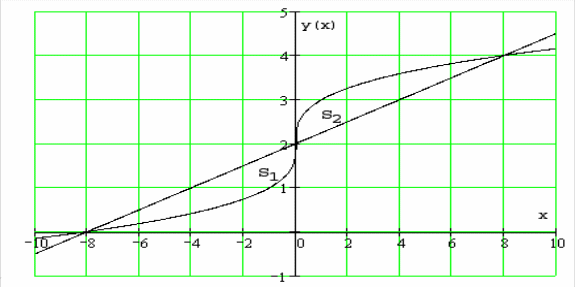
Из условия симметрии
фигуры относительно точки с координатами
![]()
,
площади
![]()
и
![]()
равны. Так как данная область является
стандартной как относительно оси
так и относительно оси
,
то ее площадь можно вычислить одним из
двух способов.
1) Выразим зависимости
в явном виде:
![]()
и ![]()
,
а стандартная
относительно оси
область

.
Тогда получаем

.
2) Заметим, что для
вычисления площади можно было
воспользоваться исходным видом
зависимостей:
![]()

.
6.1.2.
Вычислить площадь области, ограниченной
параболами
![]()
и
![]()
.
Изобразим фигуру
в декартовой системе координат

Очевидно, область
симметрична относительно оси
,
кроме того, она не является стандартной
относительно оси
и стандартной относительно оси
,
а ее площадь можно вычислить одним из
двух способов.
-
Данная область
не является стандартной относительно
оси.
Её можно разбить на две стандартные
относительно осиобласти:
![]()
,
![]()
.
Из симметрии
областей
![]()
и
![]()
относительно оси
следует, что


.
-
Относительно оси
данная область
является стандартной:

.
Снова, используя
симметрию области, получаем

.
6.1.3.
Вычислить площадь эллипса, заданного
уравнением
![]()
(![]()
,
![]()
).
Искомую площадь
можно вычислить, используя как явное
представление линии, так и параметрическое.
-
Выразив уравнение
в явном виде
![]()
,
получим,
применив подстановку
,
![]()
,
приходим к
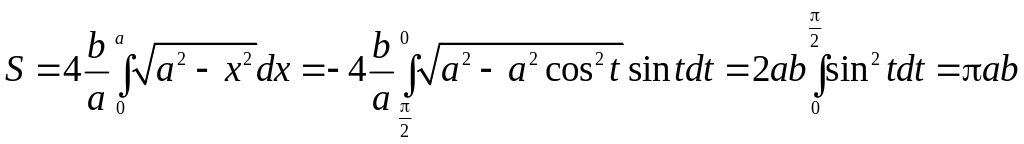
.
2) С другой стороны,
используя параметрическое представление
,
при изменении параметра
![]()
в пределах от
![]()
до
![]()
,
получаем:

.
6.1.4.
Вычислить площадь астроиды, заданной
уравнением
![]()
(![]()
,![]()
)
Изобразим кривую
в декартовых координатах:

Используя
параметрическое представление
,
при изменении параметра
в пределах от
до
,
получаем:


.
6.1.5.
Найти площадь фигуры, ограниченной
кардиоидой
![]()
,
![]()
.
Изобразим кривую
в декартовых координатах:
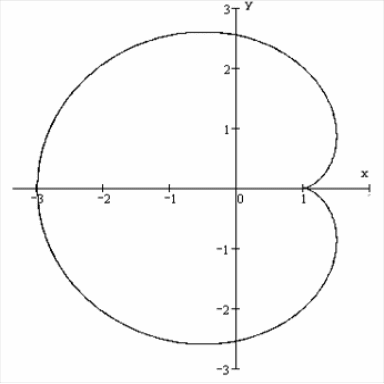
Так как кардиоида
симметрична относительно оси
,
то, используя параметрическое
представление, будем менять параметр
в пределах от
до
![]()
.
Так как
![]()
и ![]()
,
получаем по любой
из трех формул




,



,


.
Отметим, что площадь
кардиоиды задаваемой уравнением в
полярных координатах
![]()
равна

.
6.1.6.
Найти площадь области, ограниченной
кривой
![]()
.
Кривая образует
три симметричные петли, каждая из которых
ограничивает криволинейный сектор.
Изобразим ее в полярных координатах.

Рассмотрим сектор,
лежащий в первой четверти:
![]()
.
Площадь его,
очевидно, равна 1/3 площади всей области,
ограниченной данной кривой. Следовательно,

.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 мая 2018 года; проверки требует 1 правка.
Первая теорема о среднем значении — одна из теорем об определённом интеграле.
Формулировка[править | править код]
Пусть функция 
![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)



Тогда существует такое число 

.
Доказательство[править | править код]
Из неравенства 
.
Обозначив 
Так определённое число 

![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)
Замечание[править | править код]
Если функция 
![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)

можно взять её наибольшее и наименьшее значения (которые, по теореме Вейерштрасса, достигаются),
тогда по теореме о промежуточном значении существует такая точка ![cin [a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/02b8df5ba00bbc02820be401c0dbc93d73392da8)

поэтому утверждение теоремы можно переписать в виде
.
Если воспользоваться формулой Ньютона-Лейбница, то это равенство запишется как
,
где 


Обобщение[править | править код]
Пусть функции 

![[a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/68e776d74130a8890a814c1f4e74372a9110d2f9)

а вторая из них не меняет знак (то есть либо всюду неотрицательна: 

Тогда существует такое число 

.
Доказательство[править | править код]
Пусть 
,
откуда, ввиду монотонности интеграла
.
Если 

и утверждение теоремы выполняется при любом 
В противном случае положим
.
Обобщение доказано. Если функция 
![cin [a;b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/02b8df5ba00bbc02820be401c0dbc93d73392da8)
(аналогично предыдущему).
Литература[править | править код]
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: Наука, 1969. — Т. II.
- Зорич В. А. Математический анализ. Ч. I. — М.: Наука, 1981.
Оценка интеграла. Теорема о среднем. Среднее значение функции
Оценка интеграла. Теорема о среднем. Среднее значение функции.
1. Оценка интеграла. Укажем границы, между которыми наверняка заключено значение интеграла.
Теорема об оценке опеределенного интеграла. Значение определенного интеграла заключено между произведениями наименьшего и наибольшего значений подынтегральной функции на длину интервала интегрирования, т.е.
|
$$M(b-a)>int_{a}^{b}{f(x)dx}>m(b-a),$$ |
$$b>a,$$ |
где (M) и (m) – соответственно наибольшее и наименьшее значения функции (f(x)) в интервале ([a,b]): $$mleq f(x)leq M.$$
Доказательство. Возьмем две функции (M-f(x)) и (m-f(x)). Первая из них в интервале ([a,b]) неотрицательна, вторая неположительна. Значит по теореме о знаке интеграла
|
$$int_{a}^{b}{[M-f(x)]dx}>0$$ |
и |
$$int_{a}^{b}{[m-f(x)]dx}<0.$$ |
Применяя теоремы из пункта простейших свойств определенного интеграла и формулу (int_{a}^{b}{dx}=b-a), получим
|
$$M(b-a)>int_{a}^{b}{f(x)dx}$$ |
и |
$$m(b-a)<int_{a}^{b}{f(x)dx},$$ |
что и требовалось доказать. Из доказательства теоремы о знаке интеграла следует, что знаки неравенств могут перейти в знаки равенств только в том случае, когда функция (f(x)) постоянна.
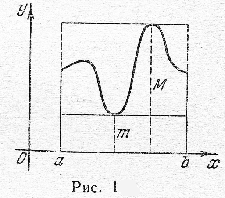
Геометрический смысл доказанных неравенств таков: площадь криволинейной трапеции больше площади прямоугольника с основанием, равным основанию трапеции, и высотой, равной наименьшей ординате трапеции, и меньше площади прямоугольника с тем же основанием и высотой, равной наибольшей ординате трапеции (рис. 1).
Находя границы для интеграла, мы, как говорят, производим его оценку. Может случиться, что весьма трудно или даже невозможно найти точное значение интеграла, а оценивая его, мы узнаем, хотя бы грубо, приближенное его значение. С такого рода оценками приходится довольно часто встречаться в математике.
Указанные в теореме об оценке определенного интеграла границы для интеграла тем более точны, чем короче интервал интегрирования и чем меньше линия (y=f(x)) отличается по положению от прямой, параллельной оси (Ox).
Пример 1. Оценим интеграл $$int_{0}^{2}{frac{5-x}{9-x^{2}}dx}.$$
Известными методами дифференциального исчисления находим, что наибольшее и наименьшее значения подынтегральной функции в интервале ([0, 2]) равны соответственно (0,6) и (0,5). Значит, $$0,5(2-0)<int_{0}^{2}{frac{5-x}{9-x^{2}}dx}<0,6(2-0)$$
т.е. интеграл заключен между (1) и (1,2). Если считать, что он равен (1,1), то предельная абсолютная ошибка равна (0,1), а относительная (frac{0,1cdot 100}{1,1}approx 9%).
Пример 2. Оценим интеграл $$int_{frac{pi }{4}}^{frac{pi }{2}}{frac{sin x}{x}dx}.$$
Легко проверить, что подынтегральная функция в интервале ([frac{pi }{4}, frac{pi }{2}]) убывает и, следовательно, $$frac{sin frac{pi }{2}}{frac{pi }{2}}cdot frac{pi }{4}<int_{frac{pi }{4}}^{frac{pi }{2}}{frac{sin x}{x}dx}<frac{sin frac{pi }{4}}{frac{pi }{4}}cdot frac{pi }{4},$$
т.е. $$frac{1}{2}<int_{frac{pi }{4}}^{frac{pi }{2}}{frac{sin x}{x}dx}<frac{1}{2}sqrt{2}.$$
Таким образом, интеграл заключен между (0,5) и (0,71), что дает нам право считать его равным (0,6) с точностью до (0,1). Более точные приемы показывают, что приближенно он равен (0,62).
Оценка интеграла. Теорема о среднем. Среднее значение функции.
Продолжение здесь
2012-11-05 • Просмотров [ 62612 ]
I. ОцеНКа интеграла. Укажем граНИцы, между которыми наверняка заключено значение интеграла.
Теорема VI (об оценке определенного интеграла). Значение определенного интеграла заключено между произведениями наименьшего и наибольшего значений подынтегральной функции на длину интервала интегрирования, т. Е.
![]()
Где Т и М — Соответственно наименьшее и наибольшее значения функции ![]() интервале
интервале ![]() :
:
![]()
Доказательство. Возьмем две функции ![]() и
и ![]() . Первая из них в интервале
. Первая из них в интервале ![]() неотрицательна, вторая неположительна. Значит, по теореме V
неотрицательна, вторая неположительна. Значит, по теореме V
![]() и
и ![]()
А по теореме I
![]() и
и ![]()
Откуда в силу того, что ![]()
![]()
И
![]()
Что и требовалось доказать.
Геометрический смысл этих неравенств таков: площадь КриволиНейной трапеции больше площади прямоугольника с основанием, РавНой оснОваНИЮ трапеции, и высотой, равной наименьшей ординате ТрапециИ, и меньше площади прямоугольника с тем же основанием и Высотой, равной наибольшей ординате Трапеции (рис. 6).
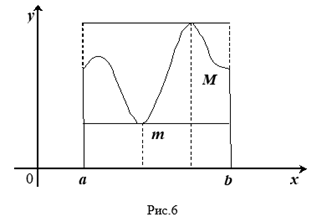
Находя границы для интеграла, мы, как говорят, производим его оценку. Может случиться, что весьма трудно или дажЕ невозможно найти точное значение Интеграла, а оценивая его, мы узнаем, ХотЯ бы грубо, приближенное его Значение. С такого, рода оценками приходится Довольно часто встречаться в математике.
УказаННые в теореме VI границы для Интеграла тем более точны, чем короче Интервал интегрирования и чем меньше линия ![]() отличается По положению от прямой, параллельной оси Ох.
отличается По положению от прямой, параллельной оси Ох.
Пример. Оценим интеграл 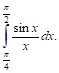
Легко проверить, что подынтегральная функция в интервале ![]() убывает и, следовательно,
убывает и, следовательно,
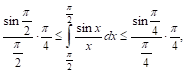
Т. е. 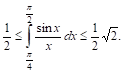
Таким образом, интеграл заключен между 0,5 и 0,71, что дает нам право считать его равным 0,6 с точностью до 0,1. Более точные приемы показывают, что приближенно он равен 0,62.
II. Обобщение теоремы об оценке интеграла. Интегрирование неравенств.
Справедлива следующая более общая теорема, чем теорема VI:
Теорема VII. Если в каждой точке Х интервала ![]()
![]()
То ![]()
Это значит, что неравенство между функциями влечет неравенство того же смысла между их определенными интегралами, или, говоря коротко, Неравенства можно интегрировать..
На доказательстве и геометрическом смысле теоремы останавливаться не будем, так как они вполне подобны предыдущим.
В частном случае, когда ![]() тождественно равно М, а
тождественно равно М, а ![]() тождественно равно Т, получаем теорему VI.
тождественно равно Т, получаем теорему VI.
III. Теорема о среднем.
Определенный интеграл обладает следующим важным свойством:
Теорема VIII (о среднем). Внутри интервала интегрирования ![]() существует, по меньшей мере, одно значение
существует, по меньшей мере, одно значение ![]() для которого
для которого
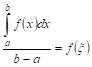 . (*)
. (*)
Доказательство. В силу теоремы VI имеем:
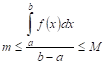
И, значит,
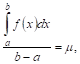
Где M — некоторое число, заключенное между наименьшим (Т) и наибольшим (М) значениями функции ![]() в интервале
в интервале ![]() , Т. Е.
, Т. Е. ![]() . Но
. Но ![]() , будучи непрерывной функцией, обязательно принимает, по меньшей мере, один раз каждое значение, лежащее между Т и М. Следовательно, при некотором
, будучи непрерывной функцией, обязательно принимает, по меньшей мере, один раз каждое значение, лежащее между Т и М. Следовательно, при некотором ![]() получит значение, равное M, т. е.
получит значение, равное M, т. е. ![]() (см. рис. 6), что и требовалось доказать.
(см. рис. 6), что и требовалось доказать.
Из равенства (*) находим:
![]()
Эта формула позволяет теорему о среднем высказать в такой форме:
ОпредЕЛенный интеграл от непрерывной функции, равен произведению значения этой функции в некоторой промежуточной точке интервала интегрирования, на длину интервала.
Дадим наглядное пояснение теоремы. При движении прямой, параллельной оси Ох (рис. 6), вверх от положения ВС площадь прямоугольника АВСК будет непрерывно возрастать от величины, меньшей площади трапеции, до величины, большей ее. Очевидно, при некотором промежуточном положении прямой — обозначим его через FG — Площадь прямоугольника AFGK окажется в точности равной площади трапеции S. Так как при ЭТом движении прямая постоянно пересекает линию, ограничивающую трапецию, то и в положении FG найдется одна или несколько (на рис.
7 две)
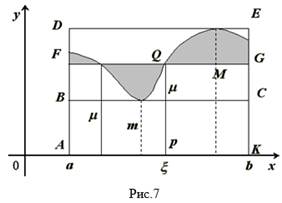
Точек пересечения Q; абсцисса любой точки пересечения и будет требуемым по теореме значением X.
Если трапецию ограничивает прямая линия, то ![]() ; отрезок PQ будет при этом средней линией прямолинейной трапеции.
; отрезок PQ будет при этом средней линией прямолинейной трапеции.
IV. Среднее арифметическое значение функции. Значение ![]() , находимое по теореме о среднем, называется средним арифметическим значением функции
, находимое по теореме о среднем, называется средним арифметическим значением функции ![]() в интервале
в интервале ![]() .
.
Определение. Средним арифметическИМ значением ![]() непрерывной функции
непрерывной функции ![]() в интервале
в интервале ![]() называется отношение определенного интеграла от этой функции к длиНЕ интервала:
называется отношение определенного интеграла от этой функции к длиНЕ интервала:
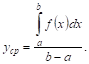
Приведем некоторые соображения в обоснование этого определения.
Пусть некоторая величина У принимает П значений: ![]() Средним арифметическим значением этой величины называется частное
Средним арифметическим значением этой величины называется частное ![]() . ТаК если температура воздуха в течение суток измеряется через каждый час, то средней температурой будет частное от деления суммы всех наблюденных температур на 24.
. ТаК если температура воздуха в течение суток измеряется через каждый час, то средней температурой будет частное от деления суммы всех наблюденных температур на 24.
Но представим себе теперь, что величина изменяется непрерывно (например, температура воздуха известна в любой момент суток) и мы хотим как-то в среднем охарактеризовать всю совокупность ее значений. Как в этом случае следует определить среднюю температуру воздуха, принимая во внимание всю известную совокупность знАЧений температуры? Вообще, ЧтО следует принять в качестве среднего значения неПРерывной фуНКции ![]() в некотором интервале
в некотором интервале ![]() ?
?
Разобьем интервал ![]() на П равных частей с помощью точек
на П равных частей с помощью точек ![]() и возьмем значения функции в этих N точках:
и возьмем значения функции в этих N точках:
![]()
Значениями нашей функции во всех остальных точках интервала пока пренебрежем. Возьмем среднее арифметическое ![]() указанных значений:
указанных значений:
![]()
Ясно, что чем больше П, тем больше значений функции учитывается при отыскании среднего значения, и поэтому естественно за среднее значение ![]() функции принять предел, к которому стремится
функции принять предел, к которому стремится ![]() При
При ![]() . Найдем этот предел.
. Найдем этот предел.
Умножив и разделив выражение для ![]() на
на ![]() , получим:
, получим:
![]()
Но так как ![]() То
То
![]()
ОТкуда, переходя к пределу, получаем указанное нами выше выражение для среднего значения:
![]()
На основании теоремы о среднем (теорема VIII) мы заключаем, ЧТо ![]() , где
, где ![]() , т. Е. что среднее значение непрерывной функции в интервале всегда (если только функция не постоянная) меньше некоторых ее значений, больше других ее значений и равно по меньшей мере одному ее значению.
, т. Е. что среднее значение непрерывной функции в интервале всегда (если только функция не постоянная) меньше некоторых ее значений, больше других ее значений и равно по меньшей мере одному ее значению.
Понятие среднего значения функции очень употребительно в техНИке. Многие величины часто характеризуются своими средними значениями; таковы, например, давление пара, сила и напряжение переменного тока, скорость химической реакции и т. п.
| < Предыдущая | Следующая > |
|---|
5.
Оценка интеграла. Теорема о среднем
Укажем границы, между которыми наверняка заключено значение интеграла.
Теорема 7. (об
оценке
определенного
интеграла).
Значение
определенного
интеграла заключено между произведениями наименьшего и наибольшего значений
подынтегральной функции на длину интервала интегрирования, т. е.
Z b
m(b − a) ≤
f (x)dx ≤ M (b − a), a < b,
a
где m и M — соответственно наименьшее и наибольшее значения функции f (x) в
интервале [а,b]:
m ≤ f (x) ≤ M.
Доказательство. Возьмем две функции M − f (x) и m − f (x) . Первая из них в
интервале [a, b] неотрицательна, вторая неположительна. Значит, по теореме 6
Z b
Z b
[M − f (x)]dx ≥ 0,
[m − f ()]dx ≤ 0.
a
a
Применяя теоремы п. 3 и формулу
Rb
dx = b − a , получим
a
Z
Z
b
M (b − a) ≥
b
f (x)dx и m(b − a) ≤
a
f (x)dx.
a
что и требовалось доказать. Из доказательства теоремы 6 следует, что если только
функция f (x) не постоянная, то нестрогие неравенства можно заменить на строгие:
Z b
m(b − a) <
f (x)dx < M (b − a).
a
Находя границы для интеграла, мы, как говорят, производим его оценку. Может
случиться, что весьма трудно или даже невозможно найти точное значение интеграла,
а оценивая его, мы узнаем, хотя бы грубо, приближенное его значение. С такого рода
оценками приходится довольно часто встречаться в математике.
Указанные в теореме 7 границы для интеграла тем более точны, чем короче интервал
интегрирования и чем меньше линия y = f (x) отличается по положению от прямой,
параллельной оси Ox .
Пример 1. Оценим интеграл
Z 2
5−x
dx.
2
0 9−x
Известными методами дифференциального исчисления находим, что наибольшее и
наименьшее значения подынтегральной функции в интервале [0,2] равны соответственно
y(2) = 0, 6 и y(2) = 0, 5 . Значит,
Z 2
5−x
dx < 0, 6(2 − 0),
0, 5(2 − 0) <
2
0 9−x
1
т. е. интеграл заключен между 1 и 1,2. Если считать, что он равен 1,1, то предельная
абсолютная ошибка равна 0,1, а относительная — 9%. Позже мы сумеем найти точное
значение приведенного интеграла. Оно равно 4/3 · ln 5 − ln 3 ≈ 1, 047 .
Пример 2. Оценим интеграл
Z π/2
sin x
dx.
x
π/4
Легко проверить, что подынтегральная функция в интервале [π/4, π/2] убывает и,
следовательно,
Z π/2
sin(π/2) π
sin x
sin(π/4) π
<
dx <
π/2 4
x
π/4 4
π/4
т. е.
√
Z π/2
1
sin x
2
<
dx <
.
2
x
2
π/4
Таким образом, интеграл заключен между 0,5 и 0,71, что дает нам право считать его
равным 0,6 с точностью до 0,1. Более точные приемы показывают, что приближенно он
равен 0,62.
Обобщение теоремы об оценке интеграла.
Интегрирование неравенств
Справедлива следующая более общая теорема, чем теорема 7.
Теорема 8. Если в каждой точке x интервала [a, b]
ψ(x) ≤ f (x) ≤ φ(x),
то
Z
Z
b
ψ(x)dx ≤
a
Z
b
b
f (x)dx ≤
a
φ(x)dx.
a
Это значит, что неравенство между функциями влечет неравенство того же
смысла между их определенными интегралами, или, говоря коротко, неравенства
можно интегрировать. Понятно хотя бы из простых геометрических соображений, что
дифференцирование неравенства может привести к нелепым результатам.
Доказательство теоремы немедленно следует из применения к неравенствам f (x) −
φ() ≤ 0 и f (x)−ψ(x) ≥ 0 теоремы 7 о знаке интеграла. Опять-таки знак равенства между
интегралами возможен только тогда, когда функции тождественно равны между собой.
В частном случае, когда φ(x) тождественно равно M , а ψ(x) тождественно равно
m , получаем теорему 7.
С помощью теоремы 8 легко получается важное неравенство, которым мы
воспользуемся в дальнейшем. При любом x
−|f (x)| ≤ f (x) ≤ |f (x)|.
(Если f (x) > 0 , то правая часть неравенства превращается в равенство, а левая часть
очевидна; если f (x) < 0 , то наоборот.) Тогда
Z b
Z b
Z b
−
|f (x)|dx ≤
f (x)dx ≤
|f (x)|dx,
a
a
a
2
или
Z
Z
b
|
b
f (x)dx| ≤
a
|f (x)|dx.
a
Модуль интеграла не превосходит интеграла от модуля функции. Предоставляем
читателю выяснить геометрический смысл этого неравенства. Напомним еще, что
аналогичное неравенство имеет место и для сумм: модуль суммы не превосходит суммы
модулей.
Теорема о среднем
Определенный интеграл обладает следующим важным свойством.
Теорема 9. (о среднем). Пусть функция f (x) непрерывна в замкнутом интервале [а,b].
Тогда внутри этого интервала существует хотя бы одно значение x = ξ , для которого
Rb
f (x)dx
a
= f (ξ).
(1)
b−a
Доказательство. Если функция f (x) постоянная, то формула (1) очевидна, причем
ξ — любая точка интервала [а,b]. Пусть теперь f (x) не постоянная, тогда в силу теоремы 7
имеем
Rb
f (x)dx
m< a
< M,
b−a
и, значит,
Rb
f (x)dx
a
= µ,
b−a
где µ — некоторое число, заключенное между наименьшим (m) и наибольшим (M )
значениями функции f (x) в интервале [a, b] .
В силу свойств непрерывных функций функция f (x) в каких-то двух точках
интервала [a, b] принимает значения m и и в какой-то точке, лежащей между ними,
принимает промежуточное значение µ . Значит, существует точка ξ ∈ (a, b) , в которой
f (ξ) = µ . Теорема доказана.
Из равенства (1) находим
Z
b
f (x)dx = f (ξ)(b − a), ξ ∈ (a, b).
a
Эта формула позволяет теорему о среднем сформулировать в такой форме:
Определенный интеграл от непрерывной функции равен произведению значения этой
функции в некоторой промежуточной точке интервала интегрирования на длину
интервала.
Среднее арифметическое значение функции
Определение 1. Средним арифметическим значением непрерывной функции y =
f (x) в интервале [а,b] называется отношение определенного интеграла от этой
функции к длине интервала:
Rb
f (x)dx
.
yc = a
b−a
3
На основании теоремы о среднем заключаем, что yc = f (ξ) , где ξ ∈ (a, b) . Среднее
значение непрерывной функции в замкнутом интервале всегда (если только функция не
постоянная) меньше некоторых ее значений, больше других ее значений и равно хотя бы
одному ее значению.
Понятие среднего значения функции очень употребительно в технике. Многие
величины часто характеризуются своими средними значениями, например: давление пара,
мощность переменного тока, скорость химической реакции и т. п.
4

