![]()
Представим выпуклый пятиугольник в виде четырехугольника с добавленным к нему треугольником. Поскольку сумма углов четырехугольника так или иначе равна 360 градусов, а сумма углов треугольника – 180 градусов, методом простого вычисления 180+360 получаем число 540: именно 540 градусов – сумма углов пятиугольника.
автор вопроса выбрал этот ответ лучшим
chipmunk
[41.4K]
9 лет назад
Сумма углов пятиугольника равна 540 градусов.
Для справки:
У шестиугольника сумма углов – 720 градусов.
У семиугольника сумма углов -900 градусов.
У восьмиугольника сумма углов -1080 градусов.
У четырехугольника сумма углов -360 градусов.
У треугольника сумма углов -180 градусов.
![]()
Oleg74
[202K]
8 лет назад
Существует формула для вычисления суммы всех углов многоугольника, благодаря которой можно вычислить сумму углов любого многоугольника, будь то треугольник, или четырехугольник, или пятиугольник и т. д.
Эта формула выглядит так :
Сумма углов = ( n – 2 ) х 180 °.
Тогда сумма углов для нашего пятиугольника будет равна ( 5 – 2 ) х 180 = 3 х 180 = 540 °.
А можно применить для такого вычисления и еще один способ, который заключается в том, что мы наш пятиугольник можем разделить на треугольники, которых будет три, а так как в треугольнике сумма углов равна 180 °, то 3 треугольника умножаем на 180 и получаем те же 540 °.

![]()
88SkyWalker88
[428K]
8 лет назад
Пятиугольником, судя по его названию, называют многоугольник с пятью углами.
Сумму углов пятиугольника можно найти по следующей формуле:
( n – 2 ) х 180 °, где n – это количество углов в многоугольнике, в нашем случае это будет пять.
Получается: (5-2) х 180 = 3 х 180 = 540
У пятиугольника с равными углами каждый угол будет равняться 108°.
![]()
gematogen
[29.9K]
8 лет назад
Сумма углов любого пятиугольников стоит 540 градусов.
В среднем величина угла около 110 градусов.
Пятиугольники в математике встречаются часто, поэтому необходимо знать формулу, если не знаете сколько градусов в фигуре.
Формула для нахождения суммы градусов в n-угольнике: (n-2)*180 градусов.

Ksyusha26
[26.8K]
8 лет назад
Существует формула, в соответствии с которой можно определить, чему равна сумма углов любого многоугольника. (n-2)*180, где n-это количество углов в нашем многоугольнике. Применим формулу: (5-2)*180=540. Верным ответом на данный вопрос будет число 540
Знаете ответ?
Чему равна сумма углов пятиугольника
Пятиугольник представляет собой геометрическую фигуру, обладающую соответствующим количеством углов. При этом для него, как и для других видов многоугольников, действуют общие правила, касающиеся в том числе суммы величин углов.

Пятиугольник представляет собой геометрическую фигуру, обладающую пятью углами. При этом, с точки зрения геометрии, в категорию пятиугольников входят любые многоугольники, обладающие этой характеристикой, вне зависимости от расположения его сторон.
Пятиугольник фактически представляет собой многоугольник, поэтому для вычисления суммы его углов можно воспользоваться формулой, принятой для исчисления указанной суммы в отношении многоугольника с любым количеством углов. Указанная формула рассматривает сумму углов многоугольника как следующее равенство: сумма углов = (n – 2) * 180°, где n – число углов в искомом многоугольнике.
Таким образом, в случае, когда речь идет именно о пятиугольнике, значение n в данной формуле будет равно 5. Таким образом, подставляя заданное значение n в формулу, получается, что сумма углов пятиугольника составит 540°. Вместе с тем, следует иметь в виду, что применение этой формулы в отношении конкретного пятиугольника связано с рядом ограничений.
Дело в том, что указанная формула для многоугольника, имеющего пять углов, как и для остальных видов этих геометрических фигур, может применяться только в том случае, если речь идет о так называемом выпуклом многоугольнике. Он, в свою очередь, представляет собой геометрическую фигуру, удовлетворяющую следующему условию: все ее точки находятся по одну сторону от прямой, которая проходит между двумя соседними вершинами.
Это определение можно несколько упростить, отметив, что в этом случае геометрическая фигура не должна иметь вершин, направленных внутрь нее. Только в этой ситуации правило, гласящее, что сумма углов пятиугольника составляет 540°, будет верным. Одним из частных случаев выпуклого пятиугольника является правильный пятиугольник, все углы которого равны, причем каждый составляет 108 градусов. В геометрии он имеет особое название, связанное с его греческим корнем – пентагон.
Таким образом, существует целая категория пятиугольников, сумма углов в которых будет отличаться от указанной величины. Так, например, одним из вариантов невыпуклого пятиугольника является геометрическая фигура звездчатой формы. Звездчатый пятиугольник также можно получить, используя всю совокупность диагоналей правильного пятиугольника, то есть пентагона: в этом случае образовавшаяся геометрическая фигура будет носить название пентаграммы, которая обладает равными углами. В этом случае сумма указанных углов будет составлять 180°.
Источники:
- Выпуклый многоугольник
Лучший ответ
cHin-cHillo
Гений
(85865)
12 лет назад
есть такая формула
сумма углов n-угольника = (n-2)*180градусов.
Отсюда:
сумма углов 5-угольника = (5-2)*180 = 3*180 = 540 градусов
Остальные ответы
Семен Аркадьевич
Высший разум
(340149)
12 лет назад
Правильного или произвольного? И что задано?
Nordeb-q
Профи
(701)
12 лет назад
Провести из одной его вершины все диагонали. Получается 2 диагонали и 3 треугольника. А сумма всех углов треугольника равна 180 градусам. Получается 180*3=540 градусов
Мама Самоделкина
Знаток
(344)
6 лет назад
есть такая формула
сумма углов n-угольника = (n-2)*180градусов.
Отсюда:
сумма углов 5-угольника = (5-2)*180 = 3*180 = 540 градусов
Вячеслав Басула
Ученик
(146)
6 лет назад
о
Даниил Козин
Ученик
(138)
6 лет назад
формула сумма углов n-угольника = (n-2)*180градусов..
Значит! сумма углов 5-угольника = (5-2)*180 = 3*180 = 540 градусов
Пятиугольник — многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы.
Площадь пятиугольника без самопересечений[править | править код]
Площадь пятиугольника без самопересечений, заданного координатами вершин, определяется по общей для многоугольников формуле.
Выпуклый пятиугольник[править | править код]
Выпуклым пятиугольником называется пятиугольник, такой, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Сумма внутренних углов выпуклого пятиугольника равна 540°.
Любые 9 точек в общем положении содержат вершины выпуклого пятиугольника, и существует множество из 8 точек в общем положении, в котором нет выпуклого пятиугольника[1].
Доказано также, что любые 10 точек на плоскости в общем положении содержат выпуклый пустой пятиугольник, и существует множество из 9 точек в общем положении, в котором нет выпуклого пустого пятиугольника[2].

Правильный пятиугольник[править | править код]
Пентагоном или правильным пятиугольником называется пятиугольник, у которого все стороны и углы равны.
Если провести в пентагоне диагонали, то он разобьётся на[3]:
- меньший пентагон (образуеся точками пересечения диагоналей) — в центре
- Вокруг меньшего пентагона — пять равнобедренных треугольников двух видов (с отношением бедра к основанию, равным золотой пропорции):
- 1) имеют острые углы в 36° при вершине и острые углы в 72° при основании
- 2) имеют тупой угол в 108° при вершине и острые углы в 36° при основании
При соединении двух первых и двух вторых треугольников их основаниями получатся два «золотых» ромба (первый имеет острый угол в 36° и тупой угол в 144°). Роджер Пенроуз использовал «золотые» ромбы для конструирования «золотого» паркета (мозаики Пенроуза).
Звездчатые пятиугольники[править | править код]
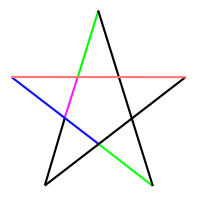
Многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника называется звёздчатым. Помимо правильного существует ещё один звёздчатый пятиугольник — пентаграмма.
Пентаграмма, как полагал Пифагор, представляет собой математическое совершенство, поскольку демонстрирует золотое сечение (φ = (1+√5)/2 = 1,618…). Если разделить длину любого цветного отрезка на длину самого длинного из оставшихся меньших отрезков, то будет получено золотое сечение φ.
См. также[править | править код]
- Правильный пятиугольник
- Пентагон
- Пентаграмма
- Пятиугольный паркет
Примечания[править | править код]
- ↑
Kalbfleisch, J.D.; Kalbfleisch, J.G. & Stanton, R.G. (1970), A combinatorial problem on convex regions, Proc. Louisiana Conf. Combinatorics, Graph Theory and Computing, vol. 1, Congressus Numerantium, Baton Rouge, La.: Louisiana State Univ., с. 180–188 - ↑ Harborth, Heiko (1978), Konvexe Fünfecke in ebenen Punktmengen, Elem. Math. Т. 33 (5): 116–118
- ↑ Плитки Пенроуза. Дата обращения: 9 февраля 2011. Архивировано 22 сентября 2013 года.
По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.
 Так как все углы правильного n-угольника равны между собой, каждый внутренний угол правильного пятиугольника равен 540º:5=108º (в частности, ∠A2A1A5=108º).
Так как все углы правильного n-угольника равны между собой, каждый внутренний угол правильного пятиугольника равен 540º:5=108º (в частности, ∠A2A1A5=108º).
Сумма внешних углов многоугольника, взятых по одному при каждой вершине, равна 360º. Поскольку все внешние углы правильного пятиугольника равны между собой, градусная мера каждого, например, угла 1, равна
∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).
Каждый центральный угол правильного пятиугольника, например, угол A1O A2, равен
∠A1O A2=360º:5=72º.
Как и любой другой правильный многоугольник, правильный пятиугольник вписан в окружность и описан около окружности.
Соединив центр правильного многоугольника с его вершинами, получим пять равных равнобедренных треугольников.
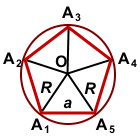
Основанием каждого такого треугольника равно стороне 5-угольника, боковые стороны равны радиусу описанной окружности, угол при вершине — центральному углу 5-угольника.
В треугольнике A1OA5
![]()
![]()
![]()
 Проведём из вершины высоту OF.
Проведём из вершины высоту OF.
По свойству равнобедренного треугольника, OF является также медианой и биссектрисой треугольника A1OA5, то есть
![]()
![]()
OF — радиус вписанной в A1A2A3A4A5 окружности: OF=r.
Рассмотрим прямоугольный треугольник A1OF.
По определению синуса,
![]()
откуда
![]()
![]()
Так как
![Rendered by QuickLaTeX.com [sin {36^o} = sqrt {frac{{5 - sqrt 5 }}{8}} ,]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-978b0fcccb82af5f73951d1811832f6d_l3.png)
то
![Rendered by QuickLaTeX.com [R = frac{a}{{2sqrt {frac{{5 - sqrt 5 }}{8}} }} = frac{{asqrt 8 }}{{2sqrt {5 - sqrt 5 } }} = frac{{a cdot 2sqrt 2 }}{{2sqrt {5 - sqrt 5 } }} = ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-37925508765b0e92c944807a15ed029f_l3.png)
![Rendered by QuickLaTeX.com [ = frac{{asqrt 2 }}{{sqrt {5 - sqrt 5 } }} = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{sqrt {5 - sqrt 5 } cdot sqrt {5 + sqrt 5 } }} = frac{{asqrt 2 cdot sqrt {5 + sqrt 5 } }}{{sqrt {{5^2} - {{(sqrt 5 )}^2}} }} = ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-3635f26a3c4a245681b619a78633459d_l3.png)
![]()
![]()
Таким образом, формула радиуса описанной около правильного пятиугольника окружности —
![]()
По определению котангенса,
![]()
![]()
Подставив значение котангенса 36°, получаем:
![]()
Итак, формула радиуса вписанной в правильный пятиугольник окружности
![]()
Применив формулу
![]()
можно найти площадь правильного пятиугольника. Здесь
![]()
следовательно, формула для нахождения площади A1A2A3A4A5
![]()
Все диагонали правильного пятиугольника равны.
Длина диагонали равна
![]()


