В данной публикации мы рассмотрим определение, свойства и признаки одной из основных геометрических фигур – прямоугольника. Также приведем формулы, с помощью которых можно найти его площадь и периметр.
- Определение прямоугольника
-
Свойства прямоугольника
- Свойство 1
-
Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Признаки прямоугольника
- Формулы
Определение прямоугольника
Прямоугольник – это четырехугольник, у которого все углы равны 90° (т.е. являются прямыми).

∠ABC = ∠BCD = ∠BAD = ADC = 90°
Прямоугольник состоит из:
- длины – более длинная пара сторон. Обычно обозначаются латинской буквой, например, a;
- ширины – более короткая пара сторон. Чаще всего обозначаются как b.
Сам прямоугольник обычно записывается путем перечисления его вершин, например, ABCD в нашем случае.
Примечание: Прямоугольник является разновидностью параллелограмма.
Свойства прямоугольника
Свойство 1
Противоположные стороны прямоугольника попарно параллельны и равны.

- AD = BC = a, AD || BC
- AB = CD = b, AB || CD
Свойство 2
Длина и ширина прямоугольника одновременно являются его высотами, т.к. они взаимно перпендикулярны.

- a – это высота h1, проведенная к стороне b
- b – это высота h2, проведенная к стороне a
Свойство 3
Если соединить середины сторон прямоугольника, то получится ромб.

Свойство 4
Квадрат диагонали (d) прямоугольника равняется сумме квадратов его смежных сторон.
d2 = a2 + b2

Это следует из теоремы Пифагора, которую можно применить к любому из прямоугольных треугольников, которые образуются в результате деления диагональю прямоугольника.
Свойство 5
Диагонали прямоугольника равны, и в точке пересечения делятся пополам.

- AC = BD = d
- AE = EC = BE = ED
Свойство 6
Около любого прямоугольника можно описать окружность, радиус (R) которой равен половине диагонали этого прямоугольника.

Следовательно, диаметр окружности равен полной длине диагонали прямоугольника.
Признаки прямоугольника
Параллелограмм является прямоугольником, если верно одно из следующих утверждений:
- Его диагонали равны.
- Все его углы равны.
- Если квадрат диагонали равен сумме квадратов его смежных сторон.
Формулы
1. Площадь прямоугольника (S):
S = a ⋅ b
2. Периметр прямоугольника (P):
P = a + a + b + b = 2a + 2b
Прямоугольник. Формулы и свойства прямоугольника
Определение.
Прямоугольник – это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.
Стороны прямоугольника одновременно является его высотами.
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
AB||CD, BC||AD
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
AC = BD
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d2 = 2a2 + 2b2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника – квадрат).
Стороны прямоугольника
Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.
Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
a = √d2 – b2
b = √d2 – a2
2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
3. Формула стороны прямоугольника (длины и ширины прямоугольника) через периметр и другую сторону:
4. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол α:
a = d sinα
b = d cosα
5. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол β:
Диагональ прямоугольника
Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.
Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d = √a2 + b2
2. Формула диагонали прямоугольника через площадь и любую сторону:
| d = | √S2 + a4 | = | √S2 + b4 |
| a | b |
3. Формула диагонали прямоугольника через периметр и любую сторону:
| d = | √P2 – 4Pa + 8a2 | = | √P2 – 4Pb + 8b2 |
| 2 | 2 |
4. Формула диагонали прямоугольника через радиус описанной окружности:
d = 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
d = Dо
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула диагонали прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d = √2S : sin β
Периметр прямоугольника
Определение.
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a + 2b
P = 2(a + b)
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a2 | = | 2S + 2b2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a + √d2 – a2) = 2(b + √d2 – b2)
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a + √4R2 – a2) = 2(b + √4R2 – b2)
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a + √Do2 – a2) = 2(b + √Do2 – b2)
Площадь прямоугольника
Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.
Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
S = a · b
2. Формула площади прямоугольника через периметр и любую сторону:
| S = | Pa – 2a2 | = | Pb – 2b2 |
| 2 | 2 |
3. Формула площади прямоугольника через диагональ и любую сторону:
S = a√d2 – a2 = b√d2 – b2
4. Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
S = a√4R2 – a2 = b√4R2 – b2
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
S = a√Do2 – a2 = b√Do2 – b2
Окружность описанная вокруг прямоугольника
Определение.
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
2. Формула радиуса окружности описанной вокруг прямоугольника через периметр квадрата и любую сторону:
| R = | √P2 – 4Pa + 8a2 | = | √P2 – 4Pb + 8b2 |
| 4 | 4 |
3. Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:
| R = | √S2 + a4 | = | √S2 + b4 |
| 2a | 2b |
4. Формула радиуса окружности описанной вокруг прямоугольника через диагональ квадрата:
5. Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:
6. Формула радиуса окружности описанной вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула радиуса окружности описанной вокруг прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
Угол между стороной и диагональю прямоугольника
Формулы определения угла между стороной и диагональю
1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:
Угол между диагоналями прямоугольника
Формулы определения угла между диагоналями прямоугольника
1. Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:
β = 2α
2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:
Чтобы найти площадь прямоугольника, надо его ширину умножить на длину.
Формула площади
S = a * b
Чтобы найти периметр прямоугольника, надо сложить все его стороны.
Формула периметра
Р = а * 2 + b * 2 или Р = (а + b ) * 2
Формулы площади и периметра для квадрата выглядят так:
S = a * a
Р = а * 4
Чтобы найти объем прямоугольного параллелепипеда, надо умножить его длину на ширину и высоту.
Формула объема
V = a * b * c
Формула объема для куба
V = a * a * a
Задачи
- Длина прямоугольника равна 5 см, а ширина – 4 см. Найдите площадь и периметр прямоугольника.
- Сторона квадрата равна 20 см. Найдите площадь и периметр квадрата.
- Вычислите периметр квадрата со стороной 6 дм.
- Вычислите площадь прямоугольника, длины сторон которого равны 12 мм и 8 мм.
- Длина прямоугольника равна 30 см, ширина – на 10 см меньше. Найдите Р и S этого прямоугольника.
- Длина одной стороны прямоугольника 4 см, а ширина в 2 раза больше. Найдите периметр и площадь прямоугольника.
- Сторона квадрата равна 10 дм. Чему равен периметр?
- Ширина прямоугольника 9 дм, а длина в 2 раз больше ширины. Найдите Р и S этого прямоугольника.
- Площадь прямоугольника 54 см², его длина 9 см. Чему равна ширина прямоугольника?
- Периметр квадрата равен 20 см. Найдите его площадь.
- Площадь прямоугольника равна 360 см², его длина 6 см. Найдите периметр этого прямоугольника.
- Периметр прямоугольника равен 40 дм. Ширина – 5 дм. Найдите его площадь?
- Сад около дома имеет ширину 20 м, а длину – 30 м. Какой длины надо поставить вокруг сада. Какова площадь сада?
- Прямоугольный параллелепипед имеет следующие грани – 6 см, 8 см, 10см. Найдите объем параллелепипеда.
- Высота комнаты 3 м, ширина 6 м, а длина 10 м. Сколько кубических метров воздуха находится в комнате? Найдите площадь пола, потолка, стен?
- Найдите объем бассейна, если его глубина 3 м, ширина 12м, длина 20 м.
- Длина аквариума 50 см, ширина – 30 см, высота 40 см. Сколько литров воды можно в него налить (до краев)?
- Найдите объем книги. Толщина – 2 см, ширина – 15 см, а длина – 20 см.
Также посмотрите дополнительные задания по темам:
Задания на таблицу умножения и деления.
Уравнения простые и составные, 3 класс.
Карточки для развития внимания на каждый день (примеры с несколькими действиями плюс упражнение на внимание).
Единицы времени.
Примеры на порядок действий (примеры с несколькими действиями).
Единицы длины и Единицы веса.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Прямоугольник – это четырехугольник, у которого все углы прямые.
На рис. 1 изображен прямоугольник АВСD.
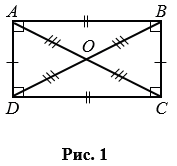
Отрезки АВ и СD, АD и ВС – противолежащие стороны прямоугольника. Противолежащие стороны прямоугольника не имеют общих точек. В прямоугольнике противолежащие стороны равны, тогда на рис. 1 в прямоугольнике АВСD: АВ = DС, АD = ВС.
Отрезки АВ и АD, АD и DC, DC и ВС, АВ и ВС – соседние или смежные стороны. Смежные стороны – стороны, которые имеют общую вершину. Смежные стороны прямоугольника имеют специальные названия: длина и ширина.
Отрезки АС и ВD – диагонали прямоугольника. Диагонали прямоугольника соединяют противолежащие вершины. Диагонали прямоугольника равны и точкой пересечения делятся пополам. Так на рис. 1 АС = ВD и ОА = ОВ = ОС = ОD.
Периметр – это сумма длин всех сторон многоугольника. Обозначается периметр буквой 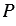 .
.
Учитывая, что в прямоугольнике противоположные стороны равны, его периметр вычисляется по формуле: 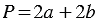 или
или 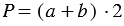 , где
, где 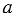 и
и 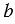 смежные стороны прямоугольника (длина и ширина).
смежные стороны прямоугольника (длина и ширина).
Площадь прямоугольника обозначается буквой 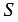 . Площадь прямоугольника равна произведению его смежных сторон, т.е. если
. Площадь прямоугольника равна произведению его смежных сторон, т.е. если 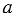 и
и 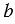 смежные стороны прямоугольника, то его площадь
смежные стороны прямоугольника, то его площадь 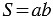 .
.
Каждая диагональ прямоугольника делит его на два равных треугольника. На рис. 2, 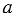 диагональ АС делит прямоугольник АВСD на два равных треугольника АВС и АDС, т.е.
диагональ АС делит прямоугольник АВСD на два равных треугольника АВС и АDС, т.е. 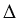 АВС =
АВС = 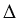 АDС, а на рис. 2, б диагональ ВD делит прямоугольник АВСD на два равных треугольника ВАD и ВСD, т.е.
АDС, а на рис. 2, б диагональ ВD делит прямоугольник АВСD на два равных треугольника ВАD и ВСD, т.е.
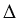 ВАD =
ВАD = 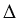 ВСD.
ВСD.
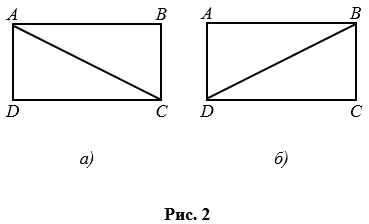
Прямоугольник, у которого все стороны равны, называют квадратом.
Ось симметрии
Прямоугольник имеет ось симметрии. Ось симметрии прямоугольника – это прямая, проходящая через средины противоположных сторон прямоугольника. У прямоугольника две оси симметрии, на рис. 3 прямые 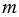 и
и 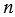 оси симметрии прямоугольника АВСD.
оси симметрии прямоугольника АВСD.
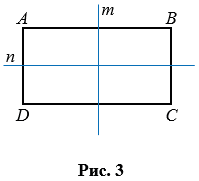
Если лист бумаги перегнуть по прямым 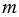 (или
(или 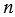 ), то две части прямоугольника, лежащие по разные стороны от прямой
), то две части прямоугольника, лежащие по разные стороны от прямой 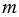 (или
(или 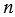 ), совпадут.
), совпадут.
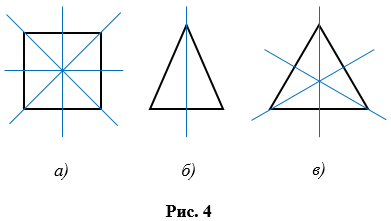
Существуют и другие фигуры, которые имеют ось симметрии, такие фигуры называют симметричными относительно прямой. Так, например, квадрат имеет четыре оси симметрии (рис. 4, 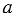 ), равнобедренный треугольник одну ось симметрии (рис. 4, б), а равносторонний треугольник – три оси симметрии (рис.4, в).
), равнобедренный треугольник одну ось симметрии (рис. 4, б), а равносторонний треугольник – три оси симметрии (рис.4, в).
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Угол. Обозначение углов
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 677,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 738,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 750,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 762,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 769,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 846,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1810,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 367,
Мерзляк, Полонский, Якир, Учебник
Номер 568,
Мерзляк, Полонский, Якир, Учебник
Номер 9,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 60,
Мерзляк, Полонский, Якир, Учебник
Номер 516,
Мерзляк, Полонский, Якир, Учебник
Номер 748,
Мерзляк, Полонский, Якир, Учебник
Номер 750,
Мерзляк, Полонский, Якир, Учебник
Номер 1180,
Мерзляк, Полонский, Якир, Учебник
Задание 72,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 495,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 706,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 725,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 758,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 19,
Мерзляк, Полонский, Якир, Учебник
Номер 20,
Мерзляк, Полонский, Якир, Учебник
Номер 82,
Мерзляк, Полонский, Якир, Учебник
Номер 379,
Мерзляк, Полонский, Якир, Учебник
Номер 410,
Мерзляк, Полонский, Якир, Учебник
Номер 411,
Мерзляк, Полонский, Якир, Учебник
Номер 663,
Мерзляк, Полонский, Якир, Учебник
Задание 305,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 401,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 502,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Номер 67,
Мерзляк, Полонский, Якир, Учебник
Номер 313,
Мерзляк, Полонский, Якир, Учебник
Номер 450,
Мерзляк, Полонский, Якир, Учебник
Загрузить PDF
Загрузить PDF
Прямоугольник — это четырехугольник (двумерная фигура) с четырьмя прямыми углами. Параллельные стороны прямоугольника равны.[1]
Прямоугольник, у которого все стороны равны, называется квадратом. Все квадраты являются прямоугольниками, но не все прямоугольники — квадраты. Периметр фигуры равен сумме значений ее сторон.[2]
Площадь фигуры равна произведению ее длины на ширину.[3]
-

1
Удостоверьтесь, что в задаче дан прямоугольник (показан на рисунке). Помните, что у прямоугольника противоположные стороны параллельны и равны (верхняя и нижняя стороны, а также боковые стороны). Более того, боковые стороны перпендикулярны (пересекают под 90°) верхней и нижней сторонам.[4]
- Если у фигуры все стороны равны, в задаче дан квадрат. Квадрат является частным случаем прямоугольника.
- Если данная в задаче фигура не соответствует приведенным условиям, она не является прямоугольником.
-

2
Запишите формулу для вычисления площади прямоугольника: S = l x w.[5]
В этой формуле S — площадь, l — длина прямоугольника, w — ширина прямоугольника. Единицами измерения площади являются квадратные единицы измерения длины, например, квадратные метры, квадратные сантиметры и так далее.- Единицы измерения площади записываются так: м2, см2 и так далее.
-

3
Найдите длину и ширину прямоугольника. Длина прямоугольника — это его верхняя или нижняя сторона. Ширина прямоугольника — это одна из его боковых сторон. Измерьте стороны прямоугольника с помощью линейки, чтобы найти длину и ширину.
- Например, длина прямоугольника равна 5 см, а ширина равна 2 см.
-

4
В формулу подставьте значения переменных и вычислите площадь. В формулу подставьте значения длины и ширины, которые вы только что нашли, а затем перемножьте их, чтобы вычислить площадь прямоугольника.
- В нашем примере: S = l x w = 5 x 2 = 10 см2.
Реклама
-

1
Удостоверьтесь, что в задаче дан прямоугольник (показан на рисунке). Помните, что у прямоугольника противоположные стороны параллельны и равны (верхняя и нижняя стороны, а также боковые стороны). Более того, боковые стороны перпендикулярны (пересекают под 90°) верхней и нижней сторонам.
- Если у фигуры все стороны равны, в задаче дан квадрат. Квадрат является частным случаем прямоугольника.
- Если данная в задаче фигура не соответствует приведенным условиям, она не является прямоугольником.
-

2
Запишите формулу для вычисления периметра прямоугольника: P = 2 (l + w).[6]
В этой формуле Р — периметр, l — длина прямоугольника, w — ширина прямоугольника. Иногда данная формула записывается так: P = 2l + 2w (эти формулы идентичны друг другу, но форма записи у них разная).- Единицами измерения периметра являются единицы измерения длины, например, метры, сантиметры и так далее.
-

3
Найдите длину и ширину прямоугольника. Длина прямоугольника — это его верхняя или нижняя сторона. Ширина прямоугольника — это одна из его боковых сторон. Измерьте стороны прямоугольника с помощью линейки, чтобы найти длину и ширину.
- Например, длина прямоугольника равна 5 см, а ширина равна 2 см.
-

4
В формулу подставьте значения переменных и вычислите периметр. В формулу подставьте значения длины и ширины, которые вы только что нашли. Периметр можно вычислить двумя способами в зависимости от выбранной вами формулы. Если вы выбрали формулу P = 2(l + w), сложите значения длины и ширины, а затем сумму умножьте на 2. Если вы выбрали формулу P = 2l + 2w, умножьте длину на 2, затем ширину умножьте на 2, а затем сложите полученные значения.
- В нашем примере: P = 2(l + w) = 2(2 + 5) = 2(7) = 14 см.
- В нашем примере: P = 2l + 2w = (2 x 2) + (2 x 5) = 4 + 10 = 14 см.
Реклама
Что вам понадобится
- Бумага
- Ручка или карандаш
- Линейка, чтобы измерять стороны
Об этой статье
Эту страницу просматривали 19 360 раз.
