Как найти среднеквадратичную скорость атома

Как найти среднеквадратичную скорость атома

Как вычислить среднеквадратичную скорость атомов???



Профи

(887),
закрыт



13 лет назад

Александр Панин

Профи

(609)


13 лет назад

Нужно знать стат. физику. Атомы в газе подчинаются статистике Больцмана, что означает, что их функция распределения пропорциональна f(p)~exp(-E/k*T), где E = p^2/(2m) – кинетическая энергия, k – постоянная Больцмана, T- температура. Коэффициент перед экспонентой в функции распределения писать не буду. Далее, чтобы найти среднеквадратичную скорость, сначала найдём среднеквадратичный импульс. Для этого вычисляем интеграл p^2 * f(p)* d^3p – интеграл по трёхмерному импульсу. Вы получите, что импульс в квадрате пропорционален температуре в квадрате p^2~(k*T)^2*m. Теперь, вас интересует скорость p=m*v -> v~k*T/sqrt(m). Вот и ответ!

Источник

Наиболее
вероятная скорость.

Наиболее вероятная
скорость молекул идеального газа
соответсвует максимуму функции f(v).
Следовательно, эта скорость может быть
найдена из выражения

(13.18)

Средняя
скорость молекул.

По определению:

Есть табличный
интеграл:

В нашем случае

Откуда получаем:

(13.19)

средняя
квадратичная скорость <Vкв>
молекул.

По определению

Есть табличный
интеграл:

В нашем случае

Получаем:

(13.20)

Скорости,
характеризующие состояние газа.

Наиболее
вероятная скорость

Средняя

средняя
квадратичная скорость

Где:
k
– постоянная Больцмана;

m0
–
масса
молекулы;

Т – термодинамическая
температура;

R
– молярная газовая постоянная;


– молярная масса.

13. 2. 4. Распределение Максвелла в безразмерном виде.

Зачатую бывает
удобно провести анализ или решение
задачи воспользовавшись распределением
Максвелла по скоростям в безразмерном
виде. Что получить распределение в такой
записи перейдем к безразмерной скорости

Тогда выражение
(13.16) примет вид

(13.21)

13. 2. 5. Распределение Максвелла по энергиям.

Преобразует
выражение (13.6) с помощью замен
(среднее значение энергии, приходящееся
на одну степень свободы) и(кинетическая энергия частицы). Тогдаи

или после перехода
к безразмерной величине

(13.22)

Это
и есть распределение Максвелла по
энергиям

13. 3. Распределение Больцмана. Газ в силовом поле.

Перейдем к
рассмот­рению газа во внешнем силовом
поле. Для простоты будем полагать, что
в любом физически малом объеме
температура газа одинакова. Выделим
в газе два равных по величине объема
(см. рис. 13.3) таких, что в каждом из них
можно полагать потенциальную энергию
неизменной.

Рисунок 13.3.

Пусть в первом
объеме молекулы газа обладают потенциальной
энергией
,
а во втором.
Согласно формулам (13.3) и (13.9) вероятности
того, что молекулы обладают такими
значениями потенциальной энергии (т.е.,
и.)
будут соответственно равны

и.

(13.23)

Здесь
– некоторый числовой множитель.

С другой стороны
эти вероятности
идолжны относиться друг к другу в той же
пропорции, что и количества частиц в
выбранных объемах при одинаковых в них
температурах

(13.24)

Подставим в левую
часть этого равенства (13.23), а числитель
и знаменатель правой дроби поделим на
величину выбранного объема
.
Тогда учтя, что концентрация частиц,
после упрощений получаем

Отсюда следует,
что

(13.25)

или

(13.26)

где
– концентрация частиц в местоположении
частиц газа с нулевой потенциальной
энергией. Данное выражениеназывается
распределение Больцмана
(при постоянной температуре).

Анализ данного
выражения показывает, что силовое
поле принуждает собираться частицы
газа в местах с минимальной потенциальной
энергией, а тепловое движение приводит
к разбрасыванию частиц по пространству.

Соседние файлы в папке физика

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Средняя квадратичная скорость молекул — среднее квадратическое значение модулей скоростей всех молекул рассматриваемого количества газа

Large vecupsilon =sqrt{frac{3kT}{m}}=sqrt{frac{3RT}{M}}


Таблица значений средней квадратичной скорости молекул некоторых газов

Средняя квадратичная скорость газа

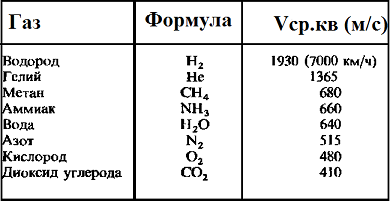
Для того чтоб понять, откуда же у нас получается эта формула, мы выведем среднюю квадратичную скорость молекул. Вывод формулы начинается с основного уравнения молекулярно кинетический теории (МКТ):

large PV=nu RT

Где nu у нас количество вещества, для более легкого доказательства, возьмем на рассмотрение 1 моль вещества, тогда у нас получается:

large PV=RT

Если посмотреть, то PV это две третьих средней кинетической энергии всех молекул (а у нас взят 1 моль молекул):

large PV=frac{2}{3}vec E_k

Тогда, если приравнять правые части, у нас получается, что для 1 моля газа средняя кинетическая энергия будет равняться:

large vec E_k =frac{3}{2}RT

Но средняя кинетическая энергия, так же находится, как :

large vec E_k =frac{1}{2}N_a m vecupsilon^2

А вот теперь, если мы приравняем правые части и выразим из них скорость и возьмем квадрат,Число Авогадро на массу молекулы , получается Молярная масса N_a m = M то у нас и получится формула для средней квадратичной скорости молекулы газа:

Large vecupsilon =sqrt{frac{3RT}{M}}

А если расписать универсальную газовую постоянную, как R=N_ak , и за одно молярную массу M=N_a m , то у нас получится?

Large vecupsilon =sqrt{frac{3kT}{m}}

В Формуле мы использовали :

vecupsilon — Средняя квадратичная скорость молекул

k=1.38cdot10^{-23} — Постоянная Больцмана

T — Температура

m — Масса одной молекулы

R=8.31 — Универсальная газовая постоянная

M — Молярная масса

nu — Количество вещества

vec E_k — Средняя кинетическая энергия молекул

N_a=6,02cdot10^{23} — Число Авогадро

Источник

Molecular speed is defined as the speed of the group of molecules in an ideal gas. Molecular speed is an important concept in the kinetic theory of gases. According to the kinetic theory of gases, the molecules of a gas are in constant motion and move in a straight line until they collide with another molecule. All the molecules of an ideal gas undergo elastic collision. It explains why small molecules diffuse more rapidly than large molecules. The molecular speed of a gas is directly proportional to its speed and inversely proportional to its molar mass. The molecular speed of a gas increases with an increase in the temperature of the gas. For example, Helium has the lowest molecular mass and thus has the highest molecular speed.

Types of Molecular Speed

The concept of molecular speed states that a cluster of atoms moves at a typical rate. The particles in an ideal gas don’t come into contact with one another. Let us see different types of molecular speed and how to calculate them. Molecular speed can be of 3 types which are as follows:

Average Molecular Speed

It is the average speed of a group of molecules in a gas. It is denoted using bar{v} . It can be calculated using the formula:

bar{v} = sqrt{frac{8RT}{pi M}}

where, 

  • T is the temperature of the gas in Kelvin
  • M is the molar mass
  • R is the Ideal gas constant, 8.314 kg*m2/s2*mol*K

Root Mean Square Speed

It is the measure of the speed of the particles in particular gas. It is denoted by vrms and can be calculated using the formula:

v_{rms} = sqrt{frac{3RT}{M}}

where,

  • T is the temperature of the gas in Kelvin
  • M is the molar mass
  • R is the Ideal gas constant, 8.314 kg*m2/s2*mol*K

Most Probable Speed

It is the speed which is acquired by most of the molecules in a gas. It is denoted by vp and can be calculated using the following formula:

v_{p} = sqrt{frac{2RT}{M}}

where,

  • T is the temperature of the gas in Kelvin
  • M is the molar mass
  • R is the Ideal gas constant, 8.314 kg*m2/s2*mol*K

Relation between Molecular Speeds

The volume of a gas molecule is little in relation to the whole volume of the container when it comes to the molecular speeds of a particle. The gas particles travel freely and with complete mobility. The force of attraction between the gaseous molecules is therefore absent.

  • The relationship between average molecular speed, root mean square speed, and most probable speed is:

v_{rms}> bar{v} > v_p

  • The ratio between average molecular speed, root mean square speed, and most probable speed is:

u_{rms}: bar{v}: u_{mp}:: 1:1.128:1.224

Maxwell Distribution of Molecular Speeds

Maxwell and Boltzmann derived an equation to find the distribution of various types of molecular speeds in a gas. The number of molecules per unit speed is indicated on the y-axis of the Maxwell-Boltzmann distribution graph. The quantity of molecules in the gas is represented by the total area under the whole curve. The peak of the graph will move to the right if we heat the gas to a greater temperature (since the average molecular speed will increase). The graph grows higher and more narrow as the gas gets colder, similar to how the graph shortens and widens as the gas heats up.

Maxwell Distribution of Molecular Speeds

Maxwell Distribution of Molecular Speeds

Inferences from the Graph

  • The most probable speed is represented by the peak of the curve. The average molecular speed is the speed that is just a little higher than the most probable speed. The root mean square speed coincides with the average kinetic energy of the gas molecules.
  • The curve will spread and flatten out when we observe the gas at increasing temperatures. 
  • The shape of the curve is dependent upon the molar mass and temperature of the gas. 
  • The curve gets taller and flatter when we consider gases of increasing molar mass.
  • With the increase in temperature, the most probable speed increases, and the peak of the curve shifts to the right. The particles of gas also tend to move faster. 

Solved Examples on Molecular Speed

Example 1: The temperature of gas with a molar mass of 2 g/mol is 900K. Calculate the root mean square speed of the particles of gas.

Solution:

Given, M = 2g/mol, T = 900K

R = 8.314

v_{rms} = sqrt{frac{3RT}{M}}

= sqrt{frac{3*8.314*900}{2}}

= √11223.9

therefore v_{rms} = 105.9 m/s

Example 2: Calculate the most probable speed of Helium gas at 800K.

Solution:

Given, T = 800K

For Helium, M = 4g/mol and R = 8.314

v_{p} = sqrt{frac{2RT}{M}}

= sqrt{frac{2*8.314*800}{4}}

= sqrt{3325.6}

therefore v_{p} = 57.66 m/s

Example 3: Determine the speed of particles of m = 1 gr/mol and temperature 1500 k.

Solution:

Given, M = 1g/mol, T = 1500K and R = 8.314

v_{rms} = sqrt{frac{3RT}{M}}

= sqrt{frac{3*8.314*1500}{1}}

= sqrt{37413}

therefore v_{rms} = 193.42 m/s

Example 4: Compare the following quantities, the RMS velocity of oxygen at 80 °C and the RMS velocity of Hydrogen at 45 °C. 

Solution:

To compare the quantities, we shall calculate the rms for oxygen and hydrogen for the given conditions.

Oxygen:

Given T = 80degree C = 353K, Molar mass of oxygen (M) = 16g/mol

v_{rms} = sqrt{frac{3RT}{M}}

= sqrt{frac{3*8.314*353}{16}}

therefore v_{rms_o} = 23.45 m/s

Hydrogen:

Given, T = 45°, C = 318K, Molar mass of Hydrogen (M) = 2g/mol

v_{rms} = sqrt{frac{3RT}{M}}

= sqrt{frac{3*8.314*318}{2}}

therefore v_{rms_h} = 62.97 m/s

Thus, rms velocity of hydrogen is more than Oxygen at the given conditions.

Example 5: Find the average molecular speed of gas with a molar mass 19 g at 500K.

Solution:

Given, T = 500K, M = 19g/mol

bar{v} = sqrt{frac{8RT}{pi M}}

= sqrt{frac{8*8.314*500}{3.14*19}}

therefore bar{v} = 23.60 m/s

FAQs on Molecular Speed

Question 1: What is meant by the kinetic theory of gases?

Solution:

Based on the notion that a gas is made up of atoms or molecules that are moving quickly, kinetic theory describes how gases behave.

Question 2: Why do smaller gas atoms travel more quickly?

Solution:

Because of the molecular mobility of molecules, smaller gas particles travel more quickly. At all temperatures higher than absolute zero, they have kinetic energy. The average kinetic energy of gas molecules and temperature are directly inversely correlated. At the same temperature and pressure, lighter gases will also move at speeds that are higher than heavier gases.

Question 3: What is meant by the degree of freedom?

Solution:

The amount of independent ways that the system’s path and configuration might vary is referred to as the degree of freedom.

Question 4: Describe mean energy.

Solution:

The mean energy or internal energy of one mole of gas is called the mean energy. It is represented by the letter U.

Last Updated :
11 Oct, 2022

Like Article

Save Article

Источник

При неизменном давлении одноатомного идеального газа среднеквадратичная скорость движения его атомов увеличилась в 2 раза. Чему равно отношение конечной плотности газа к начальной?

Спрятать решение

Решение.

Давление идеального газа можно найти по формуле p= дробь: числитель: 2, знаменатель: 3 конец дроби nE_кин.ср.. Концентрация равна n= дробь: числитель: N, знаменатель: V конец дроби = дробь: числитель: Nrho, знаменатель: m конец дроби = дробь: числитель: rho, знаменатель: m_ат конец дроби , где m  — масса всего газа, m_ат  — масса атома. Средняя кинетическая энергия атомов газа E_кин.ср.= дробь: числитель: m_атlangle v в квадрате rangle, знаменатель: 2 конец дроби . Подставим выражение для E_кин.ср. в уравнение для p и выразим плотность газа.

p= дробь: числитель: 2, знаменатель: 3 конец дроби умножить на дробь: числитель: rho, знаменатель: m_ат конец дроби умножить на дробь: числитель: m_атlangle v в квадрате rangle, знаменатель: 2 конец дроби равносильно rho= дробь: числитель: 3p, знаменатель: langle v в квадрате rangle конец дроби .

Среднеквадратичная скорость движения атомов равна корню из среднего квадрата скорости атомов v _кв= корень из: начало аргумента: langle v в квадрате rangle конец аргумента . Следовательно, при увеличении среднеквадратичной скорости движения атомов в 2 раза плотность газа уменьшается в 4 раз.

Ответ: 0,25.

Источник

Добавить комментарий