Как найти массу материальной поверхности

Макеты страниц

Приложения кратных интегралов в механике

Краткая теория

---

Масса и статистические моменты пластики

Если

 – область плоскости

, занятая пластинкой, и

 – поверхностная плотность пластики в точке

, то масса

 пластинки и ее статистические моменты

 и

 относительно осей

 и

 выражаются двойными интегралами:

Если
пластика однородна, то

Координаты центра тяжести пластики

Если

 – центр тяжести пластики, то

где

 – масса пластинки и

 – ее статистические моменты относительно осей
координат.

Моменты инерции пластики

Моменты
инерции пластинки относительно осей

 и

 соответственно равны:

Момент инерции пластики относительно
начала координат:

Полагая

, получаем геометрические моменты инерции плоской
фигуры.

Масса тела, занимающего область
 и статистические моменты тела относительно
координатных плоскостей

где

 – плоскость тела в точке

Координаты центра тяжести

Если тело
однородно, то формулах для координат центра тяжести можно положить

.

Моменты инерции относительно
осей координат

Полагая в
этих формулах

, получаем геометрические
моменты инерции тела.

Примеры решения задач

---

Задача 1

Вычислить
массу материальной пластины, занимающей область

 плоскости

, если поверхностная
плотность

 и границы области

 заданы уравнениями.

Решение

Сделаем
чертеж области

:

Искомая
масса материальной пластины:

Ответ:

---

Задача 2

Найти
статистический момент фигуры, ограниченной линиями

 и

 относительно оси абсцисс.

Решение

Сделаем
чертеж:

Статистический
момент относительно оси

:

Ответ:

---

Задача 3

Вычислить
координаты центра масс однородной

 материальной пластины

, ограниченной данными
линиями:

Решение

Сделаем
чертеж:

Масса
пластинки:

Статистические
моменты:

Искомые
координаты центра масс:

Ответ:

.

---

Задача 4

Вычислить массу тела

, ограниченного заданными поверхностями

 -плотность в
точке

.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Изобразим
тело на рисунке:

С боков
тело будет ограничено цилиндром

 и плоскостями

. Сверху плоскостью

Проекция на плоскость

:

           

Ответ:

---

Задача 5

Найти
момент инерции однородного шара

 с массой

 относительно оси

.

Решение

Момент
инерции относительно оси

 можно найти по формуле:

Шар
однородный, поэтому плотность:

Перейдем
к сферическим координатам:

Получаем:

Ответ:

Примеры решений поверхностных интегралов

В этом разделе вы найдете подробные решения по вычислению поверхностых интегралов первого и второго рода и применению их к нахождению массы поверхности:

Поверхностные интегралы 1-го рода: примеры решений

Задача 1. Вычислить интеграл
$$iint_S (x-y) dS,$$
где $S$ – часть цилиндра $x^2+y^2=a^2$, лежащая внутри цилиндра $z^2=a(a-x)$.

Задача 2. Вычислить $iint_sigma (5x-3y+3z) d sigma$, где $sigma$ – часть плоскости $P: 4x+3y+12z-12=0$, ограниченная координатными плоскостями.

Поверхностный интеграл по части плоскости

Задача 3. Вычислить интеграл $iint_S (x+y+z) dS$, $S$ – поверхность $x^2+y^2+z^2=a^2, z ge 0$.

Трудности с задачами? МатБюро поможет с интегралами.

Поверхностные интегралы 2-го рода: примеры решений

Задача 4. Вычислить поверхностные интегралы второго рода
$$iint_S (y^2+z^2) dxhat dy,$$
где $S$ – часть верхней стороны цилиндра $z=sqrt{a^2-x^2}$, $0 le y le b$.

Задача 5.

Вычислить поверхностный интеграл $iint_S z dxdy$, $S$ – внешняя сторона $x^2+y^2/4+z^2/9=1$.

Масса поверхности: примеры решений

Задача 6. Найти массу участка поверхности $z^2=x^2+y^2$, $(0 le z le 1)$, если плотность $delta=z$.

Полезные ссылки

• Интегралы – примеры решений
• Применение интегралов – примеры решений
• Двойные интегралы – примеры решений
• Тройные интегралы – примеры решений
• Криволинейные интегралы – примеры решений
• Учебник с примерами онлайн по поверхностным интегралам

Приложения определенного интеграла к решению некоторых задач механики и физики

1. Моменты и центры масс плоских кривых. Если дуга кривой задана уравнением y=f(x), a≤x≤b, и имеет плотность 1) 002.gif” />=(x), то статические моменты этой дуги Mx и My относительно координатных осей Ox и Oy равны

а координаты центра масс 009.gif” /> и — по формулам

1) Всюду в задачах, где плотность не указана, предполагается, что кривая однородна и ◄ Имеем: ◄ Имеем: Пример 3. Найти координаты центра масс полуокружности ◄Вследствие симметрии 026.gif” />. При вращении полуокружности вокруг оси Ох получается сфера, площадь поверхности которой равна 028.gif” />, а длина полуокружности равна па. По теореме Гульдена имеем Отсюда 032.gif” />, т.е. центр масс C имеет координаты CПример 4. Скорость прямолинейного движения тела выражается формулой (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.

◄ Так как путь, пройденный телом со скоростью (t) за отрезок времени [t1,t2], выражается интегралом

2. Вычисление площади плоской фигуры

Если положить в формуле (6.18) f ( x , y )=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой h = 1. Объем такого цилиндра,

как известно, численно равен площади S основания D . Получаем формулу для вычисления площади S области D :

или, в полярных координатах,

Пример 6.10. Вычислить площадь фигуры, ограниченной прямой y = 2 x + 1 и параболой y = x 2 + 1.

Решение. Решая совместно систему

Применяя формулу (6.19), будем иметь:

Решение. Переходим к полярной системе координат, полагая x = r cos φ и y = r sin φ ; тогда получаем

3. Вычисление массы плоской фигуры (пластины)

Масса плоской пластинки D с переменной плотностью γ =γ ( x , y ) находится по формуле

4. Определение статических моментов и координат центра тяжести плоской фигуры

Статические моменты фигуры D относительно осей 0 x и 0 y могут быть вычислены по формулам

а координаты центра масс фигуры – по формулам

Статические моменты широко используются в сопротивлении материалов и других технических науках.

5. Определение моментов инерции плоской фигуры

Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т.е. . Моменты инерции плоской фигуры относительно 0 x и 0 y могут быть вычислены по формулам:

Момент инерции фигуры относительно начала координат – по формуле

Пример 6.12 . Найти массу, статические моменты и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом и координатными осями. Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.

Решение. По формуле (6.21) находим массу пластины. По условию, γ =γ ( x , y )= k ∙ xy , где k – коэффициент пропорциональности.Тогда

Находим статические моменты пластинки по формулам (6.22):

Находим координаты центра тяжести пластинки, используя формулы (6.23):

6. Поверхностный интеграл I рода

Обобщением двойного интеграла является поверхностный интеграл. Пусть в трехмерном пространстве О xyz в точках некоторой поверхности площади S определена непрерывная функция u = f ( x ; y ; z ). Разобьем поверхность на конечное число n частей S_i , площади которых равны ∆ S_i , а диаметры – d_i , . Выберем в каждой части S_i произвольную точку M_i ( x_i ; y_i ; z_i ) и составим сумму произведений вида

Она называется интегральной суммой для функции f ( x ; y ; z ) по поверхности S . Если при интегральная сумма (6.26) имеет предел, который не зависит ни от способа разбиения поверхности S, ни от выбора точек M_i ( x_i ; y_i ; z_i ), то он называется поверхностным интегралом I рода от функции f ( x ; y ; z ) по поверхности S и обозначается . Следовательно,

Теорема 6.3 (о существовании поверхностного интеграла). Если поверхность S гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция f ( x ; y ; z ) непрерывна на этой поверхности, то поверхностный интеграл существует

Формула (6.28)

выражает интеграл по поверхности S через двойной интеграл по проекции S на плоскость x 0 y . Отметим, что если поверхность S задана уравнением вида y=y(x;z) или x=x(y;z), то аналогично получим:

где D ₁ и D ₂ – проекции поверхности S на координатные плоскости xО z и y О z соответственно.

Пример 6.13. Вычислить , где S – часть цилиндрической поверхности , отсеченной плоскостями z = 0 и z = 3.

Решение . Из уравнения заданной цилиндрической поверхности выразим и учтём, что при x = 0 в плоскости x О y : . Так как частные производные равны , то согласно формуле (6.30), имеем

6.1. Площадь поверхности

Если поверхность S задана уравнением z = f ( x ; y ), a ее проекция на плоскость x 0 y есть область D , в которой z = f ( x ; y ), z_x ( x ; y ) и z_y ( x ; y ) – непрерывные функции, то ее площадь S вычисляется по формуле:

Пример 6.14. Вычислить площадь части плоскости x + y + z = 4, вырезаемой цилиндром x 2 + y 2 = 4 (рис. 6.10).

Чтобы вычислить этот интеграл, введём полярные координаты. Область D определяется: . Следовательно,

Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы γ =γ ( x ; y ; z ) . Все эти величины определяются одним и тем же способом:

– данную область разбивают на конечное число мелких частей;

– делают для каждой такой части предположения, упрощающие задачу;

– находят приближенное значение искомой величины;

– переходят к пределу при неограниченном измельчении разбиения области.

Проиллюстрируем описанный способ на примере определения массы материальной поверхности.

6.2. Масса поверхности

Пусть плотность распределения массы материальной поверхности есть γ =γ ( x ; y ; z ) . Для нахождения массы поверхности:

1. Разбиваем поверхность S на n частей S_i , , площадь которых обозначим ∆ S_i .

2. Выберем произвольную точку M_i ( x_i ; y_i ; z_i ) в каждой области S_i . Предполагаем, что в переделах области S_i плотность постоянна и равна её

4. Суммируя m_i по всей области, получаем: .

5. За точное значение массы материальной поверхности S принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей S_i , то есть

6.3. Моменты и центр тяжести поверхности. С татические моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по соответствующим формулам:

Пример 6.15. Вычислить координаты центра тяжести однородной поверхности параболоида z = x 2 + y 2 , ограниченной плоскостью z = 1.

Решение. Вершина заданного параболоида совпадает с началом координат. Так как поверхность однородная (постоянная плотность массы), то, основываясь на ее симметрии, можно сделать вывод, что центр тяжести расположен на оси 0 z . Тогда x_c = 0, y_c = 0 и по формуле (6.36) аппликата . Пересечем параболоид поверхностью z = 1, спроектируем линию пересечения на плоскость x 0 y – получим окружность x 2 + y 2 =1 в качестве области D . Вычислим элемент поверхности параболоида z = x 2 + y 2 по формуле (6.31), учитывая, что :

Аналогично, переходя к полярным координатам на плоскости x 0 y , получим:

Приложения криволинейных интегралов.

1. Площадь области D, ограниченной замкнутым контуром L, находится по формуле:

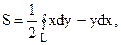
где направление обхода контура L выбрано так, что область D остается все время слева от пути интегрирования.

2. Пусть L есть плоская кривая с линейной плотностью массы m(x, y),
тогда

а) масса m кривой L вычисляется по формуле

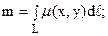
б) координаты центра тяжести кривой L вычисляются по формулам:

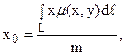
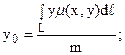
в) моменты инерции I_x, I_y и I₀ соответственно относительно осей Ox, Oy и начала координат равны:

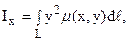
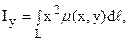
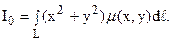( 27)

3. Пусть 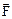= P(x, y, z) 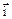+Q(x, y, z) 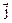+ R(x, y, z) 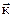есть переменная сила, совершающая работу W вдоль пути L, и функции P(x, y, z), Q(x, y, z) и R(x, y, z) непрерывны на кривой L.

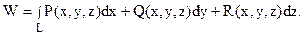
Найти массу тонкого стержня, имеющего форму линии x 2 + y 2 = 1, y > 0, если его линейная плотность в точке M(x, y) равна m(x, y) = 1 + (1/2)y.

В данном случае линия L есть верхняя половина единичной окружности, которую легко задать параметрически: x = cost, y = sint, 0

Воспользовавшись известными параметрическими уравнениями прямой, запишем уравнения линии, по которой перемещается точка приложения силы:

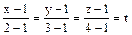Þx = 1 + t, y = 1 + 2t, z = 1 + 3t, 0 3 t,
y = asin 3 t, 0

[spoiler title=”источники:”]

http://www.sites.google.com/site/vyssaamatem/glava-vi-osnovy-integralnogo-iscislenia-funkcii-neskolkih-peremennyh/vi-3-nekotorye-prilozenia-dvojnogo-integrala

http://mydocx.ru/12-43515.html

[/spoiler]

Некоторые приложения поверхностного интеграла I рода

Приведем некоторые примеры применения поверхностного интеграла I рода.

Площадь поверхности

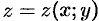Если поверхность задана уравнением , а ее проекция на плоскость 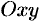есть область , в которо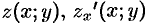й и 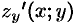— непрерывные функции, то ее площадь вычисляется по формуле

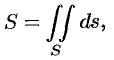
или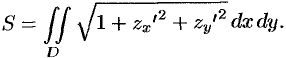

Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы 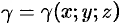. Все эти величины определяются одним и тем же способом: данную область разбивают на конечное число «мелких» частей, делая для каждой области деления упрощающие задачу предположения; находят приближенное значение искомой величины; переходят к пределу при неограниченном измельчении области деления. Проиллюстрируем описанный способ на примере определения массы материальной поверхности.

Масса поверхности

Пусть плотность распределения массы материальной поверхности есть 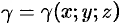. Для нахождения массы поверхности:

1. Разбиваем поверхность на частей 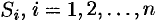, площадь которой обозначим .

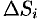2. Берем произвольную точку 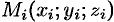в каждой области 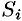. Предполагаем, что в пределах области 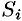плотность постоянна и равна значению ее в точке .

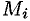3. Масса 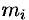области 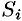мало отличается от массы 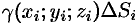фиктивной однородной области с постоянной плотностью

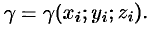
4. Суммируя 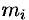по всей области, получаем: .

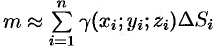5. За точное значение массы материальной поверхности принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей 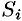, т. е.

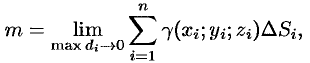
т. е.

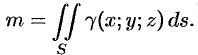
Моменты, центр тяжести поверхности

Статистические моменты, координаты центра тяжести, моменты инерции материальной поверхности находятся по соответствующим формулам:

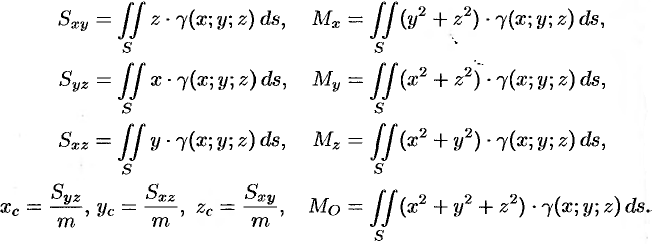
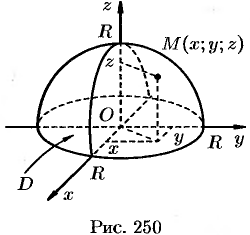
Пример №57.3.

Найти массу полусферы радиуса 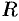, если в каждой точке поверхности плотность численно равна расстоянию этой точки от радиуса, перпендикулярного основанию полусферы.

Решение:

На рисунке 250 изображена полусфера радиуса 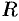. В уравнение 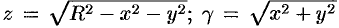— поверхностная плотность полусферы.

По формуле (57.7) находим:

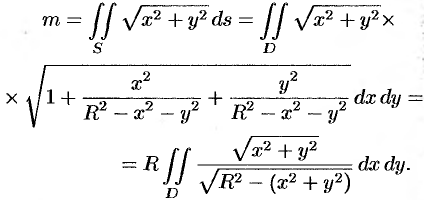
Переходим к полярным координатам:

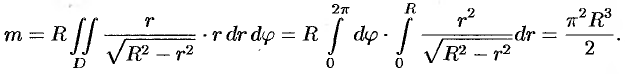
Внутренний интеграл вычислен с помощью подстановки :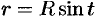

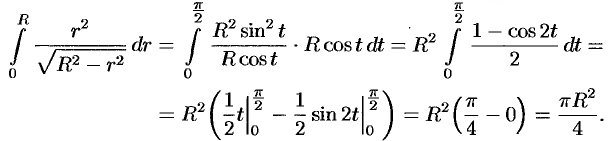
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

• Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны: