
{S = a cdot h}
Найти площадь параллелограмма
На этой странице вы можете рассчитать площадь параллелограмма с помощью калькулятора по трем формулам. Просто введите известные вам данные – основание, высоту, стороны, диагонали и углы между ними и получите ответ.
Параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Содержание:
- калькулятор площади параллелограмма
- формула площади параллелограмма через сторону и высоту
- формула площади параллелограмма через две стороны и угол между ними
- формула площади параллелограмма через диагонали и угол между ними
- примеры задач
Формула площади параллелограмма через сторону и высоту
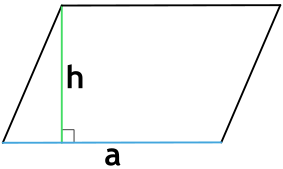
{S = a cdot h}
a – сторона параллелограмма
h – высота параллелограмма
Формула площади параллелограмма через две стороны и угол между ними

{S=a cdot b cdot sin(alpha)}
a, b – стороны параллелограмма
α – угол между сторонами a и b
Формула площади параллелограмма через диагонали и угол между ними
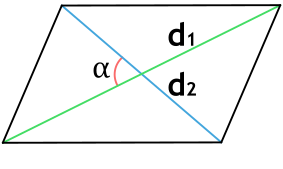
{S = dfrac{1}{2} cdot d_1 cdot d_2 cdot sin(alpha)}
d1, d2 – диагонали параллелограмма
α – угол между диагоналями
Примеры задач на нахождение площади параллелограмма
Задача 1
Найдите площадь параллелограмма, стороны которого равны 9 см и 12 см, а угол между ними 60 градусов.
Решение
Для решения задачи нам подойдет вторая формула, так как из условия нам известны стороны параллелограмма и угол между ними. Подставим значения в формулу и произведем расчет.
S = a cdot b cdot sin(alpha) = 9 cdot 12 cdot sin(60) = 108 cdot sin(60) = 108 cdot 0.866 approx 93.53074 : см^2
Ответ: 108 cdot 0.866 approx 93.53074 : см^2
Мы можем проверить ответ с помощью калькулятора .
Задача 2
Найдите площадь параллелограмма, если две его стороны равны 8 см и 12 см, а угол между ними равен 30 градусов.
Решение
Задача похожа на предыдущую, поэтому ее решение будет выглядеть аналогично.
S = a cdot b cdot sin(alpha) = 8 cdot 12 cdot sin(30) = 96 cdot sin(30) = 96 cdot 0.5 = 48 : см^2
Ответ: 48 см²
И снова проверить ответ нам поможет калькулятор .
Задача 3
Найдите площадь параллелограмма, сторона которого равна 12 см, а высота проведенная к ней 8 см.
Решение
В этом случае нам известны сторона параллелограмма и высота, поэтому воспользуемся первой формулой.
S = a cdot h = 12 cdot 8 = 96 : см^2
Ответ: 96 см²
И снова проверить ответ нам поможет калькулятор .
В прошлой статье предложила решить 4 задачки на тему площадь параллелограмма. Задания простые. Несколько заданий требуют несложных размышлений.
Посмотрим как они решаются.
Во всех четырех задачах требуется найти площадь параллелограмма ABCD.
Задание №1
Задание на знание базовой формулы нахождения площади параллелограмма (произведение высоты и стороны параллелограмма, к которой эта высота проведена):
Высота, в данном случае, отрезок ВЕ, а сторона, к которой проведена высота это AD.
В параллелограмме противолежащие стороны равны. Значит AD=BC=8.
ОТВЕТ: 32
Задание №2
В этом задании уже понадобится знание формулы вычисления площади параллелограмма через синус угла (площадь параллелограмма вычисляется как произведение смежных сторон на синус угла между ними):
Остается только найти угол между сторонами параллелограмма из исходных данных.
Заметим, что углы BCA и CAD накрест лежащие углы при параллельных прямых ВС и AD и секущей АС .
Тогда из рисунка видно, что угол BAD является суммой углов BAC и CAD:
Не забываем, что AD=ВС=12. Остается только подставить все значения в формулу и найти площадь.
Синус угла 60 градусов – табличное значение.
ОТВЕТ: 60√3
Задание №3
В этом задании знаем высоты, но не знаем ни одной стороны. Попробуем найти любую из сторон параллелограмма.
Рассмотрим образовавшийся прямоугольный треугольник ВАЕ:
В этом треугольнике один острый угол равен 60 градусов, значит второй острый угол равен 90-60=30 градусов.
А в прямоугольном треугольнике против угла 30 градусов лежит катет равный половине гипотенузы. Т.е. гипотенуза АВ в два раза больше противолежащего катета ВЕ:
Не забываем что в параллелограмме CD=AB=8. Воспользуемся формулой вычисления площади параллелограмма:
где BF – высота, СD – сторона, к которой проведена высота.
ОТВЕТ: 48
Задание №4
Сторона параллелограмма по сути нам известна (AD=AE+ED=10+4=14).
Попробуем найти высоту.
Для этого сначала посмотрим на образовавшийся выпуклый четырехугольник BEDF, в котором два угла прямые. С учетом, что сумма углов выпуклого четырехугольника равна 360 градусов, можно найти угол FDE (или тот же угол CDA, обозначенный другими буквами ):
Помним, что сумма углов параллелограмма, прилежащих одной стороне, равна 180 градусов. Значит:
Рассмотрим треугольник АВЕ (прямоугольный). Если один его острый угол равен 45 градусов, то второй:
По признаку равнобедренного треугольника получаем, что треугольник АВЕ – равнобедренный с равными сторонами АЕ и ВЕ:
ВЕ, в свою очередь, является высотой параллелограмма АВСD. Значит:
ОТВЕТ: 140
Если вы знаете того, кто готовится к ОГЭ не забудьте поделиться с ним этой информацией. Всегда пригодится.
Продолжение следует…
Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность
(✿◠‿◠)
Необходимо определить, что такое высота параллелограмма.
Это перпендикуляр, проведённый из любой точки стороны параллелограмма к прямой, содержащей противоположную параллельную сторону. Обычно высоту проводят из вершины параллелограмма. Так как параллелограмм имеет две пары параллельных сторон, то он имеет высоты двух различных длин.
Высота (BE), проведённая между длинными сторонами, короче высоты (BF), проведённой между короткими сторонами.

Так как стороны ромба одинаковы, то высоты ромба также одинаковы: (BE = BF).

Площадь произвольного параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота.

Проведём высоты из двух вершин (B) и (C) к стороне (AD) .
Прямоугольные треугольники (ABE) и (DCF) равны (равные гипотенузы как противоположные стороны параллелограмма и равные катеты как расстояние между параллельными прямыми).
Параллелограмм (ABCD) и прямоугольник (EBCF) — равновеликие, так как состоят из равных фигур:
SABCD=SABE+SEBCD;SEBCF=SEBCD+SDCF.
Значит, площадь параллелограмма определяется так же, как площадь прямоугольника:
SEBCF=BE⋅BC;SABCD=BE⋅BC=BE⋅AD.
Если обозначить сторону через (a), высоту — через (h), то:
Для определения площади параллелограмма можно использовать короткую сторону и высоту, проведённую к короткой стороне.
Диагонали ромба в точке пересечения делятся пополам, они перпендикулярны и делят ромб на четыре равных прямоугольных треугольника.

.
Формула определения площади ромба:
Эта формула справедлива для определения площади любого четырёхугольника, если его диагонали перпендикулярны.
Так как диагонали квадрата равны, то для определения площади квадрата в формуле достаточно длины одной диагонали:
Площадь произвольного треугольника
Так как диагональ параллелограмма делит его на два равных треугольника, то площадь треугольника равна половине площади параллелограмма.

, где (h) — высота (на рисунке — (BE)), проведённая к стороне (a) (на рисунке — (AD)).
Для определения площади треугольника можно использовать любую сторону и высоту, проведённую к этой стороне.
Удобно иногда использовать формулу Герона, если известны длины всех трёх сторон треугольника.
SΔ=pp−ap−bp−c;p=a+b+c2
— формула Герона, где (a), (b) и (c) — стороны треугольника, (p) — полупериметр треугольника.
Площадь прямоугольного треугольника
Так как катеты прямоугольного треугольника взаимно перпендикулярны, то один катет может быть высотой, а другой катет — стороной, к которой проведена высота. Получаем формулу:
S=a⋅b2, где (a) и (b) — катеты.
Для прямоугольного треугольника также можно применять формулы площади произвольного треугольника.
Пример:
1. вычислим площадь треугольника со сторонами (17) см, (39) см, (44) см.
Решение:
p=17+39+442=50;SΔ=50⋅50−17⋅50−39⋅50−44=50⋅33⋅11⋅6==25⋅2⋅3⋅11⋅11⋅2⋅3=5⋅2⋅3⋅11=330см2.
Чтобы легче было вычислить корень, необходимо не перемножать все числа, а раскладывать их на множители:
a⋅a=a
.
Формулу Герона можно использовать для вычисления высоты треугольника.
Пример:
2. вычислим меньшую высоту треугольника, стороны которого равны (15) см, (13) см, (4) см.
Решение:
используем две формулы вычисления площади:
SΔ=aha2
и
SΔ=pp−ap−bp−c
.
Меньшая высота в треугольнике — та, которая проведена к большей стороне, поэтому (a =) (15) см.
.
15⋅h2=24⋅215⋅h=48;h=4815=3,2(см).
Иногда формула Герона используется для вычисления площади параллелограмма, если даны стороны параллелограмма и его диагональ.
Пример:
3. дан параллелограмм со сторонами (17) см и (39) см, длина диагонали равна (44) см. Вычислим площадь параллелограмма.
Решение:
диагональ делит параллелограмм на два равных треугольника. Используем результат, полученный в первом примере:
.
Трапеция имеет одну пару параллельных сторон, следовательно, имеет одну высоту — перпендикуляр, проведённый между параллельными сторонами.
Чаще всего высоту трапеции проводят из вершин или через точку пересечения диагоналей.

Площадь трапеции определим как сумму площадей треугольников, на которые трапецию делит диагональ.

SABCD=SABD+SDBC;SABCD=AD⋅BE2+BC⋅DF2=AD⋅BE2+BC⋅BE2==AD+BC⋅BE2.
Если обозначить параллельные стороны (основания) трапеции через (a) и (b), высоту через (h), то:
Обрати внимание!
Важные следствия:
1. если высоты треугольников равны, то их площади относятся как длины оснований.
2. Если основания треугольников равны, то их площади относятся как длины высот.
3. Если высоты треугольников равны и их основания равны, то они равновелики, например, медиана делит треугольник на две равновеликие части.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Площадь
- Площадь параллелограмма
Назовем одну из сторон параллелограмма основанием, а перпендикуляр, проведенный из любой точки противоположной стороны к прямой, содержащей основание, – высотой параллелограмма.
Теорема
Площадь параллелограмма равна произведению его основания на высоту
Доказательство
Дано: ABCD – параллелограмм, S – площадь ABCD, ВН и СК – высоты
Доказать: S = AD  BH
BH
Доказательство:
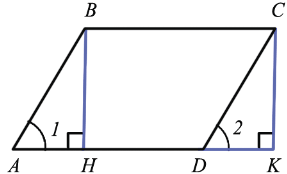
Докажем, что площадь прямоугольника НВСК также равна S. Рассмотрим трапецию АВСК: с одной стороны, она составлена из параллелограмма ABCD и треугольника DCK. Но с другой стороны, она составлена из прямоугольника НВСК и треугольника АВН. Но 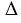 DCK =
DCK =  АВН (по гипотенузе (АВ = CD, т.к. они противоположные стороны параллелограмма) и острому углу(углы 1 и 2 как соответственные углы при пересечении параллельных прямых АВ и CD секущей AD)), а равные фигуры имеют равные площади, поэтому их площади равны.
АВН (по гипотенузе (АВ = CD, т.к. они противоположные стороны параллелограмма) и острому углу(углы 1 и 2 как соответственные углы при пересечении параллельных прямых АВ и CD секущей AD)), а равные фигуры имеют равные площади, поэтому их площади равны.
 площадь параллелограмма ABCD и прямоугольника НВСК также равны, т.е. площадь прямоугольника НВСК равна S. По теореме площадь прямоугольника равна произведению его смежных сторон, т.е. S = BC
площадь параллелограмма ABCD и прямоугольника НВСК также равны, т.е. площадь прямоугольника НВСК равна S. По теореме площадь прямоугольника равна произведению его смежных сторон, т.е. S = BC  BH, а так как BC = AD, то S = AD
BH, а так как BC = AD, то S = AD  BH. Теорема доказана
BH. Теорема доказана
Советуем посмотреть:
Понятие площади многоугольника
Площадь квадрата
Площадь прямоугольника
Площадь треугольника
Площадь трапеции
Теорема Пифагора
Теорема, обратная теореме Пифагора
Формула Герона
Площадь
Правило встречается в следующих упражнениях:
7 класс
Задание 460,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 467,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 5,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 502,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 503,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 513,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 603,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 832,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 835,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1241,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Как найти площадь параллелограмма — три основных формулы
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта статья на еще одну математическую тему. Мы расскажем, как правильно посчитать площадь параллелограмма. Эту тему подробно изучают только в 8-м классе. И это говорит, что она не такая простая.

Но для начала давайте все-таки напомним, какая фигура называется параллелограммом.
Параллелограмм – это разновидность четырехугольников, у которого противоположные стороны параллельны друг другу.
Классический параллелограмм выглядит вот так:

Впервые об этой фигуре подробно написал древнегреческий математик Евклид в своем известном произведении «Начала». Он же рассказал и о двух частных случаях параллелограмма, которые нам сегодня хорошо известны.
Это и прямоугольник, у которого противоположные стороны не только параллельны друг другу, но и пересекаются под прямым углом. И квадрат, у которого помимо параллельности противоположных сторон, все стороны еще и равны между собой.

И наконец, не лишним будет вспомнить, что подразумевается под термином «площадь».
Площадь геометрической фигуры – это размер плоскости, которая находится внутри сторон фигуры.
Ну а теперь объединим эти два понятия и расскажем, как надо считать площадь параллелограмма.
Формулы для расчета площади параллелограмма
Есть три основных формулы для вычисления площади параллелограмма:
- если известна длина стороны и высота, проведенная к ней;
- если известны длины сторон и углы между ними;
- если известны длины диагоналей и угол между ними.
Теперь о каждом из этих способов подробнее.
Как найти площадь параллелограмма, если известны сторона и высота
Возьмем для примера такой параллелограмм:
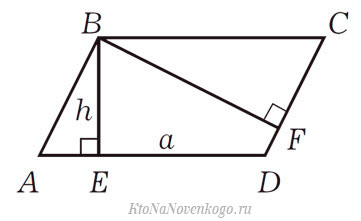
В нем указаны две высоты – BE и BF. Напомню, что высота — это отрезок, который опускается из вершины на противоположную сторону под прямым углом.
В данном случае площадь считается весьма просто. Надо всего лишь перемножить длину высоты и длину стороны, к которой она проведена.
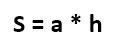
И то же самое касается, если знать длины стороны DC и высоты BF. Тогда для вычисления площади достаточно их перемножить.
Кстати, у этой формулы есть весьма интересное доказательство. Так как у параллелограмма противоположные стороны параллельны и равны, то можно взять треугольник ABE и переставить его к стороне CD. Вот так это будет выглядеть:
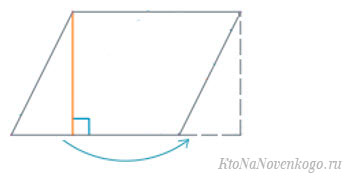
В результате мы получим прямоугольник, у которого нам известны длины обеих сторон (высота параллелограмма превратилась в одну из сторон). А как известно, площадь прямоугольника равна произведению его сторон.
Формула площади параллелограмма, если известны стороны и угол
Площадь параллелограмма можно посчитать, если известны длины обеих его сторон и величина острого угла между ними.
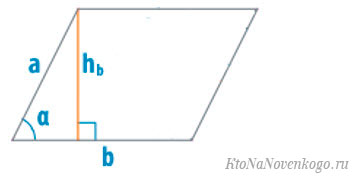
Собственно, этот способ вытекает из предыдущего, Просто по исходным данным нужно вычислить высоту параллелограмма, а уже потом по ней посчитать площадь.
Согласно тригонометрии, синус острого угла в прямоугольнике равен отношению противоположного катета к гипотенузе. В нашем примере таким катетом является высота, а гипотенузой сторона «а». И получается:
![]()
Соответственно, чтобы посчитать значение высоты надо:
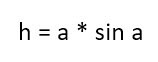
И наша конечная формула для расчета площади будет выглядеть следующим образом:
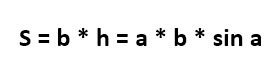
Как найти площадь параллелограмма через диагонали
Этот способ используется крайне редко, но знать его все равно нужно. Во всяком случае, на экзаменах у школьников такие примеры вполне могут встретиться.
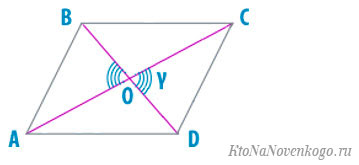
В данном случае для вывода формулы используются весьма непростые математические вычисления. И мы не будем ими вас загружать. А просто покажем конечный результат:
![]()
Соответственно, здесь d1 и d2 – длины диагоналей, а y – острый угол между ними.
Вот и все, что мы хотели рассказать о вычислении площади параллелограмма.
