Пока в цикле статей по сопротивлению материалов мы лишь немного касались геометрии сечения и её влияния на прочность конструкции. В частности, в статье о эпюре продольных сил рассматривались площадь тела, как одна из основных характеристик, влияющих на величину нормальных напряжений. Впрочем, площадь, как самостоятельная характеристика, нуждается в более детальном представлении. Именно поэтому вы попали в цикл внутри цикла, в котором мы более подробно разберёмся с геометрическими характеристиками, использующимися в сопромате и других инженерных дисциплинах.
Итак, площадь сечения.
Всегда положительна. Не зависит от выбора системы координат. Имеет размерность см2.
Здесь и далее я буду указывать размерность в сантиметрах. Это нужно лишь для того, чтобы показать степень величины, а сантиметры очень удобны для расчетов сечений строительных конструкций. Помни, согласно СИ основная единица измерения расстояния — метр!
“В предыдущих сериях” мы уже говорили о напряжениях — отношении внутреннего усилия (равного приложенной внешней силе направленной вдоль стержня, т.е. по оси x) к площади поперечного сечения стержня. А всё потому, что толстый стальной прут при прочих равных рвётся при большей нагрузке, чем тонкий, и отношение этих нагрузок — это отношение площадей.
Ответ на ключевой вопрос: “Когда же разрушится эта конструкция / деталь” может быть получен экспериментально, путем разрушения образцов из одного материала, но с разной площадью поперечного сечения. И если мы продольную силу разрыва разделим на площадь сечения образца, то найдем так называемое разрушающее напряжение.
Так что напряжение – единичная внутренняя сила, действующая в каждой точке деформированного тела. Подробнее про это можно прочитать в заметке посвященной деформациям в стержне при растяжении..
Тут встаёт вопрос о том, насколько материал “равномерный” (точнее использовать термин “изотропный”), ведь в древесине бывают сучки, в бетоне — участки с щебнем разной прочности. Даже в стали есть дефекты кристаллической решётки, которые снижают её прочность. Пока раскрывать его не буду, но упомянуть считаю нужным. Разрушение зданий, самолётов, ракет и других творений рук человеческих всегда начинается с самого слабого и нагруженного места.
Именно используя площадь мы определяем напряжения от центральных сжимающих / растягивающих нагрузок.
Когда мы говорим о площади некой области, ограниченной произвольной кривой, мы подразумеваем интеграл:
Кратко про интегрирование. Для чайников. Искушенному в мат. анализе читателю стоит пропустить до конца курсива.
Тут я говорю про вычисление определенного интеграла. Окинув взглядом странное сечение, которое нам попалось, мы в первую очередь пытаемся описать его какими-то функциями. Далее мы идём искать таблицу первообразных в поисковик, в которой стараемся найти нашу функцию — часть после знака интеграла и перед dx. Например первообразной линейной функции y=x-8 будет парабола y’=(x^2)/2-8x+C
Если эта часть была f(x), то её первообразная (производная наоборот, которая нужна нам для вычисления интеграла) будет F(x).
Тогда значение находится по этой формуле:
Кроме того: константы (числа) из под интеграла выносятся, а определенный интеграл от a до с можно рассчитать, как сумму двух определенных интегралов от a до b и от b до с
Пример:
Найдём площадь показанного выше сечения в границах x ∈ [-2;8]:
Первая часть(закрашена зелёным):
Вторая часть (оранжевый):
Третья часть (синий):
Общая площадь (минусы тут учитывать не будем, т.к. нас интересует площадь фигуры, а не её положение относительно осей):
Когда мы говорим о площади сложного сечения, состоящего из нескольких простых, мы подразумеваем их сумму:
Вот здесь мы и делим нашу сложную фигуру на несколько менее сложных и определяем их площадь по одному интегралу за раз. После этого складываем полученные площади.
Это важно, потому что очень часто на практике конструкции собирают из типовых элементов.
Вспоминая старый анекдот, если конструкция собрана из нескольких красных резиновых мячей — инженер достает таблицу характеристик красных резиновых мячей по ГОСТ на красные резиновые мячи и находит нужное значение.
На рисунке 3 приведены сечения из уголков, тавров (от буквы Т) и двутавров (в английском название понятнее — I beam) — одних из наиболее распространенных типов сечений (хотя есть еще труба и прямоугольный профиль).
На этом разговор о площади сечения, пожалуй, можно заканчивать.
Подводя итог — площадь это наиболее простая в вычислении и наиболее распространённая в расчётах характеристика сечения. Хотя с позиции математики вычисление площади в общем смысле предполагает интегрирование, на практике для поперечных сечений типовых строительных конструкций ее, с небольшой погрешностью, может найти любой школьник, используя простейшие формулы. При этом почти всегда присутствует и второй вариант — посмотреть в многочисленных сортаментах и таблицах.
На очереди чуть более длинные статьи, проливающие свет на суть, вычисление и использование таких занимательных штук, как статические моменты, моменты и радиусы инерции, моменты сопротивления. А понимание всего этого арсенала понятий обозначающихся умными терминами позволит нам расщеплять недругов на атомы определять нормальные и касательные напряжения для любых состояний рассматриваемого тела, вплоть до случаев сложного кручения в нескольких плоскостях.
Не переключайтесь!
Автор: Марк Ершов
Редактор, факт-чекер: Кирилл Овчинников
Список использованных источников
- Алгебра и начала математического анализа. 11 класс В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / [А. Г. Мордкович, Денищева Л.О., Звавич Л.И. и др. под ред. А. Г. Мордковича. — 3-е изд., стер. — М., 2009. — 264 с. : ил.
4 369
Площадь поперечного сечения
При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:
S = πR2
При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.
Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:
a2 + b2 = c2
Из нее можно вывести такую формулу:
c = S*q*r*t*(a2 + b2)
Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:
S= c*h
S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:
S=a*b
используется в тех случаях, когда сечение идет параллельно двум основаниям.
При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:
S =2R*h
где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.
Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:
S =2а*h
где 2а – значение хорды, расчета площади поперечного сечения.

Поперечным сечением называется фигура, образованная пересечением продолговатого тела с воображаемой плоскостью, расположенных перпендикулярно друг другу, т.е. когда тело рассекается строго поперек его длины.
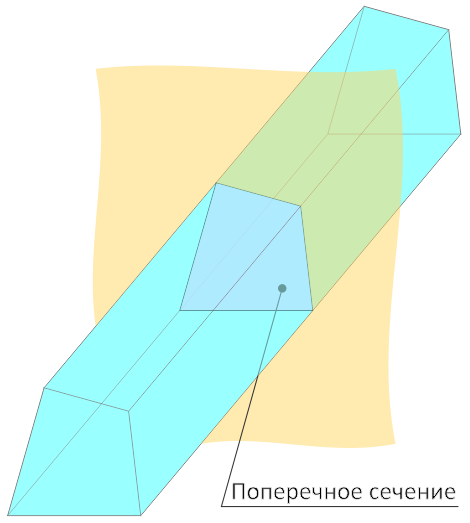
Сечение может иметь простую или сложную форму, а также быть составным.
Площадь и размеры (длина и ширина) поперечного сечения равны соответствующим размерам этой фигуры.
Площадь поперечного сечения
В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.
Формулы для расчета площади основных фигур.
Пример:
Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением.

Для расчета общей площади, сложное сечение раскладывается на простые фигуры:
Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто.

В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:
A=A1+A2+A3-A4
Площадь поперечного сечения обозначается латинскими буквами S или A, и измеряется в квадратных единицах длины, например: м2, см2 или мм2.
Площадь составного сечения
Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым.

Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.
Эти сечения сами по себе тоже являются сложными.
Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.
В результате сложив все составляющие профили, получим площадь всего сечения.
Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.
Длина поперечного сечения
Длиной поперечного сечения называют полную (габаритную) длину фигуры как расстояние по горизонтали между двумя её наиболее удаленными точками.
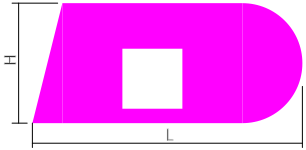
Длина поперечного сечения обозначается латинской буквой L или l и измеряется стандартно в миллиметрах или сантиметрах.
Ширина сечения определяется аналогично, но обозначается буквой H или h.
При решении задач, длину, ширину и площади поперечного сечения рекомендуется переводить соответственно в метры и м2.
Понятие «поперечное сечение» является одним из основных при расчетах на прочность в сопротивлении материалов и технической механике.
Различают два основных вида расчета площади сечений:
- Геометрический — когда требуется найти площадь сечения тела по известным размерам;
- Прочностной — расчет площади поперечного сечения бруса проводится по условию прочности.
Пример расчета поперечных сечений >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
На этой странице представлена справочная информация с формулами для вычисления площадей простых фигур (сечений) с указанием положения их центров тяжестей.
Эта страничка будет полезна при расчёте более сложных фигур (составных поперечных сечений): определении положения центра тяжести, а также общей площади.
Центры тяжести
Для всех фигур, положение центра тяжести в статье обозначается буквой – C, это наиболее используемый вариант. Также иногда центр тяжести обозначают буквой – O.
Формулы для расчёта площадей
В сопромате площадь поперечного сечения обозначается буквой – A, однако, в некоторой литературе ты можешь встретить обозначения с буквой – F.
Другую справочную информацию, размещённую на сайте – ssopromat.ru, можешь найти, перейдя по указанной ссылке.
Поскольку
площади поперечных сечений стержня на
разных его участках различны, найдем
минимально необходимое значение
из условия прочности каждого из участков.
1. На первом
участке
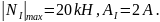
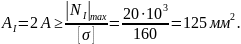
Отсюда получим
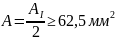
.
2. На втором участке
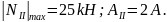
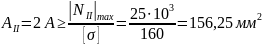
.
Отсюда следует,
что
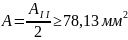
.
3. На
третьем участке
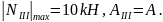
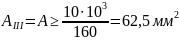
.
Из полученных
значений A
выбираем наибольшее, т.е. принимаем
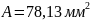
.
В итоге получим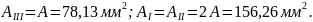
4. Построение эпюры нормальных напряжений
Построим эпюру
нормальных напряжений (т.е. график
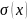
),
которая позволит проверить правильность
подбора площадей поперечных сечений
стержня.
Нормальные
напряжения в сечении стержня определяем
по формуле (2.1).
Используя эту
формулу, установим закономерности
изменения напряжений на каждом из
участков
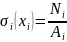
, (где i
номер участка).
I
участок
:

II
участок

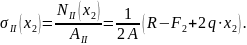
Отсюда следует:
при
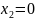

при

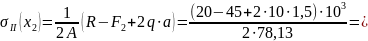

.
III
участок

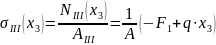
.
Отсюда получим:
при


при


.
По полученным
данным строим эпюру
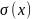
(см. рис. 6, в), порядок построения которой
аналогичен построению эпюры нормальных
сил N(x).
Анализ построенной
эпюры нормальных напряжений показывает,
что лишь в одном, наиболее нагруженном
сечении стержня напряжения достигают
допускаемой величины, а в других
поперечных сечениях напряжения меньше
допускаемых. Это свидетельствует о
правильности подбора площадей поперечных
сечений стержня.
5. Проверка выполнения условия жесткости
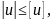
где
– осевое перемещение крайнего правого
сечения стержня.
Согласно (2.10)

.
Используя формулы
(2.8) или (2.9), определим абсолютные
удлинения (укорочения) участков стержня.
I
участок:

Поскольку

,
то используя формулу (2.9) получим
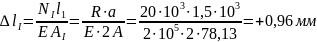
.
II
участок:
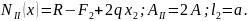
Согласно (2.8) находим
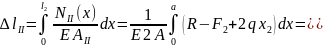

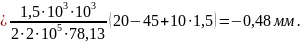
III
участок:
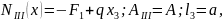
тогда
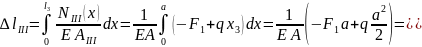
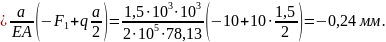
Перемещение
крайнего правого сечения стержня:

Проверяем выполнение
условия жесткости:

Требуемая
жесткость стержня обеспечена. Поэтому
в качестве окончательного принимаем
значение площади A,
установленное из условия прочности.
Примечание.
Если же условие жесткости не выполняется
и
превышает
более чем на 5 %, то значение площади A
определяют из условия жесткости. Для
этого записывают
в аналитическом виде и приравнивая к
,
находят необходимое значение площади
A.
Это значение будет больше того, что было
получено из условия прочности, и его
принимают в качестве окончательного.
2.6.2. Пример решения задачи №2.
Расчёт статически
неопределимой стержневой системы
Абсолютно жесткий
брус (рис. 7), нагруженный сосредоточенной
силой

,
опирается на шарнирно-неподвижную опору
и поддерживается стальными
шарнирно-закрепленными стержнями
круглого поперечного сечения.
Требуется:
Площади поперечных
сечений стержней
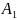
и
взять из расчета по допускаемым
напряжениям.
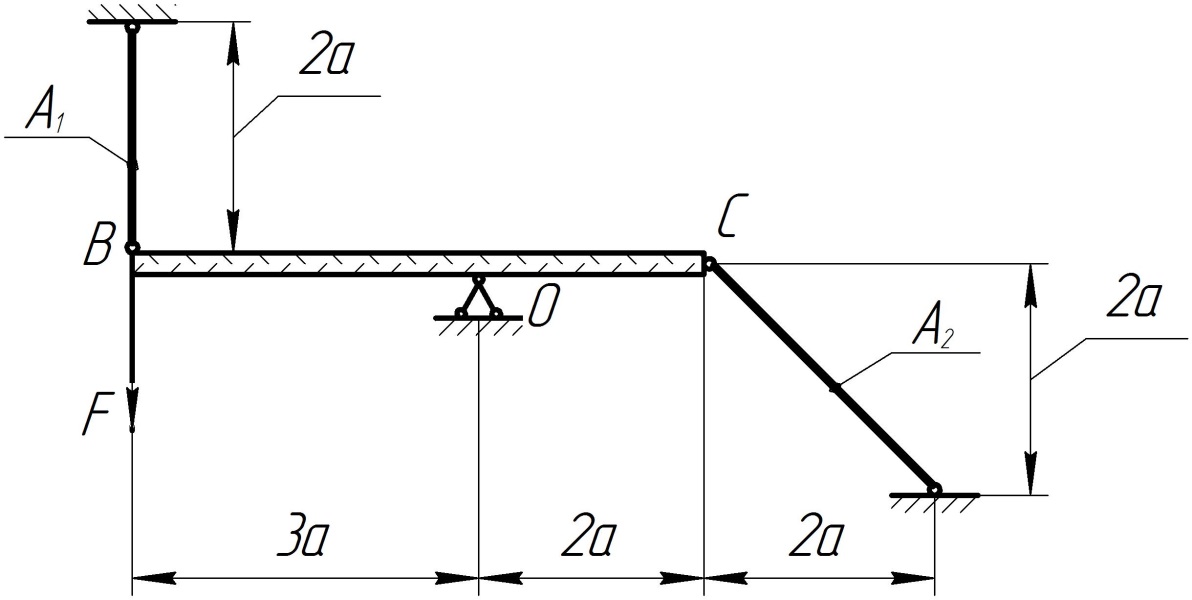
Рис. 7.
Статически неопределимая стержневая
система
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
