Полное сопротивление цепи переменного тока
В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.
Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току – Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.

Рисунок 1. Классификация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.
Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.

Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) – схема цепи; б) – сдвиг фаз тока и напряжения; в) – треугольник напряжений; д) – треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.

По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z2) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.
 (1)
(1)
Извлекая квадратный корень из обеих частей этого равенства, получим,
 (2)
(2)
Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.

Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) – схема цепи; б) – треугольник сопротивлений.
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного случая:
 (3)
(3)
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.

Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) – схема цепи; б) – треугольник сопротивлений.
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.
 (4)
(4)
Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.
 (5)
(5)
Или
 (6)
(6)
Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.

Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) – параллельное соединение R и L; б) – параллельное соединение R и C.
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
 (7)
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
 (8)
(8)
откуда:
 (9)
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
 (10)
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).

Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:
 (11)
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
 (12)
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
 (13)
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
 (14)
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Загрузить PDF
Загрузить PDF
Полное сопротивление, или импеданс, характеризует сопротивление цепи переменному электрическому току. Данная величина измеряется в омах. Для вычисления полного сопротивления цепи необходимо знать значения всех активных сопротивлений (резисторов) и импеданс всех катушек индуктивности и конденсаторов, входящих в данную цепь, причем их величины меняются в зависимости от того, как меняется проходящий через цепь ток. Импеданс можно рассчитать при помощи простой формулы.
Формулы
- Полное сопротивление Z = R или XLили XC (если присутствует что-то одно)
- Полное сопротивление (последовательное соединение) Z = √(R2 + X2) (если присутствуют R и один тип X)
- Полное сопротивление (последовательное соединение) Z = √(R2 + (|XL – XC|)2) (если присутствуют R, XL, XC)
- Полное сопротивление (любое соединение) = R + jX (j — мнимое число √(-1))
- Сопротивление R = I / ΔV
- Индуктивное сопротивление XL = 2πƒL = ωL
- Емкостное сопротивление XC = 1 / 2πƒL = 1 / ωL
-

1
Импеданс обозначается символом Z и измеряется в омах (Ом). Вы можете измерить импеданс электрической цепи или отдельного элемента. Импеданс характеризует сопротивление цепи переменному электрическому току. Есть два типа сопротивления, которые вносят вклад в импеданс:[1]
- Активное сопротивление (R) зависит от материала и формы элемента. Наибольшим активным сопротивлением обладают резисторы, но и другие элементы цепи обладают небольшим активным сопротивлением.
- Реактивное сопротивление (X) зависит от величины электромагнитного поля. Наибольшим реактивным сопротивлением обладают катушки индуктивности и конденсаторы.
-

2
Сопротивление — это фундаментальная физическая величина, описываемая законом Ома: ΔV = I * R.[2]
Эта формула позволит вам вычислить любую из трех величин, если вы знаете две другие. Например, чтобы вычислить сопротивление, перепишите формулу так: R = I / ΔV. Вы также можете измерить сопротивление при помощи мультиметра.- ΔV — это напряжение (разность потенциалов), измеряемое в вольтах (В).
- I — сила тока, измеряемая в амперах (А).
- R — это сопротивление, измеряемое в омах (Ом).
-

3
Реактивное сопротивление имеет место только в цепях переменного тока. Как и активное сопротивление, реактивное сопротивление измеряется в омах (Ом). Есть два типа реактивного сопротивления:
- Индуктивным сопротивлением XC обладают катушки индуктивности, создающие магнитное поле, которое препятствует изменению направления тока в цепи.[3]
Чем быстрее меняется направление тока, тем больше индуктивное сопротивление. - Емкостным сопротивлением XC обладают конденсаторы, которые накапливают электрический заряд. При изменении направления тока в цепи конденсатор неоднократно обнуляет и накапливает электрический заряд. Чем дольше конденсатор заряжается, тем больше емкостное сопротивление.[4]
Поэтому чем быстрее меняется направление тока, тем меньше емкостное сопротивление.
- Индуктивным сопротивлением XC обладают катушки индуктивности, создающие магнитное поле, которое препятствует изменению направления тока в цепи.[3]
-

4
Вычислите индуктивное сопротивление. Это сопротивление прямо пропорционально быстроте изменения направления тока, то есть частоты тока. Эта частота обозначается символом ƒ и измеряется в герцах (Гц). Формула для расчета индуктивного сопротивления: XL = 2πƒL, где L — индуктивность, измеряемая в генри (Гн).[5]
- Индуктивность L зависит от количества витков в катушке индуктивности.[6]
Также вы можете измерить индуктивность. - Если вы знакомы с единичной окружностью, то представьте, что один цикл переменного тока равен одному полному вращению этой окружности (на 2π радиан). Если умножить это значение на ƒ, которая измеряется в герцах (единиц в секунду), вы получите результат, измеряемый в радианах в секунду. Это единица измерения угловой скорости, которая обозначается через ω. Вы можете переписать формулу для вычисления индуктивного сопротивления так: XL=ωL[7]
- Индуктивность L зависит от количества витков в катушке индуктивности.[6]
-

5
Вычислите емкостное сопротивление. Это сопротивление обратно пропорционально быстроте изменения направления тока, то есть частоты тока. Формула для вычисления емкостного сопротивления: XC = 1 / 2πƒC.[8]
С — это емкость конденсатора, измеряемая в фарадах (Ф).- Вы можете измерить электрическую емкость.
- Эту формулу можно переписать так: XC = 1 / ωL (объяснения см. выше).
Реклама
-

1
Если цепь состоит исключительно из резисторов, то импеданс вычисляется следующим образом. Сначала измерьте сопротивление каждого резистора или посмотрите значения сопротивления на схеме цепи.[9]
- Если резисторы соединены последовательно, то полное сопротивление R = R1 + R2 + R3…
- Если резисторы соединены параллельно, то полное сопротивление R = 1 / R1 + 1 / R2 + 1 / R3 …
-

2
Сложите одинаковые реактивные сопротивления. Если в цепи присутствуют исключительно катушки индуктивности или исключительно конденсаторы, то полное сопротивление равно сумме реактивных сопротивлений. Вычислите его следующим образом:[10]
- Последовательное соединение катушек: Xtotal = XL1 + XL2 + …
- Последовательное соединение конденсаторов: Ctotal = XC1 + XC2 + …
- Параллельное соединение катушек: Xtotal = 1 / (1/XL1 + 1/XL2 …)
- Параллельное соединение конденсаторов: Ctotal = 1 / (1/XC1 + 1/XC2 …)
-

3
Вычтите индуктивные и емкостные сопротивления, чтобы получить общее реактивное сопротивление. Так как при возрастании одного типа сопротивления другое уменьшается, то они, как правило, компенсируют друг друга. Чтобы найти общее реактивное сопротивление, вычтите меньшее сопротивление из большего.[11]
- Или воспользуйтесь формулой: Xtotal = |XC – XL|
-

4
Вычислите импеданс по активному и реактивному сопротивлениям в последовательной цепи. Нельзя просто сложить эти величины, так как они меняются с течением времени, но достигают максимальных значений в разное время.[12]
Поэтому воспользуйтесь формулой:Z = √(R2 + X2).[13]
- Вычисления по этой формуле включают в себя использование векторов, но вы можете воспользоваться теоремой Пифагора, представив R и X в качестве катетов прямоугольного треугольника, а сопротивление Z — как гипотенузу.[14]
[15]
- Вычисления по этой формуле включают в себя использование векторов, но вы можете воспользоваться теоремой Пифагора, представив R и X в качестве катетов прямоугольного треугольника, а сопротивление Z — как гипотенузу.[14]
-

5
Вычислите импеданс по активному и реактивному сопротивлениям в параллельной цепи. В этом случае используются комплексные числа (это единственный способ вычислить полное сопротивление в параллельной цепи, в которой есть как активное, так и реактивное сопротивление).
- Z = R + jX, где j — мнимая единица: √(-1). Используйте j вместо i, чтобы не перепутать мнимую единицу (j) с силой тока (I).
- Складывать эти числа нельзя. Например, полное сопротивление может быть представлено так: 60 Ом + j120 Ом.
- Если у вас есть две последовательные цепи, то вы можете отдельно сложить натуральные числа и отдельно — комплексные. Например, если Z1 = 60 Ом + j120 Ом, а к этой цепи последовательно подключен резистор с Z2 = 20Ω, то Ztotal = 80Ω + j120Ω.
Реклама
Советы
- Общее сопротивление (активное и реактивное сопротивления) также может быть выражено через мнимое число.
Реклама
Об этой статье
Эту страницу просматривали 168 783 раза.
Была ли эта статья полезной?
Обычно
цепь переменного тока включает в себя
и активное сопротивление, и емкость, и
индуктивность.
Полное
сопротивление (Z)
– это векторная сумма всех сопротивлений:
активного, емкостного и индуктивного.
![]() –
–
полное сопротивление цепи.
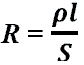 –
–
активное сопротивление.
![]() –
–
индуктивное сопротивление.
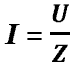 –
–
полное сопротивление определяет силу
тока в цепи по закону Ома.
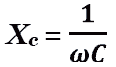 –
–
емкостное сопротивление.
I – действующее
значение силы тока (един.измер. А)
U
– действующее
значение напряжения(един.измер. В)
XL
– индуктивное
сопротивление(един.измер. Ом)
ω – циклическая
частота переменного тока(един.измер.
рад/с)
L – индуктивность(ед.из.
Гн)
C – емкость (ед.из.
Ф)
XC
– индуктивное
сопротивление (ед.из. Ом)
Z – полное сопротивление
(Ом)
R – активное
сопротивление (Ом)
ρ – удельное
сопротивление проводника (Ом/м)
l
– длина проводника (м)
S
– площадь сечения проводника (м2
47.Импеданс тканей. Физические основы реографии.
Импеданс –
основные понятия.
При прохождении
через ткани переменного тока, изменяющегося
по гармоническому закону
I(t)
=I0 cos
ωt,
падение напряжения
на биологической ткани изменяется по
закону
U
(t)=Uo⋅cos
(ωt+ϕ).
Величиной,
определяющей соотношение между
напряжением и силой переменного тока,
является импеданс
– полное электрическое сопротивление
цепи переменному току.
На опыте напряжение
отстает по фазе от тока (ϕ<0), что
характерно для электрических цепей,
состоящих из резисторов и конденсаторов.
Для биологического
объекта импеданс носит составной
(комплексный) характер Z=(R,X). Его активная
составляющая R связана, в первую очередь,
с проводимостью внутренних жидких сред,
являющихся электролитами. Различные
процессы в тканях, сопровождающиеся
необратимыми потерями энергии, также
дают вклад в величину активной составляющей
импеданса. Реактивная компонента X
определяется емкостными свойствами
исследуемой ткани, в частности, емкостью
биологических мембран. Кроме того, в
емкостную составляющую импеданса дает
вклад и область контакта стимулирующих
электродов с биологическими тканями.
Абсолютная
величина (модуль) электрического
импеданса определяется выражением
.22XRZ+=
На
опыте величина импеданса может быть
определена по измерениям амплитудных
(или эффективных) значений напряжения
Uo и
силы тока Io
⏐Z⏐
= Uo/Io
(или ⏐Z⏐ =
Uэфф/Iэфф).
Фазовый сдвиг ϕ
определяет отношение реактивной и
активной составляющих импеданса
tg ϕ = X/R.
Значения угла
сдвига фаз, полученные при частоте 1 кГц
для различных биологических объектов,
приведены в таблице 1.
Таблица 1. Угол
сдвига фаз (в градусах) для различных
видов тканей.
|
Объект |
ϕ |
|
Кожа человека, Нерв лягушки Мышцы |
-55 -64 -65 |
Составную
(комплексную) величину Z принято изображать
в виде векторной диаграммы, на которой
ось абсцисс – величина активного
сопротивления, ось ординат – величина
реактивного сопротивления.
Абсолютная
величина импеданса ⏐Z⏐ и фазовый сдвиг
ϕ являются функциями частоты переменного
тока. Зависимость электрического
импеданса от частоты носит название
дисперсии
импеданса.
Физические основы
реологии.
Величина импеданса
тканей зависит от их физиологического
состояния, в частности от их кровоснабжения.
При кровенаполнении сосудов происходит
изменение величины импеданса в такт с
работой сердца. По величине изменений
импеданса можно судить о состоянии
сердечно-сосудистой системы.
Реология
– диагностический
метод, основанный на регистрации
изменения величины импеданса тканей в
процессе сердечной деятельности.
Величина
импеданса тканей |Z| состоит из двух
составляющих |Z| = |Zo|
+ |z(t)|: постоянной – |Zo|
и изменяющейся во времени в соответствии
с работой сердца – |z(t)|.
На
практике, на исследуемый участок тела
накладывают электроды площадью несколько
см2 и
пропускают переменный ток частотой ≈
30 − 40 кГц. Выбор частоты определяется
несколькими факторами: электробезопасностью,
исключением влияния электродов и емкости
их контакта с кожей, уменьшением
зависимости величины импеданса от
механических воздействий на исследуемую
ткань. Наполнение сосудов кровью изменяет
расстояния между отдельными участками
ткани, что должно приводить к изменению
ёмкостного сопротивления. Но вклад
макроскопических объемов тканей в
реактивную составляющую импеданса
существенен только в области α- дисперсии.
Следовательно, изменения импеданса во
времени обусловлены влиянием притока
и оттока крови на активную составляющую
полного сопротивления.
При
прохождении через ткани электрического
тока I = Io⋅cos
ωt величина напряжения будет изменяться
по закону
U
= Uο cos
(ωt + ϕ) = Io⋅(
⏐Zo⏐
+ ⏐z(t)⏐ )⋅cos
(ωt +ϕ ).
Электрическими
методами выделяют из регистрируемого
сигнала составляющую, пропорциональную
|z(t)|, содержащую информацию о состоянии
кровоснабжения изучаемого участка
тканей − реограмму.
Для парных
анатомических образований проводят
запись реограммы на правой и левой
стороне тела.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Электрическая цепь.
Источник электрического тока, соединенный проводами с различными электроприборами и потребителями электрической энергии, образует электрическую цепь.
Электрическую цепь принято изображать с помощью схем, в которых элементы электрической цепи (сопротивления, источники тока, включатели, лампы, приборы и т. д.) обозначены специальными значками.
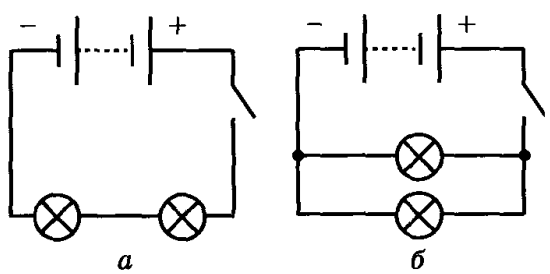
Направление тока в цепи — это направление от положительного полюса источника тока к отрицательному. Это правило было установлено в XIX в. и с тех пор соблюдается. Перемещение реальных зарядов может не совпадать с условным направлением тока. Так, в металлах носителями тока являются отрицательно заряженные электроны, и движутся они от отрицательного полюса к положительному, т. е. в обратном направлении. В электролитах реальное перемещение зарядов может совпадать или быть противоположным направлению тока, в зависимости от того, какие ионы являются носителями заряда — положительные или отрицательные.
Включение элементов в электрическую цепь может быть последовательным или параллельным.
Что такое сопротивление
Ток, протекая через провода и различные радиодетали, тратит свою энергию. Это явление количественно выражается величиной сопротивления. В электротехнике его разделяют на активное и реактивное сопротивление. В первом случае при прохождении тока часть его энергии превращается в тепловой вид, а иногда и в другие (например, проявляется в химических реакциях). Величина активного сопротивления зависит от частоты переменного электротока и возрастает с ее увеличением.
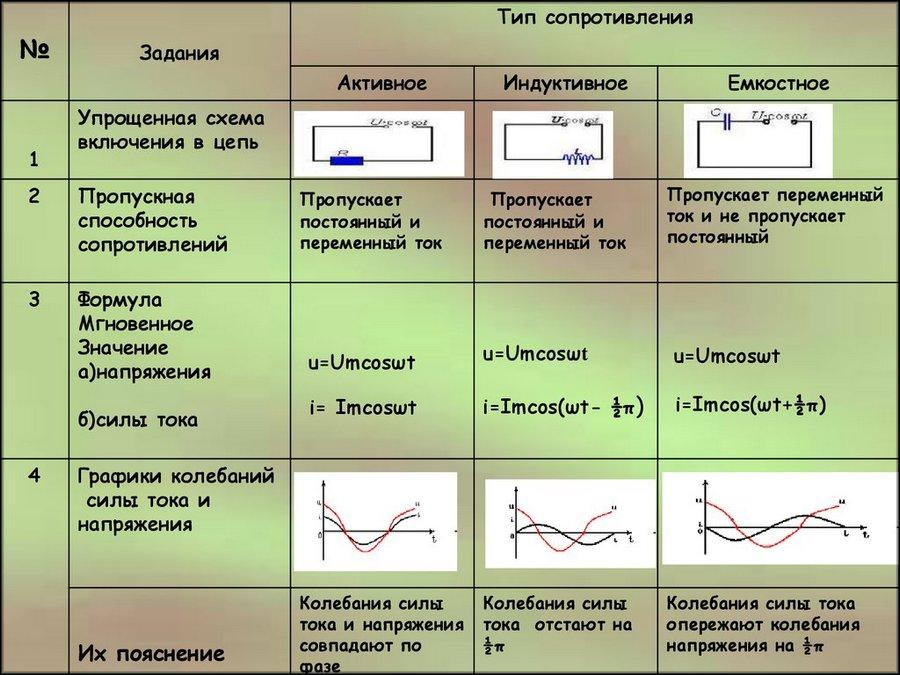
Второй тип сопротивления имеет более сложную природу и возникает в момент включения или выключения потребителя электроэнергии в сеть переменного или постоянного тока. В цепи с реактивным сопротивлением энергия электрического тока частично превращается в другую форму, а затем переходит обратно, то есть, наблюдается периодический колебательный процесс. Полное сопротивление цепи включает в себя активный и реактивный типы, которые учитываются по особым правилам.
Виды сопротивления
В электротехнике рассматривается активное электрическое сопротивление, а также две разновидности реактивного: индуктивное и ёмкостное.

Активное сопротивление
Можно представить себе электрическую цепь, в которой к клеммам батарейки через провод последовательно присоединены резистор и электрическая лампочка. Если замкнуть провода, лампочка загорится. Можно использовать вольтметр или мультиметр в соответствующем режиме работы, с помощью которых измеряется разность потенциалов между двумя точками цепи.
Измерив напряжение между клеммами и сравнив его с тем, которое имеется на проводах подсоединённых к лампочке, можно увидеть, что последнее меньше. Это связано с падением напряжения на впаянной в цепь радиодетали. Последняя оказывает противодействие электрическому току, затрудняя его прохождение.
Активным сопротивлением обладает каждая деталь, через которую проходит ток. У металлических проводов оно очень маленькое. Чтобы узнать величину сопротивления радиодетали, нужно изучить обозначение на ее корпусе. Если из рассматриваемой электроцепи убрать резистор, то сила тока, проходящего через лампочку, увеличится.
Формула для расчета активного сопротивления соответствует закону Ома:
R = U / I, где
- R — величина активного сопротивления между двумя точками в цепи;
- U — напряжение или разность потенциалов между ними;
- I — сила тока на рассматриваемом участке цепи.
Для расчета активного сопротивления проводника формула будет другая:
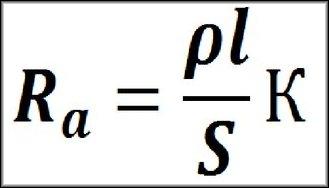
где K-коэффициент поверхностного эффекта, который равен 1,
- l — длина проводника,
- s — площадь поперечного сечения,
- p — “ро” удельное сопротивление.
Сопротивление принято измерять в Омах. Оно существенно зависит от формы и размеров объекта, через который протекает ток: сечения, длины, материала, а также от температуры. Действие активного сопротивления уменьшает энергию электрического тока, превращая её в другие формы (преимущественно в тепловую).

Реактивное сопротивление
Этот вид возникает тогда, когда переменный ток проходит сквозь элемент, который обладает индуктивностью или емкостью. Основной особенностью реактивного сопротивления является преобразование электрической энергии в другую форму в прямом и обратном направлениях. Часто это происходит циклически. Реактивное сопротивление проявляется только при изменениях силы тока и напряжения. Существует два его вида: индуктивное и емкостное.
Индуктивное сопротивление
При увеличении силы тока порождается магнитное поле, обладающее различными характеристиками. Наиболее важной из них является индуктивность. Магнитное поле, в свою очередь, воздействует на проводник, по которому протекает ток. Влияние является противоположным направлению изменения тока. То есть, если сила тока увеличилась, то магнитное поле будет уменьшать его, и наоборот, если снизилась, то поле усилит его. Когда ток не меняется, реактивное сопротивление катушки индуктивности будет равно нулю.
Индуктивное сопротивление зависит от частоты тока. Чем она выше, тем выше скорость изменения данного параметра. Это значит, что будет образовано более сильное магнитное поле. Возникающая при этом ЭДС препятствует изменению электрического тока.

Расчет реактивного индуктивного сопротивления осуществляется по такой формуле:
XL = L×w = L×2π×f, где буквами обозначаются:
- L — индуктивность магнитного поля, которое порождается изменением силы тока;
- W — круговая частота изменения, которая используется в описании синусоидального изменения силы тока;
- Π — число «пи»;
- f — частота тока в обычном смысле.
При синусоидальном изменении напряжения сила тока будет меняться, отставая от него по фазе. Поэтому реактивное сопротивление трансформатора существенно зависит от его индуктивности.

Емкостное сопротивление
Оно имеет иную природу, чем индуктивное. Это понятие удобно проиллюстрировать на примере электрической цепи, состоящей из источника питания, клеммы которого соединены с обкладками конденсатора. Сразу после подключения на них будет постепенно накапливаться заряд, создавая ток в цепи.
После достижения предельной величины, которая определяется ёмкостью детали, ток не будет проходить по цепи. Если после этого отключить провода от клемм, а затем последние соединить, то между ними начнётся перемещение зарядов до тех пор, пока разность потенциалов станет равной нулю.
Если к конденсатору подключить источник переменного тока, то будет происходить следующее. С увеличением разности потенциалов заряд на обкладках конденсатора будет расти. Когда напряжение перейдёт в фазу уменьшения, накопленный заряд начнёт стекать с них, образуя ток противоположного направления. Затем разность потенциалов станет отрицательной, но по абсолютной величине будет расти до максимального значения. При этом конденсатор начнет вновь заряжаться, но при этом знак поступающих зарядов будет не такой, который был раньше.

Когда напряжение начнёт увеличиваться (уменьшаясь по абсолютной величине), заряд с обкладок конденсатора будет стекать. Когда разность потенциалов у источника достигнет нуля и продолжит увеличиваться, начнётся новый цикл изменений.
На каждом этапе описанной ситуации ток с обкладок конденсатора будет иметь направление противоположное тому, которое порождается переменной разностью потенциалов источника питания.
Происходящее таким образом уменьшение силы тока представляет собой физический смысл ёмкостного сопротивления. Оно обозначается буквами ХС и рассчитывается по формуле:
XС = 1/(w×C) = 1/(2π×f×C), где
- C — ёмкость используемого конденсатора;
- w — круговая частота переменного тока;
- π — число «пи»;
- f — частота переменного тока.
В рассматриваемом случае изменения тока отстают от напряжения.
Полное сопротивление
При использовании нескольких разновидностей важно знать, как они сочетаются между собой. Активное сопротивление присутствует в любых схемах. Оно способствует превращению части электрической энергии в нагрев. Реактивное сопротивление возникает лишь в цепи переменного тока. Чтобы определить его величину, необходимо из индуктивного вычесть ёмкостное. Эта характеристика показывает энергию, которая пульсирует в цепи, переходя из одной формы в другую.

Полное сопротивление представляет собой сумму активного и реактивного сопротивления в цепи переменного тока, но такое сложение необходимо выполнять особым образом. Для этого нужно начертить прямоугольный треугольник, катеты в котором должны иметь длину, равную величине активного и реактивного сопротивлений соответственно.
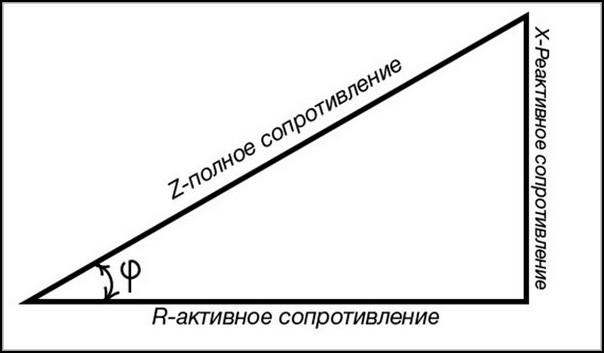
Длина гипотенузы будет численно выражать полное сопротивление электрической цепи. Для его определения используется правило, говорящее о том, что сумма квадратов катетов равна квадрату гипотенузы. Это правило называют теоремой Пифагора. Следовательно, формула, с помощью которой можно найти полное сопротивление, выглядит так:
Z = √(R^2+〖(XL-XC)〗^2 ), где
- Z — полное сопротивление;
- R — величина активной составляющей;
- XL и XC — значение индуктивного и емкостного параметра соответственно.
Следовательно, при расчёте полного сопротивления или импеданса нужно учитывать, что такое ёмкость и индуктивность и как они могут проявляться в электрических схемах. Эти величины называются еще паразитными, так как они могут отрицательно влиять на работу электроприбора. Их возникновение относят к непредсказуемым факторам. При этом емкостным или индуктивным сопротивлением, имеющим небольшое значение, при выполнении расчетов можно пренебречь.

Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
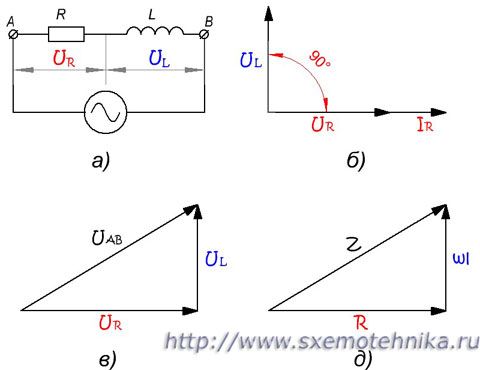
Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) – схема цепи; б) – сдвиг фаз тока и напряжения; в) – треугольник напряжений; д) – треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.

По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z2) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.

(1)
Извлекая квадратный корень из обеих частей этого равенства, получим,

(2)
Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.
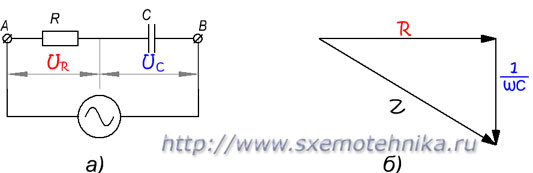
Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) – схема цепи; б) – треугольник сопротивлений.
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного случая:

(3)
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.
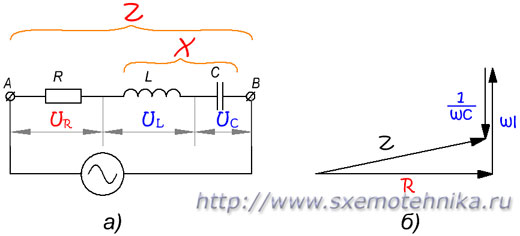
Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) – схема цепи; б) – треугольник сопротивлений.
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.
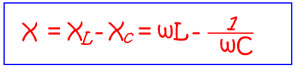
(4)
Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.

(5)
Или

(6)
Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
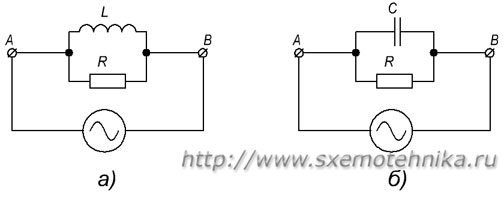
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) – параллельное соединение R и L; б) – параллельное соединение R и C.
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.

(7)
Приводя к общему знаменателю подкоренное выражение, получим:

(8)
откуда:

(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С будет равно:
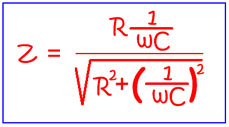
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
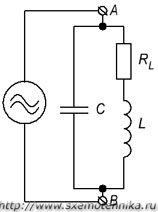
Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:

(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:

(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
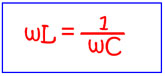
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:

(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
Закон Ома для полной цепи.
Рассмотрим электрическую цепь, состоящую из источника тока и резистора R.
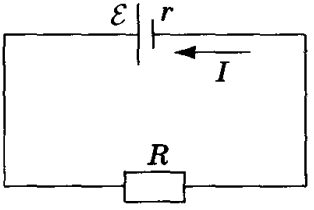
Закон Ома для полной цепи устанавливает связь между силой тока в цепи, ЭДС и полным сопротивлением цепи, состоящим из внешнего сопротивления R и внутреннего сопротивления источника тока r.
Работа сторонних сил Aст источника тока, согласно определению ЭДС (ɛ) равна Aст = ɛq, где q — заряд, перемещенный ЭДС. Согласно определению тока q = It, где t — время, в течение которого переносился заряд. Отсюда имеем:
Aст =ɛIt.
Тепло, выделяемое при совершении работы в цепи, согласно закону Джоуля — Ленца, равно:
Q = I2Rt + I2rt.
Согласно закону сохранения энергии А = Q. Приравнивая (Aст =ɛIt) и (Q = I2Rt + I2rt), получим:
ɛ = IR + Ir.
Закон Ома для замкнутой цепи обычно записывается в виде:

.
Сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Если цепь содержит несколько последовательно соединенных источников с ЭДС ɛ1, ɛ2, ɛ3 и т. д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных источников. Знак ЭДС источника определяется по отношению к направлению обхода контура, который выбирается произвольно, например, на рисунке ниже — против часовой стрелки.
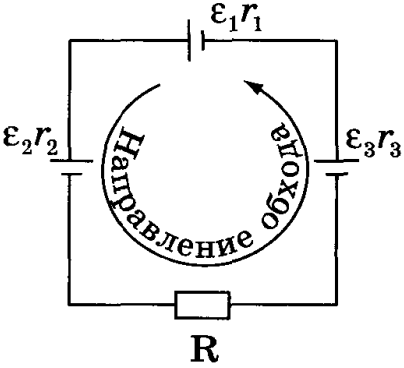
Сторонние силы внутри источника совершают при этом положительную работу. И наоборот, для цепи справедливо следующее уравнение:
ɛ = ɛ1 + ɛ2 + ɛ3 = | ɛ1| – | ɛ2| -| ɛ3| .
В соответствии с 
сила тока положительна при положительной ЭДС — направление тока во внешней цепи совпадает с направлением обхода контура. Полное сопротивление цепи с несколькими источниками равно сумме внешнего и внутренних сопротивлений всех источников ЭДС, например, для рисунка выше:
Rn = R + r1 + r2 + r3.
Как измерить полное электрическое сопротивление
Соединим все детали вместе в простую электрическую цепь. Взглянем на рисунок ниже: это цепь с источником питания постоянного тока. Ток течет через резистор. Весьма просто, верно? Чем больше сопротивление резистора в цепи, тем меньше будет ток.
Простая цепь постоянного тока с резистором
на 100 Ом для ограничения силы тока
Что произойдет, если мы добавим в электрическую цепь источник питания переменного тока, катушку индуктивности и конденсатор? Теперь в цепи есть два дополнительных компонента, каждый из которых по своему оказывает сопротивление электрическому току. Как и резистор, они оба препятствуют прохождению электрического тока, при этом также воздействуют на ток. Если суммировать активное сопротивление резистора и активное и реактивное сопротивления конденсатора и катушки индуктивности, то получится полное электрическое сопротивление или импеданс.
В цепи переменного тока последовательно соединены резистор, катушка индуктивности и конденсатора
Постойте! Чтобы рассчитать полное электрическое сопротивления недостаточно просто сложить активные и реактивные сопротивления. Обычно в большинстве учебных пособий с этого момента начинается изобилие математических формул, поэтому дальше читайте не спеша.
Практическое применение полного электрического сопротивления
Становится понятно, в конце концов, что после всех наших объяснений разобраться, что такое полное электрическое сопротивление, несложно, не так ли? Существуют десятки бесплатных калькуляторов , которые помогут вам выполнить расчеты. Что вам на самом деле нужно – это знать, что полное сопротивление работает так же, как активное сопротивление, ограничивая ток в цепи переменного тока.
Способность таких компонентов, как конденсаторы и катушки индуктивности реагировать на постоянные изменения переменного тока, делает их уникальными. Благодаря полному сопротивлению в вашей цепи можно организовать нечто похожее на электрический щит с защитными автоматами, которые реагируют на неожиданные скачки электричества, защищая от выгорания домашнюю электропроводку. Можно также сказать спасибо полному сопротивлению за то, что вы можете носить с собой ноутбук с полностью заряженным аккумулятором, не опасаясь его взрыва.
Когда дело доходит до работы с устройствами с питанием от источника переменного тока, будь то ноутбук или электрощит в вашем доме, стоит быть благодарным полному электрическому сопротивлению. И помните, полное электрическое сопротивление – это просто старший брат привычного активного сопротивления, который объединяет активное и реактивное сопротивления в одной простой формуле.
Расчет полного электрического сопротивления конденсатора
Чтобы найти полное электрическое сопротивление конденсатора, вы можете воспользоваться следующей формулой. В ней Xc – полное электрическое сопротивление, которое необходимо найти. Оно измеряется в Омах. Переменная f – это частота сигнала, проходящего через конденсатор, а C – емкость конденсатора.
Расчёт индуктивного сопротивления катушки
Любая индуктивность, в т.ч. катушка, оказывает переменному току некоторое сопротивление. Как его рассчитать, было описано выше. Из формулы XL=2pfL видно, что сопротивление дросселя в первую очередь зависит от частоты протекающего по нему тока и его индуктивности. При этом с обоими параметрами связь прямо пропорциональная.
Частота – это характеристика внешней среды, индуктивность катушки зависит от ряда её геометрических свойств:
где:
- u0 – магнитная проницаемость вакуума – 4p*10-7 Гн/м;
- ur – относительная проницаемость сердечника;
- N – количество витков дросселя;
- S – его поперечное сечение в м2;
- l – длина катушки в метрах.
Располагая вышеописанными формулами и информацией о материале и размерах катушки, можно достаточно точно прикинуть её индуктивное сопротивление без каких-либо измерительных приборов.
Дополнительная информация. Некоторые цифровые мультиметры имеют режим замера индуктивности. Подобная функция встречается редко, однако иногда оказывается очень полезной. Поэтому при выборе прибора стоит обратить внимание на то, способен ли он измерять индуктивность.
Калькулятор импеданса катушки индуктивности
Калькулятор определяет импеданс катушки индуктивности для заданной частоты синусоидального сигнала. Определяется также угловая частота.
Пример. Рассчитать импеданс катушки индуктивности 10 мкГн на частоте 25 МГц.
Введите значения индуктивности и частоты, выберите единицы измерения и нажмите кнопку Рассчитать. Для ввода значения бесконечность наберите inf.
Отметим, что величина импеданса идеальной катушки индуктивности равна ее реактивному сопротивлению. Однако это не идентичные величины, так как между током и напряжением в индуктивной цепи существует фазовый сдвиг. Для расчетов используются указанная ниже формула:
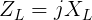
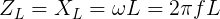
Здесь
XL — реактивное сопротивление катушки в омах (Ом),
ZL — импеданс катушки в омах (Ом),
ω = 2πf — угловая частота в рад/с,
f — частота в герцах (Гц),
L — индуктивность в генри (Гн),
j — мнимая единица.
Для расчета выберите единицы измерения и введите индуктивность и частоту. Импеданс катушки индуктивности будет показан в омах.
Катушка индуктивности представляет собой пассивный электрический элемент с двумя выводами, изготовленный, как правило, из изолированного провода в форме спирали, намотанного на магнитный сердечник или на оправку (без сердечника). Магнитный сердечник обычно изготовляется из ферромагнитного металла, например, железа или ферромагнитной керамики (феррита) и используется для усиления магнитного поля и, таким образом, для увеличения индуктивности катушки. Как и конденсаторы, катушки индуктивности используются для накопления и сохранения энергии. Однако, в отличие от конденсаторов, энергия в катушке хранится в форме окружающего ее магнитного поля. Катушки индуктивности применяются, в частности, в фильтрах для сглаживания постоянного тока или для предотвращения передачи высокочастотных помех по кабелям. Катушки индуктивности широко используются в колебательных контурах радиопередатчиков и радиоприемников, а также для изготовления трансформаторов.
Высокодобротная катушка индуктивности без сердечника, установленная в радиопередатчике
В отличие от конденсаторов, которые препятствуют изменению напряжения, приложенного к их обкладкам, катушки индуктивности препятствуют изменению текущего в них тока. В отличие от конденсаторов, которые не пропускают постоянный ток, катушки индуктивности пропускают его легко. Они препятствуют только прохождению переменного тока или иного изменяющегося тока и их способность препятствовать прохождению тока и называется индуктивностью. Индуктивность обозначается символом L в честь российского физика Эмиля Ленца и измеряется в генри — единицах, названных в честь американского ученого Джозефа Генри.
В отличие от резисторов, которые препятствуют прохождению электрического тока вследствие падения напряжения на них, пропорционального протекающему току, катушки индуктивности препятствуют изменению протекающего через них тока. На них создается падение напряжения, прямо пропорциональное скорости изменения тока. Полярность индуцированного напряжения всегда такова, что это напряжение поддерживает изменяющийся ток в его текущем состоянии. Например, если ток растет, то напряжение препятствует этому росту и старается уменьшить ток. В то же время, если ток через катушку уменьшается, напряжение мешает этому уменьшению и поддерживает более высокий ток. Чем выше скорость изменения тока, тем больше амплитуда этого обратного напряжения. В связи с указанным свойством, это напряжение часто называют индуктивными выбросами или обратным током. Для того, чтобы как-то отличить это свойство от сопротивления, используют понятие реактивного сопротивления. Если к катушке индуктивности приложено синусоидальное напряжение, то при бóльших частотах катушка оказывает току большее сопротивление, следовательно, ее реактивное сопротивление также увеличивается, как показано на графике.
График зависимости реактивного сопротивления катушки XL индуктивности и текущего через нее тока I от частоты f для нескольких величин индуктивности показывает прямую пропорциональную зависимость от частоты реактивного сопротивления и обратную зависимость от частоты протекающего через катушку тока
Полное сопротивление Z, как и реактивное сопротивление, измеряется в омах (Ом) и состоит из двух частей — действительной и мнимой. Первая из них представляет собой активное сопротивление R, которое затрудняет протекание тока в материале с плохой проводимостью и зависит от формы этого материала. Вторая часть — это рассмотренное выше реактивное сопротивление X. Оно также затрудняет протекание тока, но не вследствие свойств и формы проводящего материала, а из-за того, что протеканию тока мешает электрическое и магнитное поля.
Если реальная катушка индуктивности подключена к источнику постоянного напряжения, через нее протекает постоянный ток, ограниченный только сопротивлением провода, из которого намотана катушка. Когда катушка подключается к источнику постоянного напряжения, ток через нее медленно повышается от нуля до максимального значения, которое определяется внутренним сопротивлением источника и внутренним сопротивлением витков катушки. ЭДС самоиндукции, возникающая в катушке, препятствует резкому увеличению тока в ней. Эта ЭДС противодействует приложенному напряжению до тех пор, пока ток не достигнет максимального значения.
Если источник постоянного напряжения отключить от катушки, протекающий через нее ток постепенно падает до нуля. В этом случае опять возникает ЭДС самоиндукции, которая снова препятствует, на этот раз, уменьшению тока и которая старается поддержать ток в неизменном состоянии. В конце концов, ток постепенно уменьшается до нуля.
В чисто индуктивной цепи ток отстает от напряжения на π/2 радиан или 90°. 1 — в момент отрицательного максимума тока скорость его изменения нулевая и напряжение равно нулю; 2 — ток нулевой, скорость его изменения максимальная и напряжение равно положительному максимуму; 3 — ток положительный и максимальный, скорость его изменения нулевая и напряжение равно нулю; 4 — ток нулевой, скорость его изменения максимальная и напряжение равно отрицательному максимуму
Если к катушке индуктивности приложено переменное синусоидальное напряжение, ток отстает от напряжения на некоторый фазовый угол, как показано на графике. В идеальной катушке индуктивности этот угол будет равен точно 90° или четверти цикла. В точке (ωt = π/2), временнóй оси, где ток нулевой, напряжение на катушке достигает своего положительного максимума. Затем ток постепенно увеличивается и вокруг катушки создается магнитное поле, которое, в свою очередь, создает ЭДС самоиндукции, направленную противоположно току. Эта ЭДС является реакцией катушки на изменение протекающего через нее тока, и она максимальна, когда ток нулевой, так как в этой точке скорость изменения тока максимальная. Когда же ток достигает своего максимального значения (положительного или отрицательного), скорость изменения синусоидального тока становится нулевой и в этих точках максимумов ток ЭДС самоиндукции (определяемая этой скоростью) также равна нулю. Это приводит к тому, что синусоида напряжения не совпадает по фазе с током на угол 90° или π/2 радиан. То есть, напряжение опережает ток или ток отстает от напряжения.
Аналогичное явление можно наблюдать и в природе. Сравните: Солнце светит сильнее всего в астрономический полдень (солнечный свет — напряжение), однако самая жаркая часть дня обычно бывает через несколько часов после полудня (температура — ток). Или другой пример. День зимнего солнцестояния в северном полушарии (самый короткий день) — в конце декабря, однако самые холодные месяцы еще впереди. В зависимости от того, где вы живете, это будет январь или февраль. Вспомните поговорку «Солнце — на лето, зима — на мороз». Это как раз о поведении индуктивности, только в природной аналогии. Такой сезонный «сдвиг фаз» или отставание вызван поглощением энергии Солнца огромными массами воды в океанах. Они отдадут эту запасенную энергию, но позже — точно так же, как это делают катушки индуктивности.
День зимнего солнцестояния в северном полушарии — в конце декабря, однако самые холодные месяцы еще впереди. Именно так ведет себя ток в катушке индуктивности
Рассчитанный этим калькулятором импеданс представляет собой меру сопротивления катушки индуктивности протекающему через нее току на определенной частоте. Индуктивное реактивное сопротивление изменяется при изменении частоты приложенного переменного напряжения. Приведенные выше формула и график показывают, что реактивное сопротивление катушки индуктивности XL велико при высоких частотах и мало при низких частотах (конденсаторы ведут себя с точностью до наоборот). При высоких частотах индуктивное реактивное сопротивление становится очень большим и очень сильно противодействует протекающему току. С другой стороны, при очень низких частотах или при постоянном напряжении катушка индуктивности проводит очень хорошо — отсюда правило, которое мы выучили в школе: катушки индуктивности не пропускают переменный ток и пропускают постоянный. Если частота очень низкая, катушки индуктивности пропускают сигнал очень хорошо. Именно поэтому их устанавливают в фильтрах громкоговорителей (кроссоверах), чтобы высокие частоты не попадали на низкочастотные динамические головки.
Импеданс измеряется в омах, так же, как и сопротивление. Импеданс мешает прохождению электрического тока так же, как и сопротивление, и показывает как сильно катушка противодействует прохождению тока через нее. Но тогда возникает вопрос: в чем же разница между импедансом и сопротивлением? А разница заключается в зависимости импеданса от частоты приложенного сигнала. Сопротивление от частоты не зависит, а импеданс катушек индуктивности от частоты зависит. С увеличением частоты импеданс катушек уменьшается.
Этот калькулятор предназначен для расчета импеданса идеальных катушек индуктивности. Реальные катушки всегда имеют сопротивление, которое на эквивалентной схеме изображают включенным последовательно с индуктивностью. Для расчета импеданса реальных катушек индуктивности пользуйтесь калькулятором импеданса RL-цепей.
Катушки индуктивности в высокочастотном модуле телевизионного приемника
Предыдущая
РазноеЧто такое фазное и линейное напряжение?
Следующая
РазноеБлуждающие токи и способы борьбы с ними
 Любое вещество, находясь в разнообразных состояниях, обладает определенным сопротивлением. В некоторых случаях возникает необходимость рассчитать полное сопротивление цепи или конкретного участка. В такой ситуации следует воспользоваться формулами. Кроме того, нужно понимать основной смысл сопротивления и электропроводимости, а также зависимость этих понятий от некоторых величин.
Любое вещество, находясь в разнообразных состояниях, обладает определенным сопротивлением. В некоторых случаях возникает необходимость рассчитать полное сопротивление цепи или конкретного участка. В такой ситуации следует воспользоваться формулами. Кроме того, нужно понимать основной смысл сопротивления и электропроводимости, а также зависимость этих понятий от некоторых величин.
- Физический смысл
- Зависимость электропроводимости
- Электрические величины
- Геометрические параметры и тип вещества
- Температура проводника
- Цепь переменного тока
- Измерение сопротивления
Физический смысл
Все вещества по проводимости электрического тока (ЭТ) делятся на проводники, полупроводники и диэлектрики. Проводниками являются элементы, хорошо проводящие ЭТ. Это обусловлено наличием свободных электронов (СЭ). Полупроводники — особая группа веществ, проводимость которых зависит от внешних факторов, например, от температуры, освещенности и т. д. Диэлектриками являются все вещества, которые не проводят ЭТ из-за отсутствия или недостаточного количества СЭ. Для протекания тока по веществу требуется наличие СЭ, количество которых зависит от электронной конфигурации.
Электронная конфигурация какого-либо элемента берется из таблицы Менделеева. Ток оказывает на проводник тепловое действие, так как происходит взаимодействие СЭ с кристаллической решеткой (КР).Они замедляются, но с течением времени под действием электромагнитного поля снова ускоряются, после чего процесс взаимодействия повторяется много раз.
Процесс взаимодействия свободных заряженных частиц с КР вещества называется электрическим сопротивлением проводника. Обозначается сопротивление или электропроводимость буквой R, единицей измерения этой величины является Ом.
Зависимость электропроводимости
R зависит от внешних факторов окружающей среды, электрических величин, а также характерных особенностей проводника. Эти зависимости используются при расчетах схем и изготовлении радиодеталей. Существует несколько способов нахождения R, а иногда они комбинируются для получения эффективности и точности вычислений.
Электрические величины
 К электрическим величинам, от которых зависит величина R, относятся I, U, электродвижущая сила (ЕДС обозначается е) и тип тока. R в электрических цепях рассчитывается по закону Ома для определенного участка цепи: I, протекающая в заданном участке электрической цепи, прямо пропорциональна U на этом участке и обратно пропорциональна R выбранного участка цепи. В виде формулы его можно записать следующим образом: I = U / R.
К электрическим величинам, от которых зависит величина R, относятся I, U, электродвижущая сила (ЕДС обозначается е) и тип тока. R в электрических цепях рассчитывается по закону Ома для определенного участка цепи: I, протекающая в заданном участке электрической цепи, прямо пропорциональна U на этом участке и обратно пропорциональна R выбранного участка цепи. В виде формулы его можно записать следующим образом: I = U / R.
Исходя из следствия этого закона, можно получить сопротивление участка цепи: R = U / I. Если требуется произвести расчет R на всем участке цепи, то нужно воспользоваться формулой (следствием из закона Ома для полной цепи) с учетом внутреннего R источника питания: R = (e / I) – R внутреннее. Величина электрической проводимости рассчитывается не только при помощи законов Ома, но и с использованием геометрических параметров проводника и температуры. Кроме того, необходимо учитывать и тип тока (постоянный или переменный).
Геометрические параметры и тип вещества
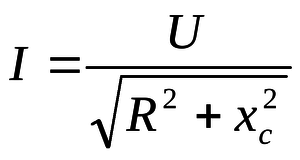 Если основными носителями заряда являются СЭ, а свойства проводимости прямо пропорционально зависят от их количества и структуры КР, то тип вещества является одним из факторов, влияющих на R проводника. Вещества и их составляющие элементы, имеющие различные электронные конфигурации, согласно таблице Менделеева обладают разными КР, что и обуславливается различным R.
Если основными носителями заряда являются СЭ, а свойства проводимости прямо пропорционально зависят от их количества и структуры КР, то тип вещества является одним из факторов, влияющих на R проводника. Вещества и их составляющие элементы, имеющие различные электронные конфигурации, согласно таблице Менделеева обладают разными КР, что и обуславливается различным R.
Зависимость от материала выражается коэффициентом, обозначающимся p. Он характеризует показатель удельного R проводника. Его значение берется из таблицы (при температуре +20 °C). Величина, обратная p, называется удельной проводимостью и обозначается σ. Взаимосвязь σ и p можно выразить формулой p = 1 / σ.
Кроме того, от площади поперечного сечения (S) также зависит R проводника. Эта зависимость обусловлена тем, что при маленьком сечении плотность потока Э протекает через проводник и взаимодействие с КР становится более частым. Площадь поперечного сечения достаточно просто вычислить. Для этого необходимо воспользоваться некоторым алгоритмом, если проводник (П) представляет собой провод цилиндрической формы:
- Измерение диаметра проводника при помощи штангенциркуля (ШЦ).
- Нахождение S при помощи формулы S = 3,1416 * sqr (d) / 4.
П может из себя представлять многожильный провод, поэтому для точного расчета необходимо найти S одной жилы, воспользовавшись алгоритмом нахождения для цилиндрической формы П, а затем результат умножить на количество жил.
Кроме того, бывают провода в форме квадрата и прямоугольника, но они встречаются редко. Для этого нужно выполнить следующие вычисления:
- Для квадратной формы нужно замерить ШЦ одну из сторон и возвести ее в квадрат: S = sqr(a).
- Для прямоугольной формы следует измерить две противолежащие стороны при помощи ШЦ, а затем произвести расчет по формуле S = a * b.
Из этих алгоритмов нахождения S можно сделать универсальный (абстрактный алгоритм). Он подходит для нахождения или расчетов величин, независимо от формы П при его разрезе, выполненном строго перпендикулярно относительно П. Алгоритм имеет следующий вид:
- Визуально определить геометрическую фигуру при разрезе П.
- Найти в справочнике формулу S.
- Произвести измерения при помощи ШЦ необходимых величин.
- Подставить в формулу и вычислить S.
Еще одной величиной является длина П, при увеличении которой R увеличивается. На основании этих величин можно вывести следующую формулу зависимости от типа вещества, длины (L) и S проводника: R = p * L / S.
Однако это значение R можно определить при температуре +20 °C. Для получения более точных расчетов нужно рассмотреть зависимость от температуры.
Температура проводника
Научно подтвержденным является факт, что p зависит от температуры. Это утверждение можно доказать практическим путем. Для проведения опыта необходимы следующие элементы, изображенные на схеме: спираль из нихрома (используется в нагревательных элементах), соединительные медные провода, источник питания, амперметр (для измерения I), вольтметр (измеряет U) и реостат.
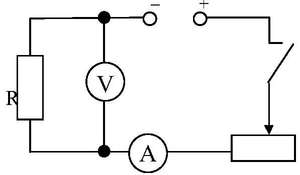
На схеме нагревательный элемент изображен в виде резистора. При его включении следует внимательно наблюдать за показаниями амперметра. Спираль начинает нагреваться, и показания амперметра уменьшаются по мере нагревания. Согласно закону Ома для участка цепи необходимо сделать вывод, что при росте R ток уменьшается (обратно пропорциональная зависимость). Следовательно, значение R зависит от температуры. При нагревании происходит увеличение ионов в КР нихромовой спирали и Э начинают чаще сталкиваться с ними.
В формуле R = p * L / S можно методом исключения найти показатель, зависящий от температуры. Последняя не оказывает влияния на длину П. По формуле вычисления S зависимость также не прослеживается, поскольку геометрия П не зависит от температуры. Остается p, который зависит от температуры. В физике существует формула зависимости p = p0 * [1 + a * (t – 20)]. Буква а является температурным коэффициентом:
- для металлов а > 0;
- для электролитов a < 0.
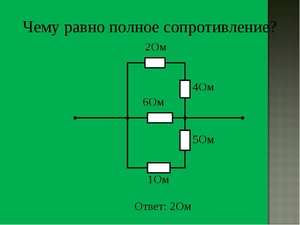 Переменная t — температура П, p0 — удельное сопротивление, взятое из справочника для конкретного материала. Кроме того, p зависит еще и от деформации П, поскольку при этом КР меняет свою структуру. Это происходит в процессе обработки металла при низких температурах и давлении. Такая деформация является пластической, при ней искажается КР, и увеличивается R течения Э.
Переменная t — температура П, p0 — удельное сопротивление, взятое из справочника для конкретного материала. Кроме того, p зависит еще и от деформации П, поскольку при этом КР меняет свою структуру. Это происходит в процессе обработки металла при низких температурах и давлении. Такая деформация является пластической, при ней искажается КР, и увеличивается R течения Э.
В этом случае происходит увеличение p. Процесс является обратимым, поэтому часть дефектов уменьшается (рекристаллический отжиг). Если на металл действуют силы растяжения или сжатия, то эта деформация является упругой. Величина p уменьшается под действием силы сжатия, при которой происходит резкое уменьшение тепловых колебаний (ТК), а Э легче двигаются. Но под действием силы растяжения происходит прямо пропорциональное увеличение p, при котором амплитуда ТК увеличивается.
Конечную формулу можно записать в виде R = p0 * [1 + a * (t – 20)] * L / S. Однако этот вариант нахождения R был рассмотрен в цепях с постоянным I, а под действием переменного I появляются новые величины, влияющие на расчеты.
Цепь переменного тока
Закон Ома применяется только для цепей постоянного тока. Для переменного U он изменен и, следовательно, существуют другие формулы нахождения R. Сопротивление в цепях с переменным I (ПТ) бывает:
- активным;
- индуктивным;
- емкостным;
- полным.

Активное сопротивление свидетельствует о том, что в цепи присутствует резистор или любая другая неемкостная или неиндуктивная нагрузка. Для его расчета необходимо произвести измерение значений амплитуд Um и Im. При помощи приборов можно получить только действующие значения этих величин. Амплитудные значения рассчитываются по формулам Um = Ud * sqrt(2) и Im = Id * sqrt(2). Для определения активного сопротивления (обозначается R) нужно воспользоваться формулой Iм = Uм / R. Из неё можно получить R = Ud * sqrt(2) / Im = Id * sqrt(2).
Если в цепи переменного I (ЦПТ) присутствуют катушка индуктивности, дроссель, контур и т. д., то появляется индуктивное R, которое обозначается Xl. Для расчета необходимо воспользоваться формулой Xl = w * L, предварительно измеряв частоту ПТ и рассчитав индуктивность.
Величина циклической частоты находится по формуле, для которой нужно измерять частоту ПТ (f): w = 2 * 3,1416 * f. Последняя измеряется при помощи осциллографа или частотомера. Для расчета индуктивности катушки необходимо воспользоваться справочником по физике или онлайн-калькулятором.
При наличии в ЦПТ емкости (конденсатора) возникает емкостное R, которое обозначается Xc. При протекании постоянного U конденсатор не пропускает I, а в ЦПТ он пропускает I и обладает емкостью (C) и Xc. Рассчитывается это значение по формуле Xc = 1 / (w * C), где:
- w — циклическая частота, которая рассчитывается аналогично вычислению Xl;
- C — емкость конденсатора, указанная на корпусе или измеренная соответствующим прибором.
Полное сопротивление цепи обозначается Z и представляет собой сумму всей нагрузки ЦПТ (активного, индуктивного и емкостного сопротивления). Для расчета нужно воспользоваться формулой полного сопротивления: Z = sqrt [sqr(R) + sqr (Xc – Xl)]. В ЦПТ величина Z зависит от:
- геометрии П;
- типа вещества, из которого сделан П;
- температуры;
- деформации различного вида;
- электрических показателей I, U, f, L, C и R.
Закон Ома для участка цепи принимает следующий вид: I = U / Z. Необязательно рассчитывать электропроводимость П, так как для этих целей существуют омметры. Расчет Xl и Xс следует производить самостоятельно.
Измерение сопротивления
 На расчет R необходимо потратить определенное время. Эту задачу упрощает прибор, который называется омметром. Он состоит из цифрового или стрелочного индикатора. Практически все современные комбинированные приборы (мультиметры) оснащены функцией измерения R. Однако есть и специализированные устройства, применяющиеся для определенных целей, например, для измерения R изоляции жил кабеля. Этот тип прибора называется мегаомметром. Омметр применяется не только для измерения величины R, но и для прозвонки радиокомпонентов, кабелей, отдельных шлейфов и других элементов на исправность и обрыв цепи.
На расчет R необходимо потратить определенное время. Эту задачу упрощает прибор, который называется омметром. Он состоит из цифрового или стрелочного индикатора. Практически все современные комбинированные приборы (мультиметры) оснащены функцией измерения R. Однако есть и специализированные устройства, применяющиеся для определенных целей, например, для измерения R изоляции жил кабеля. Этот тип прибора называется мегаомметром. Омметр применяется не только для измерения величины R, но и для прозвонки радиокомпонентов, кабелей, отдельных шлейфов и других элементов на исправность и обрыв цепи.
Для измерения R необходимо обесточить участок или радиокомпонент и проследить за разрядкой цепей, где присутствуют конденсаторы. Перед проведением измерений нужно выставить необходимый режим на приборе и закоротить щупы для проверки прибора на исправность. Некоторые модели снабжены функцией звукового сигнала. После теста прибора следует приступить к измерениям.

Для нахождения точной величины Z проводника необходимо учитывать все величины, от которых оно зависит. Вычисление Z позволяет точно рассчитать электрическую схему какого-либо устройства для избегания трудоемких измерений. Измерить омметром можно только величину активного сопротивления, а Xl и Xc следует рассчитывать самостоятельно. Однако при помощи онлайн-калькуляторов сделать это не составит особого труда.
