Время на прочтение
5 мин
Количество просмотров 157K
Доброго времени суток.
Представляю вашему вниманию перевод статьи «Algorithms on Graphs: Let’s talk Depth-First Search (DFS) and Breadth-First Search (BFS)» автора Try Khov.
Что такое обход графа?
Простыми словами, обход графа — это переход от одной его вершины к другой в поисках свойств связей этих вершин. Связи (линии, соединяющие вершины) называются направлениями, путями, гранями или ребрами графа. Вершины графа также именуются узлами.
Двумя основными алгоритмами обхода графа являются поиск в глубину (Depth-First Search, DFS) и поиск в ширину (Breadth-First Search, BFS).
Несмотря на то, что оба алгоритма используются для обхода графа, они имеют некоторые отличия. Начнем с DFS.
Поиск в глубину
DFS следует концепции «погружайся глубже, головой вперед» («go deep, head first»). Идея заключается в том, что мы двигаемся от начальной вершины (точки, места) в определенном направлении (по определенному пути) до тех пор, пока не достигнем конца пути или пункта назначения (искомой вершины). Если мы достигли конца пути, но он не является пунктом назначения, то мы возвращаемся назад (к точке разветвления или расхождения путей) и идем по другому маршруту.
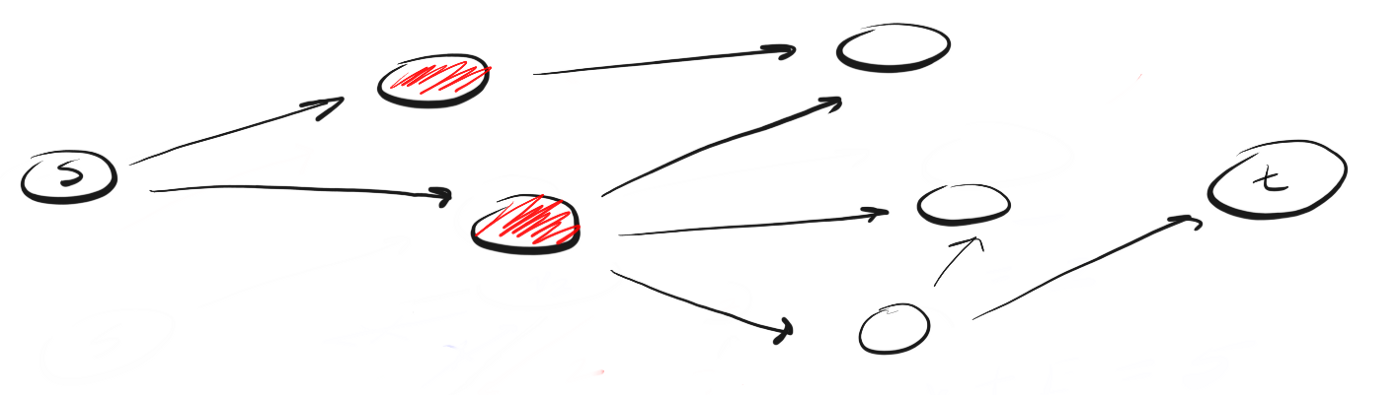
Давайте рассмотрим пример. Предположим, что у нас есть ориентированный граф, который выглядит так:

Мы находимся в точке «s» и нам нужно найти вершину «t». Применяя DFS, мы исследуем один из возможных путей, двигаемся по нему до конца и, если не обнаружили t, возвращаемся и исследуем другой путь. Вот как выглядит процесс:

Здесь мы двигаемся по пути (p1) к ближайшей вершине и видим, что это не конец пути. Поэтому мы переходим к следующей вершине.

Мы достигли конца p1, но не нашли t, поэтому возвращаемся в s и двигаемся по второму пути.

Достигнув ближайшей к точке «s» вершины пути «p2» мы видим три возможных направления для дальнейшего движения. Поскольку вершину, венчающую первое направление, мы уже посещали, то двигаемся по второму.

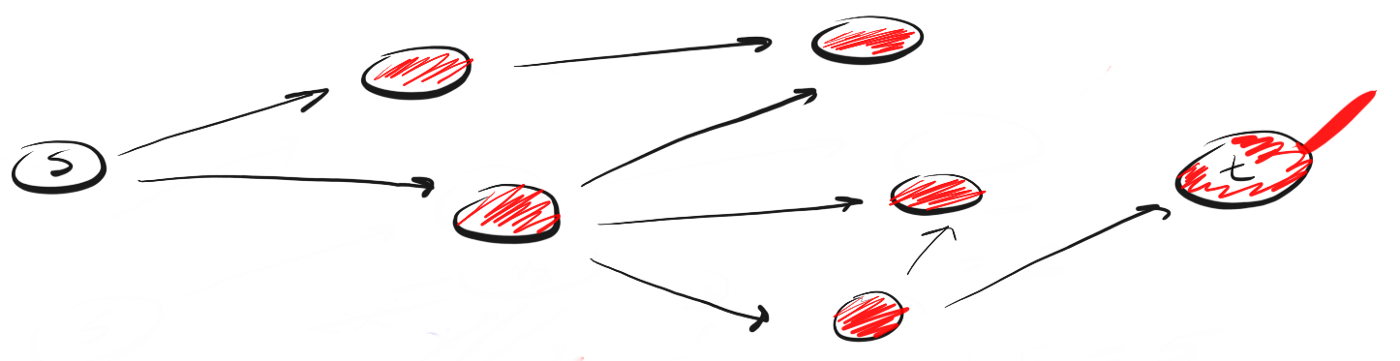
Мы вновь достигли конца пути, но не нашли t, поэтому возвращаемся назад. Следуем по третьему пути и, наконец, достигаем искомой вершины «t».

Так работает DFS. Двигаемся по определенному пути до конца. Если конец пути — это искомая вершина, мы закончили. Если нет, возвращаемся назад и двигаемся по другому пути до тех пор, пока не исследуем все варианты.
Мы следуем этому алгоритму применительно к каждой посещенной вершине.
Необходимость многократного повторения процедуры указывает на необходимость использования рекурсии для реализации алгоритма.
Вот JavaScript-код:
// при условии, что мы имеем дело со смежным списком
// например, таким: adj = {A: [B,C], B:[D,F], ... }
function dfs(adj, v, t) {
// adj - смежный список
// v - посещенный узел (вершина)
// t - пункт назначения
// это общие случаи
// либо достигли пункта назначения, либо уже посещали узел
if(v === t) return true
if(v.visited) return false
// помечаем узел как посещенный
v.visited = true
// исследуем всех соседей (ближайшие соседние вершины) v
for(let neighbor of adj[v]) {
// если сосед не посещался
if(!neighbor.visited) {
// двигаемся по пути и проверяем, не достигли ли мы пункта назначения
let reached = dfs(adj, neighbor, t)
// возвращаем true, если достигли
if(reached) return true
}
}
// если от v до t добраться невозможно
return false
}
Заметка: этот специальный DFS-алгоритм позволяет проверить, возможно ли добраться из одного места в другое. DFS может использоваться в разных целях. От этих целей зависит то, как будет выглядеть сам алгоритм. Тем не менее, общая концепция выглядит именно так.
Анализ DFS
Давайте проанализируем этот алгоритм. Поскольку мы обходим каждого «соседа» каждого узла, игнорируя тех, которых посещали ранее, мы имеем время выполнения, равное O(V + E).
Краткое объяснение того, что означает V+E:
V — общее количество вершин. E — общее количество граней (ребер).
Может показаться, что правильнее использовать V*E, однако давайте подумаем, что означает V*E.
V*E означает, что применительно к каждой вершине, мы должны исследовать все грани графа безотносительно принадлежности этих граней конкретной вершине.
С другой стороны, V+E означает, что для каждой вершины мы оцениваем лишь примыкающие к ней грани. Возвращаясь к примеру, каждая вершина имеет определенное количество граней и, в худшем случае, мы обойдем все вершины (O(V)) и исследуем все грани (O(E)). Мы имеем V вершин и E граней, поэтому получаем V+E.
Далее, поскольку мы используем рекурсию для обхода каждой вершины, это означает, что используется стек (бесконечная рекурсия приводит к ошибке переполнения стека). Поэтому пространственная сложность составляет O(V).
Теперь рассмотрим BFS.
Поиск в ширину
BFS следует концепции «расширяйся, поднимаясь на высоту птичьего полета» («go wide, bird’s eye-view»). Вместо того, чтобы двигаться по определенному пути до конца, BFS предполагает движение вперед по одному соседу за раз. Это означает следующее:

Вместо следования по пути, BFS подразумевает посещение ближайших к s соседей за одно действие (шаг), затем посещение соседей соседей и так до тех пор, пока не будет обнаружено t.

Чем DFS отличается от BFS? Мне нравится думать, что DFS идет напролом, а BFS не торопится, а изучает все в пределах одного шага.
Далее возникает вопрос: как узнать, каких соседей следует посетить первыми?
Для этого мы можем воспользоваться концепцией «первым вошел, первым вышел» (first-in-first-out, FIFO) из очереди (queue). Мы помещаем в очередь сначала ближайшую к нам вершину, затем ее непосещенных соседей, и продолжаем этот процесс, пока очередь не опустеет или пока мы не найдем искомую вершину.
Вот код:
// при условии, что мы имеем дело со смежным списком
// например, таким: adj = {A:[B,C,D], B:[E,F], ... }
function bfs(adj, s, t) {
// adj - смежный список
// s - начальная вершина
// t - пункт назначения
// инициализируем очередь
let queue = []
// добавляем s в очередь
queue.push(s)
// помечаем s как посещенную вершину во избежание повторного добавления в очередь
s.visited = true
while(queue.length > 0) {
// удаляем первый (верхний) элемент из очереди
let v = queue.shift()
// abj[v] - соседи v
for(let neighbor of adj[v]) {
// если сосед не посещался
if(!neighbor.visited) {
// добавляем его в очередь
queue.push(neighbor)
// помечаем вершину как посещенную
neighbor.visited = true
// если сосед является пунктом назначения, мы победили
if(neighbor === t) return true
}
}
}
// если t не обнаружено, значит пункта назначения достичь невозможно
return false
}
Анализ BFS
Может показаться, что BFS работает медленнее. Однако если внимательно присмотреться к визуализациям, можно увидеть, что они имеют одинаковое время выполнения.
Очередь предполагает обработку каждой вершины перед достижением пункта назначения. Это означает, что, в худшем случае, BFS исследует все вершины и грани.
Несмотря на то, что BFS может казаться медленнее, на самом деле он быстрее, поскольку при работе с большими графами обнаруживается, что DFS тратит много времени на следование по путям, которые в конечном счете оказываются ложными. BFS часто используется для нахождения кратчайшего пути между двумя вершинами.
Таким образом, время выполнения BFS также составляет O(V + E), а поскольку мы используем очередь, вмещающую все вершины, его пространственная сложность составляет O(V).
Аналогии из реальной жизни
Если приводить аналогии из реальной жизни, то вот как я представляю себе работу DFS и BFS.
Когда я думаю о DFS, то представляю себе мышь в лабиринте в поисках еды. Для того, чтобы попасть к цели мышь вынуждена много раз упираться в тупик, возвращаться и двигаться по другому пути, и так до тех пор, пока она не найдет выход из лабиринта или еду.

Упрощенная версия выглядит так:

В свою очередь, когда я думаю о BFS, то представляю себе круги на воде. Падение камня в воду приводит к распространению возмущения (кругов) во всех направлениях от центра.

Упрощенная версия выглядит так:

Выводы
- Поиск в глубину и поиск в ширину используются для обхода графа.
- DFS двигается по граням туда и обратно, а BFS распространяется по соседям в поисках цели.
- DFS использует стек, а BFS — очередь.
- Время выполнения обоих составляет O(V + E), а пространственная сложность — O(V).
- Данные алгоритмы имеют разную философию, но одинаково важны для работы с графами.
Прим. пер.: я не специалист по алгоритмам и структурам данных, поэтому при обнаружении ошибок, неточностей или некорректности формулировок, прошу написать в личку для исправления и уточнения. Буду признателен.
Благодарю за внимание.
|
|
Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. |
| График и дерево алгоритмы поиска |
|---|
|
| Списки |
|
| похожие темы |
|
В Информатика, обход графа (также известен как Поиск граф) относится к процессу посещения (проверки и / или обновления) каждой вершины в график. Такие обходы классифицируются по порядку посещения вершин. Обход дерева это частный случай обхода графа.
Резервирование
В отличие от обхода дерева, обход графа может потребовать, чтобы некоторые вершины были посещены более одного раза, так как перед переходом к вершине не обязательно известно, что она уже была исследована. Поскольку графиков становится больше плотный, эта избыточность становится все более распространенной, что приводит к увеличению времени вычислений; по мере того как графики становятся более разреженными, верно и обратное.
Таким образом, обычно необходимо помнить, какие вершины уже были исследованы алгоритмом, чтобы вершины пересматривались как можно реже (или, в худшем случае, чтобы предотвратить бесконечное продолжение обхода). Это может быть выполнено путем связывания каждой вершины графа с состоянием «цвет» или «посещение» во время обхода, которое затем проверяется и обновляется, когда алгоритм посещает каждую вершину. Если вершина уже была посещена, она игнорируется и путь больше не используется; в противном случае алгоритм проверяет / обновляет вершину и продолжает движение по текущему пути.
Некоторые частные случаи графов подразумевают посещение других вершин в их структуре и, таким образом, не требуют явной записи посещения во время обхода. Важным примером этого является дерево: во время обхода можно предположить, что все вершины-предки текущей вершины (и другие в зависимости от алгоритма) уже посещены. Оба в глубину и поиск по графу в ширину представляют собой адаптации древовидных алгоритмов, отличающиеся в первую очередь отсутствием структурно определенной «корневой» вершины и добавлением структуры данных для записи состояния посещения обхода.
Алгоритмы обхода графа
Примечание. – Если каждая вершина в графе должна быть пройдена древовидным алгоритмом (например, DFS или BFS), то алгоритм должен вызываться по крайней мере один раз для каждого связный компонент графа. Этого легко добиться, перебирая все вершины графа, выполняя алгоритм на каждой вершине, которая еще не посещена при проверке.

Невербальное описание трех алгоритмов обхода графа: случайный, поиск в глубину и поиск в ширину.
Поиск в глубину
Поиск в глубину (DFS) – это алгоритм обхода конечного графа. DFS посещает дочерние вершины перед посещением родственных вершин; то есть, он проходит глубину любого конкретного пути, прежде чем исследовать его широту. Стек (часто программный стек вызовов через рекурсия ) обычно используется при реализации алгоритма.
Алгоритм начинается с выбранной «корневой» вершины; затем он итеративно переходит от текущей вершины к соседней, непосещенной вершине, пока не перестанет находить неисследованную вершину для перехода из ее текущего местоположения. Тогда алгоритм отступления вдоль ранее посещенных вершин, пока не найдет вершину, связанную с еще более неизведанной территорией. Затем он продолжит движение по новому пути, как и раньше, с обратным отслеживанием, когда он встречается с тупиками, и завершится только тогда, когда алгоритм вернется назад мимо исходной «корневой» вершины с самого первого шага.
DFS является основой многих алгоритмов, связанных с графами, включая топологические виды и проверка планарности.
Псевдокод
- Вход: График грамм и вершина v из грамм.
- Выход: Разметка ребер связного компонента v как края открытия и задние края.
процедура DFS (грамм, v) является метка v как исследовано для всех края е в грамм.incidentEdges (v) делать если край е неизведанный тогда ш ← грамм.adjacentVertex (v, е) если вершина ш неизведанный тогда метка е как обнаруженное ребро рекурсивно вызвать DFS (грамм, ш) еще метка е как задний край
Поиск в ширину
|
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Октябрь 2012 г.) |
Поиск в ширину (BFS) – еще один метод обхода конечного графа. BFS посещает родственные вершины перед посещением дочерних вершин, а очередь используется в процессе поиска. Этот алгоритм часто используется для поиска кратчайшего пути от одной вершины к другой.
Псевдокод
- Вход: График грамм и вершина v из грамм.
- Выход: Ближайшая к v удовлетворяющие некоторым условиям, или null, если такой вершины не существует.
процедура BFS (грамм, v) является создать очередь Q ставить в очередь v на Q отметка v пока Q не пусто делать ш ← Q.dequeue () если ш это то, что мы ищем тогда возвращаться ш для всех края е в грамм.adjacentEdges (ш) делать Икс ← грамм.adjacentVertex (ш, е) если Икс не отмечен тогда отметка Икс ставить в очередь Икс на Q возвращаться ноль
Приложения
Поиск в ширину можно использовать для решения многих задач теории графов, например:
- найти все вершины в одной связный компонент;
- Алгоритм Чейни;
- найти кратчайший путь между двумя вершинами;
- тестирование графика для двудольность;
- Алгоритм Катхилла – Макки нумерация ячеек;
- Алгоритм Форда – Фулкерсона для вычисления максимальный поток в проточная сеть;
- сериализация / десериализация двоичного дерева по сравнению с сериализацией в отсортированном порядке (позволяет эффективно реконструировать дерево);
- алгоритмы создания лабиринта;
- заливка алгоритм маркировки смежных областей двухмерного изображения или n-мерного массива;
- анализ сетей и отношений.
Исследование графа
Задачу исследования графа можно рассматривать как вариант обхода графа. Это онлайн-проблема, означающая, что информация о графе раскрывается только во время выполнения алгоритма. Общая модель выглядит следующим образом: дан связный граф грамм = (V, E) с неотрицательными краевыми весами. Алгоритм начинается с некоторой вершины и знает все исходящие ребра, а также вершины на концах этих ребер, но не более того. Когда посещается новая вершина, снова становятся известны все инцидентные исходящие ребра и вершины в конце. Цель – посетить все п вершины и вернуться в исходную вершину, но сумма весов тура должна быть как можно меньше. Проблема также может быть понята как конкретная версия задача коммивояжера, где продавец должен находить график на ходу.
Для общих графов наиболее известные алгоритмы как для неориентированных, так и для ориентированных графов представляют собой простые жадный алгоритм:
- В неориентированном случае жадный тур не более чем О(ln п)в разы длиннее оптимального тура.[1] Лучшая нижняя граница, известная для любого детерминированного онлайн-алгоритма, равна 2.5 − ε;[2]
- В направленном случае жадный тур не превышает (п − 1) в разы длиннее оптимального тура. Это соответствует нижней границе п − 1.[3] Аналогичная конкурентная нижняя граница Ω(п) также выполняется для рандомизированных алгоритмов, которым известны координаты каждого узла геометрического вложения. Если вместо посещения всех узлов необходимо найти только один узел “сокровище”, то конкурентные границы будут Θ(п2) на ориентированных графах с единичным весом как для детерминированных, так и для рандомизированных алгоритмов.
Универсальные последовательности обхода
|
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Декабрь 2016 г.) |
А универсальная последовательность обхода представляет собой последовательность инструкций, составляющих обход графа для любого регулярный граф с заданным количеством вершин и для любой начальной вершины. Вероятностное доказательство было использовано Aleliunas et al. чтобы показать, что существует универсальная последовательность обхода с числом инструкций, пропорциональным О(п5) для любого регулярного графа с п вершины.[4] Шаги, указанные в последовательности, относятся к текущему узлу, а не абсолютны. Например, если текущий узел vj, и vj имеет d соседи, то в последовательности обхода будет указан следующий узел для посещения, vj+1, как яth сосед vj, где 1 ≤ я ≤ d.
Рекомендации
- ^ Rosenkrantz, Daniel J .; Стернс, Ричард Э .; Льюис, II, Филип М. (1977). «Анализ нескольких эвристик для задачи коммивояжера». SIAM Журнал по вычислениям. 6 (3): 563–581. Дои:10.1137/0206041.
- ^ Добрев, Стефан; Кралович, Растислав; Марку, Еврипид (2012). «Исследование графов онлайн с советом». Proc. 19-го Международного коллоквиума по структурной информационно-коммуникационной сложности (SIROCCO). Конспект лекций по информатике. 7355: 267–278. Дои:10.1007/978-3-642-31104-8_23. ISBN 978-3-642-31103-1.
- ^ Ферстер, Клаус-Тихо; Ваттенхофер, Роджер (декабрь 2016 г.). «Нижняя и верхняя границы конкуренции для исследования ориентированного графа в Интернете». Теоретическая информатика. 655: 15–29. Дои:10.1016 / j.tcs.2015.11.017.
- ^ Алелиунас, Р .; Karp, R .; Lipton, R .; Lovász, L .; Ракофф, К. (1979). «Случайные блуждания, универсальные последовательности обходов и сложность задач лабиринта». 20-й ежегодный симпозиум по основам компьютерных наук (SFCS 1979): 218–223. Дои:10.1109 / SFCS.1979.34.
Смотрите также
- Обход графа внешней памяти
Вес (длина) ребра – это число или несколько чисел, которые интерпретируются по отношению к ребру как длина, пропускная способность.
Вес вершины – это число (действительное, целое или рациональное), поставленное в соответствие данной вершине.
Взвешенный граф – это граф, каждому ребру которого поставлен в соответствие его вес.
Вершины (узлы) графа – это множество точек, составляющих граф.
Замкнутый маршрут – это маршрут в графе, у которого начальная и конечная вершины совпадают.
Кратные ребра – это ребра, соединяющие одну и ту же пару вершин.
Маршрут в графе – это конечная чередующаяся последовательность смежных вершин и ребер, соединяющих эти вершины.
Матрица инцидентности – это двумерный массив, в котором указываются связи между инцидентными элементами графа (ребро и вершина).
Матрица смежности – это двумерный массив, значения элементов которого характеризуются смежностью вершин графа
Мультиграф – это граф, у которого любые две вершины соединены более чем одним ребром.
Неориентированный граф (неорграф) – это граф, у которого все ребра не ориентированы, то есть ребрам которого не задано направление.
Обход графа (поиск на графе) – это процесс систематического просмотра всех ребер или вершин графа с целью отыскания ребер или вершин, удовлетворяющих некоторому условию.
Ориентированный граф (орграф) – это граф, у которого все ребра ориентированы, то есть ребрам которого присвоено направление.
Открытый маршрут – это маршрут в графе, у которого начальная и конечная вершины различны.
Петля – это ребро, соединяющее вершину саму с собой.
Поиск в глубину – это обход графа по возможным путям, когда нужно сначала полностью исследовать одну ветку и только потом переходить к другим веткам (если они останутся нерассмотренными).
Поиск в ширину – это обход графа по возможным путям, когда после посещения вершины, посещаются все соседние с ней вершины.
Простой граф – это граф, в котором нет ни петель, ни кратных ребер.
Путь – это открытая цепь, у которой все вершины различны.
Ребра (дуги) графа – это множество линий, соединяющих вершины графа.
Связный граф – это граф, у которого для любой пары вершин существует соединяющий их путь.
Смежные вершины – это вершины, соединенные общим ребром.
Смешанный граф – это граф, содержащий как ориентированные, так и неориентированные ребра.
Список ребер – это множество, образованное парами смежных вершин
Тупик – это вершина графа, для которой все смежные с ней вершины уже посещены
Цепь – это маршрут в графе, у которого все ребра различны.
Цикл – это замкнутая цепь, у которой различны все ее вершины, за исключением концевых.
