7.2.1. Общие положения
Давление грунта на стены зависит от их конструктивных особенностей (наклона и жесткости стены, наличия разгружающих элементов и т.д.), от свойств грунта, взаимодействующего со стеной, от величины и направления перемещений, поворота и прогиба стены [2].
Активное давление грунта σa реализуется при смещении стены от грунта и соответствует минимальному значению давления. Пассивное давление грунта σр реализуется при смещении стены на грунт и соответствует максимальному значению давления. При отсутствии перемещений стены реализуется давление покоя σ0. Изменение давления грунта в зависимости от перемещения стены и представлено на рис. 7.6.

Рис. 7.6. Изменение давления грунта на подпорную стенку в зависимости от ее перемещения
7.2.2. Характеристики грунта, используемые при определении давления грунта
На стенки действует боковое давление грунта нарушенного сложения. Характеристики этого грунта выражаются через соответствующие характеристики грунта ненарушенного сложения следующими соотношениями [3]:
γ’I = 0,95γI; φ’I = 0,9φI;
c‘I = 0,5cI (но не более 7 кПа);
γ’II = 0,95γII; φ’II = 0,9φII;
c‘II = 0,5cII (но не более 10 кПа);
где γI, φI, cI, γII, φII, cII — соответственно удельный вес, угол внутреннего трения и удельное сцепление грунтов ненарушенного сложения для расчетов по первой и второй группам предельных состояний, определяемые в соответствии со СНиП 2.02.01-83.
7.2.3. Активное давление грунта
А. НЕСВЯЗНЫЙ ГРУНТ
В случае свободной от нагрузки наклонной поверхности засыпки и наклонной тыловой грани стены горизонтальная σah и вертикальная σav составляющие активного давления грунта на глубине z (рис. 7.7) определяются по формулам [3, 4]:
где γ — расчетное значение удельного веса грунта; α — угол наклона тыловой грани стены к вертикали, принимаемый со знаком плюс при отклонении от вертикали в сторону стены; δ — угол трения грунта на контакте со стенкой, принимаемый для стен с повышенной шероховатостью равным φ, для мелкозернистых водонасыщенных песков и при наличии на поверхности вибрационных нагрузок равным 0, в остальных случаях равным 0,5φ (здесь φ — расчетное значение угла внутреннего трения грунта); λa — коэффициент активного давления грунта:
 ;
;
(7.3)
здесь ρ — угол наклона поверхности грунта к горизонту, принимаемый со знаком плюс при отклонении этой поверхности от горизонтали вверх: |ρ| ≤ φ.
В частном случае для гладкой вертикальной тыловой грани и горизонтальной поверхности грунта коэффициент активного давления вычисляется по формуле
λa = tg2(45° – φ/2).
(7.4)
Равнодействующие горизонтального Еah и вертикального Eav давлений грунта для стен высотой Н определяются как площади соответствующих треугольных эпюр давлений (рис. 7.7) по формулам:
Б. СВЯЗНЫЙ ГРУНТ
Горизонтальная σ’ah и вертикальная σ’av составляющие активного давления связного грунта на глубине z (см. рис. 7.7) определяются по формулам:
σ’av = σ’ahtg(α + δ),
(7.8)
где σch — давление связности:
здесь с — удельное сцепление грунта;
 .
.
(7.10)

Рис. 7.7. К определению активного давления грунта на стенку
а — несвязного; б — связного
Если значение K, вычисленное по формуле (7.10), меньше нуля, в расчетах принимается K = 0.
В частном случае при горизонтальной поверхности засыпки (ρ = 0) и вертикальной задней грани (α = 0) (или расчетной плоскости) горизонтальная составляющая активного давления грунта на глубине z определяется по формуле
σ’ah = γzλa + c(λa – 1)/tgφ.
Равнодействующая горизонтального Е‘ah и вертикального E‘av давлений грунта для стен высотой Н (см. рис. 7.7) определяется по формулам;
E‘ah = σ’ah(H – hc)/2;
(7.11)
E‘av = σ’av(H – hc)/2;
(7.12)
где
 .
.
(7.13)
В. ДАВЛЕНИЕ НА СТЕНЫ ОТ НАГРУЗКИ НА ПОВЕРХНОСТИ ЗАСЫПКИ
Сплошная равномерно распределенная нагрузка q (рис. 7.8, а). Горизонтальная σqh и вертикальная σqv составляющие активного давления грунта от этой нагрузки на глубине z для связных и несвязных грунтов определяются по формулам:
σqv = σqhtg(α + δ).
(7.15)
Сплошная (на всей призме обрушения) равномерно распределенная нагрузка q, приложенная на расстоянии а от стены (рис. 7.8, б). Горизонтальная σqh и вертикальная σqv, составляющие активного давления грунта от этой нагрузки определяются при z ≥ a/(tgα + tgΘ) по формулам (7.14) и (7.15), а при 0 ≤ z ≤ a/(tgα + tgΘ) (где Θ = 45° – φ/2) σqh = σqv = 0.
Полосовая (ширина полосы b) нагрузка q, приложенная в пределах призмы обрушения на расстоянии а от стены (рис. 7.8, в). Горизонтальная σqh и вертикальная σqv составляющие активного давления грунта от этой нагрузки определяются при a/(tgα + tgΘ) ≤ z ≤ (a + b)/(tgα + tgΘ) по формулам (7.14) и (7.15), а при 0 ≤ z ≤ a/(tgα + tgΘ) и z>(a + б)/(tgα + tgΘ), σqh = σqv = 0.
При расчете подпорных стен давления от нагрузок на поверхности засыпки, вычисленные по формулам (7.14) и (7.15), добавляются к давлениям от грунта, вычисленным по формулам (7.1), (7.2) и (7.7), (7.8).
Г. ДАВЛЕНИЕ ГРУНТА НА УГОЛКОВЫЕ ПОДПОРНЫЕ СТЕНЫ
Для уголковых подпорных стен активное давление грунта на условную поверхность определяется по двум возможным вариантам:
- – для длинной опорной плиты в предположении образования симметричной призмы обрушения (рис. 7.9, а, условная поверхность ab);
- – для короткой опорной плиты — несимметричной призмы обрушения (рис. 7.9, б, условная поверхность abc).

Рис. 7.8. К определению давления грунта от нагрузки на поверхности засыпки

Рис. 7.9. К определению активного давления грунта на угловые подпорные стены
а — при симметричной призме обрушения; б — при несимметричной призме обрушения
В обоих случаях вес грунта, заключенного между условной поверхностью и тыловой поверхностью стены, добавляется к весу стены в расчетах на устойчивость, которые выполняются так же, как и для массивных стен: α = Θ = 45°— φ/2; δ = φ.
7.2.4. Пассивное давление грунта
При горизонтальной поверхности грунта и равномерно распределенной нагрузке на поверхности горизонтальная σph и вертикальная σpv составляющие пассивного давления на глубине z от поверхности определяются по формулам:
 ;
;
(7.16)
σpv = σphtg(α + δ),
(7.17)
где q — нагрузка, равномерно распределенная на поверхности; λph — коэффициент горизонтальной составляющей пассивного давления, определяемый при горизонтальной поверхности грунта по формуле
 .
.
(7.18)
В частном случае при α = δ = 0
λph = tg2(45° + φ/2).
(7.19)
-
Определение активного и пассивного давлений грунта.
Активное давление.
Рассмотрим
простейший случай активного давления
при горизонтальной поверхности
однородного грунта и гладкой вертикальной
грани стенки, контактирующей с грунтом.
Элемент грунта, выделенный вертикальными
и горизонтальными площадками (рис. 6.3,
а), примыкающий к гладкой грани (τ = 0),
будет являться главным элементом. На
гранях этого элемента действуют главные
напряжения σz
и σx.
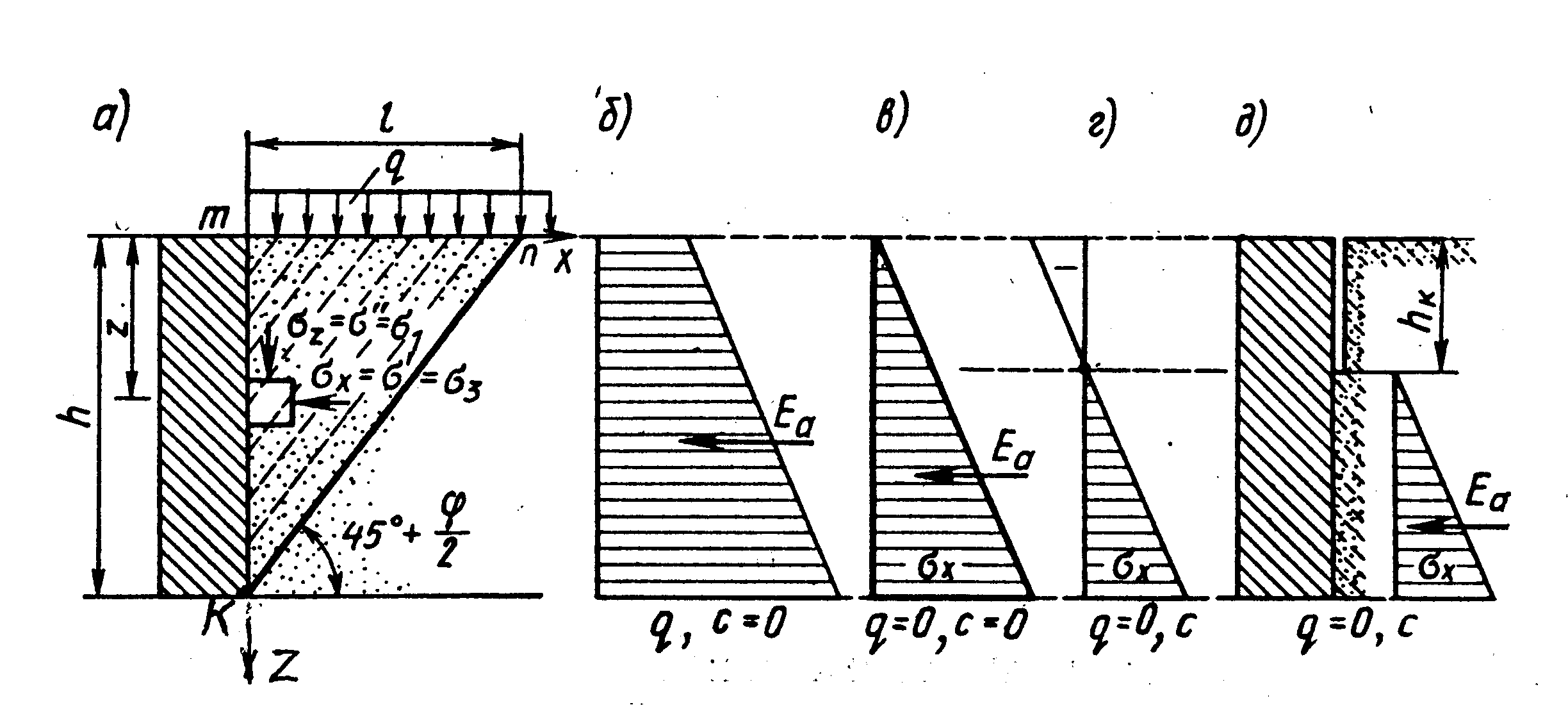
Рис.
6.3. Активное
давление грунта на вертикальную гладкую
стенку:
а —
главный элемент грунта у стенки в призме
обрушения;
б, в — давление
несвязного грунта; г, д — то же,
связного грунта.
Учитывая, что при
смещении стенки от грунта σx
уменьшается, а σz
остается неизменным (σz
= q
+ γz
= const
при z
= const)
и при этом σx
< σz,
то эти напряжения, как главные,
соответственно обозначаются σz
= σ1,
σx
= σ3.
Так как грунт за стенкой считается
находящимся в состоянии предельного
равновесия, то σz
и σx
должны удовлетворять условию предельного
равновесия, в качестве которого
применяется обычно условие Кулона.
Используя это условие в форме зависимости
(3.20/),
получим широко применяемое выражение
для интенсивности активного давления
еа
= σx
= σ3
= σ1∙tg2![]() –
–
2с∙tg![]() =
=
= (q
+ γгр
z)tg2![]() –
–
2c∙tg![]() .
.
(6.1)
По зависимости
(6.1) в случае несвязного
грунта (с =
0) при q
> 0 эпюра интенсивности активного
давления будет трапецеидальной (рис.
6.3, б), при q
= 0 — треугольной (рис. 6.3, в), а
равнодействующая активного давления,
численно равная площади эпюры еа,
при q
≠ 0
определяется выражением
Еа
=
![]() tg2
tg2![]() .
.
(6.2)
Как и давление покоя
Е0, давление Еа, определяемое
по формуле (6.2) и другим (см. ниже), является
суммарным давлением (равнодействующей
давления) на единицу длины (обычно на 1
погонный метр) стены в направлении,
перпендикулярном плоскости хz.
Как показывают
эксперименты, выполненные с несвязными
грунтами, треугольная («классическая»)
эпюра активного давления при q
= 0 (рис. 6.3,в) наблюдается, если контактная
грань стены по всей высоте получает
смещение U ≥ Uа.
В частности, при смещении стены с
поворотом от грунта, «мгновенный» центр
поворота в этом случае должен находиться
ниже подошвы стенки (ниже т.К, рис. 6.3,а),
чтобы Uк
≥ Uа.
В реальных сооружениях указанные условия
обычно обеспечиваются.
Для связного
грунта при q
= 0 зависимость (6.1) дает в верхней части
отрицательные значения давления (рис.
6.3, г), т.е. формально не грунт давит на
стенку, а стена, смещаясь, как бы тянет
за собой грунт, чего, естественно, не
может быть в действительности, между
стеной и грунтом образуется щель. Это
объясняется тем, что при получении
зависимости (6.1) принималось существование
везде предельного состояния, а на самом
деле связный грунт может в пределах
высоты, называемой критической, держать
вертикальный откос, не находясь в
предельном состоянии. Критическая
высота hк —
высота
свободно стоящего вертикального откоса
из связного грунта — легко определяется
из зависимости (6.1), принимая в ней еа
= 0 при q
= 0 и z
= hк,
откуда получаем
hк
=

. (6.3)
Определение
активного давления связного грунта
следует выполнять, полагая наличие
вертикальной
щели в
пределах высоты hк
(рис. 6.3, д). При q
= 0 суммарное активное давление с учетом
(6.1) и (6.3) определяется как площадь
треугольника на рис. 6.3, д по зависимости
![]()
При смещении стенки
от засыпки в ней образуется призма
обрушения, сползающая по поверхности
скольжения, наклоненной
к горизонтали под углом
(450
+ φ/2) (рис. 6.3, а), который легко определяется
при использовании построения круга
Мора для предельного состояния грунта
(см. раздел 3.2, рис. 3.4). Призма обрушения
на поверхности засыпки имеет размер
l
= mn = h∙tg![]() .
.
Изложенный способ
определения ea(z)
и Ea
справедлив только для случая однородной
засыпки грунта за стенкой. Для более
сложных случаев засыпки и нагрузок
применяют различные инженерные приемы,
некоторые из них приводятся ниже.
При наличии
горизонта грунтовых вод
(ГГВ) в случае засыпки из несвязного
грунта угол внутреннего трения φ
практически не меняется и необходимо
учитывать только взвешивание грунта
водой, т.е. ниже ГГВ должен приниматься
удельный вес взвешенного
в воде грунта γвзв
(см. раздел 3.3). Тогда активное давление
в т.2 (рис. 6.4, а) будет
ea
(2) = γгрh/
∙tg2![]() ,
,
а в т.3 — ea
(3) = (γгр∙h/
+ γвзв
∙h//
)∙tg2![]() .
.
Эпюра активного
давления в т.2 имеет излом тем больший,
чем больше разница между γгр
и γвзв.

Рис. 6.4.
Влияние горизонта грунтовых вод (а)
и
слоистости засыпки
(б)
на активное давление.
При слоистой
засыпке в
каждой точке перехода из слоя в слой
должны определяться две величины
давления, в точках немного выше и ниже
границы раздела слоев. Так, для схемы
на рис. 6.4,б в т.2 активное давление будет:
выше границы — ea
= γ/гр∙h/
∙tg2![]() ,
,
ниже границы — ea
= γ/гр∙h/
∙tg2![]() —
—
2c//∙tg![]() .
.
B результате на эпюре в т.2 возникает
скачок давления, причем если грунт
нижележащий прочнее вышележащего, то
скачок направлен в сторону уменьшения
давления (рис. 6.4, б, в) и наоборот (рис.
6.4, г). При большой величине с
возможно даже получение отрицательного
давления ea
(рис.6.4, в), что свидетельствует о
способности связного грунта держать
на этом участке вертикальный откос с
образованием условной щели.
Показанные на рис.
6.3 и 6.4 эпюры получены, исходя из соотношения
(3.20/)
между главными напряжениями, записанного
в форме (6.1) для определения интенсивности
активного давления ea
и затем величины равнодействующей Ea.
В более сложных случаях (наклонная
поверхность грунта и грань стенки и
т.п.) использование зависимости (6.1)
становится невозможным и широкое
распространение получил метод
Кулона,
основанный на гипотезе плоской поверхности
скольжения.
В
расчетной
схеме метода Кулона
принимается, что грунт несвязный,
поверхность скольжения плоская (рис.
6.5, а).

Рис. 6.5.
Расчетная схема метода Ш. Кулона.
По плоскости
обрушения принимается состояние
предельного равновесия, т.е. выполняется
условие Кулона, в соответствии с чем
равнодействующая R
напряжений на поверхности скольжения
отклоняется от нормали к ней на угол
внутреннего трения грунта φ. При
учете трения грунта о шероховатую грань
стенки равнодействующая активного
давления Ea
принимается отклоненной от нормали к
поверхности стены на заданный угол ω,
который обычно меньше φ (в случае гладкой
стены ω = 0). На
выделенную призму обрушения действуют
силы Ea,
R,
известные по направлению, и вес призмы
G,
который при принятом угле наклона
плоскости скольжения θ известен по
направлению и величине. Величина Ea
легко находится из условия равновесия,
т.е. из условия замыкания силового
треугольника на рис. 6.5, б. В треугольнике
стороны относятся как синусы противоположных
углов, откуда
Ea
= G![]() ,
,
(6.4)
где ε — угол,
образуемый тыловой (контактной с грунтом)
гранью стены с вертикальной плоскостью
(рис. 6.5, а).
Анализ
зависимости (6.4) показывает, что Ea
как функция угла θ имеет эстремум
(максимум). Экстремальное значение Ea
и принимается за истинную
величину активного давления. Отвечающий
истинному давлению угол θ находим из
условия
![]() .
.
(6.5)
Задача определения
активного давления по зависимости (6.4)
при подстановке θ из условия (6.5) для
простых случаев, например, для плоской
наклонной поверхности засыпки (рис.
6.5, а, пунктир), решается аналитически.
Величина Ea
определяется по формуле
Еа
=

![]()
, (6.6)
где
z
=
![]() ,
,
α — угол наклона
поверхности засыпки к горизонту, причем
в случае восходящего откоса (рис. 6.5, а,
пунктир) α > 0, в случае нисходящего
(падающего) откоса α < 0.
При значениях α =
0, ω = 0, ε = 0 из зависимости (6.5) получаем
θ =
![]() и
и
суммарное активное давление Еа
по зависимости (6.4) совпадает с величиной
Еа
по формуле (6.2).
Графические решения
задачи поиска θ с наибольшим Еа
позволяют получить активное давление
в более общих случаях неплоской
поверхности засыпки и действующих на
поверхность внешних нагрузок. На рис.
6.6 представлен графический способ К.
Кульмана. В этом способе проводятся
последовательно поверхности скольжения
под разными углами θ (рис. 6.6, а) и строятся
соответствующие силовые треугольники
(рис. 6.6, б). При построении любого
треугольника известны величина и
направление G
(в G
включаются вес грунта и внешние нагрузки,
попадающие в призму обрушения при
соответствующем принятом θ), направления
R
и Еа
(принимаются также, как и в методе
Кулона). В результате построений получают
огибающую всех величин Еа,
проводят к ней вертикальную касательную,
что соответствует выполнению условия
(6.5), и находят искомое максимальное
значение Еа.
Заметим, что в
способах Кулона и Кульмана получают
только равнодействующую активного
давления. Эпюру давления обычно принимают
треугольной формы с давлением, линейно
нарастающим с глубиной.
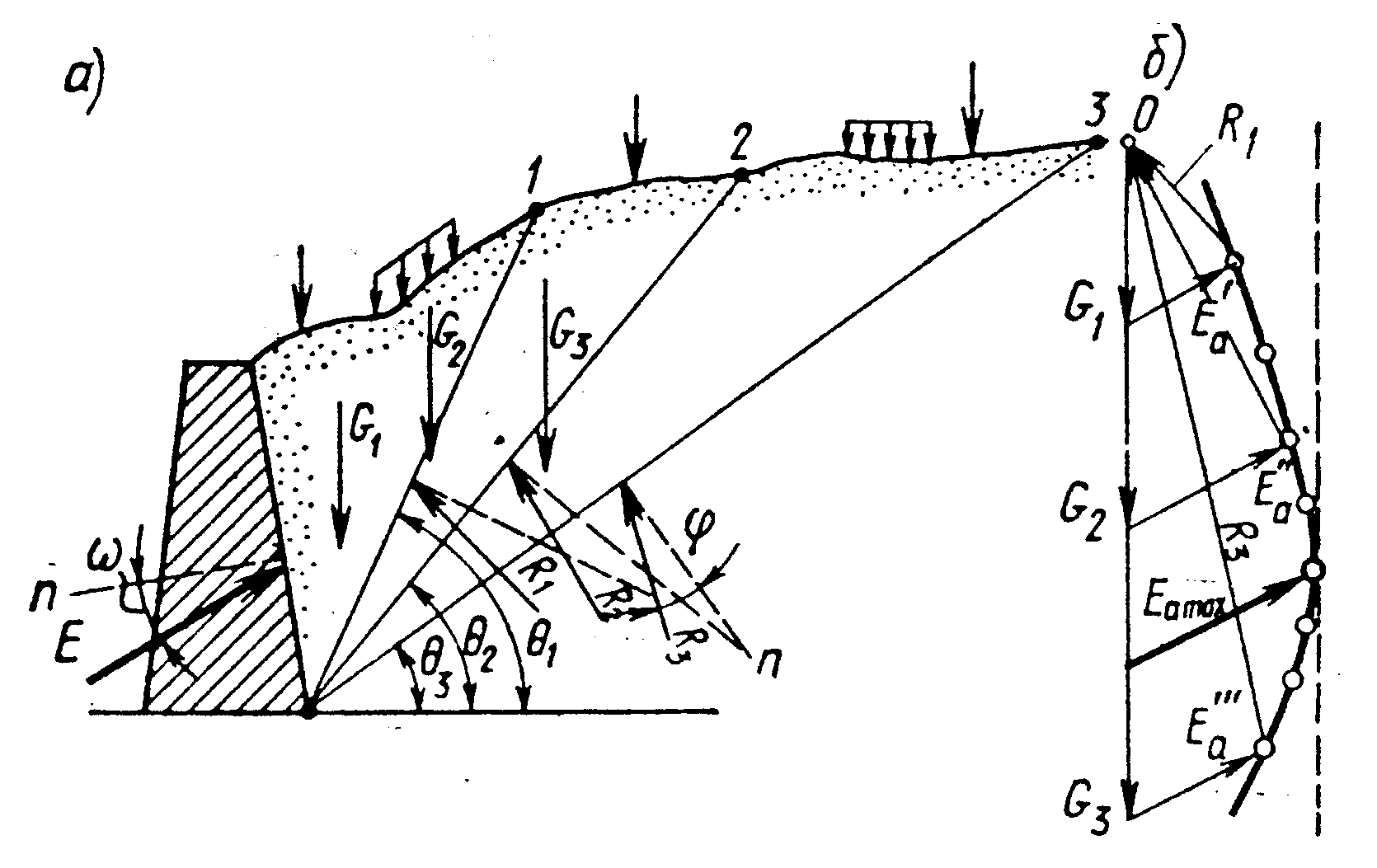
Рис.
6.6.
Графическое определение активного
давления по К. Кульману.
Пассивное
давление.
При принудительном
смещении (внешними нагрузками) стены
на грунт в главном элементе у гладкой
грани стенки (рис. 6.3, а) возникающие
горизонтальные напряжения σx
превышают вертикальные σz,
т.е. в этом случае σx
= σ1,
σz
= σ3.
Поэтому условие предельного равновесия
элемента принимаем в форме (3.20) и для
интенсивности пассивного давления
получаем зависимость
eп
= σz
∙tg2(![]() )
)
+ 2c∙tg(![]() ).
).
Для схемы рис. 6.3,
а имеем σz
= q
+ γгр∙z
и величину
eп
= (q
+ γгр∙z)tg2(![]() )
)
+ 2c∙tg(![]() ),
),
(6.7)
a равнодействующая
пассивного давления определяется
выражением
Eп
= (q∙h
+![]() γгр∙h2)
γгр∙h2)
tg2(![]() )+
)+
2c∙h∙tg(![]() ).
).
(6.8)
В
случае несвязного грунта (с
= 0) и отсутствии нагрузки q
на поверхности засыпки эпюра пассивного
давления будет согласно (6.7) треугольной,
а при наличии нагрузки q
или сцепления с
≠ 0 — трапецеидальной. Заметим, что
при q = 0, с
= 0 и
φ = 300
величина пассивного давления
eп
= γгр∙z∙tg2600
превышает в 9 раз величину активного
давления ea
= γгр∙z∙tg2300.
Поверхность скольжения, ограничивающая
призму выпора, наклонена к горизонту
под углом θ =
![]() .
.
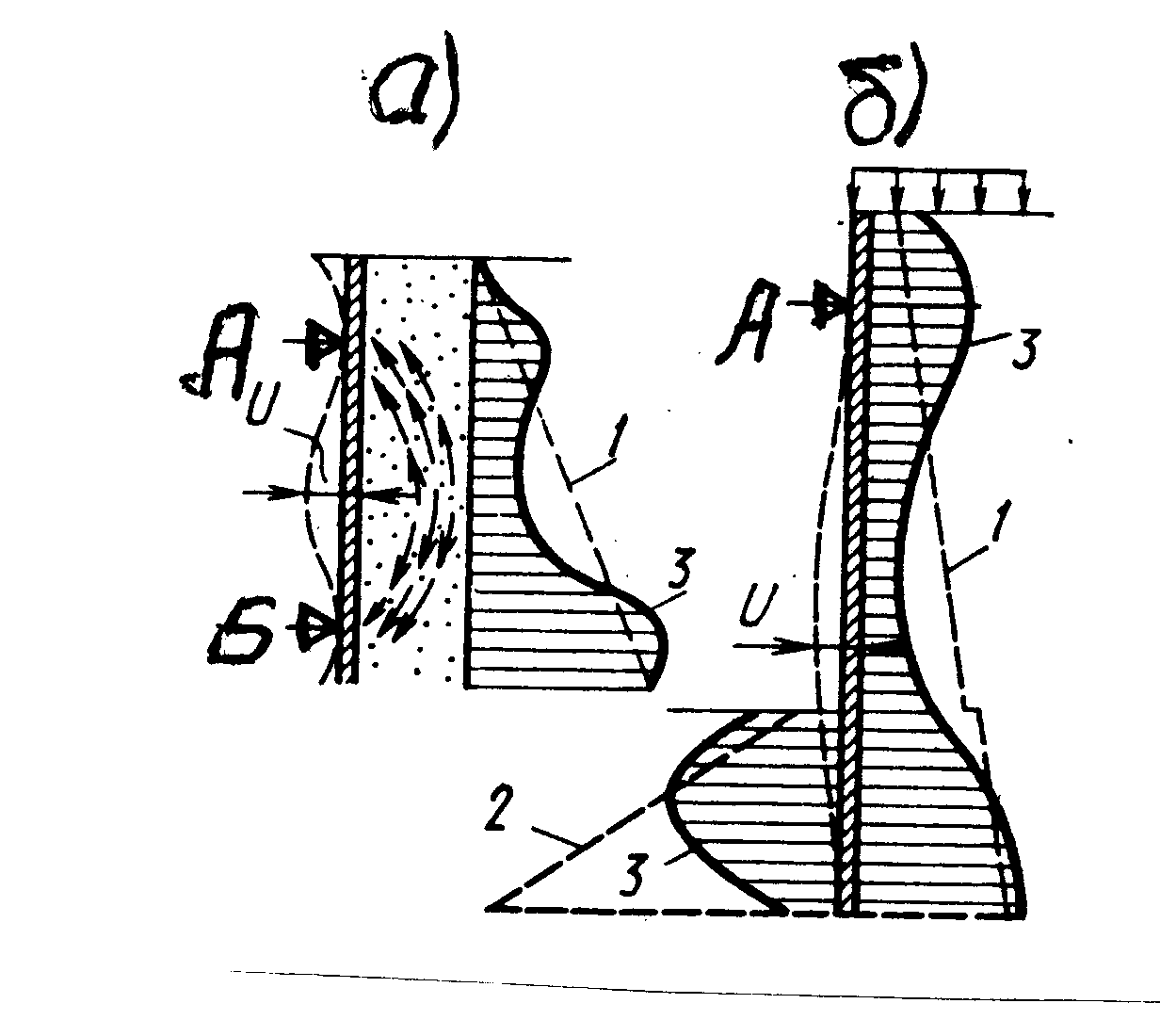
Рис. 6.7.
Влияние гибкости стены на давление
грунта:
1, 2 – активное и
пассивное давление по методу Кулона,
3 – эпюры наблюдаемых
давлений
Для
определения пассивного давления в
случае шероховатых наклонных стен и
наклонной поверхности грунта может
также применяться расчетная схема
Кулона, в которой принимается выпор
грунта по плоской поверхности скольжения.
Расчетная схема аналогична приведенной
на рис. 6.5 с учетом, что силы трения по
поверхности скольжения имеют
противоположное случаю активного
давления направление. Поэтому зависимость,
аналогичная (6.4), в этом случае принимает
вид
Еп
= G![]() .
.
Для
определения Еп
применим также графический вариант
Кульмана с использованием построения,
аналогичного приведенному на рис. 6.6
для активного давления при противоположном
направлении сил трения по поверхности
скольжения.
Приведенные выше
способы определения активного и
пассивного давлений относятся к жестким
массивным сооружениям (стенкам),
контактная с грунтом грань которых при
смещениях остается плоской.
В случаях
изгибаемых сооружений
(тонкие стены, шпунтовые ограждения и
др.) деформации изгиба существенно
влияют на распределение контактных
давлений. Так в случае изгибаемой стены
(рис. 6.7, а) в местах расположения
неподвижных опор (т. А, Б) происходит
возрастание давления выше активного,
а на участках наибольших горизонтальных
смещений U, наоборот, давление становится
меньше активного. Это объясняется
проявлением «арочного» эффекта в
грунтах, вызванного прогибом стенки.
При прогибах стены, показанной на рис.
6.7, б, давление перераспределяется по
ее высоте: уменьшается в пролетной
части, где стена прогибается, и
увеличивается (концентрируется) в зоне
опоры (т. А) и ниже уровня дна котлована.
Действительное очертание эпюры пассивного
давления на заглубленном в грунт участке
стены также не соответствует рассчитанному
по формуле (6.8). Для учета влияния
деформаций изгиба стенки на распределение
контактного давления на нее были
предложены различные инженерные методики
решения контактных задач для изгибаемых
тонких стенок как сооружений конечной
жесткости (глава 4).
В настоящее время
при расчетах изгибаемых конструкций,
подобных представленным на рис. 6.7,
успешно применяются программные
комплексы, перечисленные в гл. 4. Наиболее
совершенные из них позволяют моделировать
тонкие конструкции, определять
напряженно-деформированное состояние
грунта с учетом формирования областей
предельного напряженного состояния.
Определение
давления грунта методом теории предельного
равновесия
(ТПР) выполняется путем численного
интегрирования (В.В.Соколовский, 1960)
уравнений, включающих в случае плоской
задачи два дифференциальных уравнения
равновесия (3.2) и уравнение Кулона в
форме (3.22). Имеются решения для случая
горизонтальной поверхности засыпки из
однородного грунта и для различных
значений угла ε наклона контактной
грани стенки к вертикали и угла трения
ω грунта о стенку [12].
В случае стены с
гладкой вертикальной контактной гранью,
т.е. при ε = 0, ω = 0 (рис. 6.3, а) активное и
пассивное давления по решению ТПР
совпадает соответственно с величинами
давлений по формулам (6.2) и (6.8) приближенного
метода (метода Кулона). При значениях ε
≠ 0, ω ≠ 0 отличие в величине активного
давления по ТПР и приближенному методу
Кулона незначительное и вполне допустимо
определять активное давление по
зависимости (6.6). Влияние сил трения
грунта о стенку и наклона стенки, т.е.
углов ω и ε, существенно отражается на
величине пассивного давления. Приближенные
решения при значительных величинах ω,
ε завышают пассивный отпор по сравнению
с решением ТПР и к использованию решения
Кулона для определения пассивного
давления следует относиться осторожно
[9].
Соседние файлы в папке МГ Бугров
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рассмотрим простейший случай активного давления при горизонтальной поверхности однородного грунта за вертикальным сооружением (стенкой) и идеально гладкой поверхности стенки, т. е. случай, когда по поверхности стенки касательные напряжения равны нулю. Тогда элемент грунта, вырезанный по главным площадкам, будет располагаться на контактной поверхности, как показано на рис. 6.3, а, и ах = о’ = а3, а а2 = в” = а1.
Так как грунт за стенкой считается находящимся в состоянии предельного равновесия, то можно использовать зависимость Кулона в форме (2.48), т. е. в виде зависимости между главными напряжениями. При действии активных сил только от собственного веса грунта и равномерно распределенной нагрузки можно сделать очевидное предположение, что в этом случае всегда сг2 > ох, тогда по зависимости (2.48), т. е. при а’ <. а” а’ = ах = ог2{§2(45°—ф/2) —2с1§(45° — ф/2), или учитывая, что = ст2 = угр2 + </, получим широко применяемое выражение для активного давления.
![grunti_i_osnovania-453.jpg [image]](https://injzashita.com/images/grunti_i_osnovania/grunti_i_osnovania-453.jpg)
Рис. 6.3. Активное давление грунта на вертикальную гладкую стенку:
а — линии скольжения; б, б-—давление несвязного грунта; г, д — давление связного
Высоты засыпки возникают отрицательные давления грунта (рис. 6.3, г), т. е. формально не грунт давит на стенку, а стенка как бы тянет за собой грунт, что, конечно, никак не соответствует действительности. Это объясняется тем, что при решении задачи принято существование везде предельного напряженного состояния, а на самом деле связный грунт может в пределах высоты, называемой критической, держать вертикальный откос и не находиться в предельном напряженном состоянии. Критическая высота свободно стоящего вертикального откоса 1гк из связного грунта (рис. 6.3, г) легко определится из уравнения (6.1), принимая в нем при = 0 и г = Нк ах = 0, т. е.
По этой причине определение активного давления связного грунта следует производить, полагая наличие вертикальной щели между стенкой и засыпкой в пределах слоя толщины, равной критической высоте Нк (рис. 6.3, 5). Тогда при ^ = 0 и Нк < Н активное давление с учетом (6.1) и (6.3) определится как площадь треугольника на рис. 6.3, д, т. е.
Как было показано в § 2.3 и на рис. 2.14, в каждом элементе грунта, находящемся в предельном состоянии, образуются две площадки скольжения, направленные к главным площадкам под углами 45° +
+ ф/2 и 45° — ф/2. В условиях активного давления однородного грунта (стж < сгг) и идеально гладкой вертикальной стенки представляющая интерес для рассматриваемой задачи система прямолинейных площадок скольжения будет расположена к горизонтали под углом 45 + ф/2 (рис. 6.3, а). Вторая система прямолинейных площадок под углом 90 + ф к первой на рис. 6.3, а не приводится. Самая заглубленная площадка скольжения позволяет выделить максимальную
Рис. 6.4. Расчетная схема Ш. Кулона
призму обрушения грунта ктп и определить зону ее распространения по поверхности засыпки I = тп = (45° — ф/2).
В заключение рассмотрения этой простейшей задачи следует отметить, что принятие плоских поверхностей скольжения и получаемые решения (6.1) и (6.2) полностью соответствуют в этом частном случае строгим решениям теории предельного равновесия, элементы которой будут изложены в гл. 9. При поступательном перемещении вертикальной стенки или ее повороте вокруг нижнего ребра и малой ее шероховатости результаты расчета по зависимостям (6.1) и (6.2) хорошо согласуются с опытными данными.
В более сложных случаях, например при наличии сил трения грунта о грань наклонной стенки, образующиеся поверхности скольжения криволинейны и необходимо использовать соответствующие решения теории предельного равновесия. Однако в ряде практических задач широкое распространение получили приближенные решения, основанные на расчетной схеме, предложенной в простейшем варианте (без учета сил трения грунта о стенку) в 1773 г. Ш. Кулоном.
В расчетной схеме Кулона принимается, что грунт, несвязный„ поверхность скольжения плоская и ограничивает клин обрушения * являющийся жестким — недеформируемым телом (рис. 6.4, а). По плоскости обрушения и контактной поверхности клина обрушения с сооружением принимается, что имеет место состояние предельного равновесия, т. е. выполняется условие прочности Кулона, например, в форме (2.36). Поэтому равнодействующая активного давления Еа будет отклонена от нормали к поверхности стенки на угол со, равный углу трения грунта о стенку, а равнодействующая напряжений на поверхности скольжения отклонится от нормали к ней на угол внутреннего трения грунта <р.
В результате на сползающий клин действуют: сила веса призмы обрушения С при заданном угле наклона поверхности скольжения 9, известная по величине и направлению; активное давление грунта Еа, известное по направлению, и равнодействующая напряжений на плоскости скольжения а также известная по направлению при заданном угле 0.
Величина Еа легко находится из условия равновесия, т. е. замыкания силового треугольника на рис. 6.4, б. В треугольнике стороны относятся как синусы противоположных углов, откуда
Еа = 6 5Ш (б — <р)/зш (90° -|- ш -{- г -} ® — 6), (6.5)
где е — угол, образуемый тыловой гранью стенки с вертикальной плоскостью.
Рис. 6.5. Активное давление на наклонную стенку при плоской поверхности засыпки (а) и при различных наклонах поверхности засыпки (б, в)
Однако наклон плоскости скольжения б был выбран произвольно, и поэтому необходимо найти такую величину этого угла, при котором лктивное давление будет максимальным, т. е. выполнить условие, что на пой плоскости
йЕа1й б = 0. (6.6)
.4 а дач а определения Еа из условия (6.6) решается для простейших случаев аналитически, а для более сложных — иногда графически.
При горизонтальной поверхности грунта, вертикальной (е = 0) и гладкой (ю=0) стенках по зависимости (6.5) условие (6.6) приводит к решению б = 45 + (р/2, и выражение для Еа, по Кулону, в точности совпадает с (6.2), полученным на основе строгого решения теории предельного равновесия и предельных соотношений между главными напряжениями.
Представляет интерес случай определения активного давления на наклонную шероховатую стенку при плоской поверхности засыпки (рис. 6.5). Аналогичным путем, определяя в формуле (6.5) величину а из геометрии призмы обрушения и выполняя условие (6.6), было Получено
Е _ Чгрк2 С052 (у — 0 7а 2(1+ VI)2 сок2 г со8 (е + “) где I. = Ып((р + со)5т(ф — а)]/[соз(е + ю)со5(е — а)]; а — угол наклона поверхности грунта засыпки к горизонту.
Углы е и а при отклонении тыловой грани от вертикали или по- нерхности засыпки от горизонтали против часовой стрелки (см.
I>ис. 6.5) принимаются со знаком плюс, при отклонении по часовой ( грелке — со знаком минус. С увеличением крутизны откоса (+а) иктивное давление возрастает (рис. 6.5, б). В случае падающего откоса (—а), наоборот, с увеличением его крутизны активное давление по сравнению с давлением при горизонтальной засыпке (а = 0) существенно уменьшается. Формула (6.7) неприменима при крутых откосах (а > ф), которые сами по себе неустойчивы, и для стен с очень пологой задней гранью (при е > 70—65°). В стенках с очень пологой гранью обрушения смещение грунта происходит не по поверхности контакта стены с грунтом, а по поверхности скольжения, проходящей
внутри массива грунта, а оставшаяся часть грунта перемещается вместе со стенкой.
Рис. 6.6. Графический способ определения давления грунта (К- Кульман)
Графические решения задачи поиска 9 с наибольшим Еа позволяют получить активное давление в более общих случаях действующих нагрузок и при любой поверхности засыпки грунта за стенкой. Например, в способе К- Кульмана, проводя последовательно плоскости скольжения под различными углами 9 (рис. 6.6, а) и строя соответствующие силовые треугольники (рис. 6.6, б), можно получить огибающую всех величин Е&, а проведя к ней вертикальную касательную, т. е. выполнив графически условие (6.6), найти максимальное значение Е&. Все возможные внешние нагрузки входят в величину С.
В способах, основанных на гипотезе Кулона, т. е. для жесткого смещающегося клина, можно получить только равнодействующую активного давления. Эпюру активного давления обычно принимают треугольной формы, пропорциональной глубине расположения рассматриваемой точке грунта засыпки.
ОПРЕДЕЛЕНИЕ БОКОВОГО ДАВЛЕНИЯ ГРУНТА
ОСНОВНОЕ ДАВЛЕНИЕ ГРУНТА
Активное давление (черт. 1)
1. В случаях, ограниченных условиями: поверхность грунта плоская и ![]() , на поверхность грунта равномерно распределена нагрузка g, слои грунта за подпорной стеной параллельны поверхности (черт. 1, а), горизонтальная pah и вертикальная pav составляющие интенсивности активного давления на единицу высоты расчетной плоскости при
, на поверхность грунта равномерно распределена нагрузка g, слои грунта за подпорной стеной параллельны поверхности (черт. 1, а), горизонтальная pah и вертикальная pav составляющие интенсивности активного давления на единицу высоты расчетной плоскости при  на глубине y допускается определять исходя из гипотезы плоских поверхностей скольжения по формулам
на глубине y допускается определять исходя из гипотезы плоских поверхностей скольжения по формулам
 ; (1)
; (1)
 . (2)
. (2)


Черт. 1. Схемы к расчету активного давления грунта
а – в простых случаях;
б – в сложных случаях; 1 – расчетная плоскость;
2 – возможные поверхности обрушения; 3 – вертикальные
плоскости раздела между элементами призмы обрушения
Для связных грунтов pah должно приниматься не менее 0. Сцепление грунта по расчетной плоскости не учитывается.
В формулах (1) и (2):
![]() и C – угол внутреннего трения и удельное сцепление грунта, относимые к первой или второй группе предельных состояний;
и C – угол внутреннего трения и удельное сцепление грунта, относимые к первой или второй группе предельных состояний;
![]() – угол трения грунта по расчетной плоскости, как правило, принимаемый по абсолютной величине не более
– угол трения грунта по расчетной плоскости, как правило, принимаемый по абсолютной величине не более ![]() и не более 30° для плоскости, проходящей в грунте, и не более
и не более 30° для плоскости, проходящей в грунте, и не более ![]() – по контакту сооружения с грунтом;
– по контакту сооружения с грунтом;
py – вертикальное давление в грунте у расчетной плоскости на глубине y
 , (3)
, (3)
где ![]() и
и ![]() – соответственно удельный вес грунта (в случае насыщения грунта водой – с учетом взвешивания) и высота i-го слоя грунта у расчетной плоскости;
– соответственно удельный вес грунта (в случае насыщения грунта водой – с учетом взвешивания) и высота i-го слоя грунта у расчетной плоскости;
![]() и
и ![]() – коэффициенты горизонтальной оставляющей активного давления грунта, определяемые по формулам:
– коэффициенты горизонтальной оставляющей активного давления грунта, определяемые по формулам:
 ; (4)
; (4)
 ; (5)
; (5)
здесь
 ;
;
 ;
;
 .
.
При определении горизонтальной Eah и вертикальной Eav составляющих давления грунта суммирование эпюр интенсивности давления производится по высоте.
Если расчетная плоскость проходит в грунте, то следует определять давление при нескольких возможных ее положениях (нескольких углах ![]() ), приняв за расчетное наивыгоднейшее для рассматриваемого предельного состояния. В однородном грунте на участке, где
), приняв за расчетное наивыгоднейшее для рассматриваемого предельного состояния. В однородном грунте на участке, где  (пологая стена), расчетную плоскость допускается принимать под углом
(пологая стена), расчетную плоскость допускается принимать под углом  .
.
2. В общем случае горизонтальную Eah и вертикальную Eav составляющие активного давления грунта на расчетную плоскость (черт. 1, б) допускается определять, намечая возможные поверхности обрушения 2 от низа расчетной плоскости 1. При больших неравномерных нагрузках на поверхности грунта и слоях, резко отличающихся по характеристикам, поверхности обрушения могут быть неплоскими. Следует также рассматривать поверхности, частично или полностью проходящие по поверхности котлована или слабым прослойкам.
Для каждой поверхности обрушения определяют значение горизонтальной Eah составляющей бокового давления грунта. Наибольшее значение Eah будет искомой горизонтальной составляющей активного давления, а соответствующая этой величине поверхность обрушения – расчетной.
Для определения Eah призму обрушения разделяют вертикальными плоскостями 3 на отдельные элементы таким образом, чтобы в основании каждого был однородный грунт и основание можно было считать плоским. При ![]() элемент между расчетной плоскостью и вертикалью, проведенной через ее низ, как самостоятельный элемент не рассматривается: в зависимости от того, что может дать
элемент между расчетной плоскостью и вертикалью, проведенной через ее низ, как самостоятельный элемент не рассматривается: в зависимости от того, что может дать  значение Eah, вес этого элемента
значение Eah, вес этого элемента ![]() присоединяется к ближайшему или распределяется между остальными, например, пропорционально их весам Gi.
присоединяется к ближайшему или распределяется между остальными, например, пропорционально их весам Gi.
Горизонтальная Eah и вертикальная Eav составляющие бокового давления грунта определяют по формулам:
 ; (6)
; (6)
 , (7)
, (7)
где n – число элементов в призме обрушения;
 ; (8)
; (8)
 , (9)
, (9)
здесь Gi – сумма вертикальных составляющих нагрузок, включая вес элемента, нагрузки на его поверхности и др.,
Fh – сумма горизонтальных составляющих нагрузок в пределах ширины элемента bi, в том числе фильтрационные силы (со знаком “плюс” – при направлении в сторону расчетной плоскости),
bi – ширина элемента,
![]() – угол внутреннего трения у основания элемента,
– угол внутреннего трения у основания элемента,
ci – средневзвешенное значение удельного сцепления по высоте элемента,
![]() – угол между вертикалью и поверхностью обрушения, принимается со знаком “плюс” – по направлению часовой стрелки,
– угол между вертикалью и поверхностью обрушения, принимается со знаком “плюс” – по направлению часовой стрелки,
![]() – средневзвешенное значение угла трения по расчетной плоскости.
– средневзвешенное значение угла трения по расчетной плоскости.
Если вычисленное значение Eah < 0, то следует принимать Eah = 0. Если сила Eav < 0, то она направлена вверх.
Для определения интенсивности давления pah и точки приложения сил Eah и Eav принимают допущение, что давление на любую часть стены высотой ![]() < H можно определить тем же способом, что и для всей стены. Вследствие этого выбирают на расчетной плоскости несколько характерных точек на глубинах yj и для каждой определяют указанным выше способом давление Eahj, а затем вычисляют среднюю интенсивность давления на участке (yj – yj-1) по формулам:
< H можно определить тем же способом, что и для всей стены. Вследствие этого выбирают на расчетной плоскости несколько характерных точек на глубинах yj и для каждой определяют указанным выше способом давление Eahj, а затем вычисляют среднюю интенсивность давления на участке (yj – yj-1) по формулам:
 , (10)
, (10)
 . (11)
. (11)
Для верхних участков, которые удовлетворяют условиям применимости формул (1) и (2), можно для упрощения расчета использовать рекомендации п. 1.
Давление грунта в состоянии покоя
3. При горизонтальной поверхности и горизонтальных слоях грунтов, равномерно распределенной нагрузке g на поверхности грунта интенсивность давления на жесткую несмещаемую в горизонтальном направлении вертикальную расчетную плоскость при отсутствии трения грунта по этой плоскости определяется по формуле
 , (12)
, (12)
где py – см. формулу (3),
![]() – коэффициент бокового давления грунта в состоянии покоя.
– коэффициент бокового давления грунта в состоянии покоя.
 , (13)
, (13)
здесь ![]() – коэффициент поперечной деформации грунта, принимаемый при отсутствии опытных данных по СНиП 2.02.02-85.
– коэффициент поперечной деформации грунта, принимаемый при отсутствии опытных данных по СНиП 2.02.02-85.
4. В общем случае давление грунта на жесткую подпорную стену допускается определять как активное, принимая удельное сцепление грунта равным нулю и условное значение угла внутреннего трения по формуле
 . (14)
. (14)
Давление грунта на внутренние стены ячеек (оболочек)
(черт. 2)

Черт. 2. Схема к расчету давления грунта на внутренние
стены ячеек (оболочек)
1 – ячейка; 2 – грунт засыпки; 3 – грунт основания
5. При равномерно распределенной нагрузке q на уровне верха ячейки горизонтальная и вертикальная составляющие интенсивности давления грунта на глубине y определяются по формулам:
 ; (15)
; (15)
 , (16)
, (16)
где py – вертикальное давление на глубине ![]() :
:
 , (17)
, (17)
здесь  ; (18)
; (18)
![]() – удельный вес грунта внутри ячейки на глубине y;
– удельный вес грунта внутри ячейки на глубине y;
yi – высота i-го слоя грунта над поверхностью слоя, в пределах которого определяется pah;
py,i – вертикальное давление на поверхности слоя, в пределах которого определяется pah (для верхнего первого слоя при y <= y1 py,i = py1 = g; для второго при y > y1 вычисляется по формуле (17), принимая y = y1 и py,i = g и т.д.);
A и u – соответственно площадь и периметр ячейки (для квадратных и круглых ячеек A/u = d/4, для параллельных стен A/u = d/2 (d – расстояние между стенами ячейки или диаметр круглой ячейки);
![]() – коэффициент горизонтальной составляющей давления грунта, определяемый по формуле (4). Для жестких, не расширяющихся в горизонтальном направлении ячеек расчет ведется на условное значение угла внутреннего трения, определенное по формуле (14). Угол трения
– коэффициент горизонтальной составляющей давления грунта, определяемый по формуле (4). Для жестких, не расширяющихся в горизонтальном направлении ячеек расчет ведется на условное значение угла внутреннего трения, определенное по формуле (14). Угол трения ![]() допускается принимать постоянным в пределах высоты слоя грунта: при Ef >= 4Ec или при наличии у ячейки днища
допускается принимать постоянным в пределах высоты слоя грунта: при Ef >= 4Ec или при наличии у ячейки днища ![]() = 2/3
= 2/3![]() , при Ef < Ec
, при Ef < Ec  , если
, если ![]() , и
, и  , если y > ycr; Ef и Ec – соответственно модули деформации грунта основания и внутри ячейки; ycr – глубина, на которой осадка грунта внутри ячейки равна осадке ячейки, т.е. отсутствует вертикальное смещение грунта относительно расчетной поверхности (как правило, ycr определяется путем последовательных приближений).
, если y > ycr; Ef и Ec – соответственно модули деформации грунта основания и внутри ячейки; ycr – глубина, на которой осадка грунта внутри ячейки равна осадке ячейки, т.е. отсутствует вертикальное смещение грунта относительно расчетной поверхности (как правило, ycr определяется путем последовательных приближений).
Пассивное давление (черт. 3)

Черт. 3. Схема к расчету пассивного давления грунта
6. При плоской поверхности грунта, равномерно распределенной нагрузке g на поверхности грунта и слоях грунта, параллельных поверхности, горизонтальная pph и вертикальная ppv составляющие пассивного давления грунта на единицу высоты расчетной плоскости определяются по формулам:
 ; (19)
; (19)
 , (20)
, (20)
где py, ![]() и c – см. п. 1;
и c – см. п. 1;
![]() и
и ![]() – коэффициенты горизонтальной составляющей пассивного давления грунта;
– коэффициенты горизонтальной составляющей пассивного давления грунта;
![]() – угол наклона расчетной плоскости к вертикали, принимаемый со знаком “минус” при наклоне от грунта;
– угол наклона расчетной плоскости к вертикали, принимаемый со знаком “минус” при наклоне от грунта;
![]() – угол трения грунта по расчетной плоскости, принимаемый равным по абсолютной величине от 0 до
– угол трения грунта по расчетной плоскости, принимаемый равным по абсолютной величине от 0 до ![]() – при определении
– при определении ![]() по табл. 1 или формуле (21) и от 0 до 2/3
по табл. 1 или формуле (21) и от 0 до 2/3 ![]() – при определении
– при определении ![]() по формуле (22).
по формуле (22).
При ![]() и учете криволинейных поверхностей выпора
и учете криволинейных поверхностей выпора ![]() следует определять по табл. 1 или при
следует определять по табл. 1 или при  – по формуле
– по формуле
 . (21)
. (21)
Таблица 1
|
|
|
Коэффициенты |
||||||
|
-30 |
-20 |
-10 |
0 |
+10 |
+20 |
+30 |
||
|
5 |
0 |
1,09 |
1,12 |
1,14 |
1,18 |
1,22 |
1,26 |
1,30 |
|
5 |
1,15 |
1,18 |
1,22 |
1,27 |
1,32 |
1,37 |
1,42 |
|
|
10 |
0 |
1,20 |
1,24 |
1,33 |
1,42 |
1,51 |
1,62 |
1,75 |
|
5 |
1,34 |
1,42 |
1,47 |
1,55 |
1,62 |
1,77 |
1,91 |
|
|
10 |
1,45 |
1,51 |
1,56 |
1,63 |
1,71 |
1,79 |
1,95 |
|
|
15 |
0 |
1,30 |
1,39 |
1,55 |
1,69 |
1,93 |
2,07 |
2,34 |
|
7,5 |
1,58 |
1,72 |
1,78 |
1,95 |
2,13 |
2,39 |
2,60 |
|
|
15 |
1,80 |
1,90 |
2,05 |
2,12 |
2,32 |
2,53 |
2,84 |
|
|
20 |
0 |
1,45 |
1,60 |
1,80 |
2,04 |
2,32 |
2,79 |
3,17 |
|
10 |
1,86 |
2,06 |
2,25 |
2,51 |
2,84 |
3,28 |
3,73 |
|
|
20 |
2,27 |
2,40 |
2,61 |
2,86 |
3,15 |
3,49 |
3,86 |
|
|
25 |
0 |
1,58 |
1,74 |
2,12 |
2,46 |
3,00 |
3,68 |
4,30 |
|
12,5 |
2,23 |
2,55 |
2,79 |
3,67 |
3,86 |
4,78 |
5,77 |
|
|
25 |
2,87 |
3,16 |
3,48 |
3,94 |
4,59 |
5,36 |
5,83 |
|
|
30 |
0 |
1,72 |
2,02 |
2,43 |
3,00 |
3,70 |
4,70 |
6,10 |
|
15 |
2,74 |
3,17 |
3,71 |
4,46 |
5,45 |
7,42 |
8,66 |
|
|
30 |
3,72 |
4,23 |
4,86 |
5,67 |
6,65 |
7,82 |
9,01 |
При ![]() и
и ![]() , учете плоских поверхностей выпора – по формуле
, учете плоских поверхностей выпора – по формуле
 , (22)
, (22)
где
 . (23)
. (23)
Коэффициент ![]() определяется по формуле
определяется по формуле
 . (24)
. (24)
При значении  вертикальная составляющая интенсивности пассивного давления направлена вниз.
вертикальная составляющая интенсивности пассивного давления направлена вниз.
Горизонтальная Eph и вертикальная Epv составляющие пассивного давления грунта определяются суммированием эпюр интенсивности давления грунта по высоте.
7. В общем случае пассивное давление грунта следует определять методами, учитывающими образование в предельном состоянии криволинейных поверхностей выпора, в частности, методами, основанными на теории предельного равновесия сыпучей среды.
В сложных случаях (неплоские и непараллельные границы слоев грунта, неплоская поверхность и др.) допускается определять пассивное давление исходя из предположения об образовании плоской (для однородного грунта и ![]() ) или ломаной поверхности выпора методом, аналогичным указанному в п. 2. При этом Eph и Epv следует определять по формулам:
) или ломаной поверхности выпора методом, аналогичным указанному в п. 2. При этом Eph и Epv следует определять по формулам:
 ; (25)
; (25)
 . (26)
. (26)
За расчетное значение Eph принимается наименьшее из значений, вычисленных при различных поверхностях выпора.
При значении Epv меньше нуля вертикальная составляющая давления направлена вниз.
ДОПОЛНИТЕЛЬНОЕ (РЕАКТИВНОЕ) ДАВЛЕНИЕ ГРУНТА
8. Дополнительное (реактивное) давление грунта засыпки допускается определять расчетом сооружения во взаимодействии с упругой невесомой средой. Учитывается воздействие временных длительных нагрузок, вызывающих отпор грунта засыпки (температурные воздействия, дополнительное давление воды при наполнении камер шлюзов, деформации основания, приводящие к перемещению стены на грунт засыпки); влияние близко расположенных сооружений и скальных склонов; изменения деформативных характеристик грунта по глубине засыпки.
Деформативность грунта определяется либо модулем деформаций En и коэффициентом поперечной деформации грунта ![]() , либо коэффициентом упругого отпора K.
, либо коэффициентом упругого отпора K.
Модуль деформаций грунта следует принимать на основании данных лабораторных или полевых исследований, выполняемых в соответствии со СНиП 2.02.02-85. Допускается использовать табличные нормативные значения модулей деформаций по СНиП 2.02.01-83 для глинистых грунтов и по табл. 2 для несвязных грунтов.
Таблица 2
|
Виды грунтов |
Нормативные значения модуля деформаций несвязных грунтов En, МПа (кгс/см2), при коэффициенте пористости e |
||
|
0,45 |
0,55 |
0,65 |
|
|
Горная масса |
60 (600) |
50 (500) |
40 (400) |
|
Галечный грунт |
55 (550) |
45 (450) |
35 (350) |
|
Песок |
|||
|
гравелистый крупный |
50 (500) |
40 (400) |
30 (300) |
|
средней крупности |
45 (450) |
38 (380) |
28 (280) |
|
мелкий |
40 (400) |
30 (300) |
26 (260) |
При определении дополнительного (реактивного) давления грунта должно учитываться изменение жесткости конструкции в связи с образованием и раскрытием трещин. Расчет производится в соответствии с указаниями СНиП 2.06.08-87.
При длительно действующих и медленно изменяющихся нагрузках (например, температурное воздействие) деформационные характеристики засыпок из несвязных грунтов допускается принимать сниженными на 30% по сравнению с характеристиками при кратковременном загружении.
При расчете на температурные воздействия определение углов поворота и продольных перемещений элементов конструкций производится на действие температуры td и перепад температур ![]() .
.
Расчетную температуру td и перепад ![]() надлежит определять по общим правилам расчетов нестационарного температурного поля сооружений за шестимесячный период: от самого холодного t1 до самого теплого месяца t2.
надлежит определять по общим правилам расчетов нестационарного температурного поля сооружений за шестимесячный период: от самого холодного t1 до самого теплого месяца t2.
При таком расчете действительная криволинейная эпюра распределения температур заменяется статически эквивалентной трапецеидальной эпюрой, по которой определяются средние значения tmt1,2 и ![]() , а расчетные температуры вычисляются как разности:
, а расчетные температуры вычисляются как разности:
td = tmt2 – tmt1; (27)
 . (28)
. (28)
Приложение 10
Обязательное
Скачать документ целиком в формате PDF
