Математика – довольно непростая наука, однако усвоить ее азы нужно каждому. Без этих навыков и знаний в современном мире никуда.
Элементарные математические приемы и задачи закладываются в память школьников еще в младших классах. А «упустив» более легкий материал, решить сложные задания становится не под силу. Долгие и серьезные уроки математики делают детей особо неусидчивыми, а значит подавать информацию нужно в игровой форме, например, с помощью ребусов. Такие задания не нужно заставлять решать из-под палки, детки сами охотно будут браться за их разгадывание.
Далее вы узнаете, чем же все-таки полезны математические ребусы для школьников, научитесь составлять и разгадывать разные ребусы и головоломки вместе со своими отпрысками.
Главное в статье
- Польза ребусов на математическую тему для развития ребенка
- Правила составления математических ребусов для детей
- Как придумать математический ребус?
- Особенности математических ребусов для начальной школы
- Математические ребусы для 1 класса с ответами
- Математические ребусы для 2 класса с ответами
- Математические ребусы для 3 класса с ответами
- Математические ребусы для 4 класса с ответами
- Математические ребусы для 5 класса с ответами
- Математические ребусы для 6 класса с ответами
- Математические ребусы с цифрами с ответами
- Математические загадки, ребусы, кроссворды
- Как решать математические ребусы с буквами?
- Решение математических ребусов с буквами
- Математические ребусы и головоломки
- Самые легкие математические ребусы
- Сложные математические ребусы
Польза ребусов на математическую тему для развития ребенка
Ребусы на математическую тему – это те же загадки и головоломки, в которых используются рисунки и графика. Они бывают разные по уровню сложности в зависимости от возрастной категории школьников.
- В тех случаях, когда ребенок разгадывает, а особенно, когда составляет ребусы для своих сверстников – очень хорошо развивается логическое мышление и тренируется интеллект.
- Есть ребусы, решение которых требует немалых усилий со стороны ребятни. Пытаясь найти разгадку, дети развивают у себя нестандартное мышление. В будущем это умение здорово пригодится, когда нужно будет принять решения и найти выход из жизненных проблем.
- И самое главное: процесс разгадывания математических ребусов здорово поднимает настроение, а также помогает лучше построить отношения со сверстниками.
Правила составления математических ребусов для детей
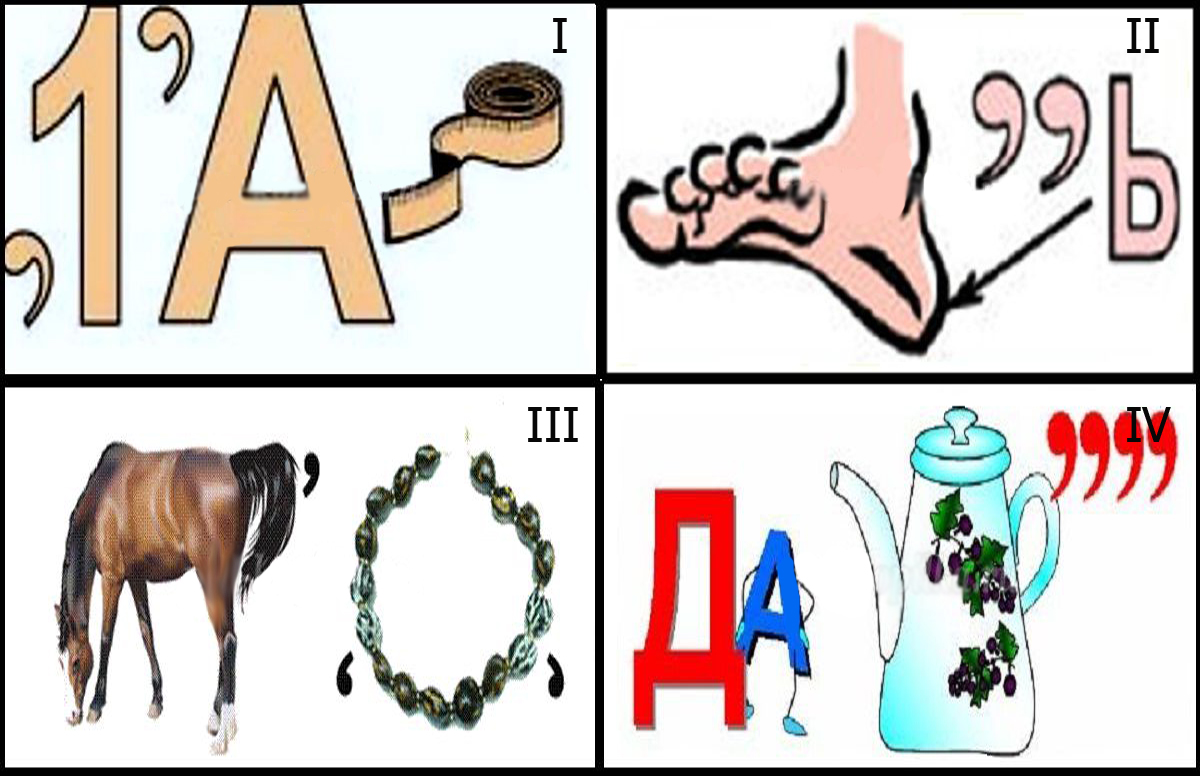
- Если вы видите перед словом или картинкой запятую, то нужно убрать первую букву с этого названия. То же самое нужно сделать, если запятая стоит в конце слова. Когда около картинки две запятых, то убирается две буквы соответственно. Например, на первой картинке изображен сок — нужно убрать первую букву «С», рука — уберите слог «ка», буква «ж» так и остается, нос — слово остается целиком, пять — уберите две первые буквы. Зашифрованное слово — «окружность».
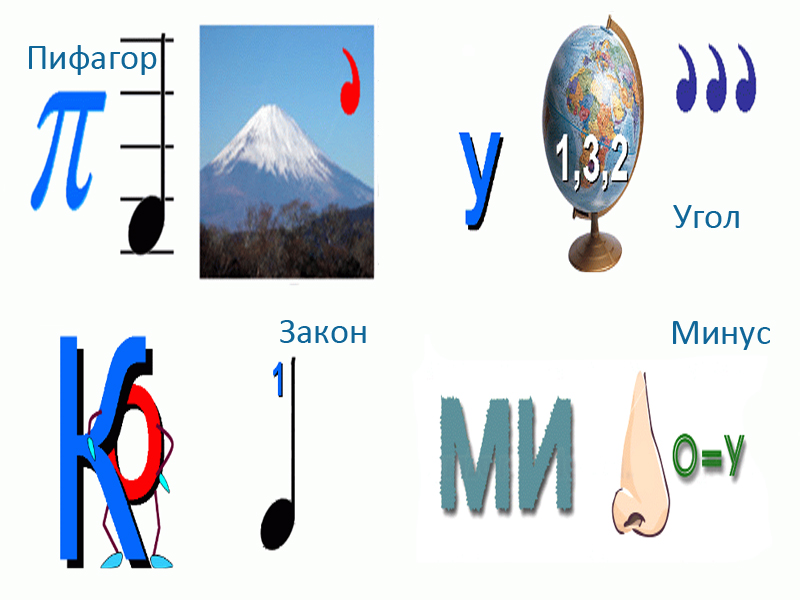
- Если цифры, обозначающие последовательность букв в слове зачеркнуты, то их необходимо выбросить из него. Тоже самое касается и букв. На втором рисунке изображен цирк — уберите последнюю букву, из слова «акула» нужно убрать букву «А», готовый ответ: «циркуль».
- Когда рядом с картинкой стоят цифры, поменянные местами, то и в названии самого предмета нужно поменять местами буквы, которые стоят в последовательности с указанными цифрами.
- Если картинка изображена вверх тормашками, то отгадку нужно читать в обратном порядке: справа-налево.
- Для ребусов используется только именительный падеж в словах.
- Указатель в виде стрелки или математический знак «равно» обозначает, что нужно заменить буквы одну другой.
- В ребусах одно значение может быть расположено внутри другой картинки, за ней или под ней. Тогда применяйте слова: В, НА, НАД, ПОД, ЗА.
- Цифры, стоящие в ряд около изображения, обозначают, что нужно использовать из этого значения буквы в указанной последовательности цифр.
Вот несколько примеров математических ребусов, соответствующих приведенным правилам:
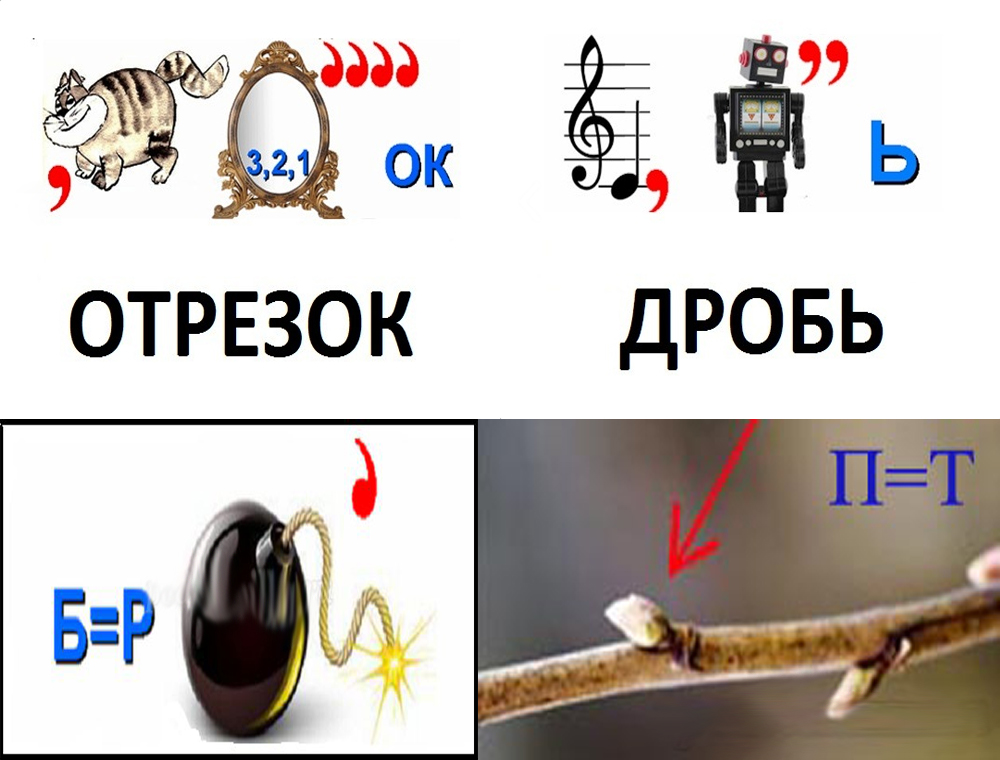
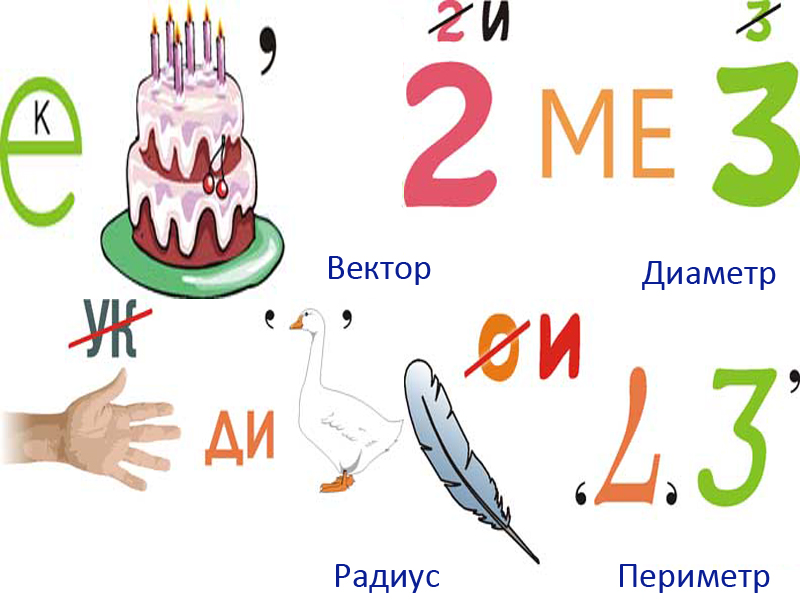
Под третьим рисунком зашифровано слово «вектор», под четвертым — «степень», под пятым — «два», под шестым — «доказательство».
Как придумать математический ребус?
Следуя общим правилам составления ребусов, попробуйте придумать для начала несложные математические задачки, используя цифры и математические термины. А затем, немного освоив простые задания, переходите к более усложненным. Вот несколько образцов ребусов по математике с ответами, которые вдохновят вас и покажут, как их нужно составлять:
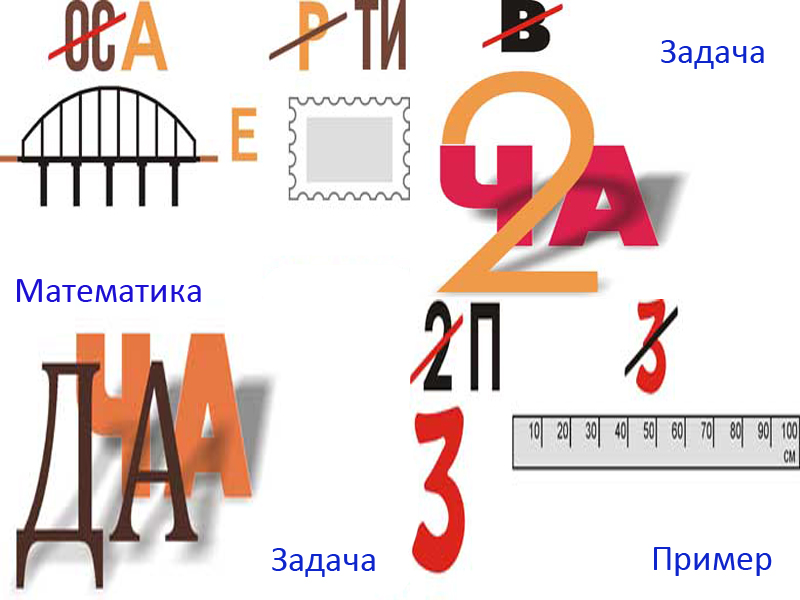
Ответы: первый ребус — «диаметр», второй — «пять», третий — «конус», четвертый — «задача».
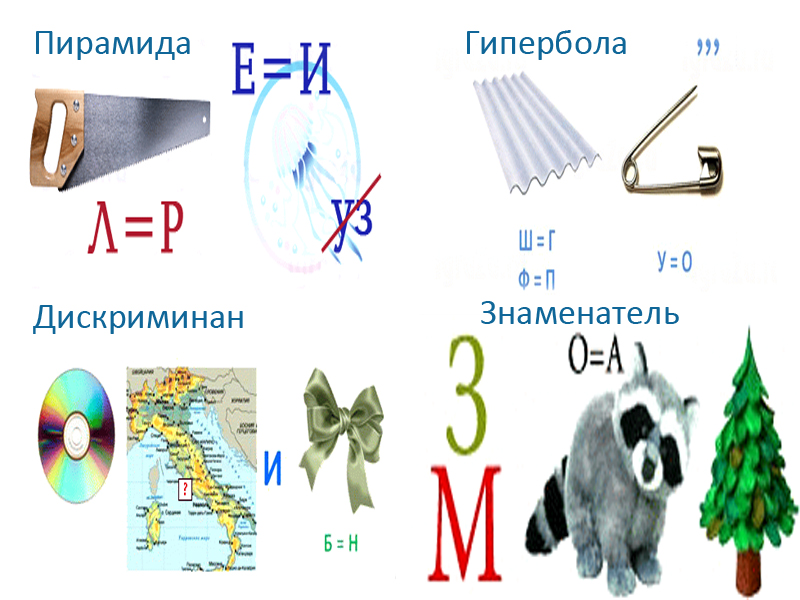
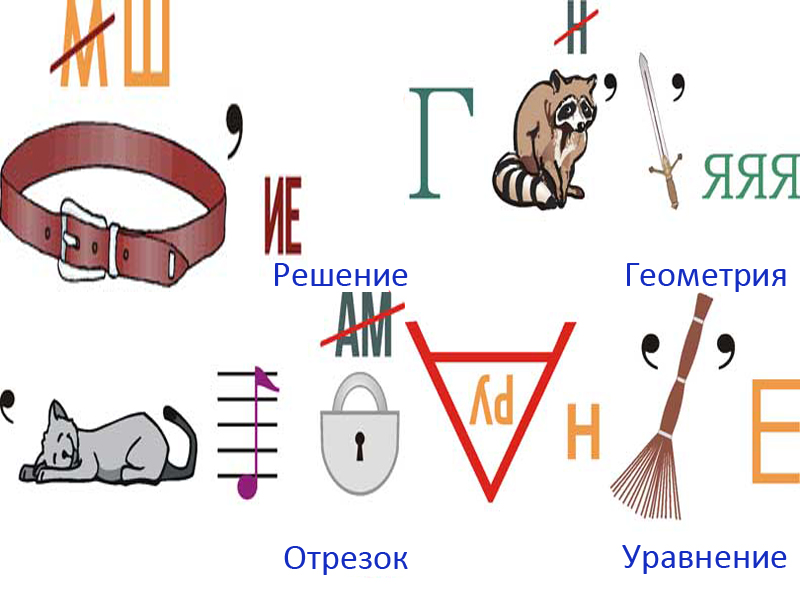
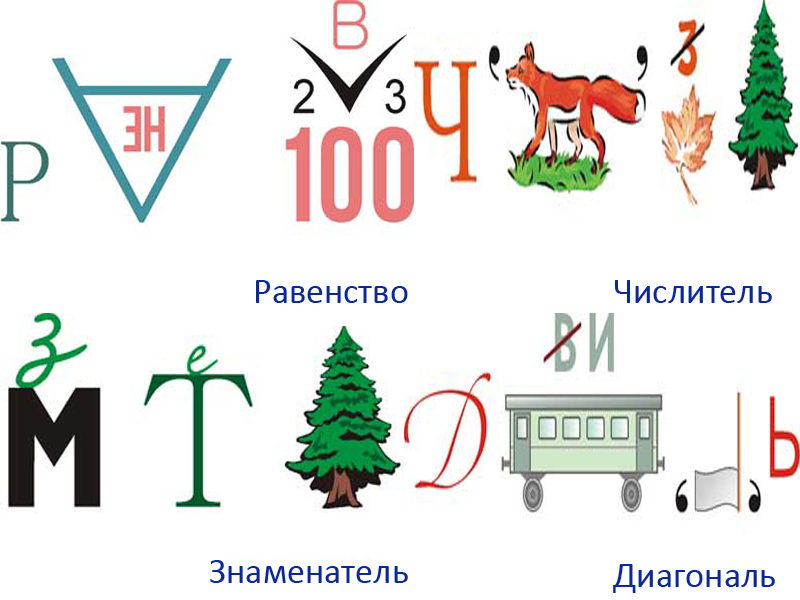
Пятая картинка — «алгебра», шестая — «геометрия», седьмая — «линейка», восьмая — «уравнение».
Девятая загадка — «диаметр», десятая — «циркуль», одиннадцатая — «транспортир», двенадцатая — «конус».
Особенности математических ребусов для начальной школы
Лучше всего приобщать ребенка к разгадыванию математических ребусов еще в детском саду, в выпускной группе. Это послужит отличной разминкой перед школой, освежит у малыша весь пройденный материал с педагогом.
Только нужно учитывать, что такие ребусы должны быть довольно легкими, и включать только те знания, которые ребенок уже усвоил и знает. Это может быть головоломка из двух-трех составляющих, ответ которой таит в себе простое математическое значение.
Эти же ребусы пригодятся для «разогрева» первоклашек. Поступление в школу – и так огромная эмоциональная нагрузка для ребенка, поэтому не стоит удручать обучение математике столь сложными ребусами. Подойдут следующие примеры:
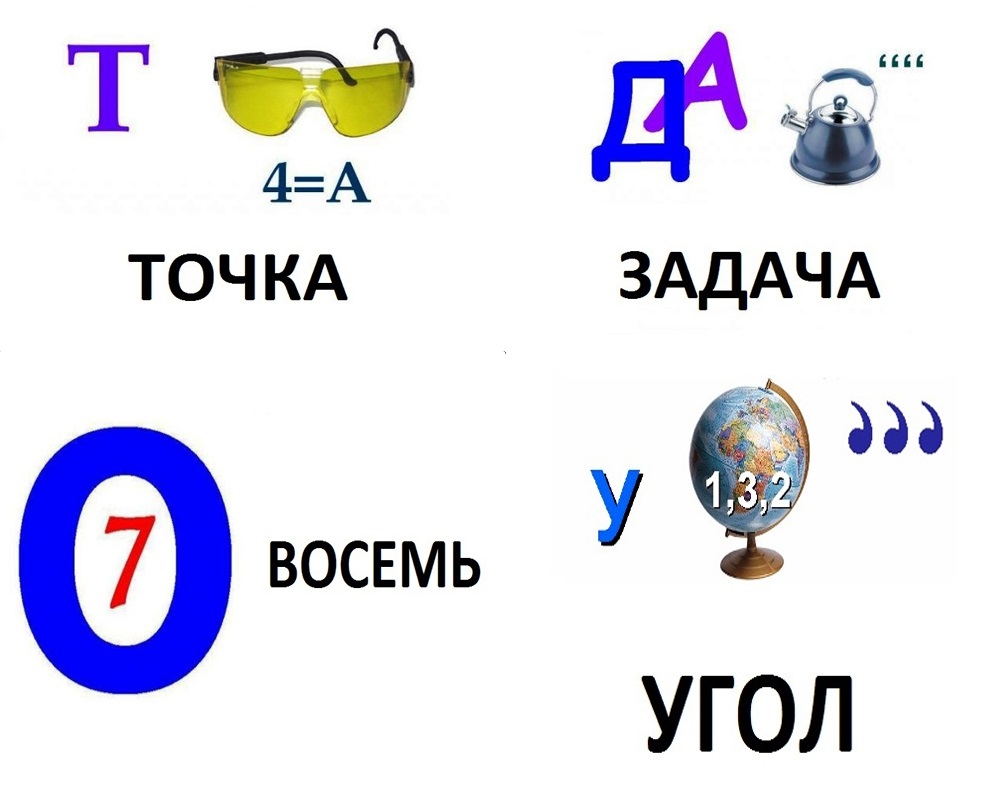
Первоклассники уже хорошо знают цифры и простые математические действия, которые можно включить в ребусы. Причем для таких ребусов характерно то, что математическое значение может присутствовать как в самой загадке, так и в ее значении. А может случиться такое, что ответ совершенно не будет связан с этой точной наукой. Предложите ребенку следующие математические ребусы:
Математические ребусы для 2 класса с ответами
Для того, чтобы составить математический ребус второкласснику, нужно ориентироваться в его знаниях, то есть предлагаемая задача должна быть ему посильной. Вот что должен знать и уметь учащийся во втором классе:
- При решении заданий использовать в правильном порядке числа от 1 до 100, правильно озвучивая их.
- Решать примеры сложения и вычитания чисел, которые не превышают цифру 20.
- В ряде случаев применять математические действия умножения и деления.
- Четко знать правила использования скобок в примерах и решать их.
- Применять в своей лексике единицы измерения длины и объема.
- Вести сравнения больше-меньше цифр в пределах 100.
- Уметь устно прибавлять и отнимать числа в пределах 100.
- Решать несложные задачи с четырьмя основными арифметическими действиями, уметь увеличивать (уменьшать) число на (в) раз (единиц).
- С помощью линейки чертить и мерить длину отрезка.
- Распознавать плоские углы.
- Узнавать и озвучивать плоские геометрические фигуры.
- Уметь вычислять периметр многоугольников.
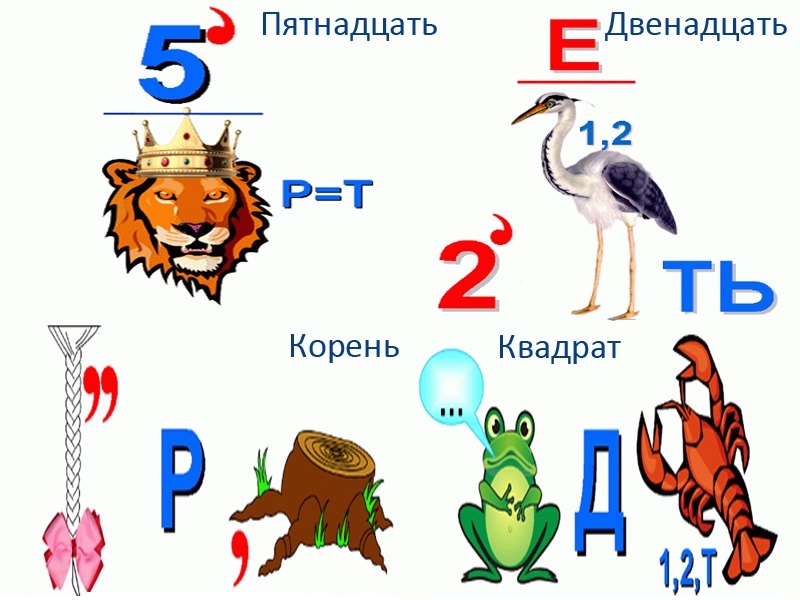
Математические ребусы для 3 класса с ответами
Чтобы разгадать посильные математические ребусы, третьеклассник на уроке математики должен:
- Считать и называть числа до тысячи.
- Выполняя основные четыре арифметические действия, называть каждую составляющую примера своим названием.
- Владеть таблицей умножения и оговаривать результат действия деления.
- Уметь решать примеры со скобками и без них.
- Знать единицы измерения величин и выражать их в разной интерпретации.
- Устно решать математические действия до значения 100.
- Делить многозначное число на однозначное, руководствуясь таблицей умножения.
- Проверять правильность расчета примеров.
- Выполнять задачи на одно-два действия.
- Придумывать задачи, обратные исходной.
- Уметь кратко записать задачу.
- Вычислять уравнения и неравенства.
- Чертить простые геометрические фигуры, согласно исходным данным задания, вычислять их периметр и площадь.
- Уметь пользоваться циркулем, чертя окружности заданных радиусов.
Математические ребусы для 4 класса с ответами
На уроках математики четвероклассник должен:
- Уметь решать задачи рациональным и нерациональным способом.
- Решать задачи, записывая ход их решения.
- Иметь представление вычисления объема и площади геометрических фигур, исходя из выученных формул.
- Чертить геометрические фигуры, обозначать их компоненты латинскими буквами.
- Строить и мерить углы транспортиром.
- Знать свойства равенства.
- Решать задания с количеством арифметических действий от одного до четырех.
- Знать свойства сторон, углов, радиусов геометрических фигур.
- Вычитать и прибавлять многозначные числа.
- Делить многозначное число на однозначное и многозначное.
- Иметь понятие натурального ряда.
- Умножать дробь на натуральное число.
- Правильно называть и писать дроби: числитель и знаменатель.
- Сравнивать дроби.
Математические ребусы для 5 класса с ответами
Программа по математике для пятиклассника схожа с предыдущим годом, только имеет более обширный характер. Недаром ведь в некоторых школах четвертый класс пропускается, а вся школьная программа за пропущенный год изучается в пятом классе.
Математические ребусы для 6 класса с ответами
- В шестом классе активно изучается геометрия, в частности ее теоремы.
- Ребенок знакомится с известными учеными в области математики и других точных наук.
- Школьник имеет дело с изучением геометрических фигур на плоскости, учится вычислять их объем и площадь по изученным формулам.
- По алгебре в ход идет решение уравнений с двумя неизвестными, неравенств.
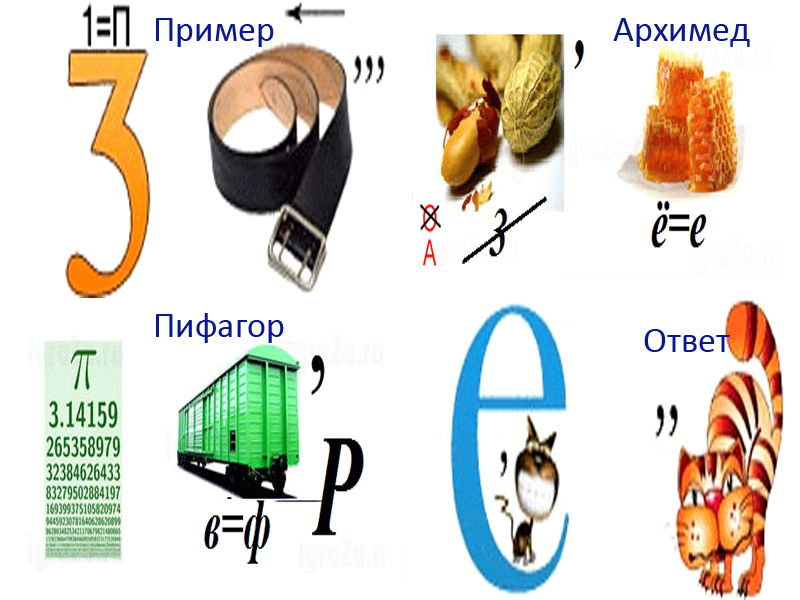
Математические ребусы с цифрами с ответами
Цифры, изображенные в математических ребусах, могут быть двух видов:
- Те, название или часть названия которых используется для ответа.
- Те, которые стоят около изображения, и указывают на то, что из названия этого изображения нужно позаимствовать буквы, соответствующие последовательности стоящих цифр в ряду.
Математические загадки, ребусы, кроссворды
Хорошо тренируют умственную активность не только ребусы по математике, но еще и логические, арифметические загадки, кроссворды. Они развивают любознательность и сообразительность у детей. А игровая форма заданий помогает достигнуть высокой скорости мышления и догадки.
Для самых маленьких подойдут такие задачки:
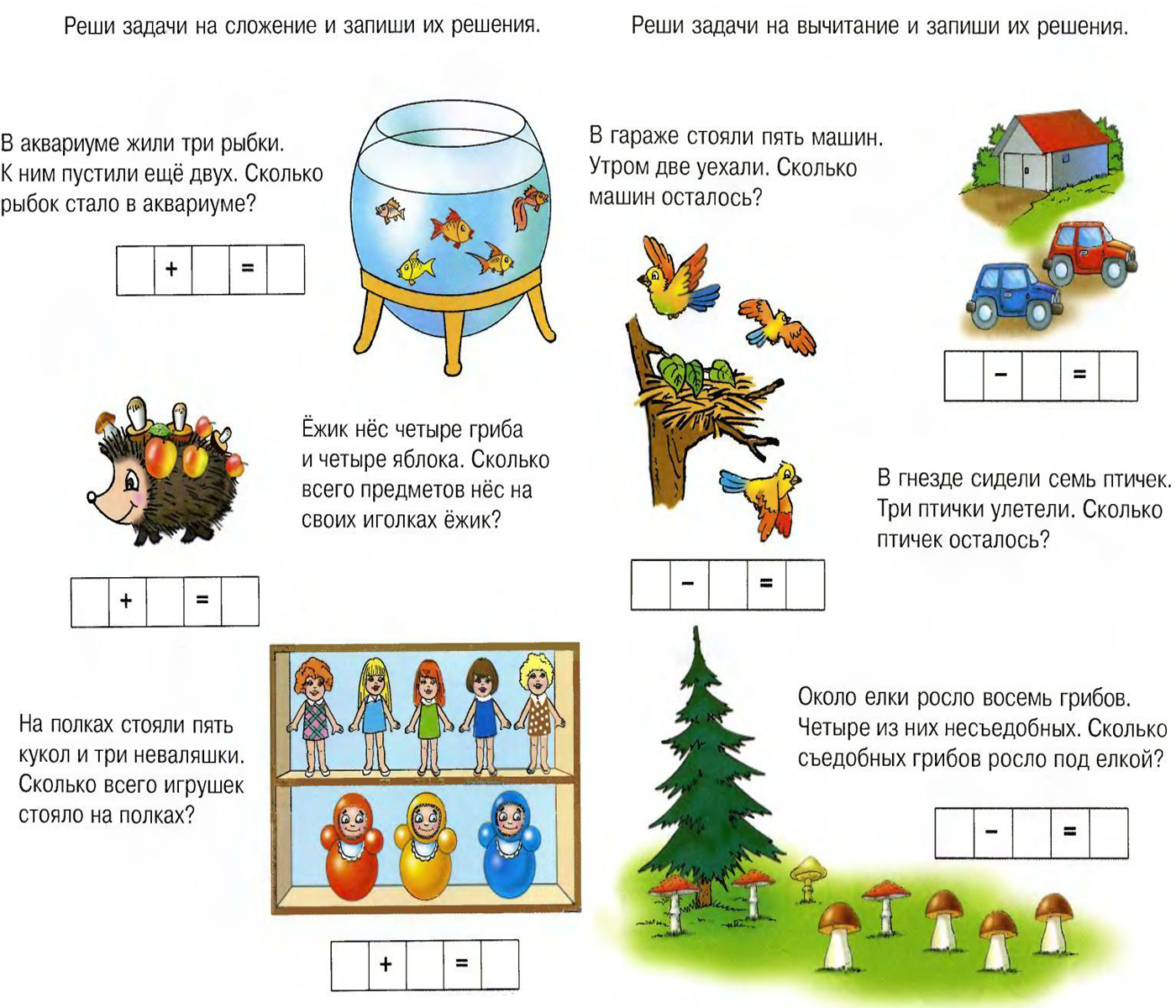
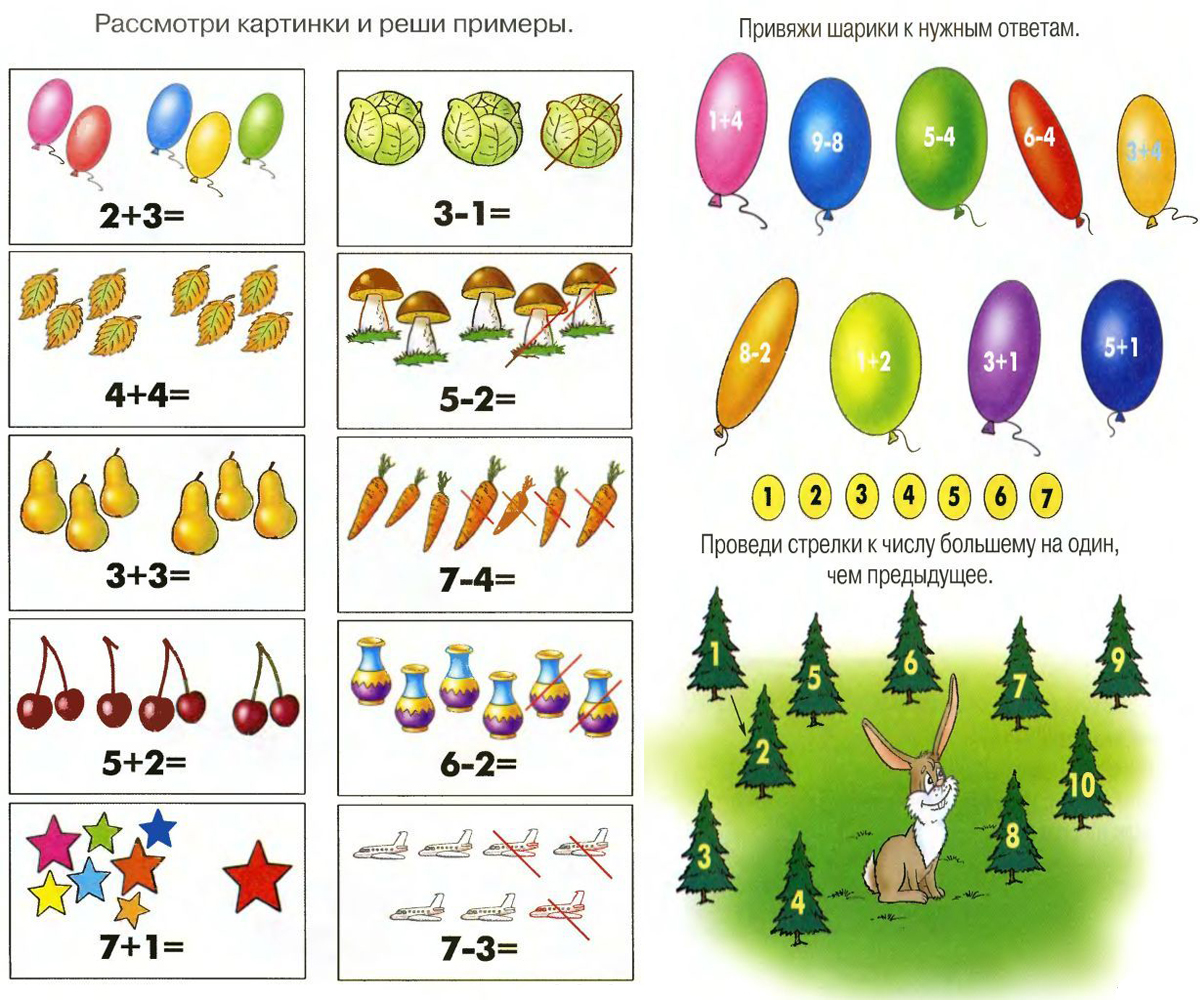Решите еще такие кроссворды и задания:
- Решите примеры, линиями соедините ответ и группу детишек, соответствующую ему (первое задание).
- Решите примеры на веслах, а затем линиями соедините каждое из них с лодками, имеющими правильный ответ (второе задание).
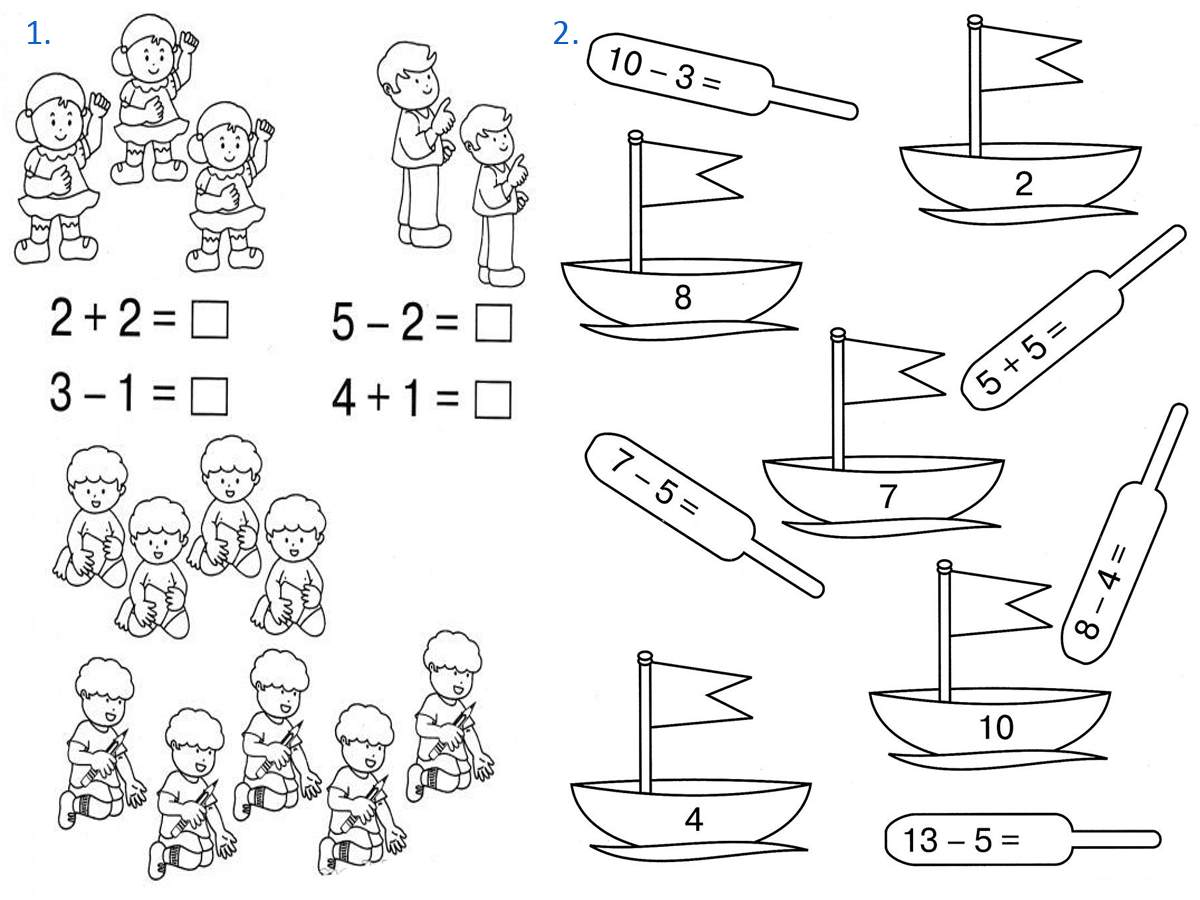
- Заполните пропущенные клеточки цифрами таким образом, чтобы по горизонтали и по вертикали всегда ответ получался 15 (третье задание).
- Заполните пропуски и решите примеры (четвертое задание).
Разгадайте кроссворды:
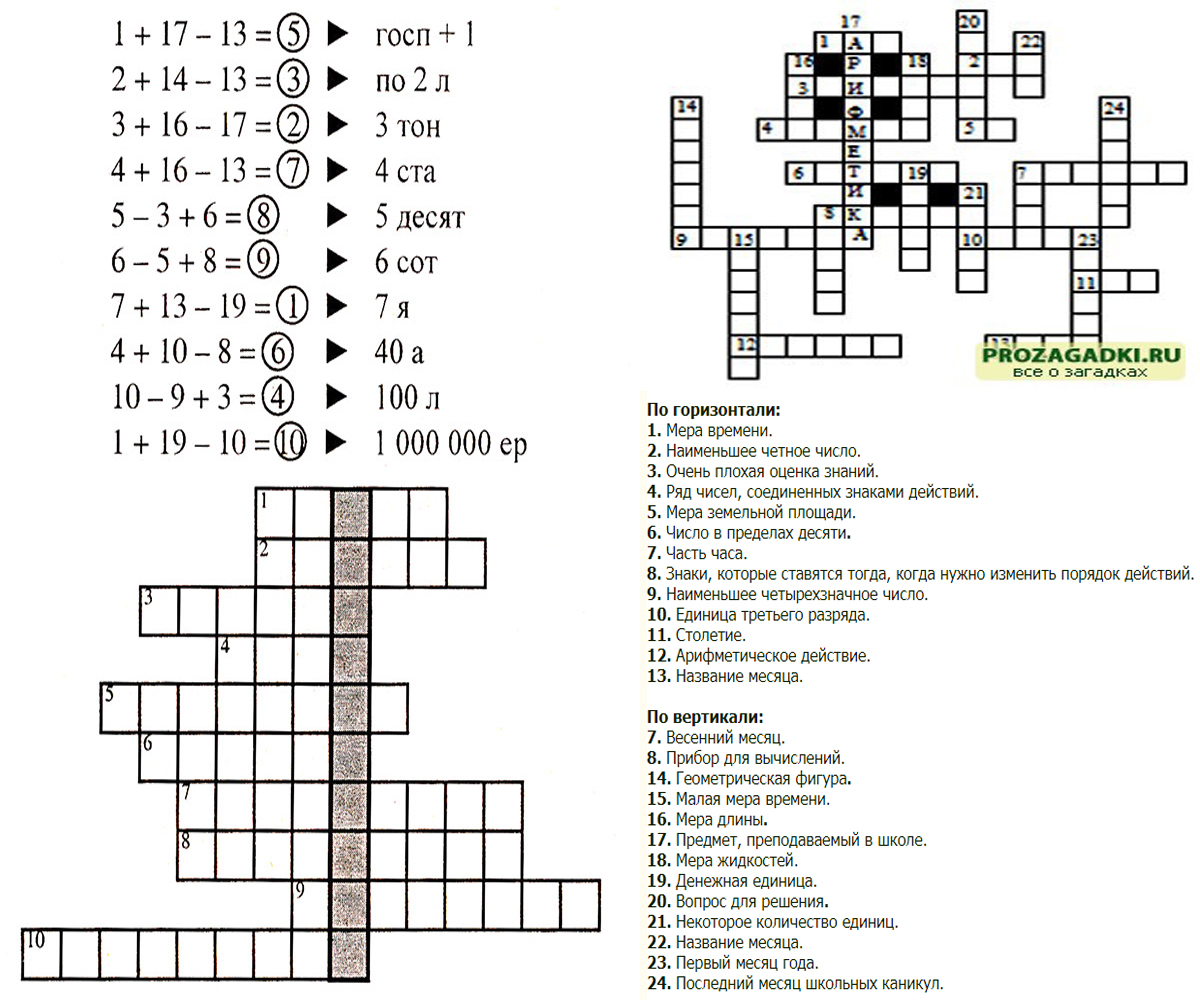
Вот более сложные ребусы:
Как решать математические ребусы с буквами?
Решение математических ребусов с буквами
Все слова состоят из букв, поэтому множество ребусов содержат в своей структуре буквы. Руководствуясь основными принципами решения ребусов, вы с легкостью осилите математические ребусы с буквами.
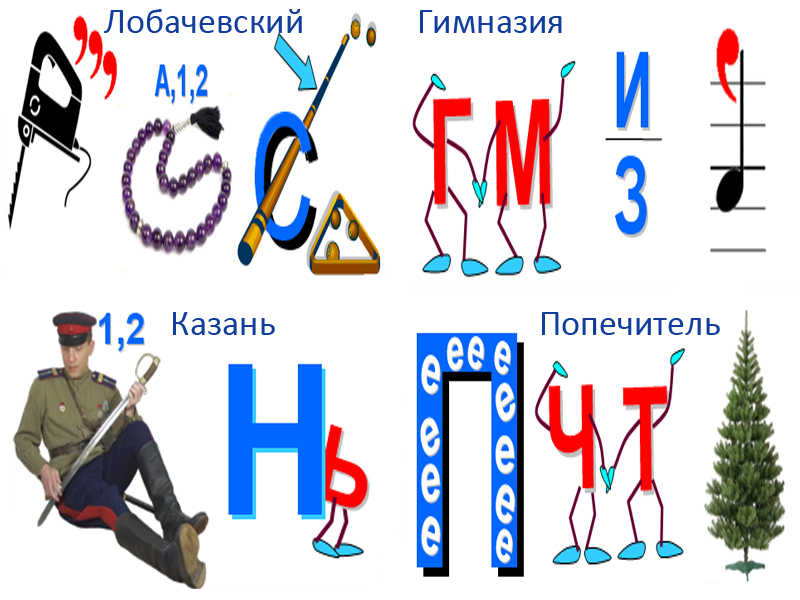
Математические ребусы и головоломки
Такие загадки и головоломки будут интересны не только школьникам, но и их родителям:
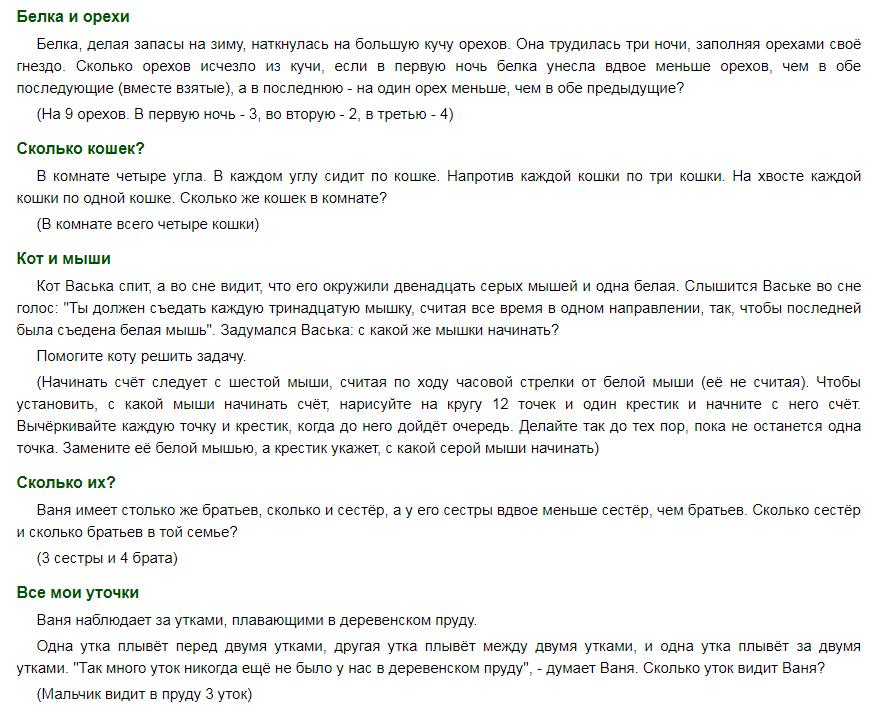
Самые легкие математические ребусы
Пусть школьник потренируется для начала на простых математических ребусах. К примеру, на таких:
Сложные математические ребусы
Попробуйте предоставить вашему сорванцу вот такие головоломки, которые позволят сконцентрировать смекалку и потренировать интеллект. Это задание предположительно для учеников пятых классов.
В нашей статье приведены примеры математических ребусов с ответами разных уровней сложности, зависящих от возраста школьника. Изучив основные правила разгадывания ребусов, попробуйте составить интересные задания своим деткам. Такого рода занятия помогут ребенку активизировать свои интеллектуальные способности, выработают усидчивость и концентрацию внимания, а также закрепят пройденный материал по математике. Это увлекательное занятие поможет сплотить родных (товарищей), и создать дружескую атмосферу в семье и школьном коллективе.
В этом генераторе ребусов можно автоматически создать ребус, зашифровав там слово или фразу на русском языке. В текстовое поле можно вводить только русские буквы, пробелы и тире. При генерации ребуса вы можете изменять его сложность. С увеличением сложности добавляется новые изображения и новые способы составления ребуса (все возможные способы присутствуют уже на 3-ем уровне, и дальше, при увеличении сложности, добавляются только изображения). По умолчанию ребус составляется без учёта пробелов, то есть фраза шифруется как единое целое. Вы можете это изменить и шифровать слова по отдельности. В этом случае каждое новое слово в ребусе будет начинаться с новой строки. При необходимости вы также можете увеличить или уменьшить максимальную ширину ребуса (холста, на котором он будет нарисован). После создания ребуса вы можете скачать его как картинку.
Что бы разгадать ребус, нужно знать правила разгадывания ребусов.
| Слово (фраза) для шифровки: | |
|
Сложность: – + Макс. ширина ребуса: px |
|
Сначала давайте выясним что такое ребус. Ребусом принято называть задачу, в которой разгадывается определенное слово. Буквы этого слова зашифрованы знаками, картинками, словами, цифрами и др. И если произнести их в слух, то мы получим зашифрованное слово или фразу. Естественно, чтобы придумать ребус нужно узнать условные обозначения, которыми в ребусах принято шифровать буквы и слоги. Для начала определяемся с шифруемым словом, потом, когда мы его подобрали, используем картинки и условные обозначения.
Например, запятыми сверху слева или сверху справа обозначается удаление букв в том слове, которое графически изображено на картинки.
В данном случае на картинке изображен компас с двумя запятыми с правой стороны. Это обозначает, что в слове нужно убрать две последние буквы. Если бы запятые были изображены справа, то нужно было убрать две первые. Итак получаем “комп”, убрав последние “ас”. Дальше прибавляем “ью”, получает “компью”. Далее смотрим на последнюю картинку на которой изображен термос и убираем в этом слове последние 3 буквы получаем “тер”. Поэтому слово, которое здесь зашифровано “компьютер”.
Еще один простой пример: в слове перечеркнута буква и указана буква ей на замену:
В слове “ложка” вместо “ж” ставим “д” и получаем слово “лодка”.
Самые простые варианты ребусов с ответами:
Зная многие приемы и правила составления ребусов, можно придумать свой. Так же можно воспользоваться специальными сайтами для составления ребусов в автоматическом режиме.
Мастер класс для учащихся
5 классов по теме:
«Решение математических ребусов»
Подготовила:
Черемисина Любовь Владимировна,
учитель математики МБОУ «Троицкая СОШ №1»
с.Троицкое,
2013 год
Пояснительная записка
Пятиклассники активно откликаются на любые предложения учителя поучаствовать во внеклассном мероприятии, олимпиаде или конкурсе. Однако, как показывают результаты, навыков решения нестандартных задач у учащихся 5 классов нет.
Ко всему прочему, в настоящее время учителя испытывают нехватку современной методической литературы, предназначенной для работы со способными учащимися по организации и проведению кружковых занятий, олимпиад по математике.
Учителя осуществляют подготовку учащихся к олимпиадам, опираясь на свой собственный опыт, взгляды, работа ведется на эмпирическом уровне без должной теоретической основы.
Между тем обучение решению нестандартных задач на раннем этапе могло бы развивать математические способности, интерес к предмету у учащихся, гибкое, вариативное мышление ребенка. Меня заинтересовали наработки методического объединения преподавателей математики, физики и информатики ГОУ лицей №1524 г. Москва по подготовке одаренных учащихся 5 класса к олимпиадам по математике. Данный мастер класс можно использовать при проведении элективных курсов, кружковых занятий и на уроках математики.
Цель мастер класса- рассмотреть технологию организации работы учащихся с арифметическими ребусами.
При работе с такими типами заданий следует учитывать несколько технологичных приемов:
1. Следует предлагать детям обратные преобразования: сначала обычный пример сделать арифметическим ребусом, заменив цифры буквами; затем ребус превратить в обычный пример, разгадав числа. Тогда дети будут понимать, откуда берутся одинаковые цифры на месте одинаковых букв, лишний старший разряд, разная цифра в суммах одинаковых слагаемых и т.д.
2. Различные “секреты” ребусов не задавать одновременно, это следует делать поочередно, причем после введения каждого “секрета” и его подробного обсуждения предлагать детям самим придумать ребус с таким “секретом”.
3. Следует учитывать возрастные особенности детей: ребусы с буквами требуют умения учащихся абстрагироваться, выполнять в уме большую часть вычислительных операций.
4. Примеры со * решаются проще, чем ребусы с буквами. Они построены по принципу “распутай клубок”. Поэтому начинать работу следует именно с таких примеров.
Оборудование к мастер классу: компьютер, мультимедийный проектор.
Содержание
-
Историческая справка.
2.Арифметические ребусы со *.
3.Арифметические ребусы с буквами.
4. Литература.
Ход мастер класса
-
Краткая историческая справка.
Слово “ребус” происходит от латинского res (вещь) и обозначает представление имен, слов и фраз изображениями, фигурами, композициями из букв и т.п. Само слово появилось из латинской фразы “Non verbis sed rebus”, что значит “Не словами, а при помощи вещей”. Иногда термин rebus ассоциируют с латинским словом rebis: res (вещь, предмет), rebis (обращение).
Математические ребусы представляют собой примеры обычных арифметических действий (сложения, вычитания, деления и умножения), в которых часть или даже все цифры заменены на точки, звездочки, буквы или другие символы. Решить ребус – означает восстановить первоначальный вид математического равенства.
Существует несколько разновидностей математических ребусов. Например, в буквенных ребусах каждой буквой зашифрована одна определенная цифра. При этом одинаковые цифры шифруются одной и той же буквой, а разным цифрам соответствуют различные буквы. Математический буквенный ребус именуют криптарифмом, если в результате шифрования получилась какая-то осмысленная фраза. Например, УДАР+УДАР=ДРАКА
В математических ребусах зашифрованных иными значками, например звездочками, каждый символ может обозначать любую цифру от 0 до 9. Причём, некоторые цифры могут повторяться несколько раз, а другие не использоваться вовсе. Такие ребусы, зачастую, называют числовыми или цифровыми.
Математический ребус – довольно старая головоломка, изобретатель её не известен.
Первое упоминание об отечественных математических ребусах, автору проекта “Ребус № 1” удалось отыскать в книге выдающегося российского, советского учёного, популяризатора физики, математики и астрономии, одного из основоположников жанра научно-популярной литературы Якова Перельмана “Занимательная арифметика. Загадки и диковинки в мире чисел“, выпущенной Ленинградским издательством “Время” в 1926 году (слайды 2-6)
2. Работа с арифметическими ребусами, где нужно заменить * недостающими цифрами и выполнить действие.
– Учитель предлагает внимательно рассмотреть примеры, записанные на доске, и найти «секрет» этих примеров.
3+ 5 = 8 8 – 2 = 6 6 + 4 = 10 10 – 7 = 3
-После того, как учащиеся выясняют, что результат каждого примера является началом следующего («цепочка» примеров), тогда учитель предлагает решить головоломку, которая называется «распутай клубок».
56 – Δ =
– 15 =
18 + 6 = Δ
+ 1 = ►
В ходе рассуждений, возникают вопросы: как решить примеры, в которых нет двух чисел? Почему задание называется «распутай клубок»?
В работе учащиеся выясняют, что один пример решить все таки можно. Таким образом, будет найдено значение Δ. Подставив его в первый пример, находим следующее число и т.д. Теперь детям понятно, почему назвали задание «распутай клубок».
Учитель предлагает детям последовательно решить следующие задания:
-
Распутать еще один «запутанный клубок
82 + = ►
+ 8 = Δ
Δ – 39 =
94 – 45 =
-
Превратить цепочку примеров в «запутанный клубок» (для этого некоторые цифры заменить геометрическими фигурами).
4 + 2 = 6 6 – 5 = 1 1 + 7 = 8 8 – 3 = 5
4 + 2 = Δ Δ – 5 = + 7 = – 3 = ►
Дети фиксируют основное правило: одинаковые цифры должны быть заменены одинаковыми значками (и наоборот).
3. Придумать самостоятельно «запутанный клубок». Для этого дети сначала должны составить цепочку примеров.
4. Вставить вместо Δ одну и ту же цифру, чтобы равенство было верным.
1Δ + 3Δ + 5Δ = 111
Дети выполняют это задание путем перебора вариантов:
1 + 1 + 1 = 3 не подходит; 2 + 2 + 2 = 6 не подходит
3 + 3 + 3 = 9 не подходит; 4 + 4 + 4 = 12 не подходит
5 + 5 + 5 = 15 не подходит; 6 + 6 + 6 = 18 не подходит
7 + 7 + 7 = 21 подходит – 21 + (10 + 30 + 50) = 111
Выполняя это задание, учащиеся, знакомятся с алгоритмом выполнения такого задания и формой записи: последовательный перебор возможных вариантов с фиксацией, подходит или нет такой вариант.
– Учитель предлагает детям следующее задание: Восстановить пример:
7 3 Δ 739
+2 6 +236
Δ 7 5 975
После выполнения задания обсудить, с чего начинали, чтобы распутать весь клубок. Выяснить, что, чтобы сложить многозначные числа, нужно сосчитать несколько примеров с однозначными числами, своеобразную цепочку. А такие задания мы выполнять умеем. Главное – найти подсказку, где «начинается клубок».
Совместно с учащимися, формулируем «секреты», которые помогают решать арифметические ребусы:
№1. Одинаковые знаки (буквы) обозначают одинаковые цифры.
№2. Чтобы решить такой пример, нужно найти начало «клубочка» (откуда будет раскручиваться логическое рассуждение).
№3. Нужно учитывать «переполнение» из соседнего разряда.
1
7 3 Δ
+ 2 6
Δ 7 5
Задания на закрепление:
1. Детям предлагается ряд примеров со *.
3 7 0 * * * 5 9 * _* 2 * 4 8 .
+ * 9 * 8 8 0 0 3 * * * *
9 * 4 0 5 0 8 * 2 * * * _ 2 *
* *
0
2. Запиши суммы обычными цифрами:
А А 0 А А В В В В К К 0 К К
+ А 0 А А А + В В В В + К К К К К
. . . 6 6 . . . 9 8 . . . . 5 4
Решая такие задания, дети выясняют еще два «секрета» арифметических ребусов, связанные с «переполнениями» из соседнего разряда:
-
откуда берется еще один разряд в сумме, и какая цифра там может быть? (только 1).
-
почему при сложении одинаковых знаков (букв) написаны (а значит, получаются) разные цифры? (виновато «переполнение» из соседнего разряда).
Открытия дополняют составленный ранее перечень «секретов»:
№4. На месте «свободного» старшего разряда в сумме может быть только цифра 1, которая получается из переполнения соседнего разряда.
№5. При сложении двух одинаковых букв могут получиться разные результаты. Виновато в этом «переполнение» из соседнего разряда.
нет переполнения 1 есть переполнение
Т Т Т Т
+ Т Т + Т Т
8 8 . 9 8
цифры одинаковые цифры разные
Значит, Т может быть равно 4, а может быть равно 9. Об этом обязательно следует помнить.
– Учитель предлагает детям решить следующие арифметические ребусы:
* * * + * = * * * * Ответ: 999+1=1000
* * * * * = * 100-99=1
* * * * * = * * * 1000-1=999
Дети сначала теряются, но потом быстро находят решение. Учитель спрашивает, почему была заминка? В чем (предположительно) ожидалась трудность? Учащиеся сообщают, что в этих ребусах нет ни одной известной цифры, только звездочки. Но смогли найти решение, потому что «секреты» арифметических ребусов, выведенные на предыдущем занятии, все равно работают.
Далее учитель предлагает детям несколько арифметических ребусов с буквами. Ребусы нужно решить и перечислить, какие «секреты» из уже известных использовались. Отдельно учитель предлагает фиксировать трудные моменты для поиска новых «секретов».
-
о х о х о
+ а х а х а
о х о х о х
Ответ: 1 0 1 0 1
+ 9 0 9 0 9
1 0 1 0 1 0 «Секреты» № 1,2, 3,4.
2) т р и
+ т р и
т р и
д ы р а
Ответ: 403
+ 403
403
1209 «Секреты» № 4, 2, 1.
Новый «секрет» №6 – если при сложении трех одинаковых цифр получается такая же, то это могут быть только цифры 0 или 5. Все зависит от того, нужно ли отсюда переполнение в более старший разряд.
-
г а
+ г о
у г у
Ответ: 9 5
+ 9 6
1 9 1 «Секреты» № 4, 2, 1.
Новые «секреты» :
№7: если при сложении двух одинаковых цифр получается такая же, то это могут быть только цифры 0.
№8: если же есть переполнение в этот разряд, то это может быть и цифра 9. Все зависит от того, нужно ли переполнение в более старший разряд. В данном ребусе не может ноль стоять в начале числа, значит, только 9.
Учитель предлагает детям буквенные ребусы на отработку всех известных «секретов». Обязательно обсуждать результат после нахождения решения: ввести форму записи «последовательности распутывания клубка».
к о ш к а 5 6 3 5 0
+ к о ш к а + 5 6 3 5 0
к о ш к а 5 6 3 5 0
с о б а к а 1 6 9 0 5 0
с – только1.
а + а + а = а только 0, так как из этого разряда не нужно переполнение.
к + к + к = к только 5.
к + к + к = о 5 + 5 + 5 (+ 1 из переполнения)= 6 – это о.
о + о + о = б 6 + 6 + 6 = либо 8 , либо 9.
Остаются цифры 2, 3, 4.
ш + ш + ш = 0 2 + 2 + 2 (+ 1 из переполнения) = 7 не подходит.
3 + 3 + 3 (+ 1 из переполнения) = 10 подходит, ш – 3.
Значит, если есть переполнение, то б – 9.
Домашнее задание: Решите ребусы:
ОДИН+ОДИН=МНОГО
РЕШИ+ЕСЛИ=СИЛЕН
ПОДАЙ-ВОДЫ=ПАША
СОТНЯ х 3 = ТРИСТА
Литература:
1.Система подготовки одаренных учащихся 5 класса к олимпиадам по математике. МО преподавателей математики, физики и информатики. ГОУ лицей №1524 г. Москва. http://do.gendocs.ru/docs/index-39863.html
2. http://rebus1.com/
ПРАВИЛА СОСТАВЛЕНИЯ РЕБУСОВ
(Памятка для учащихся)
Ребус – это игра, в которой зашифрованы слова, фразы или целые высказывания при помощи рисунков в сочетании с буквами и знаками. Название образовано от латинского rebus (вещь, предмет).
Правило 1. Изображенные на рисунках предметы и живые существа чаще всего (за редким исключением) читаются как слова в именительном падеже и единственном числе. Иногда нужный объект на картинке указывается стрелкой.
Правило 2. Если картинка нарисована вверх ногами, читаем слово в обратном порядке. Например, нарисован вверх ногами кот – читаем ТОК.
Правило 3. Запятые после картинки указывают, сколько букв нужно убрать с конца слова, обозначающего то, что изображено на картинке. Например, нарисована коза с двумя запятыми после нее – читаем КО.
Правило 4. Перевернутые запятые перед картинкой, указывают сколько букв нужно убрать в начале слова, обозначающего то, что изображено на картинке. Например, нарисован слон с запятой перед картинкой – читаем ЛОН.
Правило 5. Над картинкой или под ней могут появиться цифры. Каждая цифра – это номер буквы в слове: 1 – первая буква слова, 2 – вторая буква, 3 – третья и так далее. Определенный набор цифр под или над картинкой говорит о том, что нужно взять только эти буквы и прочитать их в указанном порядке. Перечеркнутая цифра означает, что данная буква должна быть опущена. Например, нарисован конь и цифры 2, 1 под ним – читаем ОК. При объединении примеров в правилах 3, 4 и 5 получаем загаданное слово КОЛОНОК.
Правило 6. Знак равенства между буквами означает замену определенной буквы (или сочетания букв) слова на другую букву (или на сочетание букв). Действие замены обозначается и вторым способом – буквы, которые заменяются, перечеркиваются, а над ними пишутся заменяющие. Например, нарисован крот, а рядом перечеркнутые буквы РО и сверху буква И – читаем КИТ.
Правило 7. Буквы могут быть изображены внутри других букв, над другими буквами, под и за ними. В таких случаях необходимо понять, в каких пространственных отношениях состоят изображенные буквы. Например, внутри буквы О нарисованы буквы ЛК – читаем ВОЛК (хотя можно прочесть и как ЛКВО). Сверху написаны буквы АР, снизу ОК – читаем ПОДАРОК (можно было прочесть и ОКПОДАР, НАДОКАР, АРНАДОК – но здесь уж приходится выбирать то, что подходит по смыслу). Впереди написаны буквы ДА, сзади ЧА – читаем ЗАДАЧА.
Правило 8. Буквы могут быть изображены по поверхности других букв. Например, изображена большая буква Н, а по ней разбросаны маленькие И – читаем ПОНИ (хотя можно прочитать и как ИПОН, НИЗИ или ИЗИН).
Правило 9. Перечисленные выше приемы могут объединяться друг с другом.
