Как найти сумму двух независимых событий

Учреждение
образования «Белорусская государственная

сельскохозяйственная
академия»

Кафедра
высшей математики

СЛОЖЕНИЕ
И УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ. ПОВТОРНЫЕ
НЕЗАВИСИМЫЕ ИСПЫТАНИЯ

Лекция
для студентов землеустроительного
факультета

заочной
формы обучения

Горки,
2012

Сложение
и умножение вероятностей. Повторные

независимые
испытания

1. Сложение вероятностей

Суммой
двух совместных событий
А
и В
называется событие С,
состоящее в наступлении хотя бы одного
из событий А
или В.
Аналогично суммой нескольких совместных
событий называется событие, состоящее
в наступлении хотя бы одного из этих
событий.

Суммой
двух несовместных событий
А
и В
называется событие С,
состоящее в наступлении или события
А,
или события В.
Аналогично суммой нескольких несовместных
событий называется событие, состоящее
в наступлении какого-либо одного из
этих событий.

Справедлива
теорема сложения вероятностей несовместных
событий: вероятность
суммы двух несовместных событий равна
сумме вероятностей этих событий,
т.е.
.
Эту теорему можно распространить на
любое конечное число несовместных
событий.

Из
данной теоремы следует:

сумма
вероятностей событий, образующих полную
группу, равна единице;

сумма
вероятностей противоположных событий
равна единице, т.е.
.

Пример
1.
В ящике находятся 2 белых, 3 красных и 5
синих шара. Шары перемешивают и наугад
извлекают один. Какова вероятность
того, что шар окажется цветным?

Решение.
Обозначим события:

A={извлечён
цветной шар};

B={извлечён
белый шар};

C={извлечён
красный шар};

D={извлечён
синий шар}.

Тогда
A=C+D.
Так как события C,
D
несовместны, то воспользуемся теоремой
сложения вероятностей несовместных
событий:
.

Пример
2.
В урне находятся 4 белых шара и 6 –
чёрных. Из урны наугад вынимают 3 шара.
Какова вероятность того, что все они
одного цвета?

Решение.
Обозначим события:

A={вынуты
шары одного цвета};

B={вынуты
шары белого цвета};

C={вынуты
шары чёрного цвета}.

Так
как A=B+C
и события В
и С
несовместны, то по теореме сложения
вероятностей несовместных событий
.
Вероятность события В
равна
,
где
4,

.
Подставим k
и n
в формулу и получим
Аналогично
найдём вероятность события С:
,
где
,
,
т.е.
.
Тогда
.

Пример
3.
Из колоды в 36 карт наугад вынимают 4
карты. Найти вероятность того, что среди
них окажется не менее трёх тузов.

Решение.
Обозначим события:

A={среди
вынутых карт не менее трёх тузов};

B={среди
вынутых карт три туза};

C={среди
вынутых карт четыре туза}.

Так
как A=B+C,
а события В
и С
несовместны, то
.
Найдём вероятности событий В
и С:

,
.
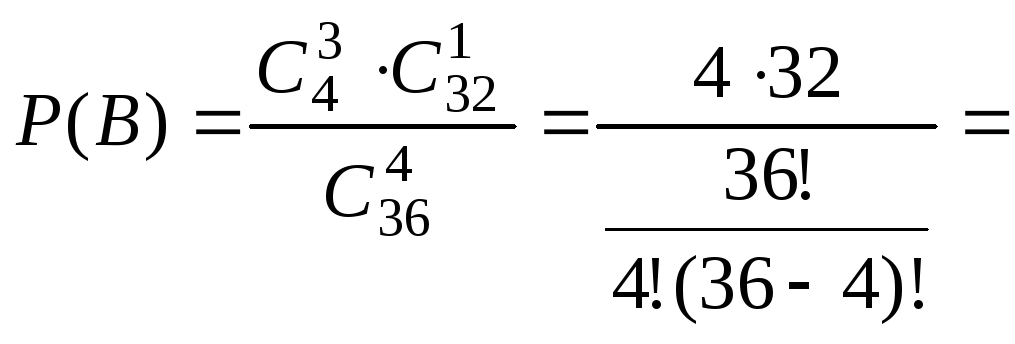
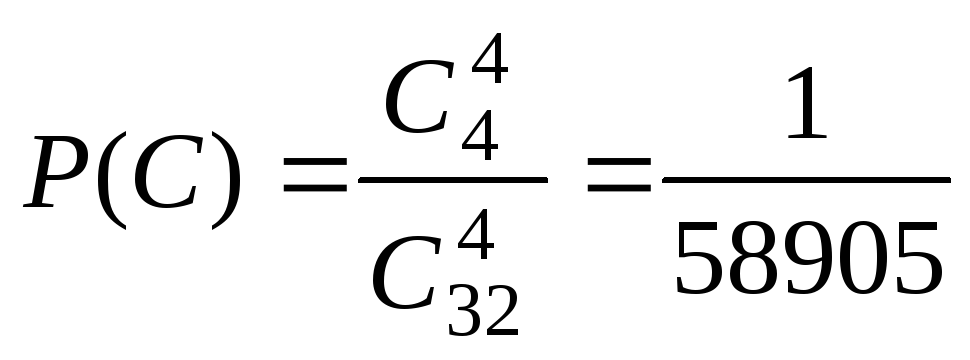Следовательно, вероятность того, что
среди вынутых карт не менее трёх тузов,
равна

0.0022.

1. Умножение вероятностей

Произведением
двух событий А
и В
называется событие С,
состоящее в совместном наступлении
этих событий:
.
Это определение распространяется на
любое конечное число событий.

Два
события называются независимыми,
если вероятность наступления одного
из них не зависит от того, произошло
другое событие или нет. События
,
,
… ,

называются независимыми
в совокупности,
если вероятность наступления каждого
из них не зависит от того, произошли или
не произошли другие события.

Пример
4.
Два стрелка стреляют по цели. Обозначим
события:

A={первый
стрелок попал в цель};

B={второй
стрелок попал в цель}.

Очевидно,
что вероятность попадания в цель первым
стрелком не зависит от того, попал или
не попал второй стрелок, и наоборот.
Следовательно, события А
и В
независимы.

Справедлива
теорема умножения вероятностей
независимых событий: вероятность
произведения двух независимых событий
равна произведению вероятностей этих
событий:
.

Эта
теорема справедлива и для n
независимых в совокупности событий:
.

Пример
5.
Два стрелка стреляют по одной цели.
Вероятность попадания первого стрелка
равна 0.9, а второго – 0.7. Оба стрелка
одновременно делают по одному выстрелу.
Определить вероятность того, что будут
иметь место два попадания в цель.

Решение.
Обозначим события:

A={первый
стрелок попадёт в цель};

B={второй
стрелок попадёт в цель};

C={оба
стрелка попадут в цель}.

Так
как
,
а события А
и В
независимы, то
,
т.е.
.

События
А
и В
называются зависимыми,
если вероятность наступления одного
из них зависит от того, произошло другое
событие или нет. Вероятность наступления
события А
при условии, что событие В
уже наступило, называется условной
вероятностью
и обозначается

или
.

Пример
6.
В урне находятся 4 белых и 7 чёрных шаров.
Из урны извлекаются шары. Обозначим
события:

A={извлечён
белый шар} ;

B={извлечён
чёрный шар}.

Перед
началом извлечения шаров из урны
.
Из урны извлекли один шар и он оказался
чёрным. Тогда вероятность события А
после наступления события В
будет уже другой, равной
.
Это означает, что вероятность события
А
зависит от события В,
т.е. эти события будут зависимыми.

Справедлива
теорема умножения вероятностей зависимых
событий: вероятность
произведения двух зависимых событий
равна произведению вероятности одного
из них на условную вероятность другого,
вычисленную в предположении, что первое
событие уже наступило,
т.е.

или
.

Пример
7.
В урне находятся 4 белых шара и 8 красных.
Из неё наугад последовательно извлекают
два шара. Найти вероятность того, что
оба шара будут чёрными.

Решение.
Обозначим события:

A={первым
извлечён чёрный шар};

B={вторым
извлечён чёрный шар}.

События
А
и В
зависимы, так как
,
а
.
Тогда
.

Пример
8.
Три стрелка стреляют по цели независимо
друг от друга. Вероятность попадания в
цель для первого стрелка равна 0.5, для
второго – 0.6 и для третьего – 0.8. Найти
вероятность того, что произойдут два
попадания в цель, если каждый стрелок
сделает по одному выстрелу.

Решение.
Обозначим события:

A={произойдут
два попадания в цель};

B={первый
стрелок попадёт в цель};

C={второй
стрелок попадёт в цель};

D={третий
стрелок попадёт в цель};

={первый
стрелок не попадёт в цель};

={второй
стрелок не попадёт в цель};

={третий
стрелок не попадёт в цель}.

По
условию примера
,
,
,

,
,
.
Так как
,
то используя теорему сложения вероятностей
несовместных событий и теорему умножения
вероятностей независимых событий,
получим:

.

Пусть
события

образуют полную группу событий некоторого
испытания, а событии А
может наступить только с одним из этих
событий. Если известны вероятности

и условные вероятности

события А,
то вероятность события А вычисляется
по формуле:

или
.
Эта формула называется формулой
полной вероятности,
а события

гипотезами.

Пример
9.
На сборочный конвейер поступает 700
деталей с первого станка и 300 деталей

со второго. Первый станок даёт 0.5% брака,
а второй – 0.7%. Найти вероятность того,
что взятая деталь будет бракованной.

Решение.
Обозначим события:

A={взятая
деталь будет бракованной};

={деталь
изготовлена на первом станке};

={деталь
изготовлена на втором станке}.

Вероятность
того, что деталь изготовлена на первом
станке, равна
.
Для второго станка
.
По условию вероятность получения
бракованной детали, изготовленной на
первом станке, равна
.
Для второго станка эта вероятность
равна
.
Тогда вероятность того, что взятая
деталь будет бракованной, вычисляется
по формуле полной вероятности

.

Если
известно, что в результате испытания
наступило некоторое событие А,
то вероятность того, что это событие
наступило с гипотезой
,
равна
,
где
–
полная вероятность события А.
Эта формула называется формулой
Байеса
и позволяет вычислять вероятности
событий

после того, как стало известно, что
событие А
уже наступило.

Пример
10.
Однотипные детали к автомобилям
производятся на двух заводах и поступают
в магазин. Первый завод производит 80%
общего количества деталей, а второй –
20%. Продукция первого завода содержит
90% стандартных деталей, а второго – 95%.
Покупатель купил одну деталь и она
оказалась стандартной. Найти вероятность
того, что эта деталь изготовлена на
втором заводе.

Решение.
Обозначим события:

A={куплена
стандартная деталь};

={деталь
изготовлена на первом заводе};

={деталь
изготовлена на втором заводе}.

По
условию примера
,
,

и
.
Вычислим полную вероятность события
А:
0.91.
Вероятность того, что деталь изготовлена
на втором заводе, вычислим по формуле
Байеса:
.

Задания
для самостоятельной работы

1. Вероятность
   попадания в цель для первого стрелка
   равна 0.8, для второго – 0.7 и для третьего
   – 0.9. Стрелки произвели по одному
   выстрелу. Найти вероятность того, что
   имеет место не менее двух попаданий в
   цель.

2. В
   ремонтную мастерскую поступило 15
   тракторов. Известно, что 6 из них нуждаются
   в замене двигателя, а остальные – в
   замене отдельных узлов. Случайным
   образом отбираются три трактора. Найти
   вероятность того, что замена двигателя
   необходима не более, чем двум отобранным
   тракторам.

3. На
   железобетонном заводе изготавливают
   панели, 80% из которых – высшего качества.
   Найти вероятность того, что из трёх
   наугад выбранных панелей не менее двух
   будут высшего сорта.

4. Три
   рабочих собирают подшипники. Вероятность
   того, что подшипник, собранный первым
   рабочим, высшего качества, равна 0.7,
   вторым – 0.8 и третьим – 0.6. Для контроля
   наугад взято по одному подшипнику из
   собранных каждым рабочим. Найти
   вероятность того, что не менее двух из
   них будут высшего качества.

5. Вероятность
   выигрыша по лотерейному билету первого
   выпуска равна 0.2, второго – 0.3 и третьего
   – 0.25. Имеются по одному билету каждого
   выпуска. Найти вероятность того, что
   выиграет не менее двух билетов.

6. Бухгалтер
   выполняет расчёты, пользуясь тремя
   справочниками. Вероятность того, что
   интересующие его данные находятся в
   первом справочнике, равна 0.6, во втором
   – 0.7 ив третьем – 0.8. Найти вероятность
   того, что интересующие бухгалтера
   данные содержатся не более, чем в двух
   справочниках.

7. Три
   автомата изготавливают детали. Первый
   автомат изготавливает деталь высшего
   качества с вероятностью 0.9, второй – с
   вероятностью 0.7 и третий – с вероятностью
   0.6. Наугад берут по одной детали с каждого
   автомата. Найти вероятность того, что
   среди них не менее двух высшего качества.

8. На
   двух станках обрабатываются однотипные
   детали. Вероятность изготовления
   нестандартной детали для первого станка
   равна 0.03, в для второго – 0.02. Обработанные
   детали складываются в одном месте.
   Среди них 67% с первого станка, а остальные
   – со второго. Наугад взятая деталь
   оказалась стандартной. Найти вероятность
   того, что она изготовлена на первом
   станке.

9. В
   мастерскую поступили две коробки
   однотипных конденсаторов. В первой
   коробке было 20 конденсаторов, из которых
   2 неисправных. Во второй коробки 10
   конденсаторов, из которых 3 неисправных.
   Конденсаторы были переложены в один
   ящик. Найти вероятность того, что наугад
   взятый из ящика конденсатор окажется
   исправным.

10. На
    трёх станках изготавливают однотипные
    детали, которые поступают на общий
    конвейер. Среди всех деталей 20% с первого
    автомата, 30% – со второго и 505 – с третьего.
    Вероятность изготовления стандартной
    детали на первом станке равна 0.8, на
    втором – 0.6 и на третьем – 0.7. Взятая
    деталь оказалась стандартной. Найти
    вероятность того, эта деталь изготовлена
    на третьем станке.

11. Комплектовщик
    получает для сборки 40% деталей с завода
    А,
    а остальные – с завода В.
    Вероятность того, что деталь с завода
    А
    – высшего качества, равна 0.8, а с завода
    В
    – 0.9. Комплектовщик наугад взял одну
    деталь и она оказалась не высшего
    качества. Найти вероятность того, что
    эта деталь с завода В.

12. Для
    участия в студенческих спортивных
    соревнованиях выделено 10 студентов из
    первой группы и 8 – из второй. Вероятность
    того, что студент из первой группы
    попадёт в сборную академии, равна 0.8, а
    со второй – 0.7. Наугад выбранный студент
    попал в сборную. Найти вероятность
    того, что он из первой группы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вероятность суммы двух событий. Независимость двух событий. Вероятность произведения двух независимых событий

Содержание

Вероятность суммы двух событий

Пусть   A   и   B   – два произвольных события в случайном эксперименте с множеством элементарных исходов  Ω .

Справедливо следующее утверждение.

УТВЕРЖДЕНИЕ 1. Вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения.

Другими словами, верна формула:

(1)

ДОКАЗАТЕЛЬСТВО. Рассмотрим диаграммы Эйлера – Венна для суммы двух событий и произведения двух событий, разместив их на одном рисунке (рис.1).

Рис.1

Проведем доказательство утверждения 1 на примере геометрического определения вероятности.

Если площадь произвольной фигуры   F   обозначить символом   S (F) ,   то из рисунка 1 легко установить справедливость равенства:

(2)

которое словами можно выразить так: «Площадь фигуры   A + B   равна сумме площадей фигур   A   и   B   минус площадь фигуры  ».

Если обе части равенства (2) разделить на число   S (Ω) ,   то мы получим равенство

В силу геометрического определения вероятности справедливы формулы

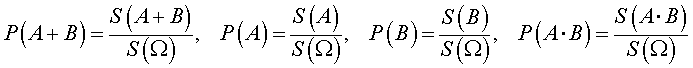
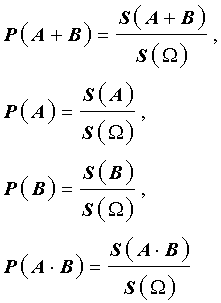
с помощью которых равенство (3) преобразуется к виду (1), что и завершает доказательство утверждения 1.

Доказательство утверждения 1 для классического определения вероятности проводится аналогичным образом, и мы оставляем его читателю в качестве полезного упражнения.

Несовместные события

ОПРЕДЕЛЕНИЕ. Два события   A   и   B   называют несовместными, если они не пересекаются.

Другими словами, события   A   и   B   несовместны, если

ЗАМЕЧАНИЕ 1. События   A   и   B   несовместны в том, и только в том случае, если событие   B   является подмножеством события   ,   то есть   .

ЗАМЕЧАНИЕ 2. События   A   и   B   несовместны в том, и только в том случае, если событие   A   является подмножеством события   ,   то есть   .

ЗАМЕЧАНИЕ 3. Если события   A   и   B   несовместны, то вероятность их произведения равна нулю.

Другими словами, для несовместных событий   A   и   B   верна формула

ЗАМЕЧАНИЕ 4. Если события   A   и   B   несовместны, то вероятность суммы событий   A + B   равна сумме вероятностей событий   A   и   B .

Другими словами, для несовместных событий   A   и   B   верна формула

P (A + B) = P (A) + P (B)

Независимость двух событий. Вероятность произведения двух независимых событий

Два события   A   и   B   называют независимыми, если появление одного из этих событий никак не влияет на вероятность появления второго события.

ЗАМЕЧАНИЕ 5. Несовместные события и независимые события – это совершенно разные понятия, и их не следует путать.

Справедливо следующее утверждение.

УТВЕРЖДЕНИЕ 2. Вероятность произведения двух независимых событий равна произведению их вероятностей.

Другими словами, для двух независимых событий   A   и   B   верна формула

(4)

Проиллюстрируем справедливость формулы (4) на примере.

ПРИМЕР 1. Случайный эксперимент состоит в подбрасывании двух игральных костей. Одна из игральных костей окрашена в синий цвет, другая – в красный. Найти вероятность того, что на синей игральной кости выпадет число   3 ,   а на красной игральной кости выпадет число   4 .

РЕШЕНИЕ. Сформируем следующую таблицу, в которой записаны все   36   возможных вариантов пар чисел, выпадающих при подбрасывании двух игральных костей. Первая строка таблицы – это числа, выпавшие при бросании синей кости, а первый столбец таблицы – это числа, выпавшие при бросании красной кости. На пересечении строки и столбца указана пара чисел, выпавших на двух костях.

	1	2	3	4	5	6
1	1, 1	1, 2	1, 3	1, 4	1, 5	1, 6
2	2, 1	2, 2	2, 3	2, 4	2, 5	2, 6
3	3, 1	3, 2	3, 3	3, 4	3, 5	3, 6
4	4, 1	4, 2	4, 3	4, 4	4, 5	4, 6
5	5, 1	5, 2	5, 3	5, 4	5, 5	5, 6
6	6, 1	6, 2	6, 3	6, 4	6, 5	6, 6

      Благоприятным является только один исход, а именно, клетка с результатом   4, 3 ,   окрашенная в таблице желтым цветом. Следовательно, вероятность события, состоящего в том, что на синей игральной кости выпадает число   3 ,   а на красной игральной кости выпадает число   4 ,   равна  .

Теперь рассмотрим случайный эксперимент, описанный в примере 1, с другой стороны. Для этого обозначим буквой   A   случайное событие, состоящее в том, что на синей игральной кости выпадает число   3 ,   а буквой   B   – случайное событие, состоящее в том, что на красной игральной кости выпадает число   4 .   События   A   и   B   являются независимыми событиями, а их вероятности равны:

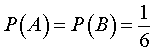
Событие     состоит в том, что на синей игральной кости выпадет число   3  ,   а на красной игральной кости выпадет число   4 .   Поскольку,

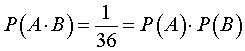
то в рассматриваемом случайном эксперименте по подбрасыванию двух игральных костей формула (4) верна.

В заключение приведем ещё одну иллюстрацию применимости формулы для вероятности суммы двух событий и формулы для вероятности произведения двух независимых событий.

ПРИМЕР 2. Два стрелка стреляют по мишени. Первый стрелок поражает мишень с вероятностью   0,9 .   Второй стрелок поражает мишень с вероятностью   0,8 .   Найти вероятность того, что мишень будет поражена.

РЕШЕНИЕ. Обозначим буквой   A   случайное событие, состоящее в том, что в мишень попадает первый стрелок, а буквой   B   обозначим случайное событие, состоящее в том, что в мишень попадает второй стрелок. Тогда событие   A + B   означает, что мишень поражена, а событие     означает, что в мишень попали оба стрелка. По условию

P (A) = 0,9   и   P (B) = 0,8  

а поскольку события   A   и   B   независимы, то в силу формулы (4)

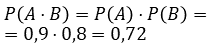
Воспользовавшись формулой (1), находим

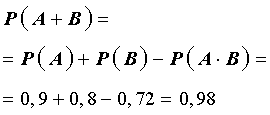
ОТВЕТ:   0,98

Продолжение статьи «Теория вероятности. Классическое определение».

В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.

Итак, теория.

Совместные и несовместные события

События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.

Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.

События называются совместными, если наступление одного из них не исключает наступления другого.

Например, бросая  игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем.   Когда выпадает три, реализуются оба события.

Сумма событий

Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

При этом сумма двух несовместных событий  есть сумма  вероятностей этих событий:

Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:

Вероятность же  суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:

Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня  в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность первого события «кофе закончится в первом автомате» также как и вероятность второго события «кофе закончится во втором автомате»  по условию равна 0,3. События являются совместными. 

Вероятность совместной реализации первых двух событий по условию равна 0,12.

Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть 

Зависимые и независимые события

Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.

Например,  при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5,  – независимые события.

Произведение вероятностей

Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Если  происходят два независимых события А и В с  вероятностями  соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:

Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле: .

Подборку задач на отработку темы смотрите здесь.

Содержание:

Теорема сложения вероятностей:

Теорема: Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т. е. если АВ = 0, то

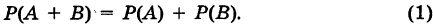
Доказательство: Пусть из общего числа п всех возможных и равновозможных элементарных исходов испытания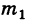

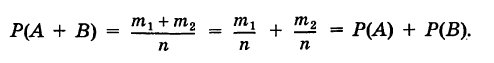
Следствие. Вероятность суммы конечного числа попарно несовместных событий равна сумме вероятностей этих событий.

Пусть, например, события А, В и С попарно несовместны, т. е. события АВ, АС, ВС невозможны.

Имеем

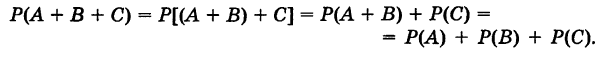
Замечание. Пусть теперь события А и В совместны. Тогда число благоприятных элементарных исходов для события А + В будет

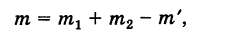
где 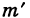— число элементарных исходов, благоприятных для события АВ. Действительно, складывая числа исходов 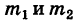, благоприятных событиям А и В, мы исходы, благоприятные событию АВ, считаем два раза; следовательно, при подсчете числа исходов для события А + В излишнее значение 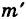следует отбросить.

Поэтому, в общем случае имеем

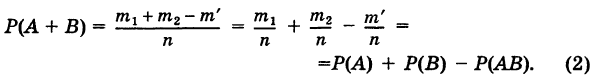
Следствие. Так как Р(АВ) 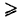0, то из формулы (2) имеем

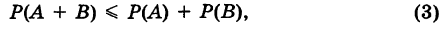
т. е. вероятность суммы двух событий никогда не превосходит суммы вероятностей этих событий.

Это утверждение, очевидно, справедливо также и для нескольких событий.

Пример:

В урне находятся 2 белых, 3 красных и 5 синих одинаковых по размеру шаров. Какова вероятность, что шар, случайным образом извлеченный из урны, будет цветным (не белым)?

Решение:

Пусть событие А — извлечение красного шара из урны, а событие В — извлечение синего шара. Тогда событие А + В есть извлечение цветного шара из урны. Очевидно, имеем

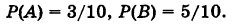
Так как события А и В несовместны (извлекается только один шар), то по теореме сложения имеем

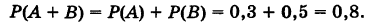
Полная группа событий:

Определение: Система событий

называется полной группой событий для данного испытания, если любым исходом его является одно и только одно событие этой группы.

Иными словами, для полной группы событий (1) выполнены следующие условия:

1)событие 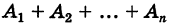достоверно;

2)события 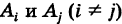попарно несовместны, т. е.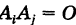 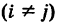, где О — событие невозможное.

Простейшим примером полной группы событий является пара событий: А и А.

Теорема: Сумма вероятностей событий полной группы равна единице.

Доказательство: Для полной группы (1) событие 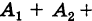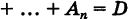достоверно, а события этой группы попарно несовместны. Отсюда на основании теоремы сложения вероятностей имеем

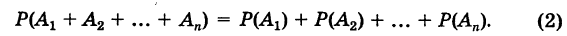
Но

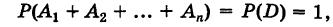
поэтому из (2) имеем

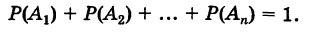
Теорема умножения вероятностей:

Определение: Вероятность события А при условии, что произошло событие В, называется условной вероятностью события А и обозначается так:

Замечание. Вероятность каждого события А в данном испытании связана с наличием известного комплекса условий. При определении условной вероятности мы предполагаем, что в этот комплекс условий обязательно входит событие В. Таким образом, мы фактически имеем другой, более обременительный комплекс условий, соответствующий испытанию в новой обстановке. Вероятность 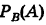появления события А при этих новых условиях называется его условной вероятностью, в отличие от вероятности Р(А), которая может быть названа безусловной вероятностью события А

Пример:

В урне находятся 7 белых и 3 черных шара.

Какова вероятность: 1) извлечения из урны белого шара (событие А); 2) извлечения из урны белого шара после удаления из нее одного шара, который является белым (событие В) или черным (событие С)?

Решение:

Здесь

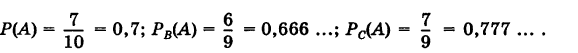
Таким образом, условная вероятность события может быть как меньше, так и больше вероятности этого события.

Определение: Два события А и В называются независимыми, если вероятность каждого из них не зависит от появления или непоявления другого, т. е.

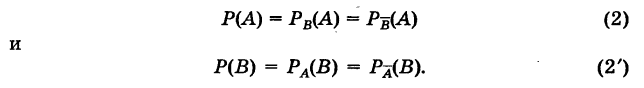
В противном случае события называются зависимыми.

Теорема: Вероятность произведения (совмещения) двух событий А и В равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое имеет место, т. е.

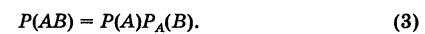
Доказательство: Пусть событию А благоприятствуют т, а событию АВ благоприятствуют k равновозможных элементарных исходов из общего их количеств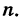а Тогда

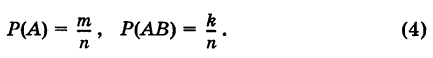
Но если событие А произошло, то в этой ситуации возможны лишь те m элементарных исходов, которые благоприятствовали событию А, причем k из них, очевидно, благоприятствуют событию В. Таким образом,

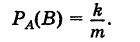
Отсюда на основании равенств (4) имеем

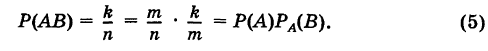
Теорема доказана.

Так как ВА = АВ, то имеем также

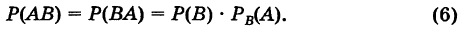
Замечание. Формула (5) формально остается верной, если событие А невозможно.

Следствие. Для любых двух событий А и В справедливо равенство

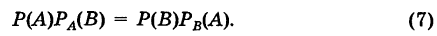
Теорема: Вероятность совместного появления двух независимых событий А и В равна произведению вероятностей этих событий:

Действительно, полагая, что 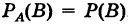, из формулы (5) получаем формулу (8).

Пример:

Вероятность поражения цели первым стрелком (событие A)равна 0,9, а вероятность поражения цели вторым стрелком (событие B)равна 0,8. Какова вероятность того, что цель будет поражена хотя бы одним стрелком?

Решение:

Пусть С — интересующее нас событие; противоположное событие 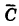, очевидно, состоит в том, что оба стрелка промахнулись. Таким образом, 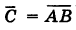. Так как события 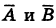независимы (при стрельбе один стрелок не мешает другому!), то

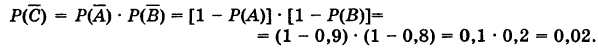
Отсюда вероятность того, что цель будет поражена хотя бы одним стрелком, есть

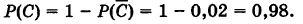
Теорема допускает обобщение на случай нескольких событий. Например, для случая трех событий А, В и С имеем

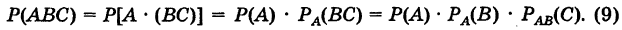
Определение: События называются независимыми в совокупности, если каждое из них и любое произведение остальных (включающее либо все остальные события, либо часть из них) есть события независимые.

События, независимые в совокупности, очевидно, попарно независимы между собой; обратное неверно.

Теорема: Вероятность произведения конечного числа независимых в совокупности событий равна произведению вероятностей этих событий.

Действительно, например, для трех независимых в совокупности событий А, В и С из формулы (9), учитывая, что

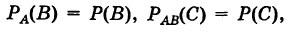
имеем

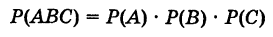
и т.п.

Теоремы сложения и умножения вероятностей

В теории вероятностей события рассматривают на фоне комплекса условий, которые его порождают. Проще говоря, событие – это результат опыта, который проистекает в природе по воле человека, независимо от нее или ей вопреки. Рассмотрим множество событий, которые можно наблюдать в эксперименте при фиксированном комплексе условий. На множестве таких событий определим следующие понятия.

Суммой событий A и B называется событие, состоящее в появлении хотя бы одного из событий A или B . Сумму событий A и B обозначают через A + B .

Приведенные понятия можно проиллюстрировать следующим образом.

Пусть комплекс условий состоит в том, что внутрь прямоугольника наугад бросают точку. Обозначим через А попадание точки внутрь левого круга, а через В – внутрь правого круга. Тогда события 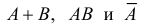состоят в попадании точки внутрь областей, закрашенных на соответствующей части рис. 2.3.1.

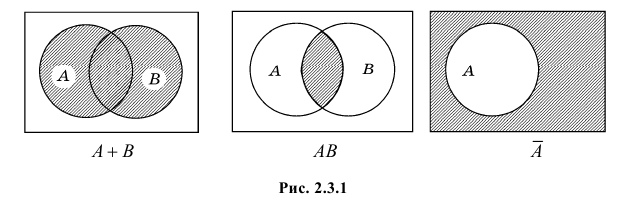
Произведением событий A и B называют событие, состоящее в появлении событий А и В в одном и том же опыте. Обозначают произведение событий A и B через AB.

Событие, состоящее в не появлении события A, называется противоположным событием и обозначается через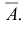

Если в каждом опыте два события A и B всегда либо оба происходят, либо оба не происходят, то такие события называют равносильными или эквивалентными и записывают: A = B .

Говорят, что события 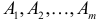образуют полную группу событий, если они попарно несовместимы и в каждом опыте непременно происходит одно и только одно из этих событий.

Словесные рассуждения можно перевести в символическую запись с помощью соответствий: «или» «+»; «и» «•»; «не A» 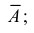«равносильно» «=».

Вероятность события A, вычисленная при условии, что событие B произошло, называется условной вероятностью события A и обозначается через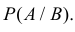

Теорема умножения вероятностей

Вероятность произведения событий равна вероятности одного события, умноженной на вероятность другого события, вычисленную при условии, что первое событие произошло, т.е.

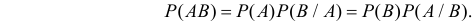
События называются независимыми, если появление одного из них не изменяет вероятности появления другого. Если события независимы, то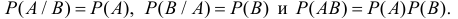 

Для любого конечного числа событий вероятность произведения событий равна произведению вероятностей этих событий, причем вероятность каждого следующего события вычисляется при условии, что предыдущие события произошли, т.е.

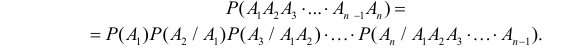
Если события независимы, то

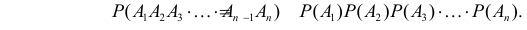
Итак, перед вычислением вероятности произведения событий необходимо установить, зависимы события или нет.

Пример №1

Вероятности попадания в цель при одном выстреле для первого, второго и третьего стрелков равны соответственно 0,3; 0,6; 0,8. Все три стрелка выстрелили в цель. Какова вероятность того, что:

а) цель поражена;

б) произошло только одно попадание;

в) произошло ровно два попадания;

г) попадут все три стрелка;

д) будет хотя бы один промах?

Решение. Обозначим через 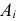– событие, состоящее в попадании в цель 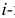го стрелка.

а) Поражение цели (событие A) равносильно появлению хотя бы одного из событий A₁ или A₂ или A₃. Поэтому 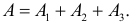Учитывая совместность событий, имеем

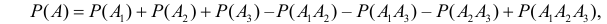
так как события независимы, то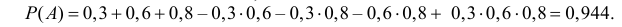

б) Рассмотрим три случая:

1) 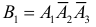– первый стрелок попал в цель и при этом второй не попал и третий не попал;

2) 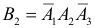– первый стрелок не попал и при этом второй попал и третий не попал;

3) 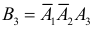– первый и второй не попали и при этом третий попал.

Только одно попадание в цель (событие В) равносильно реализации хотя бы одного из несовместных событий B₁ или B₂ или B₃ . Поэтому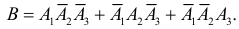

В силу независимости событий 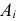имеем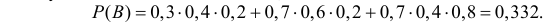

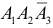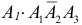в) Два попадания в цель (событие C) равносильны реализации хотя бы одного из несовместных случаев: или или 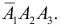В силу независимости событий 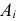получаем

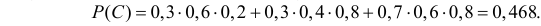
г) Все три стрелка попадут в цель (событие D), если произойдут события 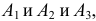т.е. 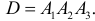В силу независимости событий 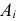имеем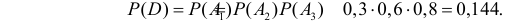

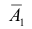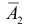д) Хотя бы один промах (событие Е) равносилен появлению хотя бы одного из событий или или 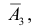т.е. 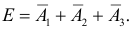Вместо вычисления вероятности суммы трех совместных событий, заметим, что событие E равносильно не появлению события D. Поэтому

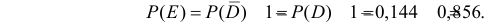
Ответ. а) 0,944; б) 0,332; в) 0,468; г) 0,144; д) 0,856.

Замечание. Значительное число вероятностных задач связано с теорией стрельб. В связи с этим уместно вспомнить изречение немецкого военного теоретика Карла Клаузевица (1780–1830): «Никакая человеческая деятельность не соприкасается со случаем так всесторонне и так часто, как война».

Пример №2

В первой урне два белых шара, четыре синих и девять красных, а во второй соответственно три, пять и шесть. Из каждой урны наугад выбирают два шара. Какова вероятность того, что будут выбраны шары одного цвета?

Решение. Событие, состоящее в выборе шаров одного цвета, обозначим через A. Обозначим через выбор из 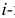й урны двух белых шаров, через 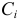обозначим выбор из 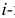й урны двух синих шаров, через 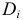выбор из 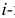й урны двух красных шаров.

Событие A произойдет, если из первой урны будут выбраны два белых шара (событие B₁) и из второй урны будут выбраны тоже два белых шара (событие B₂) или из первой урны извлекут два синих шара (событие C₁) и из второй урны будут выбраны тоже два синих шара (событие C₂) или из первой урны будут выбраны два красных шара (событие D₁) и из второй урны будут выбраны тоже два красных шара (событие D₂). Поэтому 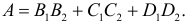События независимы и слагаемые несовместны. В итоге получаем, что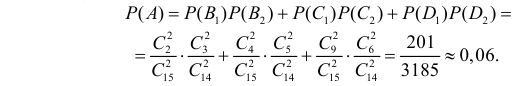

Ответ.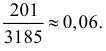

Теорема сложения вероятностей

Вероятность суммы событий A и B равна сумме вероятностей этих событий без вероятности их совместного появления: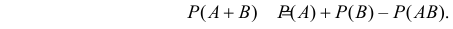

События называются несовместными, если их появление в одном и том же опыте невозможно. Если события A и B несовместны, то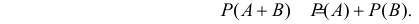

Для трех совместных событий теорема сложения вероятностей имеет вид: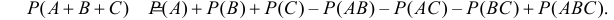

Если события несовместны, то

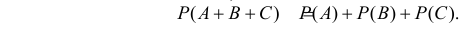
Теорему сложения можно обобщить на любое конечное число слагаемых: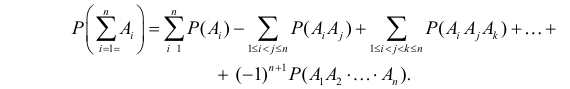

Если события несовместны, то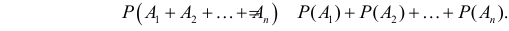

Итак, прежде чем вычислять вероятность суммы событий следует выяснить, совместны они или нет.

Указание. Желателен следующий порядок решения задач и оформления записи:

а) обозначения событий;

б) анализ взаимосвязей событий и их символическая запись;

в) вычисление вероятностей.

Пример №3

Из 20 изделий четыре имеют скрытые дефекты. Изделия выбирают наугад по одному и проверяют. Найдите вероятности следующих событий:

A – первым бракованным изделием окажется пятое по счету проверяемое изделие;

B – первыми бракованными изделиями окажутся третье и четвертое проверяемые изделия;

C – первыми бракованными изделиями окажутся третье и пятое по счету изделия.

Решение. Обозначим через 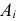– событие, состоящее в выборе годного изделия при 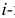м выборе. Событие A произойдет, если первые четыре изделия окажутся годными и лишь пятое по счету изделие будет бракованным. Это означает, что 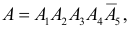причем события зависимы. Поэтому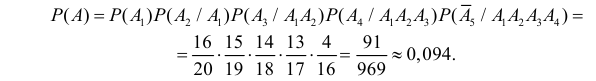

Событие B произойдет, если первые два изделия будут годными, а третье и четвертое окажутся бракованными. Символически это можно записать в виде 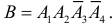В силу зависимости событий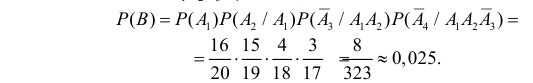

Аналогично, 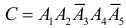и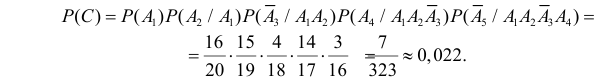

Ответ.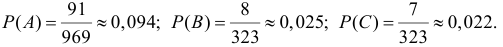

Пример №4

Имеется система соединенных между собой элементов (скажем, участок электрической цепи, поточная линия и т.д., см. рис. 2.3.2). Вероятность безотказной работы каждого элемента в течение заданного времени (надежность) равна 0,8. Элементы выходят из строя независимо друг от друга. Какова надежность системы?

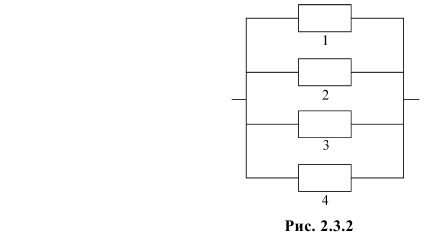
Решение. Пусть событие А состоит в безотказной работе системы в течение заданного времени, а 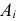означает безотказную работу 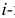го элемента в течение того же времени. Безотказная работа системы равносильна безотказной работе хоты бы одного элемента. Поэтому 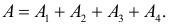События 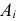совместны. Вместо вычисления вероятности 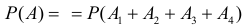по формуле вероятности суммы совместных событий вычислим вероятность противоположного события 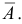Выход из строя системы эквивалентен выходу из строя всех элементов в течение заданного времени, т.е. 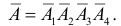Так как элементы выходят из строя независимо друг от друга, то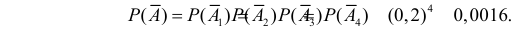

Тогда

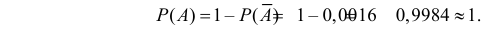
Ответ.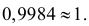

Пример №5

Имеется система соединенных между собой элементов (электрическая цепь, поточная линия и т.д., см. рис. 2.3.3). Вероятность безотказной работы (надежность) каждого элемента равна 0,9. Элементы выходят из строя независимо друг от друга. Какова надежность системы?

Решение. Пусть событие А состоит в безотказной работе системы, а 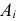– означает безотказную работу 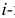го элемента. Событие А произойдет, если одновременно произойдут события 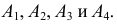Поэтому 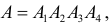а так как события независимы, то

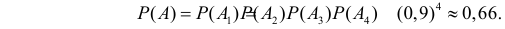
Ответ.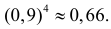

Пример №6

Два стрелка по очереди стреляют в цель до первого попадания. Вероятность попадания в цель при одном выстреле равна для них соответственно 1/3 и 1/2. Каждый стрелок имеет право только на два выстрела. Какова вероятность того, что цель будет поражена? Какова вероятность того, что цель поразит первый стрелок?

Решение. Обозначим через 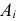попадание первого стрелка при 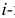м выстреле, а через – попадание второго стрелка при 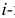м выстреле. На рис. 2.3.5 изображено «дерево» всех возможных способов протекания стрельбы.

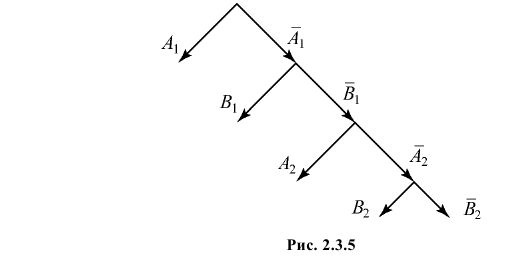
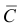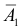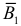Цель не будет поражена (событие ), если произойдут события и 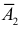и и 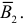 Так как события независимы, то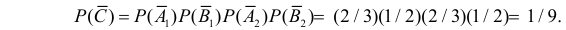

Поэтому вероятность поражения цели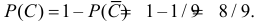

Цель поразит первый стрелок (событие A), если он попадет при первом выстреле или при первом выстреле он не попадет в цель и второй стрелок при своем первом выстреле не попадет в цель и после этого первый стрелок попадет в цель. Поэтому 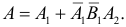События 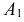и 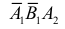несовместны. В силу независимости событий получаем

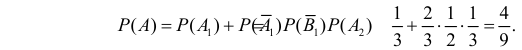
Ответ.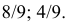

Пример №7

Урна содержит шесть занумерованных шаров с номерами от одного до шести. Шары извлекаются по одному без возвращения. Пусть событие A состоит в том, что шары будут извлечены в порядке их номеров, а событие B в том, что хотя бы один раз номер шара совпадет с порядковым номером его извлечения. Найти вероятности событий A и B и определить предельные вероятности этих событий при неограниченном увеличении числа шаров в урне.

Решение. а) Обозначим через 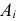– событие, состоящее в том, что порядок извлечения 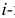го шара совпадает с его номером. Тогда событие 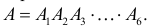Вместо рассмотрения произведения зависимых событий заметим, что шары в указанном порядке можно извлечь только одним способом, а всего равновозможных способов извлечения существует 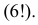Поэтому 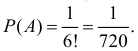При увеличении числа шаров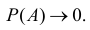

Событие B произойдет, если появится хотя бы одно из событий A₁ или A₂ или … или A₆. Поэтому 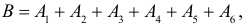причем события совместны. При переходе к противоположному событию придется рассматривать произведение шести зависимых событий  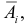что в данном случае сделать сложно. Поэтому вычислим вероятность суммы непосредственно: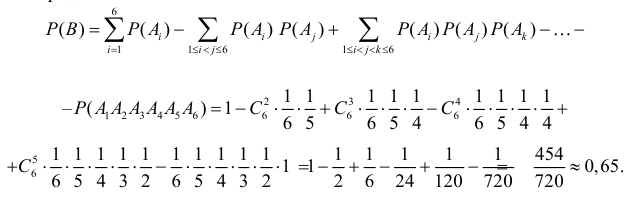

Заметим, что искомая вероятность является частичной суммой ряда Тейлора функци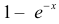и при 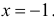Поэтому при больших 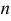имеем

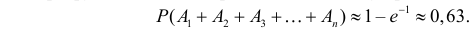
Ответ.   

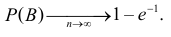
Теорема. Пусть имеем группу событий 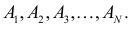Для любого целого 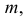удовлетворяющего условию  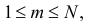вероятность 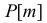одновременного появления 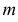из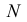 событий 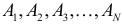определяется формулой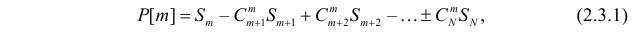 

где

 

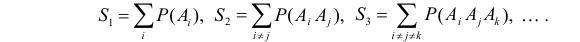
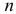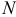К формуле (2.3.1) приводят следующие соображения. Пусть E – элементарный исход опыта. Предположим, что этот исход включен в из событий 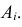Тогда вероятность этого исхода 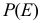входит в состав 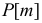только при 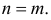Заметим, что 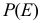входит в суммы 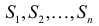и не входит в суммы 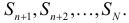Это означает, что 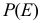не входит в правую часть (2.3.1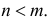) при При 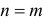вероятность 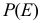входит в сумму 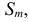а при 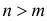члены 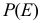в суммах 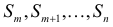взаимно уничтожаются. В самом деле, из 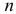событий, содержащих E, можно образовать 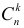групп по 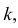поэтому 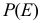входит в 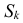с коэффициентом 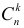. Тогда при 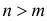вероятность 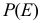входит в правую часть равенства (2.3.1) с коэффициентом

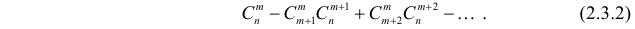
Но 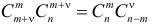(в этом легко убедиться, записав левую и правую часть равенства через факториалы). Поэтому выражение (2.3.2) преобразуется к виду

В последнем выражении в скобке имеем разложение бинома 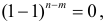так что коэффициент (2.3.2) равен нулю.

Продолжим решение примера. Установлено, что вероятность ровно 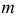 совпадений в соответствии с формулой (2.3.1) равна

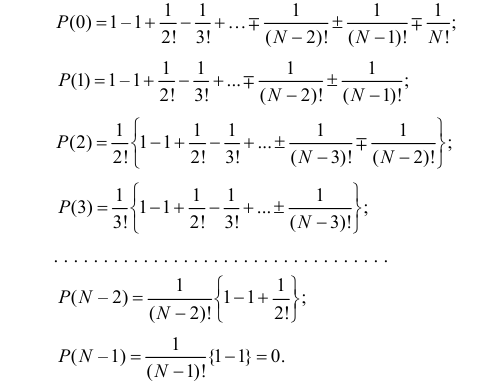
Здесь равенство нулю означает невозможность получить 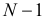совпадение без того, чтобы не было совпадений:

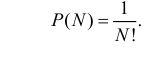
Всё о теореме умножения вероятностей

При оценки вероятности наступления какого-либо случайного события очень важно предварительно хорошо представлять, зависит ли вероятность наступления интересующего нас события от того, как развиваются остальные события. В случае классической схемы, когда все исходы равновероятны, мы уже можем оценить значения вероятности интересующего нас отдельного события самостоятельно. Мы можем сделать это даже в том случае, если событие является сложной совокупностью нескольких элементарных исходов. А если несколько случайных событий происходит одновременно или последовательно? Как это влияет на вероятность реализации интересующего нас события?

Если я несколько раз кидаю игральную кость, и хочу, чтобы выпала “шестерка”, а мне все время не везет, значит ли это, что надо увеличивать ставку, потому что, согласно теории вероятностей, мне вот-вот должно повезти? Увы, теория вероятности не утверждает ничего подобного. Ни кости, ни карты, ни монетки не умеют запоминать, что они продемонстрировали нам в прошлый раз. Им совершенно не важно, в первый раз или в десятый раз сегодня я испытываю свою судьбу. Каждый раз, когда я повторяю бросок, я знаю только одно: и на этот раз вероятность выпадения “шестерки” снова равна одной шестой. Конечно, это не значит, что нужная мне цифра не выпадет никогда. Это означает лишь то, что мой проигрыш после первого броска и после любого другого броска – независимые события.

События А и В называются независимыми, если реализация одного из них никак не влияет на вероятность другого события. Например, вероятности поражения цели первым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события “первое орудие поразило цель” и “второе орудие поразило цель” независимы.

Если два события А и В независимы, и вероятность каждого из них известна, то вероятность одновременного наступления и события А, и события В (обозначается АВ) можно посчитать, воспользовавшись следующей теоремой.

Теорема умножения вероятностей для независимых событий: Р(АВ) = Р(А)*Р(В) – вероятность одновременного наступления двух независимых событий равна произведению вероятностей этих событий.

Пример №8

Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: 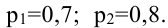Найти вероятность попадания при одном залпе обоими орудиями одновременно.

Решение:

Как мы уже видели события А (попадание первого орудия) и В (попадание второго орудия) независимы, т.е.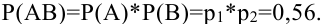

Что произойдет, с нашими оценками, если исходные события не являются независимыми? Давайте немного изменим предыдущий пример.

Пример №9

Два стрелка на соревнованиях стреляют по мишеням, причем, если один из них стреляет метко, то соперник начинает нервничать, и его результаты ухудшаются. Как превратить эту житейскую ситуацию в математическую задачу и наметить пути ее решения? Интуитивно понятно, что надо каким-то образом разделить два варианта развития событий, составить по сути дела два сценария, две разные задачи. В первом случае, если соперник промахнулся, сценарий будет благоприятный для нервного спортсмена и его меткость будет выше. Во втором случае, если соперник прилично реализовал свой шанс, вероятность поразить мишень для второго спортсмена снижается.

Для разделения возможных сценариев (их часто называют гипотезами) развития событий мы будем часто использовать схему “дерева вероятностей”. Эта схема похожа по смыслу на дерево решений, с которым Вам, наверное, уже приходилось иметь дело. Каждая ветка представляет собой отдельный сценарий развития событий, только теперь она имеет собственное значение так называемой условной вероятности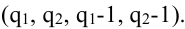

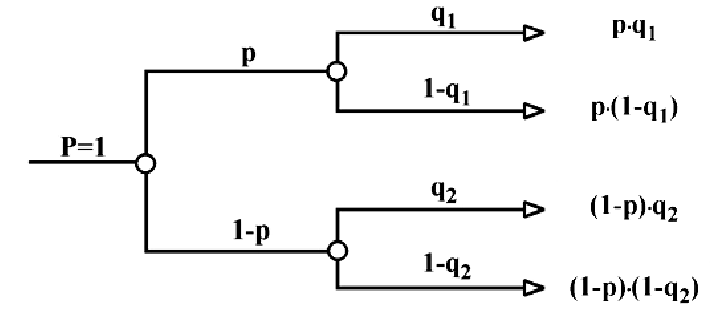
Эта схема очень удобна для анализа последовательных случайных событий.

Остается выяснить еще один немаловажный вопрос: откуда берутся исходные значения вероятностей в реальных ситуациях? Ведь не с одними же монетами и игральными костями работает теория вероятностей? Обычно эти оценки берутся из статистики, а когда статистические сведения отсутствуют, мы проводим собственное исследование. И начинать его нам часто приходится не со сбора данных, а с вопроса, какие сведения нам вообще нужны.

Пример №10

Допустим, нам надо оценить в городе с населением в сто тысяч жителей объем рынка для нового товара, который не является предметом первой необходимости, например, для бальзама по уходу за окрашенными волосами. Рассмотрим схему “дерева вероятностей”. При этом значение вероятности на каждой “ветке” нам надо приблизительно оценить. Итак, наши оценки емкости рынка: 1) из всех жителей города женщин 50%, 2) из всех женщин только 30% красят волосы часто, 3) из них только 10% пользуются бальзамами для окрашенных волос, 4) из них только 10% могут набраться смелости попробовать новый товар, 5) из них 70% обычно покупает все не у нас, а у наших конкурентов.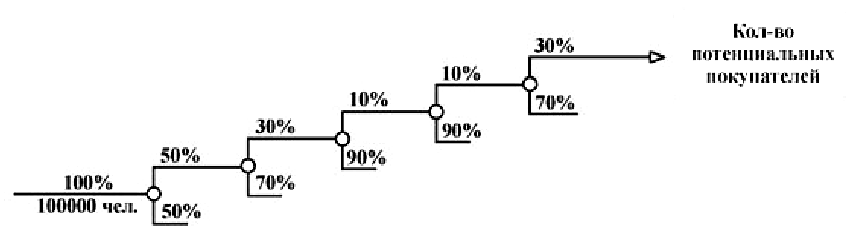

Решение:

По закону перемножения вероятностей, определяем вероятность интересующего нас события А={житель города покупает у нас этот новый бальзам} = 0,00045. Умножим это значение вероятности на число жителей города. В результате имеем всего 45 потенциальных покупательниц, а если учесть, что одного пузырька этого средства хватает на несколько месяцев, не слишком оживленная получается торговля.

И все-таки польза от наших оценок есть. Во-первых, мы можем сравнивать прогнозы разных бизнес-идей, на схемах у них будут разные “развилки”, и, конечно, значения вероятности тоже будут разные. Во-вторых, как мы уже говорили, случайная величина не потому называется случайной, что она совсем ни от чего не зависит. Просто ее точное значение заранее не известно. Мы знаем, что среднее количество покупателей может быть увеличено (например, с помощью рекламы нового товара). Так что имеет смысл сосредоточить усилия на тех “развилках”, где распределение вероятностей нас особенно не устраивает, на тех факторах, на которые мы в состоянии повлиять. Рассмотрим еще один количественный пример исследования покупательского поведения.

Пример №11

За день продовольственный рынок посещает в среднем 10000 человек. Вероятность того, что посетитель рынка заходит в павильон молочных продуктов, равна 1/2. Известно, что в этом павильоне в среднем продается в день 500 кг различных продуктов. Можно ли утверждать, что средняя покупка в павильоне весит всего 100 г?

Обсуждение:

Конечно, нельзя. Понятно, что не каждый, кто заходил в павильон, в результате что-то там купил.

Как показано на схеме, чтобы ответить на вопрос о среднем весе покупки, мы должны найти ответ на вопрос, какова вероятность того, что человек, зашедший в павильон, что-нибудь там купит. Если таких данных в нашем распоряжении не имеется, а нам они нужны, придется их получить самим, понаблюдав некоторое время за посетителями павильона. Допустим, наши наблюдения показали, что только пятая часть посетителей павильона что-то покупает. Как только эти оценки нами получены, задача становится уже простой. Из 10000 человек, пришедших на рынок, 5000 зайдут в павильон молочных продуктов, покупок будет только 1000. Средний вес покупки равен 500 грамм. Интересно отметить, что для построения полной картины происходящего, логика условных “ветвлений” должна быть определена на каждом этапе нашего рассуждения так же четко, как если бы мы работали с “конкретной” ситуацией, а не с вероятностями. Задачи для самопроверки 1. Пусть есть электрическая цепь, состоящая из п последовательно соединенных элементов, каждый из которых работает независимо от остальных.

Известна вероятность р невыхода из строя каждого элемента. Определите вероятность исправной работы всего участка цепи (событие А). 2. Студент знает 20 из 25 экзаменационных вопросов. Найдите вероятность того, что студент знает предложенные ему экзаменатором три вопроса. 3. Производство состоит из четырех последовательных этапов, на каждом из которых работает оборудование, для которого вероятности выхода из строя в течение ближайшего месяца равны соответственно 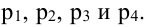Найдите вероятность того, что за месяц не случится ни одной остановки производства из-за неисправности оборудования.

Всё о теореме сложения вероятностей

В этом разделе мы начнем применять на практике математический аппарат теории вероятностей для оценки вероятности наступления интересующего нас случайного события, которое, в свою очередь, является некоторой комбинацией других случайных событий.

Классическое определение вероятности Р(А) события А как отношения числа благоприятных элементарных исходов m к числу всех элементарных исходов п предполагает, что все элементарные исходы равновероятны. Однако, это условие далеко не всегда выполняется, поэтому мы сейчас введем еще одно определение вероятности – статистическое (или частотное).

Как оценить вероятность интересующего нас события, если в процессе испытания элементарные исходы вовсе не обязаны быть равновероятными? Строго говоря, необходимо было бы много раз проделать интересующий нас опыт и узнать частоту реализации различных элементарных исходов.

В пределе, при увеличении числа испытаний, отношение числа m реализованных событий А к общему количеству испытаний n и будет определять вероятность 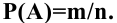Важно понимать, что статистический подход не противоречит классическому, а лишь расширяет границы возможного применения аппарата теории вероятностей. Поэтому все приемы, которые Вы уже освоили в рамках классической схемы, можно будет использовать и в дальнейшем. Для решения практических задач нам понадобятся следующие важные теоремы.

Теорема сложения вероятностей для несовместных событий:

Р(А + В) = Р(А) + Р(В) – вероятность наступления в результате эксперимента хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий.

Обсуждение:

Напомним, что события А и В называются несовместными, если в результате опыта они не могут появиться вместе. (Пожалуйста, не путайте их с независимыми событиями, которые мы обсуждали в прошлом разделе. Независимые события могут спокойно сосуществовать друг с другом.)

Пример №12

По статистике, в прошлом году 10% жителей нашего города встретили Новый год в отъезде, 40% ходили в гости или в ресторан, оставаясь в городе, остальные встречали Новый год дома. Считая, что эта тенденция сохранится, посчитайте вероятность того, что житель нашего города встретит Новый год дома.

Решение:

Здесь можно смело пользоваться теоремой сложения вероятностей, т.к. события встречи Нового года в разных местах одним и тем же человеком – несовместны. Поэтому все, кто встретит Новый год в гостях или в другом городе (они составят вместе 40% + 10%), не смогут встретить его дома. Принимая общее число жителей города за 100%, найдем, что 50% оставалось дома в прошлый раз. Полагая, что эти же пропорции сохранятся и в этом году, найдем, что вероятность встретить Новый год дома для жителя нашего города равна Р=0,5. (Заметим, что в данном случае нам было удобно посчитать сначала вероятность обратного события, а потом вычесть результат из 100%.)

Что произойдет, с нашими оценками, если исходные события не являются несовместными? Давайте немного изменим предыдущий пример.

Пример №13

Владелец фирмы частных такси хочет сделать прогноз количества клиентов на новогоднюю ночь. Пусть, по его сведениям, в прошлом году Новый год встретили дома 50%, в компании друзей или родственников, но не выезжая из города – 80%, в отъезде были 10%. Почему у него получилось в сумме больше 100%?

Видимо, каких-то жителей он посчитал больше одного раза. Скорее всего, тех, кто сидел дома, но, одновременно, принимал друзей или родственников, которые пришли к нему в гости. Поскольку эти события не являются несовместными, просто складывая вероятности, он завышает свои оценки.

Впрочем, это относится не только к оценке вероятности события, но и к решению любых задач на подсчет элементов объединения двух множеств путем сложения. Если множества частично перекрываются, сумма их элементов будет больше, чем реальное количество элементов, поскольку при арифметическом сложении элементы этого “перекрытия” мы невольно посчитали дважды, и как входящие в первое множество, и как входящие во второе. Выход здесь один: мы должны заметить, что множества частично “перекрываются”, посчитать число элементов в их общей части и вычесть это число из суммы (т.к. при суммировании мы его посчитали дважды).

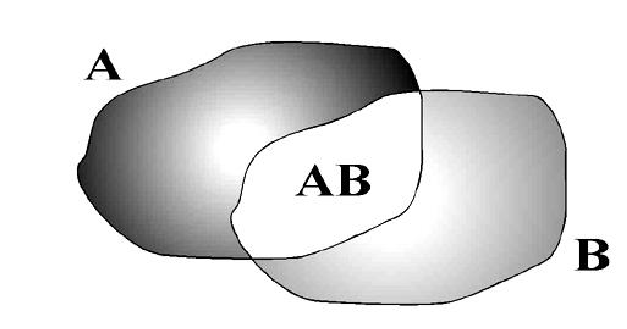
В случае подсчета вероятности события С, которое наступает или при наступлении события А, или при наступлении события В, если А и В не являются несовместными, можно воспользоваться следующей теоремой:

Общая теорема сложения вероятностей:

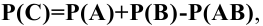где Р(АВ) – вероятность одновременного наступления и события А, и события В.

Зависимые и независимые случайные события.
Основные формулы сложения и умножения вероятностей

Понятия зависимости и независимости случайных событий. Условная вероятность. Формулы сложения и умножения вероятностей для зависимых и независимых случайных событий. Формула полной вероятности и формула Байеса.

Теоремы сложения вероятностей

Найдем вероятность суммы событий и (в предположении их совместности либо несовместности).

Теорема 2.1. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей:

Пример 1. Вероятность того, что в магазине будет продана пара мужской обуви 44-го размера, равна 0,12; 45-го — 0,04; 46-го и большего — 0,01. Найти вероятность того, что будет продана пара мужской обуви не меньше 44-го размера.

Решение. Искомое событие произойдет, если будет продана пара обуви 44-го размера (событие ) или 45-го (событие ), или не меньше 46-го (событие ), т. е. событие есть сумма событий . События , и несовместны. Поэтому согласно теореме о сумме вероятностей получаем

Пример 2. При условиях примера 1 найти вероятность того, что очередной будет продана пара обуви меньше 44-го размера.

Решение. События “очередной будет продана пара обуви меньше 44-го размера” и “будет продана пара обуви размера не меньше 44-го” противоположные. Поэтому по формуле (1.2) вероятность наступления искомого события

поскольку , как это было найдено в примере 1.

Теорема 2.1 сложения вероятностей справедлива только для несовместных событий. Использование ее для нахождения вероятности совместных событий может привести к неправильным, а иногда и абсурдным выводам, что наглядно видно на следующем примере. Пусть выполнение заказа в срок фирмой “Electra Ltd” оценивается вероятностью 0,7. Какова вероятность того, что из трех заказов фирма выполнит в срок хотя бы какой-нибудь один? События, состоящие в том, что фирма выполнит в срок первый, второй, третий заказы обозначим соответственно . Если для отыскания искомой вероятности применить теорему 2.1 сложения вероятностей, то получим . Вероятность события оказалась больше единицы, что невозможно. Это объясняется тем, что события являются совместными. Действительно, выполнение в срок первого заказа не исключает выполнения в срок двух других.

Сформулируем теорему сложения вероятностей в случае двух совместных событий (будет учитываться вероятность их совместного появления).

Теорема 2.2. Вероятность суммы двух совместных событий равна сумме вероятностей этих двух событий без вероятности их совместного появления:

---

Зависимые и независимые события. Условная вероятность

Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.

Пример 3. Монета брошена два раза. Вероятность появления “герба” в первом испытании (событие ) не зависит от появления или не появления “герба” во втором испытании (событие ). В свою очередь, вероятность появления “герба” во втором испытании не зависит от результата первого испытания. Таким образом, события и независимые.

Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.

События называются зависимыми, если одно из них влияет на вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события , вычисленная в предположении осуществления другого события , называется условной вероятностью события и обозначается .

Условие независимости события от события записывают в виде , а условие его зависимости — в виде . Рассмотрим пример вычисления условной вероятности события.

---

Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.

Решение. Обозначим извлечение изношенного резца в первом случае, а — извлечение нового. Тогда . Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.

Обозначим событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:

Следовательно, вероятность события зависит от того, произошло или нет событие .

---

Формулы умножения вероятностей

Пусть события и независимые, причем вероятности этих событий известны. Найдем вероятность совмещения событий и .

Теорема 2.3. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

---

Пример 5. Три ящика содержат по 10 деталей. В первом ящике — 8 стандартных деталей, во втором — 7, в третьем — 9. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.

Решение. Вероятность того, что из первого ящика взята стандартная деталь (событие ), . Вероятность того, что из второго ящика взята стандартная деталь (событие ), . Вероятность того, что из третьего ящика взята стандартная деталь (событие ), . Так как события , и независимые в совокупности, то искомая вероятность (по теореме умножения)

Пусть события и зависимые, причем вероятности и известны. Найдем вероятность произведения этих событий, т. е. вероятность того, что появится и событие , и событие .

Теорема 2.4. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Следствие 2.2. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.

---

Пример 6. В урне находятся 5 белых шаров, 4 черных и 3 синих. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что при первом испытании появится белый шар (событие ), при втором — черный (событие ) и при третьем — синий (событие ).

Решение. Вероятность появления белого шара при первом испытании . Вероятность появления черного шара при втором испытании, вычисленная в предположении, что при первом испытании появился белый шар, т. е. условная вероятность . Вероятность появления синего шара при третьем испытании, вычисленная в предположении, что при первом испытании появился белый шар, а при втором — черный, . Искомая вероятность

---

Формула полной вероятности

Теорема 2.5. Если событие наступает только при условии появления одного из событий , образующих полную группу несовместных событий, то вероятность события равна сумме произведений вероятностей каждого из событий на соответствующую условную вероятность события :

При этом события называются гипотезами, а вероятности — априорными. Эта формула называется формулой полной вероятности.

Пример 7. На сборочный конвейер поступают детали с трех станков. Производительность станков не одинакова. На первом станке изготовляют 50% всех деталей, на втором — 30%, на третьем — 20%. Вероятность качественной сборки при использовании детали, изготовленной на первом, втором и третьем станке, соответственно 0,98, 0,95 и 0,8, Определить вероятность того, что узел, сходящий с конвейера, качественный.

Решение. Обозначим событие, означающее годность собранного узла; , и — события, означающие, что детали сделаны соответственно на первом, втором и третьем станке. Тогда

Искомая вероятность

---

Формула Байеса

Эта формула применяется при решении практических задач, когда событие , появляющееся совместно с каким-либо из событий , образующих полную группу событий, произошло и требуется провести количественную переоценку вероятностей гипотез . Априорные (до опыта) вероятности известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е., по существу, нужно найти условные вероятности . Для гипотезы формула Байеса выглядит так:

Раскрывая в этом равенстве по формуле полной вероятности (2.1), получаем

---

Пример 8. При условиях примера 7 рассчитать вероятности того, что в сборку попала деталь, изготовленная соответственно на первом, втором и третьем станке, если узел, сходящий с конвейера, качественный.

Решение. Рассчитаем условные вероятности по формуле Байеса:

для первого станка

для второго станка

для третьего станка

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.