Истечение жидкости
через отверстие может происходить при
постоянном и переменном напоре. Если
истечение жидкости через отверстие
происходит в атмосферу или другую
газовую среду, то такое отверстие
называется незатопленным.
Если же истечение идет под уровень, а
не в атмосферу –
затопленным.
Сжатие называется
неполным,
если при подходе к отверстию поток с
одной или нескольких сторон не испытывает
сжатия.
Сжатие называется
полным
(совершенным),
если расстояние от любой стороны контура
до свободной поверхности жидкости или
края стенки, в которой расположено
отверстие, не будет меньше утроенного
поперечного размера отверстия.
Истечение
жидкости через отверстия и насадки
является одной из основных задач
гидродинамики. Задача гидравлического
расчета отверстий и насадков состоит
в определении скорости истечения и
расхода жидкости, вытекающей через
отверстие
или насадок.
Отверстие
в тонкой стенке – это отверстие, диаметр
которого минимум в 3 раза больше толщины
стенки, т.е. do>
3δ.
Насадком
называется
короткая труба длиной от 3 до 5 его
диаметров, присоединенная к отверстию.
При расчете насадков потерями напора
по длине обычно пренебрегают.
Скорость
истечения и вытекающий расход
рассчитываются по общим формулам для
отверстия и насадка, выведенным на
основе уравнения Бернулли. Общими
являются гидравлические характеристики:
коэффициенты расхода, скорости, сжатия,
сопротивления. Однако коэффициенты
расхода для отверстия и насадка различны
по величине, что связано с различной
картиной движения жидкости в них (рисунок
28).
|
|
|
|
а |
б |
|
Рисунок |
При истечении
жидкости, через отверстие в тонкой
стенке на некотором расстоянии от
стенки, происходит сжатие струи. Площадь
живого сечения струи будет меньше
площади отверстия (рисунок 27 а).
Сжатие струи обусловлено необходимостью
плавного перехода от различных направлений
движения жидкости в резервуаре, в том
числе от радиального движения по стенке,
к осевому движению струи (т.е. частицы
жидкости при входе в отверстие имеют
скорости различных направлений).
При истечении
жидкости через насадок после входа в
насадок жидкость сжимается примерно
так же, как и при истечении через отверстие
в тонкой стенке, а затем струя постепенно
расширяется до размеров отверстия и из
насадка выходит полным сечением (рисунок
27 б).
Сжатие струи
характеризуется коэффициентом
сжатия –
отношение площади сечения струи в месте
наибольшего сжатия к площади сечения
отверстия.
![]() ,
,
где Sc–
площадь живого сечения струи
![]() ;
;
S0
– площадь
отверстия,
![]() .
.
Коэффициент сжатия
ε
для круглых отверстий равен 0,64, а для
цилиндрических насадков равен 1.
4.8.1. Истечение жидкости через отверстие (или насадок) при постоянном уровне
Для вывода уравнений
расхода и скорости истечения через
отверстие и насадок при постоянном
уровне запишем уравнение Бернулли для
идеальной жидкости для двух живых
сечений 1–1
(на
свободной поверхности жидкости в сосуде)
и 2–2,
за плоскость сравнения примем сечение
2–2,
(рисунок 29):
|
|
|
|
Рисунок |
![]() ,
,
Тогда
z1=
H
, z2=0.
Скоростью в сечении
1-1
![]() ,
,
скорость в сечении 2-2![]() (
(![]() – теоретическая скорость истечения
– теоретическая скорость истечения
жидкости).
![]() ,
,
Тогда
![]() и
и![]() .
.
Пусть
у поверхности жидкости в резервуаре,
давление равно атмосферному и истечение
через отверстие происходит в пространство
с атмосферным давлением, то есть
p1
= p2
= pатм
.
И теоретическая
скорость истечения в этом случае
рассчитывается:
![]() .
.
Эта
формула была получена Эванджелиста
Торричелли,
в 1643 году.
Для реальной
жидкости учитываются потери напора в
сечении 2-2.
Они обусловлены потерей напора hп
на местном
сопротивлении и
определяются по формуле:
![]() ,
,
где ζ -коэффициент
местного сопротивления (для входа в
трубу без закругленных кромок ζ= 0,5, а с
закругленными кромками ζ= 0,1).
Тогда формула для
расчета действительной скорости
истечения через отверстие будет выглядеть
следующим образом:
![]() ,
,
Величина
![]()
называется коэффициентом
скорости и обозначается через φ.
Коэффициент
скорости φ
представляет собой отношение действительной
скорости истечения к теоретической,
определяется опытным путем.
Таким образом,
действительная скорость истечения
реальной жидкости:
![]() ,
,
Зная скорость
истечения жидкости можно определить
расход жидкости через отверстие:
![]() ,
,
где
![]()
Подставляя значения,
для скорости и коэффициента сжатия
получаем:
![]() ,
,
где ε
– коэффициент сжатия струи,
S0
– площадь отверстия,
φ
– коэффициент скорости,
Произведение
коэффициента сжатия струи на коэффициент
скорости называется коэффициентом
расхода и обозначается μр.
Следовательно:
![]() ,
,
Коэффициентом
расхода μр
называется
отношение действительного расхода к
теоретическому:
![]() ,
,
Тогда
![]() ,
,
![]() ,
,
При
истечении через малое отверстие в тонкой
стенке коэффициент скорости φ
с увеличением Re
возрастает, что связано с уменьшение
сил вязкости, что в свою очередь
сказывается на уменьшении коэффициента
сопротивления ξ.
Коэффициент сжатия
струи на выходе из насадка ε=1,
что приводит к повышению значения
коэффициента расхода μр
и соответственно
расхода жидкости.
Средние значения
коэффициентов истечения ε,
φ, μр,
ξ для малых
отверстий в тонкой стенке и насадка при
числах Re
больше 105
приведены в таблице 2.
Таблица 2 – Основные
гидравлические характеристики для
малых отверстий и насадка при числах
Re>105
|
Тип насадка или |
Коэффициенты |
|||
|
ε |
φ |
μр |
ξ |
|
|
Отверстие в |
0,62÷0,64 |
0,97 |
0,6÷0,62 |
0,06 |
|
Внешний |
1,0 |
0,82 |
0,82 |
0,5 |
В случаях, когда
число Re
меньше 105,
коэффициенты истечения находят из
графика А.Д. Альтшуля (рисунок 30),
составленного на основании опытов
разных авторов.

Рисунок 30 –
Зависимость коэффициента расхода от
значения критерия Рейнольдса для
круглого отверстия
Из графика следует,
что с увеличением числа Re
коэффициент расхода μр
сначала увеличивается, а затем, достигнув
максимального значения μр = 0,69
при Re
= 350, уменьшается и стабилизируется на
значении, близком к μр
= 0,62. Таким образом, коэффициенты истечения
при достаточно больших числах Re
зависят только от формы отверстий и
насадков [2-4,10].
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
15.05.2015135.17 Кб18генетическая карта русских.doc
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Истечение жидкости через насадки и отверстия
- gidroadmin
- 13249
Отверстие принято считать малым, если его диаметр d (для круглых отверстий)
или высота а (для прямоугольных отверстий) весьма малы по сравнению с напором Н.
При этом условии скорости во всех точках сечения струи в плоскости отверстия
практически одинаковы.
Под термином «тонкая» стенка следует понимать такую ее толщину, при которой она
не оказывает влияния на характер истечения. Опытами установлено, что толщина
стенки в этом случае не должна превышать 1—1,5 диаметра отверстия.
На расстоянии L~(0,5—l,0)d от плоскости отверстия образуется так называемое сжатое
сечение струи с—с (рис. 1), в котором течение можно считать параллельно-струйным. Площадь сжатого
сечения Sc = ε·S,
где S — площадь отверстия; ε — коэффициент сжатия.
Сжатие струи может быть совершенным, несовершенным, полным и неполным. Совершенным сжатие будет в
том случае, если боковые стенки и днище сосуда достаточно удалены от ближайшей точки контура
отверстия и не влияют на характер истечения. Можно считать, что этот случай имеет место при
неравенствах
L1≥3а и L2≥3b (рис.2. I).
Если же это условие не соблюдается (рис. 5.2, II), то сжатие называют несовершенным. Полное
сжатие струи — сжатие всестороннее, когда отверстие в достаточной мере удалено от боковых стенок
и днища сосуда. Если же часть периметра отверстия совпадает с боковой стенкой или днищем сосуда
(рис. 5.2, III), то сжатие струи называется неполным.
Скорость и расход жидкости при истечении
Скорость υ в сжатом сечении струи и расход жидкости Q определяются формулами:
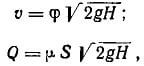
где φ — коэффициент скорости, характеризующий уменьшение действительной скорости υ по
сравнению с теоретической скоростью υт:
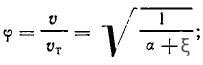
где ξ – коэффициент потери напора (сопротивления);
α – коэффициент Кориолиса, α = 1;
μ -коэффициент расхода: μ = εφ
Расчетный напор H
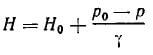
Скорость жидкости в резервуарах обычно принимается равной нулю. H0 — напор над
центром отверстия; p 0 и p — соответственно давления на поверхности жидкости в
резервуаре и в среде, куда вытекает жидкость через отверстие.
Если истечение происходит из закрытого резервуара в атмосферу,
числитель второго слагаемого представляет избыточное давление;
при истечении в атмосферу из открытого резервуара второе слагаемое обращается в нуль.
Коэффициент расхода μ, коэффициент скорости φ, и коэффициент сжатия ε
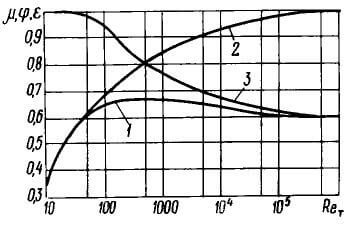
отверстия
Численные значения φ, ξ, ε и μ обычно определяются опытным путем и зависят от
расположения отверстия относительно стенок резервуара, а также от критериев подобия,
основным из которых является число Рейнольдса Re.
На рисунке 3 приведены графики зависимости μ, φ и ε и от Reт для круглого
отверстия при совершенном и полном сжатии, построенные А. Д. Альтшулем.
Кривая 1 — μ = f1(Reт); кривая 2 — φ =
f2(Reт);
кривая 3 — ε = f3(Reт).
Число Рейнольдса Reт подсчитано по теоретической скорости истечения:
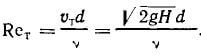
Как видно из графика, при Reт → ∞ φ → 1, а ε →
μ → 0,605.
Для маловязких жидкостей (вода, бензин, керосин), истечение которых обычно происходит при
достаточно больших числах Рейнольдса (Re> 105), коэффициенты истечения меняются в
сравнительно небольших пределах, поэтому в расчетах для случая совершенного сжатия можно
принимать следующие их усредненные значения: ε = 0,64; ξ = 0,06; φ = 0,97; μ
= 0,62.
Коэффициенты истечения практически не зависят от формы отверстия
(круглое, прямоугольное и т. д.), но изменяются при закруглении входной кромки
отверстия. При увеличении радиуса кривизны μ и ε увеличиваются.
Истечение жидкости из резервуаров может происходить также через различные типы насадков, например, цилиндрические и конические. В этом случае коэффициенты расхода и истечения можно определить по таблице.
Подробное видео по теме “Истечение жидкости через насадки и отверстия” приведено ниже.
Вильнер Я.М. Справочное пособие по гидравлике, гидромашинам и гидроприводам.
Верности творцу вам. Станьте верны творцу, создавшему вас и весь мир, чтобы жить в истине и доброте, во благо себе и всему окружающему. Если вы женского пола, то не выделяйте штанами женские ноги, не обнажайте ноги, грудь, плечи перед мужской частью населения, но носите длинное платье, длинную юбку, скрывая их. Если вы мужского пола, то не сбривайте бороду – не уподобляйте мужское лицо женскому; волосы можно подстригать, укорачивая их длину, но сохраняя видимое и осязаемое наличие на лице, на теле.И не ешьте мясо, яйца, как и не пользуйтесь вещами из кожи и меха, потому что это убийство, это зло – лишать жизни тех, кому мы её не дали. Питайтесь многообразной растительной пищей, съедобными грибами, мёдом, молочными продуктами – этим вы утолите голод, укрепите здоровье, но никому не нанесёте вред и не совершите убийство. Творец, действительно создавший вас и мир, – это не вымышленные религиозные бог, боги, которых нет. Творец не создавал никаких религий и не писал никаких религиозных книг, которые искусственно созданы людьми, отвергающими своего творца. Если вы хотите задать вопрос, я постараюсь вам ответить. Верности творцу вам. a.m_gurin@mail.ru 8-903-121-93-27 Андрей.
Спасибо за статью! Познавательно!
12-я лекция, 2010
8. ИСТЕЧЕНИЕ ЖИДКОСТИ
ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
8.1 Истечение через отверстия в тонкой стенке и насадки (короткие трубки)
при постоянном напоре.
8.2. Истечение при совершенном сжатии.
8.3 Скорость истечения при совершенном сжатии. Коэффициенты:ε, ξ, φ, μ
8.4 Истечение при несовершенном сжатии
8.5. Истечение под уровень
8.6. Истечение через насадки при постоянном напоре.
8.7 Первый режим течения.
8.8 Второй режим истечения
8.1. Истечение через
отверстия и насадки (короткие трубки)
при постоянном напоре.
Рассматривается
процесс истечение жидкости из резервуаров через отверстия и насадки в атмосферу
и в пространство, заполненное жидкостью.
При истечении запас
потенциальной энергии жидкости в
резервуаре, переходит в кинетическую энергию свободной струи, при переходе есть
потери энергии на трение и завихрение
частиц жидкости.
Задачей изучения
процесса истечения является определение скорости истечения и расхода жидкости.
Истечение
производится из резервуара с жидкостью под давлением Р0 на
свободной поверхности через круглое отверстие в тонкой стенке на глубине (во
много раз большей диаметра отверстия) Н0 >> dот (рис. 12.1).
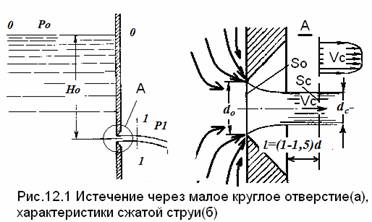
Через отверстие
жидкость вытекает в воздушное пространство с давлением Р1.
Отверстие в стенке
имеет острую кромку. Частицы жидкости приближаются к отверстию из всего
прилежащего объема, двигаясь ускоренно по различным плавным траекториям (см.
рис.12.1б). Струя отрывается от стенки у кромки отверстия и затем сжимается. Формирование
сжатого сечения струи происходит на расстоянии
примерно одного диаметра отверстия.
Сжатие струи происходит
при плавном переходе от различных направлений движения жидкости в резервуаре.
12.2. Истечение при
совершенном сжатии.
Совершенным сжатием называется наибольшее
сжатие струи, когда диаметр отверстия во
много раз меньше напора Н0.
Н0 >> dот
В этом случае боковые
стенки и свободная поверхность жидкости не влияют на поток жидкости к отверстию.
Сжатие струи оценивается
коэффициентом сжатия ε, равным отношению площади
поперечного сечения струи к площади отверстия
ε = Sc/S0 = (dc/d0)2. (12.1)
Для определения
скорости истечения и расхода из отверстия запишем уравнение Бернулли для движения
жидкости от свободной поверхности «0 – 0» в резервуаре и сечением
струи «1 – 1» (на рис.12.1а).
В рассматриваемом
случае уравнение Бернулли записывается для установившейся скорости, истечение происходит под постоянным напором,
над свободной поверхностью «0 – 0» давление
равно Р0, скорость
также равна нулю.
В сечении «1 – 1», струя примет цилиндрическую форму, давление Р1, скорость V1 предстоит определить из уравнения Бернулли для
потока реальной жидкости.
![]()
где ξ—
коэффициент, характеризующий сопротивление отверстия,  -коэффициент Кориолиса из уравнения Бернулли
-коэффициент Кориолиса из уравнения Бернулли
для потока вязкой жидкости, характеризующий неравномерность распределения
скоростей в потоке.
Если умножить
числитель и знаменатель выражения для α на ρ/2, можно убедиться, что α
является отношением действительной кинетической энергии потока в данном сечении
к кинетической энергии этого потока в этом сечения при равномерном распределении скоростей.
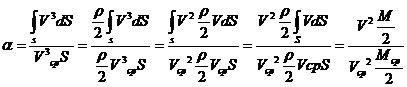
Выделив сумму
геометрического и пьезометрического напора Н = Н0 + (Р0 – Р1)/(ρg), получаем выражение,
связывающее скорость истечения и скоростной напор.
![]()
12.3 Скорость истечения
реальной жидкости при совершенном сжатии.
Коэффициенты:ε, ξ, φ, μ
Из выражения для
гидростатического напора, получим формулу для определения скорости истечения из
отверстия с острой кромкой для реальной жидкости
![]() , (12.2)
, (12.2)
где φ —
коэффициент скорости
![]() . (12.3)
. (12.3)
Для идеальной
жидкости, так как у нее отсутствует вязкость, трения и потерь на трение
нет ξ = 0, α = 1, следовательно,
φ
= 1.
Скорость
истечения идеальной жидкости из отверстия с острой кромкой
![]() (12.4)
(12.4)
Из формулы (12.2) можно заключить, что коэффициент
скорости φ есть отношение скорости истечения реальной жидкости к скорости истечения
идеальной жидкости.
![]() , (12.5)
, (12.5)
Скорость
истечения реальной жидкости меньше идеальной
из-за вязкости и трения, поэтому коэффициент скорости φ всегда меньше единицы.
Измерения
показывают, что в средней части сечения струи эпюра скоростей является
равномерной, поэтому скорость в средней части струи близка к идеальной ![]() , наружный слой жидкости притормаживается при трении о края
, наружный слой жидкости притормаживается при трении о края
стенки отверстия. Коэффициент φ
рассматривается, как коэффициент по средней скорости.
Умножив скорость истечения на площадь сечения струи, получим
выражение для расхода жидкости через отверстие с острой кромкой при совершенном
сжатии
![]() . (12.6)
. (12.6)
Коэффициентом
расхода μ называют произведение
значений коэффициентов сжатия ε и скорости
φ
μ = ε * φ.
Формула для
расхода через отверстие с острой кромкой с учетом выражения для μ
![]() (12.7) или
(12.7) или
![]() (12.8)
(12.8)
где ΔР
— расчетная разность давлений, под действием которой происходит истечение.
По этим формулам
определяется расход для всех случаев связанных с истечением из отверстия с острой кромкой и через насадки различных
форм.
Из уравнения (12.7)
следует, что
![]() (12.9)
(12.9)
Коэффициент
расхода есть отношение действительного
расхода Q к расходу идеальной
жидкости Qи,
определенному по ее скорости ![]() . Действительный
. Действительный
расход всегда меньше расхода идеальной жидкости, следовательно, коэффициент
расхода всегда меньше единицы из-за сжатия струи и трения.
Коэффициенты
сжатия струи ε, сопротивления ξ, скорости φ, расхода μ = ε * φ зависят от
типа отверстия и насадка и от числа Рейнольдса.
На рис. 12.2
показаны составленные Альтшулем зависимости
для коэффициентов ε, φ и μ
для круглого отверстия в функции
числа Rеи, подсчитанного по
скорости истечения идеальной жидкости
Rеи=Vиd/ν = ![]() .
.
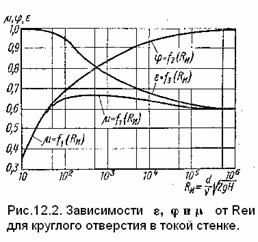
Увеличение числа Re означает
уменьшение сил вязкости, поэтому коэффициент φ возрастает в связи
с уменьшением коэффициента сопротивления ξ
(влияние трения становится меньше), коэффициент ε уменьшается из-за уменьшения торможения жидкости
у кромки отверстия и увеличения радиусов кривизны струи на входе в цилиндрическую
часть. При Rеи
→∞ значения коэффициентов приближаются к φ→1
и ε→0,6
и соответствуют истечению идеальной жидкости.
Коэффициент
расхода μ, определяемый
произведением ε на φ с увеличением Re сначала растет, что связано с сростом
φ,
а затем уменьшается в связи со
значительным падением ε
и при больших Rеи
равен μ = 0,60÷061.
В области малых Re (Rеи < 25) роль
вязкости велика, торможение жидкости у кромки значительно так, что сжатие струи отсутствует ε
= 1, φ = μ. В этом
случае можно пользоваться формулой:
![]() (12.10)
(12.10)
12.3. Истечение при
несовершенном сжатии
Несовершенным
сжатием струи тогда, когда на формирование струи оказывает влияние близость боковых
стенок резервуара.
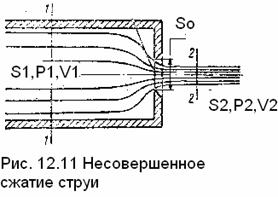
Боковые стенки успевают
направлять жидкость при подходе к отверстию, и струя сжимается в меньшей степени, чем при истечении
из резервуара неограниченных размеров при совершенном сжатии. Увеличивается коэффициент сжатия и коэффициент расхода.
При истечении из
цилиндрического резервуара через круглое отверстие, расположенное в центре торцевой
стенки при больших числах Re, коэффициент сжатия ε1 можно
находить по формуле Жуковского для идеальной жидкости
ε1 = 0,57 +0,043/(1,1 – n)
(12.11)
где n = S0/S1 отношение площади
отверстия S0 к
площади S1 поперечного
сечения резервуара.
Коэффициент
скорости φ при несовершенном сжатии мало зависит от отношения n и его
находят по графику на рис.12.2, коэффициент сопротивления отверстия ξ можно найти из формулы, связывающей ![]()
Коэффициент
расхода μ1 = ε1 φ
, уравнение Бернулли записывается для сечения «1-1» в резервуаре и сечения в
наиболее сжатой части струи, где давление равно Р0 –атмосферному.
Выразим V1 через V2 V1S1=V2 ε1S0;
V1=V2 ε1S0/S1;
V1=V2 ε1n
![]() .
.
(12.12)
Откуда получаем:
скорость для несовершенного
сжатия струи
 ; (12.13)
; (12.13)
расход для несовершенного
сжатия струи
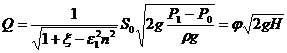 (12.14)
(12.14)
12.5. Истечение под
уровень
Истечением под
уровень называется истечение жидкости в пространство, заполненное этой же жидкостью
(рис. 12.12).

Вся кинетическая
энергия струи теряется на вихреобразование, как при внезапном расширении.
Составляя уравнение
Бернулли относительно свободных поверхностей «0 – 0» и «2 –
2» скорости считаем равными нулю, а приравнивая к
первой и второй части члены уранения для сжатого сечения получим с учетом
коффициента α :
![]() или
или
1-я сумма, 2-я сумма, 3- сжатое сечение
![]()
где Н – обозначен
расчетный напор, ξ – коэффициент сопротивления отверстия, имеющий примерно
то же значение, что и при истечении в атмосферу, V – скорость истечения в сжатом сечении
струи.
Скорость в этом
случае
![]() (12.15)
(12.15)
Расход
![]() , (12.16)
, (12.16)
где Sc – площадь
сжатого сечения струи, S0
– площадь отверстия.
Получились такие же расчетные формулы, что и при истечении в
воздух, только расчетный напор Н в данном
случае представляет собой разность
гидростатических напоров по обе стороны стенки, т.е. скорость и расход
не зависят от высоты расположения
отверстия.
Коэффициенты
сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.
12.6.
Истечение через насадки при постоянном напоре.
Внешним
цилиндрическим насадком называется короткая трубка длиной, равной l = (2÷6)d без
закругления входной кромки (рис.12.4а). Истечение через такой насадок в атмосферу может
происходить в двух режимах.
12.5.1.Первый режим течения- безотрывный:
струя после входа в насадок сжимается
примерно как при истечении через
отверстие в тонкой стенке.
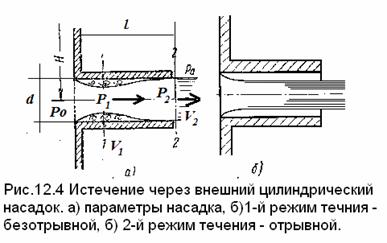
Затем сжатая часть
струи расширяется до размеров отверстия, и из насадка выходит полным сечением. Такой
режим истечения называют безотрывным. На выходе диаметр струи равен диаметру отверстия.
Для маловязких
жидкостей средние значения коэффициентов
для этого режима при больших числах Re равны: μ=φ = 0,8, ξ = 0,5-0,63.
Коэффициент μ
расхода такого насадка при этом режиме истечения жидкости зависит от относительной
длины насадка l/d и числа Re. Однако и при достаточном значении
l/d не всегда возможен
этот режим.
Пусть
истечение жидкости происходит под действием давления Р0 в среду
газа с давлением Р2. Расчетный напор в этом случае
H = (P0 – Р2)/(ρg)
В
струе на выходе из насадка давление равно Р2, в суженном месте
струи внутри насадка, где скорость увеличена, давление Р1 меньше, чем
Р2.
Чем больше напор, под которым происходит истечение и расход через насадок, тем
меньше абсолютное давление Р1.
Разность давлений Р2 – Р1
растет пропорционально напору Н.
Покажем
это, составив уравнение Бернулли для сечений 1 – 1 и 2 – 2,α = 1 (см. рис.12.4а):
![]()
Последний
член уравнения представляет собой потерю напора на расширение потока, которое в
данном случае происходит примерно так же, как и при внезапном расширении трубы (формула
Борда). Сжатие струи внутри насадка можно оценить коэффициентом сжатия ε,
как и в случае отверстия, поэтому на основании уравнения расхода
ε=S1/S2; V1S1=V2S2;
V1/V2=S2/S1=1/ ε;
V1=V2/ε. (12.17)
Заменив
с помощью этого соотношения скорость V1 в уравнении
Бернулли на скорость V2, а ее скорость V2 выражением через ![]() , найдем падение давления внутри насадка:
, найдем падение давления внутри насадка:
![]() (12.18)
(12.18)
Подставляя сюда φ = 0,8 и
ε=0.63, получаем
(Р2 – Р1 ) ≈ 0,75ρgH (12.19)
Если
истечение происходит в среду, где Р2 равно постоянному ,
например, атмосферному давлению, увеличение
напора до критической величины Нкр приводит
к уменьшению Р1 – абсолютное давление в сжатом сечение «1 – 1» внутри насадка может уменьшиться до давления насыщенных паров. Поэтому существует
величина напора, называемая критическим
напором
Hкр ≈ Р2 /(0,75ρg). (12.20)
Следовательно,
при Н
> Hкр
давление Р1 должно
стать отрицательным, но отрицательных давлений в жидкости не бывает, поэтому
первый режим истечения при
Н
> Hкр
делается невозможным. При Н ≈ Hкр происходит внезапное
изменение режима истечения, переход от первого режима ко второму (см. рис.12.4в).
12.5.2. Второй режим истечения
характеризуется тем, что струя после сжатия уже не расширяется, сохраня
цилиндрическую форму, и перемещается внутри насадка, не соприкасаясь с его
стенками. Течение становится таким же, как из отверстия в тонкой стенке, с теми
же значениями коэффициентов. Следовательно, при переходе от первого режима ко
второму скорость возрастает, расход
уменьшается, благодаря сжатию струи.
Если
через насадок происходит истечение воды в атмосферу, то
Hкр ≈ Ра /(0,75ρg) = 10,33/0,75 ≈ 14 м.
Когда
давление Рн.п.
насыщенных паров истекающей жидкости соизмеримо с давлением Р2
среды, в которую происходит истечение,
пренебречь величиной Рн.п. нельзя, в формуле (12.19) следует принять Р1
= Рн.п.
Hкр = (Ра – Рн.п.)
/(0,75ρg) (12.21)
Если
после перехода от первого режима истечения ко второму уменьшить напор Н,
то второй режим будет сохраняться вплоть до самых малых Н. Это значит, что второй
режим истечения возможен при любых напорах, следовательно, при Н < Нкр возможны оба
режима.
При
истечении через цилиндрический насадок под уровень первый режим истечения не
будет отличаться от описанного выше. Но когда абсолютное давление внутри
насадка благодаря увеличению Н падает до давления насыщенных
паров перехода ко второму режиму не происходит, а начинается кавитационный
режим, при котором расход перестает зависеть от противодавления Р2,
получается эффект стабилизации расхода. При этом чем меньше относительное противодавление
Р2/Р0
= Рвых/Рвх =![]() , которое является критерием кавитации, тем шире
, которое является критерием кавитации, тем шире
область кавитации внутри насадка и тем меньше коэффициент расхода μ.
Таким
образом, при истечении жидкости через внешний цилиндрический насадок под
уровень коэффициент является функцией трех безразмерных критериев, а именно
μ = f (l/d, Re, ![]() ).
).
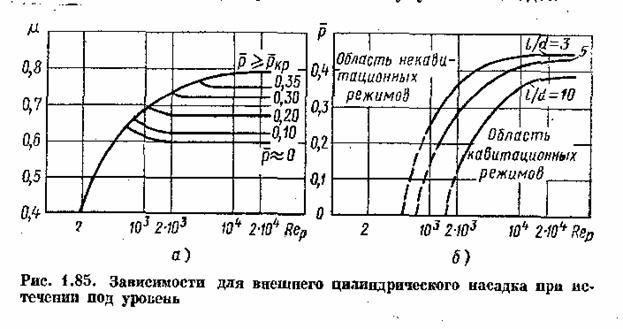
Результаты
новых экспериментальных исследований этого случаи истечения представлены в
безразмерных координатах на рис. 1.85. На рис.1.85а даны зависимости от Re при l/d = 3
для ряда значений ![]() , начиная от
, начиная от ![]() = 0 и до
= 0 и до ![]() >
> ![]() , где
, где ![]() – критическое
– критическое
значение ![]() , соответствующее началу кавитации и, следовательно,
, соответствующее началу кавитации и, следовательно,
критерию ηкр(см. п. 1.23). На рис. 1.85б показаны области кавитационных и
безкавитационных режимов истечения через насадки с l/d = 3; 5 и 10. Увеличение![]() при возрастании Re объясняется уменьшением коэффициента ε сжатия струи
при возрастании Re объясняется уменьшением коэффициента ε сжатия струи
внутри насадка, т. е. увеличением степени сжатия, а уменьшение ![]() при увеличении l/d происходит из-за возрастания давления в сжатом сечении вследствие
при увеличении l/d происходит из-за возрастания давления в сжатом сечении вследствие
увеличения потерь на трение по длине насадка.
Таким
образом, внешний цилиндрический насадок имеет существенные недостатки: на
первом режиме – большое сопротивление и недостаточно высокий коэффициент расхода,
а на втором – очень низкий коэффициент расхода. Недостатком является также двойст-венность
режима истечения в газовую среду при Н < Нкр, а следовательно двузначность
расхода при данном Н и возможность кавитации при истечении под уровень.
При
использовании цилиндрического насадка (сверления в толстой стенке), например в
качество жиклеров, дросселей или форсунок эти недостатки следует учитывать или
улучшать насадок.
Внешний
цилиндрический насадок может быть значительно улучшен путем закругления входной
кромки (см. штриховые линии на рис. 1.83) или устройства конического входа с
углом конусности около 60° (см. жиклер на рис. 1.75).
Чем
больше радиус закругления, тем выше коэффициент расхода и ниже коэффициент
сопротивления. В пределе при радиусе кривизны, равном толщине стенки, цилиндрический
насадок приближается к коноидальному насадку, или соплу.
Коноидальный
насадок (рис. 1.86) очерчивается приблизительно по форме естественно сжимающейся
струи и, благодаря этому, обеспечивает безотрывность течения внутри насадка в
параллельноструйность в выходном сечении. Это весьма распространеный насадок, так
как он имеет коэффициент расхода, близкий к единице, и очень малые потери
(коэффициент сжатия ε = 1), а также устойчивый режим течения без кавитации.
Значения
коэффициента сопротивления те же, что и при плавном сужении (см. п. 1.32), т.
е. ξ= 0,03 ÷ 0,1 (большим Re соответствуют малые ξ ‚ и наоборот). В соответствии с этим
μ =φ= 0,99÷0,96.
Диффузорный
насадок представляет собой комбинацию сопла и диффузора (рис. 1.87).

Приставка
диффузора к соплу влечет за собой снижение давления в узком месте насадка, а
следовательно, увеличение скорости и расхода жидкости через него. При том жедиаметре
узкого сечения, что и у сопла, и том же напоре диффузорный насадок может дать
значительно больший расход (увеличение до 2,5 раза), чем сопло.
Такие насадки
применяют в том случае, когда заданы диаметр узкого сечения и напор и требуется
получить возможно больший расход. Однако, использовать диффузорных насадков
можно лишь при небольших напорах Н = 1 ÷4
м, так как иначе в узком месте насадка возникает кавитация. Следствием кавитации являются увеличение
сопротивления и уменьшение пропускной способности насадка.
На рис.1.88
показано падение коэффициента расхода диффузорного насадка с увеличением напора
вследствие кавитации, возникающей в узком месте насадка при истечении воды в атмосферу.
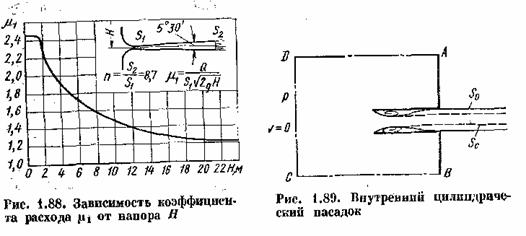
Коэффициент
расхода отнесен к площади узкого сечения, т. е. ![]() . Приведенная кривая получена в результате испытания диффузорного
. Приведенная кривая получена в результате испытания диффузорного
насадка, обладающего наивыгоднейшим углом и степенью расширения, которые
обеспечивают наибольший коэффициент расхода.
Внутренний
цилиндрический насадок или насадок Борда, изображен на рис.1.89. Там же
схематически показаны два режима истечения , аналогичные режимам истечения
через внешний цилиндрический насадок. Очертания струи при первом режиме
показаны сплошными линиями, а при втором – штриховыми. Так как частицы жидкости
приближаются к входному отверстию
насадка из всего прилежащего объема, а некоторые из них, попадающие на
периферию струи, изменяют направление своего движения на 180°, то степень
сжатия струи в данном насадке больше, а коэффициент ε меньше, чем во внешнем
цилиндрическом насадке. Значение ε в этом случае при истечении идеальной
жидкости может быть получено на основании
теоремы Эйлера об изменения количества движения (см. п. 1.15). Применим эту
теорему к фиксированному объему в виде кругового цилиндра ABCD соосного с насадком, и с основанием
CD, достаточно удаленным от насадка, где V=0. Пренебрегая толщиной стенки
насадка на основании указанной теоремы при втором режиме истечения получим
PS0 = ρSс*V2,
где
P— давление в центре
основания CD, S0 и Sс —
площади отверстия насадка и сечения струи (силы давления жидкости на кольцевые
площади оснований цилиндра ABCD уравновешиваются, а избыточное
давление по площади S0 в
плоскости АВ равно нулю.
С
другой стороны, для скорости истечения имеем
![]() 1 .
1 .
IIосле
подстановки второго уравнения в первое и сокращения на Р и ρ получим
ε = Sс / S0 = ½.
Этому
значению ε соответствуют значения коэффициентов расхода μ = 0,71 и потерь
ξ =1, что подтверждается опытами при первом режиме истечения и больших
числах Рейнольдса.















Примеры
Примеры. Пример 7. 1 определите расход и расход воды из небольшого круглого отверстия в боковой стенке большого резервуара диаметром (1 = 0, 03 м). Давление над центром отверстия равно n-1 м, а температура воды равна 20°С. Кинематическая вязкость воды v = 1 * 10 * 6 м2 / с (см. Таблицу 6) определяет число Рейнольдса, характеризующее Сток. 1/2 до 9, 81. 1 * 0. 03 Кэи = = —6 = 133, 000. Н В 1-10 6 7. 2 из рисунка для этого числа Рейнольдса: (l = 0. 59; f = 0. 98. 1 А. Д. А л ш у Л, М. Ш. Марголин / / инженерно-физический журнал. 18, № 4, 1970. 154.
Смотрите также:
- Предмет гидравлика
Скорость оттока воды из скважины o = Пример 7. 2. Если давление в баке постоянно и / / = поддерживается на уровне 4 м, определяют отверстие с острым краем диаметром= = см, а также расход и расход масла из бака через коническое сопло того же диаметра. Кинематическая вязкость масла 7 = 2 * 10-5 м2 / э. Решение. Найдите число Рейнольдса, характеризующее срок годности. 7. 2 из рисунка: ph = 0. 66; fn = 0. 90. Подача масла от отверстия В = ФН ’ / Г2 П $ = 0. 90-4. 43-2 = 8 м / с Дебит нефти /. 3. 14-0. 012 л (2ч =В-В2§ч= 0. 66-^ 4. 43-2 = 4. 6-10〜4 м3 / сек.
Смотрите также:
- Воронкообразование при истечении жидкости.
Как и при входе в трубу, наблюдается сжатие струи за отверстием. Причиной этого является инерционность жидких частиц, двигающихся к отверстию из резервуара по радиальным направлениям.
Людмила Фирмаль
Для сравнения найдите объемный расход воды при том же давлении[t = 1 * 10′ 6 м2 / с, температура 20°С (см. Приложение 2) ). 4. 43-2. 0. 01 — ^ — = 88 600; То есть примерно на 10% меньше, чем потребление нефти. Определить объемный расход масла в стоке из Коноидального сопла (в данном случае рН = fn = 0, 90 : и. .3 .14-0 .012 л Sn = Tsn) ] / 2 ^ I= 0 .90- -4 .43-2 = 6 .25-10-4 м3 / с .Объемный расход воды при тех же условиях (rv = fv = 0, 98 = 0 .98 3’1440 .012 4 .43-2 = 6 .86-10-4 М3 / С То есть примерно на 10% больше, чем потребление нефти .
Смотрите также:
Местные сопротивления в открытых руслах.
Так, в рассматриваемом случае округлость края отверстия (конического сопла) приводит к увеличению расхода масла на 26% и увеличению расхода воды на 40% .Пример 7 .3 .Охлаждающая вода поступает в пароперегреватель через бурильную трубу при температуре 20 ° С и расходе 2 (0, 00278 м3 / с) .давление воды в трубе составляет от p1 = 1 до 106 Па, а давление в корпусе протектора перегрева-2 = 0 .7XXIO6Pa .Определите, сколько отверстий D = 0, 003 м в диаметре должно быть просверлено в трубе для обеспечения заданного расхода воды .
Решение .Плотность воды составляет Р = 998, 2 кг / м3 (см .добавление 1) .Кинематическая вязкость V = 1 * 10-6 м2 / с (см .Приложение 2) .155 .Определите число Рейнольдса, характеризующее отток из отверстия .В 2D R19A У2-0 .3-10Э / 998 .2 * 0 .003 Коя=«=! .Ю-б = 73 80°- Найти 7 .2 коэффициент излучения отверстия p, = 0 .6 из рисунка .Расход воды, протекающей через 1 отверстие Количество требуемых отверстий д 0 .00278 П-Д〜10 .3-10-5 Пример 7 .4 вода течет из бассейна шириной B = 2 м, глубиной H1 = 3 м, через тонкостенное круглое отверстие, расположенное в центре, шириной= 0, м, в поддон шириной 6 = 0, 15 м, глубиной H2 = 0, 2 В .расстояние A = 0, 1 м от дна бассейна .
Определите расход воды (2 проходит через отверстие .Решение .Определить коэффициент расхода по формуле (7 .25) .От) / ’2еата-Еала + с0 + 1-2ет’ Найдите значение ямы .Площадь отверстия ы = л <* 2/4 = 0 .78-0 .01 = 0 .0078 м2 .Жилая часть бассейна=&м2; н .=(0 /&1 = 0 .0078 / 6 = 0 .0013 Живая площадь сечения лотка J2 = b / 12 = 0, 15-0, 25 = 0, 0375 м2; m = co / J2 = 0, 0078 / 0, 0375 = 0, 208 «0, 21 .чтобы определить e, используйте таблицу . 7 .2; e при n = 0 .0013 „0 .6 K .предполагаемый коэффициент расхода (=0 .06 М1 .И ’* _} / 2-0 .61 а-0, 21 а-0, 61 а-0, 0013 а+ 0 .06+ 1 −2-0 .61-0 .
В гидрогеологии и геологии вместо термина «расход воды» может использоваться термин «дебит» (например, «дебит скважины»), однако его использование носит локальный характер для этих специальностей и не распространяется, например, на родственную им гидрологию.
Людмила Фирмаль
- Поэтому коэффициент эмиссии скважины значительно ниже, чем в случае неразлива, где Р-0, 6 .Определите расход воды .< 2 = С3 <о] / 2# (# !- НГ) = 0 .507-0 .0078-4 .43 У 3-0 .25 = 0, 025 м3 / с .Пример 7 .5 температура 20°С вода вытекает из тонкостенных отверстий диаметром= = 0, 005 м .определите расход и сравните его с расходом глицерина, протекающего при тех же условиях .Высота уровня жидкости от центра отверстия I = 0, 05 м .Решение .Определите число Рейнольдса отверстий в оттоке воды и глицерина[вода V = 1 .01 −10〜6 м2 / с, глицерин V = 1, 19 10-3 м2 / С]: вода Коэффициент расхода у кромки воды показан на рисунке .
Коэффициент расхода при истечении глицерина определяется по формуле (7 .14) .Потребление глицерина < ?», = 0, 376 3° — V2 .9 .81 510-2 = 7 .3-10-6 М8 / С .В аналогичных условиях расход глицерина со значительно большей вязкостью был на 43%меньше, чем расход воды .Пример 7 .6 танка состоит из 3 соединенных между собой камерах (рис . 7 .7) .Определите расход воды и уровень воды в каждой камере .Диаметр цилиндрического сопла первой перегородки^ 1 = 0, 1 м; диаметр конического сопла 2-й перегородки<22 = 0, 2 м, угол конусности a = 10°; диаметр отверстия 3-й перегородки.




