Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 июня 2021 года; проверки требует 1 правка.
Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида.[1][2]
Её можно рассматривать как задачу об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки.
Транспортная задача по теории сложности вычислений входит в класс сложности P.
Когда суммарный объём предложений (грузов, имеющихся в пунктах отправления) не равен общему объёму спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной (открытой).
Постановка задачи[править | править код]
Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачи).
Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку).
Под названием транспортная задача, определяется широкий круг задач с единой математической моделью, эти задачи относятся к задачам линейного программирования и могут быть решены оптимальным методом. Однако, спец.метод решения транспортной задачи позволяет существенно упростить её решение, поскольку транспортная задача разрабатывалась для минимизации стоимости перевозок.
Математическая формулировка задачи[править | править код]
Однородный груз сосредоточен у 









,
,
История поиска методов решения[править | править код]
Проблема была впервые формализована французским математиком Гаспаром Монжем в 1781 году[4]. Прогресс в решении проблемы был достигнут во время Великой Отечественной войны советским математиком и экономистом Леонидом Канторовичем[5]. Поэтому иногда эта проблема называется транспортной задачей Монжа — Канторовича.
Методы решения[править | править код]
Классическую транспортную задачу можно решить симплекс-методом, но в силу ряда особенностей её можно решить проще (для задач малой размерности).
Условия задачи располагают в таблице, вписывая в ячейки количество перевозимого груза из 



Итерационное улучшение плана перевозок[править | править код]
Нахождение опорного плана[править | править код]
Требуется определить опорный план и путём последовательных операций найти оптимальное решение. Опорный план можно найти следующими методами: «северо-западного угла», «наименьшего элемента», двойного предпочтения и аппроксимации Фогеля.
Метод северо-западного угла (диагональный или улучшенный)[править | править код]
На каждом этапе максимально возможным числом заполняют левую верхнюю клетку оставшейся части таблицы. Заполнение таким образом, что полностью выносится груз из 

Метод наименьшего элемента[править | править код]
Одним из способов решения задачи является метод минимального (наименьшего) элемента. Его суть заключается в сведении к минимуму побочных перераспределений товаров между потребителями.
Алгоритм:
- Из таблицы стоимостей выбирают наименьшую стоимость и в клетку, которая ей соответствует, вписывают большее из чисел.
- Проверяются строки поставщиков на наличие строки с израсходованными запасами и столбцы потребителей на наличие столбца, потребности которого полностью удовлетворены. Такие столбцы и строки далее не рассматриваются.
- Если не все потребители удовлетворены и не все поставщики израсходовали товары, возврат к п. 1, в противном случае задача решена.
Итерации[править | править код]
После нахождения опорного плана перевозок, нужно применить один из алгоритмов его улучшения, приближения к оптимальному.
- Метод падающего камня[de]
- Метод потенциалов.
Решение с помощью теории графов[править | править код]
Рассматривается двудольный граф, в котором пункты производства находятся в верхней доле, а пункты потребления — в нижней. Пункты производства и потребления попарно соединяются рёбрами бесконечной пропускной способности и цены за единицу потока 
К верхней доле искусственно присоединяется исток. Пропускная способность рёбер из истока в каждый пункт производства равна запасу продукта в этом пункте. Цена за единицу потока у этих рёбер равна 0.
Аналогично к нижней доле присоединяется сток. Пропускная способность рёбер из каждого пункта потребления в сток равна потребности в продукте в этом пункте. Цена за единицу потока у этих рёбер тоже равна 0.
Дальше решается задача нахождения максимального потока минимальной стоимости (mincost maxflow). Её решение аналогично нахождению максимального потока в алгоритме Форда — Фалкерсона. Только вместо кратчайшего дополняющего потока ищется самый дешёвый. Соответственно, в этой подзадаче используется не поиск в ширину, а алгоритм Беллмана — Форда. При возврате потока стоимость считается отрицательной.
Алгоритм «mincost maxflow» можно запускать и сразу — без нахождения опорного плана. Но в этом случае процесс решения будет несколько более долгим. Выполнение алгоритма «mincost maxflow» происходит не более чем за 



При решении несбалансированной транспортной задачи применяют приём, позволяющий сделать её сбалансированной. Для этого вводят фиктивные пункты назначения или отправления. Выполнение баланса транспортной задачи необходимо для того, чтобы иметь возможность применить алгоритм решения, построенный на использовании транспортных таблиц.
Обобщения[править | править код]
Транспортная задача в сетевой постановке[править | править код]
В этом варианте пункты не делятся на пункты отправления и пункты потребления, все пункты равноправны, но производство задается положительным числом, а потребление — отрицательным. Перевозки осуществляются по заданной сети, в которой дуги могут соединять любые пункты, включая производитель — производитель, потребитель — потребитель.
Задача решается слегка измененным методом потенциалов, практически тем же, что и классическая постановка.
Транспортная задача с ограничениями пропускной способности[править | править код]
Вариант транспортной задачи в сетевой постановке, при котором задается максимальная пропускная способность некоторых дуг.
Задача решается слегка усложненным методом потенциалов.
Многопродуктовая транспортная задача[править | править код]
Вариант транспортной задачи, в которой присутствует несколько продуктов (пункты могут производить/потреблять несколько продуктов). Для некоторых дуг задается ограничение на пропускную способность (без этого ограничения задача распадается на отдельные задачи по продуктам).
Задача решается симплекс-методом (используется разложение Данцига — Вулфа, в качестве подзадач используются однопродуктовые транспортные задачи).
Примечания[править | править код]
- ↑ А. В. Кузнецов, Н. И. Холод, Л. С. Костевич. Руководство к решению задач по математическому программированию. — Минск: Высшая школа, 1978. — С. 110.
- ↑ Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е. — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5.
- ↑ Корбут, 1969, с. 28.
- ↑ Monge G. Mémoire sur la théorie des déblais et de remblais. Histoire de l’Académie Royale des Sciences de Paris, avec les Mémoires de Mathématique et de Physique pour la même année, pages 666—704, 1781.
- ↑ Kantorovich L. On the translocation of masses // C. R. (Doklady) Acad. Sci. URSS (N. S.), 37:199-201, 1942.
Ссылки[править | править код]
- Транспортная задача
- Алгоритмы нахождения максимального потока
- http://kb.mista.ru/article.php?id=859 Решение транспортной задачи в 1С:Предприятие 8.2
Литература[править | править код]
- Корбут А.А., Финкельштейн Ю.Ю. Дискретное программирование. — М.: Наука, 1969. — 368 с.
 Одна из самых распространенных и востребованных оптимизационных задач в логистике — транспортная задача. В классическом виде она предполагает нахождение оптимального (т. е. сопряженного с минимальными затратами) плана грузоперевозок.
Одна из самых распространенных и востребованных оптимизационных задач в логистике — транспортная задача. В классическом виде она предполагает нахождение оптимального (т. е. сопряженного с минимальными затратами) плана грузоперевозок.
Например, у нас есть сеть розничных магазинов, которым требуется определенное количество товаров. Также имеется ряд складов поставщиков, где требуемые товары хранятся. При этом на каждом складе различный объем запасов этих товаров. Кроме этого нам известны тарифы — затраты на перевозку 1 товара от каждого склада к каждому магазину.
Возникает необходимость разработать такой план перевозок, чтобы магазины получили требуемое количество товаров с наименьшими затратами на транспортировку. Вот именно в таких случаях (и во множестве других) приходится решать транспортную задачу.
Содержание:
- теоретический материал по транспортной задаче;
- общий план решения методом потенциалов;
- подробный пример решения транспортной задачи;
- практическое применение транспортной задачи.
Теоретический материал по транспортной задаче
Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.
Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления (например, складов) в пункты потребления (например, магазины), с минимальными общими затратами на перевозки.
Математическая модель транспортной задачи имеет следующий вид:
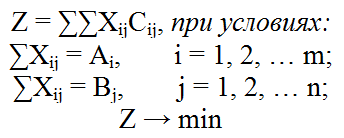
где: Z — затраты на перевозку грузов;
X — объем груза;
C — стоимость (тариф) перевозки единицы груза;
A — запас поставщика;
B — запрос потребителя;
m — число поставщиков;
n — число потребителей.
Общий план решения транспортной задачи методом потенциалов
Решить транспортную задачу можно различными методами, начиная от симплекс-метода и простого перебора, и заканчивая методом графов. Один из наиболее применяемых и подходящих для большинства случаев методов — итерационное улучшение плана перевозок.
Суть его в следующем: находим некий опорный план и проверяем его на оптимальность (Z → min). Если план оптимален — решение найдено. Если нет — улучшает план столько раз, сколько потребуется, пока не будет найден оптимальный план.
Ниже приведен алгоритм решения транспортной задачи в самом общем виде:
- Построение транспортной таблицы.
- Проверка задачи на закрытость.
- Составление опорного плана.
- Проверка опорного плана на вырожденность.
- Вычисление потенциалов для плана перевозки.
- Проверка опорного плана на оптимальность.
- Перераспределение поставок.
- Если оптимальное решение найдено, переходим к п. 9, если нет — к п. 5.
- Вычисление общих затрат на перевозку груза.
- Построение графа перевозок.
Подробная инструкция по решению транспортной задачи
1. Построение транспортной таблицы
Заполняем транспортную таблицу с исходными данными, где указываем запасы материалов, имеющиеся на складах поставщиков (Ai), и потребности заводов (Bj) в этих материалах.
В нижний правый угол ячеек таблицы заносим значение тарифов на перевозку груза (Cij).
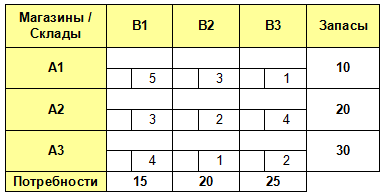
2. Проверка задачи на закрытость
Обозначим суммарный запас груза у всех поставщиков символом A, а суммарную потребность в грузе у всех потребителей — символом B.
Тогда:
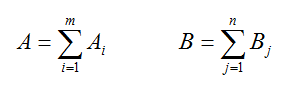
Транспортная задача называется закрытой, если A = B . Если же A ≠ B , то транспортная задача называется открытой. В случае закрытой задачи от поставщиков будут вывезены все запасы груза, и все заявки потребителей будут удовлетворены. В случае открытой задачи для ее решения придется вводить фиктивных поставщиков или потребителей.
Проверим задачу на закрытость:
A = 10 + 20 + 30 = 60.
B = 15 + 20 + 25 = 60.
A = B, следовательно данная транспортная задача — закрытая.
3. Составление опорного плана
Составляет предварительный (опорный) план перевозок. Он не обязательно должен быть оптимальный. Это просто своеобразный «черновик» или «набросок», итерационно улучшая который мы постепенно придем к оптимальному плану.
Есть разные методы нахождения опорного плана. Наиболее распространены следующие:
а) Метод Северо-Западного угла
Суть метода проста — ячейки транспортной таблицы последовательно заполняются максимально возможными объемами перевозок, в направлении сверху вниз и слева направо. То есть сперва заполняется самая верхняя левая ячейка («северо-западная» ячейка), потом следующая справа и т. д. Затем переходят на новую строку и вновь заполняют ее слева направо. И так пока таблица не будет заполнена полностью.
Подробное описание метода и пример можно посмотреть здесь.
б) Метод минимального элемента
Метод заключается в том, что для заполнения ячеек транспортной таблицы выбирается клетка с минимальным тарифом. Затем выбирается следующая клетка с наименьшим значением тарифа и так продолжается до тех пор, пока таблица не будет заполнена (все запасы и потребности при этом обнулятся).
Подробное описание метода и пример можно посмотреть здесь
в) Аппроксимация Фогеля
Основа метода в нахождении разности (по модулю) между парой минимальных тарифов в каждой строке и столбце. Затем в строке или столбце с наибольшей разностью заполняется клетка с наименьшим тарифом. Затем все эти действия повторяются заново, только при этом уже не учитываются заполненные клетки.
Подробное описание аппроксимации Фогеля и пример можно посмотреть здесь
г) Метод двойного предпочтения
Суть метода в том, что отмечаются клетки с наименьшим тарифом по строкам, а затем по столбцам. Затем ячейки заполняются в следующей очередности: сначала клетки с двумя отметками, потом с одной, наконец без отметок.
Подробное описание метода и пример можно посмотреть здесь
Выберите один из методов и пройдите по ссылке в его описании, чтобы посмотреть как в данном примере был составлен опорный план и заполнена транспортная таблица.
4. Проверка опорного плана на вырожденность
Клетки таблицы, в которые записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) — свободными.
План называется вырожденным, если количество базисных клеток в нем меньше, чем m + n — 1. Если во время решения задачи получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в базисные (общий баланс и суммарная стоимость перевозок плана при этом не изменятся).
Проводить пополнение плана, выбирая клетки произвольно, нельзя. План должен быть ациклическим!
План называется ациклическим, если его базисные клетки не содержат циклов. Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. Ниже приведен пример цикла:
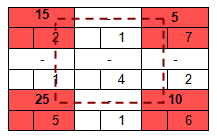
Ломаная линия может иметь точки самопересечения, но не в клетках цикла.
В нашем примере количество базисных клеток = 5; m + n — 1 = 3 + 3 — 1 = 5.
Следовательно, первоначальный план перевозок — невырожденный (5 = 5).
5. Вычисление потенциалов для плана перевозки
Для анализа полученных планов и их последующего улучшения удобно ввести дополнительные характеристики пунктов отправления и назначения, называемые потенциалами.
Этот метод улучшения плана перевозок называется методом потенциалов. Есть другие методы итерационного улучшения плана перевозок, но здесь мы их рассматривать не будем.
Итак, сопоставим каждому поставщику Ai и каждому потребителю Bj соответствующие величины Ui и Vj так, чтобы для всех базисных клеток плана было выполнено следующее соотношение: Ui + Vj = Cij.
Добавим к транспортной таблице дополнительную строку и столбец для Ui и Vj.
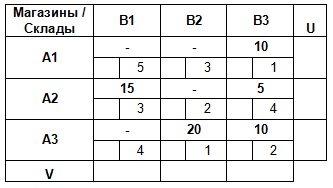
Предположим, что U1 = 0.
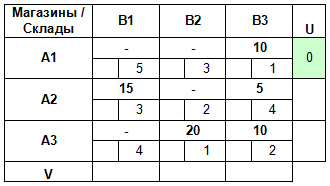
Тогда мы сможем найти V3 = C13 — U1 = 1 — 0 = 1.
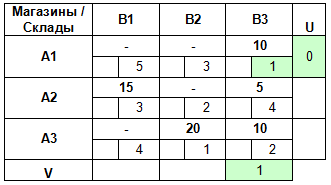
Зная V3, мы теперь можем найти U3:
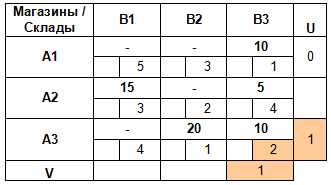
По аналогии вычисляем все оставшиеся потенциалы:
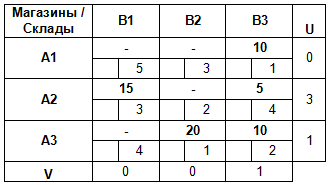
6. Проверка плана на оптимальность методом потенциалов
Для каждой свободной клетки плана вычислим разности ΔCij = Cij — (Ui + Vj ), и запишем полученные значения в левых нижних углах соответствующих ячеек.
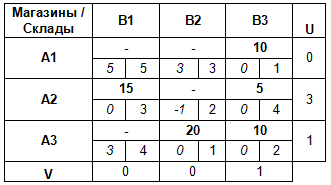
План является оптимальным, если все разности ΔCij ≥ 0.
В данном случае план — неоптимальный (ΔC22 < 0), и его следует улучшить путем перераспределения поставок.
7. Перераспределение поставок
Найдем ячейку с наибольшей по абсолютной величине (т. е. без учета знака, по модулю) отрицательной разностью ΔCij и построим цикл, в котором кроме этой клетки все остальные являются базисными. Такой цикл всегда существует и единственен.
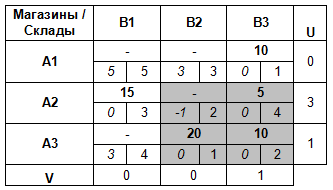
Отметим ячейку с отрицательной разностью ΔCij знаком «+», следующую знаком «–», и так далее, поочередно.
Затем находим минимальное значение груза в ячейках цикла имеющих знак «-» (здесь это 5) и вписываем его в свободную ячейку со знаком «+». Затем последовательно обходим все ячейки цикла, поочередно вычитая и прибавляя к ним минимальное значение (в соответствии со знаками, которыми эти ячейки помечены: где минус — вычитаем, где плюс — прибавляем).
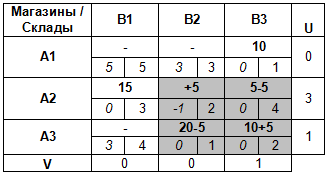
Получим новый опорный план перевозок:
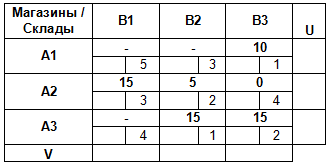
Так как базисных клеток стало больше, чем m + n — 1, то базисную клетку с нулевым значением делаем свободной:
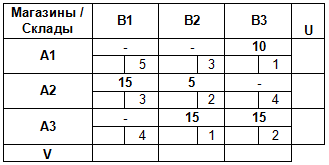
Снова вычисляем значения потенциалов и разности ΔCij:
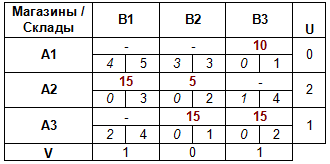
На этот раз все разности ΔCij ячеек положительные, следовательно, найдено оптимальное решение.
8. Если оптимальное решение найдено, переходим к п. 9, если нет — к п. 5.
В нашем примере оптимальное решение найдено, поэтому переходим к пункту 9.
9. Вычисление общих затрат на перевозку груза
Вычислим общие затраты на перевозку груза (Z), соответствующие найденному нами оптимальному плану, по формуле:
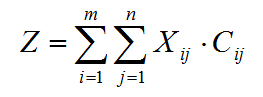
То есть нужно перемножить значения объемов грузоперевозок на соответствующие им тарифы.
Zmin = 10 ⋅ 1 + 15 ⋅ 3 + 5 ⋅ 2 + 15 ⋅ 1 + 15 ⋅ 2 = 110 ден. ед.
В результате общие затраты на доставку всей продукции для оптимального решения составляют 110 ден. ед.
10. Построение графа перевозок
Найдя оптимальный план перевозок, построим граф. Вершинами графа будут «склады» и «магазины». В вершинах укажем соответствующие объемы запасов и потребностей. Дугам, соединяющим вершины графа, будут соответствовать ненулевые перевозки. Каждую такую дугу подпишем, указав объем перевозимого груза.
В результате получится граф, аналогичный изображенному ниже:
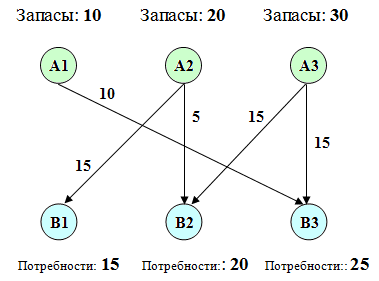
Все, транспортная задача решена. Поздравляю!
Практическое применение транспортной задачи
Транспортная задача применяется во многих случаях. В частности:
- оптимизация поставок сырья и материалов на производственные предприятия;
- оптимизация доставок товаров со складов в розничные магазины;
- оптимизация пассажирских перевозок.
Это далеко не полный перечень возможностей прикладного использования транспортной задачи.
Источники
- Галяутдинов Р. Р. Конспект лекций по логистике
- Решение транспортной задачи в 1С: Предприятие 8.2 // Волшебный форум (@romix). URL: http://kb.mista.ru/article.php?id=859 (дата обращения: 29.10.2013)
- Транспортная задача // Википедия. URL: http://ru.wikipedia.org/wiki/Транспортная_задача (дата обращения: 29.10.2013)
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Оптимальный план перевозок
|
Потребители Поставщики |
В1 |
В2 |
В3 |
В4 |
Запасы |
|
|
А1 |
1 0 |
2 60 |
3 |
4 |
60 |
0 |
|
А2 |
4 |
3 |
2 20 |
0 60 |
80 |
-1 |
|
А3 |
0 40 |
2 |
2 60 |
1 |
100 |
-1 |
|
Потребность |
40 |
60 |
80 |
60 |
240 |
|
|
|
1 |
2 |
1 |
0 |
Для
распределения, полученного в табл. 8.5,
условие
![]()
выполняется, следовательно, план —
оптимальный.
Транспортные
издержки по оптимальному плану следующие:
![]()
д.е.
Таким
образом, построением начального плана
с последующим расчетом двух итераций
получено оптимальное решение по
прикреплению пунктов отправления
грузов к пунктам назначения.
9.3. Усложненные задачи транспортного типа
Нами
рассмотрена классическая транспортная
задача, на которой показано, как
используется метод потенциалов для
нахождения оптимального плана. В
экономике предприятия такие задачи
встречаются крайне редко. Обычно при
составлении экономико – математической
модели задачи транспортного типа
приходится вводить целый ряд
дополнительных ограничений, а затем
пользоваться методом потенциалов.
Ряд
экономических задач легко сводимы к
транспортной задаче. Рассмотрим наиболее
часто встречающиеся ситуации
в экономике предприятия.
1
Отдельные поставки от определенных
поставщиков некоторым потребителям
должны быть исключены (из-за отсутствия
необходимых условий хранения,
чрезмерной перегрузки коммуникаций
и т д ) Это ограничение требует, чтобы в
матрице перевозок, содержащей оптимальный
план, определенные клетки оставались
свободными. Последнее достигается
искусственным завышением затрат на
перевозки
![]()
в клетках, перевозки
через которые следует запретить При
этом производят завышение величины
![]()
до таких значений, которые будут заведомо
больше всех и с которыми их придется
сравнивать в процессе решения задачи.
-
На
предприятии необходимо определить
минимальные суммарные затраты на
производство и транспортировку
продукции. С подобной задачей сталкиваются
при решении вопросов, связанных с
оптимальным размещением производственных
объектов. Здесь может оказаться
экономически более выгодным доставлять
сырье из более отдаленных пунктов, но
зато при меньшей его себестоимости
В таких задачах за критерий оптимальности
принимают сумму затрат на производство
и транспортировку продукции. -
Ряд
транспортных маршрутов, по которым
необходимо доставить грузы имеют
ограничения по пропускной способности.
Если например, по маршруту

можно провести не
более q
единиц груза то
Bj
-й столбец матрицы
разбивается на два столбца – Вj‘-
и Вj”
В первом столбце
спрос принимается равным разности
между действительным спросом

и ограничением
 :
: ,
,
во втором – равным
ограничению q,
т. е.
 .
.
Затраты

в обоих столбцах
одинаковы и равны данным, но в первом
столбце
 ,
,
в клетке соответствующей ограничению
i,
вместо истинного
тарифа

ставится искусственно завышенный тариф
М (клетка
блокируется) Затем задача решается
обычным способом.
-
Поставки
по определенным маршрутам обязательны
и должны войти в оптимальный план
независимо от того, выгодно это или нет
В этом случае уменьшают запас груза у
поставщиков и спрос потребителей и
решают задачу относительно тех поставок,
которые необязательны. Полученное
решение корректируют с учетом
обязательных поставок. -
Экономическая
задача не является транспортной, но в
математическом отношении подобна
транспортной, так как описывается
аналогичной моделью, например
распределение производства изделий
между предприятиями, оптимальное
закрепление механизмов по определенным
видам работы.
2. Необходимо
максимизировать целевую функцию задачи
транспортного типа. В этой ситуации при
составлении опорного плана в первую
очередь стараются заполнить клетки с
наиболее высокими значениями показателей
![]() .
.
Выбор клетки, подлежащей
заполнению при переходе от одного
допустимого плана к другому, должен
производиться не по минимальной
отрицательной разнице
![]() ,
,
а по максимальной положительной разнице
![]() .
.
Оптимальным будет план, которому в
последней таблице сопутствуют
свободные клетки с неположительными
элементами: все разности
![]() .
.
3. Необходимо
в одно время распределить груз различного
рода по потребителям. Задачи данного
типа называются многопродуктовыми
транспортными задачами. В этих задачах
поставщики т родов
грузов разбиваются на т
условных поставщиков,
а потребители п
родов грузов разбиваются
на п условных
потребителей. С учетом этой разбивки
составляют полную транспортную таблицу.
При этом заметим, что некоторые маршруты
AiBj
должны быть блокированы (закрыты),
поскольку в данной постановке задачи
грузы разного рода не могут заменять
друг друга. Этим маршрутам AiBj
должна соответствовать
очень высокая стоимость перевозки.
Многопродуктовую задачу не всегда
обязательно описывать одной моделью.
Например, если поставки грузов различного
рода независимы, то задачу можно
представить в виде комплекса транспортных
задач по каждому роду груза. Однако если
между грузами различного рода
существует связь {например, одни из
грузов можно заменить другими), то в
общем случае исходную модель (задачу)
не удается разбить на комплекс простых
транспортных задач.
Рассмотрим примеры
задач транспортного типа.
Пример
9.1. Одно
фермерское хозяйство (А1)
имеет продовольственное
зерно двух видов: 3 тыс. т — III
класса и 4 тыс. т — IV
класса. Второе фермерское хозяйство
(А2)
также имеет зерно
двух классов: 5 тыс. т — III
класса и 2 тыс. т — IV
класса. Зерно должно быть вывезено на
два элеватора: на первый элеватор (5,)
необходимо поставить 2 тыс. т пшеницы
III
класса, 3 тыс. т пшеницы
IV
класса и остальные 2 тыс. т пшеницы
любого класса.
Аналогично
второй элеватор (В2)
должен получить 8,25
тыс. т, из них пшеницы — 1 тыс. т III
класса и I,
5 тыс. т IV
класса.
Стоимость
перевозки в д. е. 1т зерна составляет: из
пункта А1
в пункты В1–и
В2
— 1 и 1,5 соответственно;
из пункта А2
в пункты В1
и В2
— 2 и 1 д. е. соответственно.
Составить оптимальный
план перевозок.
Решение
Каждого
поставщика условно разбиваем на две
части согласно двум видам зерна (![]() ),
),
аналогично потребителей
разбиваем на три части (пшеница III
класса, IV
класса и любой класс):
![]() ,
,
а также
![]() .
.
Потребности превышают
запасы, поэтому вводим фиктивного
поставщика А3.
Часть клеток в
таблице запираем большими числами М;
например, в клетке
(I;
2) стоит большое число. Это значит, что
поставщик
![]()
не может удовлетворить
потребителя
![]()
пшеницей IV
класса за счет имеющейся пшеницы III
класса.
С учетом сделанных
замечаний составим первую таблицу
(табл. 9.6).
Таблица 9.6
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Транспортная задача. Методы решения
Транспортная задача, это специальный вид задачи линейного программирования. Для решения транспортной задачи можно использовать методы решения задач линейного программирования, однако ввиду специфического вида задачи, были построены алгоритмы специально для решения этой задачи. Для решения транспортной задачи в онлайн режиме с подробными пояснениями пользуйтесь калькулятором транспортная задача онлайн.
- Содержание
- 1. Математическая постановка транспортной задачи
- 2. Определение опорного плана. Предварительные сведения
- 3. Метод северно-западного угла
- 4. Метод минимального элемента
- 5. Метод аппроксимации Фогеля
- 6. Метод потенциалов
- 7. Метод дифференциальных рент
1. Математическая постановка транспортной задачи.
Общая постановка транспортной задачи заключается в определении оптимального плана перевозок некоторого однородного груза из пунктов отправления A1, A2,…, Am в пункты назначения B1, B2,…, Bn. Критерий оптимальности берется минимальная стоимость перевозки или минимальное время доставки груза.
Рассмотрим транспортную задачу, где в качестве критерия оптимальности взята минимальная стоимость перевозок всего груза. Обозначим через Сij тарифы перевозки единицы груза из пункта отправления i в пункт назначения j. Обозначим через Ai запасы груза i-м пункте отправления, а через Bj потребности груза j-м пункте назначения, а через Xj количество единиц груза переводимого из пункта отправления i в пункт назначения j.
Тогда математическая модель транспортной задачи состоит в определении минимального значения функции
 |
(1.1) |
при условиях
 |
(1.2) |
 |
(1.3) |
 |
(1.4) |
Поскольку удовлетворяется условия (1.2)−(1.4), то обеспечивается доставка необходимого количества груза в каждый из пунктов назначения, вывоз груза из всех пунктов отправления, а также исключаются обратные перевозки.
Определение 1. Любое неотрицательное решение Xij=∥xij∥ (i=1,..,m; j=1,…,n) систем (1.2) и (1.3) называется допустимым планом транспортной задачи.
Определение 2. План  при котором функция (1.1) принимает минимальное значение, называется оптимальным планом транспортной задачи.
при котором функция (1.1) принимает минимальное значение, называется оптимальным планом транспортной задачи.
Если сумма груза у поставщиков равно общей сумме потребностей в пунктах назначения:
 |
(1.5) |
то модель транспортной задачи называется закрытой (или сбалансированной). Если (1.5) не удовлетворяется, то модель транспортной задачи называется открытой (или несбалансированной).
Теорема 1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы выполнялось условие (1.5).
В случае превышения запаса над потребностью, т.е. при
 , , |
вводится фиктивный (n+1)-ый пункт назначения с потребностью
 . . |
Соответствующие тарифы считаются равными нулю: ci n+1=0 (i=1,…,m). После этих преобразований получим закрытую модель транспортной задачи.
Аналогично, при  вводится фиктивный (m+1) пункт отправления с грузом
вводится фиктивный (m+1) пункт отправления с грузом  а тарифы полагаются равными нулю: cm+1j=0 (j=1,…,n). После этих преобразований получим закрытую модель транспортной задачи.
а тарифы полагаются равными нулю: cm+1j=0 (j=1,…,n). После этих преобразований получим закрытую модель транспортной задачи.
Мы будем рассматривать закрытую модель транспортной задачи. Если же модель транспортной задачи является открытой, то с помощью вышеизложенных преобразований строим закрытую модель транспортной задачи.
Обычно данные транспортной задачи записывают в виде таблицы:
Число переменных Xij равно mn, где m число пунктов отправнения , а n число пунктов назначения. Число уравнений в (1.2) и (1.3) равно m+n. Так как мы рассматриваем закрытую модель транспортной задачи (выполняется равенство (1.5)), то число линейно независимых уравнений равно m+n−1. Следовательно опорный план транспортной задачи может иметь не более m+n−1 отличных от нуля неизвестных.
Если в опорном плане количество отличных от нуля компонентов равно в точности m+n−1, то опорный план называется невырожденным, а если меньше − то вырожденным.
Для решения транспортной задачи сначала определяется начальный опорный план, а затем определяется оптимальный план путем улучшения текущего опорного плана.
Для определения начального опорного плана существует несколько методов. Мы рассмоьтрим три метода. Метод северно-западного угла, метод минимального элемента и метод аппроксимации Фогеля.
2. Определение опорного плана. Предварительные сведения
Опорный план транспортной задачи находим следующим образом. На каждом шаге в таблице условий задачи заполняем одну клетку, которая называется занятой. Обозначим через Kij клетку, где i -номер пункта отправления (строка), j-номер пункта назначения (столбец). Клетку Kij заполняем так, чтобы удовлетворялись полностью потребности пункта назначения j, либо обеспечивался полный вывоз груза из пункта отправления i.
В первом случае временно исключаем из рассмотрения столбец j и изменяем запас груза пункта отправления i. Во втором случае временно исключаем из рассматрения строку i и изменяем потребность груза пункта назначения j. Далее повторяем процедуру с таблицей условий с исключенной строкой или столбцом.
В m+n−1-ом шаге получаем задачу с одним пунктом отправления и одним пунктом назначения. Остается свободной одна клетка. Запасы оставшегося пункта отправления будут равны потребностям пункта назначения. Заполнив эту клетку заканчиваем m+n−1-ый шаг и получаем опорный план.
Если на некотором шаге (но не на последнем) потребности очередного пункта назначения равны запасам пункта отправления, то временно исключаем из рассмотрения либо столбец, либо строку (только одно из двух). Тогда либо запасы данного пункта отправления, либо потребности данного пункта назначения считаем равным нулю. Этот нуль при очередном шаге записываем в очередную заполняемую клетку. Данный подход обеспечивает ровно m+n−1 занятых клеток, что обеспечивает возможность проверки полученного опорного плана на оптимальность и нахождение оптимального плана.
Для нахождения опорного плана транспортной задачи в онлайн режиме тремия методами с подробными пояснениями пользуйтесь калькулятором транспортная задача онлайн.
3. Метод северно-западного угла
При нахождении опорного плана транспортной задачи методом северно-западного угла, заполнене клеток таблицы условий начинают с верхней левой клетки K11 поэтому метод и называется “метод северно западного угла”).
Рассмотрим метод на конкретном примере.
Пример 1. На три базы A1, A2, A3 поступил очередной груз в количествах равных 140, 160, 120 ед. Этот груз требуется перевезти в четыре пунктов назначения B1, B2, B3, B4 в количествах 150, 90, 100, 80. Тарифы перевозок представлена матрицей
 . . |
Найти план перевозок даной транспортной задачи методом северно-западного угла.
Решение. Запишем все данные в таблицу условий:
Число пунктов отправления m=3, а число пунктов назначения n=4. Следовательно опорный план задачи определяется числами, стоящими в m+n−1=3+4−1=6 заполненых клетках таблицы.
Наличие груза у поставщиков равно: ∑Ai=140+160+120=420.
Общая потребность в грузе в пунктах назначения равна: ∑Bj=150+90+100+80=420.
∑Ai=∑Bj. Модель транспортной задачи является закрытой. Следовательно она разрешима.
Найдем опорный план задачи методом северно-западного угла.
A1≤B1. Следовательно в клетку (A1, B1 ) помещаем число min(A1, B1)=140. Запасы пункта A1 полностью исчерпаны. Поэтому исключаем из рассмотрения строку A1 и будем считать потребности пункта B1 равными 150−140=10.
A2>B1. Следовательно в клетку (A2, B1) помещаем число min(A2, B1)=10. Потребности пункта B1 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B1 и будем считать запасы пункта A2 равными 160−10=150.
Таким образом, продолжая процедуру в m+n−1-ом шаге получим:
Запишем полученный опорный план:
При этом плане стоимость перевозок вычисляется так:
F=2·140+8·10+4·90+ 1·60+3·40+6·80=1380.
4. Метод минимального элемента
В отличие от метода северно-западного угла, в методе минимального элемента выбор пунктов отправления и пунктов назначения производится ориентируясь на тарифы перевозок, т.е. в каждом шаге нужно выбрать клетку с минимальным тарифом перевозок. Если таких клеток несколько, то выбираем один из них. Надо отметить, что при данном методе определения заполняемой клетки, стоимость перевозок как правило бывает меньше, чем при методе северно западного угла. Поэтому целесообразно начальный опорный план найти методом минимального элемента.
Рассмотрим метод минимального элемента на примере.
Пример 2. Найти опорный план транспортной задачи представленной в таблице условий ниже методом минимального элемента:
Число пунктов отправления m=3, а число пунктов назначения n=4. Следовательно опорный план задачи определяется числами, стоящими в m+n−1=3+4−1=6 заполненых клетках таблицы. Тарифы перевозок единицы груза из кажного пункта отправления во все пункты назначения задаются матрицей
Наличие груза у поставщиков равно:  .
.
Общая потребность в грузе в пунктах назначения равна:  .
.
 Модель транспортной задачи является закрытой. Следовательно она разрешима.
Модель транспортной задачи является закрытой. Следовательно она разрешима.
Минимальный тариф равный 1 находится в клетке (A1, B3). Поэтому заполняем эту клетку.
A1>B3. Следовательно в клетку (A1, B3) помещаем число 70. Потребности пункта B3 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B3 и будем считать запасы пункта A1 равными 150−70=80.
Минимальный тариф равный 1 находится в клетке (A2, B4). Поэтому заполняем эту клетку.
A2>B4. Следовательно в клетку (A2, B4) помещаем число 40. Потребности пункта B4 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B4 и будем считать запасы пункта A2 равными 100−40=60.
Таким образом, продолжая процедуру в m+n−1-ом шаге получим:
Запишем полученный опорный план:
При этом плане стоимость перевозок вычисляется так:
5. Метод аппроксимации Фогеля
Суть метода аппроксимации Фогеля заключается в следующем. Для каждой строки и для каждого столбца находим разности между двумя записанными в них минимальными тарифами. Полученные разности записываем в специально отведенные для этого столбце и в строке в таблице условий задачи.
Среди указанных разностей выбираем максимальную. В строке (или в столбце), которой данная разность соответствует, определяем минимальный тариф. Клетку, в которой он записан заполняем на данной итерации.
Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбираем ту клетку, которая соответствует наибольшей разности между двумя минимальными тарифами в данном столбце (строке).
Применение метода аппроксимации фогеля позволяет получить либо опорный план, близкий к оптимальнму, либо сам оптимальный план.
Рассмотрим метод аппроксимации Фогеля на примере 2, рассмотренной выше.
Пример 3. Найти опорный план транспортной задачи представленной в таблице условий ниже методом аппроксимации Фогеля:
Число пунктов отправления m=3, а число пунктов назначения n=4. Следовательно опорный план задачи определяется числами, стоящими в m+n−1=3+4−1=6 заполненых клетках таблицы. Тарифы перевозок единицы груза из кажного пункта отправления во все пункты назначения задаются матрицей
Наличие груза у поставщиков равно:  .
.
Общая потребность в грузе в пунктах назначения равна:  .
.
 Модель транспортной задачи является закрытой. Следовательно она разрешима.
Модель транспортной задачи является закрытой. Следовательно она разрешима.
Для каждой строки Ai найдем разности между двумя минимальными тарифами, записанными в данной строке и поместим их в соответствующем дополнительном столбце.
В строке 1 минимальный тариф равен 1, а следующий за ним равен 2, разность между ними 2−1=1. В строке 2 минимальный тариф равен 1, а следующий за ним равен 3, разность между ними 3−1=2. В строке 3 минимальный тариф равен 3, а следующий за ним равен 3, разность между ними 3−3=0.
Для каждого столбца Bj найдем разности между двумя минимальными тарифами, записанными в данном столбце и поместим их в соответствующей дополнительной строке.
В столбце 1 минимальный тариф равен 2, а следующий за ним равен 3, разность между ними 3−2=1. В столбце 2 минимальный тариф равен 3, а следующий за ним равен 4, разность между ними 4−3=1. В столбце 3 минимальный тариф равен 1, а следующий за ним равен 3, разность между ними 3−1=2. В столбце 4 минимальный тариф равен 1, а следующий за ним равен 2, разность между ними 2−1=1.
Вычислив все разности выберем наибольшую из них. В данном случае наибольшая разница равна 2. В этом столбце минимальный тариф равен 1 и находится в пересечении строки A 1 и столбца B3. Следовательно заполняем эту клетку.
A1>B3. Следовательно в клетку помещаем число 70. Потребности пункта B3 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B3 и будем считать запасы пункта A1 равными 150−70=80.
Для каждой строки Ai найдем разности между двумя минимальными тарифами, записанными в данной строке и поместим их в соответствующем дополнительном столбце.
В столбце 1 минимальный тариф равен 2, а следующий за ним равен 3, разность между ними 3−2=1. В столбце 2 минимальный тариф равен 3, а следующий за ним равен 4, разность между ними 4−3=1. В столбце 3 минимальный тариф равен 1, а следующий за ним равен 3, разность между ними 3−1=2. В столбце 4 минимальный тариф равен 1, а следующий за ним равен 2, разность между ними 2−1=1. В строке 1 минимальный тариф равен 2, а следующий за ним равен 2, разность между ними 2−2=0. В строке 2 минимальный тариф равен 1, а следующий за ним равен 3, разность между ними 3−1=2. В строке 3 минимальный тариф равен 3, а следующий за ним равен 4, разность между ними 4−3=1.
Для каждого столбца Bj найдем разности между двумя минимальными тарифами, записанными в данном столбце и поместим их в соответствующей дополнительной строке.
В столбце 1 минимальный тариф равен 2, а следующий за ним равен 3, разность между ними 3−2=1. В столбце 2 минимальный тариф равен 3, а следующий за ним равен 4, разность между ними 4−3=1. В столбце 4 минимальный тариф равен 1, а следующий за ним равен 2, разность между ними 2−1=1.
Вычислив все разности выберем наибольшую из них. В данном случае наибольшая разница равна 2. В этой строке минимальный тариф равен 1 и находится в пересечении строки A2 и столбца B4. Следовательно заполняем эту клетку.
A2>B4. Следовательно в клетку помещаем число 40. Потребности пункта B4 полностью удовлетворены. Поэтому исключаем из рассмотрения столбец B4 и будем считать запасы пункта A2 равными 100−40=60.
Таким образом, продолжая процедуру в m+n−1-ом шаге получим:
Запишем полученный опорный план:
При этом плане стоимость перевозок вычисляется так:
F=2·40+3·40+1·70+ 4·60+1·40+3·100=850.
Для определения оптимального плана транспортной задачи разработано нескольно методов. Мы расмотрим метод потенциалов и метод дифференциальных рент.
6. Метод потенциалов
Процедура нахождения оптимального плана транспортной задачи имеет два этапа. На первом этапе находят опорной план транспортной задачи. Далее последовательно улучшают найденный опорный план до получения оптимального плана.
Для определения опорного плана будем пользоваться методом северно-западного угла, методом минимального элемента или методом аппроксимации Фогеля рассмотренных выше.
Для онлайн решения задачи методом потенциалов пользуйтель калькулятором транспортная задача онлайн.
При применении этих методов получаем m+n−1 занятых клеток в исходном плане. Отметим, что в некоторых клетках могут стоять нули. Полученный план следует проверить на оптимальность.
Теорема. Если для некоторого опорного плана  (i=1,..,m; j=1,…,n) транспортной задачи существуют такие числа α1, α1, …, αm, β1, β2, …, βn, что
(i=1,..,m; j=1,…,n) транспортной задачи существуют такие числа α1, α1, …, αm, β1, β2, …, βn, что
для всех i=1,..,m; j=1,…,n, то  − оптимальный план транспортной задачи.
− оптимальный план транспортной задачи.
Определение 6.1. Числа αi и βj (i=1,..,m; j=1,…,n) называются потенциалами пунктов отправления и пунктов назначения, соответственно.
Вышеизложенная теорема позволяет построить алгоритм нахождения оптимального плана транспортной задачи.
Алгоритм состоит в следующем. Предположим, что одним из рассмотренных выше методов найден опорный план транспортной задачи. Для каждого из пунктов отправления и назначения определяют потенциалы αi и βj (i=1,..,m; j=1,…,n) из системы уравнений
где сij − тарифы транспортной задачи в заполненных клетках.
Так как число заполненных клеток равно m+n−1, то система (6.1) с m+n неизвестными содержит m+n−1 уравнений. Для решения данной задачи одно из неизвестных можно сделать равным нулю и найти остальные неизвестные. После этого, для свободных клеток определяем числа
Если среди чисел αij нет положительных, то найденный опорный план является оптимальным. Если же для некоторой свободной клетки αij>0, то данный опорный план не является оптимальным и необходимо перейти к новому опорному плану. Для этого рассматривают все свободные клетки, для которых αij>0 и среди данных чисел выбирают максимальное. Клетку с данным числом следует заполнить.
Надо учитывать, что при заполнении данной клетки необходимо изменить объем поставок в нескольких других клетках.
Определение 6.2. Циклом в таблице условий транспортной задачи называется ломанная линия, вершины которой расположены в занятых клетках таблицы, а звеня расположены вдоль строк и столбцов. В каждой вершине цикла встречается два звена, одно из которых находится в строке, а другой в столбце.
Если ломаннная линия, образующая цикл, самопересекается, то место пересечения не является вершиной. Некоторые циклы представлены на рисунке Рис.6.1.
При правильном строении опорного плана для любой свободной клетки можно построить только один цикл. После построения цикла следует перейти к новому опорному плану. Для этого в каждой из клеток, находящихся на вершине цикла записывают определенный знак “+” или “−” . В свободной клетке записывают знак “+” и поочередно проходя по циклу записывают знаки “−” и “+”. Назовем клетки с записанными в них знаками плюсовыми и минусовыми.
Далее в свободную клетку переносят меньшее из чисел xij, находящихся в минусовых клетках. Это число прибавляют к числам, стоящим в плюсовых клетках а вычисляют из чисел, стоящих в минусовых клетках. Клетка, которая была свободной, становится занятой, а минусовая клетка с минимальным из чисел xij, находящихся в минусовых клетках считается свободным.
В результате вышеуказанных перемещений груза по циклу, получим новый опорный план транспортной задачи. Описанный переход от одного опорного плана транспортной задачи к другому опорному плану называется сдвигом по циклу пересчета.
При сдвиге по циклу пересчета число занятых клеток не изменяется и равно m+n−1. Если в минусовых клетках имеется два и более одинаковых минимальных числа xij, то освобождают только одину, о остальные оставляют занятыми с нулевыми значениями.
Далее полученный опорный план проверяют на оптимальность. Для этого определяют потенциалы пунктов отправления и назначения и находят числа αij=βj−αi−cij для всех свободных клеток. Если среди них не окажется положительный, то получен оптимальный план. Если же среди них есть положительный, то нужно перейти к новому опорному плану. После конечнего числа шагов получяют оптимальный план.
Таким образом алгоритм нахождения оптимального плана содержит следующие этапы:
1. Нахождение опорного плана. При этом число заполненных клеток должно быть равным m+n−1.
2. Нахождение потенциалов αi и βj (i=1,..,m; j=1,…,n) пунктов отправления и назначения соответственно.
3. Определение числа αij для каждой свободной клетки. Если среди αij нет положительных, то получен оптимальный план транспортной задачи. Если же они имеются, то делается переход к новому опорному плану.
4. Выбор максимального среди положительных чисел αij . Определение свободной клетки, которую нужно заполнить. Построение цикла пересчета для выбранной свободной клетки. Сдвиг по циклу пересчета.
5. Проверка полученного опорного плана на оптимальность, т.е. переход к пункту 2.
Отметим, что в некотором шаге опорный план может стать вырожденным. Чтобы избежать зацикливания следует преобразовать вырожденный план в невыроженный путем замены соответствующий нулевых элементов опорного плана на сколь угодно малыми положительными числами δ и решить задачу. После решения, в оптимальном плане нужно заменить δ нулем.
Рассмотрим метод потенциалов на примере.
Пример 6.1. Решить транспортную задачу, заданную в таблице условий методом потенциалов:
Решение. Найдем сначала опорный план с помощью одного из методов описанного выше. Пусть это будет метод минимального элемента. Тогда после m+n−1 шагов получим следующую таблицу с опорным планом:
Опорный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 6 уравнений с 7 неизвестными:
Полагая α1=0, находим β2=2, β3=1, α2=-1, α3=-3, β4=0, β2=5
Для каждой свободной клетки вычисляем число αij=βj−αi−cij. α12=2, α14=-2, α22=2, α23=-3, α33=-1, α34=-3.
Полученные числа заключаем в рамки и записываем их в соотвестствующие клетки таблицы:
Среди чисел αij есть положительные. Следовательно данный опорный план не является оптимальным. Наибольшее положительное число 2 находится в пересечении строки A1 и столбца B2. Для данной свободной клетки строим цикл пересчета. Для этого вставим в эту клетку знак “+” а остальные клетки цикла поочередно знаки “−” и “+”.
Наименьшее из чисел в минусовых клетках равно 80. Клетка, в которой находится это число становится свободной. В новой таблице другие числа получаются так. Числам, находящимся в плюсовых клетках добавляется 80, а из чисел, находящихся в минусовых клентках вычитается это число.
Опорный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 6 уравнений с 7 неизвестными:
Полагая α1=0, находим β2=3, β3=1, α3=-3, β1=0, α2=-3, β4=-2
Для каждой свободной клетки вычисляем число αij=βj−αi−cij. α11=-2, α14=-4, α22=2, α23=-1, α33=1, α34=-3.
Полученные числа заключаем в рамки и записываем их в соотвестствующие клетки таблицы:
Полученные числа заключаем в рамки и записываем их в соотвестствующие клетки таблицы:
Среди чисел αij есть положительные. Следовательно данный опорный план не является оптимальным. Наибольшее положительное число 2 находится в пересечении строки A2 и столбца B2. Для данной свободной клетки строим цикл пересчета. Для этого вставим в эту клетку знак “+” а остальные клетки цикла поочередно знаки “−” и “+”.
Наименьшее из чисел в минусовых клетках равно 20. Клетка, в которой находится это число становится свободной. В новой таблице другие числа получаются так. Числам, находящимся в плюсовых клетках добавляется 20, а из чисел, находящихся в минусовых клентках вычитается это число.
Опорный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 6 уравнений с 7 неизвестными:
Полагая α1=0, находим β2=3, β3=1, α2=-1, β1=2, β4=0, α3=-1
Для каждой свободной клетки вычисляем число αij=βj−αi−cij. α11=0, α14=-2, α23=-3, α32=-2, α33=-1, α34=-3.
Среди чисел αij нет положительных. Следовательно данный опорный план является оптимальным.
Ответ. Оптимальный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
7. Метод дифференциальных рент
При нахождении решения транспортной задачи методом дифференциальных рент сначала распределяем часть груза наилучшим образом между пунктами назначения и получаем так называемое условно оптимальное распеделение. На последующих итерациях уменьшаем общий объем нераспределенных поставок. Для решения транспортной задачи методом дифференциальных рент в онлайн режиме с подробными пояснениями пользуйтесь калькулятором метод дифференциальных рент онлайн.
Начальное распределение груза определяется следующим образом. Для каждого столбца определяем минимальный тариф и заключаем в квадрат. Клетки с тарифами в квадратах заполняем максимально возможными числами. В результате получим некоторое распределение поставок груза в пункты назначения. Это распределение в общем случае не удовлетворяет ограничениям транспортной задачи. Далее шаг за шагом нужно постепенно сокращать нераспределенные поставки груза так, чтобы общая стоимисть перевозки оставалась минимальным. Для этого определяем избыточные и недостаточные строки.
Определение 7.1. Строки, соответствующие пунктом отправления, запасы которых полностью распределены а среди пунктов назначения, связанные с этим распределением есть неудовлетворенные потребности называются недостаточными или отрицательными.
Определение 7.2. Строки, запасы которых не распределены полностью называются избыточными или положительными.
После определения недостаточных и избыточных строк, в дополнительном столбце записываем величину избытка или недостатка. Избыток записывается со знаком “+”, а недостаток со знаком “-“.
В случае избытка для данной строки в дополнительном столбце записываем разность между запасом груза данного пункта отправления и суммой всех поставок данной строки. Если же данная строка недостаточная, то определяем общий объем поставок, которая недостает для удовлетворения всех потребностей пунктов назначения, связанных с данным распределением груза.
После определения избыточных и недостаточных строк, для каждого столбца находим разности между числом в квадрате и ближащим к нему тарифом, записанным в избыточной строке. Если число в квадрате стоит в избыточной строке, то разность не определяем. Все разности записываем в дополнительной строке. Среди этих разностей находим наимельшее. Это число называется промежуточной рентой. Далее переходим к новой таблице. Эта таблица получается из предыдущей таблицы прибавлением промежуточной ренты к соответствующим тарифам, стоящим в недостаточных строках. Остальные элементы оставляем прежними. Все клетки новой таблицы считем свободными и начинаем их заполнять. В новой таблице число заполненных клеток на одну больше, чем в предыдущей таблице. Эта клетка находится в столбце с промежуточной рентой.
Так как число заполненных клеток больше, чем столбцов, то при заполнении следует соблюдать специальное правило, которое состоит в следующем.
Выбираем некоторый столбец (строку), в котором имеется одна клетка с помещенным в ней квадратом. Эту клетку заполняем и исключаем из рассмотрения данный столбец (строку). После этого берем некоторую строку (столбец), в котором имеется одна клетка с помещенным в ней квадратом. Эту клетку заполняем и исключаем из рассмотрения данную строку (столбец). Продолжая так, после конечного числа шагов заполняем все клетки, в которых помещены квадраты с записанными в них числами.
Если удается распределить весь груз в пунктах отправления между пунктами назначения, то получаем оптимальный план. В противном случае переходим к новой таблице. Для этого находим извыточные и недостаточные строки, прмежуточную ренту и на основе этого строим новую таблицу.
При определении избыточности или недостаточности строк могут возникнуть трудности когда ее нераспределенный остаток равен нулю. Этот вопрос мы рассмотрим ниже на конкретном примере.
После конечного числа итераций распределенный остаток станет равным нулю. В результате получим оптимальный план данной транспортной задачи.
Пример. Найти решение транспортной задачи представленной в таблице условий методом дифференциальных рент:
Решение. Число пунктов отправления m=3, а число пунктов назначения n=4. Следовательно опорный план задачи определяется числами, стоящими в m+n−1=3+4−1=6 заполненых клетках таблицы. Тарифы перевозок единицы груза из каждого пункта отправления во все пункты назначения задаются матрицей
Наличие груза у поставщиков равно: 
Общая потребность в грузе в пунктах назначения равна: 
 . Модель транспортной задачи является закрытой. Следовательно она разрешима.
. Модель транспортной задачи является закрытой. Следовательно она разрешима.
Найдем оптимальный план транспортной задачи методом дифференциальных рент.
Итерация 1:
В каждом из столбцов таблицы находим минимальные тарифы и заключаем в рамки. Если в каком-либо столбце окажется несколько одинаковых минимальных тарифов, то выбираем какой-нибудь из них, причем неважно какой. Заполняем клетки, в которых стоят указанные числа. Сначала находим те столбцы (строки) в которых есть только одна клетка для заполнения. Заполнив ее, исключаем из рассмотрения данный столбец (строку) и переходим к заполнению следующей клетки.
Последовательность заполнения клеток следующее: A1B1, A3B2, A2B3, A2B4.
В результате заполнения отмеченных клеток получен условно оптимальный план.
После получения условно оптимального плана определяем избыточные и недостаточные строки. Строка A1 является недостаточной, поскольку запасы пункта отправления A1 распределены полностью, а потребности пункта назначения B1 удовлетворены частично. При этом величина недостатка равна 20. Строка A3 является недостаточной, поскольку запасы пункта отправления A3 распределены полностью, а потребности пункта назначения B2 удовлетворены частично. При этом величина недостатка равна 20. Строка A2 является избыточным, поскольку запасы пункта отправления A2 распределены не полностью. При этом величина избытка этой строки равна 40.
Нераспределенный остаток равен 40. Суммарный объем поставок равен 150.
После определения избыточных и недостаточных строк, по каждому из столбцов находим разности между минимальными тарифами, записанными в избыточных строках, и тарифами, стоящими в заполненных клетках.
В столбце 1 минимальный тариф в избыточных строках равно 4 а число стоящее в рамке равно 2. Cледовательно, разность для данного столбца равна 4−2=2. В столбце 2 минимальный тариф в избыточных строках равно 3 а число стоящее в рамке равно 2. Cледовательно, разность для данного столбца равна 3−2=1. Для столбца 3 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке. Для столбца 4 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке.
Избыточные и недостаточные оценки помещаем в дополнительный столбец, а разности в дополнительную строку:
Выбираем наименьшую из найденных разностей, которая является промежуточной рентой. В данном случае промежуточная рента равна 1 и находится в столбце B2. Далее переходим к следующей таблице. В этой таблице в строках (являющихся избыточными) переписываем соответствующие тарифы из предыдущей таблицы, а тарифы недостаточных строках получаются в результате прибавления к ним величину промежуточной ренты, т.е. 1.
Итерация 2:
В каждом из столбцов таблицы находим минимальные тарифы и заключаем в рамки. Заполняем клетки, в которых стоят указанные числа. Сначала находим те столбцы (строки) в которых есть только одна клетка для заполнения. Заполнив ее, исключаем из рассмотрения данный столбец (строку) и переходим к заполнению следующей клетки.
Последовательность заполнения клеток следующее: A1B1, A2B3, A2B4, A2B2, A3B2.
В результате заполнения отмеченных клеток получен условно оптимальный план.
После получения условно оптимального плана определяем избыточные и недостаточные строки. Строка A1 является недостаточной, поскольку запасы пункта отправления A1 распределены полностью, а потребности пункта назначения B1 удовлетворены частично. При этом величина недостатка равна 20. Строка A3 является избыточным, поскольку запасы пункта отправления A3 распределены не полностью. При этом величина избытка этой строки равна 20.
Нераспределенный остаток равен 20. Суммарный объем поставок равен 170.
Избыточные и недостаточные оценки помещаем в дополнительный столбец.
Определяем положительность или отрицательность нулевой строки A2. Для этого запасы этой строки увеличиваем на 1 и снова заполняем таблицу. Если суммарный объем поставок не изменится, то строка положительная, в противном случае − отрицательная.
Последовательность заполнения клеток следующее: A1B1, A2B3, A2B4,A2B2, A3B2:
Суммарный объем поставок не изменился (170). Следовательно строка A2 избыточна (положительна).
После определения избыточных и недостаточных строк, по каждому из столбцов находим разности между минимальными тарифами, записанными в избыточных строках, и тарифами, стоящими в заполненных клетках.
В столбце 1 минимальный тариф в избыточных строках равно 4 а число стоящее в рамке равно 3. Cледовательно, разность для данного столбца равна 4−3=1. Для столбца 2 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке. Для столбца 3 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке. Для столбца 4 разность не определена, так как число, записанное в рамке в данном столбце находится в положительной строке.
Выбираем наименьшую из найденных разностей, которая является промежуточной рентой. В данном случае промежуточная рента равна 1 и находится в столбце B1. Далее переходим к следующей таблице. В этой таблице в строках (являющихся избыточными) переписываем соответствующие тарифы из предыдущей таблицы, а тарифы недостаточных строках получаются в результате прибавления к ним величину промежуточной ренты, т.е. 1.
Итерация 3:
В каждом из столбцов таблицы находим минимальные тарифы и заключаем в рамки. Заполняем клетки, в которых стоят указанные числа. Сначала находим те столбцы (строки) в которых есть только одна клетка для заполнения. Заполнив ее, исключаем из рассмотрения данный столбец (строку) и переходим к заполнению следующей клетки.
Последовательность заполнения клеток следующее: A2B3, A2B4, A1B1, A2B1, A3B1,A2B2, A3B2.
В результате заполнения отмеченных клеток получен условно оптимальный план. После получения условно оптимального плана определяем избыточные и недостаточные строки.
Посмотрев на таблицу выше мы видим, что избыточных и недостаточных строк нет. Нераспределенный остаток равен 0. Суммарный объем поставок равен 190. Все имеющие запасы распределены в соответствии фактическими потребностями пунктов назначения. Следовательно получен оптимальный план.
Ответ.
Оптимальный план имеет следующий вид:
При этом плане стоимость перевозок вычисляется так:
Пример решения задачи. Решение транспортной задачи
Условие задачи
Поставщики товара – оптовые коммерческие
предприятия
имеют запасы товаров соответственно в
количестве
и розничные торговые предприятия
-подали заявки на закупку товаров в объемах
соответственно:
. Тарифы перевозок единицы
груза с каждого из пунктов поставки в соответствующие пункты потребления заданы
в виде матрицы
. Найти такой план
перевозки груза от поставщиков к потребителям, чтобы совокупные затраты на
перевозку были минимальными.
Решение задачи
Экономико-математическая модель задачи
Обозначим через
количество
груза, перевозимого от
поставщика
потребителю.
Тогда общая стоимость перевозок равна:
Ограничения
для поставщиков:
Ограничения для потребителей:
Объем суммарных поставок любого
поставщика к потребителю не может быть отрицательным числом, поэтому
справедливы ограничения:
Проверка транспортной задачи на закрытость
Стандартная транспортная задача
разрешима только в том случае, когда выполняется условие баланса:
В нашем случае:
Модель
транспортной задачи открытая. Вводим фиктивного потребителя, которому
требуется 85 единиц груза.
Правило минимального элемента
Заполняем таблицу по правилу
минимального элемента.
Просматривая таблицу замечаем, что
наименьшие затраты соответствуют маршруту
, поэтому в клетку помещаем
. В этом случае 5-й столбец в расчет не принимается.
Просматриваем оставшиеся таблицы клетки. Наименьшие тарифы имеют клетки
и
Далее действуя по аналогичной схеме:
Число занятых клеток должно быть
.
Решение транспортной задачи методом потенциалов
Решать задачу будем методом
потенциалов. Потенциал 1-й строки принимаем равным нулю. После этого мы можем
вычислить остальные потенциалы (если известны потенциал и тариф занятой клетки,
то из соотношения
легко
определить неизвестный потенциал).
Найдем оценки свободных клеток:
| S ( 1, 1)= 7-( 0+ 10)= -3 |
S ( 1, 2)= 20-( 0+ 21)= -1 |
|
S ( 2, 3)= 10-(-7+ 3)= 14 |
S ( 2, 4)= 20-(-7+ 15)= 12 |
|
S ( 2, 5)= 0-(-7+ 0)= 7 |
S ( 3, 1)= 15-( 4+ 10)= 1 |
|
S ( 3, 3)= 11-( 4+ 3)= 4 |
S ( 3, 5)= 0-( 4+ 0)= -4 |
| S ( 4, 1)= 11-(-9+ 10)= 10 |
S ( 4, 2)= 12-(-9+ 21)= 0 |
|
S ( 4, 3)= 18-(-9+ 3)= 24 |
S ( 4, 5)= 0-(-9+ 0)= 9 |
Для
клетки ( 3, 5) строим цикл.
Найдем оценки свободных клеток:
| S ( 1, 1)= 7-( 0+ 10)= -3 |
S ( 1, 2)= 20-( 0+ 21)= -1 |
| S ( 1, 5)= 0-( 0-4)= 4 |
S ( 2, 3)= 10-(-7+ 3)= 14 |
|
S ( 2, 4)= 20-(-7+ 15)= 12 |
S ( 2, 5)= 0-(-7-4)= 11 |
|
S ( 3, 1)= 15-( 4+ 10)= 1 |
S ( 3, 3)= 11-( 4+ 3)= 4 |
|
S ( 4, 1)= 11-(-9+ 10)= 10 |
S ( 4, 2)= 12-(-9+ 21)= 0 |
|
S ( 4, 3)= 18-(-9+ 3)= 24 |
S ( 4, 5)= 0-(-9-4)= 13 |
Для
клетки ( 1, 1) строим цикл.
Найдем оценки свободных клеток:
|
S ( 1, 2)= 20-( 0+ 18)= 2 |
S ( 1, 5)= 0-( 0-4)= 4 |
|
S ( 2, 3)= 10-(-4+ 3)= 11 |
S ( 2, 4)= 20-(-4+ 15)= 9 |
| S ( 2, 5)= 0-(-4-4)= 8 |
S ( 3, 1)= 15-( 4+ 7)= 4 |
|
S ( 3, 2)= 25-( 4+ 18)= 3 |
S ( 3, 3)= 11-( 4+ 3)= 4 |
|
S ( 4, 1)= 11-(-9+ 7)= 13 |
S ( 4, 2)= 12-(-9+ 18)= 3 |
|
S ( 4, 3)= 18-(-9+ 3)= 24 |
S ( 4, 5)= 0-(-9-4)= 13 |
Оценки
свободных клеток не отрицательны, следовательно, полученный план является
оптимальным:
Минимальные
транспортные издержки оптимального плана:
При
реализации оптимального плана у поставщика
останется нереализованный товар в размере 85
ед.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.



