Как найти все автоморфизмы группы

Автоморфизм группы — биективный гомоморфизм группы на себя.

Автоморфизм группы называется внутренним, если существует такой элемент , что (в этом случае иногда обозначают как ); в противном случае автоморфизм называется внешним.

Группа автоморфизмов группы обозначается множество внутренних автоморфизмов обозначается Поскольку — подгруппа в можно также доказать, что она является нормальной подгруппой. Факторгруппа называется группой внешних автоморфизмов группы. Отображение определяет гомоморфизм , ядро которого есть центр группы , так что . Все нормальные подгруппы инвариантны под действием внутренних автоморфизмов. Подгруппы, инвариантные под действием всех автоморфизмов группы, называются характеристическими.

Всякая группа, совпадающая со своей группой автоморфизмов, называется совершенной. Совершенными являются все симметрические группы при . Расширение группы с помощью группы автоморфизмов называется голоморфом.

Примеры[править | править код]

• 
• 
• (группа изоморфна мультипликативной группе кольца вычетов )
  • В частности, если p простое, (группа автоморфизмов группы является циклической из p − 1 элемента)
• 
• Если — поле, характеристика которого больше двух, то
• Группа автоморфизмов множества всех комплексных корней степеней из единицы есть группа p-адических чисел по сложению.
• Группа внешних автоморфизмов свободной группы конечного ранга порождается преобразованиями Нильсена элементов базиса
• Множество автоморфизмов группы Ли также образует группу Ли.^[1]

Примечания[править | править код]

Тут надо начинать с самых простых примеров. Общая задача нахождения Aut G по заданной группе G может быть очень сложной.

Наиболее простой класс групп — конечные циклические. Для них есть готовое описание, но я не уверен, что оно здесь требуется. Если число n простое, то группа Aut Z(n) циклична и имеет порядок n-1. Это следует из теоремы о первообразном корне по простому модулю. Для небольших значений n можно теорему не применять, а то же самое доказать вручную.

Также надо уметь находить автоморфизмы групп типа S3, или Z2xZ2 — это достаточно легко. Для общего случая симметрических групп, желательно знать теорему Гёльдера, но если она не изучалась, то таких задач предлагаться не должно.

Общая процедура основана на том, что если мы знаем, чем порождаются группы, то надо смотреть, куда порождающие могут переходить при автоморфизмах. Например, элемент порядка m может переходить только в элемент порядка m, и так далее. Чем сложнее структура группы, тем сложнее задача.

По первой задаче: здесь надо начать с выяснения того, что порождают данные подстановки. Может так оказаться, что они порождают всю группу. Тогда это надо доказывать, и далее использовать факт про Aut S5. Но в конкретном примере бросается в глаза, что квадратом первой подстановки a=(14253) является вторая подстановка b=(12345), то есть a^2=b. Равным образом, b^3=a^6=a. Это значит, что перед нами циклическая группа порядка 5. Её автоморфизмы устроены просто: их всего 4, так как у этой группы 4 образующих. Элемент b, порождающий группу, может переходить в любой из них.

Если взять автоморфизм ф, для которого ф(b)=b^2 (соответственно, ф(b^k)=b^{2k} для других элементов), то ф^2(b)=b^4, ф^3(b)=b^8=b^3, ф^4(b)=b^6=b, то есть ф^4=I есть тождественный автоморфизм. Группа Aut Z(5) циклична порядка 4 с образующим ф.

Задача основана на том, чтобы заметить равенство a^2=b в самом начале, и понять, что речь всего лишь о циклической группе, для которой всё просто.

Что касается матриц, то для общего случая может быть сложно понять, какую группу они порождают. Даже если взять две матрицы (1 2 // 0 1) и (1 0 // 2 1), то надо уметь доказывать теорему Санова о том, что они порождают свободную группу ранга 2. А описание её автоморфизмов предполагает владение техникой, которая изложена в монографии Линдона и Шуппа “Комбинаторная теория групп”. Такого предлагать бы явно никто не стал.

Если вторая задача о матрицах устроена примерно как первая (скорее всего, так и есть), то она должна решаться легко. Но конкретный вид матриц здесь важен, поэтому надо его указать.

Сам я не спец в теории групп, поэтому, возможно, буду “размазывать” некоторые вещи.

В группе [math]mathbb{Z}_5[/math] элемент [math][1]_5[/math] является порождающим элементом, то есть все остальные элементы имеют вид [math]n[1]_5=[n]_5, n=1,2,3,4,5[/math]. Пусть [math]varphi[/math] – произвольный автоморфизм группы [math]mathbb{Z}_5[/math]. Тогда

[math]varphi(n[1]_5)=nvarphi([1]_5)[/math]

Поскольку [math]varphi[/math] – изоморфизм, то среди элементов [math]nvarphi([1]_5)[/math] должны содержаться все элементы группы [math]mathbb{Z}_5[/math], то есть [math]varphi([1]_5)[/math] является порождающим элементом [math]mathbb{Z}_5[/math]. С другой стороны, очевидно, два разных автоморфизма не могут переводить один и тот же порождающий элемент в один и тот же (то есть, если [math]varphi_1, varphi_2[/math] – автоморфизмы, [math]a,b[/math] – порождающие элементы [math]mathbb{Z}_5[/math] и [math]varphi_1(a)=b, varphi_2(a)=b[/math], то [math]varphi_1=varphi_2[/math]). Значит между автоморфизмами [math]mathbb{Z}_5[/math] и порождающими элементами [math]mathbb{Z}_5[/math] есть взаимно однозначное соответствие. Поскольку всего порождающих элементов в группе [math]mathbb{Z}_5[/math] 4 (это [math][n]_5, n=1,2,3,4[/math]), то и множество [math]operatorname{Aut}mathbb{Z}_5[/math] состоит из 4-ех автоморфизмов. Обозначим [math]varphi_i, i=1,2,3,4[/math] автоморфизм, переводящий [math][1]_5[/math] в [math][i]_5[/math]. Заметим тогда, что

[math]varphi_2^2([1]_5)=varphi_2varphi_2([1]_5)=varphi_2([2]_5)=2varphi_2([1]_5)=2[2]_5=[4]_5[/math]

то есть [math]varphi_2^2=varphi_4[/math]. Аналогично легко получить, что

[math]varphi_2^3=varphi_3, varphi_2^4=varphi_1[/math]

то есть [math]varphi_2[/math] является порождающим элементом в группе [math]operatorname{Aut}mathbb{Z}_5[/math], а значит эта группа изоморфна [math]mathbb{Z}_4[/math], то есть [math]operatorname{Aut}mathbb{Z}_5=mathbb{Z}_4[/math].

Теперь самостоятельно покажите, что [math]operatorname{Aut}mathbb{Z}_4=mathbb{Z}_2[/math].

The group $mathbb{Z}/7mathbb{Z}$ has generators $1,2,3,4,5,6$. Let $psi$ be an automorphism. Then $psi$ is entirely determined by where it sends a generator. So $psi(1)$ is one of $1,2,3,4,5,6$. That choice determines the automorphism and every automorphism is determined by that choice. So there are 6 automorphisms. Furthermore, $psi(n)=psi(1)n$. So $psi$ is the “multiplication by $k$” map, where $k=psi(1)$ is one of the above 6 values.

Generalize this to get the automorphisms of $mathbb{Z}/pmathbb{Z}$ and $mathbb{Z}/6mathbb{Z}$. For the latter group, note that there are only two generators.

Edit:
Explicitly, the automorphism of $mathbb{Z}/7mathbb{Z}$ given by $psi$ where $psi(1)=5$ is the map that takes $nmod 7$ to $5nmod 7$. This is a homomorphism of the group and has inverse $xi$, where $xi$ takes $nmod 7$ to $3nmod 7$. To check that they are inverses, note that $(xicircpsi)(nmod 7)=15nmod7equiv nmod 7$.

Характеристикой
симметрии графа является его группа
автоморфизмов.

Произвольная
подстановка 
на множестве вершин графа
G,
сохраняющая отношение смежности, т.
е. такая, что
образы (u)
и (v)
вершин
u
и
v
смежны
тогда и только
тогда, когда смежны сами вершины u
и
v,
называется
автоморфизмом
графа
G.

Иными
словами, автоморфизм графа — это
изоморфизм графа
на себя.

Любой
граф G
имеет
по меньшей мере один автоморфизм
— тождественное преобразование e:
VG
->
VG,
при
котором
e(v)=v
для
любой вершины v.
Очевидно,
что если

— автоморфизм графа G,
то
и обратная подстановка
^-1
также является автоморфизмом, если же
подстановки

и 
обе суть автоморфизмы, то и их произведение

— автоморфизм. Поэтому верно следующее
(важное, хотя и очевидное)

Утверждение
11.1.
Множество
всех автоморфизмов
графа относительно операции умножения
подстановок является
группой.

Группа
автоморфизмов графа G
обозначается
через AutG.

Очевидно также

Утверждение
11.2.
Всякий
автоморфизм графа G
является также автоморфизмом
дополнительного графа
,
т. е.Aut
G
= Aut

.

Поскольку
среди двух графов G
и


хотя
бы один является
связным, то в силу утверждения 11.2, когда
мы имеем
дело с группой автоморфизмов, достаточно
рассматривать
лишь связные графы.

Введем
важное понятие орбиты группы подстановок.
Пусть
Г — произвольная группа подстановок
на множестве
V.
Определим
на V
бинарное
отношение ~, положив u
~
v
для
u,
vV
тогда
и только тогда, когда в Г существует
такая подстановка s,
что
s(u)=v.
Очевидно,
что
отношение ~
является отношением эквивалентности
и,
следовательно, множество V
разбивается
на классы эквивалентных
элементов: все элементы, входящие в один
класс,
переводятся подстановками из группы Г
друг в друга,
а элементы из разных классов друг в
друга не переводятся. Эти классы
называются орбитами
группы
Г. Разбиение
множества вершин графа G
на
орбиты группы
Aut
G
— важная
задача. В сущности, применение к
графу автоморфизма означает перенумерацию
его вершин,
причем отношение смежности должно
сохраняться. Поэтому
для любого автоморфизма 
у вершины графа v
и
ее образа (v)
«все одинаково» (степени равны, графы,
порожденные окружениями, изоморфны и
т. д.). Так что
орбиты группы Aut
G
–
это просто классы «одинаковых»
вершин. Более того, известно, что проблема
распознавания
принадлежности двух вершин произвольного
графа
одной орбите его группы автоморфизмов
и проблема изоморфизма
графов эквивалентны в том смысле, что
любой
алгоритм, эффективно решающий одну из
этих проблем,
может быть преобразован в эффективный
алгоритм для другой (см., например [18]).
К сожалению эффективные алгоритмы для
решения этих двух проблем не известны
(о том, какие алгоритмы считаются
эффективными,
см. гл. XII).

Т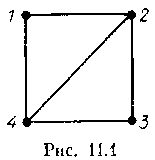рудно
сказать что-либо определенное о строениигруппы
автоморфизмов произвольного графа. Она
может быть
и «малой», и «большой». Найдем, например,
Aut
G
для
графа G,
изображенного
на рис. 11.1. Очевидно,
что любой автоморфизм либо оставляет
неподвижной вершину 1, либо переставляет
ее с вершиной 3. В любой ситуации
вершины 2 и 4 либо обе неподвижны,
либо переводятся друг в друга. Итак,
Aut
G
состоит
из четырех элементов:
e,
транспозиций
(1,3) и (2,4) и произведения
этих транспозиций — (1,3) (2,4).

Очевидно,
что каждый из двух графов, изображенныхна
рис. 11.2, имеет лишь один автоморфизм —
тождественный.
С другой стороны, очевидно, что группой
автоморфизмов
полного графа K_n
является
вся симметрическая
группа S_n.

С
1936 г. известен следующий вопрос Д. Кёнига:
какие
конечные группы являются группами
автоморфизмов графов? Этот вопрос можно
интерпретировать двояким
образом. Первый вариант: какие конечные
группы изоморфны
группам автоморфизмов графов? На этот
вопрос
почти сразу же ответил Р. Фрухт (1938 г.).

Теорема
Фрухта.
Каждая
конечная группа изоморфна
группе автоморфизмов некоторого графа.

>
Пусть Г — группа порядка n
>
1 (для n
= 1
выше приводились
примеры). Построим граф G
описанным
ниже
способом. В качество исходного множества
вершин возьмем
множество всех элементом группы Г.
Каждую упорядоченную
пару (u,
v)
несовпадающих
вершин соединим
простой цепью P_uv
длины
3, добавляя всякий раз по две новые
вершины
a_uv
и
b_uv:
P_uv
=(u,
a_uv,
b_uv,
и).
Затем
к каждой из вершин a_uv
«приклеим»
простую цепь P(a,
u,
v)
длины
l(a,
u,
v),
все вершины которой, исключая
a_uv,—
новые. Аналогично построим цепи P(b,
u,
v)
длины
l(b,
u,
v).
При
этом будем соблюдать следующее условие:
длины всех цепей попарно различны
всегда, кроме
случая, когда u^-1v
= u₁^–1v₁
,
u,
v,
u₁,
v₁Г.
В последнем
случае должно быть

l(a,
u,
v)=l(a,
u₁,
v₁),
l(b,
u,
v)
=
l(b,
u₁,
v₁).
(1)

Построенный
таким образом граф обозначим буквойG.
(На
рис 11.3 показаны соответствующие графы
для n
= 2
и
3. В этой ситуации Г — циклическая группа:
Г
={v,
v²
= e}
при
n
= 2,
Г = {v,
v²,
v³
= e}
при
n
= 3.)

Докажем,
что группы Aut G
и Г изоморфны. Вначале фиксируем в Г
какой-либо элемент w
и следующим образом определим отображение
l_w:
VG
-> VG.
Для xГ
l_w(x)=wx
— произведение элементов группы; вершины
цепи P(a,
u,
v)
переводятся в вершины цепи P(a,
wu,
wv),
причем сохраняется последовательность
вершин в цепи, т. е. l_w(a_uv)
= a_(wu)(wv)
и т. д.; аналогично для цепи P(b,
wu,
wv).
Прямая проверка подтверждает, что l_wAut
G.

Теперь
докажем равенство

Пусть

— произвольный автоморфизм графа G.
Очевидно,
что 
все концевые вершины и, следовательно,
все цепи
P_uv
переводит
друг в друга. Поэтому автоморфизм 
переставляет друг с другом вершины вида
a_uv,
а
также вершины
вида b_uv.
Следовательно,
и элементы группы Г переставляются
друг с другом. При этом из условия (1)
следует,
что если (u)=
u₁,
(v)=v₁,
то
u^-1v
= u₁^-1v₁
для всех
u,
vГ.
Из этого равенства, положив (e)=
w,
получим
(x)
= wx
для
любого xГ,
т. е. 
= l_w.
Равенство
(2) доказано.

Далее,
определим отображение :
Г -> Aut
G,
положив
(x)
= l_x
для
любого xГ.
Очевидно, что отображение

является изоморфизмом групп Г и Aut
G.
<

К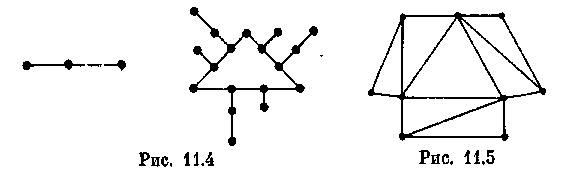онструкция,
приведенная в предыдущем доказательстве,
неэкономна в том смысле, что приводит
к графам с
большим числом элементов. Как правило,
эти графы можно
«уменьшить». Например, при n
= 2,
3 вместо графов,
приведенных на рис. 11.3. можно взять графы
на рис.
11.4. Группой автоморфизмов графа,
показанного на рис.
11.5, также является циклическая группа
порядка 3.

Можно
указать примеры групп подстановок,
которые хотя
и изоморфны по теореме Фрухта группам
автоморфизмов
графов, но сами таковыми не являются.
Рассмотрим
знакопеременную группу A_n,
состоящую
из всех четных
подстановок (n
>
3). Пусть A_nAut
G.
Легко
заметить,
что группа A_n
дважды транзитивна, т.
е. для любых i,
j,
k,
lVG,
ij,
kl,
в
A_n
существует такая подстановка
,
что (i)=
k,
(j)=l.
Если 
— автоморфизм некоторого
графа G,
то
в G
либо
любая пара вершин смежна,
т. е. G
= K_n,
либо
любая пара вершин не смежна, т. е. G
= O_n.
В
обоих случаях Aut
G
=
S_nA_n.

Естественно
возникает неизмеримо более сложный
вариант
вопроса Д. Кёнига. Этот, по-видимому,
далекий от решения
вариант известен как

Проблема
Кёнига.
Установить,
какие условия необходимы
и достаточны, чтобы для заданной на
множестве
V
группы подстановок Г
существовал
такой граф G
с
множеством вершин V,
что Aut
G
=
Г.