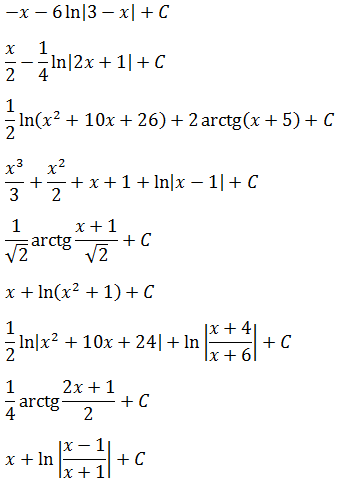Задача
нахождения неопределенного интеграла
дробно рациональной функции сводится
к интегрированию простейших дробей.
Поэтому рекомендуем для начала
ознакомиться с разделом теории разложение
дроби на простейшие.
Пример.
Найти
неопределенный интеграл ![]() .
.
Решение.
Так
как степень числителя подынтегральной
функции равна степени знаменателя, то
для начала выделяем целую часть,
проводя деление
столбиком многочлена на многочлен:
Поэтому,  .
.
Разложение
полученной правильной рациональной
дроби ![]() на
на
простейшие дроби имеет вид![]() .
.
Следовательно,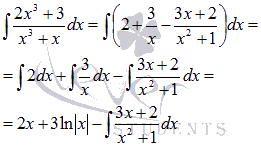
Полученный
интеграл представляет собой интеграл
простейшей дроби третьего типа. Забегая
немного вперед, отметим, что взять его
можно методом подведения
под знак дифференциала.
Так
как ![]() ,
,
то![]() .
.
Поэтому
Следовательно,

Теперь
перейдем к описанию методов интегрирования
простейших дробей каждого из четырех
типов.
Интегрирование
простейших дробей первого типа ![]()
Для
решения этой задачи идеально подходит метод
непосредственного интегрирования:![]()
Пример.
Найти
множество первообразных функции ![]()
Решение.
Найдем
неопределенный интеграл ![]() ,
,
используя свойства первообразной,
таблицу первообразных и правило
интегрирования![]() .
.

К
началу страницы
Интегрирование
простейших дробей второго типа 
Для
решения этой задачи также подходит
метод непосредственного интегрирования:

Пример.
Найдите
неопределенный интеграл  .
.
Решение.

К
началу страницы
Интегрирование
простейших дробей третьего типа ![]()
Для
начала представляем неопределенный
интеграл 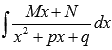 в
в
виде суммы:
Первый
интеграл берем методом подведения под
знак дифференциала:

Поэтому,

У
полученного интеграла ![]() преобразуем
преобразуем
знаменатель:
Следовательно,

Формула
интегрирования простейших дробей
третьего типа принимает вид:

Пример.
Найдите
неопределенный интеграл ![]() .
.
Решение.
Используем
полученную формулу:

Если
бы у нас не было этой формулы, то как бы
мы поступили:

9. Интегрирование простейших дробей четвертого типа
Первый
шаг – подводим под знак дифференциала:

Второй
шаг – нахождение интеграла вида  .
.
Интегралы подобного вида находятся с
использованием рекуррентных формул.
(Смотрите разделинтегрирование
с использованием рекуррентных формул).
Для нашего случая подходит следующая
рекуррентная формула:
Пример.
Найдите
неопределенный интеграл 
Решение.

Для
данного вида подынтегральной функции
используем метод подстановки. Введем
новую переменную (смотрите
раздел интегрирование
иррациональных функций):
После
подстановки имеем:

Пришли
к нахождению интеграла дроби четвертого
типа. В нашем случае имеем коэффициенты М
= 0, р = 0, q = 1, N = 1 и n
= 3.
Применяем рекуррентную формулу:

После
обратной замены ![]() получаем
получаем
результат:
10. Интегрирование тригонометрических функций.
Множество
задач сводится к нахождению интегралов
трансцендентных функций, содержащих
тригонометрические функции. В данной
статье сгруппируем наиболее часто
встречающиеся виды подынтегральных
функций и на примерах рассмотрим методы
их интегрирования.
-
Начнем
с интегрирования синуса, косинуса,
тангенса и котангенса.
Из
таблицы первообразных сразу заметим,
что ![]() и
и![]() .
.
Метод
подведения под знак дифференциалапозволяет
вычислить неопределенные интегралы
функций тангенса и котангенса:
К
началу страницы
-
Поясним,
как были найдены формулы и
и ,
,
находящиеся в таблице первообразных.
Разберем
первый случай, второй абсолютно
аналогичен.
Воспользуемся методом
подстановки:
Пришли
к задаче интегрирования
иррациональной функции. Здесь нам
также поможет метод подстановки:
Осталось
провести обратную замену ![]() иt
иt
= sinx:
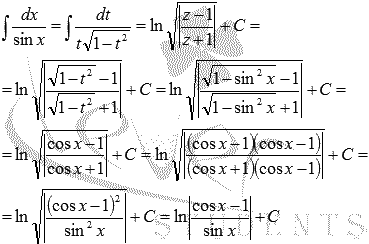
К
началу страницы
-
Отдельно
хочется остановиться на интегралах,
содержащих степени тригонометрических
функций, вида .
.
Подробно
о принципах их нахождении можете
ознакомиться в разделеинтегрирование
с использованием рекуррентных формул.
Если изучите вывод этих формул, то без
особого труда сможете брать интегралы
вида![]() ,
,
гдеm и n –
натуральные числа.
К
началу страницы
-
Когда
тригонометрические функции идут в
комбинациях с многочленами или
показательными функциями, то
применяется метод
интегрирования по частям. В этом
разделе даны рекомендации для нахождения
интегралов ,
, .
.
К
началу страницы
-
Максимум
творчества приходится вкладывать,
когда подынтегральная функция содержит
тригонометрические функции с различными
аргументами.
Здесь
на помощь приходят основные формулы
тригонометрии. Так что выписывайте их
на отдельный листочек и держите перед
глазами.
Пример.
Найти
множество первообразных функции  .
.
Решение.
Формулы
понижения степени дают ![]() и
и![]() .
.
Поэтому

Знаменатель
представляет собой формулу синуса
суммы, следовательно,
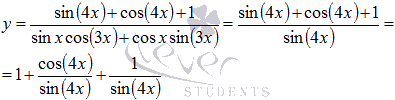
Приходим
к сумме трех интегралов.

К
началу страницы
-
Подынтегральные
выражения, содержащие тригонометрические
функции, иногда можно свести к дробно
рациональным выражениям, используя
стандартную тригонометрическую
подстановку.
Выпишем
тригонометрические формулы, выражающие
синус, косинус, тангенс через тангенс
половинного аргумента:

При
интегрировании нам также понадобится
выражение дифференциала dx через
тангенс половинного угла.
Так
как  ,
,
то
То
есть, ![]() ,
,
где![]() .
.
Пример.
Найти
неопределенный интеграл ![]() .
.
Решение.
Применим
стандартную тригонометрическую
подстановку:

Таким
образом, ![]() .
.
Разложение
на простейшие дробиподынтегральной
функции приводит нас к сумме двух
интегралов:
Осталось
провести обратную замену ![]() :
:
11.
Рекуррентные формулы – это формулы,
выражающие n-ый
член последовательности через предыдущие
члены. При нахождении интегралов они
не редко используются.
Мы
не ставим целью перечислить все
рекуррентные формулы, а хотим дать
принцип их получения. Вывод этих формул
основан на преобразовании подынтегральной
функции и применении метода
интегрирования по частям.
К
примеру, неопределенный интеграл ![]() можно
можно
взять, используя рекуррентную формулу![]() .
.
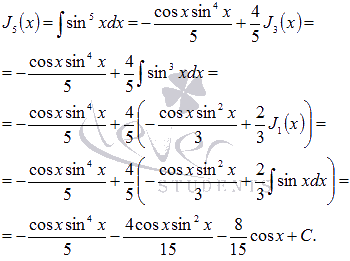
Вывод
формулы  :
:
Используя
формулы тригонометрии, можно записать:

Полученный
интеграл найдем методом интегрирования
по частям. В качестве функции u(x)возьмем cosx,
следовательно, ![]() .
.

Поэтому,

Возвращаемся
к исходному интегралу:

То
есть,

Что
и требовалось показать.
Аналогично
выводятся следующие рекуррентные
формулы:
-
Для
нахождения интегралов вида используется
используется
рекуррентная формула ,n –
,n –
натуральное число. -
Для
нахождения интегралов вида используется
используется
рекуррентная формула .
. -
Для
нахождения интегралов вида используется
используется
рекуррентная формула .
. -
Для
нахождения интегралов вида используется
используется
рекуррентная формула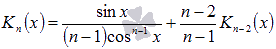 .
.
Пример.
Найти
неопределенный интеграл ![]() .
.
Решение.
Используем
рекуррентную формулу из четвертого
пункта (в нашем примере n
= 3):

Так
как из таблицы первообразных имеем ![]() ,
,
то
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Прежде, чем приступить к интегрированию простейших дробей для нахождения неопределенного интеграла дробно рациональной функции, рекомендуется освежить в памяти раздел «Разложение дроби на простейшие».
Найдем неопределенный интеграл ∫2×3+3×3+xdx .
Решение
Выделим целую часть, проведя деление столбиком многочлена на многочлен, учитывая тот факт, что степень числителя подынтегральной функции равна степени знаменателя:
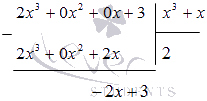
Поэтому 2×3+3×3+x=2+-2x+3×3+x . Мы получили правильную рациональную дробь -2x+3×3+x , которую теперь разложим на простейшие дроби -2x+3×3+x=3x-3x+2×2+1 . Следовательно,
∫2×3+3×3+xdx=∫2+3x-3x+2×2+1dx=∫2dx+∫3xdx-∫3x+2×2+1dx=2x+3lnx-∫3x+2×2+1dx
Мы получили интеграл простейшей дроби третьего типа. Взять его можно методом подведения под знак дифференциала.
Так как dx2+1=2xdx , то 3xdx=32dx2+1 . Поэтому
∫3x+2×2+1dx=∫3xx2+1dx+∫2×2+1=32∫dx2+1×2+1+2∫dxx2+1=32lnx2+1+2arctg x+C1
Следовательно,
∫2×3+3×3+xdx=2x+3lnx-∫3x+2×2+1dx=2x+3lnx-32lnx2+1-2arctan x+C, где С=-С1
Опишем методы интегрирования простейших дробей каждого из четырех типов.
Интегрирование простейших дробей первого типа Ax-a
Используем для решения этой задачи метод непосредственного инетгрирования:
∫Ax-adx=A∫dxx-a=A·lnx-a+C
Найдите множество первообразных функции y=32x-1.
Решение
Испльзуя правило интегрирования, свойства первообразной и таблицу первообразных, найдем неопределенный интеграл ∫3dx2x-1: ∫fk·x+bdx=1k·Fk·x+b+C
∫3dx2x-1=3∫dx2x-12=32∫dxx-12=32lnx-12+C
Ответ: ∫3dx2x-1=32lnx-12+C
Интегрирование простейших дробей второго типа Ax-an
Здесь также применим метод непосредственного интегрирования:∫Ax-andx=A∫x-a-ndx=A-n+1x-a-n+1+C=A1-nx-an-1+C
Необходимо найти неопределенный интеграл ∫dx2x-37 .
Решение
∫dx2x-37=∫dx2x-327=127∫x-32-7dx==127·1-7+1·x-32-7+1+C=127·-6·x-326+C==12·-6·26·x-326+C=-112·12x-36+C
Ответ: ∫dx2x-37=-112·12x-36+C
Интегрирование простейших дробей третьего типа Mx+Nx2+px+q, D=p2-4q<0
Первым шагом представим неопределенный интеграл ∫Mx+Nx2+px+q в виде суммы:
∫Mx+Nx2+px+qdx=∫Mxx2+px+qdx+N∫dxx2+px+q
Для того, чтобы взять первый интеграл, используем метод подведения под знак дифференциала:
∫Mxx2+px+qdx=dx2+px+q=2x+pdx=2xdx+pdx⇒2xdx=dx2+px+q-pdx⇒Mxdx=M2dx2+px+q-pM2dx==∫M2dx2+px+q-pM2dxx2+px+q==M2∫dx2+px+qx2+px+q-pM2∫dxx2+px+q==M2lnx2+px+q-pM2∫dxx2+px+q
Поэтому,
∫Mx+Nx2+px+qdx=∫Mxx2+px+qdx+N∫dxx2+px+q==M2lnx2+px+q-pM2∫dxx2+px+q+N∫dxx2+px+q==M2lnx2+px+q+2N-pM2·∫dxx2+px+q
Мы получили интеграл ∫dxx2+px+q. Проведем преобразование его знаменателя:
∫dxx2+px+q=∫dxx2+px+p22-p22+q==∫dxx+p22-p24+q=∫dxx+p22-p24+q==∫dxx+p22+4q-p24=24q-p2·arctg2x+p24q-p2+C1
Следовательно,
∫Mx+Nx2+px+qdx=M2lnx2+px+q+2N-pM2·∫dxx2+px+q==M2lnx2+px+q+2N-pM2·24q-p2·arctg2x+p24q-p2+C1
Формула интегрирования простейших дробей третьего типа принимает вид:
∫Mx+Nx2+px+qdx=M2lnx2+px+q+2N-pM4q-p2·arctg2x+p24q-p2+C
Необходимо найти неопределенный интеграл ∫2x+13×2+6x+30dx.
Решение
Применим формулу:
∫2x+13×2+6x+30dx=13∫2x+1×2+2x+10dx=M=2,N=1,p=2,q=10==1322lnx2+2x+10+2·1-2·24·10-22arctg2x+224·10-22+C==13lnx2+2x+10-19arctgx+13+C
Второй вариант решения выглядит следующим образом:
∫2x+13×2+6x+30dx=13∫2x+1×2+2x+10dx=d(x2+2x+10=(2x+2)dx==13∫2x+2-1×2+2x+10dx=13∫d(x2+2x+10)x2+2x+10=13∫dxx2+2x+10==преобразуем знаменатель=13lnx2+2x+10-13∫d(x)x+12+9==13lnx2+2x+10-19arctgx+13+C
Ответ: ∫2x+13×2+6x+30dx=13lnx2+2x+10-19arctgx+13+C
Интегрирование простейших дробей четвертого типа Mx+N(x2+px+q)n, D=p2-4q<0
Первым делом выполняем подведение под знак дифференциала:
∫Mx+Nx2+px+qdx=d(x2+px+q)=(2x+p)dx==M2∫d(x2+px+q)(x2+px+q)n+N-pM2∫dx(x2+px+q)n==M2(-n+1)·1(x2+px+q)n-1+N-pM2∫dx(x2+px+q)n
Затем находим интеграл вида Jn=∫dx(x2+px+q)n с использованием рекуррентных формул. Информацию о рекуррентных формулах можно посмотреть в теме «Интегрирование с использованием рекуррентных формул».
Для решения нашей задачи подходит рекуррентная формула вида Jn=2x+p(n-1)(4q-p2)(x2+px+q)n-1+2n-3n-1·24q-p2·Jn-1.
Необходимо найти неопределенный интеграл ∫dxx5x2-1 .
Решение
∫dxx5x2-1=∫x-5(x2-1)-12dx
Мы будем использовать для этого вида подынтегральной функции метод подстановки. Введем новую переменную x2-1=z2x=(z2+1)12dx=z(z2+1)-12dx
Получаем:
∫dxx5x2-1=∫x-5(x2-1)-12dx==∫(z2+1)-52·z-1·z·(z2+1)-12dz=∫dz(z2+1)3
Пришли к нахождению интеграла дроби четвертого типа. В нашем случае имеем коэффициенты М = 0, р = 0, q = 1, N = 1 и n = 3. Применяем рекуррентную формулу:
J3=∫dz(z2+1)3=2z+0(3-1)·(4·1-0)·z2+13-1+2·3-33-1·24·1-0·∫dz(z2+1)2==z4(z2+1)2+342z(2-1)·(4·1-0)·(z2+1)2-1+2·2-32-11·24·1-0·∫dzz2+1==z4(z2+1)2+38zz2+1+38arctg(z)+C
После обратной замены z=x2-1 получаем результат:
∫dxx5x2-1=x2-14×4+38×2-1×2+38arctgx2-1+C
Ответ: ∫dxx5x2-1=x2-14×4+38×2-1×2+38arctgx2-1+C
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
1. Интегрирование рациональных дробей.
2. Алгоритм интегрирования рациональной дроби.
3. Примеры интегрирования рациональных функций.
Интегрирование рациональных дробей
Рациональной дробью называется дробь вида

– многочлены степени m и n соответственно. Рациональная дробь называется правильной , если степень числителя меньше степени знаменателя (m<n), в противном случае дробь называется неправильной .
Простейшими элементарными дробями называются дроби следующего вида:

Пример 1

Пример 2

Интегралы, содержащие в знаменателе квадратный трехчлен, можно вычислить, применяя прием выделения полного квадрата разности или суммы. Рассмотрим пример такого интеграла.
Пример 3.

Алгоритм интегрирования рациональной дроби
1. Если дробь неправильная, надо выделить целую часть рациональной дроби, разделив числитель на знаменатель по правилу деления многочлена на многочлен, т.е. представить в виде:
 2. Знаменатель разложим на простейшие сомножители: Qn(x)
2. Знаменатель разложим на простейшие сомножители: Qn(x)

3. Представим дробь

виде суммы простейших дробей с неопределенными коэффициентами.

- Приведем все дроби в разложении к общему знаменателю и приравняем числители в обеих частях равенства.
- Составим систему уравнений, используя равенство многочленов, стоящих в числителе, приравнивая коэффициенты при одинаковых степенях x.
- Решим систему уравнений, находя некоторые коэффициенты методом частных значений, полагая равным действительным корням знаменателя.
- Подставим найденные коэффициенты A1,A2,…,Cs,Ds в разложение дроби.
- Проинтегрируем простейшие дроби.
Примеры интегрирования рациональных функций
Пример 4.


Корни знаменателя: x=1, а x2+1 = 0 не имеет действительных корней.
Тогда разложение для данной дроби имеет вид:

Приводя полученные дроби к общему знаменателю, получим тождество:

Пример 5.


Вычислим коэффициенты разложения, приравнивая коэффициенты при одинаковых степенях. Так как знаменатель имеет три действительных различных корня, то три коэффициента найдем методом частных значений.

Подставим найденные коэффициенты в разложение и проинтегрируем дроби.

Интегрирование простейших рациональных дробей
Напомним, что дробно-рациональными называют функции вида
$$
f(x) = frac{P_n(x)}{Q_m(x)},
$$
в общем случае являющиеся отношением двух многочленов %%P_n(x)%% и %%Q_m(x)%%.
Если %%m > n geq 0%%, то рациональную дробь называют правильной, в противном случае — неправильной. Используя правило деления многочленов, неправильную рациональную дробь можно представить в виде суммы многочлена %%P_{n – m}%% степени %%n – m%% и некоторой правильной дроби, т.е.
$$
frac{P_n(x)}{Q_m(x)} = P_{n-m}(x) + frac{P_l(x)}{Q_n(x)},
$$
где степень %%l%% многочлена %%P_l(x)%% меньше степени %%n%% многочлена %%Q_n(x)%%.
Таким образом, неопределенный интеграл от рациональной функции можно представить суммой неопределенных интегралов от многочлена и от правильной рациональной дроби.
Интегралы от простейших рациональных дробей
Среди правильных рациональных дробей выделяют четыре типа, которые относят к простейшим рациональным дробям:
- %%displaystyle frac{A}{x – a}%%,
- %%displaystyle frac{A}{(x – a)^k}%%,
- %%displaystyle frac{Ax + B}{x^2 + px + q}%%,
- %%displaystyle frac{Ax + B}{(x^2 + px + q)^k}%%,
где %%k > 1%% — целое и %%p^2 – 4q < 0%%, т.е. квадратные уравнения не имеют действительных корней.
Вычисление неопределенных интегралов от дробей первых двух типов
Вычисление неопределенных интегралов от дробей первых двух типов не вызывает затруднений:
$$
begin{array}{ll}
int frac{A}{x – a} mathrm{d}x &= Aint frac{mathrm{d}(x – a)}{x – a} = A ln |x – a| + C, \
\
int frac{A}{(x – a)^k} mathrm{d}x &= Aint frac{mathrm{d}(x – a)}{(x – a)^k} = A frac{(x-a)^{-k + 1}}{-k + 1} + C = \
&= -frac{A}{(k-1)(x-a)^{k-1}} + C.
end{array}
$$
Вычисление неопределенного интегралов от дробей третьего типа
Дробь третьего типа сначала преобразуем, выделив полный квадрат в знаменателе:
$$
frac{Ax + B}{x^2 + px + q} = frac{Ax + B}{(x + p/2)^2 + q – p^2/4},
$$
так как %%p^2 – 4q < 0%%, то %%q – p^2/4 > 0%%, которое обозначим как %%a^2%%. Заменив также %%t = x + p/2, mathrm{d}t = mathrm{d}x%%, преобразуем знаменатель и запишем интеграл от дроби третьего типа в форме
$$
begin{array}{ll}
int frac{Ax + B}{x^2 + px + q} mathrm{d}x &= int frac{Ax + B}{(x + p/2)^2 + q – p^2/4} mathrm{d}x = \
&= int frac{A(t – p/2) + B}{t^2 + a^2} mathrm{d}t = int frac{At + (B – A p/2)}{t^2 + a^2} mathrm{d}t.
end{array}
$$
Последний интеграл, используя линейность неопределенного интеграла, представим в виде суммы двух и в первом из них введем %%t%% под знак дифференциала:
$$
begin{array}{ll}
int frac{At + (B – A p/2)}{t^2 + a^2} mathrm{d}t &= Aint frac{t mathrm{d}t}{t^2 + a^2} + left(B – frac{pA}{2}right)int frac{mathrm{d}t}{t^2 + a^2} = \
&= frac{A}{2} int frac{mathrm{d}left(t^2 + a^2right)}{t^2 + a^2} + – frac{2B – pA}{2}int frac{mathrm{d}t}{t^2 + a^2} = \
&= frac{A}{2} ln left| t^2 + a^2right| + frac{2B – pA}{2a} text{arctg}frac{t}{a} + C.
end{array}
$$
Возвращаясь к исходной переменной %%x%%, в итоге для дроби третьего типа получаем
$$
int frac{Ax + B}{x^2 + px + q} mathrm{d}x = frac{A}{2} ln left| x^2 + px + qright| + frac{2B – pA}{2a} text{arctg}frac{x + p/2}{a} + C,
$$
где %%a^2 = q – p^2 / 4 > 0%%.
Вычисление интеграла 4 типа сложно, поэтому в этом курсе не рассматривается.
Итак, друзья, вот мы с вами, шаг за шагом, вооружившись базовыми приёмами интегрирования, плавненько подошли к весьма обширному разделу интегрального исчисления — интегрированию рациональных дробей. Этой обширной теме будет посвящён не один урок!
Несколько слов о рациональных дробях вообще.
Для начала вспомним, что же такое вообще рациональная дробь и с чем её едят. Или по-другому рациональная функция, что одно и то же.
Рациональная дробь (рациональная функция) — это просто отношение двух многочленов! И всё. Если копать глубже, то в рациональной функции над иксом производится только сложение, вычитание, умножение, деление и возведение в целую степень. Нету ни извлечения корня, ни синусов, ни логарифмов и тому подобных действий от выражения с иксом. Для понимания приведу пару примеров.
Функция
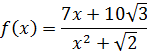
является рациональной дробью. Здесь есть корни, но под корнями стоят только числа. А вот с самим иксом при этом проделываются вполне допустимые действия — умножение на семь и возведение в квадрат.
А вот функция
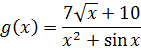
уже не является рациональной дробью, поскольку в числителе дроби присутствует извлечение корня из икса, а в знаменателе вдобавок сидит sin x.
Осознали, что такое рациональная дробь? Прекрасно! Тогда продолжаем.
Одним словом, в данном материале речь пойдёт об интегрировании функций вида
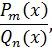
где Pm(x) и Qn(x) — какие-то многочлены. Совершенно любые. Числа-индексы m и n — степени этих многочленов.
Например:
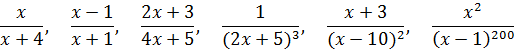
В общем, вы поняли…
Так же, как и числовые дроби, рациональные дроби бывают правильными и неправильными.
Рациональная дробь является правильной, если степень числителя строго меньше степени знаменателя. Иными словами, m<n.
Во всех остальных случаях (m≥n) дробь является неправильной. Напоминаю, что степенью многочлена P(x) является старшая степень икса в многочлене.
Посмотрим на примеры правильных и неправильных дробей?
Например, дроби из нашего списка
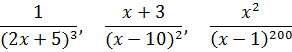
являются правильными, так как в этих дробях степень числителя (0, 1 и 2) строго меньше степени знаменателя (3, 2 и 200 соответственно).
А вот дроби
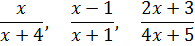
неправильные, так как в каждой из них степень числителя (первая) равна степени знаменателя (также первой).
Итак, что же это за зверь такой под названием рациональная дробь мы вспомнили. Пора теперь потихоньку переходить к вопросам их интегрирования.
В этом уроке у меня для вас есть две новости — хорошая и не очень. Начну с хорошей, пожалуй…
Новость хорошая. Мы с вами уже не раз говорили о том, что, к великому сожалению, в математике отсутствуют стандартные формулы интегрирования для дробей. В отличие от дифференцирования, где для любой дроби (даже не обязательно рациональной!) производную всегда можно вычислить по известной формуле:
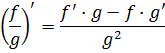
А вот в интегрировании к каждой функции – свой подход. Иногда даже уникальный. В том числе и к дробям, да.
Но есть одно существенное «но»… Если подынтегральная дробь является рациональной, (то есть, представляет собой вышеупомянутое отношение двух многочленов), то, оказывается, для такой дроби универсальный алгоритм интегрирования существует! Называется такой алгоритм – разложение на элементарные дроби с помощью метода неопределённых коэффициентов. Что это за элементарные дроби такие и что это за загадочные неопределённые коэффициенты, мы довольно скоро с вами узнаем. Всему своё время.)
А теперь новость не очень хорошая. Метод этот обычно довольно трудоёмок, громоздок и требует, порой, весьма и весьма кропотливых выкладок. В которых, между прочим, легко можно запутаться и накосячить. И поэтому обычно применяется как тяжёлая артиллерия. 🙂 Так что пока временно забудем про метод неопределённых коэффициентов и сосредоточимся лишь на самых простых дробно-рациональных функциях. Таких, где метод неопределённых коэффициентов применять не надо.
А кто ж знает, надо его применять или не надо… Согласен. Никто не знает. Но некоторые характерные случаи я вам покажу и разберу. В этом уроке.) Это только на примерах понять и прочувствовать можно. Поэтому решаем. Будем по порядочку интегрировать наши дроби, выписанные выше.
Итак, поехали!
Уровень 1.
Метод разложения числителя по степеням знаменателя. В знаменателе — линейная функция.
Очень удобный и весьма популярный способ выкрутиться при интегрировании многих дробей! Одна из разновидностей этого способа интегрирования нам уже довольно хорошо знакома. Метод «добавить/отнять» помните? В математике он называется «добавление нуля». Смысл этого манёвра прост до ужаса: от добавления/вычитания какого-то числа или выражения суть исходного выражения не меняется:
x + a — a = x
Было икс и осталось тоже икс… Добавлять/отнимать, естественно, надо то выражение, которое удобно в конкретном примере. Зачем? А затем, чтобы в числителе подынтегральной дроби (а говорим мы с вами сейчас только о дробях) выделить выражение, стоящее в знаменателе. 🙂 И, тем самым, разложить нашу исходную дробь, которую неудобно интегрировать, в сумму нескольких дробей, которые уже удобно интегрировать. Смотрим, как это делается. На примерах.
Начнём с дробно-линейных функций. То есть, таких функций, у которых в числителе и в знаменателе стоят какие-то линейные конструкции kx+b.
Инструментарий, который нам потребуется в этом параграфе, весьма скромен — подведение функции под знак дифференциала да парочка табличных интегралов:
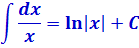
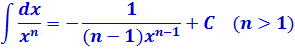
С первой формулой (натуральный логарифм) всё ясно, надеюсь. А вот вторая формула — самая обычная степенная функция. Замените дробь под интегралом на степень с отрицательным показателем (–n), проинтегрируйте по таблице — и тоже всё будет понятно.
А теперь берём самую первую дробь из нашего списка и интегрируем:
Пример 1
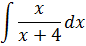
Смотрим на нашу дробь и… пока с ходу не знаем, как её интегрировать, да? Дробь неудобна для интегрирования. Что ж, будем превращать её в удобную! Методом разложения числителя.
Для этого анализируем числитель и знаменатель: сверху икс, снизу х+4. Для разложения дроби в сумму в числителе тоже хотелось бы получить х+4, но наши хотелки не должны противоречить законам математики. 🙂
Поэтому, раз уж мы в числителе решили к иксу прибавить четвёрку (это наша хотелка), то мы должны тут же её и вычесть (а так уже математике хочется). Вот так:
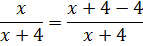
И что? Чем такой манёвр нам поможет? А тем, что теперь нашу дробь можно разложить на две:
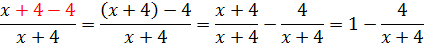
А вот в таком виде наша подынтегральная функция уже удобна для интегрирования! Почему? Да потому, что единичка интегрируется вообще в уме, а оставшаяся дробь
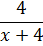
легко интегрируется подведением под дифференциал. Вперёд!
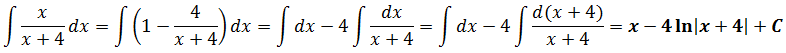
И все дела.)
Здесь я не стал второй интеграл так уж подробно расписывать:
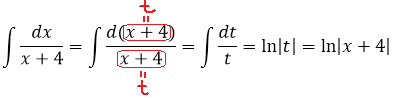
Не маленькие уже. 🙂 Кто дочитал до этой статьи, тот уже в теме, надеюсь. И в будущем подобные интегралы я сразу буду оформлять через логарифм безо всякой замены. Привыкайте.)
Продифференцируем наш ответ и проверим результат интегрирования:
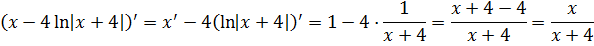
Всё ОК.
Едем дальше.)
Пример 2
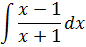
Опять анализируем числитель и знаменатель. В числителе икс минус один, а в знаменателе икс плюс один. Для продвижения в интегрировании снова выделяем в числителе выражение х+1, стоящее в знаменателе и раскладываем нашу дробь на две. Ибо так нам удобнее!
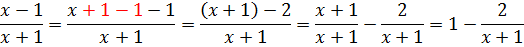
Вот так. И интеграл теперь берётся одной левой.)
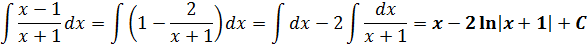
Дифференцируем ответ, не ленимся:
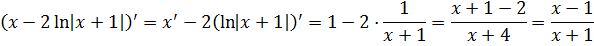
Всё гуд.)
И последний пример из этой серии. Посложнее. С кучей коэффициентов. 🙂
Пример 3
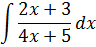
Здесь тоже хорошо бы разложить подынтегральную дробь на две. Только, это… Как же нам в числителе из 2х+3 сделать 4х+5?
Как-как… По шагам! Начнём со слагаемого с иксом. Нам надо 2х превратить в 4х. Как это сделать? Да на два домножить! Элементарно, Ватсон! 🙂
2х·2 = 4х
Но в числителе исходной дроби нету никакого 4х. Там 2х. Поэтому, чтобы от наших действий ничего не изменилось, надо что сделать? Правильно! Разделить обратно на двойку. Или, что то же самое, домножить на 1/2. Вот так:
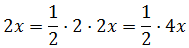
Так, с иксом расправились, 4х выделили. Следующим шагом будет выделение свободного члена. Теперь нам предстоит выделить пятёрку и организовать в числителе вот такое выражение:
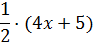
В скобках как раз находится так нужный нам знаменатель. Если сейчас раскрыть скобки, то получим:
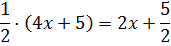
Но у нас в числителе стоит не пять вторых, а просто тройка… Непорядок! Как нам из пяти вторых получить тройку? Очень просто. Если элементарные действия с дробями помнить.)
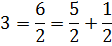
Значит, для тройки нам не хватает одной второй. Не проблема! Добавим…
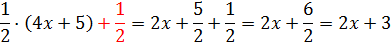
Есть! Получен исходный числитель! Это значит, что наше искусственное выделение знаменателя произведено успешно. 🙂 Вот оно:
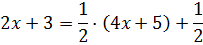
Теперь подставляем это выражение в числитель подынтегральной и с удовольствием раскладываем нашу дробь на две:
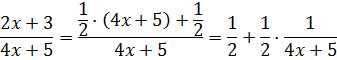
Ну вот. Теперь всё готово к интегрированию. Вперёд и с песнями! Сразу выносим 1/2 за знак интеграла и считаем. В дроби используем подведение под дифференциал (коэффициент 1/4 не теряем, да).
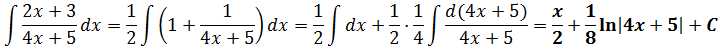
Готово дело.)
Как видите, в таких примерах всё достаточно просто. И так следует поступать с любой дробно-линейной функцией: выделяем в числителе выражение, стоящее в знаменателе, разбиваем дробь на две и интегрируем. В ответе всегда будет получаться некое слагаемое с иксом и логарифм знаменателя.
А мы идём дальше. Теперь разберём случаи, когда в знаменателе дроби стоит одинокая линейная конструкция в какой-то степени. Интегрируем следующие три дроби из нашего списка.)
Пример 4
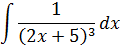
Пример совсем элементарный. Что делаем? Правильно! Подводим знаменатель 2х+5 под дифференциал и интегрируем по таблице:
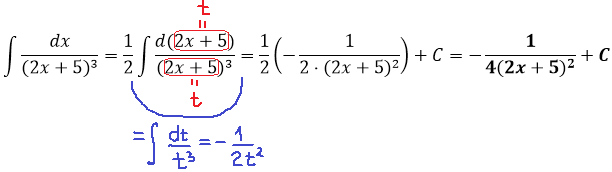
Что, думаете, этот пример я чисто для прикола дал? Вовсе нет! Такие дроби вам будут попадаться регулярно при рассмотрении интегралов от более навороченных дробей.) Думаете, ошибиться нельзя? Ну да, как же…
Здесь можно машинально влепить в показателе (и в знаменателе дроби) четвёрку вместо двойки, руководствуясь табличным выражением
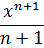
Внимание! Показатель n здесь равен -3. Минус три. Из-за того, что наша степень tn стоит в знаменателе. Стало быть, n+1 = -3+1 = -2. Минус два, а не четыре… Повторите свойства степени с отрицательным показателем!)
Также можно впопыхах забыть про коэффициент 1/2 при подведении знаменателя под дифференциал. Внимательнее надо быть, да.)
Продолжаем…
Пример 5
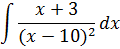
В знаменателе сидит х-10. А в числителе х+3. А хочется тоже х-10… Не проблема! Выделяем в числителе выражение х-10. Это не просто, а очень просто:
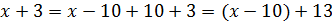
Дальше уже всё ясно.) Раскладываем нашу дробь в сумму:
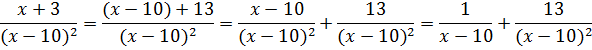
Отлично. Разложили.) А теперь вместо исходной дроби интегрируем сумму двух более простых дробей:
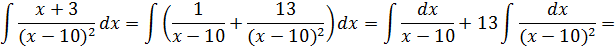
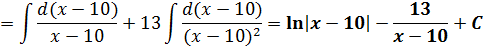
Вот и всё!
И последний пример такого типа. Самый злой, да.)
Пример 6
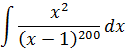
В знаменателе аж 200-я степень! Как тут не испугаться. 🙂 На самом деле, телодвижения точно такие же — выделяем в числителе линейное выражение х-1. Прямо под квадратом! Пользуемся школьной формулой квадрата суммы.)
Вот так:
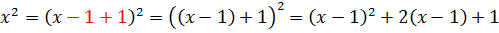
Готово дело. И теперь наша зловещая дробь разбивается на три маленьких:
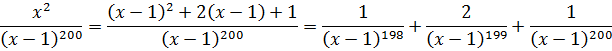
А полученные три дроби уже очень легко проинтегрировать! Буквально в уме!
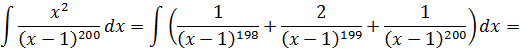
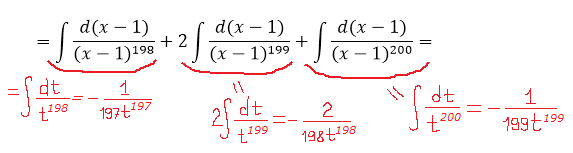
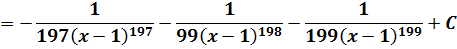
Как видите, сложного по сути ничего и нету.) А ведь как напугал в самом начале внешний вид примера!
Практический совет:
Если под интегралом рациональная дробь, в знаменателе которой стоит одиночная линейная конструкция в какой-либо степени (kx+b)n, то первым делом пробуем выделить эту же линейную конструкцию в числителе дроби. В результате этой процедуры исходный интеграл чаще всего легко сводится к комбинации табличных, либо берущихся подведением под дифференциал.
А мы переходим на следующий уровень.
Уровень 2.
В знаменателе — квадратный трёхчлен. Раскладываем числитель!
Оказывается, разложить дробь в сумму более простых методом выделения знаменателя в числителе иногда возможно и в том случае, когда в знаменателе стоит что-то покруче, чем линейная конструкция. Квадратный трёхчлен, например. Принцип тот же. Выделяем в числителе то выражение, что стоит в знаменателе, раскладываем исходную дробь в сумму дробей и — действуем!
Табличные формулы, которые нам понадобятся для решения примеров этого параграфа (формулы №7 и №8):
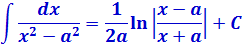
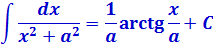
Ещё нам понадобятся школьные формулы сокращённого умножения:
(a+b)2 = a2 + 2ab + b2
(a–b)2 = a2 — 2ab + b2
(a+b)3 = a3 + 3a2b + 3ab2 + b3
(a–b)3 = a3 — 3a2b + 3ab2 — b3
и т.д. Вспоминайте, кто забыл!
Вспомнили? А теперь решаем примеры:
Пример 7
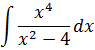
Снова, как и на предыдущем уровне, выделяем в числителе из x4 выражение x2 — 4, стоящее в знаменателе. Вот так:
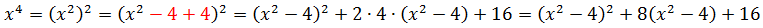
Вот и отлично. Если мы теперь числитель нашей дроби перепишем в таком виде, то наша подынтегральная дробь очень красиво разложится в сумму табличных функций. Смотрите!
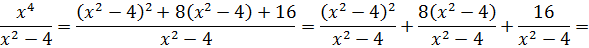
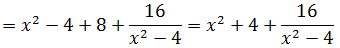
Многочлен x2+4 интегрируется в уме, а оставшаяся дробь — не что иное, как табличный интеграл! Формула №7 из таблицы, с «высоким» логарифмом.) Число «а» у нас — двойка: 4 = 22. Вот и интегрируем себе по табличке:
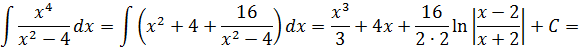
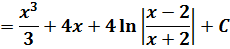
Ещё примерчик из этой оперы:
Пример 8
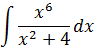
В знаменателе — одинокий квадратный трёхчлен x2+4 и больше ничего. Идём по проторенной дорожке — выделяем эту же конструкцию в числителе.
В этот раз пользуемся формулой куба разности: (a–b)3 = a3 — 3a2b + 3ab2 – b3
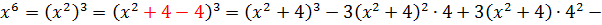
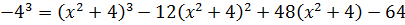
Есть. Числитель разложен по степеням (х2+4). Теперь раскладываем исходную дробь в сумму, сокращаем что сокращается, раскрываем все скобки, приводим подобные и упрощаем:
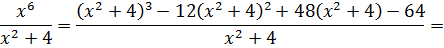
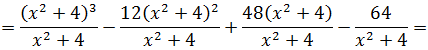
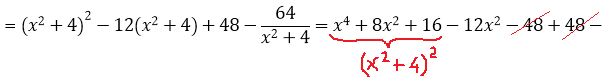
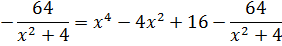
Отлично. Снова получили многочлен и табличный интеграл (формула №8, а=2). Интегрируем сумму табличных функций:
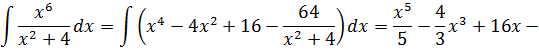
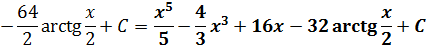
А теперь давайте поразмышляем. Как вы думаете, почему при разложении последних двух дробей в сумму у нас в обоих случаях вылез многочлен? А всё потому, что наши исходные подынтегральные дроби — неправильные! А любую неправильную рациональную дробь математика позволяет привести к сумме многочлена и правильной дроби. Посмотрим ещё разочек на наши выкладки. Что у нас получилось?
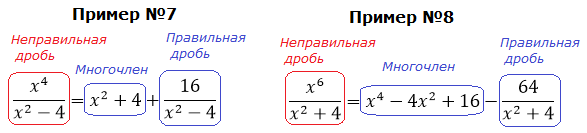
Видите? И такая структура (многочлен + правильная дробь) у нас будет получаться всегда, как только мы будем иметь дело с неправильными дробями. Сами многочлены — не что иное, как целая часть наших дробей. Так же, как и в числовых дробях.)
Понятна технология выделения знаменателя? Замечательно! Кстати, если неохота долго возиться с выделением знаменателя в числителе, есть способ-лайт (только в случае неправильной дроби!). А именно — деление числителя на знаменатель уголком. Демонстрирую на примере дроби из примера №7:
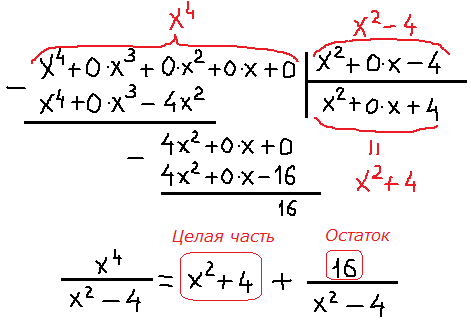
Забыли, как делить многочлен на многочлен уголком? А вы вспомните! Не сочтите за труд. 🙂
Осталось познакомиться ещё с одной полезной процедурой при интегрировании дробей. А именно — выделение полного квадрата.
Уровень 3.
В знаменателе — квадратный трёхчлен. Выделяем полный квадрат!
И сразу пример в студию! 🙂
Пример 9
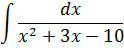
Такие интегралы всегда берутся в три шага.
1. Выделяем полный квадрат двучлена в знаменателе.
2. Подводим этот двучлен под знак дифференциала,
3. Делаем замену переменной и интегрируем по табличным формулам:
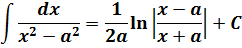
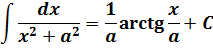
Итак, знаменателе дроби – квадратный трёхчлен. В числителе — просто dx. Работаем прямо по алгоритму.
Шаг 1. Выделяем полный квадрат в знаменателе
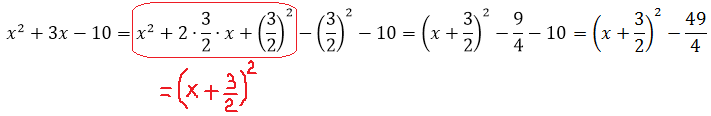
Шаг 2. Подводим двучлен под знак дифференциала
В нашем случае необходимо подвести под дифференциал образовавшуюся скобку (х+3/2). Действуем:
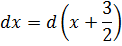
Шаг 3. Делаем замену переменной и интегрируем по таблице
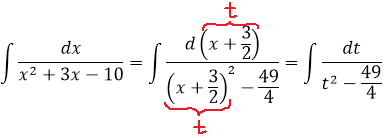
В знаменателе — разность. Значит, наша необходимая табличная формула — с логарифмом. Интегрируем:
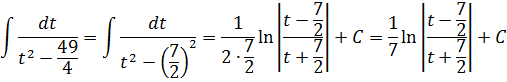
Возвращаемся обратно к переменной икс, упрощаем что упрощается и пишем окончательный ответ:
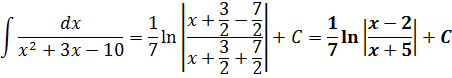
Готово дело.)
Разберём теперь пример на вторую табличную формулу.
Пример 9
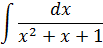
Опять действуем по шагам. Всё то же самое.)
Шаг 1. Выделяем полный квадрат в знаменателе
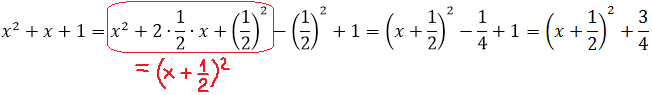
Шаг 2. Подводим двучлен под знак дифференциала
После выделения полного квадрата у нас образовалась скобка (х+1/2). Подводим её под дифференциал:
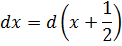
Шаг 3. Делаем замену переменной и интегрируем по таблице
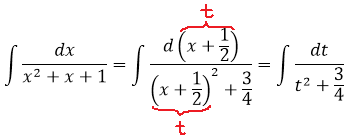
В знаменателе — сумма. Значит, пользуемся второй табличной формулой — с арктангенсом:
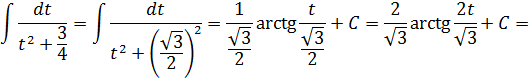
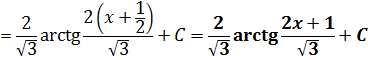
Вот такой ответ. С корнями, да… Ничего не поделать… Такой уж пример.
Что, хлопотно? Согласен, хлопотно. Но это ещё не самые трудные интегралы. Имейте в виду, что дробные и иррациональные числа при интегрировании рациональных дробей — самое обычное дело. Я специально так некрасиво подобрал коэффициенты. Чтобы вы имели представление, что делать в подобных ситуациях.
И особенно тонко прочувствуйте момент, как и зачем осуществляется выделение квадратов чисел
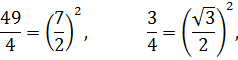
а также по какому критерию происходит выбор той или иной табличной формулы.
Что делать, если в числителе не dx, а линейная конструкция?
В этом случае процедура интегрирования усложняется ещё одним шагом. А само интегрирование — ещё одним слагаемым. Сейчас всё увидите.
Последний пример на сегодня:
Пример 10
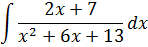
Вот такая вот дробушка… Сначала всё то же самое.
Шаг 1. Выделяем полный квадрат двучлена в знаменателе
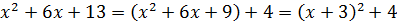
А вот следующий шаг здесь будет новым. Но хорошо знакомым.)
Шаг 2. Выделяем этот же двучлен в числителе
Такую операцию мы уже с вами неоднократно проделывали при рассмотрении предыдущих примеров. Здесь всё то же самое. Выделяем скобку (х+3) в числителе нашей дроби. Вот так:
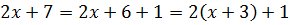
Шаг 3. Подводим двучлен под знак дифференциала
Здесь тоже всё элементарно:
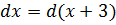
Шаг 4. Делаем замену переменной и интегрируем по таблице
А вот само интегрирование будет уже чуть сложнее, поскольку интегрировать нам придётся уже две дроби. Какие — сейчас увидите.) Начнём:
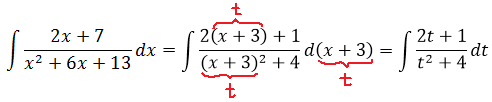
Что делать с образовавшимся новым интегралом по переменной t? Разбиваем его на сумму двух! Вот так:
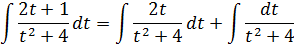
Первый интеграл легко берётся подведением знаменателя под дифференциал и далее – по известной табличной формуле. Это и есть то самое дополнительное слагаемое, о котором я говорил. А вот второй интеграл вообще проблем не вызывает, ибо он — знакомый табличный.) Раз в знаменателе сумма, значит, применяем формулу с арктангенсом. Число «а» у нас равно двойке:
а = 2
Смотрите и врубайтесь, как именно происходит интегрирование:
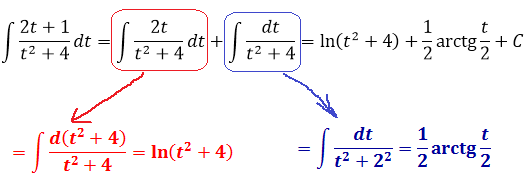
Вот и всё. Осталось лишь вернуться обратно к иксу и записать окончательный ответ:
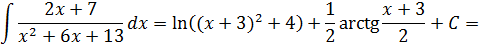
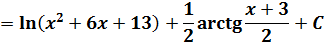
Вот всё и получилось.) Конечно, считать побольше пришлось, ну так у нас и дробь тоже посложнее.)
Сразу предупреждаю: не пытайтесь тупо выучить алгоритм! Вместо этого постарайтесь разобраться и понять каждый из этапов! Это куда полезнее, чем простое механическое зазубривание. Понимание смысла спасает всегда. В любой ситуации. И не только в интегрировании. ) А вот зубрёжка работает лишь до тех пор, пока примеры — стандартные. А при малейшем отклонении от шаблона студент может и в ступор впасть…
Что делать, если дробь – неправильная?
Что-что… Исправлять! Делать дробь правильной.) Как? Выделять целую часть. Хотя бы делением числителя на знаменатель уголком, ибо это — самый универсальный способ. От него плохо не бывает. Бывает либо хорошо, либо — никак. 🙂 Например, дана нам такая нехорошая дробь:
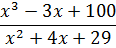
Степень числителя — тройка. Степень знаменателя — двойка. Так как степень числителя больше степени знаменателя, то, стало быть, наша дробь неправильная. Выделяем целую часть. Делим уголком числитель на знаменатель.
Напоминаю, что перед делением уголком мы должны расписать наш многочлен по всем степеням икс от старшей к младшей. В том числе и по тем степеням, которых в исходном многочлене в явном виде нет! Перед отсутствующими степенями ставим нули. В нашем многочлене х3-3х+100 нету члена с х2. Вот и пишем х2 с нулевым коэффициентом.
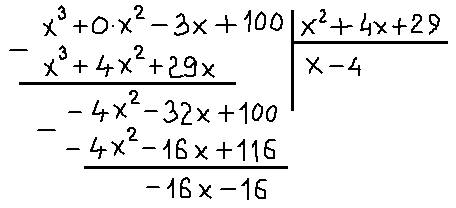
Всё. Деление закончено. Неполное частное х-4 — это целая часть, а остаток -16х-16 – это числитель правильной рациональной дроби. Поэтому после процедуры выделения целой части наша дробь распишется вот так:
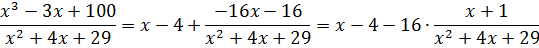
Поэтому, если бы перед нами стояла задача проинтегрировать эту дробь, то первым делом мы бы в уме проинтегрировали целую часть (многочлен х-4) и записали:
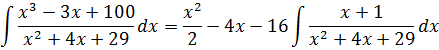
А уж что дальше делать с оставшейся непроинтегрированной правильной дробью, мы уже знаем! Выделяем полный квадрат в знаменателе и — вперёд по алгоритму! Желающие могут доинтегрировать.)
Ну, ладно. На сегодня отмучились! 🙂 На досуге порешайте следующие примерчики:
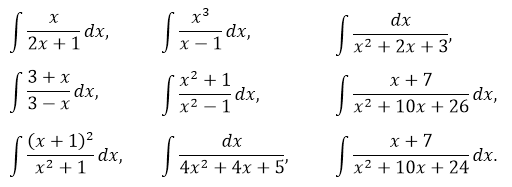
Ответы (как всегда, в беспорядке):