| Удельное электрическое сопротивление | |
|---|---|
 |
|
| Размерность |
СИ:L3MT-3I-2 СГС:T |
| Единицы измерения | |
| СИ | Ом·метр |
| СГС | с |
Уде́льное электри́ческое сопротивле́ние (удельное сопротивление) — физическая величина, характеризующая способность материала препятствовать прохождению электрического тока, выражается в Ом·метр. Удельное электрическое сопротивление принято обозначать греческой буквой ρ. Значение удельного сопротивления зависит от температуры в различных материалах по-разному: в проводниках, удельное электрическое сопротивление с повышением температуры возрастает, а в полупроводниках и диэлектриках — наоборот, уменьшается. Величина, учитывающая изменение электрического сопротивления от температуры называется температурный коэффициент удельного сопротивления. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле 

Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единицы измерения[править | править код]
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м[1]. Из соотношения 
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Зависимость от температуры[править | править код]
В проводниках удельное электрическое сопротивление увеличивается с увеличением температуры. Это объясняется тем, что с ростом температуры увеличивается интенсивность колебания атомов в узлах кристаллической решетки проводника, что препятствует движению свободных электронов[3].
В полупроводниках и диэлектриках удельное электрическое сопротивление уменьшается. Это объясняется тем, что с увеличением температуры увеличивается концентрация основных носителей заряда.
Величина, учитывающая изменение удельного электрического сопротивление от температуры называют температурным коэффициентом удельного сопротивления.
Обобщение понятия удельного сопротивления[править | править код]
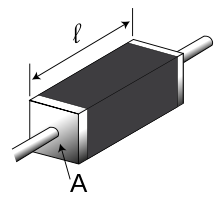
Кусок резистивного материала с электрическими контактами на обоих концах
Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля 


Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент 
В анизотропном, но однородном веществе тензор 
Тензор 



Как и для всякого симметричного тензора, для 
ортогональную систему декартовых координат, в которых матрица 






Величины 
Связь с удельной проводимостью[править | править код]
В изотропных материалах связь между удельным сопротивлением 

В случае анизотропных материалов связь между компонентами тензора удельного сопротивления 

Из этого равенства и приведённого ранее соотношения для 
где 

Удельное электрическое сопротивление некоторых веществ[править | править код]
Металлические монокристаллы[править | править код]
В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C[5].
| Кристалл | ρ1=ρ2, 10−8 Ом·м | ρ3, 10−8 Ом·м |
|---|---|---|
| Олово | 9,9 | 14,3 |
| Висмут | 109 | 138 |
| Кадмий | 6,8 | 8,3 |
| Цинк | 5,91 | 6,13 |
| Теллур | 2,90·109 | 5,9·109 |
Металлы и сплавы, применяемые в электротехнике[править | править код]
Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.
|
|
Значения даны при температуре t = 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Другие вещества[править | править код]
| Вещество | ρ, Ом·мм²/м |
|---|---|
| Сжиженные углеводородные газы | 0,84⋅1010 |
Тонкие плёнки[править | править код]
Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», 

См. также[править | править код]
- Электрическое сопротивление
- Сверхпроводимость
- Закон Ома
- Удельная проводимость
- Отрицательное сопротивление
- Импеданс
- Температурный коэффициент электрического сопротивления
Примечания[править | править код]
- ↑ 1 2 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с.
- ↑ Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд. — М.: Высшая школа, 1986. — 208 с.
- ↑ Давыдов А. С. Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с.
- ↑ Шувалов Л. А. и др. Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.
Литература[править | править код]
- Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд., переработанное и дополненное. — М.: Высшая школа, 1986. — С. 6—7. — 208 с.
Медь – основной материал для проводников
Квалифицированный выбор подходящего материала сопровождается комплексной оценкой нескольких факторов. Медный проводник не повреждается коррозией, потому что на поверхности образуется защитный слой из окислов. Структурная целостность сохраняется при малом радиусе поворота, после многократных изгибов. Отмеченные параметры пригодятся для оснащения помещений с повышенной влажностью и прокладки линий сложной конфигурации.
Тем не менее, главным преимуществом является малое сопротивление проводов из меди. Кроме улучшения токопроводимости с одновременным снижением потерь при передаче энергии, следует отметить уменьшение веса и размеров кабельной продукции, по сравнению с альтернативными вариантами.
Что такое сопротивление медного провода
В металлах ток образуется при появлении электрического поля. Оно «заставляет» двигаться электроны упорядоченно, в одном направлении. Электроны дальних орбит атома, слабо удерживаемые ядром, формируют ток.
При прохождении отрицательных частиц сквозь кристаллическую решетку молекул меди, они сталкиваются с атомами и другими электронами. Возникает препятствие или сопротивление направленному движению частиц.
Для оценки противодействия току была введена величина «электрическое сопротивление» или «электрический импеданс». Обозначается она буквой «R» или «r». Вычисляется сопротивление по формуле Георга Ома: R=, где U — разность потенциалов или напряжение, действующее на участке цепи, I — сила тока.
Важно! Чем выше значение импеданса металла, тем меньший ток проходит по нему, и именно медные проводники так широко распространены в электротехнике, благодаря этому свойству.
Исходя из формулы Ома, на величину тока влияет приложенное напряжение при постоянном R. Но резистентность медных проводов меняется, в зависимости от их физических характеристик и условий эксплуатации.
Природа сопротивления
Проводниками являются чистые металлы и их сплавы. В металле, фиксированные в единую «прочную» структуру атомы, обладают свободными электронами (так называемый «электронный газ»). Именно эти частицы в данном случае являются носителями заряда. Электроны находятся в постоянном беспорядочном движении от одного атома к другому. При появлении электрического поля (подключении к концам металла источника напряжения) движение электронов в проводнике становится упорядоченным. Движущиеся электроны встречают на своём пути препятствия, вызванные особенностями молекулярной структуры проводника. При столкновении со структурой носители заряда теряют свою энергию, отдавая её проводнику (нагревают его). Чем больше препятствий проводящая структура создаёт носителям заряда, тем выше сопротивление.
При увеличении поперечного сечения проводящей структуры для одного количества электронов «канал пропускания» станет шире, сопротивление уменьшится. Соответственно, при увеличении длины провода таких препятствий будет больше и сопротивление увеличится.
Таким образом, в базовую формулу для вычисления сопротивления входит длина провода, площадь поперечного сечения и некий коэффициент, связывающий эти размерные характеристики с электрическими величинами напряжения и тока. Этот коэффициент называют удельным сопротивлением. R= r*L/S.
Общие сведения об электрическом сопротивлении
Для начала следует рассмотреть понятие электрического сопротивления. Как известно, под действием электрического тока на проводник (а медь является одним из лучших металлов-проводников) часть электронов в нем покидают свое место в кристаллической решетке и устремляются по направлению к положительному полюсу проводника. Однако не все электроны покидают кристаллическую решетку, часть из них остаются в ней и продолжают совершать вращательное движение вокруг ядра атома. Вот эти электроны, а также атомы, расположенные в узлах кристаллической решетки, и создают электрическое сопротивление, препятствующее продвижению высвободившихся частиц.
Данный процесс, который мы вкратце обрисовали, характерен для любого металла, для меди в том числе. Естественно, что различные металлы, у каждого из которых особая форма и размеры кристаллической решетки, сопротивляются продвижению по ним электрического тока по-разному. Как раз эти различия и характеризует удельное сопротивление – показатель, индивидуальный для каждого металла.

Суть явления
Это величина, характерная для проводника, имеющего длину 1 метр и площадь поперечного сечения 1 квадратный метр/миллиметр. Ее обозначают греческой буквой ρ. Разным материалам свойственны разные удельные сопротивления. Вместе с тем сопротивление проводника будет меняться в прямой пропорциональности к длине и в обратной к площади поперечного сечения. То есть чем больше длина проводника, тем оно выше, но чем больше толщина, тем оно ниже.
Применение меди в электрических и электронных системах
Для того чтобы понять, причину популярности меди как материала для изготовления элементов электрических и электронных систем, достаточно посмотреть в таблице значение ее удельного сопротивления. У меди данный параметр равен 0,0175 Ом*мм2/метр. В этом отношении медь уступает только серебру.
Именно низкое удельное сопротивление, измеряемое при температуре 20 градусов Цельсия, является основной причиной того, что без меди сегодня не обходится практически ни одно электронное и электротехническое устройство. Медь – это основной материал для производства проводов и кабелей, печатных плат, электродвигателей и деталей силовых трансформаторов.
Низкое удельное сопротивление, которым характеризуется медь, позволяет использовать ее для изготовления электротехнических устройств, отличающихся высокими энергосберегающими свойствами. Кроме того, температура проводников из меди повышается очень незначительно при прохождении через них электрического тока.

Почему низкое удельное сопротивление – основная причина применения меди
С точки зрения физики, удельное сопротивление меди и других материалов показывает способность вещества препятствовать прохождению электрического тока, уровень потерь на единицу длины проводника. По сравнению с другими металлами, медь обладает низким удельным сопротивлением в 0,017, по данному показателю уступает только серебру. Благодаря подобным характеристикам медь является востребованным на рынке проводником:
- низкое удельное сопротивление гарантирует минимальный уровень потерь при прохождении электрического тока;
- внешние климатические нагрузки не оказывают значительного воздействия на технические характеристики металла;
- расчет сечения кабеля выполнить намного проще за счет минимальных потерь между входом и выходом;
- низкое сопротивление позволяет использовать для прокладки силовых, контрольных, специальных кабелей более тонкие проводники.
Стандартный медный провод поставляется в нескольких вариантах исполнения, отличается содержанием примесей, толщиной, характеристиками. При этом сопротивление меди может незначительно изменяться в зависимости от внешних условий.
Расчет сопротивления
Расчеты производятся при проектировании объектов разного назначения и использования, ведь жизнеобеспечение каждого происходит за счет электричества. Учитывается все, начиная с осветительных приборов, заканчивая технически сложным оборудованием. В домашних условиях также будет нелишним произвести расчет, особенно если предусматривается замена электропроводки. Для частного домостроения необходимо рассчитать нагрузку, иначе «кустарная» сборка электропроводки может привести к возгоранию.
Целью расчета является определение общего сопротивления проводников всех используемых устройств, учитывая их технические параметры. Оно вычисляется по формуле R=p*l/S, где:
R – вычисляемый результат;
p – показатель УЭС из таблицы;
l – длина провода (проводника);
S – диаметр сечения.
Что влияет на величину удельного сопротивления?
Важно знать, что существует зависимость величины удельного сопротивления от химической чистоты металла. При содержании в меди даже незначительного количества алюминия (0,02%) величина этого ее параметра может значительно возрасти (до 10%).
Влияет на этот коэффициент и температура проводника. Объясняется это тем, что при повышении температуры усиливаются колебания атомов металла в узлах его кристаллической решетки, что и приводит к тому, что коэффициент удельного сопротивления возрастает.
Именно поэтому во всех справочных таблицах значение данного параметра приведено с учетом температуры 20 градусов.
Единицы измерения
Практическое значение в технике имеет единица, равная миллионной доле ома, помноженного на метр (Ом-м), так как даже встретить провод с сечением, равным одному квадратному метру и более, довольно проблематично. Поэтому в измерениях обычно применяют микроом-метр (мкОм-м):
1 мкОм-м = 1×10^-6 Ом-м = 1 Ом-мм2/м
Как узнать сопротивление 1 метра медного провода
После выяснения всех факторов, влияющих на резистентность медного провода, можно объединить их в формуле зависимости сопротивления от сечения проводника и узнать, как вычислить этот параметр. Математическое выражение выглядит следующим образом: R= pl/s, где:
- ρ — удельное сопротивление;
- l — длина проводника, при нахождении сопротивления медного проводника длиной 1 м, l = 1;
- S— площадь поперечного сечения.
Вам это будет интересно Как проверить фазу и ноль
Для вычисления S, в случае провода цилиндрической формы, используется формула: S = π ∙ r2 = π d2/4 ≈ 0.785 ∙ d2, здесь:
- r — радиус сечения провода;
- d — его диаметр.
Если провод состоит из нескольких жил, то суммарная площадь будет равна: S = n d2/1,27, где n — количество жил.
Если проводник имеет прямоугольную форму, то S = a ∙ b, где a — ширина прямоугольника, b — длина.
Важно! Узнать диаметр сечения можно штангенциркулем. Если его нет под рукой, то намотать на любой стержень измеряемую проволоку, посчитать количество витков, желательно, чтобы их было не меньше 10 для большей точности. После этого измерить намотанную часть проводника, и разделить значение на количество витков.
Формула расчета удельного сопротивления
Расчет производят так:
ρ = (R * S) / L
, где R — сопротивление проводника (Ом); L — длина проводника (м); S — сечение проводника (мм2).
Таким образом ρ однокомпонентного отрезка провода, длина которого равняется 1 метру, а площадь поперечного сечения — 1 квадратному миллиметру, при R, равном 1 ому, составит 1 Ом-мм2/м.
R=(ρ?l)/S
где
- R — сопротивление,
- Ом; ρ — удельное сопротивление, (Ом•мм2)/м;
- l — длина провода, м;
- s — площадь сечения провода, мм2.
S=(π?d^2)/4=0.78?d^2≈0.8?d^2
- где d — это диаметр провода.
Измерить диаметр провода можно микрометром либо штангенциркулем,но если их нету под рукой,то можно плотно намотать на ручку (карандаш) около 20 витков провода, затем измерить длину намотанного провода и разделить на количество витков.
Для определения длинны провода,которая нужна для достижения необходимого сопротивления,можно использовать формулу:
l=(S?R)/ρ

Примечания:
1.Если данные для провода отсутствуют в таблице,то берется некоторое среднее значение.Как пример ,провод из никелина который имеет диаметр 0,18 мм площадь сечения равна приблизительно 0,025 мм2, сопротивление одного метра 18 Ом, а допустимый ток 0,075 А.
2.Данные последнего столбца,для другой плотности тока, необходимо изменить. Например при плотности тока 6 А/мм2, значение необходимо увеличить вдвое.
Пример 1. Давайте найдем сопротивление 30 м медного провода диаметром 0,1 мм.
Решение. С помощью таблицы берем сопротивление 1 м медного провода, которое равно 2,2 Ом. Значит, сопротивление 30 м провода будет R = 30•2,2 = 66 Ом.
Расчет по формулам будет выглядеть так: площадь сечения : s= 0,78•0,12 = 0,0078 мм2. Поскольку удельное сопротивление меди ρ = 0,017 (Ом•мм2)/м, то получим R = 0,017•30/0,0078 = 65,50м.
Пример 2. Сколько провода из манганина у которого диаметр 0,5 мм нужно чтобы изготовить реостат, сопротивлением 40 Ом?
Решение. По таблице выбираем сопротивление 1 м этого провода: R= 2,12 Ом: Чтобы изготовить реостат сопротивлением 40 Ом, нужен провод, длина которого l= 40/2,12=18,9 м.
Расчет по формулам будет выглядеть так. Площадь сечения провода s= 0,78•0,52 = 0,195 мм2. Длина провода l = 0,195•40/0,42 = 18,6 м.
Таблица удельного электрического сопротивления некоторых металлов
| Вид провода | ρ при 20℃, Ом-м |
| Серебряный | 1,59×10⁻⁸ |
| Медный | 1,67×10⁻⁸ |
| Золотой | 2,35×10⁻⁸ |
| Алюминиевый | 2,65×10⁻⁸ |
| Вольфрамовый | 5,65×10⁻⁸ |
| Никелевый | 6,84×10⁻⁸ |
| Железный | 9,7×10⁻⁸ |
| Платиновый | 1,06×10⁻⁷ |
| Стальной | 1,6×10⁻⁷ |
| Свинцовый | 2,06×10⁻⁷ |
| Дюралюминиевый | 4,0×10⁻⁷ |
| Нихромовый | 1,05×10⁻⁶ |
Удельное сопротивление абсолютно независимо от формы и размеров проводника, однако варьируется в широком диапазоне при отклонении температуры от принятого за стандартное значения, равного 20 градусам Цельсия. Практическим электротехническим путем доказано, что увеличение температуры повышает сопротивляемость металлов течению тока, с обратной стороны — вместе со снижением температуры она снижается. Примерно подсчитать, насколько существенным будет изменение, можно с учетом того, что всем металлам присущ почти одинаковый уровень прироста убыли данной величины, в среднем составляющий 0,4% на 1°С.
Если же данный показатель нужно определить точно, то можно воспользоваться этой формулой:
ρ = ρ0 x (1 + α x (t — t))
, где ρ и ρ0 — соответственно удельные сопротивления при температурах t и t (20°С, табличное значение), α — температурный коэффициент сопротивления.
| Вид провода | α |
| Никелевый | 0,005866 |
| Железный | 0,005671 |
| Молибденовый | 0,004579 |
| Вольфрамовый | 0,004403 |
| Алюминиевый | 0,004308 |
| Медный | 0,004041 |
| Серебряный | 0,003819 |
| Платиновый | 0,003729 |
| Золотой | 0,003715 |
| Цинковый | 0,003847 |
| Стальной | 0,003 |
| Нихромовый | 0,00017 |
Так, к примеру, найдя в таблицах удельное сопротивление меди при 20 градусах Цельсия и ее температурный коэффициент, можно вычислить, что при нагреве до 100℃ ее сопротивление вырастет на 32%. Практически то же самое будет происходить с удельным сопротивлением алюминиевого кабеля с тем же коэффициентом (0,004). А вот удельное сопротивление стали повысится менее значительно — на 24%.
С увеличением температуры проводник насыщается тепловой энергией, передающейся всем атомам вещества. Этим обуславливается повышение интенсивности их теплового движения. Последний фактор и приводит к повышению сопротивляемости движению свободных электронов в определенном направлении, поскольку возрастает вероятность встречи свободных электронов с атомами. Когда температура снижается, меньшее количество атомов может препятствовать направленному движению электронов, следовательно, происходит обратное. В результате колоссального спада температуры возникает интереснейшее явление, называемое «сверхпроводимостью металлов»: сопротивляемость уменьшается до нуля в условиях, близких к абсолютному нулю (-273,15℃). В таких кондициях атомы металла замирают на своих позициях, и электроны движутся без каких-либо препятствий.
Таблица удельных сопротивлений проводников
| Материал проводника | Удельное сопротивление ρ в |
| Серебро Медь Золото Латунь Алюминий Натрий Иридий Вольфрам Цинк Молибден Никель Бронза Железо Сталь Олово Свинец Никелин (сплав меди, никеля и цинка) Манганин (сплав меди, никеля и марганца) Константан (сплав меди, никеля и алюминия) Титан Ртуть Нихром (сплав никеля, хрома, железа и марганца) Фехраль Висмут Хромаль | 0,015 0,0175 0,023 0,025… 0,108 0,028 0,047 0,0474 0,05 0,054 0,059 0,087 0,095… 0,1 0,1 0,103… 0,137 0,12 0,22 0,42 0,43… 0,51 0,5 0,6 0,94 1,05… 1,4 1,15… 1,35 1,2 1,3… 1,5 |
Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм2 обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм2. Серебро — лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм2 обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:
где r — сопротивление проводника в омах; ρ — удельное сопротивление проводника; l — длина проводника в м; S — сечение проводника в мм2.
Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм2.
Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм2.
Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.
Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм2. Определить необходимую длину проволоки.
Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.
Пример 5. Проволока сечением 0,5 мм2 и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.
Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.
У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 — 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.
Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.
Температурный коэффициент сопротивления — это изменение сопротивления проводника при его нагревании, приходящееся на 1 Ом первоначального сопротивления и на 1° температуры, обозначается буквой α.
Если при температуре t0 сопротивление проводника равно r0, а при температуре t равно rt, то температурный коэффициент сопротивления
Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).
Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).
Сравнение проводимости меди и алюминия
Первый вывод можно сделать после изучения табличных данных. Сопротивление алюминия примерно на 80% выше, по сравнению с медью. В такой же пропорции хуже проводимость. Но для корректного анализа необходимо изучить дополнительно следующие факты:
- алюминий легче, но для получения аналогичных электрических параметров понадобится увеличить поперечное сечение (толщину проводника);
- медные изделия (многожильные кабели) не повреждаются неоднократным сгибанием;
- удельное сопротивление алюминия изменяется больше при повышении/ снижении температуры;
- пленка из окислов на его поверхности образуется быстрее, поэтому для надежности (долговечности) современную проводку делают из меди.
Влияние примесей на электропроводность меди
Конечно же, в наше время для выплавки этого красного металла используются гораздо более совершенные методики, чем в древности. Однако и сегодня получить совершенно чистый Cu практически невозможно. В меди всегда присутствуют разного рода примеси. Это могут быть, к примеру, кремний, железо или бериллий. Между тем, чем больше примесей в меди, тем меньше показатель ее электропроводности. Для изготовления проводов, к примеру, подходит только достаточно чистый металл. Согласно нормативам, для этой цели можно использовать медь с количеством примесей, не превышающем 0.1 %.
Очень часто в этом металле содержится определенный процент серы, мышьяка и сурьмы. Первое вещество значительно снижает пластичность материала. Электропроводность меди и серы сильно различается. Ток эта примесь совершенно не проводит. То есть является хорошим изолятором. Однако на электропроводность меди сера не влияет практически никак. То же самое касается и теплопроводности. С сурьмой и мышьяком наблюдается обратная картина. Эти элементы электропроводность меди способны снижать значительно.
Выбор сечения кабелей
Для крупных расчетов можно использовать специализированный калькулятор на справочном сайте либо соответствующее программное обеспечение. Следующий алгоритм применяют для последовательного вычисления рабочих параметров по формулам:
- при передаче в подключенную нагрузку мощности P = 1 600 Вт в линии с напряжением U = 220 V постоянный ток (I) определяют следующим образом: I = P/U ≈ 7,27А;
- сопротивление медного проводника (в обе стороны) длиной 800 м и сечением 2,5 мм кв.: R = (2*I*p)/S = (2*800*0,0175)/2,5 = 11,2 Ом;
- потери по напряжению в этой трассе: ΔU = (2*L*I)/((1/p)*S) = (2*800*7,27)/((1/0,0175)*2,5) = 11 520/ 142,86 = 80,63 V.
Удельное сопротивление
При необходимости последнее выражение несложно математически преобразовать для выбора площади поперечного сечения проводника по суммарному значению подключаемой нагрузки:
S = (2*I*L)/((1/p)*ΔU.
В рассмотренном примере потери напряжения составляют более 36%. Этот результат свидетельствует о необходимости корректировки расчета сопротивления проводника. По действующим нормативам допустимо уменьшение контрольного параметра не более, чем на 5 %. Увеличив диаметр провода, можно получить необходимый результат. При сечении 19 мм кв. напряжение уменьшится до 209,41 V (4,81%).
С учетом увеличенного сопротивления алюминиевого провода предполагаются пропорциональные изменения потерь. Выполнив аналогичный расчет, можно получить рекомендованное сечение 31 мм кв. Использование такого проводника в аналогичных условиях снизит напряжение до 209,2 V, что позволит обеспечить соответствие нормативам – 4,92%.
К сведению. Для проверки расчетных данных можно использовать мультиметр. Измерения выполняют в соответствующем диапазоне с учетом амплитуды сигнала, переменного (постоянного) тока.

При подключении источника питания переменного тока алгоритм вычислений усложняется. Для таких исходных условий пользуются формулой:
ΔU = ((Pа * Rа + Pр * Rи) *L)/ U,
где:
- Pа (Pр) – активная (реактивная) мощность;
- Rа (Rи) – относительное активное (индуктивное) сопротивление линии в Ом на километр.
Для определенных материалов проводников исходные данные берут из справочника. По аналогии с упомянутыми нормативами уменьшение напряжения не должно быть в общем случае более 5%. Дополнительные ограничения применяют с учетом особенностей электрических сетей и подключаемых потребителей (от 1% до 12%). Действующие правила уточняют по тексту последней редакции ПУЭ.
Приведенные итоги расчетов убедительно подтверждают преимущества меньшего удельного сопротивления медного провода. При использовании алюминиевого аналога значительно увеличивается количество материала для передачи электроэнергии с нормативными потерями. Для комплексного анализа следует учитывать лучшие показатели меди по прочности, гибкости.
Алюминий отличается меньшей стоимостью, легкостью. Но при работе с этим материалом следует исключить вибрационные воздействия и перемещения в процессе эксплуатации. Особо тщательно проектируют изгибы, чтобы сохранить целостность проводника. Электрический контакт нарушается образованием окислов на поверхности изделий, изготовленных из этого металла.
К сведению. В определенных ситуациях многое будет значить свободное место для прокладки трассы. По экономии пространства преимущественными параметрами обладает медь.
Выбор сечения проводника по допустимому нагреву
По мере увеличения силы тока повышается температура проводящего металла. На определенном уровне повреждается слой защитной изоляции, созданный из полимеров. Это провоцирует короткие замыкания и образование пламени. Опасные ситуации предотвращают корректным расчетом площади поперечного сечения. Определенное значение имеет способ прокладки (совместный/ раздельный).

Выбор сечения по потерям напряжения
Как показано в расчетах, при большой длине трасы нужно учитывать снижение напряжения и соответствующие энергетические потери. В крупных проектах рассматривают всю цепь тока с распределительными устройствами и подключаемыми нагрузками.

Для точного определения подходящей кабельной продукции рассматривают особенности процесса эксплуатации. Делают необходимый запас, чтобы предотвратить аварийные ситуации при подключении новых потребителей и бросках напряжения в сети питания.
Удельное сопротивление меди различных марок
Круглая медная проволока для проводов, кабелей и так далее бывает мягкой (марка ММ), твердой (марка МТ) и марки МС. Ее выпускают в диапазоне диаметров 0,02-9,42 мм. Удельное электрическое сопротивление проволоки постоянному току при 20℃ соответствует значениям, приведенным в таблице:
| Диаметр проволоки, мм | ρ при 20℃, мкОм-м | |
| ММ | МТ, МС | |
| Меньше 1,00 | — | 0,018 |
| 1,0-2,44 | 0,01724 | 0,0178 |
| 2,50 и больше | — | 0,0177 |
Преимущества меди в плане проводимости дают повод обширно применять ее на производстве проводников. Вместе с тем медь — относительно дорогой и дефицитный материал, поэтому ее все чаще заменяют другими металлами, включая алюминий.
Сплавы меди с оловом, хромом, кадмием и другие называют бронзами. Бронза при правильном подоборе состава очень выгодно отличается от чистой меди по части механических свойств.
Понятие электрического сопротивления
Этим термином называют свойство создавать препятствия прохождению в цепи электрического тока. Связь между физическими величинами описывается классической формулой R=U/I (обозначения сопротивления, напряжения и силы тока, соответственно). Движение электронов совершается под воздействием электромагнитного поля, разницы потенциалов. Повышает сопротивление металлов любое искажение кристаллической структуры молекулярной решетки. Данная причина объясняет сильную зависимость параметра от чистоты материала и температуры. Так, стандарты для трубной продукции допускают применение различных сплавов. Электротехническую медь (марка М006) создают с контролируемым количеством посторонних примесей не более 0,1%.
Квалифицированное применение этого материала предваряется оценкой всех значимых факторов. Кроме себестоимости, уточняют:
- особенности механической и других видов обработки;
- стабильность электрических параметров в определенных условиях эксплуатации;
- стойкость к внешним воздействиям, долговечность.
В некоторых ситуациях значительные начальные инвестиции оправданы продленным сроком службы, надежностью.
Сфера использования
Высокая тепло- и электропроводность меди определяет ее широкое применение в самых разных отраслях промышленности. Конечно же, чаще всего этот металл используется в электротехнике. Однако это далеко не единственная сфера его применения. Помимо всего прочего, медь может использоваться:
- в ювелирном деле;
- в архитектуре;
- при сборке водопроводных и отопительных систем;
- в газопроводах.
Для изготовления разного рода ювелирных изделий используется в основном сплав меди с золотом. Это позволяет увеличить стойкость украшений к деформациям и истиранию. В архитектуре медь может использоваться при облицовке кровель и фасадов. Основным преимуществом такой отделки является долговечность. К примеру, листами именно этого металла обшита крыша широко известной архитектурной достопримечательности — католического собора в немецком городе Хильдесхайме. Медная кровля этого здания надежно защищает его внутреннее пространство вот уже почти 700 лет.
Инженерные коммуникации
Основными преимуществами медных водопроводов также являются долговечность и надежность. Кроме того, этот металл способен придавать воде особые уникальные свойства, делая ее полезной для организма. Для сборки газопроводов и систем отопления медные трубы также подходят идеально — в основном благодаря своей коррозийной стойкости и пластичности. При аварийном повышении давления такие магистрали способны выдерживать гораздо большую нагрузку, чем стальные. Единственным недостатком медных трубопроводов является их дороговизна.
Кроме меди и алюминия, в электротехнике используются другие металлы и сплавы:
- Железо. Удельное сопротивление стали выше, но она прочнее, чем медь и алюминий. Стальные жилы вплетаются в кабеля, предназначенные для прокладки по воздуху. Сопротивление железа слишком велико для передачи электроэнергии, поэтому при расчёте сечения жилы не учитываются. Кроме того, оно более тугоплавкое, и из него изготавливаются вывода для подключения нагревателей в электропечах большой мощности;
- Нихром (сплав никеля и хрома) и фехраль (железо, хром и алюминий). Они обладают низкой проводимостью и тугоплавкостью. Из этих сплавов изготавливаются проволочные резисторы и нагреватели;
- Вольфрам. Его электросопротивление велико, но это тугоплавкий металл (3422 °C). Из него изготавливаются нити накала в электролампах и электроды для аргонно-дуговой сварки;
- Константан и манганин (медь, никель и марганец). Удельное сопротивление этих проводников не меняется при изменениях температуры. Применяются в претензионных приборах для изготовления резисторов;
- Драгоценные металлы – золото и серебро. Обладают самой высокой удельной проводимостью, но из-за большой цены их применение ограничено.
Материалы высокой проводимости
К наиболее широкораспрстраненным материалам высокой проводимости следует отнести медь и алюминий (Сверхпроводящие материалы, имеющие типичное сопротивление в 10-20 раз ниже обычных проводящих материалов (металлов) рассматриваются в разделе Сверхпроводимость).
Медь
Преимущества меди, обеспечивающие ей широкое применение в качестве проводникового материала, следующие:
- малое удельное сопротивление;
- достаточно высокая механическая прочность;
- удовлетворительная в большинстве случаев применения стойкость по отношению к коррозии;
- хорошая обрабатываемость: медь прокатывается в листы, ленты и протягивается в проволоку, толщина которой может быть доведена до тысячных долей миллиметра;
- относительная легкость пайки и сварки.
Медь получают чаще всего путем переработки сульфидных руд. После ряда плавок руды и обжигов с интенсивным дутьем медь, предназначенная для электротехнических целей, обязательно проходит процесс электролитической очистки.
В качестве проводникового материала чаще всего используется медь марок М1 и М0. Медь марки М1 содержит 99.9% Cu, а в общем количестве примесей (0.1%) кислорода должно быть не более 0,08%. Присутствие в меди кислорода ухудшает ее механические свойства. Лучшими механическими свойствами обладает медь марки М0, в которой содержится не более 0.05% примесей, в том числе не свыше 0.02% кислорода.
Медь является сравнительно дорогим и дефицитным материалом, поэтому она все шире заменяется другими металлами, особенно алюминием.
В отдельных случаях применяются сплавы меди с оловом, кремнием, фосфором, бериллием, хромом, магнием, кадмием. Такие сплавы, носящие название бронз, при правильно подобранном составе имеют значительно более высокие механические свойства, чем чистая медь.
Алюминий
Алюминий является вторым по значению после меди проводниковым материалом. Это важнейший представитель так называемых легких металлов: плотность литого алюминия около 2.6, а прокатанного — 2.7 Мг/м3. Т.о., алюминий примерно в 3.5 раза легче меди. Температурный коэффициент расширения, удельная теплоемкость и теплота плавления алюминия больше, чем меди. Вследствие высоких значений удельной теплоемкости и теплоты плавления для нагрева алюминия до температуры плавления и перевода в расплавленное состояние требуется большая затрата тепла, чем для нагрева и расплавления такого же количества меди, хотя температура плавления алюминия ниже, чем меди.
Алюминий обладает пониженными по сравнению с медью свойствами — как механическими, так и электрическими. При одинаковом сечении и длине электрическое сопротивление алюминиевого провода в 1.63 раза больше, чем медного. Весьма важно, что алюминий менее дефицитен, чем медь.
Для электротехнических целей используют алюминий, содержащий не более 0.5% примесей, марки А1. Еще более чистый алюминий марки АВ00 (не более 0.03% примесей) применяют для изготовления алюминиевой фольги, электродов и корпусов электролитических конденсаторов. Алюминий наивысшей чистоты АВ0000 имеет содержание примесей не более 0ю004%. Добавки Ni, Si, Zn или Fe при содержании их 0.5% снижают γ отожженного алюминия не более, чем на 2-3%. Более заметное действие оказывают примеси Cu, Ag и Mg, при том же массовом содержании снижающие γ алюминия на 5-10%. Очень сильно снижают электропроводность алюминия Ti и Mn.
Алюминий весьма активно окисляется и покрывается тонкой оксидной пленкой с большим электрическим сопротивлением. Эта пленка предохраняет металл от дальнейшей коррозии.
Алюминиевые сплавы обладают повышенной механической прочностью. Примером такого сплава является альдрей, содержащий 0.3-0.5% Mg, 0.4-0.7% Si и 0.2-0.3% Fe. В альдрее образуется соединение Mg2Si, которое сообщает высокие механические свойства сплаву.
Железо и сталь
Железо (сталь) как наиболее дешевый и доступный металл, обладающий к тому же высокой механической прочностью, представляет большой интерес для использования в качестве проводникового материала. Однако даже чистое железо имеет значительно более высокое сравнительно с медью и алюминием удельное сопротивление; ρ стали, т.е. железа с примесью углерода и других элементов, еще выше. Обычная сталь обладает малой стойкостью коррозии: даже при нормальной температуре, особенно в условиях повышенной влажности, она быстро ржавеет; при повышении температуры скорость коррозии резко возрастает. Поэтому поверхность стальных проводов должна быть защищена слоем более стойкого материала. Обычно для этой цели применяют покрытие цинком.
В ряде случаев для уменьшения расхода цветных металлов применяют так называемый биметалл. Это сталь, покрытая снаружи слоем меди, причем оба металла соединены друг с другом прочно и непрерывно.
Натрий
Весьма перспективным проводниковым материалом является металлический натрий. Натрий может быть получен электролизом расплавленного хлористого натрия NaCl в практически неограниченных количествах. Из сравнения свойств натрия со свойствами других проводниковых металлов видно, что удельное сопротивление натрия примерно в 2.8 раза больше ρ меди и в 1.7 раз больше ρ алюминия, но благодаря чрезвычайно малой плотности натрия (плотность его почти в 9 раз меньше плотности меди), провод из натрия при данной проводимости на единицу длины должен быть значительно легче, чем провод из любого другого металла. Однако натрий чрезвычайно активен химически (он интенсивно окисляется на воздухе, бурно реагирует с водой), почему натриевый провод должен быть защищен герметизирующей оболочкой. Оболочка должна придавать проводу необходимую механическую прочность, так как натрий весьма мягок и имеет малый предел прочности при деформациях.
Источники
- https://amperof.ru/bezopasnost/udelnoe-soprotivlenie-medi.html
- https://rusenergetics.ru/polezno-znat/soprotivlenie-mednogo-provoda-tablitsa
- https://molotok34.ru/spravochnik/udelnoe-soprotivlenie-medi.html
- http://met-all.org/cvetmet-splavy/med/udelnoe-soprotivlenie-medi.html
- https://rusenergetics.ru/ustroistvo/udelnoe-soprotivlenie-medi
- https://ntcm.ru/info/udelnoe-soprotivlenie-medi/
- https://www.calc.ru/Soprotivleniye-Provoda.html
- https://msmetall.ru/metally/provodimost-stali.html
- https://elquanta.ru/teoriya/udelnoe-soprotivlenie-medi.html
- http://bourabai.kz/toe/resistance.htm
- https://PlazmoSvarka.ru/metally/soprotivlenie-medi.html
Что такое сопротивление медного провода
В металлах ток образуется при появлении электрического поля. Оно «заставляет» двигаться электроны упорядоченно, в одном направлении. Электроны дальних орбит атома, слабо удерживаемые ядром, формируют ток.

При прохождении отрицательных частиц сквозь кристаллическую решетку молекул меди, они сталкиваются с атомами и другими электронами. Возникает препятствие или сопротивление направленному движению частиц.
Для оценки противодействия току была введена величина «электрическое сопротивление» или «электрический импеданс». Обозначается она буквой «R» или «r». Вычисляется сопротивление по формуле Георга Ома: R=, где U — разность потенциалов или напряжение, действующее на участке цепи, I — сила тока.

Важно! Чем выше значение импеданса металла, тем меньший ток проходит по нему, и именно медные проводники так широко распространены в электротехнике, благодаря этому свойству.
Исходя из формулы Ома, на величину тока влияет приложенное напряжение при постоянном R. Но резистентность медных проводов меняется, в зависимости от их физических характеристик и условий эксплуатации.
От чего зависит сопротивление
Так как мы говорим о медном проводе, то первое от чего зависит этот физический параметр, это медь, то есть, сырьевой материал. Второе – это размеры проводника, а, точнее, его диаметр или сечение (обе величины связаны между собой формулой).
Конечно, есть дополнительные физические величины, которые влияют на сопротивление проводника. К примеру, температура окружающей среды. Ведь известно, что при повышении температуры самого провода, его сопротивление увеличивается. А так как этот показатель находится в обратной зависимости от силы (плотность) тока, соответственно ток при повышении сопротивления, наоборот, снижается. Правда, это относится к тем металлам, которые являются обладателями положительного температурного коэффициента. Для примера можно привести сплав вольфрама, который используется для нити накала лампочки. Такому материалу изменения силы (плотность) тока не страшны при высоком нагреве, потому что этот металл обладает отрицательным температурным коэффициентом.
Что влияет на сопротивление медного провода
Электрический импеданс медного кабеля зависит от нескольких факторов:
- Удельного сопротивления;
- Площади сечения проволоки;
- Длины провода;
- Внешней температуры.
Последним пунктом можно пренебречь в условиях бытового использования кабеля. Заметное изменение импеданса происходит при температурах более 100°C.

Удельное сопротивление в системе СИ обозначается буквой ρ. Оно определяется, как величина сопротивления проводника, имеющего сечение 1 м2 и длину 1 м, измеряется в Ом ∙ м2. Такая размерность неудобна в электротехнических расчетах, поэтому часто используется единица измерения Ом ∙ мм2.
Вам это будет интересно Описание установленной и расчетной мощности
Важно! Данный параметр является характеристикой вещества — меди. Он не зависит от формы или площади сечения. Чистота меди, наличие примесей, метод изготовления проволоки, температура проводника — факторы, влияющие на удельное сопротивление.
Зависимость параметра от температуры описывается следующей формулой: ρt= ρ20[1+ α(t−20°C)]. Здесь ρ20— удельное сопротивление меди при 20°C, α— эмпирически найденный коэффициент, от 0°Cдо 100°C для меди имеет значение, равное 0,004 °C-1, t — температура проводника.
Ниже приведена таблица значений ρ для разных металлов при температуре 20°C.

Согласно таблице, медь имеет низкое удельное сопротивление, ниже только у серебра. Это обуславливает хорошую проводимость металла.
Чем толще провод, тем меньше его резистентность. Зависимость R проводника от сечения называется «обратно пропорциональной».
Важно! При увеличении поперечной площади кабеля, электронам легче проходить сквозь кристаллическую решетку. Поэтому, при увеличении нагрузки и возрастании плотности тока, следует увеличить площадь сечения.
Увеличение длины медного кабеля влечет рост его резистентности. Импеданс прямо пропорционален протяженности провода. Чем длиннее проводник, тем больше атомов встречаются на пути свободных электронов.

Последним элементом, влияющим на резистентность меди, является температура среды. Чем она выше, тем большую амплитуду движения имеют атомы кристаллической решетки. Тем самым, они создают дополнительное препятствие для электронов, участвующих в направленном движении.
Важно! Если понизить температуру до абсолютного нуля, имеющего значение 0° Kили -273°C, то будет наблюдаться обратный эффект — явление сверхпроводимости. В этом состоянии вещество имеет нулевое сопротивление.

Удельное сопротивление
Удельное сопротивление (ρ) — это единица, показывающая способность проводника затруднять прохождение электрического тока.
С помощью него можно оценивать параметры электрических проводников из разных материалов. ρ проводника всегда увеличивается при увеличении длины и уменьшении сечения, в интернациональной системе длина проводника равна 1 метру, а сечение -1 мм2.
Похожее: Как подключить розетку от выключателя

Как узнать сопротивление 1 метра медного провода
После выяснения всех факторов, влияющих на резистентность медного провода, можно объединить их в формуле зависимости сопротивления от сечения проводника и узнать, как вычислить этот параметр. Математическое выражение выглядит следующим образом: R= pl/s, где:
- ρ — удельное сопротивление;
- l — длина проводника, при нахождении сопротивления медного проводника длиной 1 м, l = 1;
- S— площадь поперечного сечения.
Вам это будет интересно Сколько люменов в 100 ватной лампе
Для вычисления S, в случае провода цилиндрической формы, используется формула: S = π ∙ r2 = π d2/4 ≈ 0.785 ∙ d2, здесь:
- r — радиус сечения провода;
- d — его диаметр.
Если провод состоит из нескольких жил, то суммарная площадь будет равна: S = n d2/1,27, где n — количество жил.
Если проводник имеет прямоугольную форму, то S = a ∙ b, где a — ширина прямоугольника, b — длина.
Важно! Узнать диаметр сечения можно штангенциркулем. Если его нет под рукой, то намотать на любой стержень измеряемую проволоку, посчитать количество витков, желательно, чтобы их было не меньше 10 для большей точности. После этого измерить намотанную часть проводника, и разделить значение на количество витков.

Формула сопротивления
Ток обусловлен движением электронов. Классическая формула, используемая для расчёта его силы была выведена немецким физиком Омом. Он на опыте смог подтвердить зависимость между собой тока, сопротивления и напряжения. В математическом виде связь записывают в виде формулы: I = U /R.
Согласно закону Ома, сопротивление тела электрическому току прямо пропорционально его силе и обратно пропорционально напряжению: R = I / U. Это эмпирическая формула справедлива для любого участка цепи.

Подвижные носители при хаотичном движении ведут себя как молекулы газа, поэтому в первом приближении физики считают носителей зарядов своего рода электронным газом. Как было установлено эмпирически, плотность этого газа и строение кристаллической решётки зависят от рода проводника. Соответственно, проводимость, а значит и сопротивление, определяется также и родом вещества. В свою очередь, физическое тело характеризуется и геометрическими параметрами.
Влияние размеров полупроводника объясняется зависимостью от них поперечного сечения. При его уменьшении поток зарядов становится плотнее, степень взаимодействия между частицами возрастает. Полная формула сопротивления проводника с учётом поперечного сечения выглядит так: R = (p * l) / S. Из неё становится ясно, что проводимость прямо пропорциональна площади сечения и обратно пропорциональна длине проводника.
Удельное электрическое сопротивление для многих веществ было установлено во время исследований. Существуют таблицы, в которые занесены данные, измеренные при температуре 20 градусов Цельсия. Ими часто пользуются при решении различных задач, связанных с электричеством. Вот некоторые из них:
- олово — 9,9 * 10-8 Ом * мм2/м;
- медь — 0,01724 Ом * мм2/м;
- алюминий — 0,0262 Ом * мм 2/м;
- железо — 0,098 * Ом * мм2/м;
- золото — 0,023 Ом * мм2/м.

Для проводников характерно увеличение сопротивления при росте температуры. Это связано с колебаниями атомов. В то же время с ростом температуры проводимость в полупроводниках и диэлектриках возрастает из-за увеличения концентрации носителей заряда.
Удельное сопротивление для неоднородного материала можно вычислить по формуле: p = E / J. Где: E и J напряжённость и плотность тока в конкретной точке.
Как правильно рассчитать сопротивление провода по сечению
Проектируя электрическую сеть, необходимо правильно подобрать сечение кабеля, чтобы его резистентность не была высокой. Большой импеданс вызовет падение напряжения выше допустимого значения. В результате подключенное к сети электрическое устройство может не заработать. Также, провода начнут перегреваться.
Для правильного расчета минимального сечения необходимо учесть следующие факторы:
- По стандартам ПУЭ падение напряжения не должно быть больше 5%.
- В бытовых условиях ток проходит по двум проводам. Поэтому, при расчете величину сопротивления нужно умножить на 2.
- Учитывать нужно мощность всех подключенных приборов на линии. Для развития предусмотреть запас по нагрузке.
Как вычислить сопротивление проводника по формуле? Для примера можно рассмотреть задачу. Требуется определить: достаточно ли будет медного кабеля сечением 2,5 мм2 и длиной 30 метров для подключения оборудования мощностью 9 кВт.

Задача решается следующим образом:
- Резистентность медного кабеля будет равна:
2 ∙ (ρ ∙ L) / S = 2 ∙ (0,0175 ∙ 30) / 2,5 = 0,42 Ом.
- Для нахождения падения напряжения нужно определить силу тока, по формуле: I= P/U.
Вам это будет интересно Особенности DC тока
Здесь P — суммарная мощность оборудования, U — напряжение в цепи. Тогда сила тока будет равна: I = 9000 / 220 = 40,91 А.
- Используя закон Ома, можно найти падение напряжения по кабелю: ΔU = I ∙ R = 40, 91 ∙ 0,42 = 17,18 В.
- От 220 В процент падения составит: U% = (ΔU / U) ∙ 100% = (17,18 / 220) ∙ 100% = 7, 81%>5%.
Падение напряжение выходит за пределы допустимого значения, значит необходимо использовать кабель большего сечения.
Особенности активного сопротивления
Сопротивление в электротехнике является важнейшим параметром, с помощью которого какая-то часть электрической цепи оказывает противодействие проходящему по ней току. Образованию данной величины способствуют изменения электроэнергии и ее переход в другие виды энергетических состояний.

Подобное явление характерно лишь для переменного тока, под действием которого образуются активные и реактивные сопротивления кабелей. Этот процесс представляет собой необратимые изменения энергии или передачу и распределение ее между отдельными элементами цепи. Если изменения электроэнергии принимают необратимый характер, то такое сопротивление будет активным, а если имеют место обменные процессы, оно становится реактивным. Например, электрическая плита выделяет тепло, которое обратно в электрическую энергию уже не превращается.
Данное явление в полной мере затрагивает любые виды провода и кабеля. При одинаковых условиях, они будут по-разному сопротивляться прохождению постоянного и переменного тока. Подобная ситуация возникает из-за неравномерного распределения переменного тока по сечению проводника, в результате чего образуется так называемый поверхностный эффект.
Таблица сопротивления медного провода
Узнать резистентность проводника можно по таблицам. В них содержатся готовые результаты вычислений для разных кабелей.

Например, сопротивление меди на метр для различных сечений можно определить без вычислений, из соответствующей таблицы.

Важно! Таблицы не содержат данные о всех сечениях. Если нужно узнать величину импеданса для неуказанного кабеля, то находится среднее значение между двумя ближайшими известными сопротивлениями.

Расчет сопротивления кабеля является важной задачей при проектировании электрической системы. Воспользовавшись формулами или таблицами, можно успешно ее решить.
Активные и индуктивные сопротивления проводов СИП-1, СИП-2, СИП-4
Значения активных и индуктивных сопротивлений для проводов СИП-1, СИП-2 и СИП-4 приведены в ТУ 16-705.500-2006 «Провода самонесущие изолированные и защищенные для воздушных линий электропередач» таблицы Б.1, Б.2.

Примеры решения задач
Решение примеров позволяет лучше разобраться в теме. При этом не только быстрее запоминаются формулы, но и становится понятным, где можно использовать полученные знания. Существует ряд заданий для самостоятельной проработки. Вот некоторые из них:

- На катушку электромагнита намотан медный провод сечением 0,003 мм2 длиною 200 метров. Найти сопротивление и массу обмотки. Для решения задачи нужно воспользоваться справочником по электрофизике. Из него взять значение удельного сопротивления меди и её плотность. Согласно справочным данным: p = 1,7 * 10−8 Ом * м, а V = 8900 кг/м3. В первом действии нужно определить массу. Для этого выразить её из формулы f = m / V и подставить заданные значения: m = V * f = l * S * f = 2 * 10|2 м * 3 * 10-8 м2 8,9 * 103 кг/м3 = 53,4 грамма. Теперь можно определить искомое сопротивление по формуле: R = (f * l) / S = (0,017 (Ом * мм2) / м * 200 м) / 0,03 мм2 = 3,4 / 0,003 = 113 Ом.
- Нужно изготовить провод длиною 100 метров и сопротивлением 1 Ом. Определить, из какого материала вес изделия будет меньше: меди или алюминия. Нужно вычислить, чему будет равно отношение масс: MCu / MAl. Из справочника взять данные: fAl = 2700 кг/м3; fCu = 8900 кг/м3; pAl = 2,8 * 10−8 Ом/м; pCu = 1,7 10−8 Ом/м. Для решения нужно выразить массы через плотность, длину и площадь поперечного сечения: m = f *l * S. Длина одинаковая, значит, отношения масс примет вид: (fCu * SCu) / (fAl * SAl). Площадь поперечного сечения будет вычисляться из правила нахождения сопротивления. Конечная формула примет вид: MCu / Mal = (fCu * RCu) / (fAl * RAl) = (8900 * 1,7) / (2700 * 2,8) = 2. Изделие из алюминия будет весить в 2 раза меньше.
- Имеется электрическая цепь, подключённая к сети 120 В. Если к ней подключить 2 последовательных сопротивления ток будет равен 3 A, а если параллельно — 16 А. Найти сопротивление. Задача решается с помощью закона Ома и формул вычисления сопротивления цепи: Iпосл = U / (r1 + r2); Iпар = U * (r1 + r2) / r1 * r2. Из них можно выразить искомые величины: r1 + r2 = U /Iпосл и r1 * r2 = U2 / Iпар * Iпос. Выполнив вычисления, можно найти, что r1 = 30 Ом, r2 = 10 Ом.
Решение заданий по теме обычно не вызывает трудностей. Нужно лишь внимательно переводить единицы измерения, знать формулы и иметь радиофизический справочник.
Что такое удельное сопротивление
Для начала следует рассмотреть понятие электрического сопротивления. Как известно, под действием электрического тока на проводник (а медь является одним из лучших металлов-проводников) часть электронов в нем покидают свое место в кристаллической решетке и устремляются по направлению к положительному полюсу проводника. Однако не все электроны покидают кристаллическую решетку, часть из них остаются в ней и продолжают совершать вращательное движение вокруг ядра атома. Вот эти электроны, а также атомы, расположенные в узлах кристаллической решетки, и создают электрическое сопротивление, препятствующее продвижению высвободившихся частиц.
Данный процесс, который мы вкратце обрисовали, характерен для любого металла, для меди в том числе. Естественно, что различные металлы, у каждого из которых особая форма и размеры кристаллической решетки, сопротивляются продвижению по ним электрического тока по-разному. Как раз эти различия и характеризует удельное сопротивление – показатель, индивидуальный для каждого металла.
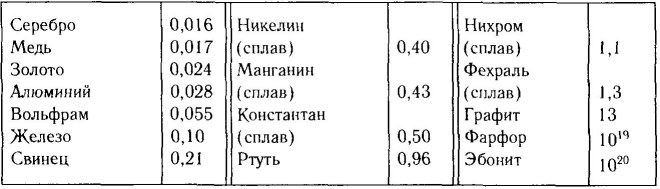
Удельное электрическое сопротивление некоторых веществ
Понятие удельного электрического сопротивления вещества следует из определения электрического сопротивления проводника R с геометрическими размерами L (длина) и S (поперечное сечение):
$ ρ = R * { S over L } $ (1).
Удельное электрическое сопротивление меди получают, пользуясь результатами измерений вольт-амперных U(I) характеристик на образцах меди различных размеров. Измерив вольтметром напряжение U, амперметром величину тока I, и применив формулу закона Ома, рассчитывают величину сопротивления образца меди:
$ R = { U over I } $ (2).
Далее, с помощью формулы (1), вычисляется величина ρ.
Медь – это один из самых первых металлов, который человек научился добывать и обрабатывать. Период с IV по III тысячелетие до н.э. называют медным веком. Считается, что в это время люди научились делать первые предметы и орудия труда из меди. Применение меди в электротехнике началось только в начале XIX века.
Медь: электропроводность материала
В спокойном состоянии все свободные электроны любого металла вращаются вокруг ядра. При подключении внешнего источника воздействия они выстраиваются в определенной последовательности и становятся носителями тока. Степень способности металла пропускать сквозь себя последний и называется электропроводностью. Единицей ее измерения в Международной СИ является сименс, определяемый как 1 См = 1 Ом-1.
Электропроводность меди очень высока. По этому показателю она превосходит все известные на сегодня неблагородные металлы. Лучше нее ток пропускает только серебро. Показатель электропроводности меди составляет 57х104 см-1 при температуре в +20 °С. Благодаря такому своему свойству этот металл на данный момент является самым распространенным проводником из всех используемых в производственных и бытовых целях.
Медь отлично выдерживает постоянные электрические нагрузки и к тому же отличается надежностью и долговечностью. Помимо всего прочего, этот металл характеризуется и высокой температурой плавления (1083,4 °С). А это, в свою очередь, позволяет меди долгое время работать в нагретом состоянии. По распространенности в качестве проводника тока конкурировать с этим металлом может только алюминий.
Сфера использования
Высокая тепло- и электропроводность меди определяет ее широкое применение в самых разных отраслях промышленности. Конечно же, чаще всего этот металл используется в электротехнике. Однако это далеко не единственная сфера его применения. Помимо всего прочего, медь может использоваться:
- в ювелирном деле;
- в архитектуре;
- при сборке водопроводных и отопительных систем;
- в газопроводах.
Для изготовления разного рода ювелирных изделий используется в основном сплав меди с золотом. Это позволяет увеличить стойкость украшений к деформациям и истиранию. В архитектуре медь может использоваться при облицовке кровель и фасадов. Основным преимуществом такой отделки является долговечность. К примеру, листами именно этого металла обшита крыша широко известной архитектурной достопримечательности — католического собора в немецком городе Хильдесхайме. Медная кровля этого здания надежно защищает его внутреннее пространство вот уже почти 700 лет.
Применение меди в электрических и электронных системах
Для того чтобы понять, причину популярности меди как материала для изготовления элементов электрических и электронных систем, достаточно посмотреть в таблице значение ее удельного сопротивления. У меди данный параметр равен 0,0175 Ом*мм2/метр. В этом отношении медь уступает только серебру.
Именно низкое удельное сопротивление, измеряемое при температуре 20 градусов Цельсия, является основной причиной того, что без меди сегодня не обходится практически ни одно электронное и электротехническое устройство. Медь – это основной материал для производства проводов и кабелей, печатных плат, электродвигателей и деталей силовых трансформаторов.
Низкое удельное сопротивление, которым характеризуется медь, позволяет использовать ее для изготовления электротехнических устройств, отличающихся высокими энергосберегающими свойствами. Кроме того, температура проводников из меди повышается очень незначительно при прохождении через них электрического тока.
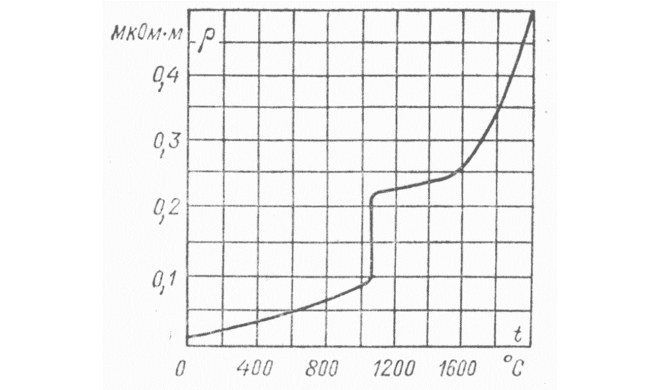
Зависимость сопротивления меди от температуры
Какое сопротивление меди и алюминия
Алюминий — это легкий металл, который легко поддается обработке и литью. Обладает высокой электропроводностью: он стоит на 4 месте после серебра, меди и золота.
Важно! Несмотря на ряд достоинств (невысокую стоимость, малый вес, простоту обработки и другие) в долгосрочной перспективе алюминиевые провода менее выгодны, чем медные.
В электротехнике значение имеют 2 термина:
- Электропроводность: отвечает за передачу тока от одной точки к другой. Чем выше проводимость металла, тем лучше он передает электричество. При +20 градусах проводимость меди составляет 59,5 миллионов сименс на метр (См/м), алюминия — 38 миллионов См/м. Проводимость медного кабеля практически не зависит от температуры.
- Электросопротивление: чем выше это понятие, тем хуже вещество будет пропускать ток. Удельное сопротивление меди составляет 0,01724-0,0180 мкОм/м, алюминия — 0,0262-0,0295.

Алюминиевые кабели востребованы не меньше медных
Иными словами, медь обладает более высокой проводимостью и меньшим сопротивлением, чем алюминий.
Что влияет на сопротивление медного провода
Важно знать, что существует зависимость величины удельного сопротивления от химической чистоты металла. При содержании в меди даже незначительного количества алюминия (0,02%) величина этого ее параметра может значительно возрасти (до 10%).
Влияет на этот коэффициент и температура проводника. Объясняется это тем, что при повышении температуры усиливаются колебания атомов металла в узлах его кристаллической решетки, что и приводит к тому, что коэффициент удельного сопротивления возрастает.
Именно поэтому во всех справочных таблицах значение данного параметра приведено с учетом температуры 20 градусов.
Электрический импеданс медного кабеля зависит от нескольких факторов:
- Удельного сопротивления;
- Площади сечения проволоки;
- Длины провода;
- Внешней температуры.
Последним пунктом можно пренебречь в условиях бытового использования кабеля. Заметное изменение импеданса происходит при температурах более 100°C.

Зависимость сопротивления
Удельное сопротивление в системе СИ обозначается буквой ρ. Оно определяется, как величина сопротивления проводника, имеющего сечение 1 м2 и длину 1 м, измеряется в Ом ∙ м2. Такая размерность неудобна в электротехнических расчетах, поэтому часто используется единица измерения Ом ∙ мм2.
Вам это будет интересно Определение плюса и минуса в электротехнике
Важно! Данный параметр является характеристикой вещества — меди. Он не зависит от формы или площади сечения. Чистота меди, наличие примесей, метод изготовления проволоки, температура проводника — факторы, влияющие на удельное сопротивление.
Зависимость параметра от температуры описывается следующей формулой: ρt= ρ20[1+ α(t−20°C)]. Здесь ρ20— удельное сопротивление меди при 20°C, α— эмпирически найденный коэффициент, от 0°Cдо 100°C для меди имеет значение, равное 0,004 °C-1, t — температура проводника.
Ниже приведена таблица значений ρ для разных металлов при температуре 20°C.
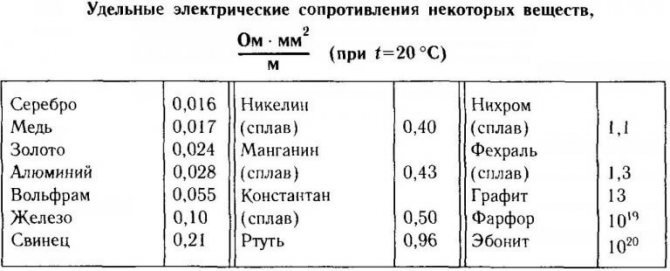
Таблица удельного сопротивления
Согласно таблице, медь имеет низкое удельное сопротивление, ниже только у серебра. Это обуславливает хорошую проводимость металла.
Чем толще провод, тем меньше его резистентность. Зависимость R проводника от сечения называется «обратно пропорциональной».
Важно! При увеличении поперечной площади кабеля, электронам легче проходить сквозь кристаллическую решетку. Поэтому, при увеличении нагрузки и возрастании плотности тока, следует увеличить площадь сечения.
Увеличение длины медного кабеля влечет рост его резистентности. Импеданс прямо пропорционален протяженности провода. Чем длиннее проводник, тем больше атомов встречаются на пути свободных электронов.

Выводы
Последним элементом, влияющим на резистентность меди, является температура среды. Чем она выше, тем большую амплитуду движения имеют атомы кристаллической решетки. Тем самым, они создают дополнительное препятствие для электронов, участвующих в направленном движении.
Важно! Если понизить температуру до абсолютного нуля, имеющего значение 0° Kили -273°C, то будет наблюдаться обратный эффект — явление сверхпроводимости. В этом состоянии вещество имеет нулевое сопротивление.
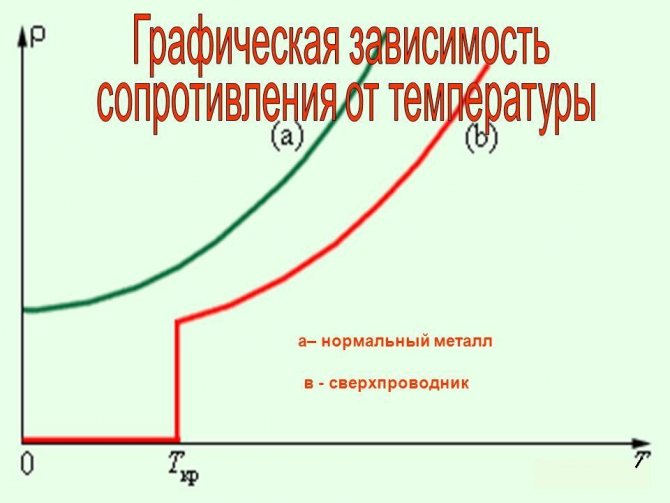
Температурная корреляция
Какое удельное сопротивление стали
Сталь — это металлический сплав железа с углеродом и другими элементами. В ее состав входит не менее 45% железа, содержание углерода колеблется от 0,02% до 2,14%. В зависимости от точного состава сталь используется в строительстве, машиностроении и приборостроении, а также во многих областях, например, в транспорте, народном хозяйстве, при производстве бытовых приборов.

Стальные провода отличаются невысокой проводимостью
Проводимость стали составляет всего 7,7 миллионов См/м, удельное сопротивление — 0,13 мкОм/м, то есть оно довольно высоко. Сталь плохо проводит электричество и не применяется при производстве непосредственно кабелей. Однако нередко можно встретить внешнюю оцинкованную стальную оплетку, которая защищает провода от механического растяжения. Такая защита нужна, если кабель проходит под дорогой или на нестабильном грунте, если есть риск резко дернуть провод.
Также из стали делают ПНСВ — провод нагревательный со стальной жилой, имеющий изоляцию из винила. Его размещают внутри конструкции до заливания бетона и используют в дальнейшем для электрообогрева готового блока. Электричество кабель практически не проводит.

Из стали производят провод ПНСВ
Как рассчитать общее сопротивление проводника?
Знать, чему равно удельное сопротивление, важно для того, чтобы проводить предварительные расчеты параметров электротехнического оборудования при его проектировании. В таких случаях определяют общее сопротивление проводников проектируемого устройства, обладающих определенными размерами и формой. Посмотрев значение удельного сопротивления проводника по справочной таблице, определив его размеры и площадь поперечного сечения, можно рассчитать величину его общего сопротивления по формуле:
R = p*l/S
В данной формуле используются следующие обозначения:
- R — общее сопротивление проводника, которое и необходимо определить;
- p — удельное сопротивление металла, из которого изготовлен проводник (определяют по таблице);
- l — длина проводника;
- S — площадь его поперечного сечения.
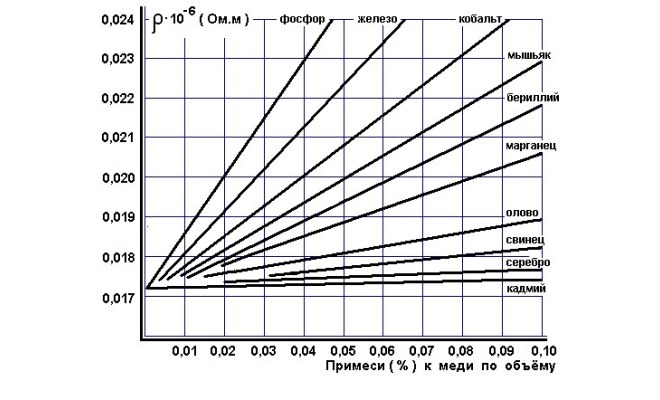
Влияние примесей на удельное сопротивление меди
Как узнать сопротивление 1 метра медного провода
После выяснения всех факторов, влияющих на резистентность медного провода, можно объединить их в формуле зависимости сопротивления от сечения проводника и узнать, как вычислить этот параметр. Математическое выражение выглядит следующим образом: R= pl/s, где:
- ρ — удельное сопротивление;
- l — длина проводника, при нахождении сопротивления медного проводника длиной 1 м, l = 1;
- S— площадь поперечного сечения.
Вам это будет интересно Сколько люменов в 100 ватной лампе
Для вычисления S, в случае провода цилиндрической формы, используется формула: S = π ∙ r2 = π d2/4 ≈ 0.785 ∙ d2, здесь:
- r — радиус сечения провода;
- d — его диаметр.
Если провод состоит из нескольких жил, то суммарная площадь будет равна: S = n d2/1,27, где n — количество жил.
Если проводник имеет прямоугольную форму, то S = a ∙ b, где a — ширина прямоугольника, b — длина.
Важно! Узнать диаметр сечения можно штангенциркулем. Если его нет под рукой, то намотать на любой стержень измеряемую проволоку, посчитать количество витков, желательно, чтобы их было не меньше 10 для большей точности. После этого измерить намотанную часть проводника, и разделить значение на количество витков.

Вычисление площади сечения
Формула сопротивления
Ток обусловлен движением электронов. Классическая формула, используемая для расчёта его силы была выведена немецким физиком Омом. Он на опыте смог подтвердить зависимость между собой тока, сопротивления и напряжения. В математическом виде связь записывают в виде формулы: I = U /R.
Согласно закону Ома, сопротивление тела электрическому току прямо пропорционально его силе и обратно пропорционально напряжению: R = I / U. Это эмпирическая формула справедлива для любого участка цепи.
Подвижные носители при хаотичном движении ведут себя как молекулы газа, поэтому в первом приближении физики считают носителей зарядов своего рода электронным газом. Как было установлено эмпирически, плотность этого газа и строение кристаллической решётки зависят от рода проводника. Соответственно, проводимость, а значит и сопротивление, определяется также и родом вещества. В свою очередь, физическое тело характеризуется и геометрическими параметрами.
Влияние размеров полупроводника объясняется зависимостью от них поперечного сечения. При его уменьшении поток зарядов становится плотнее, степень взаимодействия между частицами возрастает. Полная формула сопротивления проводника с учётом поперечного сечения выглядит так: R = (p * l) / S. Из неё становится ясно, что проводимость прямо пропорциональна площади сечения и обратно пропорциональна длине проводника.
Удельное электрическое сопротивление для многих веществ было установлено во время исследований. Существуют таблицы, в которые занесены данные, измеренные при температуре 20 градусов Цельсия. Ими часто пользуются при решении различных задач, связанных с электричеством. Вот некоторые из них:
- олово — 9,9 * 10-8 Ом * мм2/м;
- медь — 0,01724 Ом * мм2/м;
- алюминий — 0,0262 Ом * мм 2/м;
- железо — 0,098 * Ом * мм2/м;
- золото — 0,023 Ом * мм2/м.
Для проводников характерно увеличение сопротивления при росте температуры. Это связано с колебаниями атомов. В то же время с ростом температуры проводимость в полупроводниках и диэлектриках возрастает из-за увеличения концентрации носителей заряда.
Удельное сопротивление для неоднородного материала можно вычислить по формуле: p = E / J. Где: E и J напряжённость и плотность тока в конкретной точке.
Обязательны ли расчеты?
Как мы уже сказали, сечение провода выбирают исходя из предполагаемого тока и сопротивления металла, из которого изготовлены жилы. Логика выбора заключается в следующем: сечение подбирают таким способом, чтобы сопротивление при заданной длине не приводило к значительным просадкам напряжения. Чтобы не проводить ряд расчетов, для коротких линий (до 10-20 метров) есть достаточно точные таблицы:
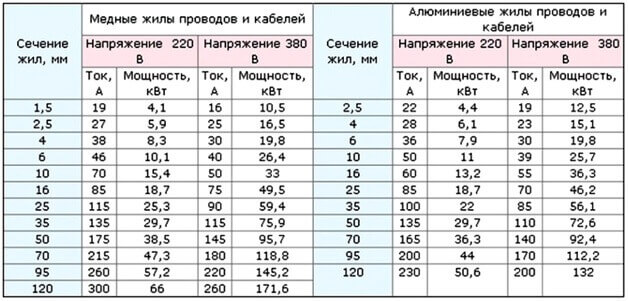
В этой таблице указаны типовые значения сечения медных и алюминиевых жил и номинальные токи через них. Для удобства указана мощность нагрузки, которую выдержит эта линия. Обратите внимание на разницу в токах и мощности при напряжении 380В, естественно, что это предполагается трёхфазная электросеть.
Напоследок рекомендуем просмотреть видео, на котором подробно рассказывается, как рассчитать сечение проводника, а также предоставлены примеры расчетных работ:
Расчет сопротивления провода сводится к использованию пары формул, при этом вы можете скачать готовые калькуляторы из Плэй Маркета для своего смартфона, например, «Electrodroid» или «Мобильный электрик». Эти знания пригодятся для расчетов нагревательных приборов, кабельных линий, предохранителей и даже популярных на сегодняшний день спиралей для электронных сигарет.
Выбор сечения кабеля
Поскольку у провода есть сопротивление, при прохождении по нему электрического тока выделяется тепло, и происходит падение напряжения. Оба этих фактора необходимо учитывать при выборе сечения кабелей.
Выбор по допустимому нагреву
При протекании тока в проводе выделяется энергия. Её количество можно рассчитать по формуле электрической мощности:
P=I²*R.
В медном проводе сечением 2,5мм² и длиной 10 метров R=10*0.0074=0.074Ом. При токе 30А Р=30²*0,074=66Вт.
Эта мощность нагревает токопроводящую жилу и сам кабель. Температура, до которой он нагревается, зависит от условий прокладки, числа жил в кабеле и других факторов, а допустимая температура – от материала изоляции. Медь обладает большей проводимостью, поэтому меньше выделяемая мощность и необходимое сечение. Определяется оно по специальным таблицам или при помощи онлайн-калькулятора.
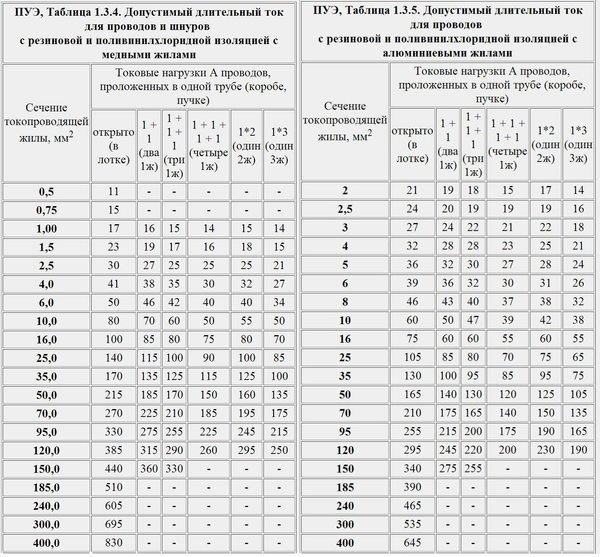
Таблица выбора сечения провода по допустимому нагреву
Допустимые потери напряжения
Кроме нагрева, при прохождении электрического тока по проводам происходит уменьшение напряжения возле нагрузки. Эту величину можно рассчитать по закону Ома:
U=I*R.
Справка. По нормам ПУЭ оно должно составлять не более 5% или в сети 220В – не больше 11В.
Поэтому, чем длиннее кабель, тем больше должно быть его сечение. Определить его можно по таблицам или при помощи онлайн-калькулятора. В отличие от выбора сечения по допустимому нагреву, потери напряжения не зависят от условий прокладки и материала изоляции.
В сети 220В напряжение подаётся по двум проводам: фазному и нулевому, поэтому расчёт производится по двойной длине кабеля. В кабеле из предыдущего примера оно составит U=I*R=30A*2*0.074Ом=4,44В. Это немного, но при длине 25 метров получается 11,1В – предельно допустимая величина, придётся увеличивать сечение.
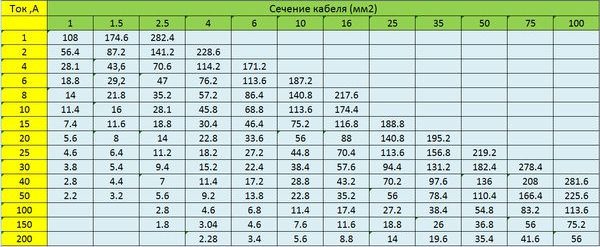
Максимально допустимая длина кабеля данного сечения
Таблица удельного сопротивления для распространенных проводников
В таблице ниже приведены показатели удельного сопротивления для различных материалов, в частности металлов, используемых для электропроводности.
Показатели удельного сопротивления приведены для таких «популярных» материалов, как медь, алюминий, нихром, сталь, свинец, золото и других.
МатериалУдельное сопротивление, ρ,при 20 °C (Ом·м)Источник
| Латунь | ~0.6 — 0.9 x 10-7 | |
| Серебро | 1.59×10−8 | [3][4] |
| Медь | 1.68×10−8 | [5][6] |
| Обожжённая медь | 1.72×10−8 | [7] |
| Золото | 2.44×10−8 | [3] |
| Алюминий | 2.65×10−8 | [3] |
| Кальций | 3.36×10−8 | |
| Вольфрам | 5.60×10−8 | [3] |
| Цинк | 5.90×10−8 | |
| Кобальт | 6.24×10−8 | |
| Никель | 6.99×10−8 | |
| Рутений | 7.10×10−8 | |
| Литий | 9.28×10−8 | |
| Железо | 9.70×10−8 | [3] |
| Платина | 1.06×10−7 | [3] |
| Олово | 1.09×10−7 | |
| Тантал | 1.3×10−7 | |
| Галлий | 1.40×10−7 | |
| Ниобий | 1.40×10−7 | [8] |
| Углеродистая сталь (1010) | 1.43×10−7 | [9] |
| Свинец | 2.20×10−7 | [2][3] |
| Галинстан | 2.89×10−7 | [10] |
| Титан | 4.20×10−7 | |
| Электротехническая сталь | 4.60×10−7 | [11] |
| Манганин (сплав) | 4.82×10−7 | [2] |
| Константан (сплав) | 4.90×10−7 | [2] |
| Нержавеющая сталь | 6.90×10−7 | |
| Ртуть | 9.80×10−7 | [2] |
| Марганец | 1.44×10−6 | |
| Нихром (сплав) | 1.10×10−6 | [2][3] |
| Углерод (аморфный) | 5×10−4 — 8×10−4 | [3] |
| Углерод (графит) параллельно-базальная плоскость | 2.5×10−6 — 5.0×10−6 | |
| Углерод (графит) перпендикулярно-базальная плоскость | 3×10−3 | |
| Арсенид галлия | 10−3 to 108 | |
| Германий | 4.6×10−1 | [3][4] |
| Морская вода | 2.1×10−1 | |
| Вода в плавательном бассейне | 3.3×10−1 — 4.0×10−1 | |
| Питьевая вода | 2×101 — 2×103 | |
| Кремний | 2.3×103 | [2][3] |
| Древесина (влажная) | 103 — 104 | |
| Деионизированная вода | 1.8×105 | |
| Стекло | 1011 — 1015 | [3][4] |
| Углерод (алмаз) | 1012 | |
| Твердая резина | 1013 | [3] |
| Воздух | 109 — 1015 | |
| Древесина (сухая) | 1014 — 1016 | |
| Сера | 1015 | [3] |
| Плавленый кварц | 7.5×1017 | [3] |
| ПЭТ | 1021 | |
| Тефлон | 1023 — 1025 |
Видно, что удельное сопротивление меди и удельное сопротивление латуни оба низкие, и с учетом их стоимости, относительно серебра и золота, они становятся экономически эффективными материалами для использования для многих проводов. Удельное сопротивление меди и простота ее использования привели к тому, что она также используется крайне часто в качестве материала для проводников на печатных платах.
Изредка алюминий и особенно медь используются из-за их низкого удельного сопротивления. Большинство проводов, используемых в наши дни для межсоединений, изготовлены из меди, поскольку она обеспечивает низкий уровень удельного сопротивления при приемлемой стоимости.
Удельное сопротивление золота также важно, поскольку золото используется в некоторых критических областях, несмотря на его стоимость. Часто золотое покрытие встречается на высококачественных слаботочных разъемах, где оно обеспечивает самое низкое сопротивление контактов. Золотое покрытие очень тонкое, но даже в этом случае оно способно обеспечить требуемые характеристики разъемов.
Серебро имеет очень низкий уровень удельного сопротивления, но оно не так широко используется из-за его стоимости и из-за того, что оно тускнеет, что может привести к более высокому сопротивлению контактов.
Однако оно используется в некоторых катушках для радиопередатчиков, где низкое удельное электрическое сопротивление серебра снижает потери. При использовании в таких целях серебро обычно наносилось только на существующий медный провод. Покрытие провода серебром позволило значительно снизить затраты по сравнению с цельным серебряным проводом без существенного снижения производительности.
Другие материалы в таблице удельного электрического сопротивления могут не иметь такого очевидного применения. Тантал фигурирует в таблице, поскольку используется в конденсаторах — никель и палладий используются в торцевых соединениях многих компонентов поверхностного монтажа, таких как конденсаторы.
Кварц находит свое основное применение в качестве пьезоэлектрического резонансного элемента. Кварцевые кристаллы используются в качестве частотоопределяющих элементов во многих осцилляторах, где высокое значение Q позволяет создавать очень стабильные по частоте схемы. Аналогичным образом они используются в высокоэффективных фильтрах. Кварц имеет очень высокий уровень удельного сопротивления и не является хорошим проводником электричества, то есть его относят к категории диэлектрикам.
Предыдущая
ТеорияКак построить векторную диаграмму токов и напряжений
Следующая
ТеорияТиристорный преобразователь частоты
Удельное сопротивление меди


4.6
Средняя оценка: 4.6
Всего получено оценок: 103.
4.6
Средняя оценка: 4.6
Всего получено оценок: 103.
Медь — это элемент таблицы Менделеева с атомным номером 29. Наряду с многими полезными свойствами (низкая температура плавления, ковкость, пластичность) медь обладает минимальным удельным электрическим сопротивлением, уступая по этому показателю только серебру. Этим объясняется его повсеместное использование для производства кабельной продукции, проводов различных сечений и контактных устройств. Удельное сопротивление меди зависит от условий эксплуатации и присутствия примесей.
Что такое удельное сопротивление
Понятие удельного электрического сопротивления вещества следует из определения электрического сопротивления проводника R с геометрическими размерами L (длина) и S (поперечное сечение):
$ ρ = R * { S over L } $ (1).
Удельное электрическое сопротивление меди получают, пользуясь результатами измерений вольт-амперных U(I) характеристик на образцах меди различных размеров. Измерив вольтметром напряжение U, амперметром величину тока I, и применив формулу закона Ома, рассчитывают величину сопротивления образца меди:
$ R = { U over I } $ (2).
Далее, с помощью формулы (1), вычисляется величина ρ.
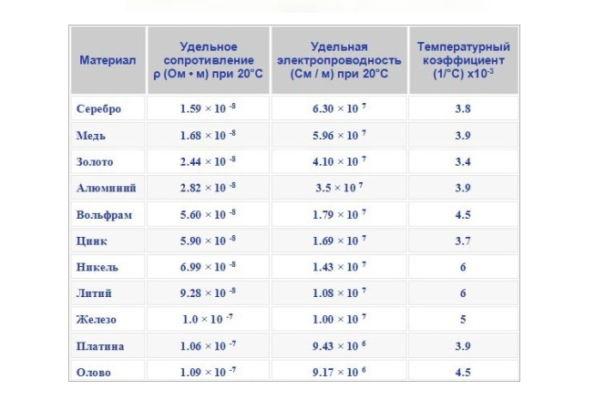
Медь – это один из самых первых металлов, который человек научился добывать и обрабатывать. Период с IV по III тысячелетие до н.э. называют медным веком. Считается, что в это время люди научились делать первые предметы и орудия труда из меди. Применение меди в электротехнике началось только в начале XIX века.
Основные параметры меди
Перечислим основные физические характеристики меди, которую делают ее столь незаменимой для электротехнической продукции:
- Главное достоинство меди — низкое удельное сопротивление, равное 0,0175 Ом*мм2м. У серебра — “рекордсмена” по этому параметру — 0,016 Ом*мм2м;
- Сравнительно небольшой температурный коэффициент α, равный 0,004 0К-1;
- Температура плавления Тпл = 10850С, что в полтора раза выше аналогичного параметра у алюминия, который тоже широко используется в электропроводке;
- Высокие пластичные свойства изделий из меди позволяют подвергать провода многократным изгибам без опасений разрушения целостности изделий;
- На поверхности меди быстро образуется пленка из окислов, которая выполняет защитную роль — предотвращает поверхность проводов от коррозии;
- Высокая механическая и ударная прочность;
- Высокая теплопроводность меди способствует быстрому отводу тепла в различных электротехнических устройствах. Например, на компьютерных платах с электрическими компонентами большой мощности (блоки питания, видеокарты) устанавливают радиаторы (кулеры) из меди для сброса тепла;
- Стоимость меди существенно меньше стоимости серебра и других драгметаллов, что определяет экономическую выгоду ее применения;
- Медь легко поддается пайке, поэтому она столь популярна среди радиолюбителей.
Примеры электротехнической продукции с применением меди
Приведем примеры использования меди в электротехнических изделиях:
- Кабельные изделия различного назначения;
- Шины (медные полосы) контактных проводов, телеграфного и телефонного оборудования, электронных плат;
- Катушки и обмотки электродвигателей;
- Первичные и вторичные обмотки трансформаторов.

Электрические параметры меди имеют сильную зависимость от количества примесей, которые оказываются центрами дефектов внутри кристаллической решетки и увеличивают удельное сопротивление. Например, присутствие 1% примеси марганца увеличивает удельное сопротивление в 3 раза. Поэтому перед массовым изготовлением продукции контролю чистоты исходной меди придается особое значение.


Что мы узнали?
Итак, мы узнали, что удельное электрическое сопротивление меди одно из самых низких среди металлических проводников. Медь является незаменимым материалом для изготовления электротехнических проводов и кабелей. В большинстве электродвигателей сегодня в качестве обмоток используется медный провод. Кроме низкого удельного сопротивления медь имеет прекрасные пластичные свойства, что позволяет изгибать медные провода при монтаже электропроводки.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Наталия Шишкина
5/5
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 103.
А какая ваша оценка?





![rho _{{11}}={frac {1}{det(sigma )}}[sigma _{{22}}sigma _{{33}}-sigma _{{23}}sigma _{{32}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/08befe7409fd1685d379b9d3045f8b7d88b62e44)
![rho _{{12}}={frac {1}{det(sigma )}}[sigma _{{33}}sigma _{{12}}-sigma _{{13}}sigma _{{32}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/023c28c36a33abc59ec81a040eeeee5d6040e007)
