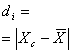Средняя арифметическая взвешенная применяется в том случае, когда отдельные значения признака (варианты) встречаются в ряду распределения не с одинаковой частотой (f1 ≠ f2 ≠ …fn) и число вариантов не совпадает с частотой их появления.
Пример расчета:
- средней арифметической взвешенной
- среднего линейного отклонения (показатель вариации)
- среднеквадратического отклонения взвешенного (показатель вариации)
При расчете средней арифметической по интервальному вариационному ряду необходимо сначала найти середину интервалов. Это и будут значения xi, а количество единиц совокупности в каждой группе fi. При наличии открытого интервала, его ширина принимается равной ширине примыкающего (рядом стоящего) интервала.
|
Стаж работника, лет |
Число работников, чел. (fi) |
Середина интервала, лет (xi) |
|
1-3 3-5 5-7 7-9 9-11 |
10 28 48 10 4 |
2 4 6 8 10 |
|
Итого |
100 |
Х |
1. Средний стаж работников предприятия определяется по средней арифметической взвешенной. Он будет равен:
![]()
![]()
![]()
2. Размах вариации R=Хmax-Хmin зависит только от двух крайних значений признака: R=11-1=10(лет).
3. Взвешенное среднее линейное отклонение (средний модуль) является средней величиной из абсолютных значений отклонений индивидуальных значений признака от общей средней арифметической величины:
![Rendered by QuickLaTeX.com [begin{array}{l} overline d = frac{{sum left| {{X_i} - overline X } right| times {f_i}}}{{sum {f_i}}} = frac{{left| {2 - 5,4} right|*10 + left| {4 - 5,4} right|*28 + left| {6 - 5,4} right|*48 + left| {8 - 5,4} right|*10 + left| {10 - 5,4} right|*4}}{{100}} = frac{{147.4}}{{100}} = 1.474; end{array}]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-0c142a6747bd17cf99a204575a921185_l3.png)
4. Взвешенное среднее квадратическое отклонение определяется как квадратный корень из дисперсии. На столько, в среднем, отклоняется средний стаж работников предприятия по каждой группе от общей средней (среднего стажа по предприятию).
![Rendered by QuickLaTeX.com [mathop sigma nolimits_X = sqrt {frac{{{{sum {left( {mathop Xnolimits_i - mathop {bar X}nolimits_{} } right)} }^2}*mathop fnolimits_i }}{{sum {mathop fnolimits_i } }}} ]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-d0ff80927f207703aa1e6d1b2d90aae5_l3.png)
или
![Rendered by QuickLaTeX.com [mathop sigma nolimits_X = sqrt {frac{{sum {{{mathop Xnolimits_i }^2}*mathop fnolimits_i } }}{{sum {mathop fnolimits_i } }} - mathop {{{bar X}^2}}nolimits_{} } ]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-0e47069c01d605d8b4e4bdd115dc96bb_l3.png)
![Rendered by QuickLaTeX.com [begin{array}{l} {sigma _x} = sqrt {frac{{{{left( {2 - 5,4} right)}^2}*10 + {{left( {4 - 5,4} right)}^2}*28 + {{left( {6 - 5,4} right)}^2}*48 + {{left( {8 - 5,4} right)}^2}*10 + {{left( {10 - 5,4} right)}^2}*4}}{{100}}} = = sqrt {frac{{340}}{{100}}} = 1,84 end{array}]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-675088cdb855b99df3fa76fe49010a3c_l3.png)
5. Коэффициент вариации характеризует колеблемость признака около средней. Если коэффициент вариации не превышает 33%, то совокупность, по рассматриваемому признаку, можно считать однородной. Данная совокупность характеризуется сильной вариацией, т.е. разброс значений по отдельным группам относительно общего среднего стажа по предприятию значителен.
![]()
Техника расчета средней арифметической «способом моментов»
![]()
|
Заработная плата |
Число рабочих f |
Центр интервала |
Х-А* |
Х’=(Х-А):К** |
Х’f |
|
до 250 250 – 275 275 – 300 300 – 325 325 и более |
10 15 18 12 5 |
237,5 262,5 287,5 312,5 337,5 |
– 50 – 25 0 +25 +50 |
– 2 – 1 0 +1 +2 |
– 20 -15 0 +12 +10 |
|
Итого |
60 |
-13 |
* – в качестве (А) обычно берут значение х, стоящее в середине вариационного ряда (А=287,5)
** -( K) обычно равно ширине интервала (K=25)
![]()
![]()
0…4
5…9
10..14
15..19
20..24
25..29
30..34
35..39
40..44
45..49
50..54
55..59
60..64
65..69
70
и старше
56,6
75,4
114,5
116,8
107,7
102,3
93,9
114,3
130,3
121
106,8
56,6
100,0
64,6
156,5
2
7
12
17
22
27
32
37
42
47
52
57
62
67
72
|
113,2 |
|
527,8 |
|
1374 |
|
1985,6 |
|
2369,4 |
|
2762,1 |
|
3004,8 |
|
4229,1 |
|
5472,6 |
|
5687 |
|
5553,6 |
|
3226,2 |
|
6200 |
|
4328,2 |
|
11268 |
36,3
31,3
26,3
21,3
16,3
11,3
6,3
1,3
3,7
8,7
13,7
18,7
23,7
28,7
33,7
|
2054,58 |
|
2360,02 |
|
3011,35 |
|
2487,84 |
|
1755,51 |
|
1155,99 |
|
591,57 |
|
148,59 |
|
482,11 |
|
1052,7 |
|
1463,16 |
|
1058,42 |
|
2370 |
|
1854,02 |
|
5274,05 |
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, руб. | До 400 | 400 – 600 | 600 – 800 | 800 – 1000 | Свыше 1000 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
Определите:
1) размах вариации;
2) средний размер вклада;
3) среднее линейное отклонение;
4) дисперсию;
5) среднее квадратическое отклонение;
6) коэффициент вариации вкладов.
Решение:
Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.
Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
| Размер вклада, руб. | 200 – 400 | 400 – 600 | 600 – 800 | 800 – 1000 | 1000 – 1200 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
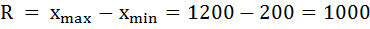
Размах вариации размера вклада равен 1000 рублей.
2) Средний размер вклада определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
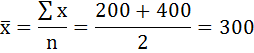
второго – 500 и т. д.
Занесём результаты вычислений в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Итого | 400 | – | 312000 |
Средний размер вклада в Сбербанке города будет равен 780 рублей:
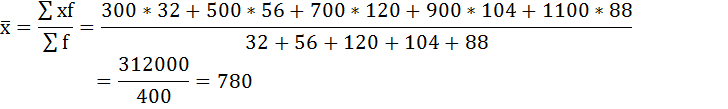
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
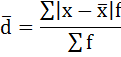
Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:
1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).
2. Определяются абсолютные отклонения вариант от средней:
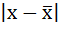
3. Полученные отклонения умножаются на частоты:
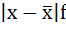
4. Находится сумма взвешенных отклонений без учёта знака:
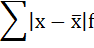
5. Сумма взвешенных отклонений делится на сумму частот:
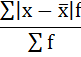
Удобно пользоваться таблицей расчётных данных:
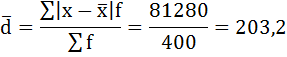
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.
4) Дисперсия – это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
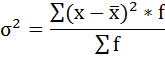
Порядок расчёта дисперсии в этом случае следующий:
1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).
2. Находят отклонения вариант от средней:

3. Возводят в квадрат отклонения каждой варианты от средней:
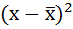
4. Умножают квадраты отклонений на веса (частоты):
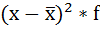
5. Суммируют полученные произведения:
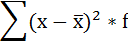
6. Полученная сумма делится на сумму весов (частот):
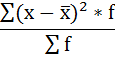
Расчёты оформим в таблицу:
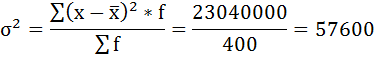
5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:
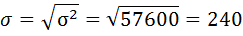
6) Коэффициент вариации – это отношение среднего квадратического отклонения к средней арифметической:
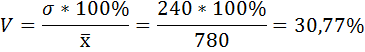
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №5.
Расчёт показателей вариации.
Студент должен:
знать:
– область применения и методику расчёта
степенных средних величин;
уметь:
– исчислять
степенные средние
величины;
– формулировать вывод по полученным
результатам.
Методические указания
Наряду со средними
величинами в статистике исчисляются показатели вариации. Вариацией в статистике
называются различия индивидуальных значений изучаемого признака. Возникает
вариация в силу того, что отдельные значения признака статистической совокупности
формируются под воздействием разнообразных факторов. Значение изучения вариации
в том, что по колеблемости признаков можно судить о качественной однородности
совокупности. Совокупности могут иметь одинаковые значения средней величины, но
отличаться колеблемостью индивидуальных значений.
Например: По имеющимся данным о дневной выработке рабочих двух бригад определить
среднюю выработку рабочего за день в каждой бригаде, сделать вывод об
однородности рассматриваемых совокупностей и надёжности их средних.
Выработка в первой
бригаде: 31, 25, 30, 26, 28 деталей.
Выработка во второй
бригаде: 27, 20, 56, 19, 18 деталей.
Решение:
Исходные данные не
сгруппированы, поэтому для расчёта средней выработки применяем среднюю
арифметическую простую. Средняя дневная выработка рабочего:
в первой бригаде ![]()
во второй бригаде ![]()
Среднедневная выработка рабочего в
обеих бригадах одинакова, но индивидуальные
значения выработки во второй бригаде подвержены значительным колебаниям. Это
вызывает необходимость измерять вариацию.
К
абсолютным показателям вариации относятся
размах вариации, среднее линейное отклонение,
дисперсия и среднее квадратическое отклонение.
Элементарным
показателем колеблемости является размах вариации, который определяется
как разность между наибольшим и наименьшим значением признака: R=Хmax – Xmin
В нашем примере размах
вариации индивидуальной выработки:
в первой бригаде R1 =31-25=6 деталей
во второй бригаде R2 =56-18=38 деталей
Сравнение этих
показателей свидетельствует о том, что размах вариации индивидуальной выработки
во второй бригаде на 32 детали больше, чем в первой бригаде. Однако размах
вариации не улавливает колеблемости вариантов внутри изучаемой совокупности.
Для получения обобщающей характеристики колеблемости всех вариантов
совокупности исчисляются другие показатели вариации.
Среднее линейное отклонение даёт обобщённую характеристику степени колеблемости признака
в совокупности относительно среднего уровня признака и рассчитывается как средняя арифметическая из индивидуальных
линейных отклонений по формуле:
–
для
невзвешенных данных 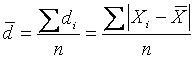
–
для
взвешенных данных 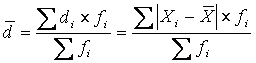
где ![]() – индивидуальное
– индивидуальное
линейное отклонение.
Показатель
среднего линейного отклонения нашел широкое применение на практике. С его
помощью анализируют состав работающих, ритмичность производства, равномерность
поставок материалов; разрабатывают системы материального стимулирования. Но
этот показатель усложняет расчёты вероятностного типа, затрудняет применение
методов математической статистики. Поэтому в статистических научных
исследованиях для измерения вариации чаще всего применяют показатель дисперсии.
В
статистике дисперсия, центральный момент второго порядка, является оценкой
одноимённого показателя теории вероятностей и оценкой дисперсии в
математической статистике, что позволяет использовать теоретические положения
этих дисциплин для анализа социально – экономических процессов. На дисперсии
практически основаны все метод математической статистики. Большое значение
имеет правило сложения дисперсий. Дисперсия рассчитывается как средний квадрат отклонений индивидуальных значений
признака от среднего
значения признака по формуле:
–
для
невзвешенных данных ![]()
–
для
взвешенных данных 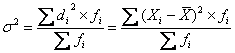
Среднее квадратическое отклонение является обобщающей характеристикой размеров вариации признака совокупности. Это – мера вариации, показатель надёжности средней. Чем меньше значение
среднего квадратического отклонения, тем лучше средняя величина представляет собой
рассматриваемую совокупность.Среднее квадратическое отклонение рассчитывается
по формуле: ![]()
Для
расчёта показателей вариации в нашем примере строим вспомогательную таблицу:
|
Первая бригада |
Вторая бригада |
||||
|
Выработка,деталей (Хi ) |
Индивидуальное линейное отклонение |
|
Выработка, деталей (Хi ) |
Индивидуальное линейное отклонение |
|
|
25 |
|-3| |
9 |
18 |
|-10| |
100 |
|
26 |
|-2| |
4 |
19 |
|-9| |
81 |
|
28 |
0 |
0 |
20 |
|-8| |
64 |
|
30 |
2 |
4 |
27 |
|-1| |
1 |
|
31 |
3 |
9 |
56 |
28 |
784 |
|
Итого: |
10 |
26 |
56 |
1030 |
Среднее
линейное отклонение:
в первой бригаде ![]() ; во второй
; во второй
бригаде ![]() .
.
Дисперсия:
в первой бригаде ![]() ; во
; во
второй бригаде ![]() .
.
Среднее квадратическое отклонение:
в первой бригаде ![]() ; во второй бригаде
; во второй бригаде ![]()
Таким образом,
выполненные нами расчёты показывают, что колеблемость индивидуальных значений
выработки во второй бригаде намного выше, чем в первой бригаде.
Для
целей сравнения колеблемости различных признаков в одной и той же совокупности
или же при сравнении колеблемости одного и того же признака в нескольких
совокупностях исчисляют показатели
вариации в относительных величинах. Базой для сравнения должна служить
средняя арифметическая. Эти показатели вычисляются как отношение размаха
вариации, среднего линейного отклонения или среднего квадратического отклонения
к средней арифметической (реже к медиане). Чаще всего они выражаются в
процентах и определяют не только сравнительную оценку вариации, но и дают
характеристику однородности совокупности. Совокупность
считается однородной, если коэффициент вариации не превышает 33% (для
распределения близкого к нормальному). Различают следующие относительные
показатели вариации:
Коэффициент осцилляции (vR) рассчитывается по формуле:
![]()
![]()
и отражает относительную меру
колеблемости крайних значений признака вокруг средней.
Линейный коэффициент вариации (vd) рассчитывается
по формуле:![]()
![]()
и отражает долю усреднённого значения
абсолютных отклонений от средней величины.
Коэффициент вариации (vσ ) как относительное квадратическое отклонение от средней величины
рассчитывается по формуле:
![]()
Рассчитаем относительные
показатели вариации для нашего примера.
Коэффициент осцилляции
Для первой бригады: Для
второй бригады:
![]()
![]()
Линейный коэффициент вариации
Для первой бригады: Для
второй бригады:
![]()
![]()
Коэффициент вариации
Для первой бригады: Для
второй бригады:
![]()
![]()
Величина рассчитанных
нами коэффициентов свидетельствует о том, что колеблемость индивидуальных
значений выработки во второй бригаде высокая. Первую совокупность можно считать
однородной, а её среднюю – надёжной. Вторую совокупность следует считать
неоднородной, а её среднюю – ненадёжной.
Рассмотрим
примеры расчёта показателей вариации для сгруппированных данных.
Пример
1. По имеющимся данным узла связи рассчитайте абсолютные и относительные
показатели вариации. Сделать вывод об однородности рассматриваемой совокупности
и надёжности её средней.
|
Количество |
Число |
|
12 13 14 15 16 17 18 |
18 22 34 26 20 13 7 |
|
Итого |
140 |
Решение:
Исходные
данные представлены в виде дискретного ряда распределения.
Для
исчисления среднего значения признака и показателей вариации строим и
рассчитываем вспомогательную таблицу:
|
Количество слов в телеграмме(Хi) |
Число телеграмм (fi) |
|
|
|
|
|
|
12 |
18 |
216 |
|
54 |
9 |
162 |
|
13 |
22 |
286 |
|
44 |
4 |
88 |
|
14 |
34 |
476 |
|
34 |
1 |
34 |
|
15 |
26 |
390 |
0 |
0 |
0 |
0 |
|
16 |
20 |
320 |
1 |
20 |
1 |
20 |
|
17 |
13 |
221 |
2 |
26 |
4 |
52 |
|
18 |
7 |
126 |
3 |
21 |
9 |
63 |
|
итого |
140 |
2035 |
199 |
419 |
1). Определяем среднее количество слов в телеграмме по
формуле средней арифметической взвешенной, так как исходные данные
сгруппированы:
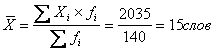
2). Определяем абсолютные показатели
вариации:
Размах вариации R=Хmax – Xmin=18-12=6 слов
Среднее линейное отклонение по
формуле для взвешенных данных:
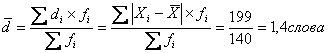
где ![]() – индивидуальное
– индивидуальное
линейное отклонение.
Дисперсию исчисляем по формуле для
взвешеных данных
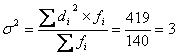
Среднее квадратическое отклонение:
![]()
3). Определяем относительные
показатели вариации:
Коэффициент осцилляции: ![]()
![]() т.е. колеблемость крайних значений признака вокруг средней
т.е. колеблемость крайних значений признака вокруг средней
составляет 40%.
Линейный коэффициент
вариации:![]()
![]() , т.е. доля усреднённого значения абсолютных отклонений от
, т.е. доля усреднённого значения абсолютных отклонений от
средней величины составляет 9,3%.
Коэффициент вариации: ![]()
Вывод:
Величина рассчитанного нами коэффициента вариации свидетельствует о том, что
колеблемость индивидуальных значений слов в телеграмме невысокая, т.е. Vσ ≤ 33%.
Поэтому совокупность можно считать
однородной, а её среднюю – надёжной.
Пример 2. Имеются следующие данные о
распределении сотрудников организации по среднемесячной заработной плате.
Рассчитать абсолютные и относительные показатели вариации. Сделать вывод об
однородности рассматриваемой совокупности и надёжности её средней.
|
Группы сотрудников по |
Количество сотрудников, чел. (fi) |
|
До 3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10 и свыше |
14 22 25 29 10 8 6 5 3 |
|
Итого: |
122 |
Решение:
Исходные данные представлены в виде
интервального ряда распределения.
Для исчисления среднего значения
признака и показателей вариации строим и рассчитываем вспомогательную таблицу:
|
Группы по ной |
Централь- ное (Хс) |
Коли- чество ников, |
|
|
|
|
|
|
До 3 |
2,5 |
14 |
35 |
|
38,36 |
7,51 |
105,14 |
|
3-4 |
3,5 |
22 |
77 |
|
38,28 |
3,03 |
66,61 |
|
4-5 |
4,5 |
25 |
112,5 |
|
18,5 |
0,55 |
13,69 |
|
5-6 |
5,5 |
29 |
159,5 |
0,26 |
7,54 |
0,07 |
1,96 |
|
6-7 |
6,5 |
10 |
65 |
1,26 |
12,6 |
1,59 |
15,90 |
|
7-8 |
7,5 |
8 |
60 |
2,26 |
18,08 |
5,11 |
40,86 |
|
8-9 |
8,5 |
6 |
51 |
3,26 |
19,56 |
10,63 |
63,76 |
|
9-10 |
9,5 |
5 |
47,5 |
4,26 |
21,3 |
18,15 |
90,74 |
|
10 и выше |
10,5 |
3 |
31,5 |
5,26 |
15,78 |
27,67 |
83,00 |
|
итого |
122 |
639 |
190 |
481,66 |
1). Определяем среднюю
заработную плату по формуле средней арифметической взвешенной для интервального
ряда распределения:
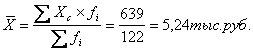
2). Определяем абсолютные показатели
вариации:
Размах вариации не рассчитываем, т.к.
нижняя граница первого интервала и верхняя граница последнего интервала не
указаны.
Среднее линейное отклонение по
формуле для взвешенных данных:
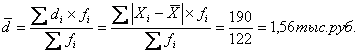
где ![]() – индивидуальное
– индивидуальное
линейное отклонение.
Дисперсию исчисляем по формуле для
взвешеных данных:
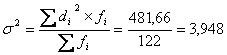
Среднее квадратическое отклонение:
![]()
3). Определяем относительные показатели вариации:
Коэффициент осцилляции (VR) не рассчитываем, т.к. не
рассчитывали размах вариации.
Линейный коэффициент вариации:![]()
![]() , т.е. доля усреднённого значения абсолютных отклонений от
, т.е. доля усреднённого значения абсолютных отклонений от
средней величины составляет 29,8%.
Коэффициент вариации: ![]()
Вывод: Величина
рассчитанного нами коэффициента вариации свидетельствует о том, что
колеблемость индивидуальных значений заработной платы высокая, т.е. Vσ ≥ 33%. Поэтому совокупность считаем неоднородной, а
её среднюю – ненадёжной.
Свойства дисперсии
Свойство 1.
Дисперсия постоянной величины равна нулю.
Свойство 2.
Уменьшение всех значений признака на одну и ту же величину А не меняет величины
дисперсии:
![]()
Значит, средний квадрат отклонений можно вычислить не по заданным
значениям признака, а по отклонениям их от какого-то постоянного числа.
Свойство 3.
Уменьшение всех значений признака в ![]() раз уменьшает
раз уменьшает
дисперсию в ![]() раз, а среднее квадратическое
раз, а среднее квадратическое
отклонение – в ![]() раз:
раз:
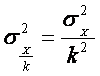
Значит, все значения признака можно разделить на какое-то постоянное
число (скажем, на величину интервала ряда), исчислить среднее квадратическое
отклонение, а затем умножить его на постоянное число:
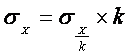
Свойство 4.
Если исчислить средний квадрат отклонений от любой величины А, в той или иной
степени отличающейся от средней арифметической (![]() ), то он всегда будет больше среднего квадрата отклонений,
), то он всегда будет больше среднего квадрата отклонений,
исчисленного от средней арифметической: ![]()
Средний квадрат отклонений при этом будет больше на вполне определенную
величину – на квадрат разности средней и этой условно взятой величины, т. е. на
![]() :
:
![]() или
или 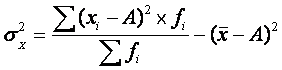
Значит, дисперсия от средней всегда меньше дисперсий, исчисленных от
любых других величин, т. е. она имеет свойство минимальности.
В случае когда А приравнивается к нулю и, следовательно, не вычисляются
отклонения, формула принимает такой вид:
![]() или
или 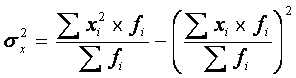
Значит, средний квадрат отклонений равен среднему квадрату значений
признака минус квадрат среднего значения признака
Виды (показатели) дисперсий и правило
их сложения
В статистическом исследовании очень
часто бывает необходимо не только изучить вариации признака по всей
совокупности, но и проследить количественные изменения признака по однородным
группам совокупности, а также и между группами. Следовательно, помимо общей
средней для всей совокупности необходимо просчитывать и частные средние
величины по отдельным группам.
Различают три вида дисперсий:
–
общая;
–
средняя
внутригрупповая;
–
межгрупповая.
Общая дисперсия (![]() ) характеризует вариацию признака всей совокупности под
) характеризует вариацию признака всей совокупности под
влиянием всех тех факторов, которые обусловили данную вариацию. Эта величина
определяется по формуле
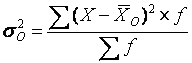
где ![]() – общая средняя
– общая средняя
арифметическая всей исследуемой совокупности.
Средняя внутригрупповая
дисперсия (![]() ) свидетельствует о случайной вариации, которая может
) свидетельствует о случайной вариации, которая может
возникнуть под влиянием каких-либо неучтенных факторов и которая не зависит от
признака-фактора, положенного в основу группировки. Данная дисперсия
рассчитывается следующим образом: сначала рассчитываются дисперсии по отдельным
группам (![]() ):
):
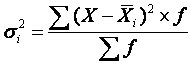 ,
,
а затем – рассчитывается средняя внутригрупповая дисперсия ![]() :
:
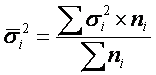
где ni –
число единиц в группе
Межгрупповая дисперсия
(![]() ) (дисперсия групповых средних) характеризует систематическую
) (дисперсия групповых средних) характеризует систематическую
вариацию, т.е. различия в величине исследуемого признака, возникающие под
влиянием признака-фактора, который положен в основу группировки. Эта дисперсия
рассчитывается по формуле:
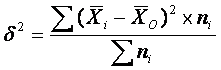
где![]() – средняя величина по отдельной группе.
– средняя величина по отдельной группе.
Все три вида дисперсии связаны между собой: общая дисперсия
равна сумме средней внутригрупповой дисперсии и межгрупповой дисперсии:
![]()
Данное соотношение отражает закон,
который называют правилом сложения дисперсий.
Согласно этому закону (правилу), общая дисперсия, которая возникает под
влиянием всех факторов, равна сумме дисперсий, которые появляются как под
влиянием признака-фактора, положенного в основу группировки, так и под влиянием
других факторов. Благодаря правилу сложения дисперсий можно определить, какая
часть общей дисперсии находится под влиянием признака-фактора, положенного в
основу группировки.
Правило сложения дисперсий широко
применяется при исчислении показателей тесноты связи, в дисперсионном анализе,
при оценке точности типической выборки и в ряде других случаев.