Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 сентября 2022 года; проверки требуют 3 правки.

Боровская модель водородоподобного атома (Z — заряд ядра), где отрицательно заряженный электрон заключен в атомной оболочке, окружающей малое, положительно заряженное атомное ядро. Переход электрона с орбиты на орбиту сопровождается излучением или поглощением кванта электромагнитной энергии (hν).
Бо́ровская моде́ль а́тома (моде́ль Бо́ра, моде́ль Бо́ра — Резерфо́рда) — полуклассическая модель атома, предложенная Нильсом Бором в 1913 г. За основу он взял планетарную модель атома, выдвинутую Эрнестом Резерфордом. Однако, с точки зрения классической электродинамики, электрон в модели Резерфорда, двигаясь вокруг ядра, должен был бы излучать энергию непрерывно и очень быстро и, потеряв её, упасть на ядро. Чтобы преодолеть эту проблему, Бор ввёл допущение, суть которого заключается в том, что электроны в атоме могут двигаться только по определённым (стационарным) орбитам, находясь на которых они не излучают энергию, а излучение или поглощение происходит только в момент перехода с одной орбиты на другую. Причём, стационарными являются лишь те орбиты, при движении по которым момент количества движения электрона равен целому числу постоянных Планка[1]: 
Используя это допущение и законы классической механики, а именно равенство силы притяжения электрона со стороны ядра и центробежной силы, действующей на вращающийся электрон, он получил следующие значения для радиуса стационарной орбиты 

Здесь 



Именно такое выражение для энергии можно получить, применяя уравнение Шрёдингера в задаче о движении электрона в центральном кулоновском поле.
Радиус первой орбиты в атоме водорода R0=5,2917720859(36)⋅10−11 м[2], ныне называется боровским радиусом, либо атомной единицей длины и широко используется в современной физике. Энергия первой орбиты 
Полуклассическая теория Бора[править | править код]
Основана на двух постулатах Бора:
Далее исходя из соображений классической физики о круговом движении электрона вокруг неподвижного ядра по стационарной орбите под действием кулоновской силы притяжения, Бором были получены выражения для радиусов стационарных орбит и энергии электрона на этих орбитах:
м — боровский радиус.
— энергетическая постоянная Ридберга (численно равна 13,6 эВ).
Формула Зоммерфельда — Дирака[править | править код]
Движение электрона вокруг атомного ядра в рамках классической механики можно рассматривать как «линейный осциллятор», который характеризуется «адиабатичным инвариантом», представляющим собой площадь эллипса (в обобщённых координатах):
где 


А квантовый постулат утверждает, что площадь замкнутой кривой в фазовой 

С точки зрения рассмотрения постоянной тонкой структуры наиболее интересным является движение релятивистского электрона в поле ядра атома, когда его масса зависит от скорости движения. В этом случае мы имеем два квантовых условия:
,
,
где 



,
.
В этом случае Зоммерфельд получил выражение для энергии в виде
.
где 


Дополнительный член 







Зоммерфельд (1916 г.) еще задолго до возникновения квантовой механики Шредингера получил феноменологичную формулу для водородных термов в виде:
,
где 




Появление тонкой структуры термов связано с прецессией электронов вокруг ядра атома. Поэтому появление тонкой структуры можно обнаружить по резонансному эффекту в области ультракоротких электромагнитных волн. В случае 
Поскольку длина электромагнитной волны равна
Поэтому для 
Достоинства теории Бора[править | править код]
- Объяснила дискретность энергетических состояний водородоподобных атомов.
- Теория Бора подошла к объяснению внутриатомных процессов с принципиально новых позиций, стала первой полуквантовой теорией атома.
- Эвристическое значение теории Бора состоит в смелом предположении о существовании стационарных состояний и скачкообразных переходов между ними. Эти положения позднее были распространены и на другие микросистемы.
Недостатки теории Бора[править | править код]
- Не смогла объяснить интенсивность спектральных линий.
- Справедлива только для водородоподобных атомов и не работает для атомов, следующих за ним в таблице Менделеева без экспериментальных данных (энергии ионизации или других).
- Теория Бора логически противоречива: не является ни классической, ни квантовой. В системе двух уравнений, лежащих в её основе, одно — уравнение движения электрона — классическое, другое — уравнение квантования орбит — квантовое.
Теория Бора являлась недостаточно последовательной и общей. Поэтому она в дальнейшем была заменена современной квантовой механикой, основанной на более общих и непротиворечивых исходных положениях. Сейчас известно, что постулаты Бора являются следствиями более общих квантовых законов. Но правила квантования широко используются и в наши дни как приближённые соотношения: их точность часто бывает очень высокой.
Экспериментальное подтверждение теории Бора[править | править код]
В 1914 году Франк и Герц поставили опыт, косвенно подтверждающий теорию Бора: атомы разреженного газа обстреливались медленными электронами с последующим исследованием распределения электронов по абсолютным значениям скоростей до и после столкновения. При упругом ударе распределение не должно меняться, так как изменяется только направление вектора скорости. Результаты показали, что при скоростях электронов меньше некоторого критического значения удары упруги, а при критической скорости столкновения становятся неупругими, электроны теряют энергию, а атомы газа переходят в возбуждённое состояние. При дальнейшем увеличении скорости удары снова становились упругими, пока не достигалась новая критическая скорость. Наблюдаемое явление позволило сделать вывод о том, что атом может или вообще не поглощать энергию, или же поглощать в количествах равных разности энергий стационарных состояний[источник не указан 1013 дней].
Примечания[править | править код]
- ↑ Планетарная модель атома. Постулаты Бора Архивная копия от 21 февраля 2009 на Wayback Machine на Портале Естественных Наук Архивная копия от 26 ноября 2009 на Wayback Machine
- ↑ Боровский радиус Архивная копия от 11 сентября 2015 на Wayback Machine согласно CODATA
Литература[править | править код]
- Борн М. Атомная физика, 2-е изд. — М.: Мир, 1967, 493 с.
- Джеммер, Макс. Эволюция понятий квантовой механики / Пер. с англ. / Под ред. Л. И. Пономарёва. — М.: Наука, 1985. — С. 11. — 384 с.
- Милантьев В. П. История возникновения квантовой механики и развитие представлений об атоме. — М.: Книжный дом «ЛИБРОКОМ», 2017, 246 с. ISBN 978-5-397-05872-8.
После
нескольких месяцев работы
Бор в 1913 г. опубликовал свою квантовую
теорию атома. Основу
этой теории составляют три постулата.
Первый
постулат Бора:
А том
том
может находиться не во всех состояниях,
допускаемых
классической физикой, а только в особых,
квантовых (или
стационарных) состояниях, каждому из
которых соответствует своя определенная
энергия Еn.
В стационарном
состоянии атом не излучает и не поглощает
энергию.
Второй
постулат Бора:
При
переходе атома из одного стационарного
состояния в
другое излучается или поглощается квант
света с энергией ћω,
равной
разности энергий стационарных состояний
(рис.25.5):
ћω
= |Еn2-Еn1|
(25.1)
Еn1
–
энергия в начальном состоянии, Еn2
–
энергия в конечном состоянии.
Третий
постулат Бора:
В стационарном
состоянии электрон может двигаться
только по такой («разрешенной») орбите,
радиус которой удовлетворяет условию:
m·υ·r=n·ћ
(25.2)
–
условие
стационарности электронных орбит, где
m·υ·r
— момент импульса электрона, n
— номер квантового состояния (n
=1, 2, 3, …).
Целое число n,
определяющее номер квантового состояния
и энергию атома в этом состоянии,
называется главным
квантовым числом.
Применив свою
теорию к простейшему из атомов — атому
водорода, Бор получил результаты,
полностью согласующиеся с экспериментальными
данными.
Рассмотрим
простейший атом — атом водорода. Он
состоит из ядра, в состав которого входит
один протон, и одного электрона,
вращающегося вокруг ядра по круговой
орбите. На электрон со стороны ядра
действует кулоновская сила притяжения,
сообщая ему центростремительное
ускорение, поэтому
![]() (25.3)
(25.3)
[е — заряд электрона
и протона, εо
— электрическая постоянная].
Поскольку должен
выполняться первый постулат Бора,
воспользуемся условием стационарности
электронных орбит. Определим из него
скорость υ
![]() (25.4)
(25.4)
возведем в квадрат
и подставим в (25.4). Из полученного
выражения найдем
![]()
отсюда радиус
орбит электрона в атоме водорода равен
![]() (25.5)
(25.5)
Подставляя в (25.5)
значения констант и считая n
= 1, получаем значение первого боровского
радиуса, который является единицей
длины в атомной физике:
rБ
= 0,528-10-10
м.
§ 25.3 Энергия атома водорода
По боровской модели
ядро атома считается неподвижным,
поэтому полная энергия Е атома является
суммой кинетической энергии Ек
вращения электрона и потенциальной
энергии Еп
взаимодействия электрона с ядром:
![]()
![]()
![]() (25.6)
(25.6)
Полученное значение
Е отрицательно, так как потенциальная
энергия двух зарядов, находящихся
на бесконечно большом расстоянии,
предполагается равной нулю. При сближении
зарядов потенциальная энергия уменьшается.
Каждое значение
энергии, которой обладает атом в том
или ином стационарном состоянии, называют
энергетическим
уровнем.
Чем больше n,
тем дальше от ядра находится электрон
и тем выше его энергетический уровень.
Энергетические
уровни атома принято изображать
горизонтальными линиями, а переходы
атома из одного стационарного состояния
в другое – стрелками (рис.25.6).
Когда атом переходит
с более высокого на более низкий
уровень (чему соответствует «перескок»
электрона на более близкую к ядру
орбиту), то происходит излучение кванта
света. При поглощении, наоборот, падающий
на атом квант (фотон) переводит атом
из состояния с меньшей в состояние с
большей энергией; сам фотон при этом
исчезает, а поглотивший его электрон
оказывается на более далекой от ядра
орбите.
С остояние
остояние
атома сn
=1 называют основным
или нормальным состоянием.
В этом состоянии энергия атома минимальна,
и он может находиться в нем (при
отсутствии внешних воздействий) сколь
угодно долго.
Все остальные
состояния с n>1
называют возбужденными.
В возбужденном состоянии атом может
находиться в течение очень малого
промежутка времени (порядка 10-8
с), после чего самопроизвольно
переходит в основное состояние (сразу
или поэтапно, уровень за уровнем),
излучая при этом соответствующие кванты.
В основном
состоянии атом водорода обладает
энергией Еі
= -13,6 эВ. При переходе в возбужденные
состояния его энергия возрастает.
Минимальную
энергию, которую нужно затратить для
удаления электрона с первой боровской
орбиты на «бесконечность», называют
энергией
ионизации Wі
или энергией связи атома водорода.
Таким образом, для
ионизации атома водорода, находящегося
в основном состоянии, ему необходимо
сообщить энергию ΔЕ
=Wі
= 13,6 эВ. Если же ему будет передаваться
энергия ΔЕ
<Wі,
то при ΔЕ=Еn—Еі
атом перейдет в состояние с энергией
Еп,
а при ΔЕ ≠ Еn—Еі
поглощения
энергии не произойдет и атом останется
в прежнем состоянии.
Такой («скачкообразный»)
характер поглощения энергии должен
наблюдаться для атомов любого химического
элемента. Для атомов ртути он был
обнаружен уже в 1913 г. немецкими
физиками-экспериментаторами Д.
Франком и Г. Герцем. Их опыты подтвердили
существование в атомах дискретных
энергетических уровней, что сыграло
важнейшую роль в развитии квантовой
теории атома.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
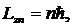 n= 1,2,3, … . (10.12)
n= 1,2,3, … . (10.12)
Данная формула была впервые постулирована астрофизиком Дж. Никольсоном в 1912 г. в его расчетах круговых орбит атомных электронов.
С учетом (10.12) энергия электрона (10.6) записывается в виде
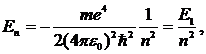 (10.13)
(10.13)
где наименьшая энергия
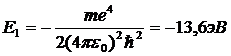 (10.14)
(10.14)
есть энергия основного состояния атома водорода. Таким образом, энергетический спектр стационарных состояний атома водорода с энергией E<0 является дискретным.
Радиус боровских орбит определяется выражением
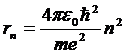 (10.15)
(10.15)
и быстро растет с увеличением n. Радиус орбиты основного состояния атома водорода (радиус первой боровской орбиты)
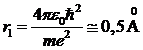 , (10.16)
, (10.16)
где 1Å=10-10м – внесистемная единица длины, называемая ангстрем.
В дальнейшем число n получило название главного квантового числа.
Энергетический спектр атома водорода приведен на рисунке 10.1. При Е<0 электрон совершает финитное (ограниченное в пространстве) движение и образует связанное (с протоном) состояние. Стационарные состояния с n>1 называются возбужденными. Точка E=0 на оси энергий является точкой сгущения для значений энергии дискретного спектра.
В области положительной энергии Е≥0 спектр является сплошным, т. е. энергия электрона вплоть до сколь угодно больших значений меняется непрерывным образом. При Е≥0 электрон совершает инфинитное (неограниченное в пространстве) движение. Переход электрона из связанного состояния дискретного спектра в состояние инфинитного движения сплошного спектра называется ионизацией атома водорода.
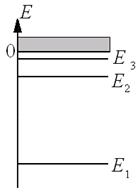
Рис.10.1
Второй постулат Бора определяет свойства процессов излучения и поглощения электромагнитных волн атомом и вводит понятие квантового скачка, когда в результате взаимодействия с окружающей средой электрон мгновенно переходит из одного стационарного состояния в другое. Рассмотрим взаимодействие атомам водорода с электромагнитным излучением. Если электрон переходит из состояния с большей энергией ![]() в состояние с меньшей энергией
в состояние с меньшей энергией ![]() , то при этом излучается фотон электромагнитной волны. Частота
, то при этом излучается фотон электромагнитной волны. Частота ![]() излучения определяется законом сохранения энергии
излучения определяется законом сохранения энергии
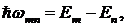
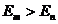 . (10.17)
. (10.17)
Если электрон переходит из состояния с меньшей энергией ![]() в состояние с большей энергией
в состояние с большей энергией ![]() , то в этом случае атом должен поглотить фотон той же частоты
, то в этом случае атом должен поглотить фотон той же частоты 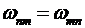 , которая входит в закон сохранения энергии (10.17).
, которая входит в закон сохранения энергии (10.17).
Линейчатые спектры излучения и поглощения атома водорода соответствуют переходам между энергетическими уровнями дискретного спектра (10.13). Все линейчатые спектры излучения можно сгруппировать в серии, которые задаются с помощью фиксированного нижнего энергетического уровня n, на который осуществляются переходы с более высоких энергетических уровней с m>n. Формулы для длин волн спектральных линий таких серий находятся с помощью формул (10.13) и (10.17).
Переходы с возбужденных уровней на основной уровень n=1 образуют серию Лаймана, относящуюся к ультрафиолетовой области спектра. Длины волн ![]() серии Лаймана определяются формулой
серии Лаймана определяются формулой
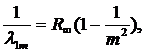
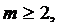 (10.18)
(10.18)
Здесь
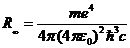 (10.19)
(10.19)
-постоянная Ридберга для случая неподвижного протона 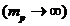 . Переходы на первый возбужденный уровень n=2 образуют серию Бальмера, длины волн которой лежат в видимой области спектра и описываются формулой Бальмера (10.11). Переходы на второй возбужденный уровень n=3 образуют серию Пашена – Бака, длины волн
. Переходы на первый возбужденный уровень n=2 образуют серию Бальмера, длины волн которой лежат в видимой области спектра и описываются формулой Бальмера (10.11). Переходы на второй возбужденный уровень n=3 образуют серию Пашена – Бака, длины волн ![]() удовлетворяют соотношению
удовлетворяют соотношению
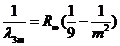 ,
, ![]() , (10.20)
, (10.20)
и принадлежат к инфракрасной области спектра.
Необходимо отметить, что в квантовой теории излучения атомов рассматриваются два типа переходов. Спонтанные (самопроизвольные) переходы с более высокого уровня на более низкий с излучением фотона, которые были введены А. Эйнштейном в 1916г. по аналогии с явлением естественной радиоактивности. Эти переходы происходят и в отсутствие внешнего электромагнитного поля на частоте перехода (10.17). Второй тип переходов – это вынужденные переходы, совершаемые только под воздействием внешнего электромагнитного поля на частоте перехода. Данные индуцированные внешним полем переходы могут происходить как с верхнего уровня на более низкий уровень с испусканием фотона, так и с низкого уровня на более высокий энергетический уровень с поглощением фотона. Понятие вынужденных переходов было введено А. Эйнштейном в 1916г. при анализе теплового равновесия между веществом и электромагнитным излучением. Вынужденное излучение возбужденных атомов лежит в основе работы лазера и определяет наиболее важные характеристики лазерного излучения.
Теория Бора относится к простейшему атому водорода и очень хорошо согласуется с экспериментальными исследованиями его спектров излучения и поглощения. Опыт показал, что представления о стационарных состояниях,
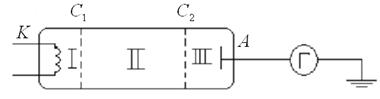
имеющих дискретные значения энергии, справедливы и для многоэлектронных атомов. В 1913г. Дж. Франк и Густав Герц поставили эксперимент, доказавший дискретность энергетического спектра многоэлектронного атома ртути, имеющего 80 электронов. В эксперименте исследовалась зависимость силы постоянного тока J от ускоряющего напряжения ![]() между катодом К и сеткой
между катодом К и сеткой ![]() (рис. 10.2). Между второй сеткой
(рис. 10.2). Между второй сеткой ![]() и анодом A приложено замедляющее напряжение
и анодом A приложено замедляющее напряжение ![]() . Напряжение между сетками
. Напряжение между сетками ![]() и
и ![]() равно нулю. Катод, анод и обе сетки помещены внутри стеклянного баллона, в котором находятся пары ртути и практически отсутствуют молекулы воздуха.
равно нулю. Катод, анод и обе сетки помещены внутри стеклянного баллона, в котором находятся пары ртути и практически отсутствуют молекулы воздуха.
В данной теме будет
рассмотрено решение задач на модель атома водорода по Бору и испускание и
поглощение света атомом.
Задача 1. Согласно теории Бора, радиус первой орбиты электрона
в атоме водорода равен 0,53 ∙ 10−10 м. Определите
радиус, скорость и частоту обращения электрона в атоме водорода для второй
орбиты.
|
ДАНО: |
РЕШЕНИЕ Радиусы стационарных Радиус второй боровской Второй закон Ньютона Сила, действующая на электрон Центростремительное ускорение электрона Тогда из второго закона Ньютона получаем, что Тогда скорость обращения электрона Частота обращения электрона |
|
|
Ответ: r2 = 2,12
∙ 10−10 м; υ2 = 1,1 ∙ 106 м/с; v2 = 8,3 ∙ 1014
Гц.
Задача 2. На диаграмме представлены энергетические уровни атома
водорода. Какой переход электрона с одной орбиты на другую сопровождается
излучением минимальной длины волны?
РЕШЕНИЕ
Кванты света излучаются только
в том случае, если переход электрона атома осуществляется с более высоких
энергетических уровней на более низкие. Поэтому переходы 2, 3 и 6 можно сразу
исключить.
Энергию кванта можно
определить, как разность энергий электрона на k и n
уровне.
Связью, между частотой и
длиной волны
Тогда
Следовательно
Теперь обратимся к
предложенной диаграмме и вспомним какие переходы соответствуют той или иной
области спектра атома водорода. И так, переход 1 — это переход с четвертого
энергетического уровня на второй, который соответствует линиям в видимой части
спектра (серия Бальмера).
Переход 4 — это переход на
первый (основной) энергетический уровень. Такой переход соответствует линиям
спектра водорода в ультрафиолетовой области (серия Лаймана).
И наконец, переход пять
соответствует линиям спектра в инфракрасной области (серия Пашена).
Теперь вспомним, что
инфракрасному излучению соответствует максимальная длина волны. Диапазон
видимого излучения лежит в пределах от 400 до 750 нм. А ультрафиолетовому
излучению соответствует диапазон длин волн от 200 до 400 нм.
Таким образом, можно
заключить, что излучению минимальной длины волны соответствует переход 4.
Ответ: излучению минимальной длины волны соответствует
переход 4.
Задача 3. Определите номер электронной орбиты, на которую
переходит электрон в атоме водорода, находившийся на втором энергетическом
уровне, при поглощении фотона с энергией 1,87 эВ. Энергия атома в основном
состоянии равна −13,6 эВ.
|
ДАНО: |
РЕШЕНИЕ Энергия электрона, находящегося на n-ой Энергия электрона, находящегося на 1-ой орбите Тогда энергия электрона, находящегося на n-ой орбите: Согласно закону сохранения энергия Тогда Номер электронной орбиты тогда определяется по формуле Полученный результат |
|
|
Ответ: электрон останется на втором энергетическом уровне.
Задача 4. Цинковую пластину освещают монохроматическим светом с
частотой, соответствующей переходу электрона в атоме водорода между уровнями с
энергией −13,6 эВ и −0,33 эВ. Вне пластинки имеется задерживающее
однородное электрическое поле напряженностью 103 В/м. На какое
максимальное расстояние от пластинки может удалиться фотоэлектрон, если работа
выхода для цинка 6,4 ∙ 10−19 Дж?
|
ДАНО: |
РЕШЕНИЕ Второй постулат Бора Уравнение Эйнштейна для фотоэффекта Теорема о кинетической энергии Работа задерживающего электрического поля Задерживающее напряжение Тогда с учетом последних трёх формул уравнение Эйнштейна Тогда |
|
|
Ответ: фотоэлектрон удалится от пластинки на 9,3 мм.
Задача 5. Протон, летящий горизонтально со скоростью 4,6 ∙
106 м/с, сталкивается с неподвижным свободным атомом гелия. После
удара протон отскакивает назад с вдвое меньшей скоростью, а атом переходит в
возбужденное состояние. Вычислите длину волны света, который излучает атом
гелия, возвращаясь в первоначальное состояние.
|
ДАНО: |
РЕШЕНИЕ При возвращении атома гелия Атом может излучать только Запишем закон сохранения энергии Закон сохранения импульса Скорость атома гелия из закона сохранения импульса равна Подставим полученное выражение в закон сохранения энергии Тогда длина волны Проверим размерность полученной формулы |
|
|
Ответ: атом гелия излучает свет с длиной волны 6,04 ∙
10−11 м.






