Расчет скорости колеса
Скорость колеса – это физическая величина, характеризующая скорость, с которой точка движется по окружности вокруг центра вращения.
Формула расчета скорости колеса:
V = 2 * π * R * n, где
V – линейная скорость;
R – радиус окружности;
n – угловая скорость.
Смотрите также перевод угловой скорости в линейную и наоборот – об/мин в м/с.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор для расчета скорости колеса по простой математической формуле в зависимости от скорости вращения и радиуса колеса. С помощью этой программы вы в один клик сможете рассчитать скорость колеса.
Угловая и линейная скорость
Переход от угловой к линейной скорости.
Сегодня смотрел на детей, катающихся на карусели, и подумал — а интересно, с какой скоростью они крутятся.
Подумав еще, понял, что ответить на этот вопрос очень просто, достаточно подсчитать, сколько оборотов в минуту они совершают.
Зная число оборотов в минуту, можно найти угловую скорость в радианах в секунду — за один оборот угол меняется на радиан, за минуту – радиан, и соответственно за секунду — радиан.
Это угловая скорость — радиан/сек. Переход к линейной тривиален — углу в 1 радиан соответствует дуга окружности равная радиусу, соответственно,
Вот и все, а ниже калькулятор. Скорость в м/с приводит к км/час, чтобы было понятнее.
Парадокс колеса
На приведённом рисунке хорошо видно, что все точки расположенные на радиусе колеса при совершении им одного оборота занимают те же самые места, на которых они были до начала вращения. Иными словами все точки радиуса колеса за один оборот перемещаются на одно и то же расстояние.
В то же время из школьного курса математики известно, что длина окружности равна:
Если прокатить колесо по поверхности и затем замерить пройденный им путь, то он будет точно соответствовать длине его окружности. Таким образом, две точки колеса: центр вращения и точка на внешней окружности проходят путь точно соответствующий приведённому расчёту. Но вот в отношении меньших радиусов мы приходим к выводу, что траектория их движения противоречит каноническому утверждению.
Так путь пройденный точкой, расположенной на половине радиуса колеса (r = R/2) должен быть равен:
C(r) = пиR, т.е. в половину меньше траектории точки расположенной на внешней окружности.
Но на самом деле она проходит фактически путь вдвое больший.
Соотношение фактически пройденной траектории и фактической дины окружности описываемый соответствующим радиусом растёт с уменьшением радиуса, фактически до бесконечности. Но в точке вращения он вновь возвращается к единице.
Самое удивительное в том, что если вырезать любую внутреннюю часть колеса и измерить его окружность, то она точно будет соответствовать вычисленной по канонической формуле.
Рассмотренный парадокс усиливается в случае, если колесо прокатывается с внешней стороны другой окружности. В этом случае траектория внутренних радиусов становится больше траектории точки на внешнем радиусе. И, наоборот, при прокатывании с внутренней стороны их траектория становится меньше.
Таким образом, можно сделать вывод о том, что траектория точек расположенных на внутренних радиусах колеса зависти не от величины собственного радиуса, а от радиуса внешней окружности. Что при этом происходит с материальными точками колеса расположенных на этих радиусах в пространстве остаётся загадкой.
Единственно разумное объяснение этого феномена предложил Галилей. Он считал, что поскольку фактическая траектория движения внутренних точек значительно больше фактической длины окружности, то точки внутренних радиусов проходят наблюдаемую траекторию с большей скоростью, чем это предписано им физикой [1]:
V = w*R, где w – угловая скорость вращения колеса.
Фактически линейная скорость внутренних точек колеса должна описываться уравнением:
V = n*w*r, где n = R/r
R – внешний радиус колеса;
r – внутренний радиус.
Иными словами линейная скорость точек внутренних радиусов является величиной постоянной и зависит только от внешнего радиуса колеса.
Вывод прямо скажем обескураживающий, но иного разумного объяснения пока ни кто не предложил.
Математически парадокс колеса в интерпретации Галилея описывается следующим уравнением:
dV = w*(R-r), где
dV – изменение скорости движения внутренних точек колеса;
R – внешний радиус колеса;
r – внутренний радиус колеса.
При r = R dV = 0
При r = 0 dV = w*R
Иными словами, изменение скорости точек расположенных на внутренних радиусах колеса меняется пропорционально от 0 на внешнем радиусе до V=w*R в центре вращения колеса. Поэтому ось колеса перемещается в пространстве с той же скоростью, которая соответствует линейной скорости вращающегося движения внешней окружности колеса при его прямолинейном движении. Соответственно такую же скорость имеют и все внутренние точки колеса.
С физической точки зрения полученный результат интерпретируется как движение жёсткого стержня, расположенного перпендикулярно направлению линейного движения оси вращения. Если рассмотреть движение такого стержня без привязки его к вращательному движению, то не трудно заметить, что все материальные точки стержня имеют одну и ту же скорость.
Преобразование вращательного движения в линейно-поступательное в данном случае решается методом рычага в рамках курса теоретической механики, которой к сожалению во времена Галилея ещё не существовало.
[1] Очевидно, именно по этому, этот парадокс практически не обсуждается в научной литературе.
Поскольку один из комментаторов так возбудился после прочтения этой статьи, что внёс меня в свои чёрные списки, и у меня нет возможности ему ответить иным путём, поэтому использую материал статьи не по назначению.
Сазонов Сергей 3 сентября 2019 года в 12:54
Писать рецензию на Вашу бредятину “Парадокс колеса” считаю излишним (много чести) – найдите в детском журнале “Квант” за 1975 год статью “ЦИКЛОИДА” . Там – примерно этот круг вопросов. Парадокса нет.
(конец цитаты)
К сожалению, найти указанный журнал в Интернете не смог, поэтому не смог лично ознакомиться со статьёй. Но уже само её название «ЦИКЛОИДА» говорит о том, Сергей Сазонов не видит разницы между прямой и циклоидой. В парадоксе колеса траектория меньшего радиуса разворачивается не в виде циклоиды, а в виде прямой линии. В этом то, как раз, и заключается парадокс. С другой стороны, то, что этим парадоксом интересовались Аристотель, Галилей, и возможно другие, не менее, замечательные умы человечества, говорит о том, что парадокс действительно существовал.
Уничижительное отношение к оппонентам явный признак ограниченной умственной деятельности. Конечно, можно было и не обращать внимание на подобные выпады, но, к сожалению, подобный уровень комментаторов встречается не так уж редко, поэтому считаю необходимым противостоять банальному хамству.
[spoiler title=”источники:”]
http://planetcalc.ru/556/
http://proza.ru/2019/09/02/1746
[/spoiler]
Условие задачи:
Найти скорость движения автомобиля, если его колесо диаметром 1,1 м делает 309 оборотов в минуту.
Задача №1.8.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(D=1,1) м, (nu=309) об/мин, (upsilon-?)
Решение задачи:
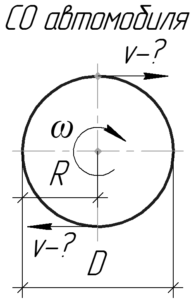Строго говоря, относительно Земли точки колеса при движении автомобиля совершают сложное движение, при котором они двигаются и поступательно, и вращательно. Но если перейти в систему отсчета (СО), связанную с автомобилем, то колеса будут уже совершать простое вращательное движение. При этом понятно, что линейная скорость крайних точек колеса равна скорости движения автомобиля (upsilon).
Эту линейную скорость можно определить по такой формуле, учитывая, что радиус равен одной второй диаметра:
[upsilon = omega R = frac{{omega D}}{2};;;;(1)]
Угловую скорость (omega) найдем, используя частоту вращения (nu), данную в условии, по такому выражению:
[omega = 2pi nu ;;;;(2)]
Подставим (2) в (1):
[upsilon = frac{{2pi nu D}}{2} = pi nu D]
Перед тем, как подставлять значения и вычислять ответ, переведем частоту вращения в систему СИ.
[309; [1/мин] = frac{{309}}{{60}}; [1/с] = frac{{103}}{{20}}; [1/с]]
[upsilon = 3,14 cdot frac{{103}}{{20}} cdot 1,1 = 17,79; м/с]
Ответ: 17,79 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.2 Какова угловая скорость вращения колеса, делающего 240 оборотов
1.8.4 С какой скоростью едет велосипедист, если колесо делает 100 об/мин. Радиус
1.8.5 Угол поворота колеса радиусом 0,2 м изменяется по закону phi=9,42t (рад)
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Связь со вторым законом Ньютона
Как вывести формулу центростремительного ускорения
Движение по циклоиде*
Немного из школьного курса математики и геометрии — как рассчитать скорость в зависимости от оборотов двигателя и выбранной передачи.
Для этого необходимо знать размерность шин и передаточные отношения главной пары и передач в коробке передач…
Формулы:
Диаметр колеса: Ширина шины, м х Профиль, % х 2 + Диаметр обода, дюймов х 2,54/100
Пример: шина 195/65R15: 0,195 х 0,65 х 2 + 15 х (2,54 / 100) = 0,63 м
Используя формулу диаметра колеса, можно посчитать на сколько изменится клиренс, поделив изменение диаметра на 2
Окружность колеса: Диаметр колеса х число Пи (3,14)
Пример: 0,63 м х 3,14 = 1,98 м
Используя формулу окружности колеса, можно посчитать на сколько процентов изменятся показания одометра и спидометра при замене дисков и/или резины, поделив новое значение окружности на старое и отняв единицу, и умножив полученное значение на сто
Скорость автомобиля при 1 000 об/мин на выбранной передаче: Окружность колеса делим на произведение передаточного отношения главной пары и передаточного отношения выбранной передачи, полученное число умножаем на 60 (минут в часе) и делим на 1 000 (метров в километре), далее полученное число умножаем на число оборотов двигателя в минуту (в нашем случае 1 000 об/мин)
Пример: [1,98 / (3,8 х 1 (пятая передача))] х (60 / 1 000) х 1 000 = 31 км/ч
Технические данные для расчетов (Hyundai Elantra MD 1.6 MPi 6AT на шинах 195/65R15):
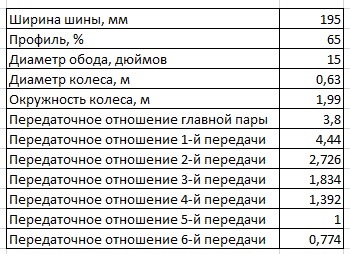
Непосредственно сами расчеты (Hyundai Elantra MD 1.6 MPi 6AT на шинах 195/65R15):
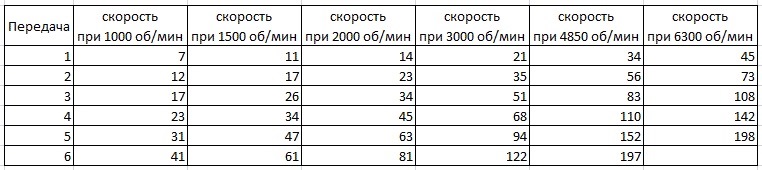
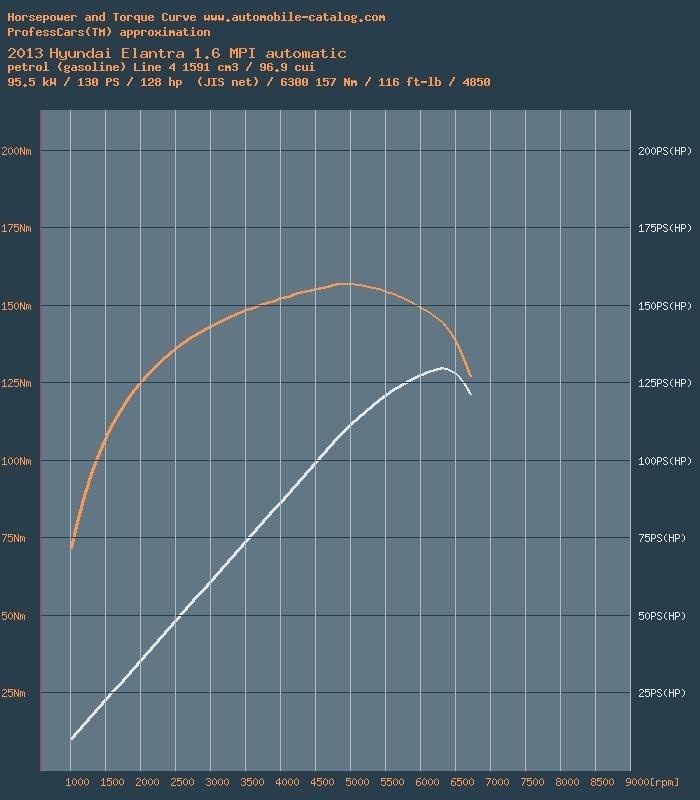
* Максимальная мощность на этом двигателе достигается при 6 300 об/мин, максимальный крутящий момент — при 4 850 об/мин
Запчасти на фото: KH130, 55006000
Технические характеристики для расчетов взяты с этого сайта www.automobile-catalog.com
Цена вопроса: 0 €
Пробег: 7 600 км
Линейная скорость через угловую, теория и онлайн калькуляторы
Линейная скорость через угловую
Определение
Мгновенной (истинной) скоростью ($overline{v}$) называют векторную физическую величину, равную производной от вектора перемещения по времени ($t$):
[overline{v}={mathop{lim }_{Delta tto 0} frac{Delta overline{r}}{Delta t}=frac{doverline{r}}{dt} }left(1right).]
$Delta overline{r}$- вектор перемещения материальной точки, это перемещение точка совершает за отрезок времени $Delta t$.
Выражение линейной скорости через угловую скорость
Скорость называют мгновенной, так как ее значение показывает величину скорости в определенный момент времени.
Так как вектор перемещения $Delta overline{r}$ направлен по хорде, которая соединяет две близкие точки криволинейной траектории движения частицы, при уменьшении расстояния между этими точками, вектор $Delta overline{r}$ занимает положение касательной к линии, по которой движется частица. Из определения (1) следует, что мгновенная скорость направлена по касательной к траектории движения.
Скорость прохождения пути ($s$) определяют:
[v={mathop{lim }_{Delta tto 0} frac{Delta s}{Delta t}=frac{ds}{dt}left(2right). }]
Мгновенную скорость называют линейной тогда, когда хотят подчеркнуть ее отличие от угловой скорости.
Если материальная точка движется по окружности, то ее положение характеризуют при помощи угла поворота ($varphi $), который образует радиус-вектор ($overline{r}$), определяющий положение рассматриваемой точки А с выделенным неизменным направлением от которого производят отсчет (рис.1).
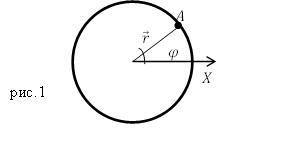
Быстроту изменения угла поворота $varphi $ характеризуют при помощи такой физической величины как угловая скорость. Обычно угловую скорость обозначают буквой $omega $. Угловая скорость равна:
[omega =frac{dvarphi }{dt}left(3right).]
Вращение называют равномерным, если угловая скорость постоянна $omega =const$. При равномерном вращении $omega $ можно называть угловой частотой.
Линейная скорость движения точки по окружности связана с угловой скоростью. Пусть точка проходит путь равный длине дуги XA (рис.1). Этот путь обозначим $s$. Если радиус окружности равен$ R=const$, то длину дуги найдем как:
[s=Rvarphi left(4right).]
Продифференцируем обе части выражения (4) по времени, имеем:
[frac{ds}{dt}=frac{dleft(Rvarphi right)}{dt}=Rfrac{dvarphi }{dt}left(5right).]
Мы видим, что в левой части получена величина линейной скорости, в правой части радиус окружности умножен на угловую скорость:
[v=Romega left(6right).]
Формула (6) будет справедлива при движении точки по криволинейной траектории отличной от окружности, но в этом случае $R$ – радиус кривизны траектории в месте нахождения частицы.
В векторном виде выражение (6) записывают так:
[overline{v}=overline{omega }times overline{r}left(7right),]
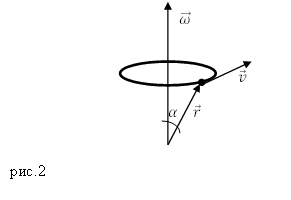
$overline{r}$ – вектор, соединяющий ось вращения и движущуюся точку (рис.2). Модуль скорости, используя формулу (7) найдем как:
[v=omega r{sin alpha left(8right), }]
где $alpha $ – угол между вектором угловой скорости и $overline{r}.$
Угловая скорость через линейную
Исходя из приведенных выше формул угловую скорость можно выразить через линейную. При движении по окружности:
[omega =frac{v}{R}left(9right).]
Или используя формулу (8) угловую скорость выразим как:
[omega =frac{v}{r{sin alpha }}left(10right).]
Примеры задач с решением
Пример 1
Задание. Диск равномерно вращается вокруг оси (O), перпендикулярной его плоскости, проходящей через его центр (рис.3). Линейная скорость точки A равна $v_1$, Точка B находится на расстоянии $Delta l$ ближе к оси и имеет лилейную скорость $v_2$. Какова угловая скорость вращения диска ($omega $)?
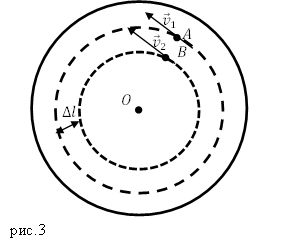
Решение. Основой для решения задачи будет формула:
[omega =frac{v}{R}left(1.1right).]
Угловые скорости движения точки A и B одинаковы (${omega }_A={omega }_B$), запишем выражение для каждой из этих скоростей используя (1.1):
[{omega }_A=frac{v_1}{R_1};; {omega }_B=frac{v_2}{R_2}left(1.2right).]
$R_1$ – расстояние от точки O до точки A; $R_2=R_1-Delta l$ – расстояние от точки B до точки O. Приравняем правые части выражений (1.2), выразим расстояние $R_1$:
[frac{v_1}{R_1}=frac{v_2}{R_1-Delta l}to R_1=frac{Delta lcdot v_1}{v_1-v_2}left(1.3right).]
Найдем угловую скорость точки A:
[{omega }_A=v_1cdot frac{v_1-v_2}{Delta lcdot v_1}=frac{v_1-v_2}{Delta l}.]
Ответ. Угловая скорость всех точек диска равна $omega =frac{v_1-v_2}{Delta l}$
Пример 2
Задание. Колесо радиусом R=1 м вращается так, что угол поворота изменяется в соответствии с
законом: $varphi left(tright)=2+5t^3(рад)$. Определите, какова линейная скорость точек обода колеса в момент времени,
равный $t’=1 (с)$.
Решение. В качестве основы для решения задачи воспользуемся формулой:
[v=Romega left(2.1right).]
Используя уравнение $varphi left(tright)$ и связь угла поворота и угловой скорости найдем $omega $:
[omega =frac{dvarphi }{dt}=frac{d}{dt}left(A+Bt^3right)=3Bt^2(2.2).]
Подставим результат (2.2) в (2.1), имеем:
[v=Rcdot 3Bt^2.]
Вычислим искомую скорость:
[v=1cdot 3cdot 5cdot 1^2=15 left(frac{м}{с}right).]
Ответ. $vleft(t’right)=15frac{м}{с}$
Читать дальше: масса и плотность вещества.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
