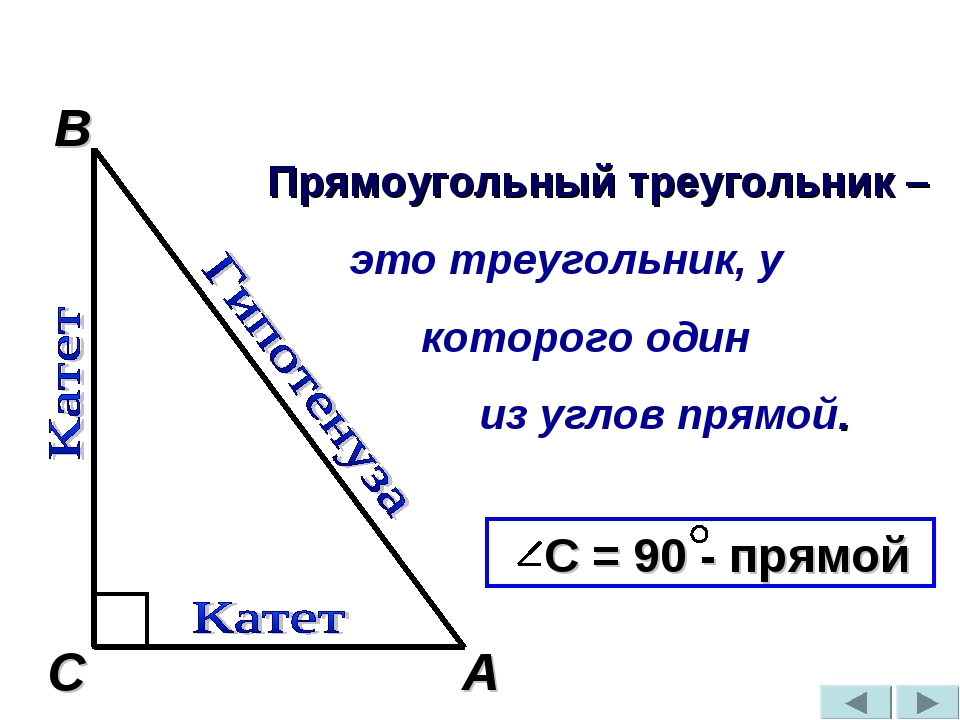
Прямоугольный треугольник – это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
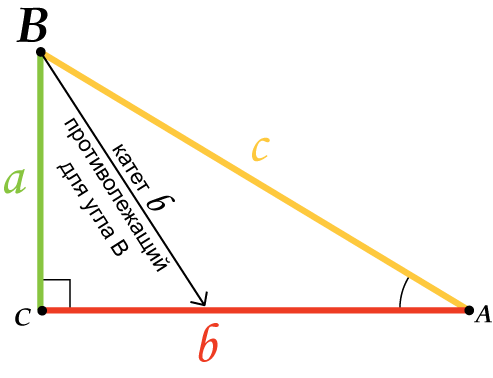
Для острого угла $В$: $АС$ – противолежащий катет; $ВС$ – прилежащий катет.
Для острого угла $А$: $ВС$ – противолежащий катет; $АС$ – прилежащий катет.
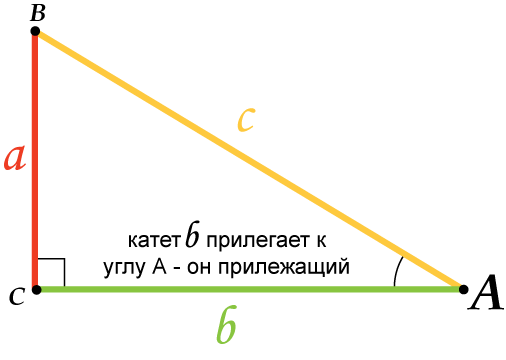
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
$sinB={AC}/{AB};$
$cosB={BC}/{AB};$
$tgB={AC}/{BC};$
$ctgB={BC}/{AC}.$
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
$sin BOA=sin BOC;$
$cos BOA=-cos BOC;$
$tg BOA=-tg BOC;$
$ctg BOA=-ctg BOC.$
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
$S={AC∙BC}/{2}$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√{91}$. Найдите косинус внешнего угла при вершине $В$.
Решение:
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
$cosABD=-cosABC$
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
$cosABC={ВС}/{АВ}$
Катет $ВС$ мы можем найти по теореме Пифагора:
$ВС=√{10^2-√{91}^2}=√{100-91}=√9=3$
Подставим найденное значение в формулу косинуса
$cos ABC = {3}/{10}=0,3$
$cos ABD = – 0,3$
Ответ: $-0,3$
Пример:
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA={4}/{5}, AC=9$. Найдите $АВ$.
Решение:
Распишем синус угла $А$ по определению:
$sinA={ВС}/{АВ}={4}/{5}$
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
$АС^2+ВС^2=АВ^2$
$9^2+(4х)^2=(5х)^2$
$81+16х^2=25х^2$
$81=25х^2-16х^2$
$81=9х^2$
$9=х^2$
$х=3$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
Ответ: $15$
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
$CD^2=DB∙AD$
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
$CB^2=AB∙DB$
$AC^2=AB∙AD$
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
$AC∙CB=AB∙CD$

Прямоугольный треугольник
Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть 90 градусов).
Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.
Связанные определения[править | править код]
- Сторона, противоположная прямому углу, называется гипотенузой (сторона c на рисунке выше).
- Стороны, прилегающие к прямому углу, называются катетами. Сторона a может быть идентифицирована как прилежащая к углу В и противолежащая углу A, а сторона b — как прилежащая к углу A и противолежащая углу В.
Типы прямоугольных треугольников[править | править код]
- Если катеты равны, то треугольник называется равнобедренным прямоугольным треугольником.
- Если длины всех трёх сторон прямоугольного треугольника являются натуральными числами, то треугольник называется пифагоровым треугольником, а длины его сторон образуют так называемую пифагорову тройку.
Признаки равенства прямоугольных треугольников[править | править код]
- По двум катетам: если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
- Этот признак немедленно следует из первого признака равенства треугольников, так как у двух треугольников будут равны по два катета и прямой угол.
- По катету и прилежащему острому углу: если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны
- Этот признак немедленно следует из второго признака равенства треугольников, так как у двух треугольников будут равен один катет, прилежащий к нему угол и прямой угол.
- По гипотенузе и острому углу: если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Этот признак следует из второго признака равенства треугольников, так как вторые острые углы будут равны по теореме о сумме углов треугольника и у треугольников будут равны гипотенузы и два прилежащих к ней угла.
- По гипотенузе и катету: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
- Этот признак докажем так. Наложим два треугольника друг на друга так, чтобы получить равнобедренный треугольник, то есть совместим их равными катетами так, чтобы углы, лежащие при этих катетах, лежали в разных плоскостях. Так как гипотенузы равны, получившийся треугольник — равнобедренный, тогда углы при основании равны. Тогда два прямоугольных треугольника будут равны по гипотенузе и острому углу.
- По катету и противолежащему острому углу: если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Этот признак доказывается так: если один из острых углов первого треугольника равен острому углу второго треугольника, то второй острый угол будет известен по теореме о сумме углов треугольника. Так как второй острый угол прилегает к катету, то далее равенство треугольников будет доказываться по предыдущей теореме.
Свойства[править | править код]
Далее предполагаем, что 


- (Теорема Пифагора)
- Площадь прямоугольного треугольника равна половине произведения двух его катетов. То есть,
Высота[править | править код]

Высота прямоугольного треугольника.
Если высота проведена к гипотенузе, то треугольник делится на два меньших треугольника, подобных исходному и подобных друг другу. Из этого следует, что в обозначениях, показанных на диаграмме:[1]
- Высота есть среднее геометрическое (среднее пропорциональное) двух образованных ею сегментов гипотенузы, то есть
-
(иногда это называют теоремой высоты прямоугольного треугольника)
- Каждый катет треугольника есть среднее геометрическое гипотенузы и проекции катета на гипотенузу, то есть
- В прямоугольном треугольнике высота, опущенная из вершины прямого угла на гипотенузу, делит гипотенузу в таком отношении, в каком находятся квадраты прилежащих катетов, то есть
Кроме того, высота, опущенная на гипотенузу, связана с катетами прямоугольного треугольника соотношением:[2][3]
и
Также если прямоугольный треугольник является равнобедренным, то высота, опущенная на гипотенузу будет равна:
-
, где
— это радиус вписанной окружности, а
— серебряное сечение.
Характеристики[править | править код]
Треугольник 





Тригонометрические соотношения[править | править код]
Тригонометрические функции для острых углов можно определить как отношения сторон прямоугольного треугольника. Для любого данного угла можно построить прямоугольный треугольник, содержащий такой угол, и со сторонами: противолежащим катетом, прилежащим катетом и гипотенузой, связанными с этим углом определёнными выше соотношениями. Эти отношения сторон не зависят от конкретного выбранного прямоугольного треугольника, а зависят только от заданного угла, так как все треугольники, построенные таким образом, являются подобными. Если для заданного угла α, противолежащий катет, прилежащий катет и гипотенузу обозначить a, b и c соответственно, то тригонометрические функции имеют вид:
И таким образом:
- Катет, противолежащий углу, равен произведению гипотенузы на синус этого угла
- Катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла
- Катет, противолежащий углу, равен произведению второго катета на тангенс угла
- Катет, прилежащий углу, равен произведению второго катета на котангенс угла
- Гипотенуза равна отношению катета к синусу противолежащего угла, и/или частному отношению катета и косинуса прилежащего угла (угла между ними)
Специальные прямоугольные треугольники[править | править код]
Значения тригонометрических функций можно точно оценить для определённых углов, используя прямоугольные треугольники с особыми значениями углов. К таким треугольникам относятся треугольник 30-60-90, который можно использовать для оценки тригонометрических функций для любых значений, кратных π/6, и треугольник 45-45-90 (равнобедренный прямоугольный), который можно использовать для оценки тригонометрических функций для значений, кратных π/4.
В частности,
- Катет, лежащий против острого угла в 30° (и соответственно, прилежащий к углу в 60°), равен половине гипотенузы.
Теорема Фалеса[править | править код]

Медиана прямого угла треугольника
Теорема Фалеса утверждает, что если какая-нибудь точка A лежит на окружности диаметра BC (за исключением самих точек B и C), то △ABC представляет собой прямоугольный треугольник с прямым углом A. Обратное утверждение таково: если прямоугольный треугольник вписан в окружность, то гипотенуза будет её диаметром. Следствием является то, что длина гипотенузы равна удвоенному расстоянию от вершины прямого угла до середины гипотенузы. Верно также, что центр окружности, описывающей прямоугольный треугольник, является серединой гипотенузы, а её радиус равен половине длины гипотенузы.
Другие свойства[править | править код]
Радиус вписанной окружности в прямоугольный треугольник с катетами a и b и гипотенузой c равен:
Если отрезки длиной p и q, исходящие из вершины C, делят гипотенузу на три равных отрезка длины c/3, то:[5]:pp. 216-217
Прямоугольный треугольник является единственным треугольником с двумя, а не тремя, отличными друг от друга вписанными квадратами.[6]
Пусть h и s (h>s) являются сторонами двух квадратов, вписанных в прямоугольный треугольник с гипотенузой c. Тогда:
Периметр прямоугольного треугольника равен сумме двух радиусов вписанной и четырёх описанных окружностей:

Если заданы S и r, то стороны треугольника находятся по формулам:
Еще важное соотношение:
, где
– длина биссектрисы, исходящей из острого угла B, с – гипотенуза.
Во всех прямоугольных треугольниках медиана, опущенная на гипотенузу, равна половине гипотенузы.
Окружность девяти точек касается описанной окружности того же треугольника в единственном случае, если треугольник прямоугольный. При этом касание двух окружностей идёт в вершине прямого угла треугольника.
Вариации и обобщение[править | править код]
- Четырёхугольники с перпендикулярными парами элементов: с 2 перпендикулярными сторонами и с 2 перпендикулярными диагоналями,- вырождаются в прямоугольный треугольник, если длина одной нужной стороны (из их 4 сторон), лежащей вблизи прямого угла или же опирающейся концами на этот угол, стремится к нулю.
- Если в прямоугольном треугольнике провести отрезок, параллельный его гипотенузе, то он разрежет этот треугольник на подобный ему же прямоугольный треугольник и трапецию. При этом сумма углов при одном из оснований трапеции будет равна 90°, а продолжения боковых сторон трапеции пересекутся под прямым углом. Тогда отрезок, соединяющий середины оснований указанной трапеции, равен полуразности оснований. Данное утверждение обобщает свойство: медиана прямоугольного треугольника, опущенная из вершины прямого угла на гипотенузу, равна половине длины гипотенузы.
Примечания[править | править код]
- ↑ Wentworth p. 156
- ↑ Voles, Roger, «Integer solutions of
,» Mathematical Gazette 83, July 1999, 269—271.
- ↑ Richinick, Jennifer, “The upside-down Pythagorean Theorem, ” Mathematical Gazette 92, July 2008, 313—317.
- ↑ Andreescu, Titu and Andrica, Dorian, «Complex Numbers from A to…Z», Birkhäuser, 2006, pp. 109—110.
- ↑ Posamentier, Alfred S., and Salkind, Charles T. Challenging Problems in Geometry, Dover, 1996.
- ↑ Bailey, Herbert, and DeTemple, Duane, «Squares inscribed in angles and triangles», Mathematics Magazine 71(4), 1998, 278—284.
Ссылки[править | править код]
- Calculator for right triangles
- Weisstein, Eric W. Right Triangle (англ.) на сайте Wolfram MathWorld.
- Wentworth, G.A. A Text-Book of Geometry (неопр.). — Ginn & Co., 1895.
Отношение сторон прямоугольного треугольника
Свойство. Сумма двух острых углов прямоугольного треугольника равна 90 0
Свойство. Катет прямоугольного треугольника, лежащий против угла в 30 0 , равен половине гипотенузы.
Теорема. Два прямоугольных треугольника равны, если катеты одного равны катетам другого.
Теорема. Два прямоугольных треугольника равны, если гипотенуза и катет одного равны гипотенузе и катету другого.
Теорема. Два прямоугольных треугольника равны, если острый угол и сторона одного равны острому углу и стороне другого.
Теорема Пифагора
Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема, обратная теореме Пифагора. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Соотношение углов и сторон прямоугольного треугольника
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Важные значения! ИХ ОБЯЗАТЕЛЬНО ЗАПОМНИТЬ!
Высота прямоугольного треугольника, проведенного из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой, проведенной из вершины прямого угла.
Прямоугольные треугольники
Прямоугольный треугольник – это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В$: $АС$ – противолежащий катет; $ВС$ – прилежащий катет.
Для острого угла $А$: $ВС$ – противолежащий катет; $АС$ – прилежащий катет.
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $<1>/<2>$ | $<√2>/<2>$ | $<√3>/<2>$ |
| $cosα$ | $<√3>/<2>$ | $<√2>/<2>$ | $<1>/<2>$ |
| $tgα$ | $<√3>/<3>$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $<√3>/<3>$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√<91>$. Найдите косинус внешнего угла при вершине $В$.
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
Катет $ВС$ мы можем найти по теореме Пифагора:
Подставим найденное значение в формулу косинуса
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA=<4>/<5>, AC=9$. Найдите $АВ$.
Распишем синус угла $А$ по определению:
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
Все формулы прямоугольного треугольника – примеры расчетов
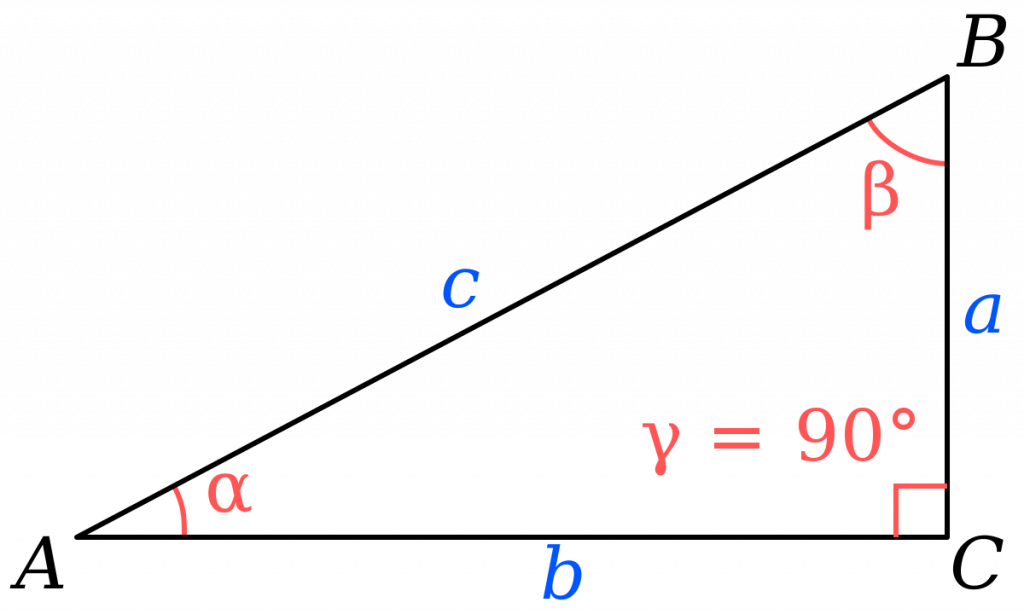
Формулы
1. Сумма острых углов прямоугольного треугольника равна 90 0 :
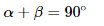
2. Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе:
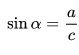
3. Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе:
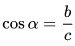
4. Тангенс острого угла равен отношению противолежащего катета к прилежащему катету:
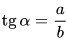
5. Котангенс острого угла равен отношению прилежащего катета к противолежащему катету:
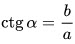
6. Секанс острого угла равен отношению гипотенузы к прилежащему катету:
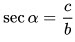
7. Косеканс острого угла равен отношению гипотенузы к противолежащему:
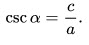
8. Катет, противолежащий углу, равен произведению гипотенузы на синус этого угла:
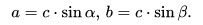
9. Катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла:
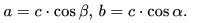
10. Катет, противолежащий углу, равен произведению второго катета на тангенс угла:
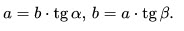
11. Катет, прилежащий углу, равен произведению второго катета на котангенс угла:
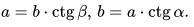
12. Гипотенуза равна отношению катета к синусу противолежащего угла, и/или частному отношению катета и косинуса прилежащего угла (угла между ними):
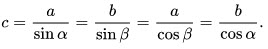
13. Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
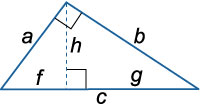


14. Медианы, проведенные к катетам прямоугольного треугольника:
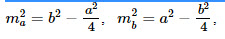
15. Медиана, проведенная к гипотенузе:
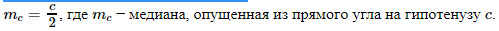
16. Радиус окружности, описанной около прямоугольного треугольника:
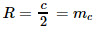
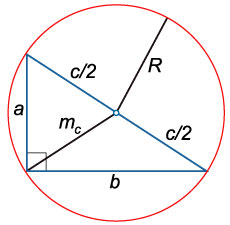
17. Радиус окружности, вписанной в прямоугольный треугольник:
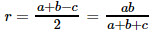
18. Площадь прямоугольного треугольника равна половине произведения катетов треугольника:
[spoiler title=”источники:”]
http://examer.ru/ege_po_matematike/teoriya/pryamougolnie_treugolniki
http://nauka.club/matematika/geometriya/formuly-pryamougolnogo-treugolnika.html
[/spoiler]
Все формулы сторон прямоугольного треугольника
Как найти,
гипотенузу или катеты в прямоугольном треугольнике.

a, b – катеты
c – гипотенуза
α, β – острые углы
Формулы для катета, (a):

Формулы для катета, (b):

Формулы для гипотенузы, (c):


Формулы сторон по теореме Пифагора, (a,b):



- Подробности
-
Автор: Administrator
-
Опубликовано: 12 октября 2011
-
Обновлено: 13 августа 2021
Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² – b²
b = √c² – a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² – 4² = √25 – 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см



















