ПРАВИЛА ПО МАТЕМАТИКЕ 2 класс
Вопрос
Правило
Пример
Компоненты
сложения:
Слагаемое
+ слагаемое = сумма
2
+ 3 = 5
Как найти
неизвестное слагаемое?
Чтобы
найти неизвестное слагаемое, надо
из суммы
вычесть известное слагаемое
?
+ 3 = 5
5
– 3 = 2
Переместительное
свойство сложения
От
перестановки слагаемых сумма не меняется.
a + b= b + a
Сочетательное
свойство сложение
Чтобы к сумме двух чисел прибавить
третье число, можно к первому числу прибавить сумму второго и
третьего числа.
(a + b) + c = a + (b + c)
Вычитание
суммы из числа
Чтобы вычесть суммы из числа, можно
сначала вычесть одно слагаемое, а потом другое.
а – (b + c) = (a – c) – b
Вычитание
числа из суммы
Чтобы вычесть число из суммы, можно вычесть
его из одного слагаемого и прибавить второе слагаемое.
(a + b) – c = f + (b – c)
Компоненты
вычитания
Уменьшаемое
– вычитаемое = разность
7 – 4 = 3
Как найти
уменьшаемое?
Чтобы
найти уменьшаемое, надо
к разности прибавить вычитаемое.
?
– 4 = 3
4
+ 3 = 7
Как найти неизвестное
вычитаемое?
Чтобы
найти вычитаемое, надо
из уменьшаемого вычесть разность.
7
– ? = 3
7
– 3 = 4
Как
узнать, на сколько одно число больше или меньше другого?
Чтобы
узнать, на сколько одно число больше или меньше другого, надо из
большего вычесть меньшее.
На
сколько 8 больше 5?
8
– 5 = 3
Однозначные
числа
Числа, которые
записывают одной цифрой называют однозначными (содержат
только разряд единиц)
2,
3, 6. 8
Двузначные
числа
Числа,
которые записывают двумя цифрами
называют двузначными.
(содержат
разряд десятков и разряд единиц)
24 = 2 десятка 4
единицы
38 = 3 десятка 8
единиц
50 = 5 десятков 0
единиц
Трёхзначные
числа
Числа,
которые записывают тремя цифрами
называют трехзначными.
(содержат
разряд сотен, разряд десятков и разряд единиц)
723 = 7 сотен 2
десятка 3 единицы
100 = 1 сотня о
десятков о единиц
Какие
числа называют круглыми?
У круглых двузначных
и трехзначных чисел в разряде единиц записывают 0
10,
20, 30, 40, 50, 600
Как к
двузначному числу прибавить двузначное число?
Чтобы
сложить двузначные числа надо
к
десяткам прибавить десятки, к единицам – единицы
23 + 35
= 58
2
дес + 3 дес = 5 дес
3
ед + 5 ед = 8 ед
5
дес 8 ед = 58
Как из
двузначного числа вычесть двузначное число?
Чтобы
вычесть из двузначного числа двузначное число надо
из
десятков вычесть десятки, из единиц – единицы
32 – 21 = 11
3
дес – 2 дес = 1 дес
2
ед – 1 ед = 1 ед
1
дес 1 ед = 11
Как к
трехзначному числу прибавить трехзначное число?
Чтобы
сложить трехзначные числа надо
к
сотням прибавить сотни, к десяткам прибавить десятки, к единицам – единицы
123 + 135
= 258
1
сот + 1 сот = 2 сот
2
дес + 3 дес = 5 дес
3
ед + 5 ед = 8 ед
2
сот 5 дес 8 ед = 158
Как из
трехзначного числа вычесть трехзначное число?
Чтобы
вычесть из трехзначного числа трехзначное число, надо
из
сотен вычесть сотни, из десятков вычесть десятки, из единиц – единицы
132 – 121 = 11
1
сот- 1 сот = 0 сот
3
дес – 2 дес = 1 дес
2
ед – 1 ед = 1 ед
1
дес 1 ед = 11
Как найти часть?
Чтобы
найти часть, надо из целого вычесть известную часть.
76
– 12 = 64
Как найти
целое?
Чтобы
найти целое, надо части сложить.
12
+ 64 = 76
Что
называют разностью?
Разностью
называют то, на сколько одно число больше или меньше другого.
12 < 23
Как найти
разность?
Чтобы
найти разность, надо из большего числа вычесть меньшее.
12 < 23
23
– 12 = 11
Что
называют умножением?
Умножение
– это сложение одинаковых слагаемых.
5
+ 5 + 5 + 5…
Как называются
компоненты умножения?
Множитель · множитель =
произведение
а · b =
с
Переместительное
свойство умножения
От
перестановки множителей произведение не изменяется.
а · b = b · а
Взаимосвязь
компонентов умножения
При
увеличении множителей произведение увеличивается.
При
уменьшении множителей произведение уменьшается.
2 · 3 =
6
3 · 4 =
12
1 · 2 =
2
Что
называют делением?
Деление
– это действие, обратное умножению.
а · b =
с
с
: а = б
с
: б = а
Название
компонентов деления
Делимое
: делитель = частное
с
: а = б
Особые
случаи умножения
При
умножении любого числа на 0 получится 0.
При
умножении любого числа на 1 получится то же самое число.
2 · 0 =
0
2 · 1 =
2
Особые
случаи деления
При
делении числа на себя получается 1.
При
делении числа на 1 получается то же самое число.
При
делении нуля на любое число, получится 0.
Делить
на 0 нельзя!
2
: 2 = 1
2
: 1 = 2
0
: а = 0
Четные
числа
Числа,
которые делятся на 2, называют четными.
2,
4, 6, 8, 10…
Нечетные
числа
Числа,
которые не делятся на 2, называют нечетными.
1,
3, 5, 7, 9, 11…
Как найти
неизвестный множитель?
Чтобы
найти неизвестный множитель, надо произведение разделить на
известный множитель.
а · ? =
с
с
: а = б
? · b =
с
с
: б = а
Увеличение
и уменьшение на несколько единиц
Увеличить
число на а единиц значит прибавить а единиц.
Уменьшить
число на а единиц
– вычесть а единиц.
с
+ а
с
– а
Увеличение
и уменьшение в несколько раз
Увеличить
число в а раз значит
умножить его на а.
Уменьшить
число в а раз –
разделить его на а.
с · а
с
: а
Порядок
действий
1.
В выражении со скобками первым выполняется действие в скобках.
2.
В выражении со скобками вторым выполняется деление или умножение.
3.
Последним выполняется действие сложение или вычитание.
Все
действия выполняются слева направо!
4
2 1 5 3
с – d ·
(b – а) + m : n
Кратное
Кратное чисел
а и б– это число с, которое делится на а и б.
12
: 2
12
: 6
12
– кратное чисел 2 и 6.
Делитель
Делитель –
это число (а или б), на которое делится с.
12
: 2
12
: 6
2
и 6 делители числа 12.
Уравнение
Уравнение
– это равенство с неизвестным компонентом.
23
+ х = 41
Что значит
решить уравнение?
Решить
уравнение – значит найти значение неизвестного компонента (корня).
х
= ?
Прямоугольник
Четырехугольник, у
которого все углы прямые, называют прямоугольником.
![]()
Квадрат
Квадрат
– это прямоугольник, у которого все стороны равны.
![]()
Длина
прямоугольника
Противоположные
стороны у прямоугольника равны. Большая сторона называется длиной.
![]()
Ширина
прямоугольника
Меньшая
сторона прямоугольника называется шириной.
Мерка
Мерка
– это единица измерения величин.
м,
см, кг, г, л, ч….
Величина
Величина
– это такое свойство предметов, которое можно измерить и результаты измерений
выразить числом.
длина,
масса, ёмкость, время, площадь
Периметр
Периметр
прямоугольника – это сумма длин всех его сторон.
P = a + a + b + b
Площадь
Площадь – это
часть плоскости, которую занимает геометрическая фигура.
![]()
Площадь
прямоугольника
Площадь
прямоугольника равняется произведению его длины и ширины.
S = a · b
Как найти
сторону прямоугольника?
Чтобы
найти длину одной стороны прямоугольника, надо площадь разделить на
длину известной стороны.
а
= S : b
b
= S : а
Виды углов
Острый (меньше
прямого угла), прямой, тупой(больше прямого угла).
![]()
![]()
![]()
![]()
![]()
![]()
- Главная
- Справочники
- Справочник по математике для начальной школы
- Вычитание
Познакомимся с вычитанием.
Рассмотрим числовой ряд и вспомним, в каком порядке идут числа.

Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.
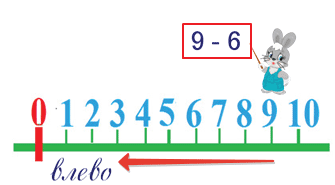
Какое действие выполняет заяц?
Вычитает число 6.
Из какого числа он вычитает число 6?
Из числа 9. Мы поставили зайчика на число 9.
В какую сторону он пойдёт?
Влево, потому что у него на табличке знак минус.
Сколько шагов влево сделает зайчик? 6.
На каком делении он остановится? На числе 3.
Когда вычитаем, становится меньше.
Чем левее, тем числа меньше.
9 – 6 = 3
Рассмотрим еще один пример.
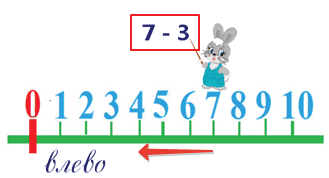
Какое действие выполняет заяц?
Вычитает число 3.
Из какого числа он вычитает число 3?
Из числа 7. Мы поставили зайчика на число 7.
В какую сторону он пойдёт?
Влево, потому что у него на табличке знак минус.
Сколько шагов влево сделает зайчик? 3.
На каком делении он остановится? На числе 4.
Когда вычитаем, становится меньше.
Чем левее, тем числа меньше.
7 – 3 = 4
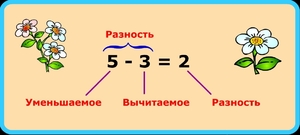
Как называются числа при вычитании?
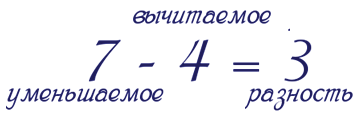
Число, из которого вычитают, становится МЕНЬШЕ, уменьшается, поэтому его называют “уменьшаемое”.
Число, которое вычитают, называют “вычитаемое”.
Число, которое получается в результате вычитания, называют “разность”.

Рассмотри рисунок.

У жонглёра было 9 шариков.
Когда несколько шариков упало, осталось ещё 5 шариков.
Сколько шариков упало?
Каким действием будем находить? Вычитанием.
9 – 4 = 5
Как называются числа при вычитании?
9 – уменьшаемое
4 – вычитаемое
5 – разность
Как найти неизвестное вычитаемое
Рассмотри рисунок.

У жонглера было 9 шариков. Когда несколько шариков упало, осталось 5. Упали, значит, убрали.
Решаем вычитанием. Что нужно найти?
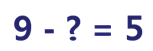
Нужно найти вычитаемое.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
9 – 5 = 4
Вычитаемое равно 4.
Упало 4 шарика.
Как найти неизвестное уменьшаемое

Что известно?
Вычитаемое – 4.
Разность – 5.
Нужно найти уменьшаемое.
Чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
5 + 4 = 9
Проверка вычитания
Если к разности прибавить вычитаемое, получится уменьшаемое.
Именно эта связь между разностью, уменьшаемым и вычитаемым используют для проверки вычитания.
Например, 35 – 15 = 20.
Правильно ли произведено вычисление? Можно проверить так:
20 + 15 = 35, мы к разности прибавили вычитаемое и получили уменьшаемое. Значит, вычисление произведено верно и пример решен правильно.
Советуем посмотреть:
Табличное вычитание
Письменное вычитание в столбик
Правило встречается в следующих упражнениях:
1 класс
Страница 25,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 53,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 66,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 71,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 73,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 16,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 30,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 34. Урок 23,
Петерсон, Учебник, часть 1
Страница 5. Урок 3,
Петерсон, Учебник, часть 2
Страница 46. Урок 24,
Петерсон, Учебник, часть 3
2 класс
Страница 81,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 5. ПР 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 25. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 58. ПР 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 59. ПР 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 40,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 41,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 24. Урок 12,
Петерсон, Учебник, часть 1
3 класс
Страница 14,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 21,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 74,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 78,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 8. Урок 2,
Петерсон, Учебник, часть 1
Страница 12. Урок 4,
Петерсон, Учебник, часть 1
Страница 103. Урок 39,
Петерсон, Учебник, часть 1
Страница 32. Урок 15,
Петерсон, Учебник, часть 3
Страница 65. Урок 28,
Петерсон, Учебник, часть 3
4 класс
Страница 40,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 8,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 52,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 43. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 84. Тест 3. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 31,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 89,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 90,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 16,
Моро, Волкова, Рабочая тетрадь, часть 2
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
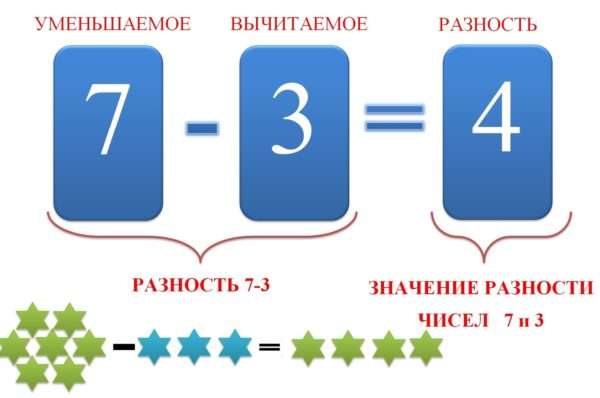 Термины
Термины
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
- разницу между двумя числами,
- это показатель того, насколько одно количество больше или меньше другого,
- это результат, полученный при выполнении вычитания такое определение предлагает школьная программа.
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
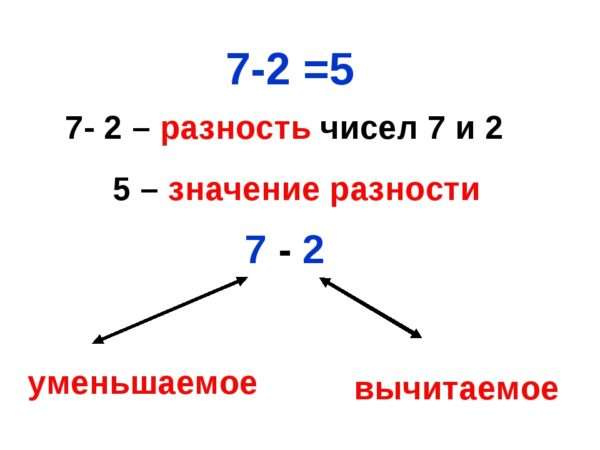
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
| Уменьшаемое | Вычитаемое | Разность | ||
| 18 | 11 | = | 7 | |
| 14 | 5 | = | 9 | |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
Памятка по математике
Название и правила нахождения компонентов при сложении, вычитании, умножении и делении
5 + 2 = 7
первое слагаемое второе слагаемое сумма
(Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое)
8 – 3 = 5
уменьшаемое вычитаемое разность
(Чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.)
4 x 6 = 24
первый множитель второй множитель произведение
(Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель)
21 : 3 = 7
делимое делитель частное
(Чтобы найти неизвестное делимое, нужно делитель умножить на частное,
Чтобы найти неизвестный делитель, нужно делимое разделить на частное)
 Слово «разность» может употребляться во многих значениях. Это может означать и разницу чего-либо, например, мнений, взглядов, интересов. В некоторых научных, медицинских и других профессиональных сферах этим термином обозначают разные показатели, к примеру, уровня сахара в крови, атмосферного давления, погодных условий. Понятие «разность», как математический термин тоже существует.
Слово «разность» может употребляться во многих значениях. Это может означать и разницу чего-либо, например, мнений, взглядов, интересов. В некоторых научных, медицинских и других профессиональных сферах этим термином обозначают разные показатели, к примеру, уровня сахара в крови, атмосферного давления, погодных условий. Понятие «разность», как математический термин тоже существует.
…
Оглавление:
- Арифметические действия с числами
- Разность в математике
- Видео: Математика 6 Делимость суммы и разности чисел
- Как найти разницу величин
- Математические действия с разностью чисел
- Видео: Математика 2 класс. Разность двухзначных чисел
- Простые примеры
- Более сложные примеры
- Математика для блондинок
- Видео: Разность двух отрицательных целых чисел. Математика 6 класс.
Арифметические действия с числами
Основными арифметическими действиями в математике являются:
- сложение;
- вычитание;
- умножение;
- деление.
Каждый результат этих действий также имеет своё название:
- сумма — результат, получившийся при сложении чисел;
- разность — результат, получившийся при вычитании чисел;
- произведение — результат умножения чисел;
- частное — результат деления.
Это интересно: что такое модуль числа?
Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:
- сумма — прибавить;
- разность — отнять;
- произведение — умножить;
- частное — разделить.
Разность в математике
Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:
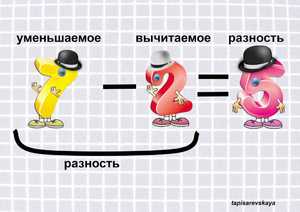 Разность чисел означает, насколько одно из них больше другого.
Разность чисел означает, насколько одно из них больше другого.- Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.
- Это вычитание одного числа из другого.
- Это цифра, составляющая остаток при минусовании двух величин.
- Это величина, являющаяся результатом вычитания двух значений.
- Разность показывает количественное различие между двумя цифрами.
- Это результат одного из четырёх арифметических действий, которым является вычитание.
- Это то, что получится, если из уменьшаемого отнять вычитаемое.
Видео: Математика 6 Делимость суммы и разности чисел
И все эти определения являются верными.
Как найти разницу величин
Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:
- Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.
Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:
- Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.
Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?
- Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).
- Вычитаемое — это математическое число, которое вычитают из уменьшаемого.
Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:
- Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
- Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
Математические действия с разностью чисел
Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.
Видео: Математика 2 класс. Разность двухзначных чисел
Простые примеры
- Пример 1. Найти разницу двух величин.
Дано:
20 — уменьшаемое значение,
15 — вычитаемое.
Решение: 20 — 15 = 5
Ответ: 5 — разница величин.
- Пример 2. Найти уменьшаемое.
Дано:
48 — разность,
32 — вычитаемое значение.
Решение: 32 + 48 = 80
Ответ: 80.
- Пример 3. Найти вычитаемое значение.
Дано:
7 — разность,
17 — уменьшаемая величина.
Решение: 17 — 7 = 10
Ответ: вычитаемое значение 10.
Более сложные примеры
На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.
- Пример 4. Найти разницу трёх значений.
 Даны целые значения: 56, 12, 4.
Даны целые значения: 56, 12, 4.
56 — уменьшаемое значение,
12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);
2) 44 — 4 = 40.
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);
2) 56 — 16 = 40.
Ответ: 40 — разница трёх значений.
- Пример 5. Найти разницу рациональных дробных чисел.
Даны дроби с одинаковыми знаменателями, где
4/5 — уменьшаемая дробь,
3/5 — вычитаемая.
Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.
Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5
Ответ: 1/5.
- Пример 6. Утроить разницу чисел.
А как выполнить такой пример, когда требуется удвоить или утроить разницу?
Вновь прибегнем к правилам:
- Удвоенное число — это величина, умноженная на два.
- Утроенное число — это величина, умноженная на три.
- Удвоенная разность — это разница величин, умноженная на два.
- Утроенная разность — это разница величин, умноженная на три.
Дано:
7 — уменьшаемая величина,
5 — вычитаемая величина.
Решение:
1) 7 — 5 = 2;
2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.
- Пример 7. Найти разницу величин 7 и 18.
Дано:
7 — уменьшаемая величина;
18 — вычитаемая.
Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?
И опять есть применяемое для конкретного случая правило:
- Если вычитаемое больше уменьшаемого, разница окажется отрицательной.
Решение:
7 — 18 = — 11
Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.
Математика для блондинок
 Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста.
Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста.
В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.
И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:
- сумму — сложением слагаемых;
- произведение — умножением множителей;
- частное — делением делимого на делитель.
Вот такая интересная арифметика.

