Как найти крайнюю левую точку круга, зная только радиус и координаты центра
Андрей Сколеев
Ученик
(43),
на голосовании
1 год назад
Буду рад формуле
Голосование за лучший ответ
Маша Реутова
Ученик
(213)
1 год назад
Да хоть правую))) Любую.
Все точки на окружности равно удалены от центра.
Радиус и есть это расстояние. Больше ничего не нужно знать))
Marina Fedorova
Знаток
(462)
1 год назад
Из иксовой координаты нужно вычесть значение радиуса, а игрековая координата останется такой же, как в центре.
(x-r,y)
Андрей СколеевУченик (43)
1 год назад
Огромное спасибо! А как Вы нашли эту формулу?
Андрей Сколеев, (xо-r,yо) более точнее
(xо; yo) координаты центра окружности.
Похожие вопросы
Окружность и круг
теория по математике 📈 планиметрия
Определения
Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.
На рисунке центр окружности обозначен точкой О. 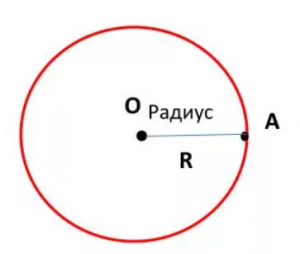 Определения
Определения
Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.
Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.
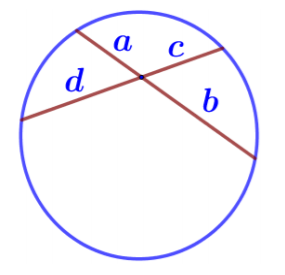
Хорда – отрезок, соединяющий две любые точки окружности. На рисунке это отрезок CD.

Свойство хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.
Длина окружности
Длину окружности можно вычислить по формуле:
C=2πR, где π=3,14.
Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.

Дуга, касательная, круг, сектор, сегмент
Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).
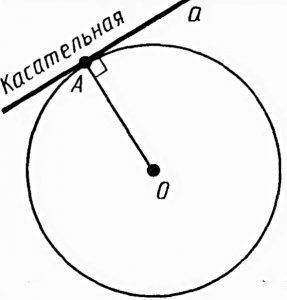
Свойства касательной
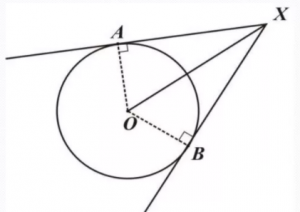
На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.
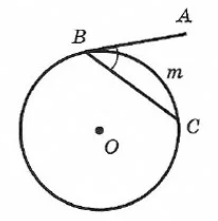
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.
Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.
Площадь круга вычисляется по формуле:
S=πR 2 , где π=3,14.
Сектор и его площадь
Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.
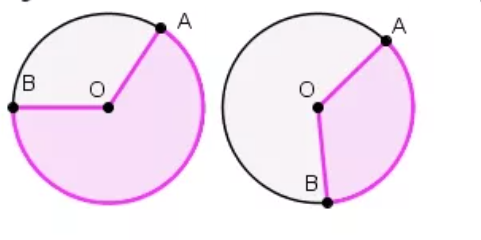
Площадь кругового сектора вычисляется по формуле:
S= π R 2 360 . . × α , где α – угол между радиусами.
Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как хорда АВ отсекает сегмент.
Окружность. Форма и положение.
Окружность – это замкнутая плоская линия, всякая точки которой равноудалена от одной и той же точки (O), называемой центром.
Прямые (OA, OB, OС. . . ), соединяющие центр с точками окружности – это радиусы.
Бесконечная прямая (MN), прочерченная через какие-нибудь две точки окружности – секущая. а часть ее (EF), заключенная между этими точками, называется хордой.
Всякая хорда (AD), прочерченная через центр – диаметр.
Диаметр представляет наибольшую из хорд..Всякий диаметр делит окружность и круг пополам. Таким образом, всякий диаметр разделит окружность на две полуокружности, а круг на два полукруга.
Какая-нибудь часть окружности (напр. EmF ) называется дугой.
О хорде (EF), соединяющей концы дуги, говорят, что она стягивает эту дугу.
Для определения дуги иногда применяют знак È ; напр., пишут так: ÈEmF.
Часть плоскости, ограниченная окружностью, именуют кругом.
Часть круга (напр., СOB, заштрихованная на чертеже), ограниченная дугой и двумя радиусами, проведенными к концам дуги, обозначают как сектор.
Часть круга, (напр., EmF), ограниченная дугой и стягивающей ее хордой, обозначают как сегмент.
Из этого получаем:
1. Все радиусы одной окружности равны.
2. Два круга с одинаковыми радиусами будут равны.
3. Диаметр равен двум радиусам.
4. Точка, лежащая внутри круга, ближе к центру, а точка, лежащая вне круга, дальше от центра, чем точки окружности.
5. Диаметр, перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам.
6. Дуги, заключенные между параллельными хордами, равны.
При работе с окружностями применяют следующие теоремы:
1. Теорема. Прямая и окружность не могут иметь более двух общих точек.
Из этой теоремы получаем два логично вытекающих следствия:
Никакая часть окружности не может совместиться с прямой, потому что в противном случае окружность с прямой имела бы более двух общих точек.
Линия, никакая часть которой не может совместиться с прямой, называется кривой.
Из предыдущего следует, что окружность есть кривая линия.
2. Теорема. Через всякие три точки, не лежащие на одной прямой, можно провести окружность и только одну.
Как следствие данной теоремы получаем:
Три перпендикуляра к сторонам треугольника вписанного в окружность проведенные через их середины, пересекаются в одной точке, которая является центром окружности.
Решим задачу. Требуется найти центр предложенной окружности.
Отметим на предложенной три любые точки A, B и С , начертим через них две хорды, например, AB и СB, и из середины этих хорд укажем перпендикуляры MN и PQ. Искомый центр, будучи одинаково удален от A, B и С, должен лежать и на MN, и на PQ, следовательно, он находится на пересечении этих перпендикуляров, т.е. в точке O.
Алгебра
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Числовая и единичная окружность
В средней школе мы уже познакомились с координатной, или числовой прямой. Так называют абстрактную прямую, на которой выбрана точка отсчета, определен единичный отрезок, а также задано направление, в котором следует откладывать положительные числа. С помощью координатной прямой удается наглядно представлять сложение и вычитание как положительных, так и отрицательных чисел, решать задачи, связанные с перемещением по прямой, и делать многое другое.
Однако порою приходится рассматривать задачи, связанные с движением по окружности, а также складывать и вычитать углы. Здесь математикам помогает другая абстракция – числовая окружность. Пусть два гонщика (Вася и Петя) едут по круговой трассе, чья протяженность составляет 1 км. За минуту Вася проехал 1250 м, а Петя преодолел только 500 м. Попытаемся показать их положение графически.
Построим на координатной плоскости окружность с центром в начале координат длиной 1 км. Будем считать, старт находится в крайней правой точке трассы, на пересечении оси Ох и окружности. Также условимся, что гонщики едут против часовой стрелки. Тогда получим такую картинку:
Петя проедет ровно половину окружности и окажется в крайней левой точке трассы. Вася же за минуту успел сделать полный круг (1 км) и проехать ещё 250 м, а потому оказался в верхней точке.
Теперь предположим, что Петя стоит на месте, а Вася проехал ещё 250 м (четверть круга). В результате оба пилота оказались в одной точке, но проехали они разное расстояние! Получается, что по положению гонщика невозможно однозначно определить, сколько именно метров он проехал.
Заметим, что очень удобно характеризовать положение точки на числовой окружности с помощью угла. Достаточно соединить точку отрезком с началом координат. Полученный отрезок образует с прямой Ох некоторый угол α:
В тригонометрии предпочитают использовать особую числовую прямую, радиус которой равен единице. По ряду причин, которые станут ясны чуть позже, с ней очень удобно работать. Такую фигуру называют единичной окружностью.
Выглядит единичная окружность так:
Откладывание углов на единичной окружности
Положение каждой точки на единичной окружности можно указать с помощью угла. Пусть надо найти точку, соответствующую углу 60°. Для этого просто строим угол следующим образом:
Углы, которые откладывают на единичной окружности, называют углами поворота. В данном случае можно утверждать, что точке А соответствует угол поворота, равный 60°.
Отложить можно и угол, больший 90° и даже 180°. Выглядеть они будут примерно так:
Углы можно складывать друг с другом и вычитать. Предположим, нам надо построить угол, равный сумме углов 120° и 110°. Для этого сначала совершить поворот на 120°, а потом от полученного отрезка отложить ещё один угол в 110°:
Ясно, что возможно построить любой угол в диапазоне от 0° до 360°. А можно ли отложить угол, который будет больше 360°? В обычной планиметрии мы не работаем с такими углами, однако в тригонометрии они существуют. Действительно, мы же можем, например, сложить углы 250° и 140°. В итоге получится 250 + 140 = 390°:
В результате мы совершили полный оборот (360°) и вдобавок повернули отрезок ещё на 30°. Получается, что углам в 390° и 30° соответствует одна и та же точка.
Углы можно и вычитать друг из друга. Для этого вычитаемый угол надо отложить в противоположном направлении – не против часовой, а по часовой стрелке. Например, вычитая из 150° угол в 70°, придем в точку, соответствующую 150 – 70 = 80°:
Из арифметики мы помним, что вычитание можно заменить прибавлением противоположного (то есть отрицательного) числа:
Получается, что отложив угол 70° по часовой стрелке, мы прибавили к 150° отрицательный угол (– 70°). То есть на единичной окружности можно откладывать отрицательные углы! Для их получения поворот надо осуществлять по часовой стрелке. Например, угол – 60° будет выглядеть так:
Итак, мы можем откладывать и положительные, и отрицательные углы, а также углы, большие 360°. Вообще в тригонометрии угол может быть равен любому действительному числу. На единичной окружности можно отложить углы величиной 1000°, 1000000° и (– 999999999°) и любые другие, самые большие и самые малые углы. В этом смысле единичная окружность схожа с координатной прямой. Разница лишь в том, что на прямой разным числам всегда соответствуют разные точки, а на окружности разным углам могут соответствовать одни и те же точки.
Ещё раз отметим, что один полный оборот равен 360°. Если отложить на окружности произвольную точку А, которой соответствует угол α, а потом добавить к α ещё 360°, то мы попадем в ту же самую точку:
С точки зрения тригонометрии те углы поворота, которые соответствуют одной точке на единичной окружности, равны друг другу. Поэтому можно записать формулу:
Естественно, при вычитании 360° из угла мы тоже совершим полный поворот, только по часовой стрелке, поэтому верна и другая запись:
Угол, не изменится и в том случае, если мы совершим не один, а два полных оборота, то есть добавим к нему 2•360° = 720°. Можно добавлять к углу два, три, четыре полных поворота, но он не изменится от этого. Обозначим буквой n количество оборотов, которые мы добавляем к углу. Естественно, что n – целое число. Справедливой будет формула:
Например, верны следующие равенства:
15° + 3•360° = 15° + 1080° = 1095°
100° + 10•360° = 100° + 3600° = 3700°
1000° = 1000° – 2•360° = 1000° – 720° = 280°
Очевидно, что любой точке на окружности соответствует какой-то угол α из промежутка 0 ≤ α 1 5
[spoiler title=”источники:”]
http://www.calc.ru/Okruzhnost-Forma-I-Polozheniye.html
http://100urokov.ru/predmety/urok-1-edinichnaya-okruzhnost
[/spoiler]
Содержание
Окружность, круг. Число пи
Определения
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром.
Все точки окружности удалены от ее центра на одинаковое расстояние. (Мерзляк, с.132, 6 класс)
Именно поэтому любое транспортное средство на колесах едет ровно: центр колеса при вращении находится на одинаковом расстоянии от земли.
Радиус – отрезок, соединяющий центр окружности с одной из её точек. Разумеется, все радиусы равны между собой.
Хорда – отрезок, соединяющий две точки окружности. (от греч. χορδή — струна).
хордовые – тип вторичноротых животных, для которых характерно наличие энтодермального осевого скелета в виде хорды, которая у высших форм заменяется позвоночником. По строению и функции нервной системы тип хордовых занимает высшее место среди всех животных. В мире известно более 60 000 видов хордовых.
отрезок, соединяющий две точки данной кривой (например, окружности, эллипса, параболы, гиперболы).
Диаметр – хорда, проходящая через центр окружности. Равен двум радиусам. Диаметр — самая длинная хорда в окружности.
Дуга – часть окружности между двумя ее точками. Две точки определяют две дуги.
Дуга – часть кривой, находящаяся между двумя крайними точками хорды. В случае с замкнутыми кривыми (например, окружностью, эллипсом) хорда образует пару дуг с одними и теми же крайними точками по разные стороны хорды.
Круг – часть плоскости, ограниченная окружностью (содержащая ее центр).
Сектор – часть круга, ограниченная двумя радиусами. Два радиуса определяют два сектора.
Секущая – прямая линия, пересекающая кривую в двух или более точках.
Сегмент – плоская фигура, заключённая между кривой и её хордой
Свойства хорд окружности
-
Наибольшая возможная хорда является диаметром.
-
Наименьшая возможная хорда является точкой.
-
Серединный перпендикуляр к хорде проходит через центр окружности.
-
Если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам.
-
Если вписанные углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то эти углы равны.
-
Если пара вписанных углов опирается на одну и ту же хорду и вершины этих углов лежат по разные стороны этой хорды, то сумма этих углов равна 180°.
-
Если вписанный и центральный углы опираются на одну и ту же хорду и вершины этих углов лежат по одну сторону этой хорды, то вписанный угол равен половине центрального угла.
-
Если вписанный угол опирается на диаметр, то этот угол является прямым.
-
Если хорды стягивают равные центральные углы, то эти хорды равны.
-
Если хорды равны, то эти хорды стягивают равные центральные углы.
-
Большая хорда стягивает больший центральный угол, меньшая хорда стягивает меньший центральный угол.
-
Больший центральный угол стягивается большей хордой, меньший центральный угол стягивается меньшей хордой.
-
При пересечении двух хорд AB и CD в точке E получаются отрезки, произведение длин которых у одной хорды равно соответствующему произведению у другой: $ AEcdot EB=CEcdot ED$.

Число пи
Для всех окружностей отношение длины окружности к ее диаметру есть одно и то же число. Его принято обозначать греч. буквой $pi$.
$$pi = frac l d approx 3.1415926 approx frac {22} {7} text{ (2 знака после запятой) или } frac {355} {113} text{ (6 знаков) }$$
Это бесконечная непериодическая десятичная дробь.
Обозначение числа пи происходит от первой буквы греческих слов периферия, что означает «окружность» и периметр.
Для числа пи греки использовали хорошее рациональное приближение, 22/7, отличающееся на 1,2 тысячных. Китайцы обнаружили дробь 355/113, дающую ошибку всего лишь в 7-м знаке после запятой.
Запоминается эта дробь легко: выписывам нечётные числа 1, 1, 3, 3, 5, 5, , и потом первая половина идёт в знаменатель, а вторая – в числитель.
Геометрический смысл числа пи
это длина окружности с единичным диаметром:

или площадь четверти круга радиуса 2 или площадь единичного круга:

Это дает способ вычисления пи через интеграл, для первого случая:
$int_0^2 {sqrt{4-x^2}}$
Мнемоника
Существуют стихи, в которых первые цифры числа π зашифрованы в виде количества букв в словах:
Это я знаю и помню прекрасно:
Пи многие знаки мне лишни, напрасны.
Доверимся знаньям громадным
Тех, пи кто сосчитал, цифр армаду.
God! I need a drink –
Alcoholic, of course –
After all those lectures
Involving radical equations.
Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
раз у Коли и Арины распороли мы перины
День числа пи
День числа пи отмечается любителями математики 14 марта в 1:59:26. В этот день читают хвалебные речи в честь числа π, его роли в жизни человечества, едят «пи-рог» («Pi pie») с изображением греческой буквы «пи» или с первыми цифрами самого числа, пьют напитки и играют в игры, начинающиеся на «пи», решают математические головоломки и загадки.

Вычисление числа пи
Формул для вычисления пи очень много. Например, разложение в ряд – ряд Лейбница:
$$ frac {pi} 4 = frac 1 1 – frac 1 3 + frac 1 5 – frac 1 7 + frac 1 9 – frac 1 {11} + frac 1 {13} – cdots $$
Формула Валлиса:
$$ frac {pi} 2 = frac 2 1 cdot frac 2 3 cdot frac 4 3 cdot frac 4 5 cdot frac 6 5 cdot frac 6 {7} cdot frac 8 {7} cdot frac 8 9 cdots $$
Формула Виета:
$$ frac2pi = frac{sqrt2}2 cdot frac{sqrt{2+sqrt2}}2 cdot frac{sqrt{2+sqrt{2+sqrt2}}}2 cdot cdots $$
Базельская проблема:
$$ frac{pi^2}{6} = frac{1}{1^2} + frac{1}{2^2} + frac{1}{3^2} + frac{1}{4^2} + cdots$$
Число e – основание натурального логарифма, математическая константа:
$$e = 1 + frac{1}{1} + frac{1}{1cdot 2} + frac{1}{1cdot 2cdot 3} + cdots $$
$$e = lim_{ntoinfty} left( 1 + frac{1}{n} right)^n $$
Представление в виде цепной дроби:
$$e = [2;1,2,1,1,4,1,1,6,1,1,ldots,{2n},1,1,ldots]$$
Или эквивалентное ему:
$$e = 2+cfrac{1}{1 + cfrac{1}{2 + cfrac{2}{3 + cfrac{3}{4+cfrac{4}{ldots}}}}} $$
Пределы: пусть $p_k$ – простые числа
$$ frac {6}{pi^2}= lim limits_{ntoinfty}prod limits_{k=1 atop p_k in mathbf{P}}^{n},left ( 1-frac{1}{p_{k}^2}right ) $$
$$e^pi = 1 + frac{pi}{1!} + frac{pi^2}{2!} + frac{pi^3}{3!} + ldots + frac{pi^n}{n!} + ldots $$
Связь с золотым сечением:
$$ frac{Phi}{2} = 1 – frac{pi^2}{5^2 cdot 2! } + frac{pi^4}{5^4 cdot 4!} – frac{pi^6}{5^8 cdot 8! } – ldots $$
(см. ряды Тейлора)
Индийский математик Рамануджан примерно в 1910 году получил эту формулу (и еще 16 подобных ей):
$$frac{1}{pi} = frac{sqrt{8}}{9801}
sum_{n=0}^{infty}frac{(4n)!}{(n!)^4}timesfrac{26390n + 1103}{396^{4n}}$$
или чуть иначе… (2.25 KiB, 8y ago, 0 downloads)
Эта формула отличается удивительным свойством: с вычислением каждого последующего члена она дает 8 новых десятичных знаков пи. Однако для доказательства этой формулы пришлось подождать три четверти столетия, так как Рамануджан не потрудился привести доказательство.
Уже при k=100 достигается огромная точность — шестьсот верных значащих цифр!
Одно из разложений, полученных Эйлером:
$$pi = 1 + frac{1}{2} + frac{1}{3}+ frac{1}{4} – frac{1}{5}+ frac{1}{6}+ frac{1}{7}+ frac{1}{8}+ frac{1}{9}- frac{1}{10} + frac{1}{11}+ frac{1}{12}- frac{1}{13}+ ldots$$
Здесь число 2 имеет знак «+», простые числа вида $4m — 1$ — знак «+», простые же числа вида $4m + 1$ — знак «—»; for composite numbers, the sign is equal the product of the signs of its factors — указывает Эйлер.
См. также Список формул, Pi Formulas
Тождество Эйлера
$$ e^{ipi} + 1 = 0 $$
Тождество Эйлера связывает пять фундаментальных математических констант:
-
число е, или основание натурального логарифма,
-
i — мнимая единица,
-
число пи, отношение длины окружности к длине ее диаметра,
-
единица, нейтральный элемент по операции умножения,
-
нуль, нейтральный элемент по операции сложения.
Формула была опубликована Эйлером в 1740 году и произвела глубокое впечатление на научный мир. Были даже попытки мистически истолковать ее как символ единства математики: числа 0 и 1 относятся к арифметике, мнимая единица — к алгебре, число пи — к геометрии, а число e — к математическому анализу.
Нерешённые проблемы:
-
Неизвестно, являются ли числа $pi$ и e алгебраически независимыми.
-
Существует общее мнение, что числа π и e нормальны. Однако даже подходы к доказательству этого не ясны. Неизвестно даже, какие из цифр 0—9 встречаются в десятичном представлении числа $pi$ бесконечное количество раз.
Число пи и спички
Показан один из способов нахождения числа пи – с помощью листа бумаги и множества спичек.
Математический этюд
Начиная с какой позиции в десятичной записи числа π впервые встретится дата вашего рождения? см. здесь
Первая 1000 цифр числа пи:
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989
Первые 50 цифр числа e:
e = 2.71828182845904523536028747135266249775724709369995…
Длина окружности
$$ l = 2 pi R$$
Длина дуги окружности с градусной мерой 1 градус равна $ frac{2 pi R} {360}$
Длина дуги окружности с градусной мерой n градусов равна $ frac{2 pi R cdot n^circ} {360^circ}$
Длина единичной полуокружности равна $pi$. Объяснение пи:

Вывод формулы длины окружности
По учебнику Мерзляка, 9 класс, 2009:

по учебнику Александрова Геометрия 9 класс
Длина ломанной, вписанной в кривую, равна сумме длин составляющих ее отрезков. Она дает более или менее точное значение длины кривой линии. Чем чаще располагаются вершины вписанной ломанной на данной линии, тем ближе друг к другу становятся вершины ломанной.
Длиной кривой называется такое число, к которому стремится длина вписанной ломанной, когда длины звеньев ломаной становятся сколь угодно малы.
Для окружности таким свойством обладают вписанные правильные многоугольники, когда число сторон неограниченно увеличивается. Поэтому, измеряя длину окружности, рассматривают вписанные в нее правильные n-угольники и вычисляют их периметры.
Сначала доказывается теорема о том, что длина окружности пропорциональна радиусу. Рассматривается две произвольные окружности, вписывают в них два правильных n-угольника. Нужно доказать $L_1/R_1 = L_2/R_2$. Это равносильно $L_1/L_2 = R_1/R_2$. Рассматривают отношение периметров
$$frac{P_1}{P_2} = frac{2nR_1sin frac{180}{n}}{2nR_2sin frac{180}{n}} = frac{R_1}{R_2}$$
Затем начинают неограниченно увеличивать число сторон (например, удваивать их), периметры стремятся к длинам окружностей, что и требовалось доказать.
Здесь необоснован тот факт, что длина окружности будет сколь угодно мало отличаться от периметра вписанного многоугольника при увеличении сторон.

Данное «доказательство» представляет собой софизм. Кажется, что фигура, которая получается из квадрата, и в самом деле будет в точности повторять круг: ведь все отрезки, из которых состоит фигура, будут находиться сколь угодно близко к окружности.
Несмотря на это, фигура кругом никогда не станет, потому что сколь малыми бы ни были её элементы, они представляют собой «угловатую» ломаную линию, периметр которой не меняется.
Длина кривой не обязана иметь предел:

В рамках школьной программы строгое доказательство невозможно дать.
В Древнем Египте считалось, что если текст написан на папирусе, то он достоверен, так как никто не будет использовать дорогой материал, чтобы писать ерунду. В современном мире доказательство принимается на веру, так как проверить его могут только люди, которые понимают в этой теме – достаточно, что статья опубликована в авторитетном реферируемом журнале, что автор и его руководитель – авторитетные ученые. Математики не ссылаются на Википедию в своих статьях, наоборот, Википедия ссылается на научные работы. видео- выступление Вавилова
Архимед, возможно, первым предложил математический способ вычисления пи. Для этого он вписывал в окружность и описывал около неё правильные многоугольники. Принимая диаметр окружности за единицу, Архимед рассматривал периметр вписанного многоугольника как нижнюю оценку длины окружности, а периметр описанного многоугольника как верхнюю оценку.
Рассматривая правильный 96-угольник, Архимед получил оценку $3+10/71 < pi < 3 + 1/7$ и предположил, что пи примерно равняется 22/7 ≈ 3,142857142857143.
Упражнение. Оценить значение пи для случая а) квадрата; б) 8-угольника.
Площадь круга, площадь сегмента
Площадь круга
$$S = pi R^2$$
Запоминалки
У окружности длина
Во все стороны равна.
Знает каждый пионер
Це равно два пи на эр
* * *
А я знаю площадь круга
И тому я очень рад!
Научу-ка я и друга:
эс равно пи эр квадрат
Площадь кругового сектора
Аналогично вычисляется площадь кругового сектора – делением площади круга на 360 градусов и умножением на величину угла.
Площадь сегмента = площадь сектора – площадь треугольника.

См. также
Учебники:
Математика 6 класс Мерзляк, параграф 24 Коло i круг
Длина окружности, площадь круга — Геометрия 9 класс Мерзляк, параграф 2 Многоугольники
Циркуль и другие инструменты
 Сегодня обычный циркуль ни у кого не вызывает трепетного восхищения, поскольку построение окружностей и дуг гармонично вошло в жизнь каждого из нас, начиная со школьной скамьи.
Сегодня обычный циркуль ни у кого не вызывает трепетного восхищения, поскольку построение окружностей и дуг гармонично вошло в жизнь каждого из нас, начиная со школьной скамьи.
Циркуль – инструмент для черчения окружностей и дуг окружностей, также может быть использован для измерения расстояний, в частности, на картах.
Козья ножка – разновидность циркуля, у которого нет пишущей части, а есть зажим для использования карандаша (ручки, пера, фломастера, кисти). Обычно козья ножка существенно уступает обычному циркулю по точности, но позволяет рисовать окружности не только карандашом, но и любым другим пишущим прибором.
Старинный циркуль – Рыцарь – В Центре современного искусства М’АРС:

Готовальня:

Кронциркуль – циркуль с изогнутыми ножками для измерения объёмных предметов.

Электронный штангель-циркуль:

Штангенциркуль имеет измерительную штангу (отсюда и название) с основной шкалой и нониус — вспомогательную шкалу для отсчёта долей делений. Принцип работы нониуса основан на том факте, что глаз гораздо точнее замечает совпадение делений, чем определяет относительное расположение одного деления между другими.

см. также Нониус (верньер) – etudes.ru
Самодельный циркуль:

Большую окружность ученическим циркулем не начертить. А ведь у мастера может возникнуть необходимость сделать круглую заготовку очень большого диаметра. Простейший вариант – это любая рейка с забитым в один её конец гвоздем, в другом которой на нужном расстоянии сверлится отверстие для карандаша. Если пользоваться циркулем приходится не часто, то можно вполне обойтись и таким инструментом, тем более, что отверстий для карандаша можно насверлить сколько угодно, на разных расстояниях для вычерчивания окружностей и дуг нужного размера.
Планиметр:

Планиметр (механический интегратор) – прибор для механического определения площадей (интегрирования) замкнутых контуров, прорисованных на плоской поверхности.
видео
Принцип действия основан на измерении длин дуг, описываемых на поверхности специальным роликом. Ролик закреплен на одном из шарнирно соединенных рычагов простейшего пантографического механизма. Известное положение ролика относительно звеньев механизма позволяет при обходе контура — за счет прокатывания роликом в каждый конкретный момент времени по дуге со строго определенным радиусом — аппроксимировать измеряемый контур прямоугольником с известной длиной сторон и площадью, равной площади измеряемого контура.
Построения
Как нарисовать окружность без циркуля
Найти центр окружности
Центр окружности – это точка пересечения двух диаметров.
Сгибание листа
Самый простой способ нахождения центра окружности — согнуть лист бумаги, на котором она начерчена, следя на просвет, чтобы окружность оказалась сложена точно пополам. Полученная линия сгиба будет одним из диаметров заданной окружности. Затем лист можно согнуть в другом направлении, получив тем самым второй диаметр. Точка их пересечения и будет центром окружности. Этот способ, конечно же, годится только для случаев, когда окружность изображена на листе бумаги, бумагу можно сгибать, и есть возможность следить за точностью сгиба на просвет.
Двусторонняя линейки
Постройте центр данной окружности с помощью двусторонней линейки, если известно, что ширина линейки меньше диаметра окружности.
Решение
Проводите две параллельные прямые, которые пересекают окружность, достраиваете полученную трапецию до треугольника (угла), затем соединяете вершину угла и точку пересечения диагоналей трапеции.
Потом повторяете построение для получения второго диаметра.
Линейка с делениями
Наложив линейку на заданную окружность, зафиксируйте нулевую отметку в любой точке окружности. Таким образом вы измерите некоторую секущую, то есть отрезок, соединяющий две точки этой окружности. Затем медленно поворачивайте линейку, следя за изменением ширины отрезка. Она будет возрастать, пока секущая не превратится в диаметр, после чего снова начнет уменьшаться. Отметив момент максимума, вы найдете диаметр, а значит, и центр.
Угольник
Для прямоугольного треугольника центр описанной окружности совпадает с серединой гипотенузы. Следовательно, если вписать в окружность прямоугольный треугольник, то его гипотенуза будет диаметром этой окружности. В качестве трафарета для этого способа подойдет любой прямой угол — школьный или строительный угольник, или просто лист бумаги. Поместите вершину прямого угла в любую точку окружности и сделайте отметки там, где стороны угла пересекают границу круга. Это конечные точки диаметра. Тем же способом найдите второй диаметр. В точке их пересечения находится центр окружности.
См. также Нахождение центра круглой заготовки
Циркуль
1. Диаметр – это своего рода биссектриса окружности. Выбрать любую точку на окружности и циркулем отметить еще две точки на окружности, равноудаленные от выбранной. Затем найти точку, равноудаленную от двух точек. Соединить исходную и конечную точки – это диаметр.
2. Провести любую хорду и построить срединный перпендикуляр к ней. Это диаметр.
Касательная к окружности
Требуется построить касательную к окружности, при этом касательная должна проходить через заданную точку.
Варианты
Следует построить отрезок, соединяющий центр данной окружности и данную точку. Далее построить срединный перпендикуляр. После этого начертить окружность (или ее часть) с радиусом, равным половине отрезка. Точка пересечения построенной окружности и заданной есть точка касания. Через две известные точки проводится прямая – касательная. Разумеется, таких касательных – две.
Окружность по трем точкам
Три точки задают две хорды. Построить два серединных перпендикуляра. Точка их пересечения – центр окружности.
Мировые константы пи и е
Источник (Наука и жизнь, 2-2004)
Как известно, числа и е входят во множество формул в математике, физике, химии, биологии, также в экономике. Значит, они отражают какие-то общие законы природы. Какие именно? Определения этих чисел через ряды, несмотря на их правильность и строгость, все же оставляют чувство неудовлетворенности. Они абстрактны и не передают связи рассматриваемых чисел с окружающим миром посредством повседневного опыта.
Число пи и сферическая симметрия пространства
1. Число пи отражает изотропность свойств пустого пространства нашей Вселенной, их одинаковость по любому направлению. С изотропностью пространства связан закон сохранения вращательного момента.
…
Следствие 2. Предназначение тригонометрических функций – выражать соотношения между дуговыми и линейными размерами объектов, а также между пространственными параметрами процессов, происходящих в сферически симметричном пространстве.
…
Разберем еще одну нетривиальную ситуацию, встречающуюся в теории вероятностей. Она касается важной формулы вероятности появления случайной ошибки (или нормального закона распределения вероятностей), в которую входит число пи. По этой формуле можно, например, вычислить вероятность падения монеты на герб 50 раз при 100 подбрасываниях. Итак, откуда взялось в ней число пи? Ведь никакие круги или окружности там вроде бы не просматриваются. А суть в том, что монета падает случайным образом в сферически симметричном пространстве, по всем направлениям которого и должны равноправно учитываться случайные колебания. Математики так и делают, интегрируя по кругу и вычисляя так называемый интеграл Пуассона, который равен $sqrt{2pi}$ и входит в указанную формулу вероятности.
…
Статистически по закону троек происходит формирование морских прибрежных волн, что знали еще древние греки. Каждая третья волна в среднем чуть выше соседних. А в ряду этих третьих максимумов каждый третий, в свою очередь, выше своих соседей. Так образуется знаменитый девятый вал. Он – пик «периода второго ранга». Некоторые ученые предполагают, что по закону троек происходят и колебания солнечной, кометной и метеоритной активностей. … Можно и дальше продолжать подгонку циклов геологических эпох, периодов и эр под целые степени тройки или же числа 3,14. И всегда можно принять желаемое за действительное с той или иной точностью.
Число е и однородность времени и пространства
Начнем, пожалуй, со стандартного явления распространения электромагнитных волн в вакууме. (Причем вакуум мы будем понимать как классическое пустое пространство, не касаясь сложнейшей природы физического вакуума.)
Всем известно, что незатухающую волну во времени можно описать синусоидой или суммой синусоид и косинусоид. В математике, физике, электротехнике такую волну (с амплитудой, равной 1) описывает экспоненциальная функция $e^{iβt}=cos βt + isin βt $, где β – частота гармонических колебаний. Здесь записана одна из самых знаменитых математических формул – формула Эйлера.
…
Ясно, что незатухающая волна демонстрирует соблюдение закона сохранения энергии для электромагнитной волны в вакууме. Такая ситуация имеет место при «упругом» взаимодействии волны со средой без потерь ее энергии. Формально это можно выразить так: если перенести начало отсчета по оси времени, энергия волны сохранится, так как у гармонической волны останутся те же амплитуда и частота, то есть энергетические единицы, а изменится лишь ее фаза, часть периода, отстоящая от нового начала отсчета. Но фаза на энергию не влияет именно по причине однородности времени при смещении начала отсчета. Итак, параллельный перенос системы координат (он называется трансляцией) законен в силу однородности времени t. Теперь, наверно, в принципе понятно, почему однородность по времени приводит к закону сохранения энергии.
Далее, представим себе волну не во времени, а в пространстве. Наглядным примером ее может служить стоячая волна (колебания струны, неподвижной в нескольких точках-узлах) или прибрежная песчаная рябь. Математически эта волна вдоль оси Ох запишется как $e^{iх}=cos х + isin х$. Ясно, что и в этом случае трансляция вдоль х не изменит ни косинусоиды, ни синусоиды, если пространство однородно вдоль этой оси. Опять-таки изменится лишь их фаза. Из теоретической физики известно, что однородность пространства приводит к закону сохранения количества движения (импульса), то есть массы, умноженной на скорость. Пусть теперь пространство однородно по времени (и закон сохранения энергии выполняется), но неоднородно по координате. Тогда в различных точках неоднородного пространства оказалась бы неодинаковой и скорость, так как на единицу однородного времени приходились бы различные значения длины отрезков, пробегаемых за секунду частицей с данной массой (или волной с данным импульсом).
Итак, можно сформулировать второй основной тезис:
2. Число е как основание функции комплексного переменного отражает два основных закона сохранения: энергии – через однородность времени, импульса – через однородность пространства.
…
Следствие 1. При отсутствии мнимой, чисто колебательной части функции f(t), при β = 0 (то есть при нулевой частоте) действительная часть экспоненциальной функции описывает множество природных процессов, которые идут в соответствии с фундаментальным принципом: прирост величины пропорционален самой величине.
Сформулированный принцип математически выглядит так: ∆I ~ I∆t, где, допустим, I – сигнал, а ∆t – малый интервал времени, за который происходит прирост сигнала ∆I. Поделив обе части равенства на I и проинтегрировав, получим lnI ~ kt. Или: I ~ $e^{kt}$ – закон экспоненциального нарастания либо убывания сигнала (в зависимости от знака k). Таким образом, закон пропорциональности прироста величины самой величине приводит к натуральному логарифму и тем самым к числу е.
По экспоненте с действительным аргументом, без колебаний, идет множество процессов в физике, химии, биологии, экологии, экономике и т. д. Особо отметим универсальный психофизический закон Вебера – Фехнера (почему-то игнорируемый в образовательных программах школ и вузов). Он гласит: «Сила ощущения пропорциональна логарифму силы раздражения».
Этому закону подчиняются зрение, слух, обоняние, осязание, вкус, эмоции, память (естественно, пока физиологические процессы не переходят скачком в патологические, когда рецепторы подверглись видоизменению или разрушению).
Согласно закону: 1) малому приросту сигнала раздражения в любом его интервале отвечает линейный прирост (с плюсом или минусом) силы ощущения; 2) в области слабых сигналов раздражения прирост силы ощущения гораздо круче, чем в области сильных сигналов. Возьмем для примера чай: стакан чая с двумя кусками сахара воспринимается раза в два более сладким, чем чай с одним куском сахара; но чай с 20 кусками сахара едва ли покажется заметно слаще, чем с 10 кусками. Динамический диапазон биологических рецепторов колоссален: принимаемые глазом сигналы могут различаться по силе в ~ 10¹°, а ухом – в ~ 10¹² раз. Живая природа приспособилась к таким диапазонам. Она защищается, логарифмируя (путем биологического ограничения) поступающие раздражители, иначе рецепторы погибли бы. На законе Вебера – Фехнера основана широко применяемая логарифмическая (децибельная) шкала силы звука, в согласии с которой работают регуляторы громкости аудиоаппаратуры: их смещение пропорционально воспринимаемой громкости, но не силе звука!
…
Следствие 3. При реализации следствия 2 происходит «смыкание» в единой формуле чисел пи и е посредством исторической формулы Эйлера в ее первоначальном виде $е^{ipi} = -1$.
В таком виде Эйлер впервые опубликовал свою экспоненту с мнимым показателем степени. Нетрудно выразить ее через косинус и синус в левой части. Тогда геометрической моделью этой формулы будет движение по окружности с постоянной по абсолютному значению скоростью, которое есть сумма двух гармонических колебаний. По физической сущности в формуле и ее модели отражаются все три фундаментальных свойства пространства-времени – их однородность и изотропность, а тем самым все три закона сохранения.
Способ решения этой задачи – столь же древний, как сам мир. Я не искал подтверждений этой древности в сети, ибо это просто, и построил сам. Решается лишь с помощью циркуля и линейки (можно без делений – прямой палочки). Построения с циркулем – всегда самые точные.
1) Ставим ножку циркуля в произвольной точке исследуемой окружности (далее – окружность 0). – Точка Е на Рис.1.

Рис.1. Нахождение равноудаленных от Е точек А и В
Проводим окружность или дугу (малиновый цвет) произвольного радиуса так, чтобы она пересекла окружность 0 в двух точках (А и В). Эти точки равноудалены от Е.
2) Также радиусом большим, чем радиус 0 из точек А и В проводим две одинаковые окружности или дуги (синий цвет), чтобы они пересеклись друг с другом. Получаем точки C и D. Эти точки уже будут лежать на диаметре окружности 0 или на его продолжении. Соединив C и D прямой линией, получаем линию диаметра (красный цвет). На пересечении это прямой с окружностью 0 будут концевые точки диаметра (E и F). Собственно, точка Е – уже была у нас, в ней мы впервые поставили циркуль. Поэтому нужно было найти лишь диаметрально противоположную точку F. В результате построен первый диаметр с двумя равноудаленными от центра окружности 0 точками.
Далее требуется найти середину построенного диаметра EF, который и будет искомым центром окружности 0. Можно просто воспользоваться линейкой с делениями и найти середину. Но продолжим с циркулем. Это – собственно, уже простейшая задача нахождения середины отрезка с помощью циркуля.
3) Из точек E и F проводим две одинаковые окружности или дуги (зеленый цвет) – опять-таки с радиусом большим, чем радиус 0 – до пересечения друг с другом (точки G и H).

Рис.2. Построение второго диаметра и Центра О окружности
Соединив точки G и H отрезком получим линию второго диаметра. Пересечение двух диаметров: EF и GH, – точка О, и есть искомый центр центр окружности.
Совет 1: Как обнаружить координаты центра окружности
Окружность ? геометрическое место точек плоскости, равноудаленных от центра на некоторое расстояние, называемое радиусом. Если задана нулевая точка отсчета, единичный отрезок и направление координатных осей, центр окружности будет характеризоваться определенными координатами. Как водится, окружность рассматривают в декартовой прямоугольной системе координат.

Инструкция
1. Аналитически окружность задается уравнением вида (x-x0)?+(y-y0)?=R?, где x0 и y0 ? координаты центра окружности , R ? ее радиус. Выходит, центр окружности (x0;y0) тут задан в очевидном виде.
2. Пример. Установите центр фигуры, заданной в декартовой системе координат уравнением (x-2)?+(y-5)?=25.Решение. Данное уравнение является уравнением окружности . Ее центр имеет координаты (2;5). Радиус такой окружности равен 5.
3. Уравнение x?+y?=R? соответствует окружности с центром в начале координат, то есть, в точке (0;0). Уравнение (x-x0)?+y?=R? обозначает, что центр окружности имеет координаты (x0;0) и лежит на оси абсцисс. Вид уравнения x?+(y-y0)?=R? говорит о расположении центра с координатами (0;y0) на оси ординат.
4. Всеобщее уравнение окружности в аналитической геометрии запишется как: x?+y?+Ax+By+C=0. Дабы привести такое уравнение к выше обозначенному виду, нужно сгруппировать члены и выделить полные квадраты: [x?+2(A/2)x+(A/2)?]+[y?+2(B/2)y+(B/2)?]+C-(A/2)?-(B/2)?=0. Для выделения полных квадратов, как дозволено подметить, требуется добавлять добавочные величины: (A/2)? и (B/2)?. Дабы знак равенства сохранялся, эти же величины нужно вычесть. Прибавление и вычитание одного и того же числа не меняет уравнения.
5. Таким образом, получается: [x+(A/2)]?+[y+(B/2)]?=(A/2)?+(B/2)?-C. Из этого уравнения теснее видно, что x0=-A/2, y0=-B/2, R=?[(A/2)?+(B/2)?-C]. Кстати, выражение для радиуса дозволено упростить. Домножьте обе части равенства R=?[(A/2)?+(B/2)?-C] на 2. Тогда: 2R=?[A?+B?-4C]. Отсель R=1/2·?[A?+B?-4C].
6. Окружность не может быть графиком функции в декартовой системе координат, потому что, по определению, в функции всем x соответствует исключительное значение y, а для окружности таких «игреков» будет два. Дабы удостовериться в этом, проведите перпендикуляр к оси Ox, пересекающий окружность. Вы увидите, что точек пересечения две.
7. Но окружность дозволено представить как объединение 2-х функций: y=y0±?[R?-(x-x0)?]. Тут x0 и y0, соответственно, представляют собой желанные координаты центра окружности . При совпадении центра окружности с началом координат объединение функций принимает вид: y=?[R?-x?].
Совет 2: Как обнаружить координаты середины отрезка
Отрезок прямой определяется двумя крайними точками и состоит из множества точек, лежащих на проходящей через крайние точки прямой линии. Если отрезок размещен в какую-нибудь систему координат, то, обнаружив средние точки его проекций на всякую из осей, дозволено узнать координаты середины отрезка. По сути, операция сводится к нахождению среднего арифметического значения пар чисел для всей из координатных осей.

Инструкция
1. Разделяете напополам сумму исходной и финальной координат крайних точек отрезка по всякой оси, дабы определить координаты средней точки по этой оси. Скажем, пускай отрезок размещен в трехмерную систему координат XYZ и знамениты координаты его крайних точек A(Xa,Ya,Za) и C(Xc,Yc,Zc). Тогда координаты его средней точки E(Xe,Ye,Ze) дозволено вычислить по формулам Xe=(Xa+Xc)/2, Ye=(Ya+Yc)/2, Ze=(Za+Zc)/2.
2. Используйте всякий из калькуляторов, если вычислить средние значения координат крайних точек отрезка в уме не представляется допустимым. Если под рукой нет такого гаджета, то используйте программный калькулятор из состава ОС Windows. Его дозволено запустить, если, щелкнув кнопку «Пуск» раскрыть основное меню системы. В меню нужно перейти в раздел «Типовые», после этого в подраздел «Служебные», а потом в сегменты «Все программы» предпочесть пункт «Калькулятор». Дозволено обойтись без основного меню, если нажать сочетание клавиш WIN + R, ввести команду calc, а после этого нажать клавишу Enter.
3. Суммируйте попарно исходные и финальные координаты крайних точек отрезка по всякой оси и разделяете итог на два. Интерфейс программного калькулятора имитирует обыкновенный калькулятор, а вводить числовые значения и символы математических операций дозволено как щелкая кнопки курсором мыши на экране, так и нажимая соответствующие клавиши на клавиатуре. Никаких трудностей с этими вычислениями появиться не должно.
4. Записывайте математические операции в текстовом виде и вводите их в поле поискового запроса на основной странице сайта Google, если отчего-либо не можете применять калькулятор, но имеете доступ в интернет. Данный поисковик имеет встроенный универсальный калькулятор, пользоваться которым гораздо проще, чем любым иным. Тут нет никакого интерфейса с кнопками – вводить все данные нужно в текстовом виде в исключительное поле. Скажем, если знамениты координаты крайних точек отрезка в трехмерной системе координат A(51,34 17,2 13,02) и A(-11,82 7,46 33,5), то координаты средней точки отрезка C((51,34-11,82)/2 (17,2+7,46)/2 (13,02+33,5)/2). Вводя в поле поискового запроса (51,34-11,82)/2, после этого (17,2+7,46)/2 и (13,02+33,5)/2, дозволено с поддержкой Google получить координаты С(19,76 12,33 23,26).
Совет 3: Как обнаружить уравнение окружности
Стандартное уравнение окружности дозволяет узнать несколько значимых сведений об этой фигуре, скажем, координаты ее центра, длину радиуса. В некоторых задачах, напротив, по заданным параметрам требуется составить уравнение.

Инструкция
1. Проверьте, указаны ли в условиях задачи координаты центральной точки окружности и длина радиуса в очевидном виде. В этом случае вам довольно подставить данные в стандартную запись уравнения, дабы получить результат.
2. Определите, какими сведениями об окружности вы располагаете, исходя из данной вам задачи. Запомните, что финальной целью является надобность определить координаты центра, а также диаметр. Все ваши действия обязаны быть направлены на достижение именно этого итога.
3. Используйте данные о наличии точек пересечения с координатными прямыми либо другими прямыми. Обратите внимание, что, если окружность проходит через ось абсцисс, вторая точка пересечения будет иметь координату 0, а если через ось ординат – то первая. Эти координаты дозволят вам обнаружить координаты центра окружности, а также вычислить радиус.
4. Не забывайте об основных свойствах секущих и касательных. В частности, особенно пригодной оказывается теорема о том, что в точке касания радиус и касательная образуют прямой угол. Но обратите внимание на то, что вас могут попросить подтвердить все использованные в ходе решения теоремы.
5. Прорешайте особенно типовые типы задач, дабы обучиться сразу видеть, как применять те либо иные данные для приобретения уравнения окружности. Так, помимо теснее указанных задач с прямо заданными координатами и теми, в условиях которых даны данные о наличии точек пересечения, для составления уравнения окружности дозволено воспользоваться познаниями о центре окружности, длине хорды и уравнения прямой, на которой эта хорда лежит.
6. Для решения постройте равнобедренный треугольник, основанием которого будет данная хорда, а равные стороны – радиусами. Составьте систему уравнений, из которой вы легко обнаружите нужные данные. Для этого довольно воспользоваться формулой для нахождения длины отрезка в координатной плоскости.
Видео по теме
Совет 4: Как обнаружить координаты точки в окружности
Под окружностью понимают фигуру, которая состоит из множества точек плоскости, равноудаленных от ее центра. Расстояние от центра до точек окружности именуется радиусом.

Вам понадобится
- – примитивный карандаш;
- – тетрадь;
- – транспортир;
- – циркуль;
- – ручка.
Инструкция
1. Раньше чем обнаружить координаты той либо другой точки окружности , постройте заданную окружность. При ее построении вам могут встретиться уйма новых представлений. Так хорда – это отрезок, тот, что соединяет две точки окружности , причем хорда, проходящая через центр окружности – максимальная (она носит наименование диаметра). Помимо того, к окружности может быть проведена касательная, которая представляет собой прямую, перпендикулярно расположенную к радиусу окружности , тот, что проведен к точке пересечения касательной и рассматриваемой геометрической фигуры.
2. Если по условию задания вестимо, что построенную вами окружность пересекает иная окружность (она поменьше по размерам), изобразите это графически: на рисунке должно быть изображено, что две эти окружности пересекаются, то есть имеют ряд всеобщих точек. Центр первой окружности обозначьте точкой 1 (ее координаты (X1,Y1)), а ее радиус – R1. Таким образом, центр 2-й окружности должен быть обозначен точкой 2 (координаты этой точки (X2,Y2)), а радиус – R2. В точках пересечения фигур поставьте точки 3 (X3,Y3) и 4 (X4,Y4). Центральная точка пересечения должна быть обозначена 0: ее координаты (X,Y).
3. Для того дабы обнаружить координаты пресечения данных окружностей, а следственно и точку, принадлежащую и первой, и 2-й из них, вам придется решить квадратное уравнение. Разглядите два образовавшихся треугольника (?103 и ?203) и проанализируйте их показатели. Гипотенузы этих треугольников – R1 и R2 соответственно. Зная значение гипотенуз, обнаружьте отрезок D, соединяющий центр первой окружности с центром 2-й. Выбранный способ расчета напрямую зависит от того, какими получились анализируемые вами треугольники. Если они прямоугольные, то квадрат длины гипотенузы всякого из них будет равен сумме квадратов катетов данного треугольника. К тому же, длину катета дозволено обнаружить по формуле: a = ccos ?, где с – длина гипотенузы, а cos? – косинус прилежащего угла. Обнаружив значение катетов, определите координаты волнующей вас точки.
Видео по теме
Обратите внимание!
Будьте внимательны, рассчитывая значения катетов: не допустите ошибку.
Полезный совет
Не позабудьте: один из углов прямоугольного треугольника прямой, то есть равен 90о.
Обратите внимание!
Две окружности, имеющие центром точку с одними и теми же координатами, именуются концентрическими. Если они заданы уравнениями (x-x0)?+(y-y0)?=R? и (x-x0′)?+(y-y0′)?=R’?, тогда x0=x0′, y0=y0′. В всеобщем уравнении для концентрических окружностей A1=A2 и B1=B2.
Полезный совет
Кстати, в физике окружность может рассматриваться как тонкое однородное кольцо. Центр этого кольца будет являться центром масс (либо центром инерции) такого тела. Если кольцо имеет массу m и радиус r, а через центр перпендикулярно плоскости кольца провести ось, то момент инерции кольца касательно оси будет равен mr?. Момент инерции твердо главен при рассмотрении вращательного движения тела.
