Введите а — длину прямоугольника в сантиметрах (см):
Введите b — ширину прямоугольника в сантиметрах (см):
Площадь прямоугольника равна:
Как рассчитать площадь прямоугольника, если известны длины его сторон?
Прямоугольник — это четырехугольник, у которого все углы составляют по 90 градусов.
Прямоугольник — это частный случай параллелограмма, у которого хотя бы один из внутренних углов равен 90 градусов.
Если известна длина сторон прямоугольника, то площадь можно рассчитать по формуле:
S = a x b
S — площадь прямоугольника;
a — длина прямоугольника;
b — ширина прямоугольника .
Если длины сторон известны в сантиметрах, то площадь прямоугольника в метрах квадратных рассчитывается по формуле:
S (м2) = a(см) x b(см) / 10 000
aсм — длина прямоугольника в сантиметрах (см).
bсм — ширина прямоугольника в сантиметрах (см).
Sм2 — площадь прямоугольника в квадратных метрах (м2).
Загрузить PDF
Загрузить PDF
Определить площадь плоских фигур в квадратных сантиметрах (также обозначаемых как см2) достаточно просто. В самом легком случае, когда требуется рассчитать площадь квадрата или прямоугольника, она вычисляется произведением длины и ширины. Площадь других фигур (кругов, треугольников и так далее) можно определить с помощью целого ряда специальных математических формул. Также, если потребуется, можно без труда перевести площадь в квадратные сантиметры из других единиц измерения.
-

1
Определите длину измеряемой площади. У квадратов и прямоугольников по четыре стороны, расположенных под прямыми углами относительно друг друга. В случае с прямоугольниками, их противоположные стороны равны между собой, тогда как у квадратов равны все стороны. Измерьте одну из сторон квадрата или большую из сторон прямоугольника, чтобы определить ее длину в сантиметрах.[1]
-

2
Определите ширину измеряемой площади. Далее измерьте в сантиметрах любую из сторон, смежных с той, которую вы измерили в первую очередь. Эта сторона будет находиться под углом в 90 градусов к первой. Вторая мерка будет обозначать ширину квадрата или прямоугольника.[2]
- Так как у квадрата все стороны одинаковы, его длина будет равна ширине. Поэтому у квадрата можно изначально измерить только одну сторону.
-

3
Умножьте длину на ширину. Просто перемножьте длину и ширину фигуры, чтобы определить площадь квадрата или прямоугольника в квадратных сантиматрах.[3]
- Например, допустим, что длина прямоугольника составляет 4 см, а ширина – 3 см. В таком случае площадь фигуры рассчитывается следующим образом: 4 × 3 = 12 квадратных сантиметров.
- В случае с квадратом (по причине равных сторон) можно просто умножить саму на себя длину одной из его сторон (другими словами, возвести ее “в квадрат” или “во вторую степень”), чтобы определить площадь фигуры в квадратных сантиметрах.
Реклама
-

1
Найдите площадь круга по формуле: S = π × r2. Чтобы найти площадь круга в квадратных сантиметрах, необходимо знать расстояние в сантиметрах от центра круга до линии его окружности. Это расстояние называется радиусом окружности. Как только радиус будет известен, обозначьте его буквой r из вышеупомянутой формулы. Умножьте значение радиуса само на себя и на число π (3,1415926…), чтобы узнать площадь круга в квадратных сантиметрах.[4]
- Например, площадь круга с радиусом 4 см составит 50,27 квадратных сантиметра в результате перемножения 3,14 и 16.
-

2
Вычислите площадь треугольника по формуле: S = 1/2 b × h. Площадь треугольника в квадратных сантиметрах вычисляется умножением половины длины его основания b (в сантиметрах) на его высоту h (в сантиметрах). Основанием треугольника выбирается одна из его сторон, тогда как высота треугольника – это перпендикуляр, опущенный к основанию треугольника из противоположной к нему вершины. Площадь треугольника можно вычислить через длину основания и высоту по любой из сторон треугольника и противоположной к ней вершине.[5]
- Например, если длина основания треугольника составляет 4 см, а высота, проведенная к основанию – 3 см, площадь составит: 2 x 3 = 6 квадратных сантиметра.
-

3
Найдите площадь параллелограмма по формуле: S = b × h. Параллелограммы подобны прямоугольникам за одним исключением – их углы не обязательно равны 90 градусам. Соответственно, расчет площади параллелограмма производится аналогичным для прямоугольника способом: длина стороны основания в сантиметрах умножается на высоту параллелограмма в сантиметрах. За основание берут любую из сторон, а высота определяется длиной перпендикуляра к ней из противоположного тупого угла фигуры.[6]
- Например, если длина основания параллелограмма составляет 5 см, а его высота – 4 см, его площадь составит: 5 x 4 = 20 квадратных сантиметров.
-

4
Вычислите площадь трапеции по формуле: S = 1/2 × h × (B+b). Трапеция – это четырехугольник две стороны которого параллельны между собой, а остальные две – нет. Чтобы определить площадь трапеции в квадратных сантиметрах, необходимо знать три мерки (в сантиметрах): длину более длинной параллельной стороны B, длину более короткой параллельной стороны b и высоту трапеции h (определяемую как кратчайшее расстояние между ее параллельными сторонами по перпендикулярному к ним отрезку). Сложите между собой длины двух параллельных сторон, поделите сумму пополам и умножьте на высоту, чтобы получить площадь трапеции в квадратных сантиметрах.[7]
- Например, если более длинная из параллельных сторон трапеции равна 6 см, более короткая – 4 см, а высота – 5 см, площадь фигуры составит: ½ x (6+4) х 5 = 25 квадратных сантиметров.
-

5
Найдите площадь правильного шестиугольника: S = ½ × P × a. Приведенная формула верна только для правильного шестиугольника с шестью равными сторонами и шестью одинаковыми углами. Буквой P обозначается периметр фигуры (или произведение длины одной стороны на шесть, что справедливо для правильного шестиугольника). Буквой a обозначается длина апофемы – расстояние от центра шестиугольника до середины одной из его сторон (точки, расположенной посередине между двумя соседними вершинами фигуры). Перемножьте периметр и апофему в сантиметрах и поделите результат на два, чтобы найти площадь правильного шестиугольника.[8]
- Например, если у правильного шестиугольника шесть равных сторон по 4 см (то есть его периметр P = 6 x 4 = 24 см), а длина апофемы равна 3,5 см, то его площадь составит: ½ x 24 x 3,5 = 42 квадратных сантиметра.
-

6
Вычислите площадь правильного восьмиугольника по формуле: S = 2a² × (1 + √2). Для расчета площади правильного восьмиугольника (с восемью равными сторонами и восемью одинаковыми углами) нужно знать только длину одной из сторон фигуры в сантиметрах (обозначенной в формуле буквой “a”). Подставьте соответствующее значение в формулу и вычислите результат.[9]
- Например, если длина стороны правильного восьмиугольника равна 4 см, то площадь этой фигуры составляет: 2 х 16 x (1 + 1,4) = 32 x 2,4 = 76,8 квадратных сантиметров.
Реклама
-

1
Переведите все мерки в сантиметры, прежде чем производить расчет площади. Чтобы сразу рассчитать площадь в квадратных сантиметрах, необходимо подставлять все параметры в формулу расчета площади также в сантиметрах (это касается, длины, высоты, апофемы и так далее). Поэтому, если ваши исходные данные выражены в других единицах измерения (например, в метрах), сначала их следует перевести в сантиметры. Ниже приведены соотношения наиболее популярных единиц измерения.
- 1 метр = 100 сантиметров
- 1 сантиметр = 10 миллиметров
- 1 дюйм = 2,54 сантиметра
- 1 фут = 30,48 сантиметра
- 1 сантиметр = 0,3937 дюйма
-

2
Чтобы перевести площадь из квадратных метров в квадратные сантиметры, ее следует умножить на 10000 (то есть площадь одного квадратного метра в сантиметрах), или на произведение 100 см на 100 см. Если вы знаете площадь фигуры в квадратных метрах, ее можно перевести в квадратные сантиметры умножением на 10000.[10]
- Например, 0,5 квадратного метра = 0,5 x 10000 = 5000 квадратных сантиметров.
-

3
Чтобы перевести в квадратные сантиметры площадь, выраженную в квадратных дюймах, умножьте ее на 6,4516. Как уже упоминалось, 1 дюйм равен 2,54 сантиметра, тогда как квадратный дюйм составляет 6,4516 квадратных сантиметров (или 2,54 x 2,54). Таким образом, если вам необходимо конвертировать в квадратные сантиметры площадь, равную 10 квадратным дюймам, следует умножить 10 на 6,4516, и у вас получится 64,5 квадратных сантиметров.[11]
- Также следует упомянуть, что в одном гектаре содержится 10000 квадратных метров, тогда как каждый квадратный метр равен 10000 квадратных сантиметров. Поэтому, чтобы выразить один гектар в сантиметрах, следует умножить 10000 на 10000 и получится 100 миллионов квадратных сантиметров.
Реклама
Об этой статье
Эту страницу просматривали 153 899 раз.
Была ли эта статья полезной?
Онлайн калькулятор. Площадь прямоугольника
Используя этот онлайн калькулятор, вы сможете найти площадь прямоугольника.
Воспользовавшись онлайн калькулятором для вычисления площади прямоугольника, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Найти площадь прямоугольника
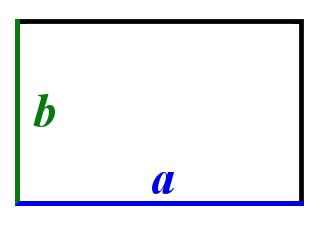
a =
b =
Площадь в
Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.
Калькулятор для расчета площади
Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:
|
|
Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.
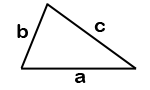
Способ нахождения площади треугольника:
| a= |
|
| b= | |
|
c= |
Вычислить
Рассчитать площадь круга, если известен:
| r= |

|
Вычислить
Способ нахождения площади параллелограмма:
| a= |

|
|
h=
|
|
Вычислить
Рассчитать площадь сектора круга, если известен:
|
r= |

|
|
θ= |
Вычислить
Способ нахождения площади трапеции:
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.
| Метрические единицы измерения площади: | |
| Квадратный метр, производная единица системы СИ 1 м2 = | 1 са (сантиар) |
| Квадратный километр – 1 км2 = | 1 000 000 м2 |
| Гектар – 1 га = | 10 000 м2 |
| Ар (сотка) – 1 а = | 100 м2 (сотка как правило применяется для измерения земельных участков и равна 100 м2 или 10м х 10м) |
| Квадратный дециметр, 100 дм2 = | 1 м2; |
| Квадратный сантиметр, 10 000 см2 = | 1 м2; |
| Квадратный миллиметр, 1 000 000 мм2 = | 1 м2. |
Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.
Как рассчитать площадь прямоугольника
На данной странице калькулятор поможет рассчитать площадь прямоугольника онлайн. Для расчета задайте длину сторон или длины диагоналей и угол между ними.
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).
Через стороны
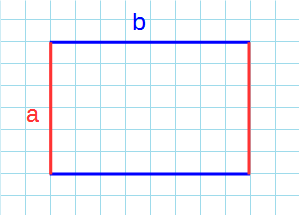
Формула для нахождения площади прямоугольника через стороны:
a, b – стороны прямоугольника.
Через диагонали и угол между ними
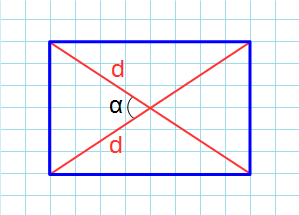
Формула для нахождения площади прямоугольника через диагонали и угол между ними:
d – диагональ; α – угол между диагоналями.
