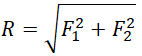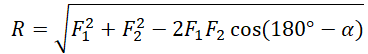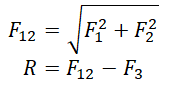Искать “а” ради “ускорения”-пустое занятие. Искать надо F-Силу,которая вызывает движение,и изменяет его. S/tt=F/m. S,t,m можно измерить. F=?
Ошибка Ньютон: S=att/2. S=att ! (без /2).
“а”-это ЭНЕРГИЯ движения. Она НЕ зависит от графика движения, и численно = S/tt (V/t).
У падающего “яблока..” несколько скоростей: нач. скорость, кон.скорость,средняя скорость, at, 2at. “средняя скорость”-(S/t)-это та-же скорость at,но выраженная через ЭНЕРГИЮ и ВРЕМЯ: F/m*t.
ВСЕ расчёты на движение надо делать ТОЛЬКО из СРЕДНЕЙ скорости! (Энергия одинакова, и НЕ зависит от графика движения). И нет “надобности” в “интегралах”. …Задачка: машина m=1165 кг, прошла 250 м. за 18 с.(набрала скорость от 0 до 27,7 м/с за 18 сек.) (“Жигули”). Вопрос: какая мощность мотора?
Всякий механизм имеет КПД. КПД ДВС (у бензиновых двс=16%).Решение: S/tt=F/m. 250/324=F/1165, (или 13,9/18=F/1165). F=900 кг.м/сс. Это 12 л.с. при 100% КПД ! При 16% мощность=75 л.с. (а,Да! “ускорение”? оно =0,77 м/сс….). Но и без “а”не обойтись…
Грубая ошибка, находить “а”: Vo=0. V кон.=27,7. t=18 сек. а=(27,7-0)/18. а=1,5 м/сс. Мощность мотора=150 л.с.
То-же с “яблоком…” Vo=0, Vкон.=9,8. t=1 c. Правильно: (0+9,8)/2t. a=4,9 м/cc S=4,9 м.
“Если тело упало на Землю с высоты h, то S/tt ВСЕГДА !!! РАВНО числу 4,9… Это число 4,9 м/сс и ЕСТЬ “УСКОРЕНИЕ СВОБОДНОГО ПАДЕНИЯ”! Скорость: м/с. Ускорение-м/сек.сек. 9,8-это скорость,(но НЕ ускорение).
Сколько ошибок (и слёз) при решении задач:
Vo=5. t=10. a=2. S=? a=? V кон.=?
Решение: S=Vot+att. S=5/10+2*10*10. S=250. a=S/tt. a=2,5. V кон.=Vo+2at. Vкон.=5+2*2*10. V кон.=45. Проверка:S=att. 2,5*10*10=250. S=(v+V)/2*t. (5+45)/2*10. S=250 м.
По принятым формулам: S=(vo+att/2)*t. S=5*10+2*10/10/2=150 м. a=2S/tt. 300/100=3 м/сс
V кон.=v0+at. 5+20=25. S=(5+5+25)*10. S=350 м. (“ОГОРОД!”)
Инертность, масса, ускорение
m1, m2 – массы взаимодействующих тел
a1, a2 – ускорение
Сила, масса, ускорение
F – сила
m – масса
a – ускорение
Сила тяжести
N – сила тяжести
m – масса
g – ускорение свободного падения
Сила трения
F_тр – сила трения
μ – коэффициент трения
N – сила тяжести
Сила трения
F_тр – сила трения
μ – коэффициент трения
m – масса
g – ускорение свободного падения
Закон всемирного тяготения
F – сила
G – гравитационная постоянная
m1, m2 – массы взаимодействующих тел
r – расстояние
Центростремительное ускорение спутника
a – ускорение
v – скорость
R – радиус земли
h – высота
Скорость спутника
v – скорость
G – гравитационная постоянная
M – масса Земли
R – радиус земли
h – высота
Первая космическая скорость (движение по круговой орбите)
v – скорость
g – ускорение свободного падения
R – радиус земли
Вторая космическая скорость (преодоление гравитации)
v – скорость
g – ускорение свободного падения
R – радиус земли
Третий закон Кеплера
T1, T2 – периоды обращения двух планет вокруг Солнца
a1, a2 – длины больших полуосей их орбит
Ускорение свободного падения на поверхности земли
g – ускорение свободного падения
G – гравитационная постоянная
M – масса Земли
R – радиус земли
Вес тела
P – вес
m – масса
g – ускорение свободного падения
Вес тела: невесомость
Вес тела, когда ускорение тела совпадает по направлению с ускорением свободного падения
P – вес
m – масса
g – ускорение свободного падения
a – ускорение
Вес тела: перегрузка
Вес тела, когда ускорение тела противоположно направлению ускорения свободного падения
P – вес
m – масса
g – ускорение свободного падения
a – ускорение
Время торможения
t – время
m – масса
v – скорость
F_тр – сила трения
Время торможения
t – время
v – скорость
μ – коэффициент трения
g – ускорение свободного падения
Путь торможения
s – путь
m – масса
v – скорость
F_тр – сила трения
Путь торможения
s – путь
v – скорость
μ – коэффициент трения
g – ускорение свободного падения
Сила трения качения
F_тр – сила трения качения
μ – коэффициент трения качения
N – сила тяжести
R – радиус
Сила упругости
F_упруг – сила упругости
k – жёсткость
x – удлинение (сокращение) предмета
Кинетическая энергия вращающегося тела
W_k – кинетическая энергия
J – момент инерции
ω – угловая скорость
Три закона Ньютона
Динамика — раздел механики, изучающий причины движения тел и способы определения их ускорения. В нем движение тел описывается с учетом их взаимодействия.
Большой вклад в развитие динамики внес английский ученый Исаак Ньютон. Он первым смог выделить законы движения, которым подчиняются все макроскопические тела. Эти законы называют законами Ньютона, законами механики, законами динамики или законами движения тел.
Внимание! Законы Ньютона нельзя применять к произвольным телам. Они применимы только к точке, обладающей массой — к материальной точке.
Основное утверждение механики
Для описания движения тела можно взять любую систему отсчета. Обычно для этого используется система отсчета, связанная с Землей. Если какое-то тело меняет свою скорость, рядом с ним всегда можно обнаружить другое тело, которое на него действует. Так, если поднять камень и отпустить, он не останется висеть в воздухе, а упадет вниз. Следовательно, на него что-то подействовало. В данном случае сама Земля притянула камень к себе. Отсюда следует основное утверждение механики:
Основное утверждение механики
Изменение скорости (ускорение) тела всегда вызывается воздействием на него других тел.
Согласно утверждению, если на тело не действуют никакие силы, его ускорение будет нулевым, и оно будет либо покоиться, либо двигаться равномерно и прямолинейно (с постоянной скоростью).
Но в нашем мире мы не всегда это наблюдаем. И этому есть объяснение. Если тело покоится, оно действительно не меняет свою скорость. Так, мяч лежит на траве до тех пор, пока его не пнут. После того, как его пнут, он начинает катиться, но затем останавливается. Пока мяч катится, к нему больше не прикасаются. Казалось бы, согласно основному утверждению механики, мяч должен катиться вечно. Но этого не происходит, потому что на мяч действует сила трения, возникающая между его поверхностью и травой.
Основное утверждение механики можно проиллюстрировать в открытом космосе в месте, где сила притяжения космических тел пренебрежимо мала. Если в космосе придать телу скорость и отпустить, оно будет двигаться с такой скоростью по прямой линии до тех пор, пока на него не подействуют другие силы. Ярким примером служат межгалактические звезды, или звезды-изгои. Гравитационно они не связаны ни с одной из галактик, а потому движутся с постоянной скоростью. Так, звезда HE 0437-5439 удаляется от нашей галактики с постоянной скоростью 723 км/с.
Свободное тело — тело, на которое не действуют другие тела. Свободное тело либо покоится, либо движется прямолинейно и равномерно.
Первый закон Ньютона
Исаак Ньютон, изучая движение тел, заметил, что относительно одних систем отсчета свободные тела сохраняют свою скорость, а относительно других — нет. Он разделил их на две большие группы: инерциальные системы отсчета и неинерциальные. В этом кроется первый закон динамики.
Первый закон Ньютона
Существуют такие системы отсчета, называемые инерциальными, относительно которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, если на них не действуют другие тела или их действие компенсировано.
Примером инерциальной системы отсчета служит система отсчета, связанная с Землей (геоцентрическая). Другой пример — гелиоцентрическая система отсчета (связанная с Солнцем).
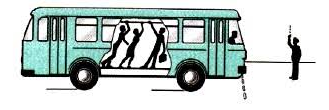
Неинерциальная система отсчета — система отсчета, в которой тела могут менять свою скорость при отсутствии на них действия других тел.
Примером неинерциальной системы отсчета служит автобус. Когда он движется равномерно и прямолинейно, стоящие внутри пассажиры находятся относительно него в состоянии покоя. Но когда автобус останавливается, пассажиры падают вперед, т. е. меняют свою скорость, хотя на них не действуют другие тела.
Второй закон Ньютона
В примере с автобусом видно, что пассажиры стараются сохранить свою скорость относительно Земли — инерциальной системы отсчета. Такое явление называется инерцией.
Инерция — явление, при котором тело сохраняет состояние покоя или равномерного прямолинейного движения.
Инертность — физическое свойство, заключающееся в том, что любое тело оказывает сопротивление изменению его скорости (как по модулю, так и по направлению).
Не все тела одинаково инертны. Вы можете взять мячик и придать ему большое ускорение. Но вы не можете придать такое же ускорение гире, хотя она обладает похожим размером. Но мячик и гиря различаются между собой массой.
Масса — скалярная физическая величина, являющаяся мерой инертности тела. Чем больше масса, тем больше инертность тела.
Масса обозначается буквой m. Единица измерения массы — кг. Прибор для измерения массы — весы.
Чтобы придать одинаковую скорость двум телам с разной инертностью, к телу с большей инертностью придется приложить больше силы. Попробуйте сдвинуть с места стол, а затем — шкаф. Сдвинуть с места стол будет проще.
Если же приложить две одинаковые силы к телам с разной инертностью, будет видно, что тело с меньшей инертностью получает большее ускорение. Если приставить к пружине теннисный шарик, а затем сжать ее и резко отпустить, шарик улетит далеко. Если вместо теннисного шарика взять железный, он лишь откатится на некоторое расстояние.
Описанные выше примеры показывают, что между силой, прикладываемой к телу, и ускорением, которое оно получает в результате прикладывания этой силы, и массой этого тела есть взаимосвязь. Она раскрывается во втором законе Ньютона.
Второй закон Ньютона
Сила, действующая на тело, равна произведению массы этого тела на ускорение, которое сообщает эта сила.
F = ma
где F — сила, которую прикладывают к телу, a — ускорение, которое сообщает эта сила, m — масса тела
Сила — количественная мера действия тел друг на друга, в результате которого тела получают ускорения.
Сила — векторная физическая величина. Обозначается F. Единица измерения — Н (Ньютон). Прибор для измерения силы — динамометр.
Пример №1. Определить, с какой силой действует Земля на яблоко, если, упав с ветки, оно получило ускорение 9,8 м/с2. Масса яблока равна 200 г.
Сначала переведем массу яблока в кг. 200 г = 0,2 кг. Теперь найдем силу, действующую на яблоко со стороны Земли, по второму закону Ньютона:
F = ma = 0,2 ∙ 9,8 = 1,96 (Н)
Равнодействующая сила
Иногда на тело действуют несколько сил. Тогда при описании его движения вводится понятие равнодействующей силы.
Определение
Равнодействующая сила — векторная сумма всех сил, действующих на тело одновременно.
R = F1 + F2 + F3 + …
В этом случае второй закон Ньютона формулируется так:
Второй закон Ньютона через равнодействующие силы
Если на тело действует несколько сил, то их равнодействующая R будет равна произведению массы на ускорение этого тела.
ma = R = F1 + F2 + F3 + …
Правила сложения сил и их проекций
|
Сложение двух сил, направленных вдоль одной прямой в одну сторону |
|
 |
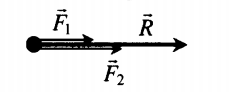Если F1↑↑F2, то:
R = F1 + F2 Равнодействующая сила сонаправлена с обеими силами. |
|
Сложение двух сил, направленных вдоль одной прямой во взаимно противоположных направлениях |
|
 |
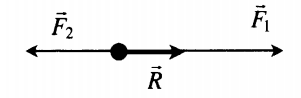Если F1↑↓F2, то:
R = |F1 – F2| Равнодействующая сила направлена в сторону направления большей по модулю силы. |
|
Сложение двух сил, перпендикулярных друг к другу |
|
 |
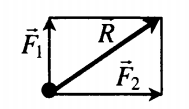Если F1 перпендикулярна F2, то равнодействующая сила вычисляется по теореме Пифагора:
|
|
Сложение двух сил, расположенных под углом α друг к другу |
|
 |
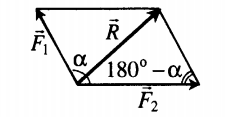Если F1 и F2 расположены под углом α друг к другу, равнодействующая сила вычисляется по теореме косинусов:
|
|
Сложение трех сил |
|
 |
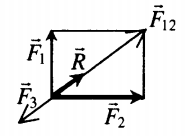Способ сложения определяется правилами сложения векторов. В данном случае:
|
|
Сложение проекций сил |
|
 |
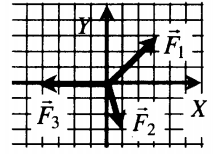Проекция на ось ОХ:
F1x + F2x – F3x = 0 Проекция на ось OY: F1y – F2y = 0 |
Третий закон Ньютона
Когда одно тело действует на другое, начинается взаимодействие этих тел. Это значит, если тело А действует на тело В и сообщает ему ускорение, то и тело В действует на тело А, тоже придавая ему ускорение. К примеру, если сжать пружину руками, то руки будут чувствовать сопротивление, оказываемое силой упругости пружины. Если же, находясь в лодке, начать тянуть за веревку вторую лодку, то обе лодки будут двигаться навстречу друг другу. То есть, вы, находясь в своей лодке, тоже будете двигаться навстречу второй лодке.
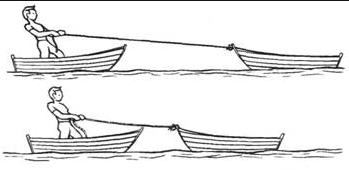
Иногда на тело действует сразу несколько сил, но тело продолжает покоиться. В этом случае говорят, что силы друг друга компенсируют, то есть их равнодействующая равна нулю.
Две силы независимо от их природы считаются равными по модулю и противоположно направленными, если их одновременное действие на тело не меняет его скорости.
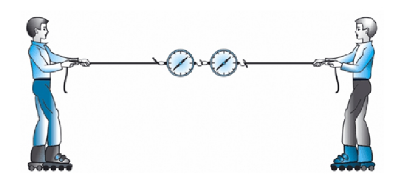
Примером такого явления служит ситуация, когда при перетягивании каната его никто не может перетянуть в свою сторону. Если взять два каната и присоединить между ними два динамометра, а затем начать игру в перетягивание, выяснится, что показания динамометра всегда будут одинаковыми. Это значит, что независимо от масс и придаваемых ускорений два взаимодействующих тела оказывают друг на друга равные по модулю силы. В этом заключается смысл третьего закона Ньютона.
Третий закон Ньютона
Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны.
FA = –FB
Используя второй закон Ньютона, третий закон механики можно переписать иначе:
m1a1 = –m2a2
Отсюда следует:
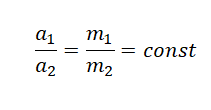
Отношение модулей ускорений a1 и a2 взаимодействующих друг с другом тел определяется обратным отношением их масс и совершенно не зависит от характера действующих между ними сил.
Пример №2. Определить ускорение, с которым движется Земля к падающему на нее яблоку. Масса яблока равна 0,2 кг. Ускорение свободного падения принять равной за 10 м/с2. Массу Земли принять равно 6∙1024 кг.
Согласно третьему закону Ньютона модули сил, с которыми взаимодействуют Земли и яблоко, равны. Поэтому:
F1 = F2
Отсюда:
m1a1 = m2a2
Пусть тело 1 будет яблоко, а тело 2 — Земля. Тогда a1 будет равно g. Отсюда ускорение, с которым движется Земля к падающему на нее яблоку, равна:
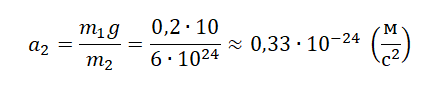
Задание EF17993
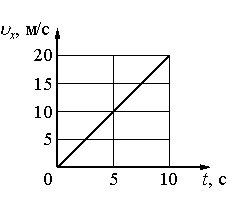Скорость тела массой 5 кг, движущегося вдоль оси Ох в инерциальной системе отсчёта, изменяется со временем в соответствии с графиком (см. рисунок). Равнодействующая приложенных к телу сил в момент времени t=2,5 с равна…
а) 2Н
б) 8 Н
в) 10 Н
г) 20 Н
Алгоритм решения
1.Записать исходные данные.
2.Проанализировать задачу.
3.Записать второй закон Ньютона.
4.Определить ускорение по графику проекции скорости от времени.
5.Подставить найденное ускорение в формулу второго закона Ньютона и произвести вычисления.
Решение
Запишем исходные данные:
Так как графиком скорости является прямая, непараллельная ось времени, тело движется с постоянным ускорением. Если ускорение постоянно, равнодействующая сил тоже будет постоянной в любой момент времени. Поэтому нам достаточно использовать координаты любой, более удобной для их определения точки. К примеру, в точке, соответствующей моменту времени 10 с.
Запишем второй закон Ньютона:
F = ma
Ускорение тела определяется как отношение изменения скорости ко времени, в течение которого эта скорость менялась. Согласно графику, за 10 секунд скорость изменилась на 20 м/с. Следовательно, ускорение равно:
a = 20/10 = 2 (м/с2)
Теперь можем вычислить равнодействующую сил:
F = ma = 5∙2 = 10 (Н)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18915
Необходимо собрать экспериментальную установку, с помощью которой можно определить коэффициент трения скольжения стали по дереву. Для этого школьник взял стальной брусок с крючком. Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?
а) деревянная рейка
б) динамометр
в) мензурка
г) пластмассовая рейка
д) линейка
Алгоритм решения
1.Проанализировать задачу. Выяснить, какие предметы необходимы для проведения опыта.
2.Вывести формулу для коэффициента трения.
3.Определить, какую величину нужно измерить, чтобы рассчитать коэффициент трения, и какой прибор для этого нужен.
Решение
Для определения коэффициента трения стали по дереву, нужен не только стальной груз, но и деревянная поверхность. То есть, понадобится деревянная рейка.
Сила трения определяется формулой:
Отсюда коэффициент трения равен:
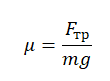
Ускорение свободного падения известно. Массу можно измерить на весах, но весов в вариантах ответа нет. Силу трения можно измерить динамометром. Следовательно, для опыта нужны только динамометр и деревянная рейка. Рейка из пластика не понадобится, так как цели расчета коэффициента трения стали по пластику нет. Мензурка используется для определения объема жидкости. В данном опыте она тоже не нужна.
Ответ: аб
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17589
Система отсчёта, связанная с Землёй, считается инерциальной. В этом случае систему отсчёта, связанную с самолётом, можно считать инерциальной, если самолёт движется:
а) равномерно и прямолинейно, набирая высоту
б) с постоянным ускорением по горизонтали
в) равномерно, выполняя поворот
г) по взлетной полосе при взлете
Алгоритм решения
- Сформулировать первый закон Ньютона об инерциальных системах отсчета.
- На основании закона сделать вывод, при каких условиях система отсчета, связанная с самолетом, может считаться инерциальной.
- Проанализировать все 4 ситуации, приведенные в вариантах ответа.
- Выбрать тот вариант, который описывает ситуацию, не противоречащую условию, выведенному в шаге 2.
Решение
Первый закон Ньютона формулируется так:
«Существуют такие системы отсчета, называемые инерциальными, относительно которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, если на них не действуют другие тела или их действие компенсировано».
Чтобы система отсчета, связанная с самолетом, была инерциальной, она должна быть неподвижной или двигаться относительно Земли — инерциальной системы отсчета — равномерно и прямолинейно.
Когда самолет движется равномерно и прямолинейно, набирая высоту, самолет движется с собственным ускорением, которое компенсируется ускорением свободного падения. И это единственный верный ответ, так как:
- Самолет, двигаясь с постоянным ускорением по горизонтали, движется неравномерно, что противоречит условию.
- Самолет, двигаясь равномерно во время поворота, движется непрямолинейно (с центростремительным ускорением).
- Самолет, двигаясь по взлетной полосе при взлете, движется прямолинейно, но неравномерно, так как он разгоняется из состояния покоя.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22791
Погрешность прямого измерения силы динамометром, на котором висит груз, равна цене деления. Каков вес груза?
Ответ: ( ± ) Н.
Внимание! Записывать ответ следует последовательностью цифр без запятых.
Алгоритм решения
1.Записать исходные данные.
2.Определить цену деления шкалы.
3.Записать значение измерения с учетом погрешности.
Решение
Из условий задачи известно, что погрешность равна цене деления шкалы. Цена деления шкалы определяется отношением разности двух ближайших числовых обозначений на шкале и количеству делений между ними. Возьмем ближайшие значения 1,0 и 1,5. Между ними 5 делений. Следовательно, цена деления шкалы динамометра равна:
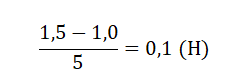
Так как погрешность равна цене деления, она также равна 0,1 Н.
Стрелка динамометра показывает 1,1 Н. Следовательно, вес груза равен: 1,1±0,1. Но по условию задачи ответ нужно записать без запятых и прочих знаков. Следовательно, верный ответ: 1101.
Ответ: 1101
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17484
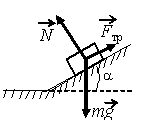Тело массой m скользит по шероховатой наклонной опоре с углом α к горизонту (см. рисунок). На него действуют 3 силы: сила тяжести mg, сила упругости опоры N и сила трения Fтр. Если скорость тела не меняется, то модуль равнодействующей сил Fтр и mg равен:
а) N cosα
б) N
в) N sinα
г) mg + Fтр
Алгоритм решения
- Запись второго закона Ньютона в векторном виде.
- Вывод формулы равнодействующей силы трения и силы тяжести.
- Нахождение модуля равнодействующей силы трения и силы тяжести.
Решение
Записываем второй закон Ньютона в векторном виде с учетом того, сто скорость тела не меняется (ускорение равно 0):
N + mg + Fтр = 0
Отсюда равнодействующая силы трения и силы тяжести равна:
mg + Fтр = –N
Следовательно, равнодействующая силы трения и силы тяжести направлена противоположно силе реакции опоры, но равна ей по модулю. Отсюда:
|mg + Fтр| = N
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18548
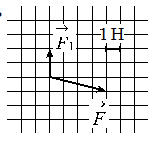На тело действуют две силы: F1 и F2. По силе F1 и равнодействующей двух сил F = F1 + F2 найдите модуль второй силы (см. рисунок).
Алгоритм решения
- Изобразить на рисунке второй вектор с учетом правил сложения векторов.
- Записать геометрическую формулу для расчета модуля вектора по его проекциям.
- Выбрать систему координат и построить проекции второй силы на оси ОХ и ОУ.
- По рисунку определить проекции второй силы на оси.
- Используя полученные данные, применить формулу для расчета вектора по его проекциям.
Решение
Построим вектор второй силы. Его начало должно совпадать с концом вектора первой силы, а его конец — с концов равнодействующей этих сил. Этот вывод следует из сложения векторов правилом треугольника.
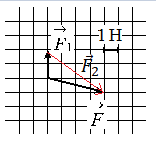
Модуль вектора равен корню из суммы квадратов его проекций на оси ОХ и ОУ:
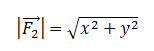
Выберем систему координат и построим проекции второй силы на оси ОХ и ОУ:
Согласно рисунку, проекция второй силы на ось ОХ равна: x = 4 (Н). Ее проекция на ось ОУ равна: y = 3 (Н).
Подставим известные данные в формулу и вычислим модуль вектора второй силы:
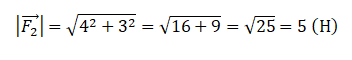
Ответ: 5
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 16.5k
Физика — серьезная наука, которая состоит из нескольких крупных разделов и множества менее объемных подразделов. Проще всего с каждым из них знакомиться отдельно, чтобы избежать путаницы в голове. В этой статье подробно поговорим о динамике.
Что такое динамика в физике
Динамика в физике — это раздел механики, который изучает взаимодействие тел и причины возникновения/изменения движения.
Динамика, которая опирается на законы Ньютона, называется классической. Этот раздел изучает движение объектов со скоростями в пределах от миллиметров в секунду до километров в секунду. В классической механике причинами движения всегда выступают силы. Законы динамики изучают также:
- движение упруго и пластически деформируемых тел;
- жидкостей;
- газов.
Не все виды движения можно описать законами динамики. Например, движение элементарных частиц при скоростях, близких к скорости света, подчиняется другим физическим законам.
В ходе изучения динамики конкретных объектов, возникли специальные дисциплины:
- баллистика;
- небесная механика;
- динамика корабля и самолёта и др.
Основные понятия и определение
Классическая механика изучает такие понятия, как:
- масса;
- энергия;
- импульс;
- момент импульса;
- сила;
- равнодействующая сила и др.
Масса — это скалярная физическая величина, которая является характеристикой такого свойства объекта, как инертность, и определяет количество вещества в теле.
Энергия — это количественная мера, характеризующая движение и взаимодействие объектов, а также их способность воздействовать на окружающий мир.
Импульс — это векторная физическая величина, измеряющая механическое движение тела, которая рассчитывается по формуле: vec p=mtimesvec v
Момент импульса — это количественная характеристика вращательного движения.
Сила — это векторная величина, которая является причиной изменения скорости тела или его деформации, а также количественной мерой взаимодействия тел.
Любая сила в физике характеризуется 3 параметрами:
- точкой приложения;
- направлением;
- численным значением или модулем.
Линией действия силы называют прямую, вдоль которой эта сила действует.
Равнодействующая сила — это сила, которая оказывает на тело такое же действие, как все другие вместе взятые силы, воздействующие на него. Величина рассчитывается по формуле:
(vec F=vec F_1+vec F_2+vec F_3 )
В том случае, когда объект находится в состоянии покоя, равнодействующая всех сил, действующих на него, равна нулю.
В динамике встречаются следующие виды сил:
- Тяжести. Приложена к центру массы тела и направлена вертикально вниз (всегда перпендикулярно горизонту). Рассчитывается по формуле: (F=mtimes g) где (m) — масса тела, (g) — ускорение свободного падения.
- Трения. Приложена к поверхности касания тела и опоры и направлена в противоположную сторону той, куда направлены другие силы, действующие на тело. Вычисляется по формуле: (F=mutimes N), где (mu) — коэффициент трения, (N) — сила реакции опоры.
- Сопротивления. Возникает при движении тела в газе или жидкости, всегда направлена против скорости движения.
- Реакции опоры. Действует на тело со стороны опоры, направлена перпендикулярно от нее.
- Натяжения нити. Направлена от тела вдоль нити.
- Упругости. Возникает при деформации тела, направлена против деформации. Вычисляется она согласно закону Гука по формуле: (F=ktimesDelta l), где (k) — коэффициент упругости, (Delta l) — удлинение тела при деформации.
Основные законы динамики, формулы
Законы, на которых строится динамика, были впервые сформулированы Исааком Ньютоном в 1687 году. Именно поэтому их чаще всего и называют законами Ньютона.
Законы Ньютона верны только для описания движений, которые происходят в инерциальных системах отсчета (ИСО). Инерциальной называют такую систему отсчета, в которой тела двигаются равномерно и прямолинейно.
Первый закон Ньютона
Согласно первому закона Ньютона, тело остается в покое или равномерно прямолинейно движется, если на него не действуют никакие силы или равнодействующая всех сил равна нулю.
Инерцией называется способность тел сохранять скорость движения при отсутствии воздействия на него других объектов. Иногда первый закон Ньютона называют еще законом инерции.
Второй закон Ньютона
Второй закон Ньютона считается основным законом динамики и представляет собой формулу нахождения ускорения: ускорение, которое приобретает тело, прямо пропорционально равнодействующей сил (F), воздействующих на тело и обратно пропорционально массе ((m)) этого тела:
(vec a=frac{vec F}m)
Когд на тело действуют сразу несколько сил, под силой в этом уравнении подразумевается равнодействующая всех сил.
Третий закон Ньютона
Третий закон Ньютона гласит: тела воздействуют друг на друга с силами, которые равны по модулю и противоположны по направлению, лежат на одной прямой и имеют одну физическую природу:
(vec F=-vec F)
Данные силы не могут уравновесить друг друга, так как приложены к разным телам. По этой же причине их нельзя складывать.
Методы решения задач, алгоритм
Как правило, все задачи из раздела динамики решаются с использованием законов Исаака Ньютона.
Для того, чтобы существенно упростить процесс решения задач по динамике, нужно:
- Внимательно прочитать условие задачи, разобраться, какие силы воздействуют на тела, указанные в задании.
- Нарисовать рисунок, на котором изобразить все векторные силы и указать их направление.
- Выбрать систему отсчета: одну координатную ось направить по направлению ускорения рассматриваемого тела, другую — перпендикулярно ускорению.
- Вспомнить второй закон Ньютона: (vec F_1+vec F_2+vec F_3=mtimes vec a)
- Записать скалярную форму уравнения, учитывая, что силы, которые направлены против выбранных осей координат, будут иметь отрицательные значения. Получится такая система уравнений: (left{begin{array}{l}F_{1x}+F_{2x}+F_{3x}=mtimes a_x\F_{1y}+F_{2y}+F_{3y}=mtimes a_yend{array}right.)
- При необходимости дополнить решение задачи другими уравнениями.
- Произвести математические вычисления.
Если в задаче указаны несколько движущихся тел, анализировать силы и записывать системы уравнений необходимо сделать для каждого из них.
Примеры решения задач по динамике
Основные формулы, используемые для решения задач на поступательное и вращательное движение в динамике:
Приведем несколько наглядных примеров решения задач по динамике.
Задачи по динамике поступательного движения с решениями
Задача № 1:
Объект массой 3 килограмма передвигается горизонтально с ускорением, равным (4 м/с^2). Определите силу, действующую на тело.
Решение:
- Запишем вводные данные: (m=3 кг) , (a=4 м/с^2, F=?)
- Находим силу по формуле, иллюстрирующей второй закон Ньютона: (F=mtimes a.)
- Подставляем числовые данные в формулу и получаем ответ: (12 Н.)
Задача №2:
Задачи по динамике вращательного движения с решениями
Решение задач на вращательное движение производится при помощи законов Ньютона, также важно помнить основное уравнение динамики вращательного движения:
(vec M=Jtimesvecepsilon)
где (M) — момент силы, которая действует на тело, (J) — инерция, (epsilon) — угловое ускорение.
Задача:
Задачи по физике могут изрядно испортить настроение, если предмет не нравится, а суть его остается неясной. В таком случае за помощью можно обратиться к образовательному сервису Феникс.Хелп. Наши специалисты с легкостью разбираются в любых темах.
Динамика изучает причины, по которым движение происходит именно так, а не иначе. Ее интересуют силы, которые действуют на тела. У динамики есть прямая и обратная задачи. Прямая – по известному характеру движения определить равнодействующую всех сил, действующих на тело. Обратная – по заданным силам определить характер движения тела. Конечно, мы должны познакомиться с понятием силы, инерциальной системы отсчета, законами Ньютона. Но обо всех основах динамики по порядку. В данной статье рассмотрим основные законы динамики и приведем пример решения задачи по основам динамики.
В чем сила, брат?
Красота – страшная сила! А еще, конечно, сила в правде, а у кого-то в деньгах. Но мы-то знаем, что все это заблуждения и домыслы. Сила – в Ньютонах!
Сила – векторная физическая величина, количественная мера интенсивности взаимодействия тел.
Единицей измерения силы в системе СИ является Ньютон. Один Ньютон – это такая сила, которую мы можем приложить к телу массой один килограмм. При этом она изменит скорость тела на 1 м/с за одну секунду.
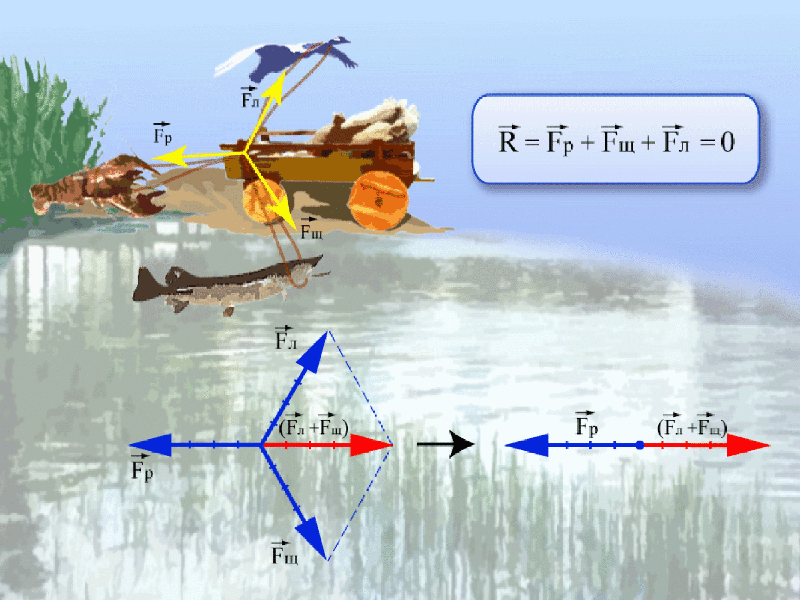
Бывает , что на тело действует сразу несколько сил. В принципе, в мире нет тел и предметов, на которые не действуют вообще никакие силы. Вот с утра едем мы на экзамен, и так бы нам хотелось, чтоб никакие силы нас не трогали и оставили в покое… Но нет. Притяжение давит вниз, ветер сдувает вбок, кто-то еще нагло толкает в метро. В таком случае можно все эти силы представить как одну, но оказывающую то же действие, что и все. Векторная сумма всех сил, действующих на тело, называется равнодействующей силой.
Например, на рисунке ниже равнодействующая сил равна нулю, потому как лебедь рак и щука так никуда и не сдвинули воз.
Масса и Вес
Масса – скалярная аддитивная физическая величина, являющаяся количественной мерой инертности тела, то есть его способности сохранять постоянную скорость.
В системе СИ измеряется в килограммах. Если не ищете легких путей и хотите быть особенно экстравагантным, можете измерять в фунтах, пудах и унциях.
Важно! Не стоит путать массу тела и вес. Ведь масса – скалярная величина, а вес – это сила, с которой тело действует на опору или подвес. Другими словами, масса всегда остается постоянной, это собственная характеристика тела. А вот вес может меняться. Например, Ваш лунный вес будет отличаться от земного, т.к. ускорение свободного падения на планетах различно.
Вы все еще читаете? Поздравляем, Вы просто молодцы! Давайте переходить к законам Ньютона, ведь рассматривая основы динамики невозможно обойти их стороной. Законы Ньютона – основные законы динамики.
Первый закон Ньютона
Как мы уже знаем, движение осуществляется в системе отсчета. Так вот, существуют такие системы отсчета, которые называются инерциальными (ИСО). Что это значит? Это тоже идеализация, наподобие материальной точки. Существование ИСО постулируется первым законом Ньютона, который собственно гласит вот что:
Существуют системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно или покоятся, если на них не действуют никакие силы, или действие других сил скомпенсировано (равнодействующая равна нулю).
Если в инерциальной системе отсчета мы разгоним автомобиль до скорости 60 км/ч, пренебрежем силой трения колес об асфальт и сопротивлением воздуха, а потом выключим двигатель, авто продолжит катиться по прямой со скоростью 60 км/ч бесконечно долго, пока не закончится дорога.
Второй закон Ньютона
Второй закон Ньютона еще называют основным законом динамики. Самая простая его формулировка такова:
В ИСО ускорение, приобретаемое телом, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратно пропорционально массе тела.
Еще одна формулировка второго закона Ньютона: производная импульса материальной точки по времени равна действующей на материальную точку силе. Импульс – мера количества движения, равняется произведению массы на скорость.
Действительно, вспомним кинематику (производная от скорости равна ускорению) и запишем:
Третий закон Ньютона
В ИСО тела действуют друг на друга с силами, лежащими на одной прямой, противоположными по направлению и равными по модулю.
Напоследок, как всегда, приведем пример решения задачи на основы динамики.
Брусок массой 5кг тянут по горизонтальной поверхности за веревку, составляющую угол 30 градусов с горизонтом. Сила натяжения веревки – 30 Ньютонов. За 10 секунд, двигаясь равноускоренно, брусок изменил скорость с 2 м/с до 12 м/с. Найти коэффициент трения бруска о плоскость.
Решение:
Нарисуем брусок. На него действуют сила тяжести, сила нормальной реакции опоры, сила трения и сила натяжения веревки. Веревку будем считать нерастяжимой. Первым делом найдем ускорение бруска, а затем вычислим проекцию сил на горизонтальную ось и запишем второй закон Ньютона.
Основы динамики в физике очень важны для понимания процесса движения. Помните, друзья, в экстремальных условиях сессии наши авторы всегда готовы поддержать Вас и облегчить учебную нагрузку. Удачи Вам!
