Содержание:
Гидростатическое взвешивание:
На этом принципе основан метод так называемого гидростатического взвешивания. Если в мензурку опустить деревянный брусок, то он будет плавать, но уровень воды поднимется. Объем этой воды равен объему погруженной части бруска, а ее вес – весу бруска. Зная объем и плотность воды, можно рассчитать вес воды и вес тела. Для случая, когда тело тяжелее воды, изготавливают специальный поплавок, дающий возможность телу плавать по поверхности воды.
Гидростатическое взвешивание
Гидростатическое взвешивание — это метод измерения плотности жидкости или твёрдого тела, основанный на законе Архимеда. Плотность твёрдых тел определяют методом двойного взвешивания тела: сначала в воздухе, а потом в жидкости, плотность которой известна. Если определяют плотность жидкости, то в ней взвешивают тело известной массы и объёма.
Если исследуемое сплошное твёрдое тело тонет в воде, то для выполнения задания нужен лишь лабораторный динамометр (или равноплечие весы) и сосуд с водой.
Сначала определяют вес Р исследуемого тела в воздухе: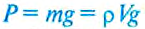 
Потом твёрдое тело погружают в сосуд с жидкостью, плотность которой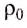 
известна (в случае использования дистиллированной или чистой воды 
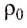= 1000 
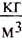), и определяют вес тела 
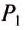в жидкости, который по закону Архимеда меньше веса тела в воздухе на значение силы Архимеда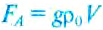 
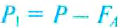отсюда 
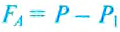, или 
.
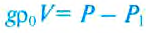Из этой формулы можно определить плотность жидкости, если она неизвестна, а объём тела известен: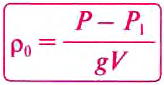
Объём жидкости, вытесненной телом, равен объёму тела, но
поскольку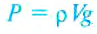 
то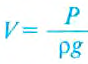 
. Подставим это в выражение
для архимедовой силы, получим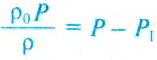 
, отсюда и вытекает искомая формула для определения плотности вещества твёрдого тела: 
.
Пример №1
Купаясь в реке с илистым дном, можно заметить, что ноги больше вязнут на мелких местах, чем на глубоких. Объясните, почему.
Ответ: так как на глубоких местах действует большая выталкивающая сила.
Пример №2
Определите, какая архимедова сила действует на тело объёмом
5 м3 , погружённое полностью в воду?
Дано:
V = 5м3
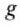= 9,81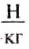 
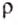= 1000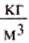 
FА = 49,05 кН
FА = ?
Решение:
По формуле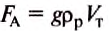 
определим архимедову силу:
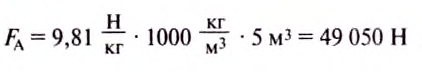
Ответ: = 49,05 кН.
Пример №3
Нужно ли учитывать загрузку судна при переходе его из моря в реку? Догружать или разгружать нужно судно, чтобы его осадка была не глубже ватерлинии?
Ответ: при переходе судна из моря в реку нужно учитывать загрузку судна, так как плотность воды уменьшается. Судно нужно разгружать.
- Заказать решение задач по физике
Теоретические сведения
Гидростатическое взвешивание издавна применяется для определения плотности различных веществ. Для этого используют закон Архимеда. Плотность твердых тел определяют двойным взвешиванием: сначала тело взвешивают в воздухе (при этом в большинстве случаев выталкивающей силой воздуха пренебрегают), а потом — в жидкости, плотность которой известна (например, в воде). Рассмотрим методы определения плотности.
1. Если исследуемое тело тонет в воде (его плотность рт превышает плотность воды рв), то в таком случае используют динамометр и стакан с водой.
Сначала исследуемое тело взвешивают в воздухе (рис. 120, а):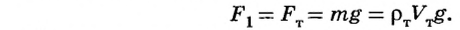 
В этом случае архимедовой силой, действующей на тело в воздухе, можно пренебречь, так как плотность воздуха намного меньше плотности тела и воды.
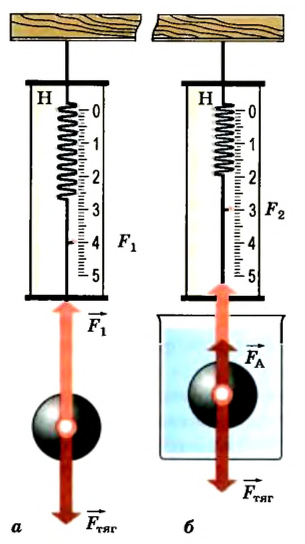
Потом тело опускают в стакан с водой (рис. 120, б), плотность воды известна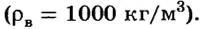 
В этом случае на тело, кроме сил тяжести 
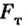и упругости пружины динамометра 
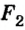, действует сила Архимеда 
:
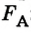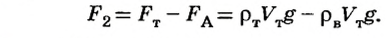
Таким образом,
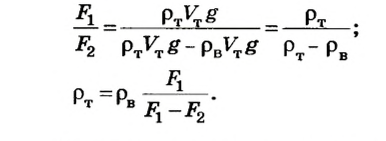
2. Для измерения плотности неизвестной жидкости можно воспользоваться также телом, которое не тонет в воде и исследуемой жидкости, например карандашом или другим телом правильной формы. Чтобы карандаш в жидкости занимал вертикальное положение, к его нижнему концу можно приколоть несколько кнопок или намотать несколько витков проволоки.
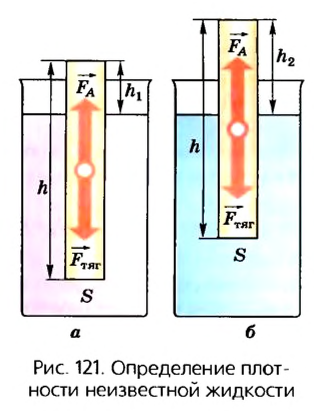
Если карандаш плавает в воде (рис. 121, а), то сила тяжести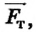 
действующая на него, равна силе Архимеда 
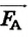. В этом случае
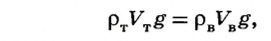
где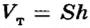 
— объем тела, a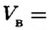 
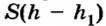— объем вытесненной телом воды (объем погруженной части тела).
Если тело опустить в неизвестную жидкость (рис. 121, б), плотность которой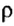 
, то
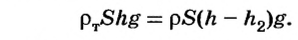
С этого уравнения имеем
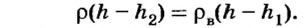
Отсюда
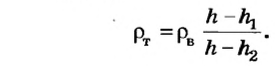
3. Плотность неизвестной жидкости можно определить с помощью резиновой нити, тела, которое тонет в воде и неизвестной жидкости, и линейки. Последовательность действий при этом показана на рисунке 122.
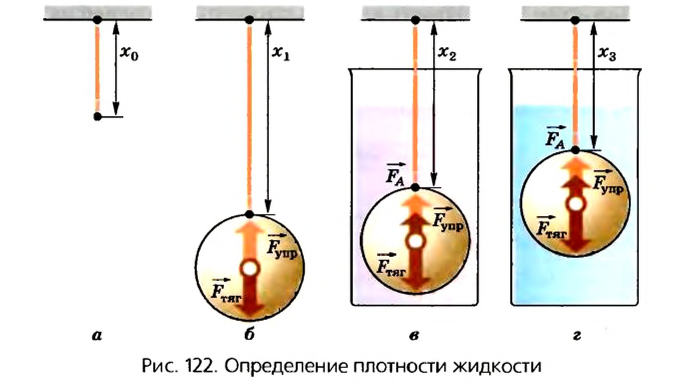
Длина резиновой нити (или пружины) без нагрузки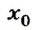 
(рис. 122, а). Если к ней прикрепить тело в воздухе (рис. 122, б), то сила тяжести 
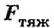будет равна по значению силе упругости 
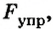возникшей в нити. Тело будет в состоянии равновесия.
Теперь, если тело опустить в воду (рис. 122, в), то на него будет действовать еще сила Архимеда:
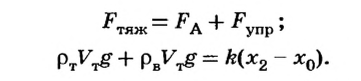
Опустим тело в жидкость, плотность которой нужно определить (рис. 122, г).
4. Для определения плотности твердого тела или неизвестной жидкости можно использовать рычаг. Для этого нужно иметь две гирьки, плотность одной из них массой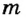 
необходимо определить, рычаг, линейку, стаканы с водой и неизвестной жидкостью. Последовательность действий показана на рисунке 123.
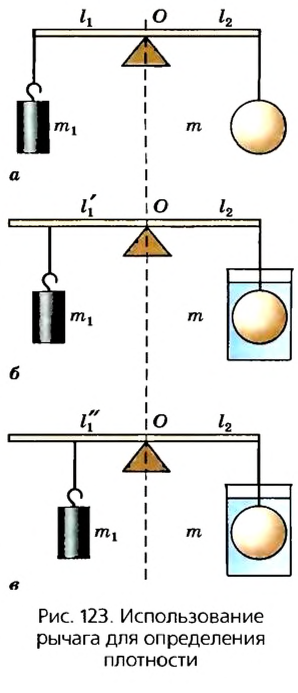
Для определения плотности тела используем формулу
Для определения плотности неизвестной жидкости можно использовать формулу
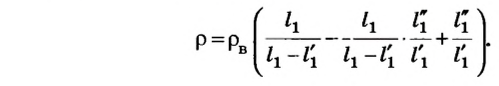
- Воздухоплавание в физике
- Машины и механизмы в физике
- Коэффициент полезного действия (КПД) механизмов
- Тепловые явления в физике
- Барометры в физике
- Жидкостные насосы в физике
- Выталкивающая сила в физике
- Условия плавания тел в физике
Цель работы:
Научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы:
Измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайки, фарфоровые ролики, кусочки металла и др.), нитки.
Указания к работе:
1. Определите цену деления мензурки.
2. Налейте в мензурки столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте её объём.
3. Опустите тело, объём которого надо измерить, в воду, удерживая его за нитку (рис. 201), и снова измерьте объём жидкости.
4. Проделайте опыты, описанные в пунктах 2 и 3, с некоторыми другими имеющимися у вас телами.
5. Результаты измерений запишите в таблицу 9.
Дополнительное задание.
Если тело неправильной формы не входить в мензурку, то его объём можно определить с помощью отливного сосуда (рис. 202). Перед измерением сосуд наполняют водой до отверстия отливной трубки. При погружении в него тела часть воды, равная объёму тела, выливается. Измерив мензуркой её объём, определяют объём погружённого в жидкость тела.
Таблица 9.
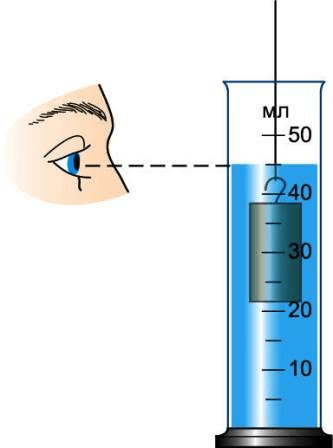
рис. 201
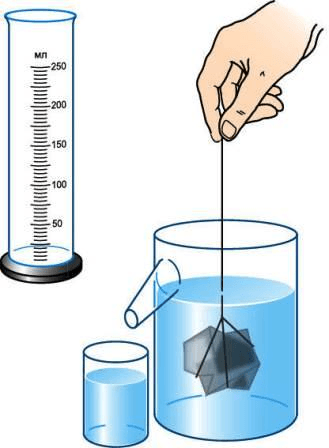
рис. 202
reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1
Решение
Объём тела неправильной формы точно измерить с помощью измерительных приборов нельзя. Поэтому для измерения объема воспользуемся мензуркой. Тело, полностью погружённое в жидкость, вытесняет объём жидкости, который равен объёму самого тела. Воспользуемся этим законом и найдем объёмы некоторых тел следующим образом. Нальем достаточное количество воды в мензурку, а затем погрузим полностью туда наше тело. Разница между первоначальным объёмом и объёмом жидкости, в которое погружено тело, равна объёму этого тела.
V
=
V
2
−
V
1
, где
V
2
− объём воды и тела,
V
1
− начальный объём воды в мензурке.
- Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30.
Таким образом, цена каждого деления будет равна
30
−
202
=
10
= 5 мл.
2 - В мензурку нальём столько воды, чтобы тело можно было полностью погрузить в воду. Начальный объём воды равен 70
с
м
3
. - Опустим тело, объём которого надо измерить (шарик, брусок, цилиндр), в воду, удерживая его за нитку, и снова измерим объём жидкости.
Вычисления.
V
б
р
=
95
−
70
=
25с
м
3
V
ц
=
85
−
65
=
20с
м
3
V
ш
=
75
−
60
=
15с
м
3
- Результаты измерений запишем в таблицу 9.
Таблица 9.
| № опыта | Название тела | Начальный объём воды в мензурке
V 1 , с м 3 |
Объём воды и тела
V 2 , с м 3 |
Объём тела V,
с м 3 V = V 2 − 1 |
|---|---|---|---|---|
| 1 | Брусок | 70 | 95 | 25 |
| 2 | Цилиндр | 65 | 85 | 20 |
| 3 | Шарик | 60 | 75 | 15 |
Вывод. В ходе лабораторной работы мы научились измерять объёмы тел с помощью измерительного цилиндра и выяснили, что объём тел равен разнице объёма воды, в которое погружено тело, и первоначального объёма воды.
Ответ
Проверено экспертом
Дано:
Fₐ = 120,5 кПа = 120 500 Па
ρ = 1000 кг/м³ – плотность воды
__________________
V – ?
Сила Архимеда
Fₐ = ρ*g*V
Объем:
V = Fₐ / (ρ*g) = 120 500 / (1000*10) ≈ 12 м³
Ответы и объяснения
|
При растворении в воде соли плотность жидкости увеличивается. График зависимости плотности солёной воды от массы растворённой в ней соли приведён на рисунке. Из оливкового дерева, плотность которого равна 960 кг/м3, вырезали брусок размерами 15 см х 10 см х 5 см и опустили его плавать в чистую воду. Брусок плавает так, что его самое короткое ребро расположено вертикально.
автор вопроса выбрал этот ответ лучшим Знаете ответ? |
Задачи на силу Архимеда с решениями
Формулы, используемые на уроках «Задачи на силу Архимеда», «Сообщающиеся сосуды».
Название величины |
Обозначение |
Единица измерения |
Формула |
Объем тела |
V |
м3 |
Vт = FA / pg |
Плотность жидкости |
p |
кг/м3 |
pж = FA / (Vg) |
Сила Архимеда |
FA |
Н |
FA = pж Vт g |
Постоянная |
g ≈ 10 Н/кг |
Н/кг |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Тело объемом 2 м3 погружено в воду. Найдите архимедову силу, действующую на тело.
Задача № 2.
Определить выталкивающую силу, действующую на деревянный плот объемом 12 м3, погруженный в воду на половину своего объема.
Задача № 3.
Каков объем железобетонной плиты, если в воде на нее действует выталкивающая сила 8000 Н?
Задача № 4.
Какую силу надо приложить, чтобы удержать под водой бетонную плиту, масса которой 720 кг?
Задача № 5.
Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?
Задача № 6.
Вес тела в воздухе равен 26 кН, а в воде — 16 кН. Каков объем тела?
Задача № 7.
Какую силу нужно приложить, чтобы удержать в воде кусок гранита объемом 40 дм3?
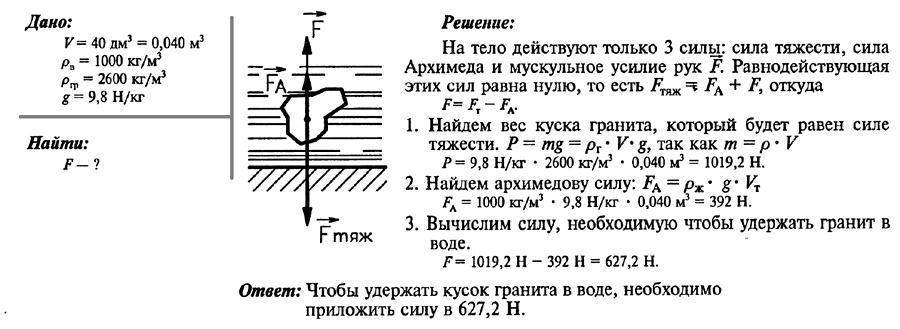
Задача № 8.
Определите объем куска меди, который при погружении в керосин выталкивается силой 160 Н.
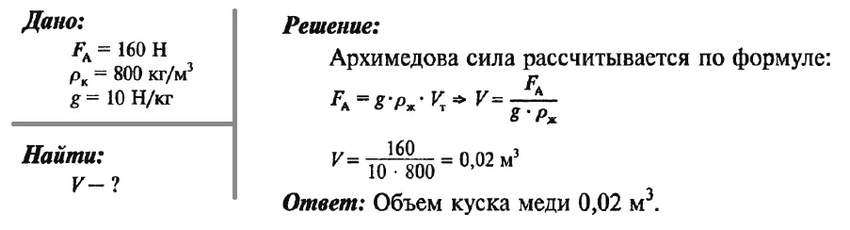
Задача № 9 (повышенной сложности).
Медный шар в воздухе весит 1,96 Н, а в воде 1,47 Н. Сплошной этот шар или полый?
Задача № 10 (повышенной сложности).
Рассчитайте, какой груз сможет поднять шар объемом 1 м3, наполненный водородом. Какой примерно объем должен иметь шар с водородом, чтобы поднять человека массой 70 кг? (Вес оболочки не учитывать.)
Задача № 11.
Деревянный цилиндр плавает на поверхности воды так, что он погружен в воду на 90%. Какая часть цилиндра будет погружена в воду, если поверх воды налить слой масла, полностью закрывающий цилиндр? Плотность масла 800 кг/м3.
Дано: V – объем цилиндра (V = Sh); h – высота цилиндра; S – площадь основания цилиндра; V1 – объем цилиндра, погруженного в масло (V1 = V – V2 = Sh1); h1 – высота части цилиндра, погруженной в масло; V2 – объем цилиндра, погруженного в воду после добавления масла; рв – плотность воды (1000 кг/м3); рм – плотность масла (800 кг/м3)
Найти: (h – h1) / h — ?
Решение. F – сила, выталкивающая цилиндр из воды до добавления масла F = 0,9pвgV
F1 – сила, выталкивающая цилиндр из масла F1 = pмgV1
F2 – сила, выталкивающая цилиндр из воды после добавления масла F2 = pвgV2
Баланс сил: F – F1 = F2
0,9pвgV – pмgV1 = pвgV2 V1 = V – V2 ⇒ 0,9pвV – pм(V – V2) = pвV2
V(0,9pв – pм) = V2(pв – pм) V = Sh; V1 = Sh1 ⇒
Ответ: 1/2 часть цилиндра будет погружена в воду (50%).
Задача № 12.
Плоская льдина плавает в воде, выступая над уровнем воды на 3 см. Человек массой 70 кг зашел на льдину. В результате, высота выступающей части над льдиной уменьшилась в 3 раза. Найти площадь льдины.
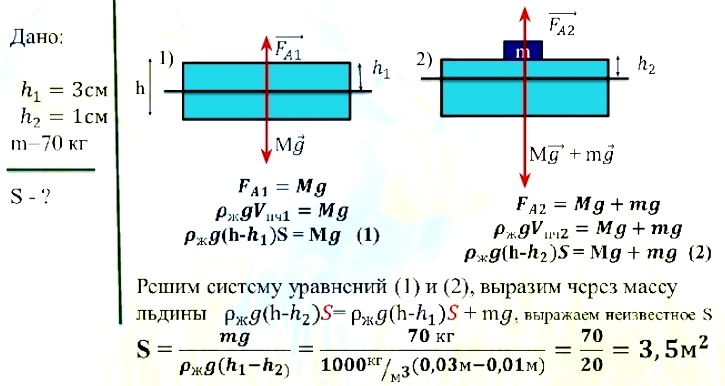
Ответ: 3,5 м3.
Теория для решения задач.
Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = ратм + p*g*h
Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.
Конспект урока «Задачи на силу Архимеда с решениями».
Следующая тема: «Задачи на механическую работу».
