
Сверху вниз:
фокусное расстояние собирающей линзы — положительное;
фокусное расстояние рассеивающей линзы — отрицательное;
фокусное расстояние вогнутого зеркала — положительное;
фокусное расстояние выпуклого зеркала — отрицательное
Фо́кусное расстоя́ние — физическая характеристика оптической системы, определяющая её основные свойства и, главным образом, увеличение и угловое поле[1].
Для центрированной оптической системы, состоящей из сферических поверхностей, описывает способность собирать лучи в одну точку при условии, что эти лучи идут из бесконечности параллельным пучком параллельно оптической оси.
Для системы линз, как и для простой линзы конечной толщины, фокусное расстояние зависит от радиусов кривизны поверхностей, показателей преломления оптических материалов и толщин элементов системы.
Определяется как расстояние от передней главной точки до переднего фокуса (для переднего фокусного расстояния), и как расстояние от задней главной точки до заднего фокуса (для заднего фокусного расстояния)[2]. При этом под главными точками подразумеваются точки пересечения передней (задней) главной плоскости с оптической осью.
Величина заднего фокусного расстояния является основным параметром, которым принято характеризовать любую оптическую систему.
Главное фокусное расстояние[править | править код]
Главное фокусное расстояние объектива — расстояние от главного фокуса до главной задней плоскости, обозначается 


Главное фокусное расстояние определяет масштаб изображения при установке объектива на «бесконечность».
См. также[править | править код]
- Фокальная плоскость
- Эквивалентное фокусное расстояние
- Заднее фокусное расстояние
- Вершинное фокусное расстояние
- Сопряжённое фокусное расстояние
Примечания[править | править код]
- ↑ Справочник кинооператора, 1979, с. 146.
- ↑ Фотокинотехника, 1981, с. 351.
Литература[править | править код]
- Гордийчук О. Ф., Пелль В. Г. Раздел III. Киносъёмочные объективы // Справочник кинооператора / Н. Н. Жердецкая. — М.: «Искусство», 1979. — С. 143—173. — 440 с.
- Е. А. Иофис. Фотокинотехника / И. Ю. Шебалин. — М.: «Советская энциклопедия», 1981. — С. 351. — 447 с.
Ссылки[править | править код]
- Alexandr Sukhov. Просто о сложном – как работает зеркальный фотоаппарат. Персональный сайт (май 2016). Дата обращения: 9 мая 2016.
- Что такое фокусное расстояние объектива. Статья с наглядными примерами.
Фо́кусное
расстоя́ние —
физическая характеристика оптической
системы.
Для центрированной оптической системы,
состоящей из сферических поверхностей,
описывает способность собирать лучи в
одну точку при условии, что эти лучи
идут из бесконечности параллельным
пучком параллельно оптической
оси.
Для
системы линз, как и для простой линзы конечной
толщины, фокусное расстояние зависит
от радиусов кривизны поверхностей,
показателей преломления стёкол и толщин.
Определяется
как расстояние от передней главной
точки до переднего
фокуса (для
переднего фокусного расстояния), и как
расстояние от задней главной точки
дозаднего
фокуса (для заднего
фокусного расстояния).
При этом, под главными точками
подразумеваются точки пересечения
передней (задней) главной
плоскости соптической
осью.
Величина заднего
фокусного расстояния является
основным параметром, которым принято
характеризовать любую оптическую
систему.

![]()
Парабола (или параболоид вращения)
фокусирует параллельный пучок лучей в
одну точку
Фо́кус (от лат. focus —
«очаг») оптической (или работающей с
другими видами излучения)
системы — точка, в которой пересекаются
(«фокусируются»)
первоначально параллельные лучи после
прохождения через собирающую систему
(либо где пересекаются их продолжения,
если система рассеивающая). Множество
фокусов системы определяет её фокальную
поверхность. Главный фокус системы
является пересечением её главной оптической
оси и
фокальной поверхности. В настоящее
время[1],
вместо термина главный
фокус (передний
или задний) используются термины задний
фокус и передний
фокус.
Опти́ческая
си́ла —
величина, характеризующая преломляющую
способность осесимметричных линз и
центрированных оптических
систем из
таких линз. Измеряется оптическая сила
в диоптриях (в СИ):
1 дптр=1 м-1.
Обратно
пропорциональна фокусному
расстоянию системы:
![]()
где ![]() —
—
фокусное расстояние линзы.
Оптическая
сила положительна у собирающих систем
и отрицательна в случае рассеивающих.
Оптическая
сила системы, состоящей из двух находящихся
в воздухе линз с оптическими силами ![]() и
и![]() ,
,
определяется формулой[1]:
![]()
где ![]() —
—
расстояние между задней главной
плоскостью первой линзы и передней
главной плоскостью второй линзы. В
случае тонких линз![]() совпадает
совпадает
с расстоянием между линзами.
Обычно
оптическая сила используется для
характеристики линз, используемых
в офтальмологии,
в обозначениях очков и для упрощённого
геометрического определения траектории
луча.
Для
измерения оптической силы линз используют
диоптриметры[2],
которые позволяют проводить измерения
в том числе астигматических и контактных
линз.
18. Формула сопряжённых фокусных расстояний. Построение изображения линзой.
Сопряжённое
фо́кусное расстоя́ние —
расстояние от задней главной
плоскости объектива до
изображения объекта, когда объект
расположен не в бесконечности, а на
некотором расстоянии от объектива.
Сопряженное фокусное расстояние ![]() всегда
всегда
большефокусного
расстояния объектива ![]() и
и
тем больше, чем меньше расстояние от
объекта допередней
главной плоскости объектива ![]() .
.
Эта зависимость приведена в таблице, в
которой расстояния![]() и
и![]() выражены
выражены
в величинах![]() .
.
|
Изменение |
|
|
Расстояние |
Расстояние |
|
4f |
1,33f |
|
2f |
2f |
|
1,5f |
3f |
|
1,2f |
6f |
|
1,1f |
11f |
Для линзы эти
расстояния связаны отношением,
непосредственно следующим из формулы
линзы:
![]()

или,
если d и R выразить в величинах фокусного
расстояния ![]() :
:
![]()
б) Построение
изображения в линзах.
Для
построения хода луча в линзе применяются
те же законы, что и для вогнутого зеркала.
Луч, параллельный
оси,
проходит через фокус и наоборот.
Центральный луч (луч, идущий через
оптический центр линзы) проходит через
линзу без
отклонения;
в толстых
линзах
он немного смещается параллельно самому
себе (как в плоскопараллельной пластинке,
см. рис. 214). Из обратимости хода лучей
следует, что каждая линза имеет два
фокуса, которые находятся на одинаковых
расстояниях от линзы (последнее верно
лишь для тонких линз). Для тонких
собирающих линз и центральных лучей
справедливы следующие законы
построения изображений:
g >2F; изображение
обратное, уменьшенное,
действительное, b >F (рис.221).
g = 2F; изображение
обратное, равное, действительное, b = F.
F <g < 2F;
изображение обратное, увеличенное,
действительное, b > 2F.
g < F; изображение
прямое, увеличенное, мнимое, – b > F.
При g < F лучи
расходятся, на продолжении пересекаются
и дают мнимое

изображение.
Линза действует как увеличительное
стекло (лупа).
Изображения
в рассеивающих линзах всегда мнимые,
прямые и уменьшенные (рис.223).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Мы уже познакомились с явлением преломления света на границе двух плоских сред. Но на практике особый интерес представляет явление преломления света на сферических поверхностях линз.
Определение
Линза — прозрачное тело, ограниченное сферическими поверхностями.
Какими бывают линзы?
По форме различают следующие виды линз:
- Выпуклые — линзы, которые посередине толще, чем у краев.
- Вогнутые — линзы, которые посередине тоньше, чем у краев.
Выпуклые линзы тоже имеют разновидности:
- Двояковыпуклая — линза, ограниченная с обеих сторон выпуклыми сферическими поверхностями (СП). Такая линза изображена ниже на рисунке 1.
- Плосковыпуклая — линза, ограниченная выпуклой СП с одной стороны и плоской поверхностью с другой (рис. 2)
- Вогнуто-выпуклая — линза, ограниченной с одной стороны вогнутой СП, а с другой — выпуклой СП (рис. 3).
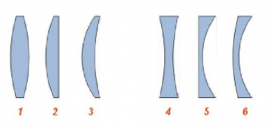
Разновидности вогнутых линз:
- Двояковогнутая — линза, ограниченная с обеих сторон вогнутыми СП (рис. 4).
- Плосковогнутая — линза, ограниченная вогнутой СП с одной стороны и плоской поверхностью с другой (рис. 5)
- Выпукло-вогнутая — линза, ограниченной с одной стороны выпуклой СП, а с другой — вогнутой СП (рис. 6).
Тонкая линза
Мы будем говорить о линзах, у которых толщина l = AB намного меньше радиусов сферических поверхностей этой линзы R1 и R2. Такие линзы называют тонкими.
Определение
Тонкая линза — линза, толщина которой пренебрежимо мала по сравнению с радиусами сферических поверхностей, которыми она ограничена.
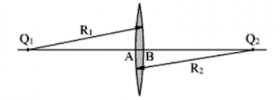
Главная оптическая ось тонкой — прямая, проходящая через центры сферических поверхностей линзы (на рисунке она соответствует прямой O1O2).
Оптический центр линзы – точка, расположенная в центре линзы на ее главной оптической оси (на рисунке ей соответствует точка О). При прохождении через оптический центр линзы лучи света не преломляются.
Побочная оптическая ось — любая другая прямая, проходящая через оптический центр линзы.
Изображение в линзе
Подобно плоскому зеркалу, линза создает изображения источников света. Это значит, что свет, исходящий из какой-либо точки предмета (источника), после преломления в линзе снова собирается в точку (изображение) независимо от того, какую часть линзы прошли лучи.
Определение
Оптическое изображение — картина, получаемая в результате действия оптической системы на лучи, испускаемые объектом, и воспроизводящая контуры и детали объекта.
Практическое использование изображений часто связано с изменением масштаба изображений предметов и их проектированием на поверхность (киноэкран, фотоплёнку, фотокатод и т. д.). Основой зрительного восприятия предмета является его изображение, спроектированное на сетчатку глаза.
Изображения разделяют на действительные и мнимые. Действительные изображения создаются сходящимися пучками лучей в точках их пересечения (см. рисунок а). Поместив в плоскости пересечения лучей экран или фотоплёнку, можно наблюдать на них действительное изображение.
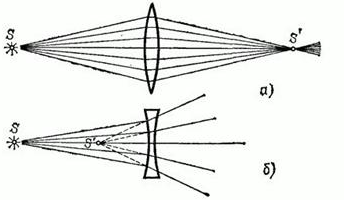
Если лучи, выходящие из оптической системы, расходятся, но если их мысленно продолжить в противоположную сторону, они пересекутся в одной точке (см. рисунок б). Эту точку называют мнимым изображением точки-объекта. Она не соответствует пересечению реальных лучей, поэтому мнимое изображение невозможно получить на экране или зафиксировать на фотоплёнке. Однако мнимое изображение способно играть роль объекта по отношению к другой оптической системе (например, глазу или собирающей линзе), которая преобразует его в действительное.
Собирающая линза
Обычно линзы изготавливают из стекла. Все выпуклые линзы являются собирающими, поскольку они собирают лучи в одной точке. Любую из таких линз условно можно принять за совокупность стеклянных призм. В воздухе каждая призма отклоняет лучи к основанию. Все лучи, идущие через линзу, отклоняются в сторону ее главной оптической оси.
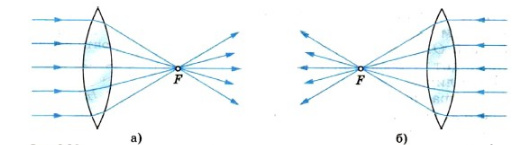
Если на линзу падают световые лучи, параллельные главной оптической оси, то при прохождении через нее они собираются на одной точке, лежащей на оптической оси. Ее называют главным фокусом линзы. У выпуклой линзы их два — второй главный фокус находится с противоположной стороны линзы. В нем будут собираться лучи, которые будут падать с обратной стороны линзы.
Главный фокус линзы обозначают буквой F.
Определение
Фокусное расстояние — расстояние от главного фокуса линзы до их оптического центра. Оно обозначается такой же букой F и измеряется в метрах (м).
В однородных средах главные фокусы собирающих линз находятся на одинаковом расстоянии от оптического центра.
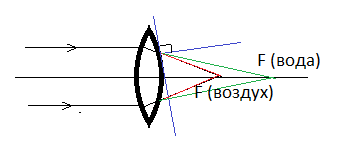
Пример №1. Что произойдет с фокусным расстоянием линзы, если ее поместить в воду?
Вода — оптически более плотная среда, поэтому преломленные лучи будут располагаться ближе к перпендикуляру, восстановленному к разделу двух сред. Следовательно, фокусное расстояние увеличится. На рисунке лучам, выходящим из линзы в воздухе, соответствуют красные линии. Лучам, выходящим из линзы в воде — зеленые. Видно, что зеленые линии больше приближены к перпендикуляру, восстановленному к разделу двух сред, что соответствует закону преломления света.
Направим три узких параллельных пучка лучей от осветителя под углом к главной оптической оси собирающей линзы. Мы увидим, что пересечение лучей произойдет не в главном фокусе, а в другой точке (рисунок а). Но точки пересечения независимо от углов, образуемых этими пучками с главной оптической осью, будут располагаются в плоскости, перпендикулярной главной оптической оси линзы и проходящей через главный фокус (рисунок б). Эту плоскость называют фокальной плоскостью.
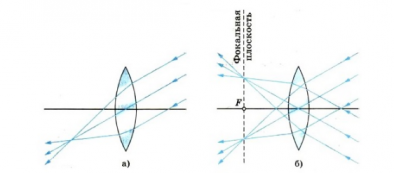
Поместив светящуюся точку в фокусе линзы (или в любой точке ее фокальной плоскости), получим после преломления параллельные лучи.
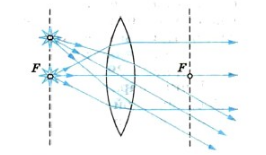
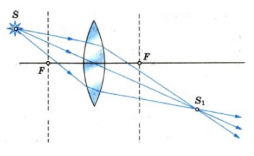
Если сместить источник дальше от фокуса линзы, лучи за линзой становятся сходящимися и дают действительное изображение.
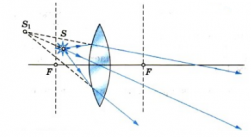
Когда же источник света находится ближе фокуса, преломленные лучи расходятся и изображение получается мнимым.
Рассеивающая линза
Вогнутые линзы обычно являются рассеивающими (лучи, выходя из них, не собираются, а рассеиваются). Это бывает если, поместить вогнутую линзу в оптически менее плотную среду по сравнению с материалом, из которого изготовлена линза. Так, стеклянная линза в воздухе является рассеивающей.
Если направить на вогнутую линзы световые лучи, являющиеся параллельными главной оптической оси, то образуется расходящийся пучок лучей. Если провести их продолжения, то они пересекутся в главном фокусе линзы. В этом случае фокус (и изображение в нем) является мнимым. Этот фокус располагается на фокусном расстоянии, равном F.
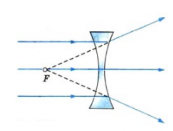
Другой мнимый фокус находится по другую сторону линзы на таком же расстоянии при условии, что среда по обе стороны линзы одинаковая.
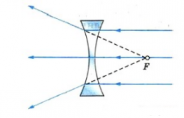
Оптическая сила линзы
Оптическая сила линзы — величина, характеризующая преломляющую способность симметричных относительно оси линз и центрированных оптических систем, состоящих из таких линз.
Обозначается оптическая сила линзы буквой D. Единица измерения — диоптрий (дптр). Оптической силой в 1 дптр обладает линза с фокусным расстоянием 1 м.
Оптическая сила линзы равна величине, обратной ее фокусному расстоянию:
D=±1|F|
D > 0, если линза собирающая, D < 0, если линза рассеивающая. Чем ближе к линзе ее фокусы, тем сильнее линза преломляет лучи, собирая или рассеивая их, и тем больше оптическая сила линзы.
Пример №2. Найти фокусное расстояние линзы, если ее оптическая сила равна –5 дптр.
Так как оптическая силы линзы отрицательная, речь идет о рассеивающей линзе. Следовательно, будем использовать формулу:
D=−1|F|
Отсюда:
|F|=−1D=−1−5=0,2 (м)
Задание EF18041
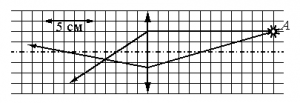 На рисунке показан ход двух лучей от точечного источника света А через тонкую линзу. Какова приблизительно оптическая сила этой линзы?
На рисунке показан ход двух лучей от точечного источника света А через тонкую линзу. Какова приблизительно оптическая сила этой линзы?
Ответ:
а) 14 дптр
б) 20 дптр
в) 17 дптр
г) 33 дптр
Алгоритм решения
1.Записать формулу для нахождения оптической силы линзы.
3.Найти точку на главной оптической оси точку главного фокуса линзы.
4.Вычислить фокусное расстояние и перевести его в СИ.
5.Вычислить оптическую силу линзы.
Решение
Оптическая сила линзы определяется формулой:
D=1F
На рисунке видно, что 5 клеток = 5 см. Следовательно, 1 клетка = 1 см. После прохождения сквозь линзу лучи света, параллельные главной оптической оси, фокусируются в главном фокусе, который лежит на этой оси. Значит, фокус находится в точке пересечения этой оси и луча. От него до линзы 3 клетки. Следовательно, фокусное расстояние равно 3 см, или 0,03 м.
Отсюда:
D=10,03≈33 (дптр)
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17706
![]() Стеклянную линзу (показатель преломления стекла nстекла = 1,54), показанную на рисунке, перенесли из воздуха (nвоздуха = 1) в воду (nводы = 1,33). Как изменились при этом фокусное расстояние и оптическая сила линзы?
Стеклянную линзу (показатель преломления стекла nстекла = 1,54), показанную на рисунке, перенесли из воздуха (nвоздуха = 1) в воду (nводы = 1,33). Как изменились при этом фокусное расстояние и оптическая сила линзы?
Ответ:
а) Фокусное расстояние уменьшилось, оптическая сила увеличилась.
б) Фокусное расстояние увеличилось, оптическая сила уменьшилась.
в) Фокусное расстояние и оптическая сила увеличились.
г) Фокусное расстояние и оптическая сила уменьшились.
Алгоритм решения
1.Установить характер преломления лучей линзой при ее перемещении из воздуха в воду.
2.Выяснить, как от этого зависят фокусное расстояние и оптическая сила линзы.
Решение
Чтобы узнать, что произойдет с лучами света при прохождении их сквозь линзу, погруженную воду, найдем относительные показатели преломления:
nвоздух−стекло=nстеклоnвоздух=1,541=1,54
nвода−стекло=nстеклоnвода=1,541,33≈1,16
Видно, что относительный показатель преломления уменьшился. Значит, преломленный линзой луч будет менее отклоняться от нормали, проведенной в точке падения на линзу. Следовательно, чтобы достигнуть главной оптической оси, ему придется пройти большее расстояние. Это говорит о том, что фокусное расстояние линзы увеличится.
Оптическая сила линзы — величина, обратная ее фокусному расстоянию. Если оно увеличится, то оптическая сила уменьшится.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18076
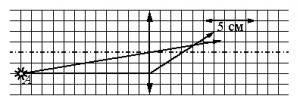 На рисунке показан ход лучей от точечного источника света А через тонкую линзу.
На рисунке показан ход лучей от точечного источника света А через тонкую линзу.
Какова приблизительно оптическая сила этой линзы?
Ответ:
а) –33,3 дптр
б) 7,7 дптр
в) 25,0 дптр
г) 33,3 дптр
Алгоритм решения
1.Записать формулу для нахождения оптической силы линзы.
2.Рассчитать длину 1 клетки.
3.Найти точку на главной оптической оси точку главного фокуса линзы.
4.Вычислить фокусное расстояние и перевести его в СИ.
5.Вычислить оптическую силу линзы.
Решение
Оптическая сила линзы находится по формуле:
D=1F
На рисунке видно, что 5 соответствуют 5 см. Следовательно, 1 клетка равна 1 см. После прохождения сквозь линзу лучи света, параллельные главной оптической оси, фокусируются в фокусе, который лежит на этой оси. Из рисунка видно, фокус находится в точке пересечения этой оси и луча, параллельного ей. Эту точку и линзу разделяют 3 клетки. Следовательно, фокусное расстояние равно 3 см, или 0,03 м.
Отсюда:
D=10,03≈33,3 (дптр)
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.7k
Условие задачи:
Определить главное фокусное расстояние рассеивающей линзы, если известно, что изображение предмета, помещенного перед ней на расстоянии 50 см, получилось уменьшенным в 5 раз?
Задача №10.5.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(d=50) см, (Gamma = frac{1}{5}), (F-?)
Решение задачи:
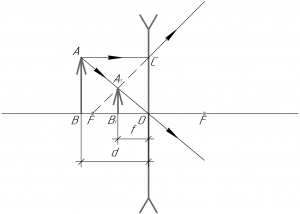 Чтобы построить изображение точки A в рассеивающей линзе, нужно провести через точку A два луча: один параллельно главной оптической оси, а второй через главный оптический центр O. Первый луч, преломившись в линзе в точке C, пойдет дальше таким образом, что его продолжение влево пройдет через передний фокус линзы. Второй луч проходит через линзу, не преломляясь. На пересечении этих лучей и будет находиться точка A1. Проекция этой точки на главную оптическую ось есть точка B1. Вот и все, изображение построено. Как мы видим, оно получилось мнимым (поскольку получается на расходящемся пучке лучей), прямым и уменьшенным ((Gamma < 1)).
Чтобы построить изображение точки A в рассеивающей линзе, нужно провести через точку A два луча: один параллельно главной оптической оси, а второй через главный оптический центр O. Первый луч, преломившись в линзе в точке C, пойдет дальше таким образом, что его продолжение влево пройдет через передний фокус линзы. Второй луч проходит через линзу, не преломляясь. На пересечении этих лучей и будет находиться точка A1. Проекция этой точки на главную оптическую ось есть точка B1. Вот и все, изображение построено. Как мы видим, оно получилось мнимым (поскольку получается на расходящемся пучке лучей), прямым и уменьшенным ((Gamma < 1)).
Запишем формулу тонкой линзы:
[ – frac{1}{F} = frac{1}{d} – frac{1}{f};;;;(1)]
В этой формуле (F) – фокусное расстояние линзы, знак перед ним “-“, поскольку линза – рассеивающая, (d) – расстояние от линзы до предмета, знак перед ним “+”, поскольку предмет – действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), (f) – расстояние от линзы до изображения, знак перед ним “-“, поскольку изображение – мнимое (то есть образуется на расходящемся пучке лучей – смотрите рисунок).
Поперечное увеличение предмета в линзе (Gamma) определяют по формуле (это можно вывести из подобия треугольников AOB и A1OB1):
[Gamma = frac{f}{d} = frac{H}{h}]
Тогда:
[f = Gamma d;;;;(2)]
Подставим выражение (2) в уравнение (1):
[ – frac{1}{F} = frac{1}{d} – frac{1}{{Gamma d}}]
Приведем в правой части под общий знаменатель:
[ – frac{1}{F} = frac{{Gamma – 1}}{{Gamma d}}]
[frac{1}{F} = frac{{1 – Gamma }}{{Gamma d}}]
Окончательно получим такой ответ:
[F = frac{{Gamma d}}{{1 – Gamma }}]
Численный ответ задачи:
[F = frac{{0,2 cdot 0,5}}{{1 – 0,2}} = 0,125;м = 12,5;см]
Ответ: 12,5 см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.5.42 Предмет находится на расстоянии 1,5F от линзы. Его приблизили к линзе на расстояние 0,7F
10.5.44 Предмет расположен на расстоянии 0,5F от рассеивающей линзы с фокусным расстоянием
10.5.45 Главное фокусное расстояние рассеивающей линзы 12 см. Изображение предмета
Главное фокусное расстояние
Главное фокусное расстояние
Если направить на собирательную (например, двояковыпуклую) линзу пучок лучей света, параллельных главной оптической оси линзы, как показано на рис. 7, в левом верхнем углу, то после преломления в линзе эти лучи соберутся в главном фокусе. Расстояние от линзы до главного фокуса и есть главное фокусное расстояние линзы.
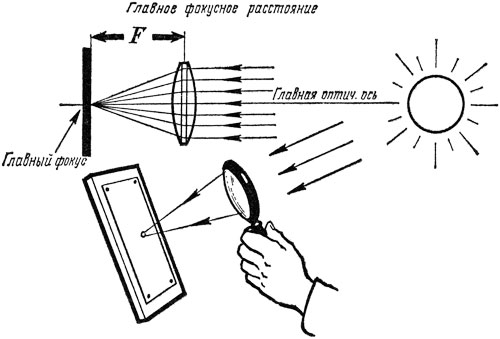
Рис. 7. Таким способом можно приблизительно определить главное фокусное расстояние линзы
С достаточным приближением его можно определить, если поместить линзу или объектив на пути солнечных лучей, которые практически параллельны, и получить на бумаге резкое изображение солнца. Расстояние между линзой и бумагой и будет главным фокусным расстоянием линзы. Его можно измерить линейкой.
Почему же это расстояние называется главным?
Пользуясь линзой, можно заметить, что с изменением расстояния между предметом и линзой расстояние от линзы до изображения предмета также изменяется.
Проделаем следующий опыт. Возьмем двояковыпуклую линзу и лист белой бумаги и, поместив линзу на небольшом расстоянии от горящей лампы, получим на бумаге резкое изображение лампы. Измерив расстояние между линзой и бумагой, начнем отходить от лампы все дальше, поддерживая резкость изображения. Легко заметить, что расстояние между линзой и бумагой сначала будет сокращаться довольно быстро, а затем все медленнее, как бы затухая, и наконец наступит момент, когда оно перестанет сокращаться. И как бы далеко мы не отошли от лампы, расстояние от линзы до бумаги практически сокращаться уже не будет. Оно останется таким же и в том случае, если мы попробуем получить на бумаге резкое изображение удаленных домов, далеких гор, облаков или даже солнца. Иными словами, это расстояние является самым коротким из всех, при которых возможно получить резкое изображение предметов. Для линз с разной оптической силой это расстояние будет разным, но для каждой линзы оно постоянное, что позволяет пользоваться им как основной оптической характеристикой данной линзы. Поэтому оно и называется главным.
Сказанное относится и к любому фотографическому объективу. Независимо от числа линз, из которых он состоит, каждый фотообъектив представляет собой собирательную оптическую систему, т. е. действует подобно одиночной линзе. Поэтому объектив прежде всего характеризуется величиной его главного фокусного расстояния. Это расстояние обозначается буквой f или F и выражается в сантиметрах (иногда в миллиметрах). Итак, обозначение «F = 5 см» показывает, что главное фокусное расстояние данного объектива равно 5 см.
Для упрощения главное фокусное расстояние обычно называют просто фокусным расстоянием.

Рис. 8. Масштаб изображения прямо пропорционален величине главного фокусного расстояния
Каково же практическое значение фокусного расстояния объектива? Прежде всего от него зависит масштаб получаемого изображения[5]. Он прямо пропорционален величине фокусного расстояния объектива. Сравните два снимка, помещенных на рис. 8. Оба они были сделаны одним и тем же аппаратом с одного и того же расстояния, но в первом случае фокусное расстояние объектива было вдвое меньше, чем во втором. Как видите, линейный масштаб изображения на первом снимке получился вдвое меньше. На этом явлении основано применение в одних и тех же фотоаппаратах так называемых сменных объективов с разными фокусными расстояниями, что позволяет, не сходя с места, т. е. с одной и той же точки, вести съемку в разных масштабах. Позже мы познакомимся с такими объективами более подробно.
Каждый фотоаппарат выпускается в продажу только с одним объективом, но у фотоаппаратов разных форматов объективы имеют разные фокусные расстояния. У фотоаппаратов марки «Смена» объективы имеют фокусное расстояние 4 см, у других малоформатных фотоаппаратов — 5 см. У фотоаппарата «Любитель» и почти у всех других фотоаппаратов формата 6 х 6 см объективы имеют фокусное расстояние 7,5-8 см, а фотоаппараты формата 6 х 9 см снабжены объективами с фокусным расстоянием 10,5 см.
Как видите, между форматом фотоаппарата и величиной фокусного расстояния объектива имеется связь: чем больше формат фотоаппарата, тем больше и фокусное расстояние установленного на нем объектива. Можно также обнаружить, что связь эта закономерна и что фокусное расстояние объектива обычно равно или близко к диагонали того кадра, для которого объектив предназначен. И в самом деле диагональ кадра фотоаппарата формата 24 x 36 мм (малоформатные аппараты) равна 43,3 мм и фокусное расстояние объективов таких фотоаппаратов обычно находится в пределах от 4 до 5 см. Диагональ кадра 6 x 9 см равна 10,8 см и объективы у таких фотоаппаратов имеют почти такое же фокусное расстояние. Чем же это объясняется?
Площадь, на которой объектив дает изображение, ограничена размерами кадра, т. е. форматом фотоаппарата.
Фотографический кадр всегда представляет собой прямоугольник или квадрат, а наибольшей линейной величиной в таких геометрических фигурах служит диагональ. Зная диагональ кадра и величину фокусного расстояния объектива, можно с помощью простого графического построения определить одно очень важное свойство объектива: под каким углом он охватывает снимаемое пространство. Для этого достаточно начертить на листе бумаги в натуральную величину прямоугольник размером с кадр, как это показано на рис. 9, и провести диагональ этого прямоугольника AB, опустить к середине диагонали перпендикуляр и, отложив на нем отрезок OC, равный фокусному расстоянию объектива, соединить точку C с концами диагонали АВ. Угол АСВ и есть искомый угол, называемый углом поля изображения.
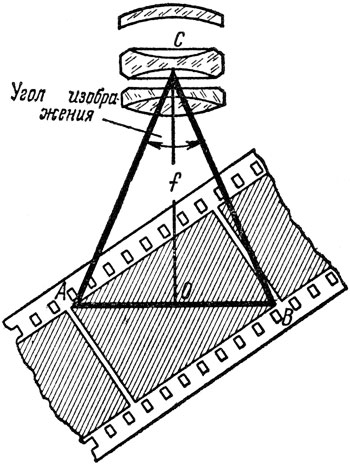
Рис. 9. Таким построением легко определить угол поля изображения объектива
Проделав такое построение для объективов, установленных на фотоаппаратах разных форматов, можно увидеть, что угол поля изображения у всех объективов примерно одинаков и находится в пределах 40-55°. В величине этого угла и кроется секрет закономерности, о которой было сказано выше.
Опыт показал, что наиболее удобны для подавляющего большинства фотосъемок объективы, угол поля изображения которых находится в указанных выше пределах. Разница между величинами фокусных расстояний объективов различных по формату фотоаппаратов объясняется не чем иным, как стремлением конструкторов сохранить у всех фотоаппаратов один и тот же наиболее удобный угол поля изображения. Объективы с таким углом поля изображения называются нормальными. Их часто называют универсальными. Именно с такими объективами, как основными, фотоаппараты и выпускаются в свет.
Один из начинающих фотолюбителей пытался уверить другого в том, что чем больше формат фотоаппарата, тем большее пространство можно им охватить при съемке. Мне хочется предостеречь вас от такого заблуждения. Все фотоаппараты с нормальными объективами охватывают почти одинаковое пространство. Два снимка, показанных на рис. 10, это убедительно подтверждают. Один из них был сделан фотоаппаратом формата 24 x 36 мм, другой — с той же точки фотоаппаратом формата 6 x 9 см. Хотя размеры снимков и масштабы изображения на них различны, границы сфотографированного пространства у них одинаковы.

Рис. 10. Все фотоаппараты с нормальными объективами охватывают при съемке одинаковое пространство
От фокусного расстояния зависит также не менее важная техническая характеристика объектива — его светосила.
Как видите, с фокусным расстоянием связаны очень важные свойства объектива. Не случайно величину его всегда обозначают на оправе объектива. Но, выбирая фотоаппарат, менее всего следует руководствоваться величиной фокусного расстояния его объектива. Вы уже знаете, что фокусное расстояние основного объектива наилучшим образом согласовано с форматом кадра и подобрано в соответствии с наиболее удобным углом поля изображения. Выбирать аппарат по величине фокусного расстояния объектива было бы бесполезным занятием, но знать это расстояние и его практическое значение важно.
