Содержание:
- Формула
- Примеры вычисления периметра равностороннего треугольника
Формула
Чтобы найти периметр равностороннего треугольника, надо длину его стороны умножить на три.
Периметр равностороннего треугольника – это сумма длин его сторон. У равностороннего треугольника
все стороны равны. Поэтому чтобы найти периметр равностороннего треугольника
$ABC$, со стороной
$a$ нужно воспользоваться формулой
$$P_{Delta A B C}=a+a+a=3 a$$
Примеры вычисления периметра равностороннего треугольника
Пример
Задание. Найти периметр треугольника
$ABC$ со стороной, равной 5 дм.
Решение. Воспользуемся формулой для нахождения периметра равностороннего треугольника:
$$P_{Delta A B C}=3a$$
Тогда искомый периметр равен:
$P_{Delta A B C}=3 cdot 5=15$ (дм)
Ответ. $P_{Delta A B C}=15$ (дм)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Периметр равностороннего треугольника
$ABC$ равен
27 см. Найти длины его стороны.
Решение. Периметр равностороннего треугольника вычисляется по формуле:
$$P_{Delta A B C}=3 a$$
Подставим в нее заданное значение периметра и выразим из полученного уравнения искомую длину
$a$:
$27=3 a Rightarrow a=27: 3=9$ (см)
Ответ. $a=9$ (см)
Читать дальше: как найти периметр круга.
Чтобы найти периметр равностороннего треугольника(или найти периметр правильного треугольника), нужно знать его сторону.
В общем случае для нахождения периметра треугольника используют формулу
![]()

Поскольку в равностороннем треугольнике все три стороны равны, формула упрощается:
![]()
Таким образом, формула периметра равностороннего треугольника:
![]()
(а — длина его стороны).
Примеры.
1) Найти периметр равностороннего треугольника, сторона которого равна 10 см.
Решение:
По формуле Р=3а имеем: Р=3∙10=30 (см).
2) Периметр равностороннего треугольника равен 21 см. Найти его сторону.
Решение:
Р=3а, значит, а=Р:3. Таким образом, длина стороны треугольника равна а=21:3= 7 (см).
 3) Найти периметр правильного треугольника АВС, если АВ=25 см.
3) Найти периметр правильного треугольника АВС, если АВ=25 см.
Решение:
По формуле P=3a, P=3∙АВ=3∙25=75 (см).
Периметр равностороннего треугольника


4.4
Средняя оценка: 4.4
Всего получено оценок: 325.
4.4
Средняя оценка: 4.4
Всего получено оценок: 325.
Равносторонний треугольник занимает особое место среди треугольников. Для того, чтобы найти значение периметра, площади, углов или радиусов окружностей вписанной и описанной у равнобедренного треугольника, достаточно знать величину стороны. С одной стороны, это значительно облегчает решение, с другой составители задач редко дают значение стороны и приходится искать обходные пути решения.
Формула нахождения периметра равностороннего треугольника
Формула периметра равностороннего треугольника вытекает из определений. Что такое периметр? Периметр это сумма всех сторон фигуры. Равносторонний треугольник – это треугольник, все стороны которого равны.
Значит,для того, чтобы найти значение периметра достаточно умножить величину стороны на количество сторон:
P=3*a
Решим несколько разных по сложности задач, чтобы разобраться, какие проблемы могут встречаться на пути нахождения периметра.
Задача 1
- В равностороннем треугольнике сторона равна 6. Найти периметр треугольника.
Это самый простой вариант задачи. Достаточно подставить значение в формулу и получить результат. Такая задача не должна вызывать затруднений:
P=3*a=3*6=18
Задача 2
- В равнобедренном треугольнике острый угол при основании равен 60 градусам, площадь треугольника равна $${64oversqrt{3}}$$.
Особое внимание нужно обращать на вид фигуры, который указан в условии задачи.
В данной задаче дан равнобедренный треугольник. Чтобы воспользоваться общей формулой, необходимо доказать, что этот равнобедренный треугольник является еще и равносторонним.
Обратим внимание на величину угла. Угол при основании равен 60. При этом углы у основания равнобедренного треугольника равны, а сумма углов любого треугольника равна 180 градусов. Значит у основания два угла по 60 градусов. Рассчитаем угол при вершине:
180-60-60=60 – угол при вершине так же равен 60 градусам.
Значит, данный треугольник будет равносторонним, так как все углы равны 60 градусам.
Углы по 60 градусов характерны только для равностороннего треугольника. Именно сочетание 3 равных сторон образует 3 равных угла. В любых других ситуациях, хотя бы один угол будет отличаться.
Для площади равностороннего треугольника имеется отдельная формула:
$$S=a^2*{sqrt{3}over 4}={64oversqrt{3}}$$ – где а значение стороны, которое нам и нужно выразить из этой формулы.
$$а^2={Sover{sqrt{3}over 4}}$$
$$a^2={4Soversqrt{3}}$$
$$a=sqrt{4Soversqrt{3}}$$
$$a={sqrt{4*{64oversqrt{3}^2}}oversqrt{3}}=sqrt{4*64}=16$$
Подставим полученное значение в формулу:
P=3*a=3*16=48
Задача 3
- В равностороннем треугольнике высота равна $$3*sqrt{3}$$. Найти периметр треугольника.
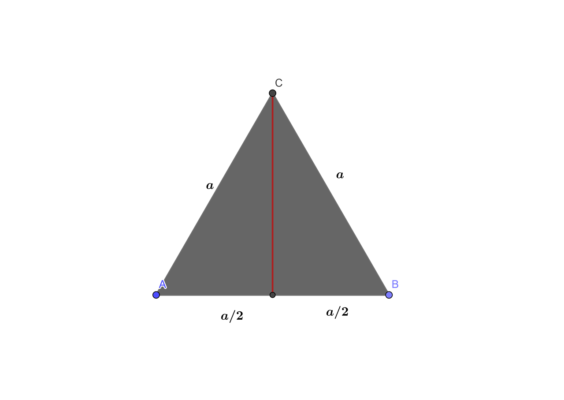
Для данной задачи нужно воспользоваться методом решения, который часто используется в задачах с равнобедренным треугольником. Из любой вершины опустим высоту, которая будет медианой и биссектрисой.
В одном из получившихся треугольников выразим значение высоты через сторону с помощью теоремы Пифагора:
$$h^2=a^2-({aover2})^2$$
$$h^2=a^2-{a^2over4}$$
Вычтем подобные слагаемые:
$$h^2={3over4}*a^2$$
Из получившейся формулы выразим значение стороны:
$$a^2={4over3}*h^2$$
$$a=sqrt{{4over3}*h^2}$$
$$a=sqrt{{4over3}*(3*sqrt{3})^2}$$
$$a=sqrt{{4over3}*(9*3)}$$
$$a=sqrt{4*9}$$
a=6
Подставим получившееся значение в формулу периметра равностороннего треугольника.
P=3*a=3*6=18

Что мы узнали?
Мы обсудили формулу для нахождения периметра равностороннего треугольника. Выделили проблемы, которые приходится решать при нахождении стороны равностороннего треугольника для дальнейшего решения задачи. Рассмотрели различные пути решения задач на нахождение периметра равностороннего треугольника.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Марго Дудченко
4/5
-

Татьяна Коробейникова
5/5
-

Наташа Новак
4/5
-

Марина Безобразова
4/5
-

Даниил Толыпин
5/5
-

Ибрагим Вафя-Сулим
5/5
-

Наталия Левина
4/5
-

Исмаил Тагиев
5/5
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 325.
А какая ваша оценка?
Выбирайте формулу в зависимости от известных величин.
1. Как найти периметр треугольника, зная три стороны
Просто посчитайте сумму всех сторон.
- P — искомый периметр;
- a, b, c — стороны треугольника.
2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности
Умножьте площадь треугольника на 2.
Разделите результат на радиус вписанной окружности.
- P — искомый периметр;
- S — площадь треугольника;
- r — радиус вписанной окружности.
3. Как вычислить периметр треугольника, зная две стороны и угол между ними
Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:
- Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
- Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
- Найдите корень из результата.
Теперь прибавьте к найденной стороне две ранее известные стороны.
- P — искомый периметр;
- b, c — известные стороны треугольника;
- ɑ — угол между известными сторонами;
- a — неизвестная сторона треугольника.
4. Как найти периметр равностороннего треугольника, зная одну сторону
Умножьте сторону на 3.
- P — искомый периметр;
- a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание
Умножьте боковую сторону на 2.
Прибавьте к результату основание.
- P — искомый периметр;
- a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
- b — основание треугольника (это сторона, которая отличается длиной от остальных).
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту
Найдите квадраты боковой стороны и высоты.
Отнимите от первого числа второе.
Найдите корень из результата и умножьте его на 2.
Прибавьте к полученному числу две боковые стороны.
- P — искомый периметр;
- a — боковая сторона треугольника;
- h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).
7. Как вычислить периметр прямоугольного треугольника, зная катеты
Найдите квадраты катетов и посчитайте их сумму.
Извлеките корень из полученного числа.
Прибавьте к результату оба катета.
- P — искомый периметр;
- a, b — катеты треугольника (стороны, которые образуют прямой угол).
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу
Посчитайте квадраты гипотенузы и катета.
Отнимите от первого числа второе.
Найдите корень из результата.
Прибавьте катет и гипотенузу.
- P — искомый периметр;
- a — любой катет прямоугольника;
- c — гипотенуза (сторона, которая лежит напротив прямого угла).

Как найти периметр равностороннего треугольника
Поиск периметра равностороннего треугольника означает расчет расстояния вокруг самой фигуры. Самый простой способ – это сложить все стороны. Однако бывают случаи, когда известна лишь высота треугольника или одна сторона, как быть в таких ситуациях? Статья подскажет, как быстро находить периметр треугольника при разных условиях.
1
Равносторонний треугольник – что собой представляет
Такой треугольник имеет три конгруэнтные стороны и три равных угла. Зная размер одной из сторон, можно найти остальные. Поскольку треугольник имеет три соразмерные стороны, он автоматически имеет три идентичных угла. Они в сумме дают 180º, которую, согласно их идентичности, следует разделить на 3. Это означает, что любой угол треугольника равен 60 º. Можно сделать заключение, что равносторонний треугольник является острой фигурой.
2
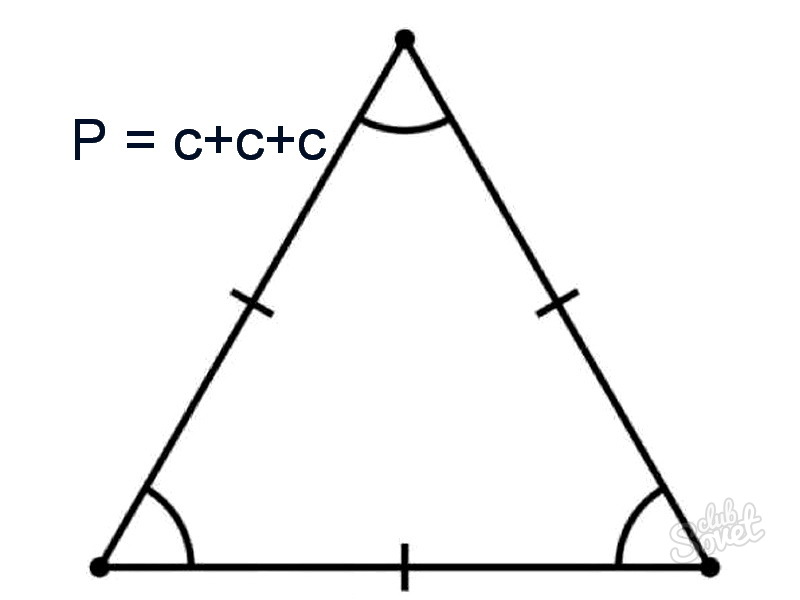
Как найти периметр равностороннего треугольника
Поскольку стороны равностороннего треугольника конгруэнтны, для вычисления его периметра требуется длина одной стороны. Можно сказать, что простая формула периметра равносторонней фигуры : Р = c+c+c, где с – длина одной из сторон.
- Узнайте периметр треугольника с конгруэнтными сторонами, если размер одной – 7 дм.
- Из условия известно, что сторона фигуры 7 дм, т.е. другие стороны идентичны.
- Согласно формулы периметр треугольника: Р = с + с + с, Р = 7+7+7 = 21 дм.
3
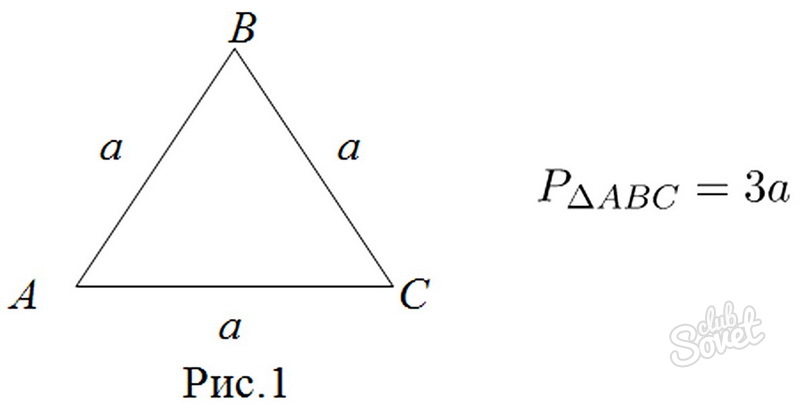
Упрощенный способ нахождения периметра равностороннего треугольника
Конечно, более простой способ найти границы треугольника – это умножить длину каждой стороны на три. Формула будет состоять: P = 3 х а, где а – длина стороны.
- Оцените периметр равностороннего треугольника с заданной стороной 7 дм.
- Подставьте значения согласно формулы: P = 3 х а , P = 3 х 7
P = 21 - Периметр треугольника составляет 21 дм.
- Когда изначально стороны треугольника заданы в сантиметрах, ваш ответ также должен быть в сантиметрах. В приведенном примере длина сторон составляет 7 дм, поэтому правильное значение периметра будет 21 дм.
4
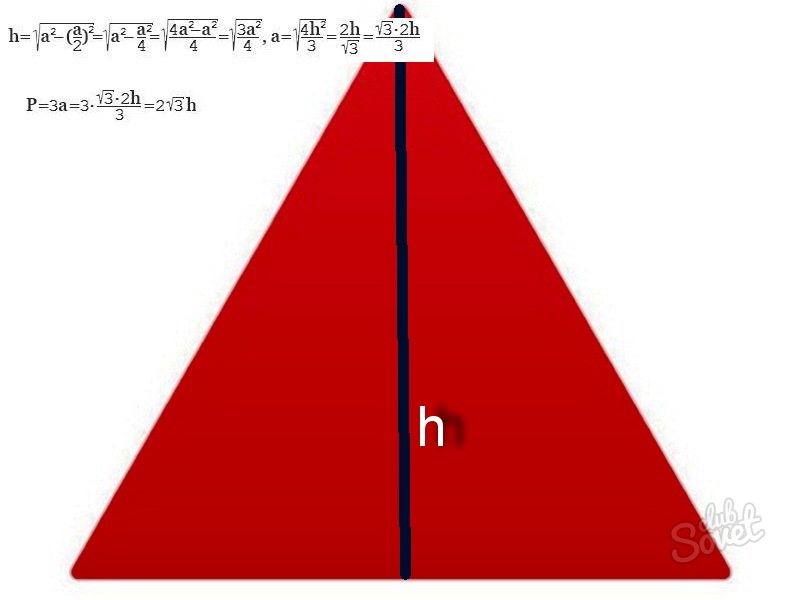
Как найти периметр равностороннего треугольника через высоту
Рассчитать периметр равностороннего треугольника возможно, если дана одна высота. Следуя теореме Пифагора, найдите одну из сторон через высоту.
- Высота треугольника с равными сторонами 7 см, найдите периметр.
- Согласно условия h = 7 см, следуя формуле:
- Р= 2√3 х 7 = 24,249 см.
5
Онлайн расчет периметра равностороннего треугольника
Существует несколько сайтов (например, справочный портал Калькулятор или познавательный портал 2mb), которые помогут быстро рассчитать периметр треугольника, достаточно лишь ввести его параметры.
6
Как найти периметр равностороннего треугольника – обратный расчет
Бывают случаи, когда в школе требуется найти сторону равностороннего треугольника, когда в условии указан периметр фигуры. Примените полученные знания : Р = 3 х с, значит с = Р : 3
- Найдите длину стороны равностороннего треугольника, когда периметр 24 см.
- Исходя из формулы: с = Р : 3, с = 24 : 3 = 8 см
- Длина сторон заданного треугольника 8 см.

Нахождение периметра равностороннего треугольника не составит труда, если правильно применять основные формулы расчета.
