Как найти угол к нормали решетки

определите угол к нормали решетки, под которым наблюдается максимум первого порядка, если…

5.124

Свет с длиной волны

падает нормально
на длинную прямоугольную щель ширины

.
Найти угловое
распределение интенсивности света при
фраунгоферовской дифракции, а также
угловое положение минимумов.

Решение:

Мысленно
разобьем щель на множество одинаковых
полосок и изобразим, имея ввиду первый
рисунок, цепочку соответствующих
элементарных векторов – для определенного
угла дифракции
.
Если

достаточно мал,

цепочка образует дугу радиуса R
(второй рисунок). Пусть длина цепочки

и результирующий вектор
.
Тогда как видно из второго рис
,
где

разность фаз между крайними векторами
цепочки. Исключив R из
этих равенств получим

Отсюда интенсивность ()

,

Где

интенсивность в центре дифракционной
картины (=0),
.
С ростом угла

увеличивается
,
и цепочка будет закручиваться. Когда

цепочка замыкается один, два,… k
раз, и мы приходим к условию
,
k=1,2…

5.125

Монохроматический
свет падает нормально на щель ширины

=11
мкм. За щелью
находится тонкая линза с фокусым
расстоянием
=150
мм, в фокальной
плоскости которой расположен экран.
Найти длину волны света, если расстояние
между симметрично расположенными
минимумами третьего порядка (на экране)
равно
=50
мм.

Решение:

условие
минимумов на щели

где

угол под которым лучи выходят из щели.
В нашем случае можно записать
,
надо найти
.
Из прямоугольного треугольника

=0,6
мкм.

5.126

Свет с диной волны

=0,50
мкм падает на щель
ширины
=10
мкм под углом

к её нормали. Найти
угловое положение первых минимумов,
расположенных по обе стороны центрального
фраунгоферова максимума.

Решение:

д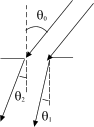ля
минимума m=1 разность хода
,
для m= -1
.
Отсюда
=33,
=27
градусов.

5.128

Монохроматический
свет падает на отражательную дифракционную
решетку с периодом d=1,0
мм под углом скольжения
.
Под углом скольжения

образуется фраунгоферов максимум
второго порядка. Найти длину волны
света.

Решение:

найдем
разность хода, она будет равно двум
длинам волны, так как максимум второй.
Итак разность хода

.

5.129

Изобразить примерную
дифракционную картину, возникающую при
дифракции Фраунгофера от решетки из
трех одинаковых щелей, если отношение
периода решетки к ширине щели равно: а)
двум; б) трем.

а)
Так как
,
то каждый второй максимум будет пропадать.
Самый большой максимум – центральный,
отсчет начинаем со следующего главного
максимума. Количество побочных максимумов
N-2, т.е. 1. Линия сверху, это
график от одной щели.

б) Так как
,
то каждый 3 максимум будет пропадать.
Количество побочных максимумов
N-2, т.е. в нашем случае 1.

5.130

При нормальном
падении света на дифракционную решетку
угол дифракции для линии
=0,65
мкм во втором
порядке равен 45 градусов. Найти угол
дифракции для линии
=0,50
мкм в третьем
порядке.

Решение: условие максимумов для
решетки
,
отсюда находим, что
.

5.131

Свет с длиной волны
535 нм падает нормально на дифракционную
решетку. Найти ее период, если одному
из фраунгоферовых максимумов соответствует
угол дифракции 35 градусов и наибольший
порядок спектра равен пяти.

Решение:

Условие максимума для решетки
,
k=1,2,3… У нас максимальный
порядок равен 5, это значит

(квадратные скобки-это целая часть).
Отсюда можно заключить, что
.
Подставим угол 35 градусов и найдем какой
максимум ему соответствует.
,
так как m это целое число,
делаем вывод, что m=3. теперь
подставим это в условие максимумов и
найдем период решетки
.

5.132

Определить длину
волны монохроматического света, падающего
нормально на дифракционную решетку с
периодом
,
если угол между направлениями на
фраунгоферовы максимумы первого и
второго порядков
.

Решение: условие
максимумов для решетки

Отсюда находим
.
Раскладываем второе уравнение как синус
суммы, получим

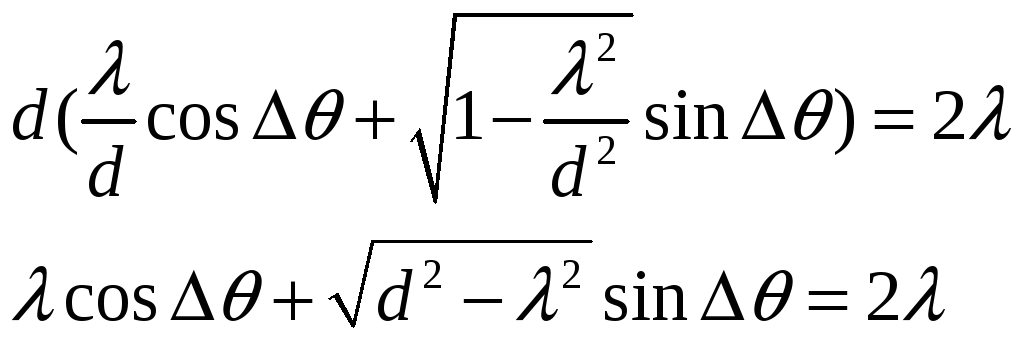
Переносим первое слагаемое вправо и
возводим в квадрат

5.133

Свет с длиной волны
530 нм падает на прозрачную дифракционную
решетку, период которой равен 1,50 мкм.
Найти угол с нормалью к решетке, под
которым образуется фраунгоферов максимум
наибольшего порядка, если свет падает
на решетку: а) нормально; б) под углом 60
градусов к нормали

Решение:

а)
Максимальный порядок
.
Разность хода

б) запишем разность хода

.
Пинимая во внимание, то что максимальное
значение

это 1, получаем m=5.

.

№5.141

Свет с длиной волны

падает на дифракционную решетку. Найти
ее угловую дисперсию в зависимости от
угла дифракции
.

Решение:

Поскольку мы имеем дело с дифракционной
решеткой, то запишем условие главных
фраунгоферовых максимумов : .

Как известно угловая дисперсия
дифракционной решетки:

Выразив отношение

из первого уравнения и подставив его
во второе, получим, что

■

№5.146

Свет падает
нормально на дифракционную решетку
ширины
,
имеющую 200 штрихов на миллиметр.
Исследуемый спектр содержит спектральную
линию с
,
которая состоит из двух компонент,
отличающихся на
.
Найти:

А) в каком порядке
спектра эти компоненты будут разрежены;

Б) наименьшую
разность длин волн, которую может
разрешить эта решетка в области
.

Решение:

А) Как известно, разрешающая способность
,
также мы знаем, что для дифракционной
решетки
,
где
-кол-во
штрихов решетки,
– порядок спектра.

Определим сколько штрихов у нашей
решетки:
,
где

кол-во штрихов на миллиметр.

Тогда окончательно для
получаем:
■

Б) Мы знаем, что разрешающая способность
.

Для нахождения минимальной разности
длин волн, которую может разрешить эта
решетка, нам надо найти максимальный
порядок спектра, что мы сделаем из
условия максимума на решетке:

,
возьмем

Тогда для

получаем, что ■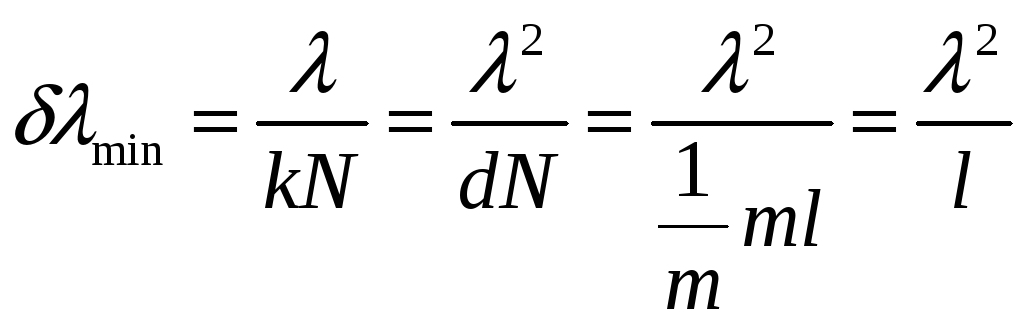

(здесь мы воспользовались тем, что период
решетки
)

№5.147

При нормальном
падении света на дифракционную решетку
ширины 10мм обнаружено, что компоненты
желтой линии натрия (589.0 и 589.6 нм)
оказывается разрешенными, начиная с
пятого порядка спектра. Оценить:

А) период этой
решетки;

Б) при какой ширине
решетки с таким же периодом можно
разрешить в третьем порядке дублет
спектральной линии с
,
компоненты которого отличаются на
0.13нм.

Решение:

Пусть как и прежде
–
это количество штрихов на миллиметр,
тогда разрешающая способность

,
где
-ширина
решетки.

Мы знаем, что период решетки ■

Б) Воспользуемся, найденным значением

из первого пункта, после чего легко
получаем, что

■

Соседние файлы в папке 11

• #
• #
• #
• #
• #
• #

Дифракционные решетки

Дифракционные решетки, пропускающие и отражательные, предназначены для пространственного деления электромагнитной волны в спектр. Когерентные пучки интерферируют, претерпевая дифракцию на периодической структуре. В пропускающих дифракционных решетках периодическая структура является множеством плотно расположенных узких щелей. При решении задачи о распределении интенсивности и записи ответа в виде функции, зависящей от длины волны и координаты на множестве щелей, получается общее выражение, которое справедливо для всех дифракционных решеток при θ_i = 0°:

        (1)

Это выражение также называют уравнением дифракционной решетки. Оно означает, что дифракционная решетка с периодом a преломляет свет дискретно, прошедшие лучи составляют с нормалью угол дифракции θ_m в зависимости от значения mλ, m – номер главного максимума. При заданном порядке m различные длины волн излучения будут выходить из решетки под разными углами. Для белого света происходит разложение в непрерывный спектр, зависящий от угла.

Пропускающая решетка

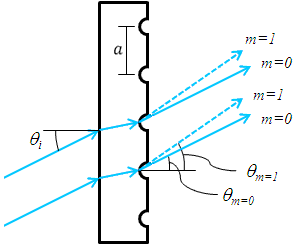
Рисунок 1. Пропускающая решетка

Один из распространенных типов решеток – пропускающая решетка. Периодическая структура решеток создается путем вырезания или гравировки на прозрачной подложке параллельных штрихов. На такой поверхности свет может рассеиваться. Пример пропускающей решетки приведен на рис. 1.

Пропускающая решетка, показанная на рис. 1, обладает периодической структурой благодаря узким штрихам с периодом a. Падающий свет попадает на решетку под углом θ_i, который отсчитывается от нормали к поверхности. Свет порядка m выходит из решетки под углом θ_m, который также определяется от нормали. Используя некоторые геометрические соотношения и общее выражение для дифракционной решетки (1), для пропускающей дифракционной решетки получим:

        (2)
 

где углы θ_i и θ_m положительны, если падающий и дифрагированный свет оказываются на противоположных сторонах нормали к поверхности решетки, как показано на рис. 1. Если эти лучи находятся на той же стороне нормали решетки, то углы следует считать отрицательными.

Отражательная решетка

Рисунок 2. Отражательная решетка

Другой распространенный тип решеток – отражательная решетка. Отражательные решетки получают путем нанесения металлического покрытия на подложку и формирования параллельных штрихов на полученной поверхности. Также существует технология производства из эпоксидных и/или пластиковых оттисков от контрольного шаблона. Во всех случаях свет отражается от поверхности с нанесенными штрихами под разными углами, которые соответствуют разным порядкам и длинам волн. Пример отражательной решетки показан на рис. 2. Используя геометрическую схему, аналогичную приведенной выше, получается уравнение отражательной решетки:

Оба типа решеток обладают одинаковым недостатком: нулевой порядок не подвергается дифракции и соответствует отражению или пропусканию поверхности. Решая уравнение (2) при условии, что θ_i = θ_m , находится единственное решение, при котором m = 0 независимо от длины волны или периода решетки. При этом условии никакой информации о длине волны, то есть весь свет или отражается от поверхности, или проходит сквозь нее.

Описанная проблема может быть решена с помощью особого рельефа, наносимого на поверхность вместе со штрихами. Дифракционные решетки такого типа называют рельефно-фазовыми. Их пример приведен на рис. 3.

Рельефно-фазовые (нарезные) решетки

Рисунок 3. Геометрия рельефно-фазовой решетки

Рисунок 4. Отражение нулевого порядка от рельефно-фазовой решетки

Рельефно-фазовые решетки (также известные как эшелетты) – особый вид отражательной или пропускающей дифракционной решетки, которые используют для достижения максимальной эффективности решетки в определенном порядке дифракции. Таким образом можно повысить мощность излучения при дифракции, минимизировав потери излучения других порядков (в частности нулевых). Благодаря своей конструкции, рельефно-фазовые решетки работают с определенной длиной волны, которую также называют длиной волны блеска.

Длина волны блеска – одна из основных характеристик рельефно-фазовых решеток. К таковым характеристикам также относятся другие два параметра, указанные на рис. 3: a – расстояние между гранями, γ – угол блеска (угол наклона грани штриха). Угол блеска может быть измерен от нормали к поверхности и от нормали к грани.

Геометрия концентрирующих решеток сходна с пропускающими и отражательными решетками. Углы падения θ_i и отражения θ_m максимумов порядка m отсчитываются от нормали к поверхности решетки. Существенное отличие заключается в том, что угол отражения зависит от угла блеска, но не от нормали поверхности решетки. Таким образом можно регулировать эффективность дифракции, изменяя только угол блеска дифракционной решетки.

Отражение нулевого порядка от рельефно-фазовой решетки показано на рис. 4. Падающий под углом θ_i луч отражается под углом θ_m при m = 0. Из уравнения (3) выводится единственное решение θ_i = – θ_m, что аналогично отражению от плоской поверхности.

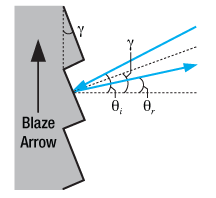
Рисунок 5. Отражение света от грани рельефно-фазовой решетки

Рисунок 6. Нормальное падение света на рельефно-фазовую решетку

Отражение от рельефно-фазовой решетки отличается от отражения света в случае плоской поверхности за счет профиля штрихов, как видно из рис. 5. Зеркальное отражение от рельефно-фазовой решетки происходит из-за угла блеска. Этот угол считается отрицательным, если он находится на той же стороне нормали поверхности решетки, что и угол падения. Выполнив несколько простых геометрических преобразований, можно обнаружить следующее:

        (4)

Рис. 6 иллюстрирует случай нулевого угла падения, при котором свет падает перпендикулярно поверхности решетки. В этом случае нулевой порядок отражения получается при 0^о. Используя уравнения (3) и (4), получаем уравнение решетки с удвоенным углом блеска:

        (5)

Схема Литтроу

Рельефно-фазовые решетки с конфигурацией Литтроу широко применяются в монохроматорах и спектрометрах из-за особенности периодической структуры. Пусть при падении света под углом θ_i эффективность решетки максимальна. По схеме Литтроу угол падения равен углу дифрагированных лучей, вышедших из решетки, θ_i = θ_m, тогда для ненулевых порядков дифракции получим:

        (6)

Рисунок 7. Схема Литтроу

Угол Литтроу θ_L отсчитывается от точки наибольшей интенсивности (m = 1), λ_D – рабочая длина волны, a – постоянная решетки. Легко увидеть, что угол в схеме Литтроу равен углу блеска для рабочей длины волны. Соответствующие сведения даны в таблицах спектральных характеристик решеток.

        (7)

Также можно вывести, что увеличение углового разделения длины волны сопровождается ростом порядка дифракции для света с нормальным падением, то есть при нулевом угле падения θ_m растет так же, как порядок m. Существует два основных недостатка дифракционной картины более высокого порядка по сравнению с дифракционной картиной низкого порядка: во-первых, уменьшение эффективности дифракции более высоких порядков, во-вторых, уменьшение свободного спектрального диапазона, определяемого соотношением:

        (8)

где λ – центральная длина волны, m – порядок.

Первая проблема, возникающая при наблюдении дифракционных картин высоких порядков, решается с помощью использования эшелеттов. Этот тип решеток обладает наибольшим углом блеска и относительно низкой плотностью штрихов, благодаря чему удается достичь достаточной концентрации энергии излучения при дифракции излучения высоких порядков. Второй недостаток компенсируют, добавляя в систему специальную дополнительную оптику: решетку, рассеивающую призму или иную оптику, обладающую рассеивающими свойствами.

Голографические решетки

Рисунок 8. Голографическая решетка

Рельефно-фазовые решетки обладают наибольшей эффективностью при использовании на рабочей длине волны. Однако на их работу серьезно влияют периодические ошибки – дублирование, большая доля рассеянного света. Все это негативно сказывается на измерениях, требующих высокой точности. Потому во многих экспериментах применяют голографические решетки, эффективность которых ниже, однако стабильность выше.

Голографические решетки в промышленном масштабе производят тем же способом, что и нарезные: копированием контрольного образца. Шаблон голографической решетки изготавливают методом фотолитографии: действием на светочувствительный материал двух интерферирующих лазерных пучков. При этом интерференционная картина экспонируется на поверхность в виде периодической структуры. Пример голографической решетки приведен на рис. 8.

Замечание: дисперсия зависит от числа штрихов на мм, но не от формы самих штрихов. Следовательно, уравнение решетки для расчета углов можно применять и в случае голографических решеток.

Факторы, которые необходимо учитывать при выборе дифракционной решетки:

1. Эффективность

Нарезные решетки демонстрируют более высокую производительность в сравнении с голографическими решетками, однако последние имеют более широкий рабочий диапазон. Обычно нарезные решетки применяют в исследованиях флуоресценции и в опытах, связанных с переизлучением.

2. Длина волны блеска

Нарезные решетки имеют пилообразный профиль, который получается вследствие нанесения штрихов на подложку. В результате пик интенсивности таких решеток достигается при излучении, близком к длине волны блеска. Голографические решетки имеют синусоидальный профиль, потому пик интенсивности достигается на рабочей длине волны. Нарезные решетки в основном применяются в приложениях с узким волновым диапазоном.

3. Светорассеяние

Из-за различия в способах нанесения штрихов голографические и нарезные решетки имеют разницу в светорассеянии. Промышленное нанесение штрихов нарезным способом повышает вероятность ошибок, а фотолитографический способ изготовления решеток более стабилен, в связи с чем голографические решетки имеют меньшее светорассеяние. Их применяют в рамановской спектроскопии.

4. Разрешающая способность

Разрешающая способность решетки – расстояние, на котором возможно различить две длины волны. Оно определяется согласно критерию Рэлея применительно к дифракционному максимуму. Две длины волны различимы, когда максимум одной длины волны совпадает с минимумом второй. Хроматическая разрешающая способность определяется из соотношения R = λ/Δλ = nN, где Δλ – разрешаемая разница длин волн, n – порядок дифракции, N – число подсвеченных штрихов. Благодаря низкой плотности штрихов эшеллеты имеют высокое разрешение.

Правила работы с дифракционными решетками

Поверхность дифракционных решеток легко повреждается отпечатками пальцев, аэрозолями, после контакта с влагой. Малейший контакт с абразивными частицами также приводит к неисправностям. Необходимо соблюдать строгие требования по эксплуатации: например, переносить решетку можно только держа за боковые стороны. Необходимы латексные перчатки или любые другие меры защиты рабочей поверхности от отпечатков пальцев. Контакт с растворителями также следует исключить. Не предпринимайте иных попыток чистить решетку, кроме сдувания пыли чистым, сухим воздухом или азотом. Незначительные дефекты на поверхности решетки обычно не влияют на производительность.

© Thorlabs Inc.

Компания INSCIENCE помогает своим заказчикам решать любые вопросы и потребности по продукции Thorlabs на территории РФ

Предмет: Физика,


автор: maksim69545

Ответы

Автор ответа: DedStar

2

Ответ:

Объяснение:

Дано:

m = 1

λ = 610 нм = 610·10⁻⁹ м

N = 1000 штрихов/мм

_______________

φ – ?

1) Находим постоянную решетки:

d = 1 мм/1000 = 1 · 10⁻⁶ м

2) Запишем формулу дифракционной решетки:

d·sin φ = m·λ

3) Величина угла:

sin φ = m·λ / d

sin φ = 1·610·10⁻⁹ / 1 · 10⁻⁶ ≈ 0,16

φ ≈ 9°

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Математика,
автор: zarinaaslanogly97

Ркшите устнл неполние х-4=0​

4 года назад

Предмет: Другие предметы,
автор: Аноним

зээээээээээээээээээээээээээээээээээээээээээээээээээээээээээээээээээээээээээээээээээээээ пжжжжжжжжжжжжжжж

4 года назад

Предмет: Русский язык,
автор: sveta15551555

перипесать выберая н или нн. указать в этих словах причастие это или прилагательное:1)сумка потеря(н,нн)а. 2)собака найде(н,нн)а. 3)картофель испечё(н,нн). 4)яблоки съезде(н,нн)в. 5)деньги утраче(н,нн)ы​

4 года назад

Предмет: География,
автор: Аноним

почему москву называют портом 5 морей

6 лет назад

Предмет: Математика,
автор: kristinalobano

Помогите сократить, пожалуйста)

6 лет назад

Как определить угол дифракции

Световые волны отклоняются от своего прямолинейного пути при прохождении через малые отверстия или мимо таких же малых препятствий. Это явление возникает, когда размеры препятствий или отверстий сравнимы с длиной волны, и называется дифракцией. Задачи на определение угла отклонения света приходится решать чаще всего применительно к дифракционным решеткам – поверхностям, в которых чередуются прозрачные и непрозрачные участки одинаковых размеров.

Инструкция

Выясните период (d) дифракционной решетки – так называют суммарную ширину одной прозрачной (a) и одной непрозрачной (b) ее полос: d = a+b. Эту пару обычно называют одним штрихом решетки, а измеряют в количестве штрихов на один миллиметр. Например, дифракционная решетка может содержать 500 штрихов на 1 мм, и тогда d = 1/500.

Для вычислений имеет значение угол (α), под которым свет падает на дифракционную решетку. Он отсчитывается от нормали к поверхности решетки, а в формуле участвует синус этого угла. Если в исходных условиях задачи сказано, что свет падает по нормали (α=0), этой величиной можно пренебречь, так как sin(0°)=0.

Выясните длину волны (λ) падающего на дифракционную решетку света. Это одна из наиболее важных характеристик, определяющих угол дифракции. Нормальный солнечный свет содержит целый спектр длин волн, но в теоретических задачах и лабораторных работах, как правило, речь идет о точечном участке спектра – о «монохроматическом» свете. Видимой области соответствуют длины примерно от 380 до 740 нанометров. Например, один из оттенков зеленого цвета имеет длину волны, равную 550нм (λ=550).

Прошедший через дифракционную решетку свет отклоняется на разные углы, образуя при этом неоднородную картину распределения с чередующимися максимумами и минимумами освещенности – дифракционный спектр. Каждому максимуму соответствует собственный угол дифракции. Выясните: угол которого максимума (k) требуется рассчитать. Отсчет ведется от нулевого – центрального – уровня. Например, условия могут требовать расчета искомой величины для второго (k=2) максимума дифракционного спектра.

Воспользуйтесь формулой, связывающей длину волны падающего на дифракционную решетку света с углом дифракции (φ) максимумов определенного порядка: d*(sin(φ)-sin(α)) = k*λ. Выведите из нее определение угла φ – у вас должно получиться такое равенство: φ = arcsin(sin(α)+(k*λ)/d). Подставьте определенные на предыдущих шагах значения в эту формулу и произведите расчеты.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?