Как найти мощность множества букв

Достаточно часто в математической науке возникает ряд трудностей и вопросов, причем многие ответы не всегда проясняются. Не исключением стала такая тема, как мощность множеств. По сути, это не что иное как численное выражение количества объектов. В общем смысле множество является аксиомой, у него нет определения. В основе лежат любые объекты, а точнее их набор, который может носить пустой, конечный или бесконечный характер. Кроме этого, он содержит числа целые или натуральные, матрицы, последовательности, отрезки и прямые.

О существующих переменных

Нулевой или пустой набор, не имеющий собственного значения, считается элементом мощности, так как это подмножество. Сбор всех подмножеств непустого множества S является множеством множеств. Таким образом, набор мощности заданного множества считается многим, мыслимым, но единым. Это множество называется множеством степеней S и обозначается P (S). Если S содержит N элементов, то P (S) содержит 2 ^ n подмножеств, так как подмножество P (S) является либо ∅, либо подмножеством, содержащим r элементов из S, r = 1, 2, 3, … Составленное из всего бесконечного множества M называется степенным количеством и символически обозначается P (M).

Элементы теории множеств

Эта область знаний была разработана Джорджем Кантором (1845-1918 годы жизни). Сегодня она используется почти во всех отраслях математики и служит ее фундаментальной частью. В теории множеств элементы представлены в форме списка и заданы типами (пустой набор, одноэлементный, конечные и бесконечные множества, равные и эквивалентные, универсальные), объединение, пересечение, разность и дополнение чисел. В повседневной жизни часто говорится о коллекции таких объектов, как куча ключей, стая птиц, пачка карточек и т. д. В математике 5 класса и не только, встречаются натуральные, целые, простые и составные числа.

Можно рассмотреть следующие множества:

• натуральные числа;
• буквы алфавита;
• первичные коэффициенты;
• треугольники с разными значениями сторон.

Видно, что эти указанные примеры представляют собой четко определенные множества объектов. Рассмотрим еще несколько примеров:

• пять самых известных ученых мира;
• семь красивых девушек в обществе;
• три лучших хирурга.

Эти примеры мощности множества не являются четко определенными коллекциями объектов, потому, что критерий “наиболее известных”, “самых красивых”, “лучших” варьируется от человека к человеку.

Наборы

Это значение представляет собой четко определенное количество различных объектов. Предположив, что:

• набор слов является синонимом, агрегатом, классом и содержит элементы;
• объекты, члены являются равными по значению терминами;
• наборы обычно обозначаются прописными буквами A, B, C;
• элементы набора представлены маленькими буквами a, b, c.

Если «a» – элемент множества A, то говорится, что «a» принадлежит A. Обозначим фразу «принадлежит» греческим символом «∈» (epsilon). Таким образом, выходит, что a ∈ A. Если ‘b’ – элемент, который не принадлежит A, это представляется как b ∉ A. Некоторые важные наборы, используемые в математике 5 класса, представляют, используя три следующих метода:

• заявки;
• реестров или табличные;
• правило создания построения.

При детальном рассмотрении форма заявления основана на следующем. В этом случае задано четкое описание элементов множества. Все они заключены в фигурные скобки. Например:

• множество нечетных чисел, меньших 7 – записывается как {меньше 7};
• набор чисел больше 30 и меньше 55;
• количество учеников класса, вес которых больше, чем учителя.

В форме реестра (табличной) элементы набора перечислены в паре скобок {} и разделены запятыми. Например:

1. Пусть N обозначает множество первых пяти натуральных чисел. Следовательно, N = → форма реестра
2. Набор всех гласных английского алфавита. Следовательно, V = {a, e, i, o, u, y} → форма реестра
3. Множество всех нечетных чисел меньше 9. Следовательно, X = {1, 3, 5, 7} → форма реестра
4. Набор всех букв в слове «Математика». Следовательно, Z = {M, A, T, H, E, I, C, S} → Форма реестра
5. W – это набор последних четырех месяцев года. Следовательно, W = {сентябрь, октябрь, ноябрь, декабрь} → реестр.

Стоит отметить, что порядок, в котором перечислены элементы, не имеет значения, но они не должны повторяться. Установленная форма построения, в заданном случае правило, формула или оператор записываются в пару скобок, чтобы набор был корректно определен. В форме set builder все элементы должны обладать одним свойством, чтобы стать членом рассматриваемого значения.

В этой форме представления набора элемент множества описывается с помощью символа «x» или любой другой переменной, за которой следует двоеточие («:» или «|» используется для обозначения). Например, пусть P – множество счетных чисел, большее 12. P в форме set-builder написано, как – {счетное число и больше 12}. Это будет читаться определенным образом. То есть, «P – множество элементов x, такое, что x является счетным числом и больше 12».

Решенный пример с использованием трех методов представления набора: количество целых чисел, лежащих между -2 и 3. Ниже приведены примеры различных типов наборов:

1. Пустой или нулевой набор, который не содержит какого-либо элемента и обозначается символом ∅ и считывается как phi. В форме списка ∅ имеет написание {}. Пустым является конечное множество, так как число элементов 0. Например, набор целых значений меньше 0.
2. Очевидно, что их не должно быть <0. Следовательно, это пустое множество.
3. Набор, содержащий только одну переменную, называется одноэлементным множеством. Не является ни простым, ни составным.

Конечное множество

Множество, содержащее определенное число элементов, называется конечным либо бесконечным множеством. Пустое относится к первому. Например, набор всех цветов в радуге.

Бесконечное количество – это набор. Элементы в нем не могут быть перечислены. То есть, содержащий подобные переменные, называется бесконечным множеством. Примеры:

• мощность множества всех точек в плоскости;
• набор всех простых чисел.

Но стоит понимать, что все мощности объединения множества не могут быть выражены в форме списка. К примеру, вещественные числа, так как их элементы не соответствуют какой-либо конкретной схеме.

Кардинальный номер набора – это число различных элементов в заданном количестве A. Оно обозначается n (A).

Например:

1. A {x: x ∈ N, x <5}. A = {1, 2, 3, 4}. Следовательно, n (A) = 4.
2. B = набор букв в слове ALGEBRA.

Эквивалентные наборы для сравнения множеств

Две мощности множества A и B являются таковыми, если их кардинальное число одинаково. Символом для обозначения эквивалентного набора является «↔». Например: A ↔ B.

Равные наборы: две мощности множества A и B, если они содержат одни и те же элементы. Каждый коэффициент из A является переменной из B, и каждый из B является указанным значением A. Следовательно, A = B. Различные типы объединения множеств в мощности и их определения объясняются с помощью указанных примеров.

Сущность конечности и бесконечности

Каковы различия между мощностью конечного множества и бесконечного?

Для первого значения характерно следующее название, если оно либо пустое, либо имеет конечное число элементов. В конечном множестве переменная может быть указана, если она имеет ограниченный счет. Например, с помощью натурального числа 1, 2, 3. И процесс листинга заканчивается на некотором N. Число различных элементов, отсчитываемых в конечном множестве S, обозначается через n (S). А также называется порядком или кардинальным. Символически обозначается по стандартному принципу. Таким образом, если множество S является русским алфавитом, то оно содержит в себе 33 элемента. Также важно запомнить, что элемент не встречается более одного раза в наборе.

Бесконечное количество в множестве

Множество называется бесконечным, если элементы не могут быть перечислены. Если оно имеет неограниченное (то есть несчетное) натуральное число 1, 2, 3, 4 для любого n. Множество, которое не является конечным, называется бесконечным. Теперь можно обсудить примеры рассматриваемых числовых значений. Варианты конечного значения:

1. Пусть Q = {натуральные числа меньше 25}. Тогда Q – конечное множество и n (P) = 24.
2. Пусть R = {целые числа между 5 и 45}. Тогда R – конечное множество и n (R) = 38.
3. Пусть S = {числа, модуль которых равен 9}. Тогда S = {-9, 9} является конечным множеством и n (S) = 2.
4. Набор всех людей.
5. Количество всех птиц.

Примеры бесконечного множества:

• количество существующих точек на плоскости;
• число всех пунктов в сегменте линии;
• множество положительных целых чисел, кратных 3, является бесконечным;
• все целые и натуральные числа.

Таким образом, из приведенных выше рассуждений понятно, как различать конечные и бесконечные множества.

Мощность множества континуум

Если провести сравнение множества и других существующих значений, то к множеству присоединено дополнение. Если ξ – универсальное, а A – подмножество ξ, то дополнение к A является количеством всех элементов ξ, которые не являются элементами A. Символически обозначается дополнение A относительно ξ как A’. К примеру, 2, 4, 5, 6 являются единственными элементами ξ, которые не принадлежат A. Следовательно, A’= {2, 4, 5, 6}

Множество с мощностью континуум имеет следующие особенности:

• дополнением универсального количества является пустое рассматриваемое значение;
• эта переменная нулевого множества является универсальным;
• количество и его дополнение являются непересекающимися.

Например:

1. Пусть количество натуральных чисел является универсальным множеством и А – четное. То, тогда A ‘{x: x – множество нечетное с такими же цифрами}.
2. Пусть ξ = множество букв в алфавите. A = набор согласных. Тогда A ‘= количество гласных.
3. Дополнением к универсальному множеству является пустое количество. Можно обозначить через ξ. Тогда ξ ‘= Множество тех элементов, которые не входят в ξ. Пишется и обозначается пустое множество φ. Поэтому ξ = φ. Таким образом, дополнение к универсальному множеству является пустым.

В математике «континуум» иногда используется для обозначения реальной линии. И в более общем плане, для описания подобных объектов:

• континуум (в теории множеств) – вещественная линия или соответствующее кардинальное число;
• линейный – любое упорядоченное множество, которое разделяет определенные свойства реальной прямой;
• континуум (в топологии) – непустое компактное связное метрическое пространство (иногда хаусдорфово);
• гипотеза о том, что никакие бесконечные множества больше целых чисел, но меньшие, чем действительные числа;
• мощность континуума – кардинальное число, представляющее размер множества действительных чисел.

По существу дела, континуум (измерение), теории или модели, которые объясняют постепенные переходы из одного состояния в другое без каких-либо резких изменений.

Проблемы объединения и пересечения

Известно, что пересечение двух или более множеств – это количество, содержащее все элементы, которые являются общими в этих значениях. Задачи Word на множествах решаются, чтобы получить основные идеи о том, как использовать свойства объединения и пересечения множеств. Решенные основные проблемы слов на множествах выглядят так:

1. Пусть A и B – два конечных множества. Они представляют собой такие, что n (A) = 20, n (B) = 28 и n (A ∪ B) = 36, находится n (A ∩ B).

Связь в наборах с использованием диаграммы Венна:

1. Объединение двух множеств может быть представлено заштрихованной областью, представляющей A ∪ B. A ∪ B, когда A и B – непересекающиеся множества.
2. Пересечение двух множеств может быть представлено диаграммой Венна. С затененной областью, представляющей A ∩ B.
3. Разность двух наборов может быть представлена диаграммами Венна. С заштрихованной областью, представляющей A – B.
4. Связь между тремя наборами, использующими диаграмму Венна. Если ξ представляет универсальное количество, то A, B, C – три подмножества. Здесь все три набора являются перекрывающимися.

Обобщение информации о множестве

Мощность множества определяется как общее количество отдельных элементов в наборе. А последнее указанное значение описывается как количество всех подмножеств. При изучении подобных вопросов требуются методы, способы и варианты решения. Итак, у мощности множества примерами могут служить следующие:

Пусть A = {0,1,2,3}| | = 4, где | A | представляет мощность множества A.

Теперь можно найти свой набор мощности. Это тоже довольно просто. Как уже сказано, набор мощности установлен из всех подмножеств заданного количества. Поэтому нужно в основном определить все переменные, элементы и другие значения A, которые {}, {0}, {1}, {2}, {3}, {0,1}, {0,2}, {0,3}, {1,2}, {1,3}, { 2,3}, {0,1,2}, {0,1,3}, {1,2,3}, {0,2,3}, {0,1,2,3}.

Теперь мощность выясняет P = {{}, {0}, {1}, {2}, {3}, {0,1}, {0,2}, {0,3}, {1,2}, {1,3}, {2,3}, {0,1,2}, {0,1,3}, {1,2,3}, {0,2,3}, {0,1,2,3}}, который имеет 16 элементов. Таким образом, мощность множества A = 16. Очевидно, что это утомительный и громоздкий метод решения этой проблемы. Однако есть простая формула, по которой, непосредственно, можно знать количество элементов в множестве мощности заданного количества. | P | = 2 ^ N, где N – число элементов в некотором A. Эта формула может быть получена применением простой комбинаторики. Таким образом, вопрос равен 2 ^ 11, поскольку число элементов в множестве A равно 11.

Итак, множеством является любое численно выраженное количество, которое может быть всевозможным объектом. К примеру, машины, люди, числа. В математическом значении это понятие шире и более обобщенное. Если на начальных этапах разбираются числа и варианты их решения, то в средних и высших стадиях условия и задачи усложнены. По сути, мощность объединения множества определена принадлежностью объекта к какой-либо группе. То есть один элемент принадлежит к классу, но имеет одну или несколько переменных.

2.
Декартово произведение. Мощность
множества.

2.1.
Декартово
произведение множеств.

Упорядоченная пара

определяется как совокупность, состоящая
из двух элементов x
и y,
расположенных в определенном порядке.
Две пары

и

считаются равными тогда и только тогда,
когда x=u
и y=v.

Определение 2.1.
Пусть A
и B
– два множества. Прямым
(декартовым) произведением
двух множеств A
и B
называется множество всех упорядоченных
пар, в котором первый
элемент каждой пары принадлежит A,
а второй
принадлежит B:

.

Пример ..
Пусть

и
.
Тогда

.

.



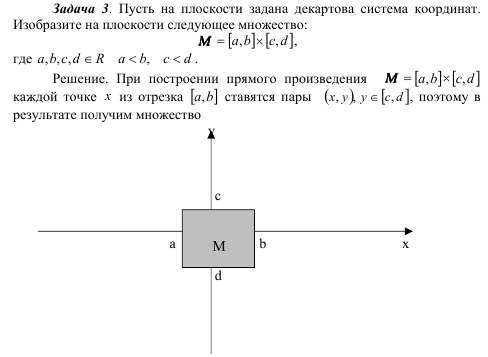
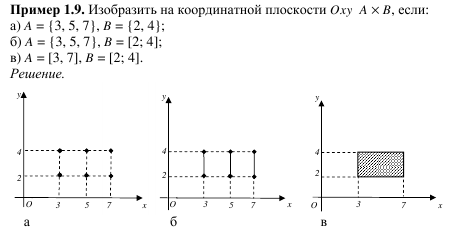
Пример ..
На координатной плоскости построить
следующее множество:

(-1; 3×1;
3)

Решение.
Первое множество помещаем на оси OX,
второе на оси OY.
Множество всех пар, т.е. декартово
произведение, изображается точками
заштрихованного прямоугольника, но без
левой и нижней стороны.



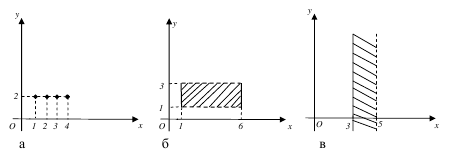
В
общем случае, точка на плоскости может
быть задана упорядоченной парой
координат, то есть двумя точками на
координатных осях. Поэтому координатную
плоскость можно задать в виде
.
Метод координат ввел в употребление
Рене Декарт (1596-1650), отсюда и название
«декартово произведение».

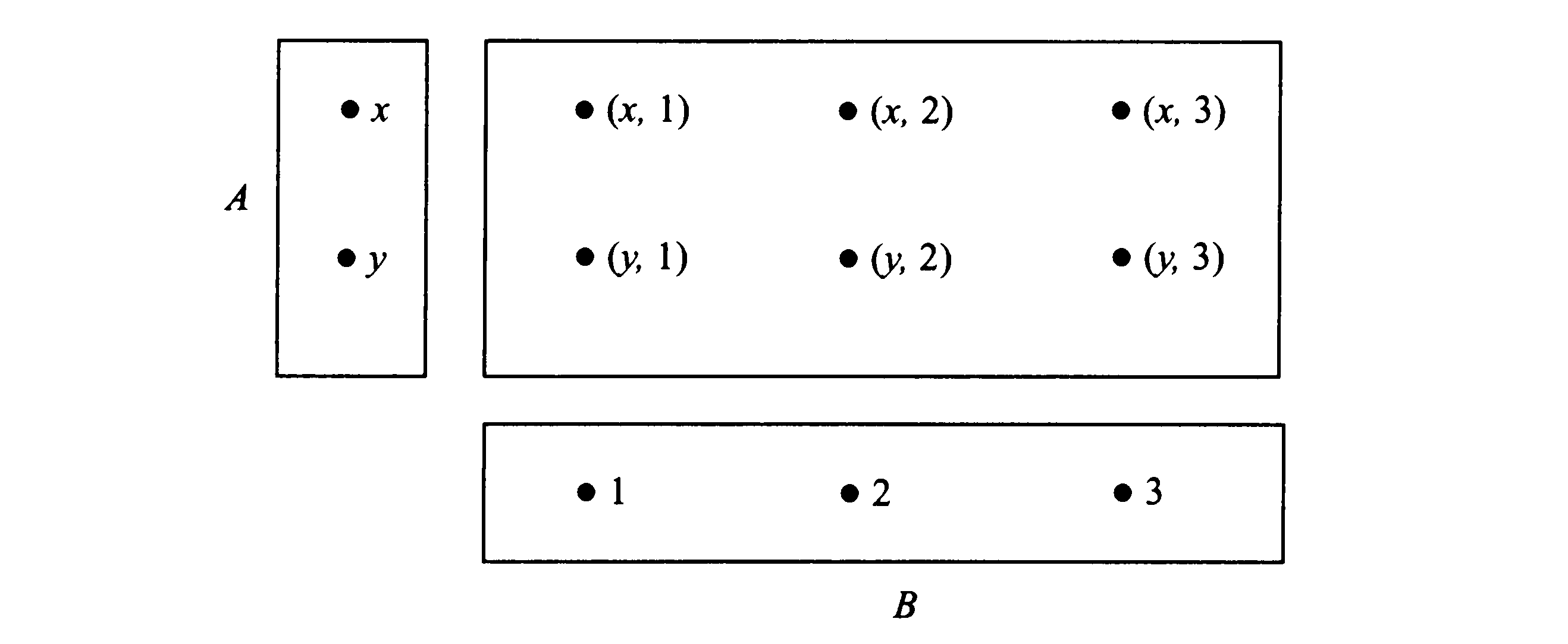
Диаграмма
Венна, иллюстрирующая декартово
произведение АхВ

В частности, если A
пусто или B
пусто, то, по определению, AB
пусто.

Понятие прямого
произведения допускает обобщение.

Прямое произведение
множеств A₁,
A₂,
…, A_n
– это множество наборов (кортежей):

.

Множества A_i
не обязательно различны.

Степенью
множества A
называется его прямое произведение
самого на себя. Обозначение:

.

Соответственно,

и вообще
.

Пример ..
Пусть B=0,
1.
Описать множество Bⁿ.

Решение.
Множество Bⁿ
состоит из последовательностей нулей
и единиц длины n.
Они называются строкой
бит или битовой
строкой длины n.



2.2. Мощность
множества.

Говорят, что между
множествами A
и B
установлено взаимно
однозначное соответствие,
если каждому элементу множества A
соответствует один и только один элемент
множества B
и каждому элементу множества B
соответствует некоторый элемент
множества A.
В этом случае говорят также, что множества
A
и B
изоморфны
и используют обозначение AB.

Определение 2.2. Два
множества A
и B
называются эквивалентными,
или равномощными,
если между этими множествами может быть
установлено взаимно однозначное
соответствие. В этом случае пишут: AB,
или A=B,
и говорят, что множества A
и B
имеют равные мощности.

Пример ..

1) Множество десятичных
цифр равномощно множеству пальцев на
руках человека.

2) Множество четных
натуральных чисел (2N)
равномощно множеству всех натуральных
чисел (N).

Определение 2.3. Множество
A
называется конечным,
если оно эквивалентно J_n
при некотором n,
где J_n=1,
2, …, n
– множество n
первых натуральных чисел.

Определение 2.4. Мощностью
конечного
множества A,
которое содержит k
элементов, называется число его элементов.
Она обозначается A=k.
Пустое множество считается конечным с
числом элементов равным нулю, т.е. =0.

Таким образом, если
множество A
конечно, т.е. A=k,
то элементы A
всегда можно перенумеровать,
то есть поставить в соответствие
элементам номера из отрезка натурального
ряда 1..k
с помощью некоторой процедуры. Наличие
такое процедуры подразумевается, когда
употребляется запись A=a₁,
a₂,
…, a_k.

Пример ..
В компьютере все множества реальных
объектов конечны: множество адресуемых
ячеек памяти, множество исполнимых
программ, множество тактов работы
процессора.

Множества, которые не
являются конечными, называются
бесконечными.
Если некоторое множество A
равномощно множеству натуральных чисел
N,
т.е. AN,
то множество A
называется счетным.
Счетное множество A
– это такое множество, все элементы
которого могут быть занумерованы в
бесконечную последовательность a₁,
a₂,
…, a_n,
…, так, чтобы при этом каждый элемент
получил лишь один номер n
и каждое натуральное число n
было бы номером лишь одного элемента
множества A.

Мощность счетного
множества принято обозначать через

(
– первая буква древнееврейского
алфавита, называемая «алеф», символ

читается: «алеф-нуль»).

Наименьшая бесконечная
мощность – мощность
множества натуральных чисел

N=.

Пример .7.
Множество Z
– множество целых чисел также счетно.

Решение.
Рассмотрим множество целых чисел Z:

…,
n,
…, 3,
2,
1,
0, 1, 2, 3, …, n,
… .

На первый взгляд, кажется,
что это множество невозможно перенумеровать.
Однако эту нумерацию можно осуществить,
применив следующую хитрость: двигаясь
не в одном направлении, а все время
менять его.

Иными словами, будем
нумеровать так: числу 0 дадим номер 1,
числу 1 – номер 2, числу 1
– номер 3, числу 2 – номер 4, числу 2
– номер 5, и т.д. Таким образом, получаем
взаимно однозначное соответствие между
множеством Z
и N.
А значит, множество Z
счетно.

Множество A
называется несчетным,
если его мощность больше мощности
множества N.
В таком случае множество A
называется континуальным
или континуумом.
Мощность континуума обозначается
.
Следующую теорему примем без доказательства.

Теорема 2.1.
Множество всех действительных чисел
имеет мощность континуума, т.е. R=C.

2.3. Теоремы
сложения и умножения.

Формула
включений и исключений.

Теорема 2.2.
(Теорема сложения)

Пусть

– конечные попарно непересекающиеся
множества, т.е.
.
Тогда

(2.3.1.)

Доказательство.
Докажем теорему методом математической
индукции.

Базис индукции.
Пусть n=2.
Пусть множества X₁=A
и X₂=B,
мощности которых соответственно равны
k₁
и k₂,
т.е. A=k₁,
B=k₂.
Так как AB=,
то

.

Индуктивный переход.
Пусть теорема верна для n.
Покажем, что для n+1
будет тоже справедливо. Тогда

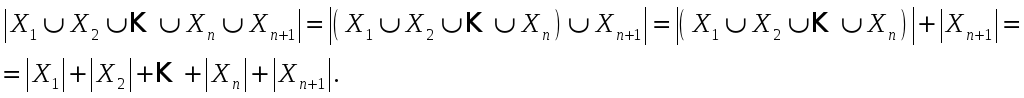
Теорема 2.3.
(Теорема умножения)

Пусть заданы конечные
множества
.
Тогда

(2.3.2.)

т.е.
число элементов декартова произведения
множеств равно произведению количеств
элементов сомножителей.

Доказательство.
Докажем теорему методом математической
индукции.

Базис индукции.
Пусть n=2.
Пусть множества X₁=A
и X₂=B,
мощности которых соответственно равны
k₁
и k₂,
т.е. A=k₁,
B=k₂.
Первый компонент упорядоченной пары
можно выбрать k₁
способами, второй – k₂
способами. Таким образом, всего имеется
k₁k₂
различных упорядоченных пар. Значит,

.

Индуктивный переход.
Утверждение теоремы справедливо для
n.
Покажем, что оно будет справедливо и
для n+1.
Имеем:

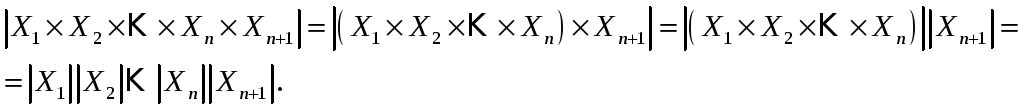
Пример ..
Сколько существует целых чисел между
0 и 1000, содержащих ровно одну цифру 6?

Решение.
Пусть S
– множество целых чисел между 0 и 1000,
содержащих ровно одну цифру 6. Рассмотрим
три подмножества S₁,
S₂
и S₃
множества S.

S₁
– множество, которое содержит число,
состоящее из одной цифры, и эта цифра
6;

S₂
– множество, содержащее двузначные
числа ровно с одной цифрой, равной 6;

S₃
– множество, содержащее трехзначные
числа ровно с одной цифрой, равной 6.

Множество S₁
содержит только один элемент – число
6. Значит, 
S₁=1.

В множестве S₂
каждый элемент, содержащей 6, имеет ее
либо первой, либо второй цифрой. Если 6
– вторая цифра, то существует 8 различных
чисел, которые будут стаять на первом
месте, поскольку первое число не может
быть 0 или 6. Если 6 – первая цифра, то
таких чисел 9, поскольку вторая цифра
не может быть 6. Таким образом, S₂
содержит 8+9=17 элементов, т.е. 
S₂=17.

Элемент из S₃
содержит 6 как первою, вторую или третью
цифру.

Если 6 – первая цифра,
то существует 9 вариантов выбора второй
цифры и 9 вариантов выбора третьей цифры.
Согласно комбинаторному принципу
умножения, S₃
содержит 99=81
чисел с первой цифрой 6.

Если 6 – вторая цифра,
то имеются 9 вариантов выбора третьей
цифры и 8 вариантов выбора первой цифры,
поскольку первая цифра не может быть
нулем. Следовательно, S₃
содержит 98=72
числа, у которых 6 – вторая цифра.

Аналогично, S₃
содержит 72 числа, у которых 6 – третья
цифра. Следовательно, всего S₃
содержит 81+72+72=225 элементов, т.е. S₃=225.

Поскольку

и множества S₁,
S₂
и S₃
попарно непересекающиеся, то

.



Поставим задачу подсчитать
число элементов в объединении

X=X₁X₂…X_m

конечных
множеств
,
которые могут иметь непустые пересечения
между собой, т.е. объединение может быть
не разбиением.

Теорема 2.4.
(Формула включений
и исключений).

Для конечных множеств
,
справедлива формула включений
и исключений.

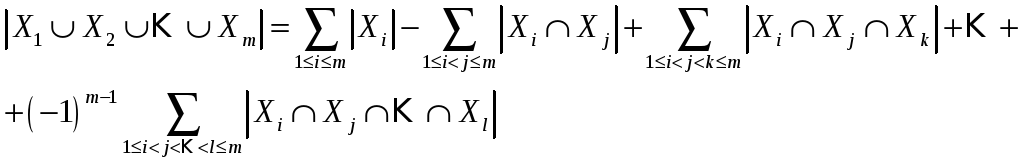
(2.3.3.)

В частности для двух
множеств эта формула примет вид:

.

Для трех множеств формула
включений и исключений примет вид:

.

Название этой теоремы
подчеркивает использование последовательных
включений и исключений элементов
подмножеств.

Пример ..
Сколько положительных целых чисел,
меньших 101, делятся на 2 или на 3?

Решение.
Пусть X
– множество положительных целых чисел,
которые делятся на 2 или 3. Рассмотри два
подмножества X₁
и X₂
множества X.

X₁
– множество положительных целых чисел,
которые делятся на 2. Число элементов
или мощность этого множества равно
.

X₂
– множество положительных целых чисел,
которые делятся на 3. Число элементов
или мощность этого множества равно
.

Тогда множество X₁X₂
– множество положительных целых чисел,
которые делятся и на 2 и на 3. Число
элементов или мощность этого множества
равно
.

Воспользуемся формулой
включения и исключения, чтобы найти
число элементов множества X.

Получаем

.

Соседние файлы в папке Лекции_2

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вспомним некоторые известные нам факты: Множество символов, с помощью которых записывается текст, называется алфавитом.  Число символов в алфавите – это его мощность.  Формула определения количества информации: N=2 i  , где N – мощность алфавита (количество символов), i – количество бит (информационный вес символа).  В алфавит мощностью 256 символов можно поместить практически все необходимые символы. Такой алфавит называется достаточным.  Т.к. 256 = 28, то вес 1 символа – 8 бит.  Единице измерения 8 бит присвоили название 1 байт:  1 байт = 8 бит.  Двоичный код каждого символа в компьютерном тексте занимает 1 байт памяти.

Задачи: 1) Алфавит содержит 32 буквы. Какое количество информации несет одна буква? Дано: Мощность алфавита N = 32 Решение:  1. 32 = 2 5, значит вес одного символа i = 5 бит.  Ответ: одна буква несет 5 бит информации.  2) Сообщение, записанное буквами из 16 символьного алфавита, содержит 10 символов. Какой объем информации в битах оно несет?  Дано: Мощность алфавита N = 16 текст состоит из 10 символов. Решение:  1. 16 = 2 4 2. Всего символов 10, значит объем информации 10 * 4 = 40 бит.  Ответ: сообщение несет 40 бит информации (8 байт). 3) Информационное сообщение объемом 300 бит содержит 100 символов. Какова мощность алфавита?  Дано: Объем сообщения = 300 бит текст состоит из 100 символов Решение:  1. Определим вес одного символа: 300 / 100 = 3 бита.  2. Мощность алфавита определяем по формуле: 2 3  = 8 Ответ: мощность алфавита N = 8.