Посчитать диагональ прямоугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Посчитать диагональ прямоугольника
Чтобы посчитать диагональ прямоугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор

Посчитать чему равна диагональ (d) любого прямоугольника (в том числе и квадрата) можно зная длины его сторон (a и b).
Просто подставьте их в калькулятор и получите результат.
Чему равна диагональ прямоугольника если сторона
a = ,
а сторона
b = ?
Ответ: d =
0
Теория
Чему равна диагональ прямоугольника d если известны длина стороны a и длина стороны b?
Формула
d = √a2 + b2
Пример
Если сторона a = 10 см, а сторона b = 5 см, то:
d = √102 + 52 = √100 + 25 ≈ 11.18 см
См. также
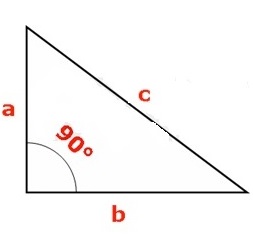
Прямоугольник — четырёхугольник, у которого все углы равны 90 градусов, т. е. прямые.
Диагональ прямоугольника — прямая проложенная из противоположных вершин прямоугольника.
Диагонали прямоугольника равны и они делят прямоугольник на два равных прямоугольных треугольника.
Чтобы найти диагональ прямоугольника необходимо вспомнить теорему Пифагора, ведь диагональ — это гипотенуза прямоугольного треугольника, а стороны (длина и ширина) прямоугольника являются катетами треугольника.
Как найти диагональ прямоугольника
Воспользуемся теоремой Пифагора и формулой
d= sqrt{a^2 + b^2}
d — диагональ квадрата
a — длина прямоугольника
b — ширина прямоугольника
Подставив в формулу вместо a длину прямоугольника, а вместо b — ширину прямоугольника и произведя расчет мы получим диагональ прямоугольника. Следует помнить, что у прямоугольника две диагонали и они равны между собой.
Диагональ прямоугольника онлайн калькулятор
Чтобы найти диагональ с помощью калькулятора введите длину и ширину прямоугольника и нажмите кнопку Рассчитать. В результате вы получите ответ и подробное решение.
Нахождение диагонали прямоугольника используется в различных жизненных ситуациях. К примеру, при проектировании фундамента дома необходимо проверить его диагонали — они должны быть равны между собой. Также на сайте можно рассчитать диагональ квадрата.
Ваша оценка
[Оценок: 171 Средняя: 3.1]
Диагональ прямоугольника Автор admin средний рейтинг 3.1/5 – 171 рейтинги пользователей
Посчитать диагональ прямоугольника
Онлайн калькулятор

Посчитать чему равна диагональ (d) любого прямоугольника (в том числе и квадрата) можно зная длины его сторон (a и b).
Просто подставьте их в калькулятор и получите результат.
Теория
Чему равна диагональ прямоугольника d если известны длина стороны a и длина стороны b?
Формула
Пример
Если сторона a = 10 см, а сторона b = 5 см, то:
Диагональ треугольника – формула
Очень часто в начале изучения фигуры ученики путают значение диагонали прямоугольника и треугольника. Поэтому, чтобы не путаться в обозначениях, лучше разобраться в тематике раз и навсегда.

Треугольник
Треугольник – это фигура, состоящая из трех сторон и трех углов. Треугольник имеет три характеризующих отрезка:
Треугольник не может иметь диагональ в принципе. Дело в том, что диагонали могут быть проведены только в многоугольниках, количество сторон которых больше 3.
Почему так? Потому что диагональ это отрезок, соединяющий противоположные вершины. В треугольнике противоположных вершин нет и быть не может. Существует сторона, противоположная вершине, но сами по себе вершины всегда смежные, т.е. соединенные одной стороной. Значит, диагонали треугольника не существует

Рис. 1. Три медианы в треугольнике.
Прямоугольник
Прямоугольник – это первая фигура школьного курса математики, которая имеет диагональ. Так же, как диагональ имеет и квадрат.
Диагональ прямоугольника или квадрата всегда:
- Делит фигуру на две равных прямоугольных треугольника.
- В полученных треугольниках диагональ будет являться гипотенузой
- Диагональ будет равняться корню квадратному из суммы квадратов катетов согласно теореме Пифагора
Диагоналей в любом четырехугольнике 2, а в квадрате и прямоугольнике обе диагонали равны между собой.
При этом правило не касается других четырехугольников. Например, диагонали параллелограмма всегда неравны между собой. Запомните, если перед вами произвольный четырехугольник использовать утверждение о равенстве диагоналей без доказательства нельзя. Любое утверждение в геометрии, кроме аксиом должно быть доказано.
Кроме прямоугольника и квадрата равными диагоналями обладает ромб. При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.
Многоугольник
На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.
Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.

Рис. 2. Диагонали многоугольника.
В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.
Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.
Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.
Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.
Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:
$P=>$ – где n это число сторон многоугольника.
Проверим для квадрата:

Рис. 3. Диагонали квадрата.
Что мы узнали?
Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.
Диагональ прямоугольника
Прямоугольник — четырёхугольник, у которого все углы равны 90 градусов, т. е. прямые.
Диагональ прямоугольника — прямая проложенная из противоположных вершин прямоугольника.
Диагонали прямоугольника равны и они делят прямоугольник на два равных прямоугольных треугольника.
Чтобы найти диагональ прямоугольника необходимо вспомнить теорему Пифагора, ведь диагональ — это гипотенуза прямоугольного треугольника, а стороны (длина и ширина) прямоугольника являются катетами треугольника.
Как найти диагональ прямоугольника
Воспользуемся теоремой Пифагора и формулой
d — диагональ квадрата
a — длина прямоугольника
b — ширина прямоугольника
Подставив в формулу вместо a длину прямоугольника, а вместо b — ширину прямоугольника и произведя расчет мы получим диагональ прямоугольника. Следует помнить, что у прямоугольника две диагонали и они равны между собой.
Диагональ прямоугольника онлайн калькулятор
Чтобы найти диагональ с помощью калькулятора введите длину и ширину прямоугольника и нажмите кнопку Рассчитать. В результате вы получите ответ и подробное решение.
Нахождение диагонали прямоугольника используется в различных жизненных ситуациях. К примеру, при проектировании фундамента дома необходимо проверить его диагонали — они должны быть равны между собой. Также на сайте можно рассчитать диагональ квадрата.
[spoiler title=”источники:”]
http://sprint-olympic.ru/uroki/matematika-uroki/15430-diagonal-treygolnika-formyla.html
http://calculat.ru/diagonal-pryamougolnika
[/spoiler]
Расчет диагонали
Расчет диагонали
Скачать, сохранить результат
Выберите способ сохранения
-
Вы можете сохранить результат расчёта в формате PDF на ваше устройство.
-
Распечатайте результат расчёта конструкции на бумагу любого формата.
-
Отправьте результат расчета в формате PDF на ваш е-мейл.
Информация
Профессиональное проектирование и формирование фундамента, стен, а также полноценной системы крыши дома требует чёткого выставления геометрических углов и расчёта диагоналей сегментов конструкций. От точности вычислительных манипуляций напрямую зависит безопасность, устойчивость, прочность и долговечность здания. Интерактивный калькулятор диагоналей для расчёта фундамента и крыш поможет безошибочно выполнить все расчётные операции на этапе проектирования дома всего за несколько секунд.
Преимущества калькулятора диагоналей
- Помогает безошибочно рассчитать квадрат конкретной секции фундамента всего в несколько кликов.
- Позволяет самостоятельно выполнить расчёт диагонали прямоугольника или треугольника.
- Помогает быстро рассчитать общую длину и ширину фундамента, а также стен дома.
- Результаты расчётных операций гарантируют чёткое выставление геометрических углов в 90° при монтаже конструкционных элементов фундамента, стен и крыши.
- Экономит уйму времени, сил нервов и средств в процессе проектирования строений всех категорий.
- Расчёт диагоналей основания обеспечивает безупречное обустройство фундамента, что дарит дому безопасность, надёжность и долговечность.
- Возможность бесплатно получить результаты расчётных операций в формате PDF на свой E-mail или мгновенно распечатать их в режиме онлайн.
Безошибочно рассчитайте геометрические параметры фундамента, стен и конструкционных элементов системы крыши уже сегодня. Бесплатно задействуйте онлайн калькулятор диагоналей — сэкономьте силы, время и деньги прямо сейчас!
Добавить комментарий
Одна из основных фигур курса математики – прямоугольник.
Впервые о нем заговорили еще в Древнем Египте, а позже и в
Древней Греции. Именно свойства его диагоналей помогают
решить многие задания учебного курса. Подход, который
сейчас используется в геометрии разработал Евклид. Формулы,
представленные в данной статье, пригодятся как при решении
домашних упражнений, так и на ЕГЭ. Именно такие задачки
помогают набрать недостающие баллы, поэтому ими не стоит пренебрегать.
- Диагональ прямоугольника через его стороны
- Диагональ прямоугольника через площадь и известную сторону
- Диагональ прямоугольника через периметр и сторону
- Диагональ прямоугольника через диаметр описанной окружности
- Диагональ прямоугольника через радиус описанной окружности
- Диагональ прямоугольника через площадь и острый угол между диагоналями
- Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу
- Диагональ прямоугольника через угол прилегающей диагонали и длину стороны противоположной этому углу
- Что такое диагональ прямоугольника, когда требуется ее вычисление
Диагональ прямоугольника через его стороны
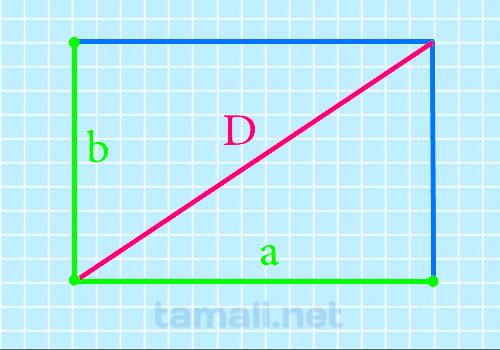
Если заданы хотя бы 2 стороны, то вычислить линию, соединяющую противоположные вершины, будет довольно просто. Применяется классическая теорема Пифагора. Достаточно подставить приведенные в дано числовые параметры в виде суммы квадратов под корнем:
![]()
Где a, b – это стороны, а d – прямая, которую мы ищем.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через площадь и известную сторону
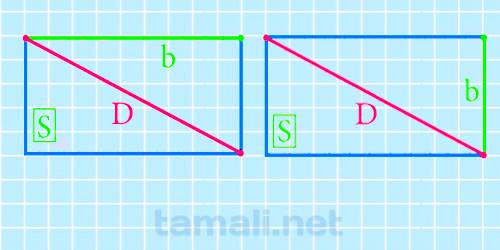
Когда в дано есть S и одна сторона, то узнать искомое значение можно используя следующее равенство:
![]()
Где D – это прямая, которую необходимо найти, a и b – любая заданная сторона, а S – площадь.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через периметр и сторону
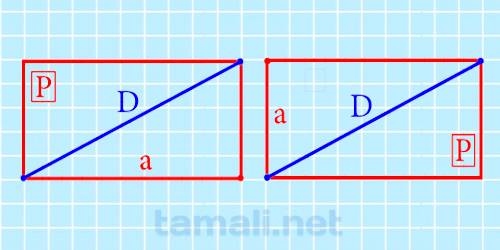
Когда задан периметр (сумма сторон) и, хотя бы одна сторона, отрезок, соединяющий несмежные точки высчитывают так:
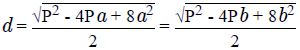
Где P – сумма сторон, a и b – любая заданная сторона.
Рассчитать искомый отрезок можно и через соотношение сторон и площадь.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через диаметр описанной окружности
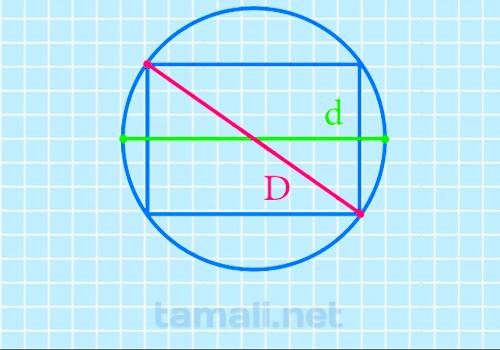
Поиск отрезка через описанную окружность еще более прост, здесь даже не придется проводить расчеты: D = d
Где d – это обозначенный диаметр.
Различить вписанную/описанную окружность легко. Когда геометрическое тело вписано куда-то, то оно всегда будет находиться в другой фигуре. Когда окружность описана, то она находится снаружи, она как бы описывает другое геометрическое тело. Описанные фигуры задевают собой точки, а вписанные – касаются сторон.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через радиус описанной окружности
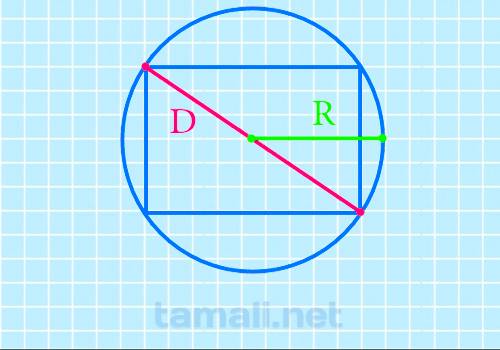
Для расчета искомого отрезка через описанную окружность нужно провести вычисления, где: D = 2R
Где R – это заданный радиус.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через площадь и острый угол между диагоналями
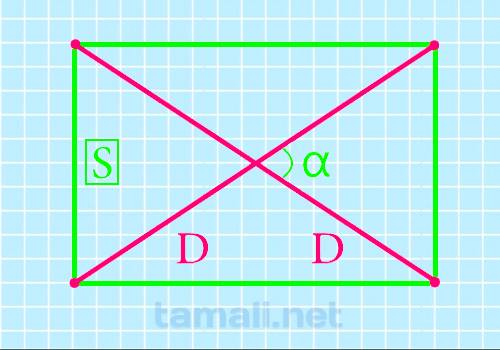
Если необходимо узнать прямую, соединяющую вершины 4-хугольника, это можно осуществить с помощью двух диагоналей. Для получения ответа к задаче понадобится sin β между ними и S (произведение длины и ширины).
Расчет проводится с равенством:
![]()
Где соответственно S – это площадь, а sin β – это острый угол, расположенный внутри фигуры (меж пересекающимися прямыми).
Если в 4-хугольнике расчертить 2 отрезка, объединяющие несмежные вершины, то они будут равны меж собой (все 4 отрезка), а точка пересечения разделит их пополам.
Пересечение всегда происходит в геометрическом центре самой фигурки. Этот же центр является центром описанной окружности.
Площадь (S):
Цифр после запятой:
Результат в:
Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу
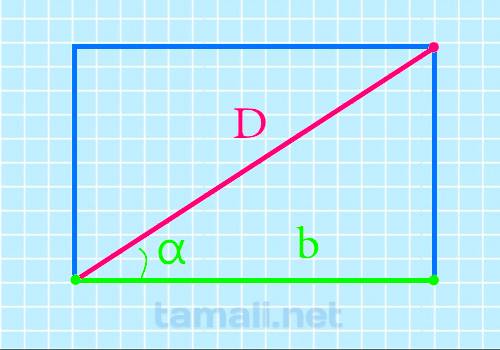
Когда одна из сторон 4-хугольника прилегает к углу, то просчитать отрезок, соединяющий вершины тоже возможно:
![]()
Где b – это сторона, прилегающая к углу, а cos a – это тот самый угол.
Косинус угла в треугольнике с прямым углом рассчитывается по формуле – длина соседней стороны, разделенная на гипотенузу. Синус – это противолежащий катет, разделенный на гипотенузу. Либо можно поступить еще проще, подсмотрев в таблицу Брадиса.
Цифр после запятой:
Результат в:
Диагональ прямоугольника через угол прилегающей диагонали и длину стороны противоположной этому углу
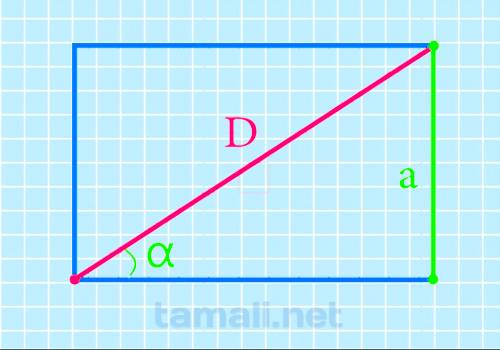
Чтобы найти нужный отрезок внутри четырехугольника, должен быть задан угол, прилегающий к искомому отрезку и сторона, противоположная углу:
![]()
Где a – это сторона четырехугольника, а sin a – это прилегающий угол.
Длинная сторона 4-хугольника– это длина, а короткая – его ширина. Помните, что каждая сторона одновременно является высотой.
Цифр после запятой:
Результат в:
Что такое диагональ прямоугольника, когда требуется ее вычисление
Прямоугольник – это частный случай параллелограмма. Иначе 4-хугольник с попарно равными сторонами, параллельными друг другу, а также равными прямыми углами по 90⁰. Сумма углов четырехугольника составляет 360⁰.
Диагональ разделяет фигуру на два новых элемента – треугольники с прямым углом. Это прямая, объединяющая противоположные вершины. Имея 2 прямоугольных треугольника, отрезок уже можно рассчитать по теореме Пифагора. По теореме гипотенуза – это квадрат из суммы катетов (обозначенных сторон треугольника), возведенных в квадрат.
Линии, соединяющие противоположные точки в четырехугольнике всегда пересекаются друг с другом.
Отрезок обозначают как d или D. Если названы все точки, то его можно называть в соответствии с ними – AC или BD.
Знания о линии, проходящей через несмежные точки 4-хугольника может понадобиться в легких геометрических упражнениях, так и в более сложных многоуровневых задачках, которые появляются на ЕГЭ. Свойства данного отрезка помогают находить важные параметры прямоугольника. Зная данные обеих линий, соединяющих противоположные углы, можно рассчитать S геометрического тела.
Перед решением любой геометрической задачки рекомендуется сделать чертеж и обозначить всю заданную информацию. Так будет значительно проще сосредоточиться на искомом значении.
Если регулярно решать тесты по геометрии, то формулы легче запомнятся, а их применение будет доведено до автоматизма.
