
Линейную производственную функцию часто называют производственной функцией с бесконечной эластичностью замещения производственных факторов.
Уравнения изокванты линейной производственной функции определяются уравнением
|
Y |
A* |
b |
(1.31) |
|||||
|
K = |
L . |
|||||||
|
a |
a |
a |
||||||
|
Семейство изоквант линейной производственной функции имеет вид |
||||||||
|
параллельных прямых с угловым коэффициентом |
b |
(рис.1.4). |
||||||
|
a |
||||||||
0
Несмотря на указанные недостатки линейной производственной функции, они получили широкое распространение при моделировании крупномасштабных производственных систем, такие как отрасли промышленности и национальная экономика, когда производство агрегированного продукта обеспечивается
29

одновременным функционированием огромного множества разнообразных технологических процессов.
Перейдём к рассмотрению основных свойств и характеристик степенной производственной функции (1.21). Эта функция 1 предложена П. Дугласом и Ч. Коббом в 1928 г. Степенная производственная функция применяется для решения разнообразных теоретических и прикладных задач благодаря своей структурной простоте. Степенная производственная функция относится к классу мультипликативных производственных функций.
Логарифмируя производственную функцию (1.21), получаем линейное соотношение
|
lnYt=lnA+ ln Kt+ lnLt. |
(1.32) |
Преимущество этой формы записи состоит в том, что для оценки неизвестных параметров A, ,  по эмпирическим данным можно применять классические методы линейной множественной регрессии и использовать широко распространенные программные продукты для реализации методов наименьших квадратов.
по эмпирическим данным можно применять классические методы линейной множественной регрессии и использовать широко распространенные программные продукты для реализации методов наименьших квадратов.
При использовании классической степенной производственной функции предполагается выполнение следующих условий:
1)допускается возможность замещения одним фактором производства другого;
2)неизменность эффективности единиц труда и капитала;
3)неизменность эффективности использования факторов производства (условие отсутствия научно-технического прогресса).
Для степенной производственной функции (1.21) все свойства 1 – 4 выполняются.
Определим основные характеристики степенной производственной функции по формулам (1.5) – (1.11), (1.18) и (1.19):
1 Cobb, Charles W. and Paul H. Douglas (1928) A theory of production. American Economic Review 18: p. 139 – 165.
30

|
AyK |
= |
Y |
= |
F( K ,L ) |
= |
A K |
L |
= A·K |
·L ; |
||||||||||||||||||||||||||||||||||||||||||||||
|
K |
K |
K |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
AyL |
= |
Y |
= |
F( K ,L ) |
= |
A K |
L |
= A·K |
·L |
||||||||||||||||||||||||||||||||||||||||||||||
|
L |
L |
L |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
My = |
Y |
= |
F( K ,L ) |
= |
A K |
1 L |
Y |
; |
|||||||||||||||||||||||||||||||||||||||||||||||
|
K |
K |
K |
K |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
My = |
Y |
= |
F( K ,L ) |
= |
Y |
; |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
L |
L |
L |
L |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
MyK |
≤ 1 (MyK ≤ AyK); |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
AyK |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
MyL |
≤ 1 (MyL ≤ AyL); |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
AyL |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
EK |
Y |
Y |
Y |
K |
MyK |
= |
; |
||||||||||||||||||||||||||||||||||||||||||||||||
|
K |
K |
K |
Y |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
AyK |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
E |
Y |
L |
MyL |
= |
; |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
L |
L |
Y |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
AyL |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
hLK |
M yL |
= |
K |
; |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
M yK |
L |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
d( K / L ) |
d( K / L ) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= |
( K / L ) |
= |
( K / L ) |
1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
dh |
( |
/ |
) |
d( K / L ) |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
h |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
( |
/ |
) ( K / L ) |
(1.33)
(1.34)
(1.35)
(1.36)
(1.37)
(1.38)
(1.39)
(1.40)
(1.41)
(1.42)
|
Из формул |
(1.33) – (1.36) |
следует, что |
с увеличением затрат |
|
производственного |
фактора средняя |
и предельная |
производительность для |
|
31 |

степенной производственной функции монотонно уменьшается при фиксированном значении дополнительного фактора производства. Кроме того, выполнение неравенств (1.37) и (1.38) указывает на то, что и для степенной производственной функции предельный продукт фактора меньше среднего продукта при фиксированных величинах затрат факторов.
Для степенных производственных функций эластичности выпуска продукции по факторам K и L являются соответственно постоянные параметры и . Это следует из соотношений (1.39) и (1.40).
Из соотношений (1.39) и (1.40) следует, что постоянные параметры и степенной производственной функции совпадают с соответствующими
и степенной производственной функции совпадают с соответствующими
коэффициентами эластичности выпуска продукции по факторам K и L:
EK = ;
EL = .
Для степенной производственной функции (1.21) линии постоянного уровня выпуска Y=Y0 образуют семейство изоквант, уравнение которых можно получить из (1.21), принимая, например, K как функцию L:
|
Y0 |
1 / |
||
|
K( L ) |
(1.43) |
||
|
A L |
|||
Из этого уравнения видно, что изокванты имеют асимптотами оси координат. Величина K(L), определяемая изоквантой (1.43), характеризует объём основного капитала, необходимый для получения заданного выпуска продукции Y0 в зависимости от численности занятых в производстве. Функция K(L) является монотонно убывающей функцией. Необходимо отметить, что это свойство не определяется конкретным видом производственной функции (1.21),
|
а |
присуще |
всем |
производственным |
функциям |
с |
двумя |
|
производственными факторами. |
||||||
|
Согласно соотношению (1.41) предельные нормы замещения |
||||||
|
производственных |
факторов для |
степенной |
производственной |
функции |
||
|
являются линейными |
функциями |
отношения |
объёмов производственных |
32

факторов. При пропорциональном росте объёмов производственных факторов предельная норма замещения не изменяется.
Из (1.41) получаем уравнения изоклиналей для степенной производственной функции
Следовательно, изоклинали степенной производственной функции представляют собой лучи, исходящие из начала координат.
Графики изоквант и изоклиналей степенной производственной функции в общем случае совпадают с видом изоквант и изоклиналей, представленных на рис. 1.1 – 1.3.
Величина эластичности замещения труда капиталом для степенной производственной функции, как следует из (1.42), всегда равна единице
= 1.
Это означает, что в случае степенной производственной функции при увеличении капиталовооруженности труда на 1%, предельная норма замещения труда капиталом также увеличится на 1%.
Для степенной производственной функции эластичность замещения факторов имеет особенно простую геометрическую интерпретацию: поскольку изоклинали этой производственной функции — прямые линии, то отношение
|
K/L характеризуется тангенсом угла |
наклона изоклинали (рис.1.3). Поэтому |
|||
|
величина |
показывает, на |
сколько процентов |
необходимо |
повернуть |
|
изоклиналь (то есть изменить tg |
), чтобы tg изменился на 1%. |
|||
|
Подчеркнём ещё раз, |
что в |
определении |
эластичности |
замещения |
(K, L) производная берётся вдоль изокванты, проходящей через точку (K, L). Постоянство эластичности замещения производственных факторов
многих производственных функций позволяет охарактеризовать с её помощью возможность замещения факторов в целом (а не при каком-то конкретном соотношении факторов, как это удаётся на основе предельной нормы замещения h). Чем больше величина , тем в более широких пределах производственные ресурсы могут замещать друг друга.
33

Равенство единице эластичности замещения факторов в степенных производственных функциях вне зависимости от коэффициентов A, ,  является одним из важнейших свойств производственных функций этого вида. Оно показывает, что характеристика замещения одного фактора другим при выборе степенной производственной функции задана заранее вне зависимости от желания исследователя. Это является одним из недостатков степенной производственной функции.
является одним из важнейших свойств производственных функций этого вида. Оно показывает, что характеристика замещения одного фактора другим при выборе степенной производственной функции задана заранее вне зависимости от желания исследователя. Это является одним из недостатков степенной производственной функции.
Возможность замещения одного производственного фактора другим (равенство единице эластичности замещения производственных факторов и неограниченная компенсация недостатка одних факторов другими) часто вступает в противоречие со свойствами моделируемого объекта исследования. В связи с этим в моделировании используется обобщённая производственная функция с постоянной эластичностью замещения производственных факторов, которая получила название производственной функции с постоянной эластичностью замещения факторов (функция ПЭЗ), или производственная функция CES (от англ. Constant Elasticity of Substitution). Такая производственная функция характеризуется показателем эластичности замещения производственных факторов, не равным единице. Впервые производственная функция CES была введена К. Эрроу и Р. Соллоу в 1961 г.1
Производственная функция CES имеет следующий вид:
|
Y A 1 K |
( 1 1 ) L |
(1.45) |
|||
|
. |
|||||
Вкратце отметим, что A есть параметр масштаба, обозначающий эффективность технологии; β1 – означает степень капиталоёмкости технологии и определяется в интервале 0< β1<1; > 0 – представляет степень однородности производственной функции или отдачу на масштаб производства;  -1.
-1.
Производственная функция CES удовлетворяет всем четырём свойствам
(1.1) – (1.4).
Рассмотрим вопрос о замещении факторов. Предельная норма замещения согласно (1.17) имеет вид
1Экономико-математическое моделирование : учебник для студентов вузов / под общ. ред. И. Н. Дрогобыцкого. М. : Экзамен, 2004. С. 618 – 667
34

|
1 |
||||||||
|
( 1 |
1 |
) K |
(1.46) |
|||||
|
h1 |
. |
|||||||
|
1 |
L |
|||||||
Таким образом, предельная норма замещения производственных факторов зависит от отношения факторов, причём так же, как и в случае степенных производственных функций, изоклинали являются прямыми, а при пропорциональном увеличении количеств обоих факторов предельная норма замещения не изменяется.
Можно показать, что для производственной функции CES эластичность замещения труда капиталом имеет вид
|
LK = |
1 |
. |
(1.47) |
|
|
1 |
||||
Таким образом, хотя производственная функция CES по-прежнему имеет постоянную эластичность замещения производственных факторов, эта эластичность замещения, в отличие от степенных производственных функций, не равна единице и меняется при изменении параметра от единицы (при = 0) до нуля (при → +∞).
Эластичность замещения труда капиталом LK – это мера «кривизны» изоквант (линий уровня) производственной функции. Точнее, «кривизну»
измеряет величина 1 .
|
Обратим внимание на тот факт, что при |
→ 0 все |
характеристики |
|
производственной функции CES (имеются в виду EK, EL, hLK, |
) стремятся к |
|
|
соответствующим характеристикам степенной производственной функции. |
||
|
Производственная функция CES при = 1 и |
→ -1 стремится к линейной |
|
|
производственной функции (1.20): |
Y=A*+a·K+b·L.
35

Линейная производственная функция 1 имеет нулевую «кривизну» и, соответственно, бесконечную эластичность замещения LK.
Заканчивая рассмотрение производственных функций, отметим, что степенные производственной функции используются чаще производственных функций CES, поскольку параметры степенных производственный функций оценить значительно легче и работать со степенными функциями проще. А неправдоподобность поведения степенных производственный функций в области малых количеств факторов не так уж важна, поскольку в исследованиях представляют интерес значения факторов, достаточно близкие к уже использующимся в производстве в данный момент2.
1.1.4. Методы соизмерения характеристик статических производственных функций
Несовершенство традиционных методов выбора и оценивания производственных функций сдерживает их широкое применение в
|
экономических исследованиях. |
В |
зависимости |
от выбранного |
вида |
|
производственной функции |
будут |
получены |
различные числовые |
характеристики одного и того же экономического процесса. Так, у линейной производственной функции, как показано ранее, предельная эффективность постоянная, эластичность выпуска переменная, а эластичность замещения производственных факторов равна бесконечности. В случае же степенной производственной функции эти характеристики соответственно являются переменной, постоянной и равной единице. Что касается средних эффективностей факторов, то они совпадают для всех видов производственных функций. Всё сказанное справедливо для производственных функций с постоянными параметрами.
В действительности все перечисленные числовые характеристики в результате влияния технического прогресса и неучтённых факторов являются переменными. Поэтому переменными будут и все оцениваемые параметры в производственных функциях. Поскольку производственные функции
1Замков О. О., Толстопятенко А. В., Черемных Ю. Н. Математические методы в экономике : учебник. М. : МГУ им. М.В.Ломоносова; ДИС, 1997. С. 157 – 173.
2 Лотов А. В. Введение в экономико-математическое моделирование. М. : Наука, 1984. С. 67 –
96.
36
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Производственная функция Кобба-Дугласа. Изокванты и изокосты
- Факторы производства и производственная функция
- Степенная производственная функция Кобба-Дугласа
- Изокванты – линии равного выпуска
- Изокосты – линии равной стоимости
- План производства с минимальными затратами на ресурсы
Факторы производства и производственная функция
В современном мире нам не удастся выжить, орудуя одной лишь «палкой-копалкой», верно служившей нашим далёким предкам. Стол, кресло, компьютер, одежда, посуда, – всё стало настолько сложным, что одному человеку никак не справиться, и одновременно настолько простым, что десятки тысяч этих товаров каждую секунду сходят с конвейеров по всему миру.
Чтобы произвести что-нибудь, нужны ресурсы: сырьё, материалы, оборудование, энергия, информация, деньги, труд людей.
Факторы производства – это используемые в процессе производства ресурсы.
В простейшей модели производства рассматривают два основных фактора:
- Труд (L – labor);
- Капитал (K – capital).
Результат производства – это некоторое количество Q выпущенного продукта.
Производственная функция – это зависимость количества выпущенного продукта от величины затрат факторов производства:
Q = f(K,L)
Например:
Пусть $Q = 1,5 sqrt{KL}$.
Тогда при затратах K = 100 ед. капитала и L = 16 ед. труда, будет получено $Q = 1,5 cdot sqrt{100 cdot 16} = 1,5 cdot 10 cdot 4 = 60$ ед. продукции.
Степенная производственная функция Кобба-Дугласа
Производственные функции можно строить по-разному.
Часто используется модель, в которой оба фактора – труд и капитал – входят в виде произведения степеней:
$$ Q = A cdot K^a L^{1-a} $$
где A – технологический коэффициент (зависит от применяемой технологии);
$0 le a le 1$ – коэффициент эластичности.
Такие производственные функции называют функциями Кобба-Дугласа в честь американских исследователей, которые получили:
$$ Q = 1,4 cdot K^{frac{1}{4}} L^{frac{3}{4}}$$
в 1927 году для обрабатывающей промышленности США.
Свойства производственной функции Кобба-Дугласа:
1. Если K = 0 или L = 0, то Q = 0, т.е. производство невозможно при отсутствии хотя бы одного фактора производства.
2. При увеличении затрат фактора производства, величина выпуска продукции возрастает: $K uparrow Rightarrow Q uparrow, L uparrow Rightarrow Q uparrow$
Например:
Пусть $Q = 2,5 cdot K^{frac{1}{4}} L^{frac{3}{4}}$.
Тогда при затратах K=81 ед. капитала и L=16 ед. труда, будет получено $Q = 2,5 cdot sqrt[4]{81 cdot 16^3} = 2,5 cdot 3 cdot 8 = 60$ ед. продукции.
Изокванты – линии равного выпуска
Пусть предприятие планирует выпустить $Q_0$ единиц продукции.
В этом случае, мы можем найти зависимость затрат капитала от затрат труда.
Выведем формулу:
$$ Q_0 = A cdot K^a L^{1-a} Rightarrow K^a = frac{Q_0}{A L^{1-a}} = frac{Q_0}{A} L^{a-1} Rightarrow Κ = Biggl( frac{Q_0}{A} L^{a-1}Biggr)^{1/a} $$
$$ Κ = Biggl( frac{Q_0}{A}Biggr)^{frac{1}{a}} L^{frac{a-1}{a}} $$
Эту зависимость можно изобразить на плоскости LOK в виде кривой.
Для каждого плана выпуска будет отдельная кривая.
Множество точек (L;K) на плоскости LOK, которые соответствуют одному плану выпуска, называют изоквантой или линией равного выпуска.
Например:
Пусть $Q = 2,5 cdot K^{frac{1}{4}} L^{frac{3}{4}}$.
Построим изокванты для $Q_0 = {25;50;75;100 }$ единиц готовой продукции.
$$ a = frac{1}{4}, frac{1}{a} = 4, frac{a-1}{a} = -3, frac{Q_0}{A} = frac{Q_0}{2,5} = 0,4 Q_0, Κ = frac{(0,4Q_0 )^4}{L^3} $$

Свойства изоквант
1. Чем больше используется труда, тем меньше нужно капитала для производства заданного количества продукции. И наоборот: чем меньше труда, тем больше капитала. Труд и капитал взаимно заменяют друг друга.
2. Через каждую точку (L;K) проходит единственная изокванта.
3. Изокванты, соответствующие разным количествам продукции $Q_1 neq Q_2$, не пересекаются.
Изокосты – линии равной стоимости
Согласно полученному выше графику, произвести $Q_0$ = 100 единиц продукции можно потратить 50 единиц труда и 20 единиц капитала, или же по 40 единиц труда и капитала, или же множество других сочетаний L и K.
Как нам определить, какое из сочетаний будет самым удачным? Очевидно, исходя из цены каждого ресурса. Пусть r – цена единицы капитала, а w – цена единицы труда. Тогда для некоторого набора ресурсов (L,K ), их общая стоимость:
C = rK+wL
В этом случае:
$$ K = – frac{w}{r} L+ frac{C}{r} $$
На плоскости LOK это будет прямая с угловым коэффициентом $k = -frac{w}{r}$.
Множество точек (L;K) на плоскости LOK, которые соответствуют одной величине затрат на ресурсы (бюджету), называют изокостой или линией равной стоимости.
Например:
Пусть цена ресурсов r = 5, w = 3.
Построим изокосты для общей суммы затрат C = {200;250;300;350}
$$ frac{w}{r} = frac{3}{5} = 0,6, frac{C}{r} = frac{C}{5} = 0,2C, K = -0,6L+0,2C $$

Свойства изокост
1. Угловой коэффициент изокосты равен отношению цен на ресурсы $k = -frac{w}{r}$.
2. Изокоста для данного бюджета затрат C проходит через точки $(frac{C}{w},0)$ и $(0;frac{C}{r})$.
3. Для заданных цен на ресурсы изокосты для $C_1 neq C_2$ являются параллельными прямыми.
План производства с минимальными затратами на ресурсы
Теперь поставим главную задачу:
При заданном плане производства $Q_0$, известных ценах на ресурсы r и w, найти такое сочетание труда L и капитала K, при котором затраты на эти ресурсы минимальны:
$$ {left{ begin{array}{c} Q_0 = A cdot K^a L^{1-a} \ C = wL+rK rightarrow min end{array} right.} $$
При заданном плане производства $Q_0$, известных ценах на ресурсы r и w, затраты на ресурсы будут минимальными в точке $(L_0,K_0)$, в которой изокоста $C_0 (L_0,K_0)$ является касательной для изокванты $Q_0 (K,L)$, т.е. имеет с ней только одну общую точку.
Величина затрат для оптимальной изокванты:
$$ C_0 = frac{Q_0}{A} cdot left(frac{w}{1-a}right)^{1-a} cdot left(frac{r}{a}right)^a $$
Оптимальный объем ресурсов:
$$ L_0 = frac{C_0}{left(frac{w}{1-a}right)}, K_0 = frac{C_0}{left(frac{r}{a}right)}$$
Например:
Пусть $Q = 2,5 cdot K^frac{1}{4} L^frac{3}{4}$. План выпуска продукции $Q_0 = 100$ единиц.
Цена ресурсов r = 5, w = 3.
Найти оптимальное отношение труда к капиталу $frac{L_0}{K_0}$, при котором затраты на ресурсы будут минимальными.
Оптимальный бюджет:
$$ C_0 = frac{100}{2,5}left(frac{3}{3/4}right)^{frac{3}{4}}left(frac{5}{1/4}right)^{frac{1}{4}} = 40 cdot 4^{frac{3}{4}} cdot 20^{frac{1}{4}} = 40 cdot sqrt[4]{64 cdot 20} = 40 sqrt[4]{2^6 cdot 5 cdot 2^2} = $$
$$ = 40 cdot 2^2 cdot sqrt[4]{5} = 160 sqrt[4]{5} $$
Оптимальный объем ресурсов:
$$ L_0 = frac{160 sqrt[4]{5}}{left(frac{3}{3/4}right)} = 40 sqrt[4]{5}, K_0 = frac{160 sqrt[4]{5}}{left(frac{5}{1/4}right)} = 8 sqrt[4]{5} $$
Искомое отношение:
$$ frac{L_0}{K_0} = frac{40 sqrt[4]{5}}{8 sqrt[4]{5}} = 5 $$
Объем труда в 5 раз больше объема капитала при оптимальных затратах.
В плоскости LOK:
$$ Κ = frac{(0,4Q_0 )^4}{L^3} = frac{40^4}{L^3}, K = -0,6L+0,2C = -0,6L+32 sqrt[4]{5} $$

Таким образом, точка $(40 sqrt[4]{5};8 sqrt[4]{5})$ является точкой касания изокосты с минимальным бюджетом затрат $C_0 = 160 sqrt[4]{5}$ и изокванты с планом выпуска $Q_0 = 100$.

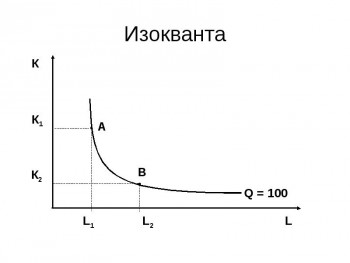
График изокванты, где объём выпуска Q3 > Q2 > Q1. Обычно под факторами производства X и Y понимают труд и капитал соответственно. Требуется больше фактора X, фактора Y или обоих факторов, чтобы перейти от изокванты Q1 к Q2, или от Q2 к Q3
Изокванта — это кривая равного выпуска продукта (кривая безразличия для производителей). Все точки на этой кривой показывают различное сочетание факторов производства для выпуска одинакового количества продукции.[1]
В теории производственных функций изокванта — это геометрическое место точек в пространстве ресурсов, в которых различные сочетания производственных ресурсов дают одно и то же количество выпускаемой продукции[2].
Свойства изоквант[править | править код]
- Изокванты не могут пересекаться.
- Каждая следующая изокванта, проходящая дальше от начала координат, отражает бо́льшую величину выпуска, чем предыдущая. Совокупность этих изоквант образует карту изоквант.
- Изокванты имеют отрицательный наклон.
- Предельная норма технического замещения MRTS одного ресурса другим уменьшается при движении вдоль изокванты.
- Изокванты выпуклы по отношению к началу координат.
Пример[править | править код]
Фермер может произвести 50 т зерна, используя пять комбайнов и труд пяти работников или четыре комбайна и труд 10 работников. Изокванта имеет нисходящий наклон вправо, что отражает возможность заменять один фактор производства на другой. Изокванта изогнута относительно начала координат, поскольку факторы не являются абсолютными субститутами, хотя и взаимозаменяемы. Таким образом, предельная норма технического замещения одного фактора другим снижается по мере продвижения по кривой вниз слева направо. Изокванта схожа с кривой безразличия. Точка касания изокосты и изокванты показывает такое сочетание факторов, при котором данное количество продукции будет произведено с наименьшими затратами.[3]
Виды изоквант[править | править код]
Графическое отображение изоквант определяется сочетанием взаимозаменяемости и взаимодополняемости ресурсов, используемых при производстве.
В случае жёсткой взаимозаменяемости ресурсов (совершенной субституции), изокванта принимает линейный вид. В случае жёсткой взаимодополняемости ресурсов (комплементарности), изокванта сводится к точке.[4]
См. также[править | править код]
- Кривая безразличия
- Изокоста
Примечания[править | править код]
- ↑ Вадейко Е. И. 350 терминов и понятий рыночной экономики: Справочное учебное пособие, издательство МГУ, 2005 г. Дата обращения: 13 июня 2013. Архивировано 4 марта 2016 года.
- ↑ Бизнес-словарь, 2001 г. Дата обращения: 13 июня 2013. Архивировано 5 марта 2016 года.
- ↑ Новый англо-русский словарь-справочник. Экономика. О. В. Сиполс. — М. Флинта, Наукa 712 с. Дата обращения: 13 июня 2013. Архивировано 5 марта 2016 года.
- ↑ Экзамен | Сайт для учёбы. 39. Изокванта. Карта изоквант
Нина Афонина
Эксперт по предмету «Микро-, макроэкономика»
преподавательский стаж — 4 года
Задать вопрос автору статьи
Сущность понятий «изокванта» и «изокоста» продукта
Определение 1
Изокванта продукта – это кривая, отражающая сочетания факторов производства, используемых в создании определенного объема конечного продукта.
Изокванта часто именуется линией равного выпуска.
Функциональная роль изокванты в производственном процессе сводится к выполнению той же роли, что и кривых безразличия в потреблении, поэтому они имеют сходство в следующих аспектах:
- отрицательный наклон кривых и изокванты;
- наличие определенных пропорций в замещении факторов;
- отсутствие точек пересечения кривых;
- чем дальше расположены изокванта и кривая безразличия от начала координат, тем больший результат производства подлежит фиксации.
Графическое представление изокванты имеет следующий вид:
Рисунок 1. Изокванта. Автор24 — интернет-биржа студенческих работ
Вогнутый характер изокванты иллюстрирует эластичность замещения факторов при выпуске заданного объема продукта и фиксирует то, насколько легко возможна замена факторов производства. Если изокванта приобретает вид прямого угла, то вероятность замещения одного фактора другим крайне низкая. Когда она имеет вид прямой линии с наклоном вниз, то это свидетельствует о высокой степени вероятности замены одного фактора другим. По сути, изокванта отражает замену одного фактора производства другим или замену определенной доли фактора производства. Тогда как, кривая безразличия выступает отражением замены благ потребителями.
« Изокванта, изокоста. Равновесие производителя»
При этом выпуклость изокванты в сторону начала координат является постоянной, поскольку полная взаимозаменяемости факторов производства не может быть реализована.
Изокванты бывают различных видов:
- линейная изокванта – отражает полноценное замещение факторов производства;
- изокванта в форме угла – отражает жесткую дополняемость ресурсов, носящую обязательный характер (невозможно реализовать производственный процесс без нее);
- изокванта в виде ломаной кривой – отражает ограниченную возможность замещения ресурсов, т. е. ресурсы могут взаимозаменяться в лимитированном количестве;
- изокванта в виде гладкой кривой – отражает общие случаи взаимодействия факторов производства.
Изокванта смещается в то или иное положение в случаях увеличения ресурсов хозяйствующего субъекта и при изменении технологий производства. Наклон изокванты приобретает иной вид при данных обстоятельствах и отражает предельную норму технического замещения одного фактора другим (МRТS). Эта норма отражает величину снижения объемов потребления того или иного фактора производства за счет применения дополнительных единиц другого фактора /факторов и сохранения объемов производства на том же уровне. Расчет предельной нормы технического замещения факторов производства реализуется по формуле:
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
Определение 2
Изокоста – это линия, отражающая сочетания производственных факторов, которые могут быть приобретены за определенную денежную сумму.
Изокоста является отражением равных издержек. Графически изокосты представляются в виде параллельных прямых. Это демонстрирует возможности приобретения фирмой бесконечного количества сочетаний факторов производства в пределах имеющегося денежного лимита.
При построении графика изокоста может иметь точку пересечения с изоквантой. Каждая точка на линии изокосты характеризуется одними и теми же общими издержками. Точка пересечения изокванты и изокосты отражает оптимальную позицию фирмы. При этом изокванта не пересекает изокосту, а только касается ее. Данная точка отражает оптимальную комбинацию факторов производства, гарантирующую минимизацию производственных издержек, которые требуется понести при создании определенного вида и объема продукции.
Рисунок 3. Изокоста и изокванта. Автор24 — интернет-биржа студенческих работ
С изокостой и изоквантой связано достижение равновесия производителя.
Равновесие производителя
Определение 3
Равновесие производителя – это состояние производственного процесса, при котором использование факторов производства обеспечивает получение максимального объема выпуска при минимальных затратах.
Графическое представление равновесного состояния производителя имеет вид изокванты, занимающей самую отдаленную позицию от начала координат и касается изокосты – прямой линии, отражающей сочетание, применяемых факторов производства. Получается, что точка касания изокванты и изокосты и является отражением равновесия производителя. В ней отражается максимальный объем выпуска, который может быть достигнут при минимальных затратах.
Графическое представление равновесия производителя имеет вид:
Рисунок 4. Равновесие производителя. Автор24 — интернет-биржа студенческих работ
Данный график отражает наименьшую отдачу от факторов производства изоквантой, расположенной ближе к началу координат, т. е. использование данного сочетания факторов производства позволяет производить незначительный объем продукции. Изокванты, расположенные выше и правее изокванты Q2, предполагают прирост факторов производства, который невозможен в силу лимита финансовых ресурсов производителя. В точке касания изокванты и изокосты – Е отражается оптимальное сочетание факторов производства, обеспечивающее получение максимального объема выпуска.
При этом, возникает такая ситуация, как эффект масштаба. Он отражает отдачу от производства, связанную с изменением стоимости единицы продукции в зависимости от масштабов ее производства фирмой. Данный эффект актуален для долгосрочного периода. В это время фирмы ориентируются на расширение производства. Путем снижения затрат на единицу достигается укрупнение производства. Реализуется политика экономии на масштабе: производство больше – затрат меньше. Эффект масштаба может быть:
- Положительным. Происходит рост объемов выпуска в больших пропорциях, чем рост затрат, которые фирма несет на его реализацию, т. е. чем потребление факторов производства.
- Стабильным. Такой эффект связан с изменением объема выпуска в равных долях с изменением величины издержек – факторов производства.
- Отрицательным. Он отражает рост объемов производства в меньших объемах, чем рост производственных затрат, т. е. рост потребления факторов производства превышает прирост объема выпуска продукции.
Возникновение эффекта масштаба связано с:
- переменным характером факторов производства, что не позволяет реализовать закон убывающей отдачи;
- стабильностью соотношения факторов производства.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Добавлено в закладки: 0
Что такое изокванта? Описание и определение понятия.
Изокванта – это график, который являет собой кривую, которая показывает разные комбинации затрат при постоянном объёме производства продукта. Другое наименование изоквант – характерные линии равного выпуска или кривые равного продукта. Эти графики дают возможность понять, как получить наибольшую выгоду при сбережении объёмов производства при помощи комбинирования нескольких типов затрат. При этом рассматривают различные уровни самих издержек. Позитивный наклон изокванты свидетельствует о прямой связи меж увеличением разных издержек. Негативный же говорит, что при снижении одного затратного фактора будет неизбежно увеличен другой.
Изокванта — это кривая равного выпуска продукта (кривая безразличиая для производителей). Все точки на данной кривой указывают различное сочетание факторов производства для выпуска одинакового числа продукции.
 В теории производственных функций изокванта — это геометрическое место точек в пространстве ресурсов, в которых разные сочетания производственных ресурсов дают одинаковое число выпускаемой продукции.
В теории производственных функций изокванта — это геометрическое место точек в пространстве ресурсов, в которых разные сочетания производственных ресурсов дают одинаковое число выпускаемой продукции.
Характеритсики изоквант
- Изокванты не могут пересекаться.
- Каждая следующая изокванта, которая проходит дальше от начала координат, отражает бо́льшую величину выпуска, нежели предыдущая. Совокупность данных изоквант образует карту изоквант.
- Изокванты имеют негативный наклон.
- Граничная норма технического замещения MRTS одного ресурса другим снижается при передвижении вдоль изокванты.
- Изокванты выпуклы в отношении к началу координат.
Пример
Фермер может произвести 50 тонн зерна, применяя пять комбайно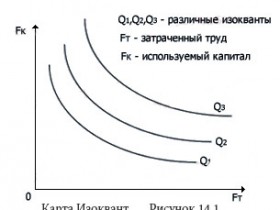 в и труд пяти сотрудников или труд 10 работников и четыре комбайна. Изокванта имеет нисходящий правый наклон, что показывает на возможность заменять один фактор производства на другой. Изокванта изогнута в отношении начала координат, так как факторы не являются абсолютными субститутами, хотя и являются взаимозаменяемыми. Таким образом, граничная норма технического замещения одного фактора другим уменьшается по мере продвижения по кривой слева направо вниз. Изокванта похожа на кривую безразличия. Точка касания изокванты и изокосты показывает такое сочетание факторов, при котором данное число продукции произведут с минимальными затратами.
в и труд пяти сотрудников или труд 10 работников и четыре комбайна. Изокванта имеет нисходящий правый наклон, что показывает на возможность заменять один фактор производства на другой. Изокванта изогнута в отношении начала координат, так как факторы не являются абсолютными субститутами, хотя и являются взаимозаменяемыми. Таким образом, граничная норма технического замещения одного фактора другим уменьшается по мере продвижения по кривой слева направо вниз. Изокванта похожа на кривую безразличия. Точка касания изокванты и изокосты показывает такое сочетание факторов, при котором данное число продукции произведут с минимальными затратами.
Типы изоквант
Графическое отображение изоквант определяет сочетание взаимодополняемости и взаимозаменяемости ресурсов, которые используются при производстве.
При жёсткой взаимозаменяемости ресурсов (совершенной субституции), изокванта имеет линейный вид. При жёсткой взаимодополняемости ресурсов (комплементарности), изокванта является точкой.
Рассмотрим, более детально, что значит изокванта.
Для простоты анализа будем полагать, , как и прежде, что:
- технология производства в течение полного рассматриваемого периода не изменяется
- факторы производства в определенных границах будут взаимозаменяемыми
- исследуемая функция изготовления связана с двумя факторами: трудом и капиталом и является частным случаем функции Кобба-Дугласа
Есть несколько комбинаций капитала и труда, которые обеспечивают в определенных границах заданный объем выпуска. К примеру, возможно получить, применяя комбинацию (1,4), (4,1) и (2,2).
Если отложить по горизонтальной оси количество единиц труда, а по вертикальной — количество единиц капитала, затем обозначить точки, в которых фирма выпускает один и тот же объем, то получится кривая, которая называется изоквантой.
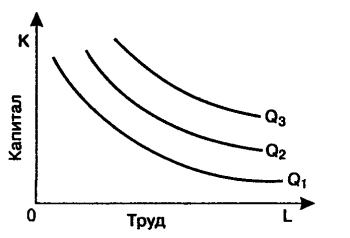 Каждая точка изокванты отвечает комбинации ресурсов, при которой компания производит заданный объем продукции.
Каждая точка изокванты отвечает комбинации ресурсов, при которой компания производит заданный объем продукции.
Набор изоквант, который характеризет эту производственную функцию, карта изоквант.
Характеристики стандартных изоквант тождественны характеристикам кривых безразличия:
- Изокванта, равно, как и кривая безразличия, непрерывная функция, а не набор дискретных точек.
- Для каждого заданного объема выпуска можно провести свою изокванту, отражающую разные комбинации экономических ресурсов, которые обеспечивают производителю один и тот же объем производства (изокванты, которые описывают эту производственную функцию, не пересекаются никогда).
- У изоквант нет участков возрастания (Если бы существовал участок возрастания, то при передвижении вдоль него увеличивалось бы число как первого, так и второго ресурса).
Граничная норма технологического замещения
Граничная норма технологического замещения одного ресурса на другой (к примеру, труда на капитал) указывает на степень замещения капиталом труда, при котором остается неизменным объем выпуска.
Алгебраическое выражение, которое показывает степень, в которой производитель выражает готовность уменьшить количество капитала в обмен на увеличение труда, которая достаточна для сбережения прежнего объема выпуска указывает на то, что объем производства неизменен. Это значит, что уменьшение выпуска в итоге уменьшения затрат капитала компенсируется тем, что увеличивается выпуск за счет применения добавочного количества труда.
Уменьшение выпуска в итоге уменьшения затрат капитала равняется произведению на граничный продукт капитала. Увеличение выпуска благодаря использованию добавочного числа труда в свою очередь равняется произведению на предельный продукт труда.
Производственная функция, которая связывает меж собой количество труда, капитала и объем выпуска, дает возможность рассчитать также граничную норму технологического замещения через производную этой функции: .
Это означает, что в любой точке изокванты графически предельная степень технологического замещения равняется тангенсу угла наклона касательной к изокванте в данной точке.
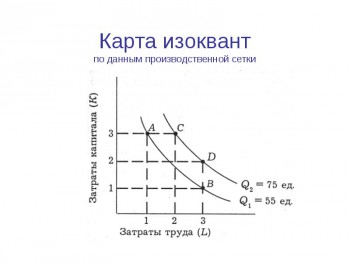 Очевидно, что степень замещения труда капиталом не остается постоянной при движении вдоль изокванты. При перемещении вниз по кривой абсолютное значение MRTS труда капиталом убывает, так как все большее количество труда приходится использовать, чтобы компенсировать снижение затрат капитала (Так, в приведенном выше примере при L=1 MRTS=-10, а при L=10 MRTS=-0.1.)
Очевидно, что степень замещения труда капиталом не остается постоянной при движении вдоль изокванты. При перемещении вниз по кривой абсолютное значение MRTS труда капиталом убывает, так как все большее количество труда приходится использовать, чтобы компенсировать снижение затрат капитала (Так, в приведенном выше примере при L=1 MRTS=-10, а при L=10 MRTS=-0.1.)
В дальнейшем MRTS достигает своего предела (MRTS=0), а изокванта приобретает горизонтальный вид. Очевидно, что дальнейшее снижение затрат капитала приведет лишь к сокращению объемов выпуска. Количество капитала в точке Е — минимально допустимое для данного объема производства (аналогичным образом минимально допустимое для производства данного объема количество труда имеет место в точке А).
Убывание MRTS одного ресурса другим является характерным для большей части производственных процессов и характерно для всех изоквант стандартного типа.
Особенные случаи производственной функции (изокванты нестандартного типа)
Абсолютная взаимозаменяемость ресурсов. Когда ресурсы, применяемые в процессе изготовления, являются полностью заменяемыми, то стабильна во всех точках изокванты. Пример такого производства — производство, которое допускает, как полную автоматизацию, так и ручное изготовление какого-нибудь продукта).
Фиксированная структура применения ресурсов. Когда технологический процесс исключает замещение факторов и требует применение обоих ресурсов в фиксированных строго пропорциях, производственная функция имеет тип латинской буквы
Пример подобного типа — это работа землекопа (один человек и одна лопата). Увеличение одного из факторов без необходимого изменения числа другого фактора нерационально, потому технически эффективными будут только угловые комбинации ресурсов (угловая точка — точка, где пересекаются соответствующие вертикальная и горизонтальная линии).
Мы коротко рассмотрели изокванту, ее характеристики, нахождение MRTS. Оставляйте свои комментарии или дополнения к материалу.





