Как найти производную комплексных чисел – Сайт, где вы сможете решить свои вопросы

Дифференцирование функций комплексного переменного

Правила дифференцирования

Так как производная функции комплексного переменного определяется, как и в действительной области, т.е. в виде предела $f'(z_0)= lim_{Delta zto0}frac{Delta f(z_0)}{Delta z}$ , то, используя это определение и свойства пределов, несложно убедиться в справедливости правил дифференцирования, известных из математического анализа. А именно имеет место следующее утверждение.

Утверждение 2.5

1. Сумма, произведение функций, дифференцируемых в точке, есть функция, дифференцируемая в этой точке, и справедливы равенства:

$begin{aligned}bigl(f_1(z)+f_2(z)bigr)'&= f'_1(z)+ f'_2(z),\ bigl(f_1(z)cdot f_2(z)bigr)'&= f'_1(z)cdot f_2(z)+ f_1(z)cdot f'_2(z). end{aligned}$

Из этого свойства и очевидного равенства c'=0~(c=text{const}) следует

$left(sum_{k=1}^{n}c_kf_k(z)right)'= sum_{k=1}^{n}bigl(c_kcdot f'_k(z)bigr).$

2. Частное функций, дифференцируемых в точке, есть функция, дифференцируемая в этой точке, при условии, что знаменатель в точке не равен нулю:

$left(frac{f_1(z)}{f_2(z)}right)'= frac{f'_1(z)cdot f_2(z)-f_1(z)cdot f'_2(z)}{f_2^2(z)},.$

3. Сложная функция комплексного переменного f(varphi(z)) дифференцируема в точке z_0 , если в этой точке дифференцируема функция , а функция f(u) дифференцируема в точке u_0 , где u_0=varphi(z_0) и u=varphi(z) . При этом в точке z_0 имеет место формула

bigl(f(varphi(z))bigr)'= f'(varphi(z))cdot varphi'(z).

▼ Примеры 2.29-2.31

Пример 2.29. Доказать дифференцируемость во всей плоскости функций: a) w=z ; б) w=z^n . Найти их производные.

Решение

а) По определению производной для любой точки zin mathbb{C} записываем $lim_{Delta zto0}frac{(z+Delta z)-z}{Delta z}=1$ ; предел существует для любой точки zinmathbb{C} и z'=1 .

б) Для любой точки $z_0inmathbb{C}$ и любого приращения Delta z рассмотрим

$lim_{Delta zto0}frac{Delta w}{Delta z}= lim_{Delta zto0}frac{(z_0+Delta z)^n-z_0^n}{Delta z},.$

Выражение (z_0+Delta z)^n раскрываем по формуле бинома Ньютона:

$(z_0+Delta z)^n= z_0^n+ ncdot z_0^{n-1}+ frac{n(n-1)}{2!}cdot (Delta z)^2cdot z_0^{n-2}+ ldots+ (Delta z)^n,$

в результате получаем

$begin{aligned}lim_{Delta zto0}frac{(z_0+Delta z)^n-z_0^n}{Delta z}&= lim_{Delta zto0}frac{Delta z left(nz_0^{n-1}+ frac{n(n-1)}{2!}Delta zcdot z_0^{n-2}+ ldots+ (Delta z)^{n-1}right)}{Delta z }=\ &=lim_{Delta zto0}! left(nz_0^{n-1}+ frac{n(n-1)}{2!}Delta zcdot z_0^{n-2}+ ldots+ (Delta z)^{n-1}right)= nz_0^{n-1}.end{aligned}$

Предел существует, следовательно, функция дифференцируема в точке z_0 . Так как z_0 — произвольная точка плоскости, то доказана дифференцируемость z^n ( — натуральное) при любом и получена формула $(z^n)'=nz^{n-1}$ .

Пример 2.30. Исследовать дифференцируемость функций комплексного переменного:

а) P_n(z) — многочлен степени ; б) R(z) — рациональная функция.

Решение

а) Дифференцируемость многочлена в любой точке zin mathbb{C} следует из дифференцируемости функции z^n (пример 2.29) и п. 1 утверждения 2.5.

б) Дифференцируемость рациональной функции $R(z)=frac{P_n(z)}{Q_n(z)}$ отношения двух многочленов в любой точке из области определения, т.е. за исключением нулей знаменателя, получается из результата п. “а” и п. 2 утверждения 2.5.

Пример 2.31. Найти модуль и аргумент производной f'(z) в точке z_0 , если

а) f(z)=2iz-3i ; б) $f(z)=frac{z-4i}{z+2i},~z_0=1-i$ ; в) f(z)=z^2 .

Решение

а) Используя правила дифференцирования, находим f'(z)=2i . Поэтому f'(z_0)=2i для любой точки z_0 и $|f'(z_0)|=2,~ arg f'(z_0)= frac{pi}{2}$ .

б) Используя правила дифференцирования частного, находим

$f'(z)= frac{z+2i-(z-4i)}{(z+2i)^2}= frac{6i}{(z+2i)^2},quad f'(z_0)= frac{6i}{(z_0+2i)^2}= f'(1-i)= frac{6i}{(1+i)^2}= frac{6i}{2i}=3.$

Поэтому в результате имеем |f'(1-i)|=3,~ arg f'(1-i)=0 .

в) Используя результат примера 2.29, находим (z^2)'=2z , поэтому f'(z_0)= 2z_0 и |f'(z_0)|=2|z_0|,~ arg f'(z_0)= 2arg z_0 .

Условия Коши-Римана дифференцируемости функции

Очевидно, между свойствами дифференцируемости функции комплексного переменного как функции точки плоскости и дифференцируемостью ее действительной и мнимой частей как функций двух действительных переменных существует тесная связь.

Утверждение 2.6

1. Если функция f(z) дифференцируема в точке, то в этой точке существуют частные производные ее действительной u(x,y) и мнимой v(x,y) частей и выполняются условия Коши-Римана:

$begin{cases}dfrac{partial u}{partial x}= dfrac{partial v}{partial y},\[9pt] dfrac{partial u}{partial y}= -dfrac{partial v}{partial x}.end{cases}$

(2.19)

2. Если u(x,y) и v(x,y) дифференцируемы в точке (x_0,y_0) и в этой точке выполняются условия (2.19), то функция f(z)=u+iv дифференцируема в точке z_0=x_0+iy_0 .

3. Производная дифференцируемой функции может быть записана по одной из формул:

$begin{array}{ll}f'(z)=dfrac{partial u}{partial x}+ i,dfrac{partial v}{partial x},&quad f'(z)= dfrac{partial v}{partial y}- i,dfrac{partial u}{partial y},\[10pt] f'(z)=dfrac{partial u}{partial x}- i,dfrac{partial u}{partial y},&quad f'(z)= dfrac{partial v}{partial y}+ i,dfrac{partial v}{partial x}. end{array}$

(2.20)

Доказательство этих утверждений не представляет трудностей и опирается только на определения дифференцируемости функций f(z),~ u(x,y),~ v(x,y) .

Анализ утверждения 2.6 позволяет сделать следующие полезные для исследования функций на дифференцируемость замечания.

Замечания 2.7

1. Выполнение условий (2.19) является необходимым условием дифференцируемости функции f(z) в точке. Следовательно, их невыполнения достаточно для утверждения о том, что функция не является дифференцируемой в соответствующей точке.

2. Условия (2.19) не являются достаточными. Согласно п.2 утверждения 2.6 в соответствующей точке должны быть дифференцируемы функции u(x,y) и v(x,y) . Напомним, что условием дифференцируемости функции двух действительных переменных в точке является существование и непрерывность частных производных в этой точке.

Из утверждения 2.6 и замечаний 2.7 следует правило исследования функции на дифференцируемость.

Правило 2.1. Для исследования функции на дифференцируемость и нахождения ее производной следует выполнить следующие операции.

1. Для заданной функции f(z) найти действительную и мнимую части:

u=operatorname{Re}f(z),quad v=operatorname{Im}f(z),qquad u=u(x,y),quad v=v(x,y).

2. Найти частные производные функций u(x,y),~v(x,y) .

3. Проверить выполнение условий Коши-Римана. Точки, в которых эти условия не выполняются, являются точками, где функция не дифференцируема. Точки, в которых условия (2.19) выполняются и частные производные являются непрерывными, принадлежат области, где функция дифференцируема.

4. Записать выражение производной в точках дифференцируемости по одной из формул (2.20).

▼ Примеры 2.32-2.34

Пример 2.32. Исследовать на дифференцируемость функцию f(z)= sqrt{|xcdot y|} .

Решение

Для решения выделим два случая.

Первый случай. Рассмотрим произвольную точку zne0 . Исследование проводим по правилу 2.1.

1. По условию u(x,y)=sqrt{|x|}cdotsqrt{|y|},~ v(x,y)equiv0 .

2. Очевидно, $dfrac{partial v}{partial x}=0,~ dfrac{partial v}{partial y}=0$ для любой точки. Находим частные производные функции u(x,y) . Для нахождения $dfrac{partial u}{partial x}$ положим y=text{const} и, учитывая определение модуля, рассмотрим два случая: x>0 (тогда |x|=x ) и x<0 (тогда |x|=-x ). Получаем

$dfrac{partial u}{partial x}= sqrt{|y|}cdot frac{1}{2sqrt{x}}$ при x>0 и $dfrac{partial u}{partial x}= sqrt{|y|}cdot frac{-1}{2sqrt{-x}}$ при x<0 .

Аналогично при любом x=text{const} имеем

$dfrac{partial u}{partial y}= sqrt{|x|}cdot frac{1}{2sqrt{y}}$ при y>0 и $dfrac{partial u}{partial y}= sqrt{|x|}cdot frac{-1}{2sqrt{-y}}$ при y<0 .

3. Проверяем условие (2.19). Условие $dfrac{partial u}{partial x}= dfrac{partial v}{partial y}$ выполняется в точках прямой y=0 при любом xne0 . Условие $dfrac{partial u}{partial y}=-dfrac{partial v}{partial x}$ выполняется в точках прямой x=0 при любом yne0 . Вместе эти условия не выполняются ни в одной точке. Согласно п.2 замечаний 2.7 функция не является дифференцируемой.

Второй случай. Рассмотрим точку z=0 .

1,2. Найдем частные производные функции u=sqrt{|xcdot y|} в точке M_0(0;0) , используя определение:

$left.{dfrac{partial u}{partial x}}right|_{M_0}= lim_{Delta xto0} frac{u(Delta x,0)-u(0;0)}{Delta x}= lim_{xto0} frac{u(x,0)-u(0;0)}{x}= 0$ , так как u(x,0)=0 при любом .

Аналогично $left.{dfrac{partial u}{partial y}}right|_{M_0}= 0$ , так как v(x,y)=0 , то $dfrac{partial v}{partial x}=0$ и $dfrac{partial v}{partial y}=0$ .

3. Условие Коши-Римана (2.19) в точке M_0 (то есть z=0 ) выполняется.

Согласно п.2 замечаний 2.7 следует проверить дифференцируемость функций u(x,y),~ v(x,y) в точке M_0 . Это можно сделать, установив непрерывность частных производных в точке z=0 , для чего следует рассмотреть пределы всех найденных в п. “а” производных при zto 0 , то есть xto0,~ yto0 .

В данном случае удобнее проверить дифференцируемость f(z) в точке z=0 по определению производной. В точке z_0=0 рассмотрим произвольное приращение Delta z и составим приращение функции Delta f(0)= f(Delta z)-f(0)= f(Delta z) . Далее записываем предел

$lim_{Delta zto 0}frac{Delta f(0)}{Delta z}= lim_{Delta zto 0}frac{f(Delta z)}{Delta z}= lim_{zto0}frac{f(z)}{z}= lim_{zto0}frac{sqrt{|xcdot y|}}{x+iy},.$

Производная в точке z=0 существует, если этот предел имеет одно и то же значение при любом стремлении к 0, при этом нельзя ограничиться никаким специальным классом путей.

Выберем сначала в качестве пути простейший — прямую y=kx или в комплексной форме z=x(1+ki) . Тогда выражение для предела принимает вид

$lim_{zto0}frac{sqrt{kx^2}}{x(1+ik)}= lim_{zto0}frac{|x|cdot sqrt{|k|}}{x(1+ik)},,$

из чего следует, что значение предела зависит от , от наклона прямой — т.е. от выбранного пути. В частности, при k=1 , т.е. для прямой y=x , можно записать

$lim_{Delta zto0}frac{Delta f(0)}{Delta z}= lim_{xto0}frac{sqrt{x^2}}{x(1+i)}= lim_{xto0} frac{|x|}{x(1+i)},$

поэтому

при $x>0~~ lim_{Delta zto0} frac{Delta f(0)}{Delta z}= frac{1}{1+i}$ , а при $x<0~~ lim_{Delta zto0} frac{Delta f(0)}{Delta z}= -frac{1}{1+i}$ .

По определению $lim_{Delta zto0} frac{Delta f(0)}{Delta z}$ не существует и функция f(z)= sqrt{|xcdot y|} не дифференцируема в точке z=0 .

Объединяя результаты пунктов “а” и “б” , получаем окончательный ответ: данная функция не дифференцируема всюду.

Пример 2.33. Исследовать на дифференцируемость функции: а) f(z)=|z|^2 ; б) f(z)=overline{z} .

Решение

а) Найдем решение, используя правило 2.1.

1. Находим $u=operatorname{Re}f(z),~ v=operatorname{Im}f(z),~ u=x^2+y^2,~ v=0$ .

2. Определяем частные производные: $frac{partial u}{partial x}=2x,~ frac{partial u}{partial y}=2y,~ frac{partial v}{partial x}= 0,~ frac{partial v}{partial y}= 0$ .

3. Условия Коши-Римана (2.19) выполняются только в точке z=0 , где x=0 и y=0 . Непрерывность частных производных очевидна. Следовательно, функция f(z)=|z|^2 дифференцируема только в одной точке z=0 .

б) Найдем решение, используя также правило 2.1.

1. Находим operatorname{Re}overline{z} и operatorname{Im} overline{z} , то есть u=x и v=-y .

2,3. Условия (2.19) не выполняются ни в одной точке, так как $frac{partial u}{partial x}=1,~ frac{partial v}{partial y}=-1$ . Следовательно, функция не дифференцируема всюду.

Пример 2.34. Исследовать на дифференцируемость функцию e^z . Найти производную.

Решение

1. Из равенства e^z=e^x(cos y+isin y) находим u=e^xcos y,~ v=e^xsin y .

2. Находим частные производные:

$frac{partial u}{partial x}= e^xcos y,quad frac{partial u}{partial y}= -e^xsin y,quad frac{partial v}{partial x}= e^xsin y,quad frac{partial v}{partial y}= e^xcos y.$

3. Условия (2.19) выполняются в любой точке zinmathbb{C} , и частные производные, очевидно, непрерывны всюду. Поэтому функция e^z дифференцируема всюду в .

4. Надо полагать, что (e^z)'=e^z . Действительно, записываем производную По формуле (2.20), используя найденные частные производные

$f'(z)= frac{partial u}{partial x}+ i,frac{partial v}{partial x}= e^x(cos y+isin y)= e^xcdot e^{iy}=e^z.$

Условия Коши-Римана в полярных координатах

Пример 2.35. Записать условия Коши-Римана в полярных координатах.

Решение. Пусть f(z)= u(x,y)+iv(x,y) дифференцируема в точке и $z=r,e^{ivarphi}$ . Находим частные производные сложных функций u=u(x,y),~ v=v(x,y) , где $begin{cases}x=rcosvarphi,\ y=rsinvarphi, end{cases}$

$begin{aligned}dfrac{partial u}{partial r}&= dfrac{partial u}{partial x}cdot dfrac{partial x}{partial r}+ dfrac{partial u}{partial y}cdot dfrac{partial y}{partial r}= dfrac{partial u}{partial x}cdot cosvarphi+ dfrac{partial u}{partial y}cdot sinvarphi,;\[5pt] dfrac{partial u}{partial varphi}&= dfrac{partial u}{partial x}cdot dfrac{partial x}{partial varphi}+ dfrac{partial u}{partial y}cdot dfrac{partial u}{partial varphi}= dfrac{partial u}{partial x}cdot(-rsinvarphi)+ dfrac{partial u}{partial y}cdot rcosvarphi,. end{aligned}$

или, в силу условий (2.19), $dfrac{partial u}{partial varphi}= -r left(dfrac{partial v}{partial y}cdot sinvarphi+ dfrac{partial v}{partial x}cdot cosvarphiright)$

$begin{aligned}dfrac{partial v}{partial r}& = dfrac{partial v}{partial x}cdot dfrac{partial x}{partial r}+ dfrac{partial v}{partial y}cdot dfrac{partial y}{partial r}= dfrac{partial v}{partial x}cdot cosvarphi+ dfrac{partial v}{partial y}cdot sinvarphi,;\[5pt] dfrac{partial v}{partial varphi}&= dfrac{partial v}{partial x}cdot dfrac{partial x}{partial varphi}+ dfrac{partial v}{partial y}cdot dfrac{partial y}{partial varphi}= dfrac{partial v}{partial x}cdot(-rsinvarphi)+ dfrac{partial v}{partial y}cdot rcosvarphi,. end{aligned}$

или, используя условия (2.19): $dfrac{partial v}{partial varphi}= r left(dfrac{partial u}{partial x}cdot cosvarphi+ dfrac{partial u}{partial y}cdot sinvarphiright)$

Сравнивая равенства для $dfrac{partial u}{partial r}$ и $dfrac{partial v}{partial varphi}$ , имеем $dfrac{partial v}{partial varphi}=rcdot dfrac{partial u}{partial r}$ , а из равенств для $dfrac{partial u}{partial varphi}$ и $dfrac{partial v}{partial r}$ получаем $dfrac{partial u}{partial varphi}=-rcdot dfrac{partial v}{partial r}$ . Выписываем результат:

$begin{cases}dfrac{partial u}{partial r}= dfrac{1}{r}cdot dfrac{partial v}{partial varphi},\[9pt] dfrac{partial u}{partial varphi}= -rcdot dfrac{partial v}{partial r}.end{cases}$

(2.21)

Это и есть искомые условия Коши-Римана в полярных координатах.

▼ Примеры 2.36-2.37

Пример 2.36. Записать производную функции f(z) для случая $z=r,e^{ivarphi}$ в полярных координатах.

Решение

Пусть f(z)=u+iv,~ u=u(r,varphi),~ v=v(r,varphi) и $r=sqrt{x^2+y^2},~ varphi= operatorname{arctg}frac{y}{x}$ . Запишем частные производные по правилу дифференцирования сложной функции:

$dfrac{partial u}{partial x}= dfrac{partial u}{partial r}cdot dfrac{partial r}{partial x}+ dfrac{partial u}{partial varphi}cdot dfrac{partial varphi}{partial x},qquad dfrac{partial u}{partial y}= dfrac{partial u}{partial r}cdot dfrac{partial r}{partial y}+ dfrac{partial u}{partial varphi}cdot dfrac{partial varphi}{partial y}.$

Используя условия (2.21), запишем выражение для $f'(z)colon, f'(z)= dfrac{partial u}{partial x}-i,dfrac{partial u}{partial y}$ . Получим

$f'(z)= dfrac{partial u}{partial r}left(dfrac{partial r}{partial x}- i,dfrac{partial r}{partial y}right)- r, dfrac{partial v}{partial r}left(dfrac{partial varphi}{partial x}-i,dfrac{partial varphi }{partial y}right)!.$

Далее находим производные функций $r(x,y)= sqrt{x^2+y^2},~ varphi(x,y)= operatorname{arctg}frac{y}{x}$ и выписываем выражения, стоящие в скобках:

$begin{aligned}dfrac{partial r}{partial x}- i,dfrac{partial r}{partial y}&= frac{x}{sqrt{x^2+y^2}}- i,frac{y}{sqrt{x^2+y^2}}= frac{overline{z}}{r};\[5pt] dfrac{partial varphi}{partial x}-i,dfrac{partial varphi }{partial y}&= frac{-y}{x^2+y^2}-i,frac{x}{x^2+y^2}= -frac{i(x-iy)}{x^2+y^2}= frac{-icdot overline{z}}{zcdot overline{z}}= -frac{icdot overline{z}}{r^2},.end{aligned}$

Для производной получаем выражение

$f'(z)= frac{overline{z}}{r} left(dfrac{partial u}{partial r}+ i,dfrac{partial v}{partial r}right)quad Leftrightarrowquad f'(z)= frac{r}{z} left(dfrac{partial u}{partial r}+ i,dfrac{partial v}{partial r}right)!.$

(2.22)

Пример 2.37. Исследовать на дифференцируемость функцию f(z)= ln z,~ 0<arg z<2pi . Найти производную.

Решение

В области Dcolon, 0<arg z<2pi — плоскости с разрезом по действительной положительной полуоси, функция однозначная (см. рис. 2.5). Исследуем ее на дифференцируемость по правилу 2.1, используя запись в полярных координатах.

1. Из равенства ln z= ln r+i,varphi имеем u(r,varphi)= ln r,~ v(r,varphi)=varphi .

2. Находим частные производные: $dfrac{partial u}{partial r}= frac{1}{r},~ dfrac{partial u}{partial varphi}=0,~ dfrac{partial v}{partial r}=0,~ dfrac{partial v}{partial varphi}=1$ .

3. Условия (2.21) выполняются в любой точке области , следовательно, функция дифференцируема в области . Заметим, что, очевидно, дифференцируемой в соответствующей области будет любая однозначная ветвь логарифма, ln z=ln r+i(arg z+2kpi),~ kinmathbb{Z} . Используя формулу (2.22), записываем производную

$(ln z)'= frac{r}{z}cdot! left(frac{1}{r}+icdot0right)= frac{1}{z},.$

Геометрический смысл модуля и аргумента производной

Производная f'(z) как функция комплексного переменного определяет отображение некоторой области — области дифференцируемости функции f(z) на область . В каждой точке z_0in D определено комплексное число f'(z_0) , следовательно, определены |f'(z_0)| и arg f'(z_0) , если f'(z_0)ne0 . Геометрически число — длина радиуса-вектора точки f'(z_0) , a — угол наклона этого радиуса-вектора к действительной оси.

Возникает вопрос, как характеризуют эти величины само отображение w=f(z) в точке z_0 . Как известно, для функции действительной переменной аналогичный вопрос решается просто: производная f'(x_0) определяет угловой коэффициент касательной, проведенной к кривой y=f(x) в точке (x_0,f(x_0)) .

Рассмотрим геометрические свойства величин k=|f'(z_0)| и alpha= arg f'(z_0) , полагая f'(z_0)ne0 , а функцию f(z) дифференцируемой в окрестности точки z_0 . Так как по определению производной $f'(z_0)= lim_{Delta zto0} frac{Delta w}{Delta z}$ предел в точке не зависит от направления и способа стремления Delta z к нулю, то можно взять произвольную гладкую кривую gamma , проходящую через точку z_0 , и на ней любую точку из окрестности точки z_0 .

Образ кривой gamma при отображении w=f(z) обозначим Gamma , образы точек z_0 и через w_0 и соответственно; из непрерывности отображения очевидно, что w_0inGamma и winGamma . Приращения переменных Delta z=z-z_0 и Delta w=w-w_0 геометрически есть векторы (рис. 2.13,а), их длины — |Delta z|,~|Delta w| .

Из определения производной и свойства предела $lim_{Delta zto0}frac{Delta w}{Delta z}= f'(z)$ имеем $frac{Delta w}{Delta z}=f'(z_0)+alpha$ , следовательно,

$left|frac{Delta w}{Delta z}right|= bigl|f'(z_0)+alphabigr|leqslant bigl|f'(z_0)bigr|+ |alpha|$ , или $left|left|frac{Delta w}{Delta z}right|-bigl|f'(z_0)bigr|right|leqslant |alpha|< varepsilon$ для z_0in O(z_0) .

Последнее неравенство, согласно определению, означает $|f'(z_0)|= lim_{Delta zto0}left|frac{Delta w}{Delta z}right|$ . Перепишем его следующим образом:

$bigl|f'(z_0)bigr|= lim_{Delta zto0}left|frac{Delta w}{Delta z}right|= lim_{Delta zto0}frac{Delta l_{Gamma}}{Delta l_{gamma}}= frac{d,l_{Gamma}}{d,l_{gamma}},$

где $Delta l_{Gamma}$ и $Delta l_{gamma}$ — длины соответствующих дуг кривых Gamma и gamma , как известно, эквивалентных при |Delta z|to0 стягивающим их хордам |Delta w| и ; $d,l_{Gamma}$ и $d,l_{gamma}$ — элементы длин дуг Gamma и gamma в точках w_0 и z_0 соответственно.

Производная на комплексной плоскости

Отношение $frac{d,l_{Gamma}}{d,l_{gamma}}$ определяет изменение масштаба (растяжение, сжатие) в точке z_0 при отображении w=f(z) . В этом заключается геометрический смысл модуля производной.

Величина |f'(z_0)| не зависит от вида кривой gamma , поэтому отмеченное свойство имеет место и для любой другой гладкой кривой, проходящей через точку z_0 .

Следовательно, величина k=|f'(z_0)| модуля производной есть величина постоянная для данной функции f(z) и данной точки z_0 .

Для аргумента производной имеет место равенство arg f'(z_0)=theta-varphi , где theta и varphi — углы между действительными осями в плоскостях (w) и (z) соответственно и касательными, проведенными к кривым Gamma в точке w_0 и gamma в точке z_0 (рис. 2.13,а).

Если точки w_0 и z_0 совместить, то alpha=arg f'(z_0)= theta-varphi — угол поворота кривой gamma в точке z_0 при отображении w=f(z) (рис. 2.13,б).

В этом заключается геометрический смысл аргумента производной аналитической функции.

Это свойство, очевидно, имеет место и для любой другой гладкой i кривых gamma_1 и Gamma_1 проходящих через точки z_0 и w_0 соответственно, alpha=theta_1-varphi_1 . Из равенств alpha=theta-varphi и получаем theta_1-theta= varphi_1-varphi . Это означает, что угол beta между кривыми Gamma_1 и Gamma,~ beta=theta_1-theta — в равен углу между кривым gamma_1 и gamma,~ beta=varphi_1-varphi (рис. 2.14). Следовательно, при отображении сохраняются углы между кривыми.

Отображение, сохраняющее углы между кривыми, называется конформным.

Кривые, проходящие через точку, на комплексной

Полученные результаты сформулируем в виде утверждения.

Утверждение 2.7

1. Модуль |f'(z_0)| производной функции f(z) , дифференцируемой в окрестности точки z_0 , есть коэффициент линейного растяжения кривой в точке z_0 при отображении w=f(z) .

2. Аргумент производной в точке есть угол поворота кривой в этой точке при отображении w=f(z) .

3. Отображение с помощью дифференцируемой в окрестности точки z_0 функции f(z) , удовлетворяющее условию f'(z_0)ne0 , является конформным в точке z_0 . Оно обладает свойством постоянства растяжения и сохранения углов. Причем углы сохраняются как по величине, так и по направлению отсчета.

▼ Примеры 2.38-2.40

Пример 2.38. Найти коэффициент растяжения и угол поворота в точке z=2i при отображении $w=frac{z+1}{z+i}$ .

Решение

Находим производную $w'=frac{z+i-z-1}{(z+i)^2}$ , ее значение в точке $2icolon, w'(2i)= frac{1-i}{9}$ . Коэффициент растяжения равен модулю производной, $k=|w'(2i)|= frac{1}{9}sqrt{2}$ , угол поворота — аргументу производной $arg w'(2i)=-frac{pi}{4}$ .

Пример 2.39. Определить, какая часть плоскости при отображении w=z^2 растягивается, а какая — сжимается.

Решение

Находим производную w'=2z , коэффициент растяжения в любой точке равен |w'(z_0)=2|z_0|,~ k=2|z_0| . Множество точек z_0 , для которых k>1 , то есть $2|z_0|>1Rightarrow |z_0|>frac{1}{2}$ , очевидно, образует часть плоскости, которая при отображении растягивается. Следовательно, при отображении w=z^2 внешность круга $|z|>frac{1}{2}$ растягивается, а внутренняя часть $|z|<frac{1}{2}$ сжимается.

Пример 2.40. Показать, что при отображении w=z^2 координатная сетка плоскости (w) соответствует двум ортогональным семействам кривых плоскости (z) .

Решение

Так как f'(z)=2z , то отображение w=z^2 конформно всюду, кроме точки z=0 . Координатная сетка плоскости (w) — это совокупность линий u=text{const},~ v=text{const} . Очевидно, любая пара таких линий в точках пересечения образует прямой угол (рис. 2.15,а). Прообразами этих линий в плоскости (г) будут два семейства гипербол: x^2-y^2=c,~ cne0 и 2xy=c,~ cne0 (рис. 2.15,б). Они получаются из равенства w=z^2 , то есть u+iv=(x+iy)^2 или u=x^2-y^2,~ v=2xy . Линии рассматриваются при любых значениях cne0 . Заметим, что при c=0 линии y=pm x,~ y=0,~ x=0 проходят через точку z=0 , где f'(0)=0 .

Покажем, что гиперболы x^2-y^2=c_2 и 2xy=c_1 при любых c_1,c_2~(c_1ne0,,c_2ne0) пересекаются под прямым углом, т.е. прямой угол образуют касательные к этим кривым в точке пересечения кривых (например, точка на рис. 2.15,б). Угловой коэффициент кривой первого семейства — производную точке A(x_0, y_0) — находим по правилу дифференцирования неявной функции $y'_1(x_0)=-frac{2x_0}{-2y_0}= frac{x_0}{y_0}$ для кривой второго семейства $y'_2(x_0)=-frac{c_1}{2x_0^2}$ . Но в точке пересечения (x_0,y_0) верно равенство 2x_0y_0=c_1 , поэтому $y'_2(x_0)=-frac{2x_0y_0}{x_0^2}=-frac{y_0}{x_0}$ .

Условие ортогональности касательных выполнено: y'_1(x_0)cdot y'_2(x_0)=-1 .

Семейства прямых и гипербол на комплексной плоскости

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

1.3.1. Определение производной

Пусть
задана однозначная функция

на области D
(открытом связном множестве) комплексной
плоскости.

Определение.
Производной
функции

в точке z
называется предел отношения приращения
функции к приращению аргумента при
стремлении приращения аргумента к нулю

Если
этот предел существует, то функция

называется дифференцируемой
в точке

Если
функция

является дифференцируемой в каждой
точке области

,
то говорят, что она аналитическая
в области

Поскольку
определение производной функции
комплексного переменного полностью
аналогично определению производной
функции действительной переменной, то
в случае дифференцируемости функции

,
все известные правила дифференцирования
остаются в силе.

1.3.2. Необходимые и достаточные условия дифференцируемости функции комплексного переменного

Теорема
1 (Условия
Коши – Римана).
Для того,
чтобы функция

,
определенная в некоторой области

,
была дифференцируема в точке

этой области, как функция комплексного
переменного, необходимо и достаточно,
чтобы функции

были дифференцируемы в той же точке
(как функции действительных переменных)
и, чтобы, кроме того, выполнялись условия:

При
выполнении условий теоремы, производная
функции

может быть представлена в виде:

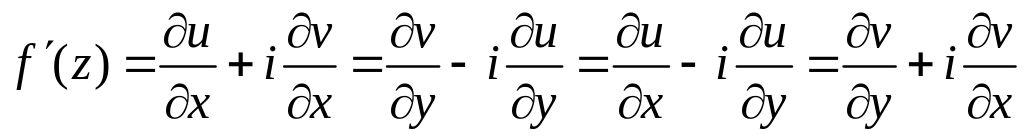
1.3.3. Производные основных элементарных функций

Показательная
функция

.

Имеем

Действительная
и мнимая части

будут, соответственно,

Находим
частные производные:

.
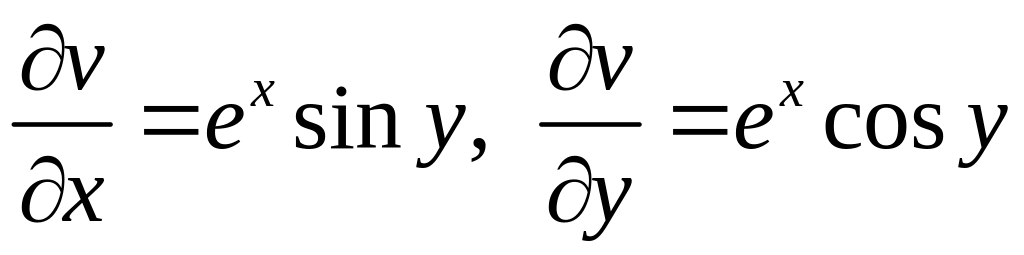
Следовательно,

,
т.е. условия Коши-Римана выполнены,
значит, функция

аналитическая, и ее производная:

Функция

.

По
определению:

.
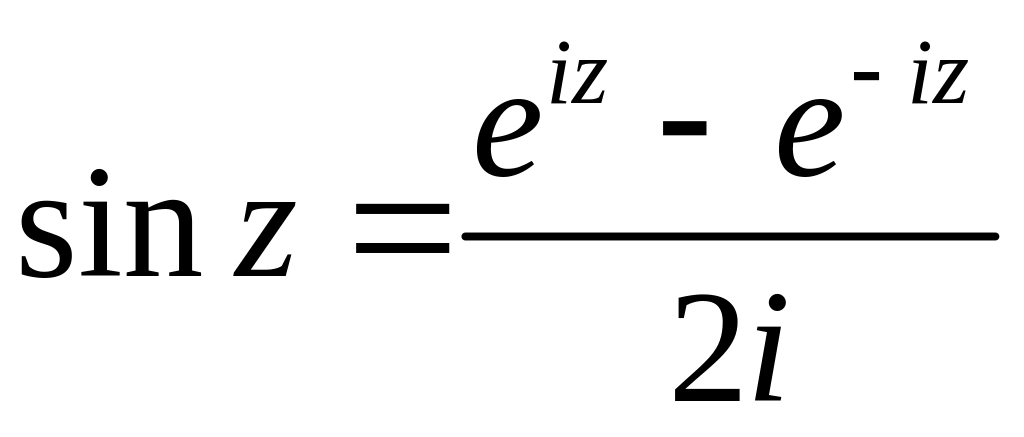
Т.е. является аналитической функцией,
тогда, пользуясь правилами дифференцирования,
получим:

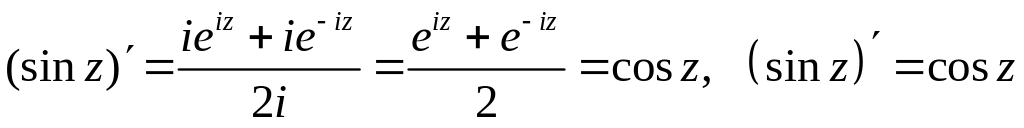
Функция

.

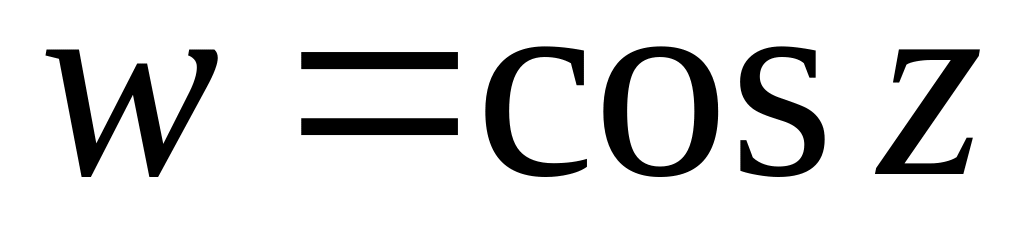
Аналогично
предыдущему:

Функция
.

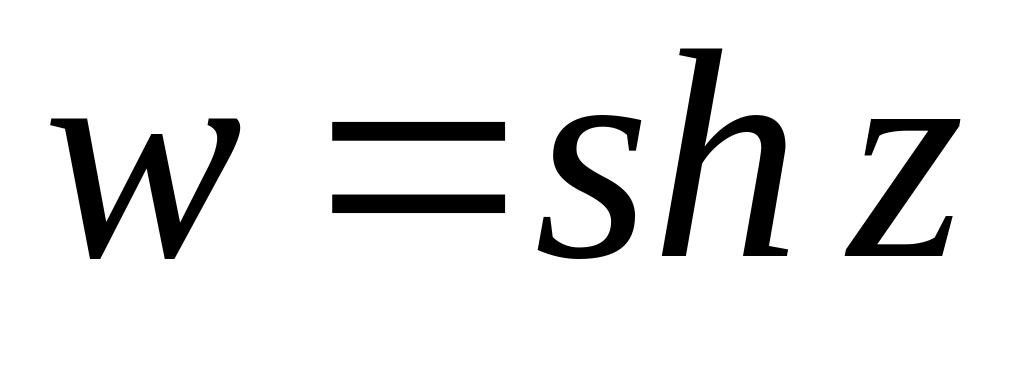
Функция

.

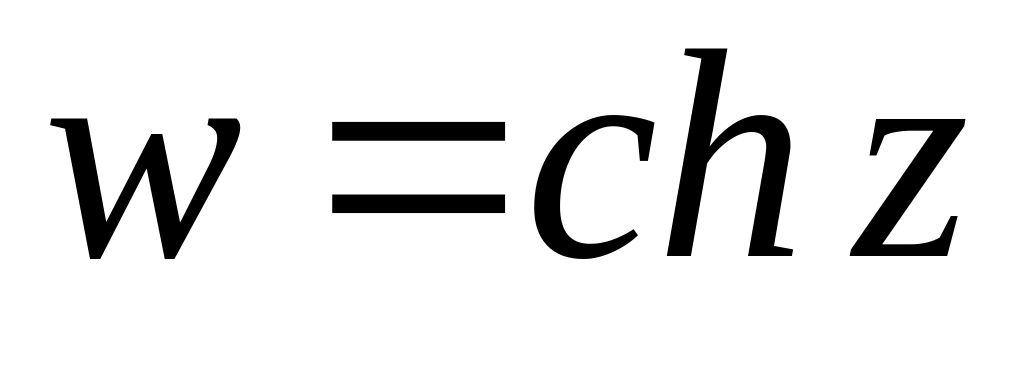
Функция
.

Логарифмическая
функция является обратной к показательной
функции, а значит – аналитической.
Воспользуемся правилом дифференцирования
обратной функции.

Имеем:

,
тогда

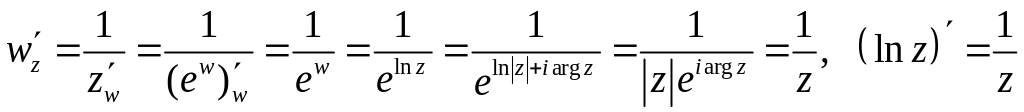
Функция

.

Производную
степенной функции вычислим непосредственно
по определению:

.
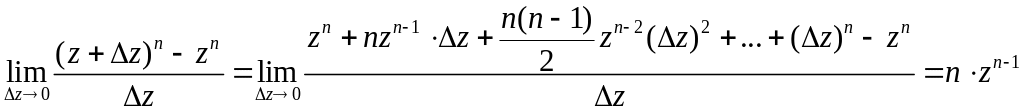
Предел
существует, следовательно,
функция

аналитическая, и ее производная:

Таким
образом, мы показали, что основные
элементарные функции комплексного
переменного являются аналитическими
функциями. Следовательно, всякая функция
комплексного переменного, являющаяся
композицией конечного числа основных
элементарных функций, будет аналитической
или дифференцируемой в области своего
определения.

Пример.
Вычислить
производную функции

.

Решение.
Имеем:

=

=

.

1.3.4. Восстановление аналитической функции по известной действительной или мнимой части

Условия,
при которых функция комплексного
переменного дифференцируема, достаточно
жесткие. Поэтому, аналитическая функция,
с точностью до постоянного слагаемого,
может быть задана свой действительной
или мнимой частью.

Действительная
и мнимая части функции

,
аналитической в некоторой области D,
связаны условиями Коши – Римана:

Пусть
известна одна из частей аналитической
функции, например

.
Из условия:

можно найти

(с точностью до неизвестной функции

).
Эту функцию

,
с точностью до постоянного слагаемого,
найдем из второго условия

.

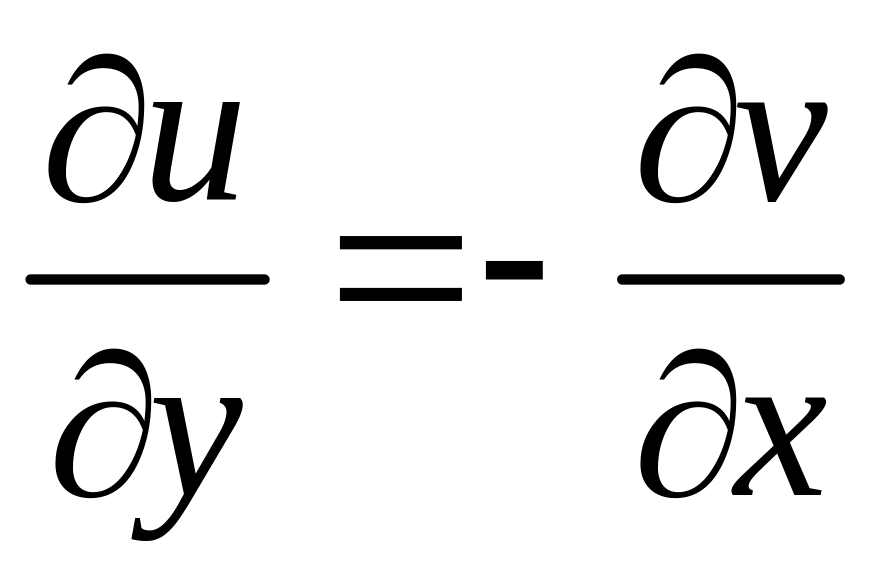
А
именно,

или

.

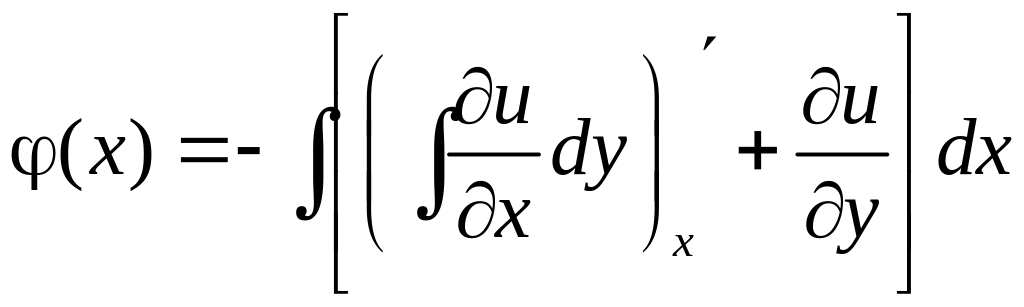
Пример.
Найти
аналитическую функцию

,
если известна её мнимая часть

.

Решение.
Так как

,
то из условия

находим:

.
Следовательно,

,
где функция

пока
неизвестна. Для нахождения функции

дифференцируем
это равенство по y
и приравниваем
к известной производной, используя
условие

,
откуда

Следовательно,

Окончательно получаем

=
.

Ответ.

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Пусть задана однозначная функция на области (открытом связном
множестве) комплексной плоскости .

Производной от функции в точке называется предел

(1)

когда
любым
образом стремится к нулю.

Далеко не всякая функция
комплексного переменного имеет производную. Существование предела (1) – очень сильное
требование: при подходе к по любому пути каждый раз должен
существовать указанный в (1) предел.

Функцию , имеющую непрерывную
производную в любой точке области комплексной плоскости, называют аналитической
функцией на этой области.

Можно доказать, что если
производная аналитической функции не равна нулю на области , то множество
значений функции
также
есть область. Мы будем пользоваться этим свойством.

Дадим геометрическое
представление производной , когда она не равна нулю. Кроме плоскости , введем еще другую
плоскость точек .
Опишем из точки открытый
круг радиуса
с
центром в ней (рис. 131).

Рис. 131

Произвольная точка имеет вид , где – произвольное
комплексное число с модулем, меньшим . Запишем в показательной форме

. (2)

При помощи функции круг перейдет в некоторую
область плоскости
. Область
состоит
из точек ,
где приращения соответствуют
всевозможным указанным приращениям (см. рис. 131).

Из (1) следует равенство

,
где .

Умножая левую и правую части
последнего равенства на , получаем

. (3)

Произведение стремится к нулю при быстрее чем . Поэтому, если , то первый член правой
части (3) является главным. Приближенно, с точностью до бесконечно
малых высшего порядка (по сравнению с ), при достаточно малых можно написать

Число запишем в показательной
форме

. (4)

Поэтому, учитывая (2), получим

Мы видим, что модуль , с точностью до
бесконечно малой высшего порядка, в раз больше модуля :

а
аргумент (тоже
с точностью до бесконечно малой высшего порядка) получается из аргумента прибавлением к
нему числа (рис.
132):

Таким образом, для того чтобы
представить себе, куда перешли точки с при помощи функции надо 1) повернуть
круг на
угол и
2) растянуть его в раз. Каждая точка , , при помощи этих двух
операций перейдет в некоторую точку, которую надо еще сдвинуть на величину – бесконечно малую
высшего порядка чем .

Пусть и – гладкие кривые, выходящие
из точки .
Касательные к ним образуют с осью углы соответственно (отсчитываемые от
оси против
часовой стрелки). Образы этих кривых на плоскости (рис. 133) при помощи
функции имеют
касательные в точке , образующие с осью абсцисс
соответственно углы (которые отсчитываются тоже против
часовой стрелки).

Рис. 132

При
этом (в силу свойства 1))

,
,

откуда
следует свойство

выражающее,
как говорят, что данное отображение сохраняет углы и притом с
сохранением направления отсчета (если , то ).

Рис. 133

Кроме того, как мы видели выше,
данное отображение осуществляет в каждой точке , где , растяжение, не зависящее от
направления.

Отображение, обладающее (с
точностью до бесконечно малых высшего порядка) свойством сохранения углов (с
сохранением направления отсчета) и свойством постоянства растяжений,
называется конформным отображением.

Из вышеизложенного следует, что отображение
с помощью аналитической функции является конформным во всех
точках, где .

Замечание 1. Если функция комплексной
переменной имеет
всюду на области производную , то
автоматически эта производная непрерывна всюду на , т. е. аналитическая
на .
Этим утверждением мы будем пользоваться, хотя доказывать его не будем.

Замечание 2. Из равенства (3)
следует, что если функция имеет производную в точке , то она непрерывна
в этой точке (т. е. при ).

Производная от функции порядка обозначается через
и
определяется по индукции

Зная, что у аналитической на
области функции
производная
непрерывна на ,
нам будет в дальнейшем нетрудно заключить, что имеет на непрерывные производные
любого порядка

Употребляют еще такую
терминологию: функция называется аналитической в точке
, если
она аналитическая на некоторой окрестности этой точки. Наконец, говорят, что
функция аналитическая
на замыкании области
, если
существует область , содержащая в себе , на которой аналитическая.

Приведем основные свойства
производных функций комплексного переменного, аналогичные соответствующим
свойствам производных для функций действительного переменного, которые и
доказываются аналогично:

, (5)

, (6)

, (7)

. (8)

Формулу (8) надо понимать так:
если есть
функция комплексного
переменного ,
имеющая производную , a – функция от комплексной переменной , имеющая
производную ,
то производная сложной функции

вычисляется
по формуле (8).

Ниже мы приводим некоторые
элементарные функции комплексного переменного.

Степенная функция

–
целое.

Эта функция имеет производную,
вычисляемую по формуле

При ее удобно вычислить как предел

применяя
формулу бинома Ньютона.

При теперь можно воспользоваться формулой
(7).

Функция при аналитическая на всей
плоскости ,
а при на
всей плоскости с выколотой из нее точкой .

Функции , , , .

Первые три из этих функций
определены в нашей книге «Высшая математика. Дифференциальное и интегральное
исчисление», § 9.13, как суммы степенных рядов:

Радиус сходимости каждого из этих
рядов равен .
Поэтому производные от этих функций могут быть получены для любого почленным
дифференцированием соответствующих рядов:

Формулы для тригонометрических
функций суммы комплексных аргументов остаются такими же, как и в случае
действительного переменного.

Функция определяется по формуле

Ее производная равна

что
следует из формулы (7).

Функция () может быть определена по формуле

Ее производная вычисляется на
основании формулы (8) о производной сложной функции:

Гиперболические функции , , определяются формулами

,
, .

Отсюда следует, что

,
. (9)

Заменяя в (9) на , получаем

,
. (10)

Отметим еще легко проверяемую
формулу

Формулы сложения для
гиперболических функций легко получить из (9) и (10) соответствующих формул для
тригонометрических функций от комплексного переменного. Например:

Производные от этих функций
вычисляются на основании формул (5), (7), (8):

,
,

Пример. Выделить действительную и
мнимую части у функции и найти нули этой функции.

Пусть , .

Имеем .

Таким образом, , .

Чтобы найти нули функции , мы должны приравнять
нулю ее действительную и мнимую части:

Решим эту систему. Так как для любого действительного
, то из
первого уравнения получаем .

Из второго уравнения при получаем, что . При
действительных косинус
и синус не обращаются одновременно в нуль, поэтому при система решений не имеет.
Если же ,
то и
второе уравнение удовлетворяется при любых . Таким образом, нули функции расположены на
действительной оси и совпадают с нулями .

Замечание 3. Из этого утверждения
следует, что нули функции совпадают с нулями функции , где .

Замечание 4. Отметим еще § 6.15,
посвященный линейной и дробно-линейной функциям; его можно читать и
непосредственно после настоящего § 6.2.

Источник

Дифференцируемость[править]

Определение. ${textstyle f:uleft(z_{0}right)rightarrow mathbb {C} }$ называется ${textstyle mathbb {C} }$ дифференцируемой в точке ${textstyle z_{0}}$ , если ${textstyle exists lim _{Delta zrightarrow 0}{frac {fleft(z_{0}+Delta zright)-fleft(z_{0}right)}{Delta z}}=f^{prime }left(z_{0}right)}$ .

Пример. ${textstyle f(z)=z^{n};quad lim _{Delta zrightarrow 0}{frac {left(z_{0}+Delta zright)^{n}-z_{0}^{n}}{Delta z}}=lim _{Delta zrightarrow 0}{frac {Delta zleft(left(z_{0}+Delta zright)^{n-1}+cdots +z_{0}^{n-1}right)}{Delta z}}=nz_{0}^{n-1}}$

Пример. ${textstyle f(z)={overline {z}};lim _{Delta Zrightarrow 0}{frac {{overline {z_{0}+Delta z}}-{overline {z_{0}}}}{Delta z}}=lim _{Delta zrightarrow 0}{frac {overline {Delta z}}{Delta z}}}$

Этот предел не существует, так как если брать ${textstyle Delta z}$ вида ${textstyle Delta z=Delta x}$ , то есть только действительная часть, то ${textstyle lim _{Delta zrightarrow 0}{frac {overline {Delta z}}{Delta z}}=lim _{Delta xrightarrow 0}{frac {Delta x}{Delta x}}=1}$ ;

если брать ${textstyle Delta z}$ вида ${textstyle Delta z=iDelta y}$ , то ${textstyle lim _{Delta zrightarrow 0}{frac {overline {Delta z}}{Delta z}}=lim _{Delta yrightarrow 0}{frac {-iDelta y}{iDelta y}}=-1}$ .

Определение. ${textstyle sqsupset z=x+iy,f(z)=u(x,y)+iv(x,y)}$ . ${textstyle f}$ называется ${textstyle mathbb {R} }$ -дифференцируемой в точке ${textstyle z_{0}}$ , если:

${textstyle left{{begin{array}{l}{uleft(x_{0}+Delta x,y_{0}+Delta yright)-uleft(x_{0},y_{0}right)=aDelta x+bDelta y+oleft({sqrt {Delta x^{2}+Delta y^{2}}}right)}\{vleft(x_{0}+Delta x,y_{0}+Delta yright)-vleft(x_{0},y_{0}right)=cDelta x+dDelta y+oleft({sqrt {Delta x^{2}+Delta y^{2}}}right)}end{array}}right.}$

Теорема. ${textstyle sqsupset f=u+iv:uleft(z_{0}right)rightarrow mathbb {C} ,}$ ” ${textstyle f}$ ${textstyle mathbb {C} }$ -дифференцируема в точке ${textstyle z_{0}}$ тогда и только тогда, когда:

${textstyle f}$ ${textstyle mathbb {R} }$ -дифференцируема в точке ${textstyle z_{0}}$ ;
выполняются условия Коши Римана:

${textstyle left{{begin{array}{c}{u_{x}left(z_{0}right)=v_{y}left(z_{0}right)}\{u_{y}left(z_{0}right)=-v_{x}left(z_{0}right)}end{array}}right.}$

Доказательство. ${textstyle f}$ ${textstyle mathbb {C} }$ -дифференцируема тогда и только тогда, когда ${textstyle fleft(z_{0}+Delta zright)-fleft(z_{0}right)=f^{prime }left(z_{0}right)Delta z+o(Delta z)(Delta zrightarrow 0)}$

${textstyle uleft(z_{0}+Delta zright)-uleft(z_{0}right)+ileft(vleft(z_{0}+Delta zright)-vleft(z_{0}right)right)=(a+ib)(Delta x+iDelta y)+oleft({sqrt {x^{2}+y^{2}}}right)}$

Следовательно:

${textstyle left{{begin{array}{l}{uleft(z_{0}+Delta zright)-uleft(z_{0}right)=aDelta x-bDelta y+oleft({sqrt {x^{2}+y^{2}}}right)}\{vleft(z_{0}+Delta zright)-vleft(z_{0}right)=bDelta x+aDelta y+oleft({sqrt {x^{2}+y^{2}}}right)}end{array}}right.}$

Видно,что:

${textstyle u_{x}left(z_{0}right)=a,u_{y}left(z_{0}right)=-b,v_{x}left(z_{0}right)=b,v_{y}left(z_{0}right)=a}$ ,

то есть:

${textstyle left{{begin{array}{c}{u_{x}left(z_{0}right)=v_{y}left(z_{0}right)}\{u_{y}left(z_{0}right)=-v_{x}left(z_{0}right)}end{array}}right.}$

Пример. (выполнены условия Коши–Римана, но нет ${textstyle mathbb {C} }$ -дифференцируемости)

Возьмём функцию ${textstyle f=u+iv}$ ,где ${textstyle u}$ функция, на действительной и мнимой осях равная ${textstyle 1}$ , а вне их равная ${textstyle 0}$ , а ${textstyle vequiv 0}$ . Возьмём точку ${textstyle z_{0}=0}$ :

${textstyle left{{begin{array}{l}{v_{x}(0)=0}\{v_{y}(0)=0}\{u_{x}(0)=0}\{u_{y}(0)=0}end{array}}right.}$

Условия КошиРимана выполняются, но ${textstyle f}$ не ${textstyle mathbb {C} }$ -дифференцируема, так как разрывна.

Замечание. ${textstyle mathbb {C} }$ -дифференцируемость в точке ${textstyle z_{0}}$ влечёт за собой непрерывность в точке ${textstyle z_{0}}$ .

Правила дифференцирования[править]

${textstyle {(fpm g)^{prime }=f^{prime }pm g^{prime }}}$
${textstyle {(alpha f)^{prime }=alpha f^{prime }}}$
${textstyle (gf)^{prime }=f^{prime }g+fg^{prime }}$
${textstyle {left({frac {f}{g}}right)={frac {fg-gf}{g^{2}}}}}$
${textstyle {left(fleft(gleft(z_{0}right)right)right)=f^{prime }left(gleft(z_{0}right)right)g^{prime }left(z_{0}right)}}$
${textstyle {left(f^{-1}right)left(z_{0}right)={frac {1}{f^{prime }left(f^{-1}left(z_{0}right)right)}}}}$

Пример. Рассмотрим функцию ${textstyle e^{Z}}$ :

${textstyle e^{z}=e^{x}(cos y+isin y)}$

${textstyle left{{begin{array}{l}{u=e^{x}cos y}\{v=e^{x}sin y}end{array}}right.}$

${textstyle mathbb {R} }$ –дифференцируемость в любой точке очевидна, проверим условия Коши Римана:

${textstyle {begin{aligned}u_{x}=&e^{x}cos y=v_{y}\u_{y}=&-e^{x}sin y=-v_{x}end{aligned}}}$

Итак, экспонента ${textstyle mathbb {C} }$ -дифференцируема. Найдём её производную ${textstyle left(e^{z}right)^{prime }left(z_{0}right)=lim _{Delta zrightarrow 0}{frac {e^{z_{0}+Delta z}-e^{z_{0}}}{Delta z}}}$ .

Экспонента ${textstyle mathbb {C} }$ -дифференцируема, значит, этот предел одинаков по всем направлениям, в частности, по чисто действительному направлению ${textstyle Delta z=Delta x}$ :

${textstyle lim _{Delta zrightarrow 0}{frac {e^{z_{0}+Delta z}-e^{z_{0}}}{Delta z}}=lim _{Delta xrightarrow 0}{frac {e^{z_{0}+Delta z}-e^{z_{0}}}{Delta z}}={frac {partial e^{z}}{partial x}}=e^{x_{0}}left(cos y_{0}+isin y_{0}right)=e^{z_{0}}}$

Значит, ${textstyle left(e^{z}right)^{prime }=e^{z}}$ , и, вообще, если ${textstyle f(z)}$ ${textstyle mathbb {C} }$ -дифференцируема в точке ${textstyle z_{0}}$ , то ${textstyle f^{prime }left(z_{0}right)={frac {partial f}{partial x}}left(z_{0}right)=-i{frac {partial f}{partial y}}left(z_{0}right)}$

Пример. Вычислим производные синуса и косинуса:

${textstyle {begin{aligned}(sin z)^{prime }&=left({frac {e^{iz}-e^{-iz}}{2i}}right)^{prime }={frac {ie^{iz}+ie^{-iz}}{2i}}={frac {e^{iz}+e^{-iz}}{2}}=cos z\(cos z)^{prime }&=left({frac {e^{iz}+e^{-iz}}{2}}right)={frac {ie^{iz}-ie^{-iz}}{2}}={frac {-e^{iz}+e^{-iz}}{2i}}=-sin zend{aligned}}}$

Пример. (Функция, которая ${textstyle mathbb {C} }$ -дифференцируема везде, кроме нуля, а в нуле выполняются условия Коши-Римана)

${textstyle {begin{array}{c}{f(z)=left{{begin{array}{c}{e^{-{frac {1}{z^{4}}}},quad zneq 0}\{0,quad z=0}end{array}}right.}\{f(x)=e^{-{frac {1}{x^{4}}}}}\{f_{x}(0)=lim _{Delta xrightarrow 0}{frac {e^{-{frac {1}{Delta x^{4}}}}}{Delta x}}=0}end{array}}}$

Значит,

${textstyle {begin{array}{c}{u_{x}=v_{x}=0}\{f(iy)=e^{-{frac {1}{y^{4}}}}}\{f_{y}(0)=lim _{Delta yrightarrow 0}{frac {e^{-{frac {1}{Delta y^{4}}}}}{Delta y}}=0}end{array}}}$

Теорема. (Лумана-Меньшова, без доказательства): ${textstyle sqsupset D}$ область, ${textstyle f:Drightarrow mathbb {C} }$ непрерывна в ${textstyle D}$ и удовлетворяет условиям Коши Римана в ${textstyle D}$ . Тогда ${textstyle f}$ ${textstyle mathbb {C} }$ -дифференцируема в ${textstyle D}$ .

Условия Коши-Римана в комплексной форме[править]

${textstyle sqsupset f=u+iv}$

${textstyle fleft(z_{0}+Delta zright)-fleft(z_{0}right)=uleft(z_{0}+Delta zright)-uleft(z_{0}right)+ileft(vleft(z_{0}+Delta zright)-vleft(z_{0}right)right)}$

${textstyle {begin{array}{l}{uleft(z_{0}+Delta zright)-uleft(z_{0}right)+ileft(vleft(z_{0}+Delta zright)-vleft(z_{0}right)right)=u_{x}Delta x+u_{y}Delta y+oleft({sqrt {x^{2}+y^{2}}}right)+ileft(v_{x}Delta x+v_{y}Delta y+right.}\{+oleft({sqrt {x^{2}+y^{2}}}right))=u_{x}{frac {Delta z+{overline {Delta z}}}{2}}+u_{y}{frac {Delta z-{overline {Delta z}}}{2i}}+ileft(v_{x}{frac {Delta z+{overline {Delta z}}}{2}}+v_{y}{frac {Delta z-{overline {Delta z}}}{2i}}right)+oleft({sqrt {x^{2}+y^{2}}}right)=}end{array}}}$

${textstyle {begin{array}{l}{={frac {Delta z}{2}}left(u_{x}-iu_{y}+iv_{x}+v_{y}right)+{frac {overline {Delta z}}{2}}left(u_{x}+iu_{y}+iv_{x}-v_{y}right)+oleft({sqrt {x^{2}+y^{2}}}right)={frac {Delta z}{2}}left(u_{x}+iv_{x}-ileft(u_{y}+iv_{y}right)right)+}\{+{frac {overline {Delta z}}{2}}left(u_{x}+iv_{x}+ileft(u_{y}+iv_{y}right)right)+oleft({sqrt {x^{2}+y^{2}}}right)=Delta z{frac {1}{2}}left({frac {partial f}{partial x}}-i{frac {partial f}{partial y}}right)+{overline {Delta z}}{frac {1}{2}}left({frac {partial f}{partial x}}+i{frac {partial f}{partial y}}right)+oleft({sqrt {x^{2}+y^{2}}}right)}end{array}}}$

Введём такие обозначения:

${textstyle {frac {partial f}{partial z}}={frac {1}{2}}left({frac {partial f}{partial x}}-i{frac {partial f}{partial y}}right)}$

${textstyle {frac {partial f}{partial {overline {z}}}}={frac {1}{2}}left({frac {partial f}{partial x}}+i{frac {partial f}{partial y}}right)}$

${textstyle Delta z{frac {1}{2}}left({frac {partial f}{partial x}}-i{frac {partial f}{partial y}}right)+{overline {Delta z}}{frac {1}{2}}left({frac {partial f}{partial x}}+i{frac {partial f}{partial y}}right)+oleft({sqrt {x^{2}+y^{2}}}right)={frac {partial f}{partial z}}Delta z+{frac {partial f}{partial {overline {z}}}}{overline {Delta z}}+oleft({sqrt {x^{2}+y^{2}}}right)}$

Запишем производную ${textstyle f}$ :

${textstyle {frac {partial f}{partial z}}=lim _{Delta zrightarrow 0}{frac {fleft(z_{0}+Delta zright)-fleft(z_{0}right)}{Delta z}}=lim _{Delta zrightarrow 0}{frac {{frac {partial f}{partial z}}Delta z+{frac {partial f}{partial {overline {z}}}}{overline {Delta z}}+oleft({sqrt {x^{2}+y^{2}}}right)}{Delta z}}={frac {partial f}{partial z}}+lim _{Delta zrightarrow 0}left({frac {partial f}{partial {overline {z}}}}{frac {overline {Delta z}}{Delta z}}right)}$

${textstyle lim _{Delta zrightarrow 0}left({frac {partial f}{partial {overline {z}}}}{frac {overline {Delta z}}{Delta z}}right)=0}$

${textstyle lim _{Delta zrightarrow 0}left({frac {overline {Delta z}}{Delta z}}right)}$ не существует, поэтому это возможно только если ${textstyle {frac {partial f}{partial {overline {Z}}}}=0}$ . Это и есть условие Коши Римана в комплексной форме.

${textstyle {frac {partial f}{partial {overline {z}}}}=0}$

${textstyle {frac {partial f}{partial {overline {Z}}}}={frac {1}{2}}left(f_{x}+if_{y}right)=0}$

${textstyle {begin{array}{c}{f_{x}=-if_{y}}\{u_{x}+iv_{x}=-ileft(u_{y}+iv_{y}right)}\{u_{x}+iv_{x}=v_{y}-iu_{y}}\{quad quad v_{x}=-u_{y}}\{quad v_{x}=-u_{y}}end{array}}}$

Голоморфные функции[править]

Определение. ${textstyle f}$ называется голоморфной (аналитической) в точке ${textstyle z_{0}}$ , если она ${textstyle mathbb {C} }$ –дифференцируема в точке ${textstyle z_{0}}$ .

Определение. ${textstyle f}$ , определённая в области ${textstyle D}$ , называется голоморфной (аналитической) в области ${textstyle D}$ , если она ${textstyle mathbb {C} }$ –дифференцируема во всех точках ${textstyle D}$ . Голоморфность в области ${textstyle D}$ обозначается так: ${textstyle fin O(D)}$ или ${textstyle fin A(D)}$ .

Утверждение. ${textstyle sqsupset D}$ область, ${textstyle fin O(D)}$ и ${textstyle operatorname {Re} f=uequiv 0}$ .

Тогда ${textstyle fequiv i*const}$

Доказательство. *пока нет*

Голоморфность в бесконечности[править]

Определение. ${textstyle sqsupset f:uleft(z_{0}right)rightarrow {overline {mathbb {C} }},fleft(z_{0}right)=infty }$ . ${textstyle fin O(z_{0})}$ , если ${textstyle {frac {1}{f}}in Oleft(z_{0}right)}$

Пример. ${textstyle f(z)={frac {1}{z}}}$ в точке ${textstyle z_{0}=0}$ . ${textstyle {frac {1}{f(z)}}=z}$ голоморфна в точке ${textstyle z_{0}=0}$ , значит, и ${textstyle f(z)}$ голоморфна в точке ${textstyle 0}$ .

Определение. ${textstyle f:u(infty )rightarrow {overline {mathbb {C} }}}$ называется голоморфной в бесконечности, если ${textstyle fleft({frac {1}{z}}right)in O(0)}$ . Голоморфность ${textstyle f}$ в бесконечности обозначается: ${textstyle f(z)in O(infty )}$ .

Пример. ${textstyle f(z)={frac {az+b}{cz+d}}}$

${textstyle f(infty )={frac {a}{c}},quad fleft({frac {1}{z}}right)={frac {a+bz}{c+dz}}in O(0)}$ , значит, ${textstyle f(z)in O(infty )}$

Пример. ${textstyle f(z)=z}$

${textstyle f(infty )=infty ,quad fleft({frac {1}{z}}right)={frac {1}{z}}in O(0)}$ , значит, ${textstyle f(z)in O(infty )}$

Конформность голоморфных отображений[править]

Определение. ${textstyle sqsupset f=u+iv:uleft(z_{0}=x_{0}+iy_{0}right)rightarrow mathbb {C} ,f}$ – ${textstyle mathbb {R} }$ -дифференцируема в точке ${textstyle z_{0}}$ . ${textstyle f}$ конформна в точке ${textstyle z_{0}}$ , если дифференциал ${textstyle f}$ обладает свойствами сохранения ориентированных углов и постоянства расстояния, то есть матрица Якоби ${textstyle J=left({begin{array}{ll}{u_{x}}&{u_{y}}\{v_{x}}&{v_{y}}end{array}}right)}$ ортогональная матрица с положительным определителем.

Примечание. В этом курсе лекций мы называем матрицу ортогональной, если её столбцы как векторы ортогональны; определитель не обязательно равен 1.

Утверждение. ${textstyle f}$ конформно в точке ${textstyle z_{0}Longleftrightarrow f}$ ${textstyle mathbb {C} }$ -дифференцируема в точке ${textstyle z_{0}}$ и ${textstyle f^{prime }left(z_{0}right)neq 0}$ .

Доказательство. ${textstyle f}$ конформно в точке ${textstyle z_{0}Longleftrightarrow }$

${textstyle f}$ ${textstyle mathbb {R} }$ -дифференцируема
${textstyle left({begin{array}{ll}{u_{x}}&{u_{y}}\{v_{x}}&{v_{y}}end{array}}right)=left({begin{array}{cc}{a}&{-b}\{b}&{a}end{array}}right)}$
${textstyle a^{2}+b^{2}neq 0}$

${textstyle left({begin{array}{ll}{u_{x}}&{u_{y}}\{v_{x}}&{v_{y}}end{array}}right)=left({begin{array}{cc}{a}&{-b}\{b}&{a}end{array}}right)}$ ${textstyle Longleftrightarrow }$ выполняются условия Коши Римана ${textstyle Longleftrightarrow }$

${textstyle f}$ ${textstyle mathbb {C} }$ -дифференцируема
${textstyle u_{x}^{2}+v_{x}^{2}neq 0}$

${textstyle left|f^{prime }left(z_{0}right)right|=left|f_{x}left(z_{0}right)right|=left|u_{x}+iv_{x}right|=u_{x}^{2}+v_{x}^{2}neq 0}$

Значит, ${textstyle left|f^{prime }left(z_{0}right)right|neq 0}$ и ${textstyle f^{prime }left(z_{0}right)neq 0}$ .

Геометрический смысл производной[править]

${textstyle left|f^{prime }left(z_{0}right)right|}$ коэффициент растяжения бесконечно малых векторов

${textstyle arg f'left(z_{0}right)}$ угол, на который поворачиваются бесконечно малые вектора

Определение. ${textstyle f}$ голоморфна в области ${textstyle D}$ ${textstyle Longleftrightarrow }$ ${textstyle fin O(D)}$ , ${textstyle forall zin D:f^{prime }(z)neq 0}$ ${textstyle f(z)}$ конформна в точке ${textstyle z}$ .

В ${textstyle mathbb {R} ^{2}}$ много конформных отображений.

Теорема. (Лиувилль, без доказательства)

${textstyle sqsupset f}$ область в ${textstyle mathbb {R} ^{n}}$ , ${textstyle ngeq 3,f:Drightarrow mathbb {R} ^{n}}$ конформна в любой точке из ${textstyle D}$ . Тогда ${textstyle f}$ является композицией параллельного переноса, инверсии, поворота и гомотетии.

Источник

Дифференцирование функций комплексного переменного

Правила дифференцирования

Условия Коши-Римана дифференцируемости функции

Условия Коши-Римана в полярных координатах

Геометрический смысл модуля и аргумента производной

1.3.1. Определение производной

1.3.2. Необходимые и достаточные условия дифференцируемости функции комплексного переменного

1.3.3. Производные основных элементарных функций

1.3.4. Восстановление аналитической функции по известной действительной или мнимой части

Дифференцируемость[править]

Правила дифференцирования[править]

Условия Коши-Римана в комплексной форме[править]

Голоморфные функции[править]

Голоморфность в бесконечности[править]

Конформность голоморфных отображений[править]

Геометрический смысл производной[править]

Вам также может понравиться

Как найти алфею винкс

Как найти длину нити маятника если

Как найти домоуправителя в скайриме

Добавить комментарий Отменить ответ