Умножение дробей онлайн
Чтобы умножить дробь на дробь нужно перемножить их числители и знаменатели, первое произведение записать числителем, а второе знаменателем.
Правила умножения дробей
Произведение двух дробей равно дроби. В числителе которой произведение числителей, а в знаменателе произведение знаменателей.
Как умножать обыкновенные дроби
Для умножения обыкновенных дробей нужно найти произведение числителей и произведение знаменателей. Первое произведение записать числителей а второе знаменателем.
Разберём пример: умножим дроби 1/4 × 1/3. Для этого перемножим числители 1 × 1 = 1 и знаменатели 4 × 3 = 12 в итоге у нас получится дробь 1/12
Как умножать натуральное число на дробь
Чтобы умножить дробь на натуральное число нужно числитель умножить на это число а знаменитель оставить без изменения.
Как умножать 3 и более дробей
При умножении 3 и более дробей мы пользумеся теми же правилами что и при умножении двух дробей.
Разберём пример: умножим правильную дробь 1/4 на натуральное число 5 и на смешанную дробь 3 целые 1/8.
Перед умножением нужно смешанную дробь перевести в неправильную 3 целые 1/8 = 25/8. Затем перемножить числители 1*5*25 = 125 и знаменатели 4*8 = 32. Полученное записать в виде дроби 125/32. При необходимости сократить и перевести в смешанную дробь.
Как умножить смешанную дробь на целое число
Чтобы умножить смешанную дробь на целое число нужно смешанную дробь перевести в неправильную. Затем числитель неправильной дроби умножить на целое число. Знаменатель оставить без изменения.
Разберём пример: умножим смешанную дробь 2 целые 1/4 на целое число 6.
Перед умножением нужно смешанную дробь перевести в неправильную 2 целые 1/4 = 9/4. Затем умножить числитель неправильной дроби на целое число 9*6 = 54 а знаменатель останется без изменения 4. При необходимости сократить и перевести в смешанную дробь.
Как перемножить смешанные дроби
Чтобы перемножить смешанные дроби, нужно их перевести в неправильные. Затем перемножить числители и знаменатели.
Разберём пример: умножим смешанную дробь 1 целая 2/5 на смешанную дробь 2 целые 1/3.
Переведём смешанные дроби в нерпавильные 1 целая 2/5 = 7/5 и 2 целые 1/3 = 7/3. Затем перемножим числители 7*7 = 49 и знаменатели 5*3 = 15. Получится дробь 49/15. При необходимости сократить и перевести в смешанную дробь.
Похожие калькуляторы
Перед тем как перейти к умножению дробей, вспомним теоретические основы. Итак, дробь — это форма записи числа:
где a — числитель, b — знаменатель.
Дробь называется правильной — если числитель меньше знаменателя (к примеру, 4/5), неправильной — если числитель больше знаменателя (например, 8/7).
Как умножать обыкновенные дроби?
Умножение дробей — это арифметическое действие, в результате которого получается новое число, содержащее произведение заданных чисел. Разберем на конкретных примерах: как находить произведение дробей, как натуральное число умножить на дробь, познакомимся с умножением смешанных дробей.
Многие по аналогии со сложением и вычитанием, считают, что существует какая-то разница между умножением дробей в зависимости от их знаменателей. На самом деле её нет. Сейчас на примерах мы в этом убедимся.
Как умножать дроби с одинаковым знаменателем?
Умножение дробей с одинаковыми знаменателями сводится к умножению и числителей и знаменателей и в общем виде выглядит следующим образом:
Пример 1:
2 5
×
3 5
Решение:
2 5
×
3 5
=
2 ∙ 3 5 ∙ 5
=
6 25
Как умножать дроби с разными знаменателями?
Умножение дробей с разными знаменателями заключается в умножении и числителей и знаменателей. В общем виде выглядит следующим образом:
Пример 2:
5 6
×
4 5
Решение:
5 6
×
4 5
=
5 ∙ 4 6 ∙ 5
=
20 30
=
2 3
Как вы могли заметить, разницы между умножением дробей с разными и одинаковыми знаменателями — нет, а сам алгоритм сводится к умножению обоих компонентов.
Как умножить дробь на целое число?
Чтобы умножить дробь на число необходимо числитель умножить число, а знаменатель оставить без изменения. Т.е.:
Пример 3:
5 ×
3 4
Решение:
5
×
3 4
=
5 ∙ 3 4
=
15 4
=
3
3 4
Таким образом, умножение дроби на целое число, сводится к умножению числителей.
Как умножать смешанные дроби?
Умножение смешанных дробей сводится к переводу их к неправильному виду и дальнейшим действиям согласно вышеописанным алгоритмам. Перевод смешанного числа в неправильную дробь, в общем виде, выглядит следующим образом:
Пример 4:
6
3 5
×
6 4
Решение:
6
3 5
×
6 4
=
6 ∙ 5 + 3 5
×
6 4
=
33 5
×
6 4
=
33 ∙ 6 5 ∙ 4
=
198 20
=
99 10
=
9
9 10
Правила умножения дробей
Резюмируя вышесказанное, выведем общий алгоритм умножения дробей:
- Если дробь смешанная — приводим её к неправильному виду;
- Неважно одинаковые или разные знаменатели у дробей — перемножаем и числители и знаменатели;
- При необходимости сокращаем и приводим к неправильному виду.
Смотрите также:
- Смотрите также
- Калькуляторы
- Последние примеры
Калькулятор умножения дробей
Оцените материал:
Загрузка…
Умножение смешанных дробей
Чтобы умножить смешанные дроби, надо записать их в виде неправильных дробей, а затем умножить их числители, а затем их знаменатели.
Пример Умножить смешанные дроби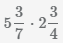 
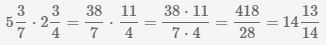
Сократим дробь 
с помощью нахождения наибольшего общего делителя числителя и знаменателя и деления полученного числа на числитель и знаменатель, НОД(418,28)=2.
Пример Умножить смешанное число на дробь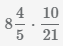 
.
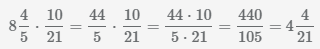В результате умножения получили смешанную дробь.
Примеры умножения нескольких дробей
Пример Умножить 3 дроби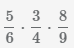 
.
Пример Найти произведение дробей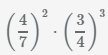 
Первая дробь во 2 степени, вторая дробь в 3 степени, чтобы найти произведение дробей, возведем первую дробь в квадрат, потом возведем вторую дробь в куб и перемножим дроби между собой.
.
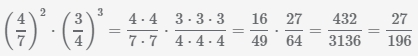Сократим дробь 
с помощью нахождения наибольшего общего делителя числителя и знаменателя и деления полученного числа на числитель и знаменатель, НОД(432,3136)=16.
Умножение дробей
Как научиться легко и быстро умножать дроби, можно ли научиться делать это в уме и как успешно подготовиться к контрольной – разбираем тему из школьной программы по математике вместе с экспертом
Как высчитать, чему равно произведение пяти восьмых и трех девятых? Или как умножить семь тринадцатых на четыре? Школьники России учатся этому, проходя одну из основных тем программы по математике – умножение дробей. Разберемся, для чего пригодится это умение, и узнаем у эксперта, как успешно подготовиться к контрольной.
Полезная информация об умножении дробей
| Умножение дробей – одна из базовых тем школьной программы по математике | Согласно Федеральным государственным образовательным стандартам (ФГОС) 2022 года, дроби и основные действия с ними изучают в 5 классе. |
| Умножение дробей можно изучать на визуальных примерах | Используя счетный материал, рисунки или реальные предметы (например, отрезать две трети от половинки пиццы или четверть от трети торта). |
| Дроби умножать удобнее, если их предварительно сократить | При наличии такой возможности перед умножением дробей желательно их сократить (разделить числитель и знаменатель на одно и то же число). |
Умножение обыкновенных дробей
Для умножения дроби на дробь необходимо умножить знаменатель первой дроби на знаменатель второй, а числитель – на числитель. Полученные результаты составят знаменатель и числитель результата соответственно.
Полезные факты:
- Если числитель одной из дробей имеет общий делитель со знаменателем другой, то можно произвести сокращение произведения до выполнения умножения.
- Если одна или обе дроби являются смешанными, то перед выполнением действия можно перевести их в неправильные, либо представить смешанную дробь в виде суммы целого числа и правильной дроби, провести умножение, а после представить результат вновь в виде смешанной дроби.
Примеры
Сначала сократим первую дробь на 5 (числитель и знаменатель поделили одновременно на 5), числа стали меньше, действия с ними уже сделать намного проще. Во втором действии мы также не умножили сразу, а сократили на тройку в числителе и тройку в знаменателе.
В этом примере подробно рассмотрено сокращение дробей, сначала на 5, а затем на 7. Здесь в результате получилась неправильная дробь. Ее, в зависимости от задания, можно либо перевести в десятичную, получится 1,5, либо перевести в смешанное число 1 1/2.
Еще один, более сложный, пример умножения правильной дроби на смешанное число путем представления смешанного числа в виде суммы целого и дроби. После получения произведения дроби на сумму приводим полученные слагаемые к единому знаменателю путем домножения первого слагаемого на три. Далее складываем и выделяем целую часть.
Данный пример вычисляется без сокращения: первым действием перемножаем числители и знаменатели дробей, вторым – выделяем целую часть неправильной дроби, превращая ее в смешанную.
Умножение дроби на натуральное число
Умножение дроби на натуральное число – пожалуй, самый простой вариант умножения дробей. Чтобы выполнить это действие, нужно умножить числитель дроби на это число, а знаменатель оставить без изменений. После подсчета можно выделить целую часть, превратив обыкновенную дробь в смешанную.
Если число-множитель делится нацело на знаменатель дроби, то в результате получится целое число.
Примеры
В первом примере для умножения дроби на целое число проводим умножение числителя дроби на число-множитель, а знаменатель остался без изменений. Во втором примере можем сократить произведение на 4, получив в результате целое число.
Умножение смешанных дробей
Для умножения смешанных дробей необходимо перевести их обе в вид обыкновенных и далее действовать по стандартному алгоритму: произведение знаменателей станет знаменателем результата, произведение числителей – числителем.
Далее производится сокращение и перевод обратно в смешанную дробь.
Примеры
При умножении смешанной дроби на число удобно представить дробь в виде суммы целой и дробной части, произвести умножение и сложить полученные результаты.
Для перемножения двух смешанных дробей переводим обе в неправильные, затем умножаем по стандартным правилам. Вторым действием производим сокращение (делим числитель и знаменатель произведения на 7), а в полученном результате выделяем целую часть.
В данном примере не удалось провести сокращение, поэтому итоговый результат содержит четырехзначные числа. Приводим его к более простому виду, выделив целую часть.
Советы эксперта, как подготовиться к контрольной работе по умножению дробей
Альбина Бабурчина, репетитор по математике, автор курсов по подготовке к ЕГЭ и ОГЭ по математике:
Дроби бывают обыкновенные (с дробной чертой) и десятичные (с запятой). Чтобы умножить две обыкновенные дроби, нужно просто перемножить числитель одной дроби с числителем другой, а знаменатель со знаменателем. Если получится сначала сократить дроби, а потом их перемножить, то это освободит вас от действий с большими числами. Поэтому везде, где можно, сначала лучше упростить и только потом делать основное действие.
Популярные вопросы и ответы
Отвечает Альбина Бабурчина
Почему умножение дробей начинают изучать в 5 классе?
Тема дробей раскрывается именно в 5 классе, так как к этому моменту ученики уже имеют в своем арсенале все необходимые для этого знания. Дроби – это азы. Без понимания этой темы дальнейшее изучение математики практически невозможно.
Зачем изучать умножение дробей?
После того как дети в школе изучают дроби, далее ни одна тема не обходится без них. По моему многолетнему опыту могу сказать, что если дроби не усвоены вовремя и на должном уровне, то все следующие темы без исключения будут «хромать». То есть без преувеличения, дроби (сначала обыкновенные, а затем и десятичные) – важнейшая тема в математике. И моя большая рекомендация для ребят в 5 классе – максимально сконцентрировано и детально изучать эту тему, уметь применять в разных ситуациях и задавать учителю все возникающие вопросы и сомнения.
Можно ли научиться умножать дроби в уме?
Все действия с дробями, разумеется, можно выполнять и в уме, все зависит от способностей конкретного ученика. А также существует много лайфхаков, которые упрощают умножение.
Содержание:
- Умножение дроби на число
- Умножение дробей
- Умножение смешанных дробей
Умножение дроби на число
Умножение дроби $frac{a}{b}$ на число
$n$ равносильно сложению одинаковых слагаемых:
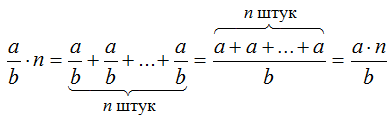
Итак, можно сделать вывод, что чтобы умножить дробь на число, надо числитель этой
дроби умножить на это число, а знаменатель оставить без изменения.
Пример
Задание. Найти произведение
$frac{1}{3} cdot 4$
Решение. Выполним умножение по описанному выше правилу
$frac{1}{3} cdot 4=frac{1 cdot 4}{3}=frac{4}{3}=1 frac{1}{3}$
Ответ. $frac{1}{3} cdot 4=1 frac{1}{3}$
Аналогично выполняется умножения числа на дробь.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти произведение
3$cdot frac{1}{4}$
Решение. Выполним умножение по описанному выше правилу
$3 cdot frac{1}{4}=frac{3 cdot 1}{4}=frac{3}{4}$
Ответ. $3 cdot frac{1}{4}=frac{3}{4}$
Умножение дробей
Определение
Произведением дробей называется такая дробь, числитель которой равен произведению числителей
исходных дробей, а знаменатель – произведению их знаменателей:
$frac{a}{b} cdot frac{c}{d}=frac{a cdot c}{b cdot d}$
Таким образом, чтобы умножить дробь на дробь, надо умножить числитель первой дроби на числитель второй и результат
записать в числитель; а также перемножить знаменатели и результат записать в знаменатель.
Замечание. При выполнении умножения по возможности следует сокращать. Сокращать можно только
числа стоящие в числителе с числами, стоящими в знаменателе. Числитель с числителем и знаменатель со знаменателем сокращать нельзя.
Пример
Задание. Найти произведение дробей
$frac{1}{3}$ и
$frac{4}{5}$
Решение. Выполним умножение дробей по описанному выше правилу
$frac{1}{3} cdot frac{4}{5}=frac{1 cdot 4}{3 cdot 5}=frac{4}{15}$
Ответ. $frac{1}{3} cdot frac{4}{5}=frac{4}{15}$
Пример
Задание. Умножить
$frac{13}{14}$ на
$frac{14}{39}$
Решение. Необходимо найти произведение
$frac{13}{14} cdot frac{14}{39}$ . Как видим, числа 13 и 39 можно сократить на
общее число 13. Для этого сами указанные величины зачеркиваем, а над ними пишем число, которое получается после деления.
Аналогично поступает со знаменателем первой дроби и числителем второй:
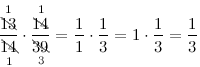
Ответ. $frac{13}{14} cdot frac{14}{39}=frac{1}{3}$
Умножение смешанных дробей
Чтобы перемножить смешанные дроби, нужно представить их в виде
неправильных дробей, а затем уже выполнить умножение как
обыкновенных дробей.
Пример
Задание. Найти произведение дробей
3$frac{1}{3} cdot 4 frac{2}{5}$
Решение. Выполним умножение смешанных дробей по описанному выше правилу
$3 frac{1}{3} cdot 4 frac{2}{5}=frac{3 cdot 3+1}{3} cdot frac{4 cdot 5+2}{5}=frac{10}{3} cdot frac{22}{5}=$
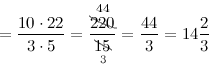
Ответ. $3 frac{1}{3} cdot 4 frac{2}{5}=14 frac{2}{3}$
Для умножения смешанной дроби на целое число поступают либо аналогично и далее умножают дробь на число,
либо на целое число отдельно умножают целую часть, и отдельно дробную часть смешанного числа.
Пример
Задание. Умножить смешанную дробь
3$frac{3}{4}$ на
2
Решение. Выполним умножение смешанной дроби на число по описанному выше правилу
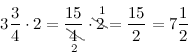
Либо
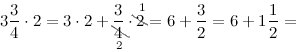
$=(6+1)+frac{1}{2}=7+frac{1}{2}=7 frac{1}{2}$
Ответ. $3 frac{3}{4} cdot 2=7 frac{1}{2}$
Читать следующую тему: деление дробей.
