Выделить максимальную линейно независимую…
Задание:
Выделить максимальную линейно независимую подсистему векторов в R4:
a1 = (1, −1, 2, 0), a2 = (2, 3, −4, 2), a3 = (3, 2, −2, 2), a4 = (1, 4, −6, 2), a5 = (4, 1, 0, 2).
Решение. Определим, является ли система векторов a1, a2, a3, a4, a5 линейно зависимой или нет. Для этого составим линейную комбинацию:
α1a1 + α2a2 + α3a3 + α4a4 + α5a5.
Подставим числовые значения векторов a1, a2, a3, a4, a5 и приравняем линейную комбинацию к нулевому вектору в R4, получим:
α1(1, −1, 2, 0) + α2(2, 3, −4, 2) + α3(3, 2, −2, 2) + α4(1, 4, −6, 2) + α5(4, 1, 0, 2) = (0, 0, 0, 0).
В левой части равенства каждый из векторов умножим на соответствующий коэффициент и сложим векторы, получим:
(α1 + 2α2 + 3α3 + α4 + 4α5, −α1 + 3α2 + 2α3 + 4α4 + α5, 2α1 − 4α2 − 2α3 − 6α4,
2α2 + 2α3 + 2α4 + 2α5) = (0, 0, 0, 0).
Два вектора равны, если равны их соответствующие компоненты, поэтому полученное равенство эквивалентно системе:

Если эта система линейных однородных уравнений имеет единственное решение, то векторы a1, a2, a3, a4, a5 линейно независимы. Если решений бесконечно много, то векторы линейно зависимы. Решим полученную систему уравнений методом Гаусса:
 Так как переменные α3, α4, α5 являются свободными, то исходная система имеет ненулевое решение. Следовательно векторы a1, a2, a3, a4, a5 линейно зависимы. Найдем, как один из этих векторов выражается через остальные. Исходная система линейных уравнений эквивалентна следующей:
Так как переменные α3, α4, α5 являются свободными, то исходная система имеет ненулевое решение. Следовательно векторы a1, a2, a3, a4, a5 линейно зависимы. Найдем, как один из этих векторов выражается через остальные. Исходная система линейных уравнений эквивалентна следующей:

Из этой системы находим, что

Подставляя α3 = 1, α4 = α5 = 0 получаем, что пятерка (−1, −1, 1, 0, 0) является решением системы. Тогда справедливо равенство: −a1 − a2 + a3 = 0.
Вектор a3 линейно выражается через векторы a1 и a2, следовательно его можно отбросить. Получим систему векторов a1, a2, a4, a5. Снова определим, является ли эта система векторов линейно независимой. Составим линейную комбинацию: β1a1 + β2a2 + β3a4 + β4a5.
Найдем, при каких значениях неизвестных β1, β2, β3, β4 эта линейная комбинация равна нулю. Подставив числовые значения векторов a1, a2, a4, a5 и сложив получившиеся векторы, получим:
(β1 + 2β2 + β3 + 4β4, −β1 + 3β2 + 4β3 + β4, 2β1 − 4β2 − 6β3, 2β2 + 2β3 + 2β4) = (0, 0, 0, 0).
Система линейных однородных уравнений, которой эквивалентно равенство, имеет следующий вид:

Будем решать эту систему методом Гаусса. Для этого надо в точности повторить те преобразования матрицы коэффициентов, которые мы делали в предыдущем случае:

Неизвестные β3, β4 являются свободными, следовательно исходная система линейных уравнений имеет бесконечно много решений. Тогда векторы a1, a2, a4, a5 линейно зависимы. Найдем, как один из этих векторов выражается через остальные. Исходная система
линейных уравнений эквивалентна следующей:

Находим, что четверка (1, −1, 1, 0) является решением исходной системы. Следовательно справедливо равенство: a1 − a2 + a4 = 0.
Вектор a4 линейно выражается через векторы a1 и a2, следовательно его можно отбросить. Получим систему векторов a1, a2, a5. Снова определим, являются ли они линейно независимыми. Составляем линейную комбинацию: γ1a1 + γ2a2 + γ3a5.
Подставляя числовые значения векторов a1, a2, a5 и приравнивая линейную комбинацию к нулевому в R4 вектору, получим: (γ1 + 2γ2 + 4γ3, −γ1 + 3γ2 + γ3, 2γ1 − 4γ2, 2γ2 + 2γ3) = (0, 0, 0, 0).
Это равенство эквивалентно следующей системе линейных однородных уравнений:

Будем решать эту систему уравнений методом Гаусса. Снова повторяем преобразования матрицы коэффициентов, которые делали в предыдущих случаях:

Неизвестная γ3 является свободной, следовательно исходная система линейных уравнений имеет бесконечно много решений. Тогда векторы a1, a2, a5 линейно зависимы. Исходная система уравнений эквивалентна следующей:

Находим, что тройка (−2, −1, 1) является решением исходной системы. Следовательно справедливо равенство: −2a1 − a2 + a5 = 0.
Вектор a5 линейно выражается через векторы a1 и a2, следовательно его можно отбросить. Получим систему векторов a1, a2. Снова определим, является ли она линейно независимой. Составляем линейную комбинацию: ζ1a1 + ζ2a2.
Подставляя числовые значения векторов a1, a2 и приравнивая линейную комбинацию к нулевому вектору в R, получим: (ζ1 + 2ζ2, −ζ1 + 3ζ2, 2ζ1 − 4ζ2, 2ζ2) = (0, 0, 0, 0).
Это равенство эквивалентно следующей системе линейных однородных уравнений:

Решаем эту систему методом Гаусса:

Обе неизвестные ζ1, ζ2 являются главными, следовательно исходная система уравнений имеет только нулевое решение (0, 0). Тогда векторы a1, a2 линейно независимы. Они образуют максимальную линейно независимую подсистему.
Ответ. a1, a2.
Ранг системы столбцов (строк) матрицы
Пусть дана система столбцов размеров
. Рангом системы столбцов называется максимальное число линейно независимых столбцов этой системы и обозначается
. Максимальной линейно независимой подсистемой столбцов (или базой системы столбцов) называется линейно независимая подсистема, состоящая из
столбцов. Максимальность здесь понимается в том смысле, что любое большее количество столбцов данной системы образует линейно зависимую подсистему.
Для нахождения максимальной линейно независимой подсистемы столбцов надо выполнить следующие действия.
1. Составить из данных столбцов матрицу размеров
.
2. Найти базисный минор этой матрицы.
3. Столбцы, в которых расположен базисный минор, образуют искомую подсистему (т.е. базу данной системы столбцов).
Замечания 3.6.
1. Ранг системы столбцов равен рангу матрицы, составленной из этих столбцов:
2. У системы столбцов может быть несколько максимальных линейно независимых подсистем, но все они состоят из одинакового количества столбцов.
3. Столбцы, в которых расположен базисный минор матрицы , можно найти методом Гаусса. Для этого приводим матрицу
к ступенчатому виду, используя только преобразования ее строк. В матрице ступенчатого вида выбираем базисный минор. Столбцы, в которых расположен базисный ми нор матрицы
, совпадают (по номерам) со столбцами, в которых расположен базисный минор матрицы ступенчатого вида (см. следствие 2 теоремы 3.4 о ранге матрицы).
4. Пусть дана система строк размеров
. Рангом системы строк называется максимальное число линейно независимых строк этой системы. Для нахождения максимальной линейно независимой подсистемы строк нужно составить из этих строк матрицу и найти ее базисный минор (например, используя только элементарные преобразования ее столбцов). Строки, в которых расположен базисный минор, образуют искомую подсистему. Другим путем решения задачи является ее сведение к нахождению максимальной линейно независимой системы столбцов
(см. следствие 1 теоремы 3.4 о ранге матрицы).
Пример 3.9. Дана система столбцов
Найти ранг системы и максимальную линейно независимую подсистему столбцов.
Решение. 1. Составляем из данных столбцов матрицу
2. Находим базисный минор этой матрицы. Для этого приводим ее к ступенчатому виду, преобразовывая только строки:
Следовательно, — базисный минор этой матрицы (один из них) и
. Второй и четвертый столбцы преобразованной матрицы линейно независимы. Так как преобразования выполнялись только над строками, то второй и четвертый столбцы исходной матрицы
также линейно независимы (см. следствие 2 теоремы 3.4). Поэтому ранг системы столбцов равен 2. Следовательно,
— максимальная линейно независимая подсистема системы столбцов
. В примере 3-3 были найдены и другие максимальные линейно независимые подсистемы, каждая из которых состоит из двух столбцов.
Пример 3.10. Дана система строк
Найти ранг и максимальную линейно независимую подсистему строк.
Решение. 1. Составляем из данных строк матрицу
2. Преобразуем матрицу, используя элементарные преобразования ее столбцов:
Хотя это не ступенчатый вид, нетрудно заметить, что минор — базисный (один из них) и
. Поэтому ранг данной системы строк равен 3. Первые три строки преобразованной матрицы линейно независимы. Так как преобразовывались только столбцы матрицы, делаем вывод, что первые три строки исходной матрицы также линейно независимы. Поэтому
— максимальная линейно независимая подсистема строк данной системы.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Максимальные линейно независимые подсистемы систем элементов линейных пространств, базис линейного пространства
Пусть 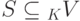 . Наиболее важные для нас случаи:
. Наиболее важные для нас случаи:
а) S – конечное подмножество элементов в K V ;
б) S = K V.
Подсистема 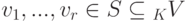 называется максимальной линейно независимой подсистемой в S, если:
называется максимальной линейно независимой подсистемой в S, если:
1) v1,…,vr – линейно независимая система;
2) v1,…,vr,v – линейно зависимая система для всякого 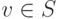 , или, что эквивалентно,
, или, что эквивалентно,
2′) любой элемент 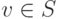 является линейной комбинацией элементов v1,…,vr.
является линейной комбинацией элементов v1,…,vr.
Максимальная линейно независимая подсистема v1,…,vr в S = KV (если в K V существует такая конечная система) называется базисом линейного пространства K V. Линейное пространство K V с конечным базисом v1,…,vr называется конечномерным линейным пространством (при этом будет показано, что любой другой базис линейного пространства содержит то же самое число элементов).
Пример 9.3.1. Как мы уже видели, система строк
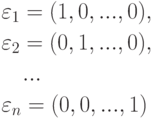
является базисом линейного пространства строк Kn.
Лемма 9.3.2. Любую линейно независимую подсистему v1,…,vr в 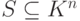 можно дополнить до максимальной линейно независимой подсистемы в
можно дополнить до максимальной линейно независимой подсистемы в 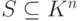 .
.
Доказательство. Если v1,…,vr – максимальная линейно независимая подсистема в 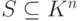 , то все доказано. Если нет, то найдется элемент
, то все доказано. Если нет, то найдется элемент 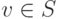 такой, что v1,v2,…,vr,v=vr+1 – линейно независимая подсистема в S. После конечного числа шагов процесс остановится, так как любые системы из n+1 элементов в линейном пространстве Kn оказываются линейно зависимыми.
такой, что v1,v2,…,vr,v=vr+1 – линейно независимая подсистема в S. После конечного числа шагов процесс остановится, так как любые системы из n+1 элементов в линейном пространстве Kn оказываются линейно зависимыми.
Следствие 9.3.3. Любой ненулевой элемент 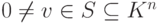 дополняем до максимальной линейно независимой подсистемы в S.
дополняем до максимальной линейно независимой подсистемы в S.
Следствие 9.3.4. В S= Rn (или S=Kn для бесконечного поля K ) бесконечно много различных базисов. Если поле K конечно, |K|=q (например, K= Z2 ), то число элементов в Kn равно qn, и поэтому число базисов в Kn конечно. Найдите их число.
Замечание 9.3.5. Пусть строки 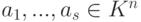 линейно независимы, s<n. Тогда существуют такие строки
линейно независимы, s<n. Тогда существуют такие строки 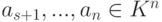 , что {a1,…,an} – базис линейного пространства Kn. Практическое нахождение строк as+1,…,an можно осуществить следующим образом. Запишем строки a1,…,as по столбцам и приведем полученную матрицу к ступенчатому виду:
, что {a1,…,an} – базис линейного пространства Kn. Практическое нахождение строк as+1,…,an можно осуществить следующим образом. Запишем строки a1,…,as по столбцам и приведем полученную матрицу к ступенчатому виду: 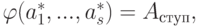 , где
, где 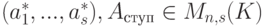 ,
, 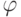 – последовательность элементарных преобразований строк. Так как строки a1,…,as линейно независимы, то в
– последовательность элементарных преобразований строк. Так как строки a1,…,as линейно независимы, то в  имеется ровно s ненулевых строк (первые s строк). Пусть
имеется ровно s ненулевых строк (первые s строк). Пусть 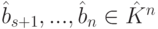 – столбцы, на i -м месте которых стоит 1, а остальные элементы равны 0, i=s+1,…,n. Припишем эти столбцы справа к матрице
– столбцы, на i -м месте которых стоит 1, а остальные элементы равны 0, i=s+1,…,n. Припишем эти столбцы справа к матрице  . Пусть
. Пусть 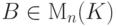 – полученная матрица. Применяя к матрице B последовательность элементарных преобразований строк, обратную к
– полученная матрица. Применяя к матрице B последовательность элементарных преобразований строк, обратную к 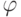 , приходим к матрице
, приходим к матрице 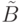 . При этом
. При этом  – матрица, в которой первые s строк – это a1,…,as, а последующие строки дополняют их до базиса линейного пространства Kn.
– матрица, в которой первые s строк – это a1,…,as, а последующие строки дополняют их до базиса линейного пространства Kn.
Пример 1. Доказать, что следующее
множество образует векторное пространство
над полем
![]()
относительно операций сложения матриц
и умножения матриц на число.
Найти его базис и размерность.
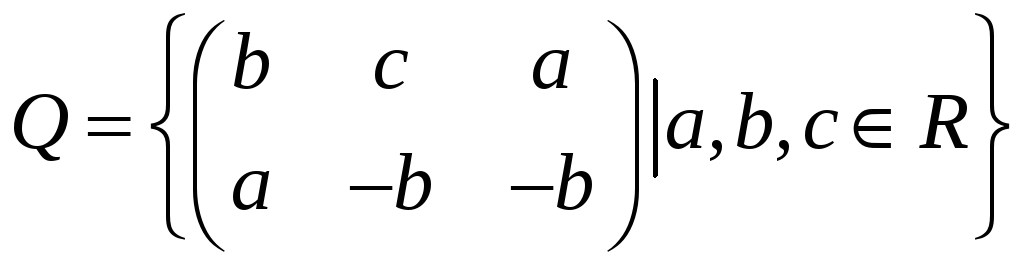 .
.
Решение.
![]()
является непустым подмножеством
пространства матриц размерности
![]() .
.
Докажем, что
![]()
является подпространством в
![]() ,
,
пользуясь критерием подпространства.
Пусть
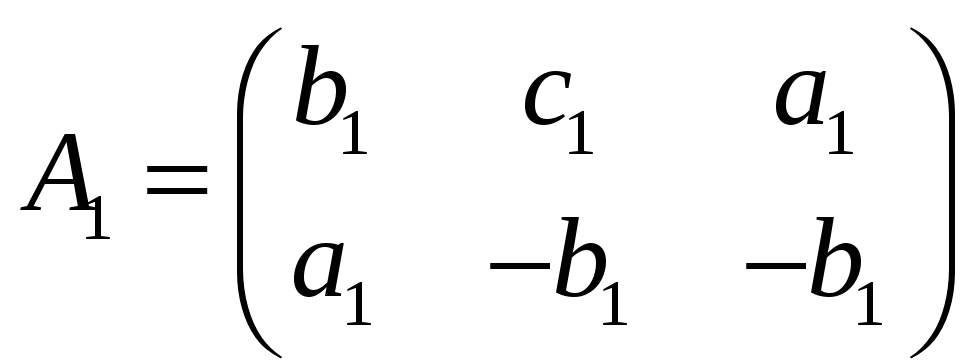
и
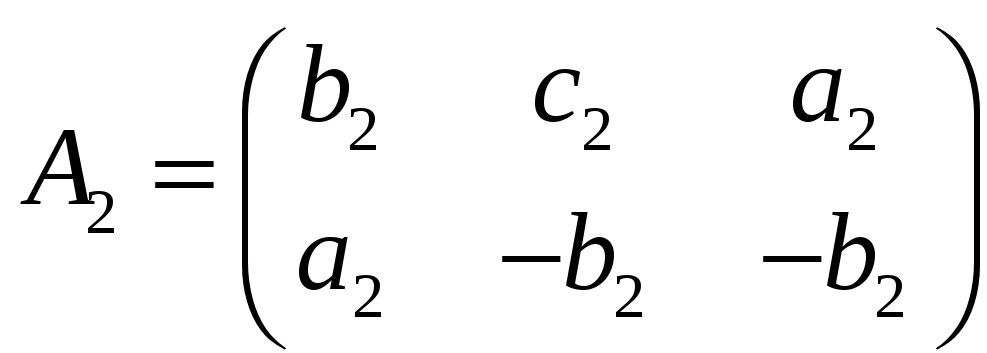
произвольные матрицы из
![]() .
.
Рассмотрим их сумму
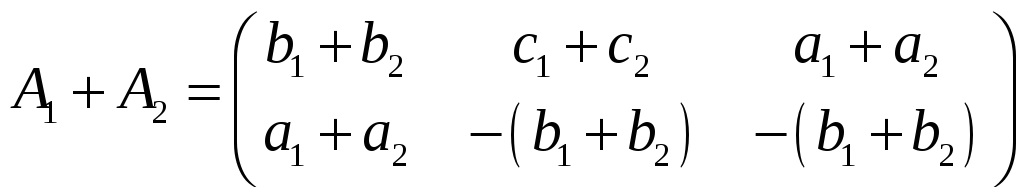 .
.
Очевидно
![]() .
.
Произведение
![]()
на любое число
![]()
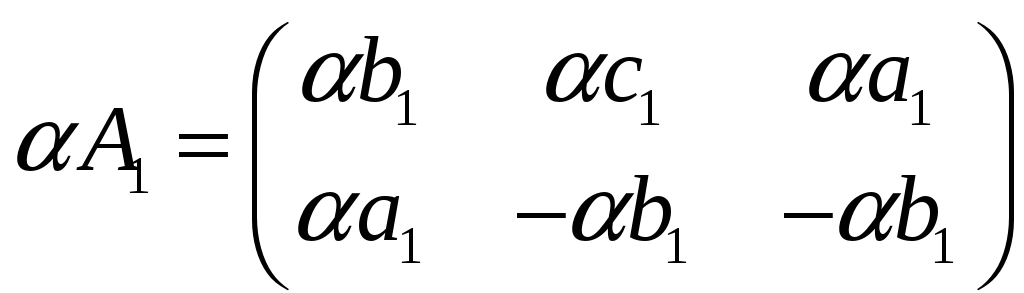
также принадлежит
![]() .
.
Итак,
![]()
является подпространством пространства
![]() ,
,
а значит, само является пространством.
Найдем базис этого пространства.
Ясно, что в базис можно включить,
например,
![]()
, так как
![]() .
.
Так как ![]()
, то
![]()
нельзя получить в виде
![]() .
.
Поэтому в качестве второго базисного
вектора можно взять
![]() .
.
Рассмотрим вектор
![]() .
.
Его нельзя представить в виде линейной
комбинации
![]()
и
![]() ,
,
так как
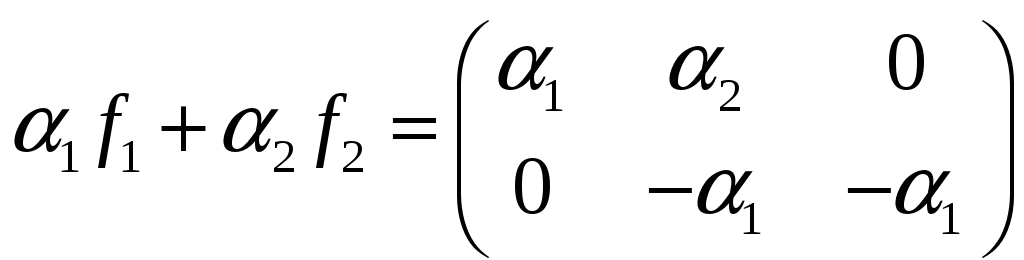 .
.
Поэтому в качестве третьего базисного
вектора возьмем
![]() .
.
Всякий другой вектор
![]()
можно представить в виде линейной
комбинации
![]() .
.
![]() .
.
Следовательно, система векторов
![]()
является системой образующих пространства
![]() .
.
По построению, эта система линейно
независима. Значит, она является базисом.
Пример2. Выяснить, является ли
система векторов
![]()
линейно зависимой. Найти коэффициенты
линейной зависимости.
Решение. Пусть
![]() ,
,
где
![]()
— некоторые числа. Подставляем в это
равенство векторы
![]() .
.
![]() .
.
После выполнения операции над векторами
получаем
![]() ,
,
откуда
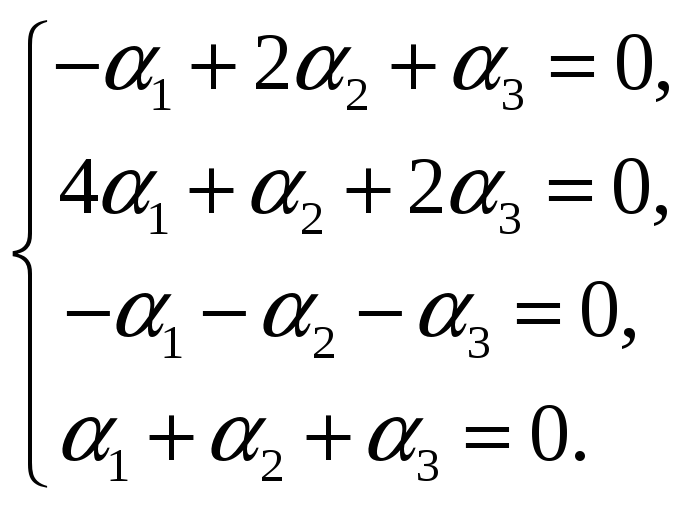
Эту систему линейных уравнений решаем
методом Гаусса:
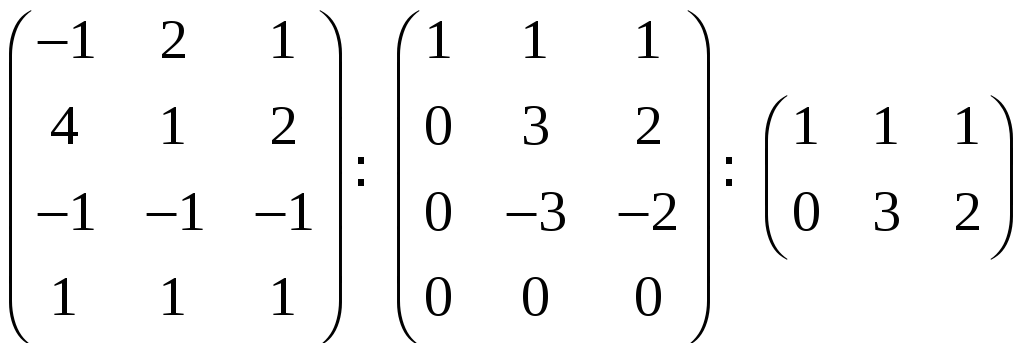 .
.
Получилась трапецеидальная система
уравнений. Она является неопределенной
и потому имеет ненулевые решения (кроме
нулевого). Таким образом, система
![]()
линейно зависима. Найдем коэффициенты
линейной зависимости. Для этого решаем
однородную систему линейных уравнений,
приведенную к трапецеидальному виду
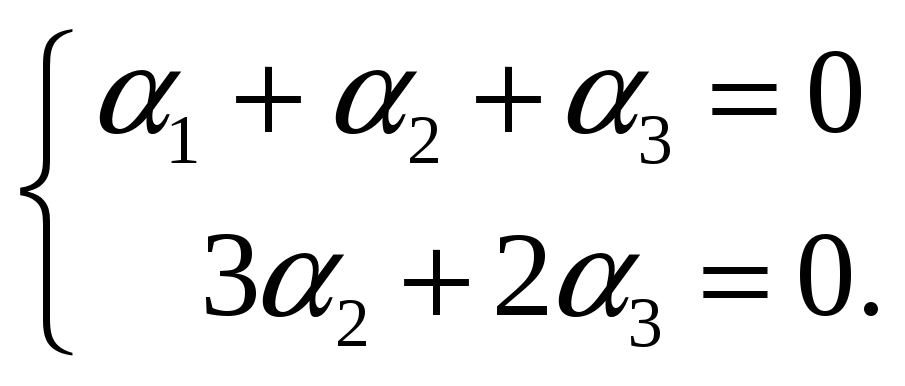
Общее решение этой системы имеет вид
![]() .
.
Найдем частное решение, придавая
![]()
произвольное значение, отличное от
нуля, например, -3. Получим
![]() .
.
Таким образом,
![]() .
.
Очевидно, коэффициенты линейной
зависимости определяются неоднозначно.
Пример 3. Найти какую-нибудь
максимальную линейно независимую
подсистему данной системы векторов, а
остальные векторы выразить через нее.
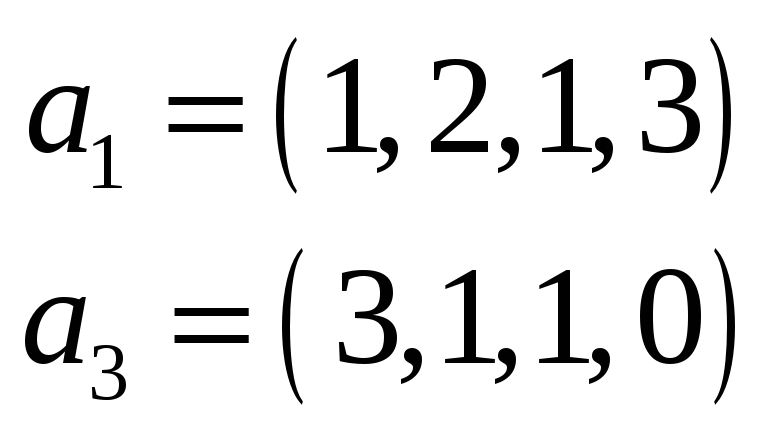
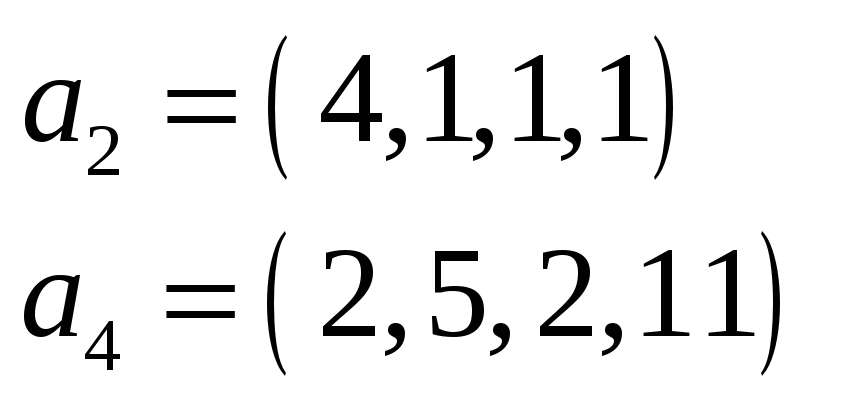
Решение. Составим матрицу
![]() ,
,
столбцами которой являются данные
векторы, и найдем ее ранг. Будем делать
элементарные преобразования только
над строками.

Первую строку, умноженную на соответствующие
числа -2, -1, -3, прибавили ко второй, третьей,
четвертой. Третью строку, умноженную
на соответствующие числа -2, -4, прибавили
ко второй и четвертой. И наконец, третью,
умноженную на 2, прибавили к четвертой.
Так как минор третьего порядка
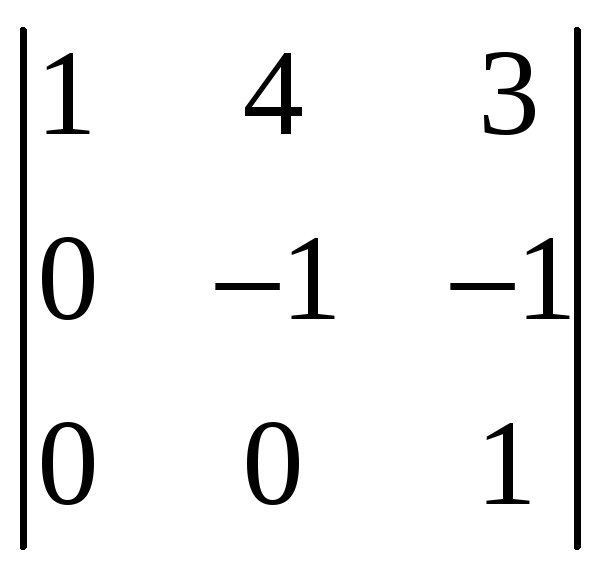
Отличен от нуля, а определитель четвертого
порядка равен нулю, то ранг последней
матрицы, а значит, ранг матрицы
![]()
равен 3. Отсюда следует, что ранг данной
системы равен 3.
Три вектора входят в максимальную
линейно независимую подсистему данной
системы. Очевидно, что это векторы
![]() .Действительно,
.Действительно,
выразим вектор
![]()
через
![]() :
:
![]() .
.
Подставим в это уравнение выражения
векторов
![]() .
.
После выполнения операций над векторами
получим:
![]() .
.
Приравнивая соответствующие координаты,
получим систему линейных уравнений:
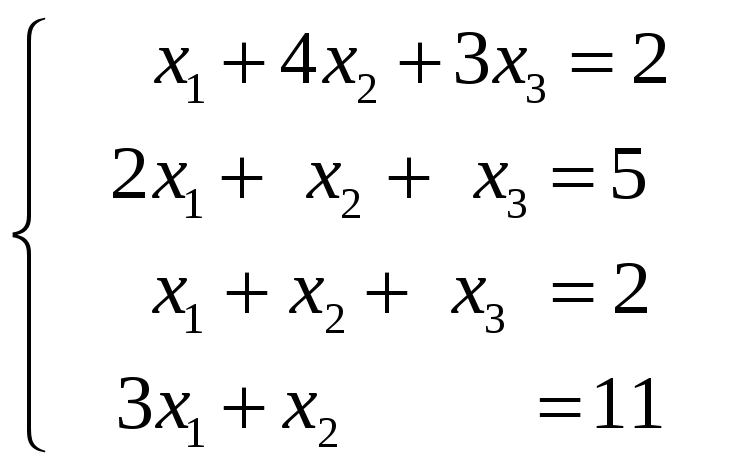 .
.
Решаем эту систему методом Гаусса.
Составим расширенную матрицу
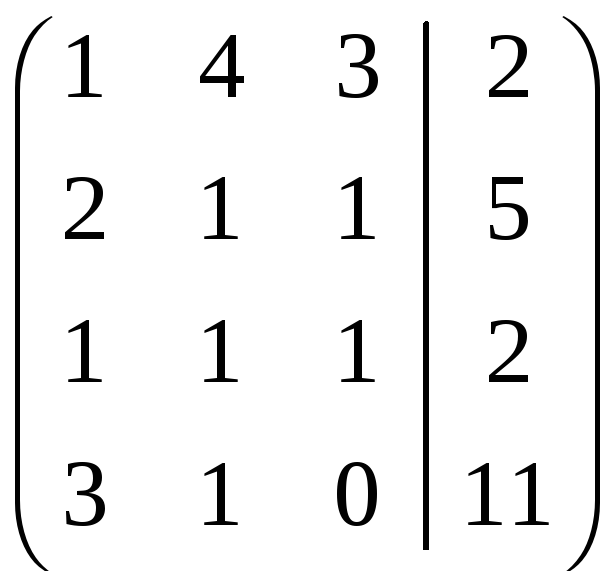 .
.
Эта матрица совпадает с матрицей
![]() .
.
Так как мы проделываем элементарные
преобразования над строками матрицы
![]() ,
,
то эта система эквивалентна системе
линейных уравнений, соответствующей
последней матрице:
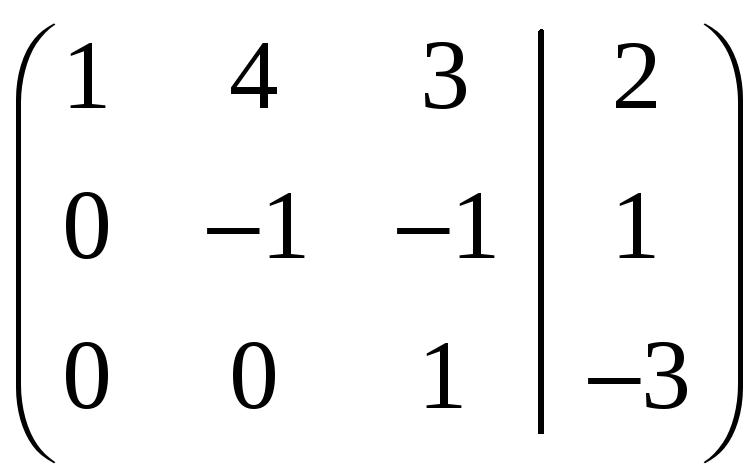
, то есть системе
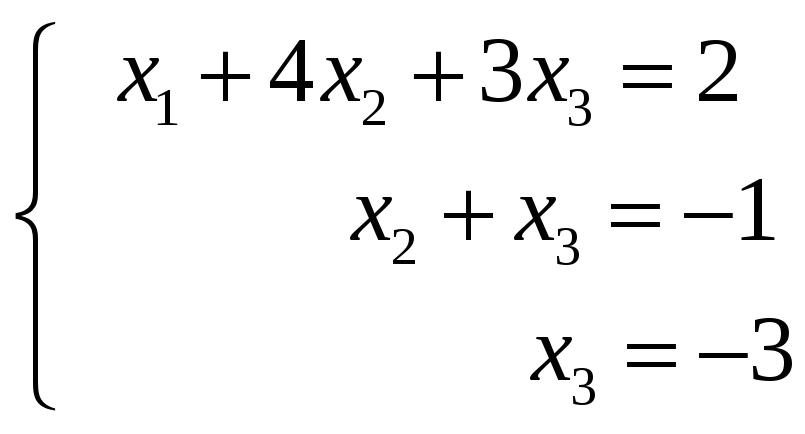
, откуда
![]() ,
,
а следовательно,
![]() .
.
Пример 4. Векторы
![]()
заданы своими координатами в некотором
базисе
![]() .
.
Показать, что векторы
![]()
сами образуют базис, и найти координаты
вектора
![]()
в этом базисе.
Решение. Так как система любых трех
линейно независимых векторов является
базисом 3-мерного пространства, то
достаточно доказать, что система
![]()
линейно независима. Для этого составим
матрицу
![]() ,
,
столбцами которой являются координаты
векторов
![]() ,
,
и найдем ее ранг.
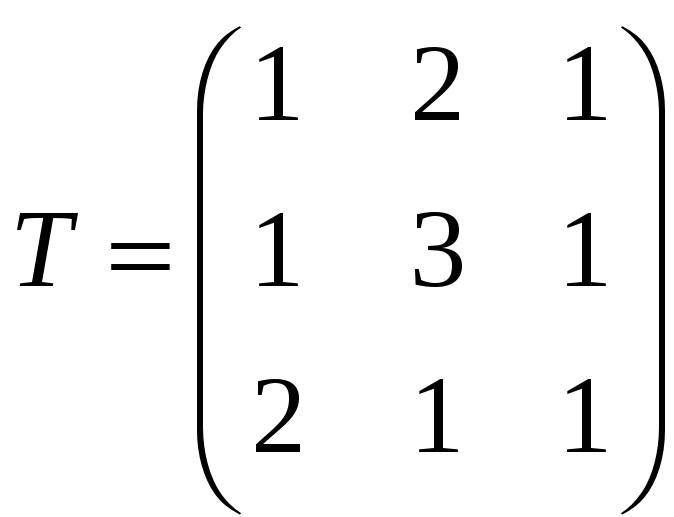 .
.
Определитель этой матрицы
![]() ,
,
а значит, по теореме о ранге, ранг матрицы
равен 3, что доказывает линейную
независимость системы
![]() .
.
Таким образом,
![]()
образуют базис и
![]() -матрица
-матрица
перехода от базиса
![]()
к базису
![]() .
.
Для нахождения координат вектора в
базисе
![]()
воспользуемся формулой преобразования
координат, приведенной в
![]() :
:
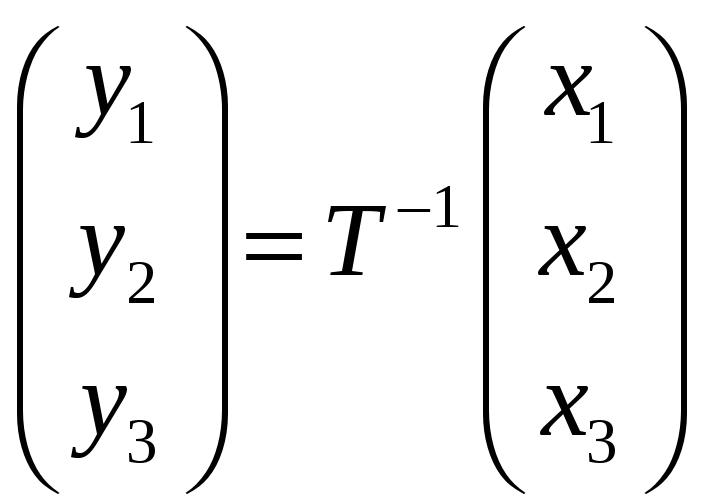
, где
![]()
— матрица перехода от базиса
![]()
к базису
![]() ;
;
![]()
— координаты вектора в базисе
![]() ;
;
![]()
— координаты вектора
![]()
в базисе
![]() .
.
Так как здесь
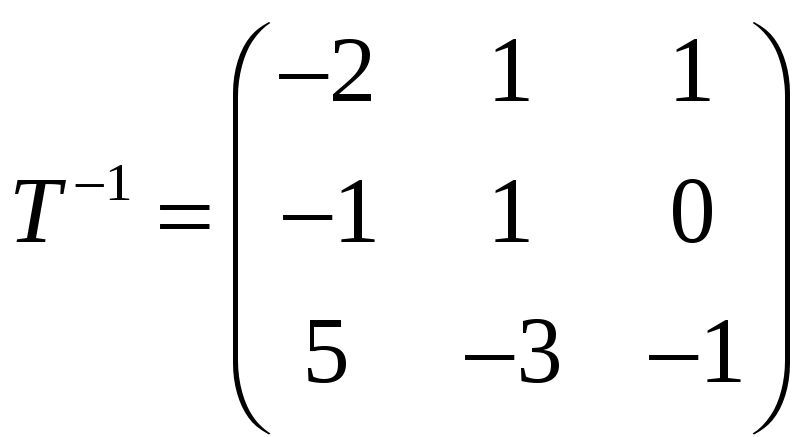 ,
,
то
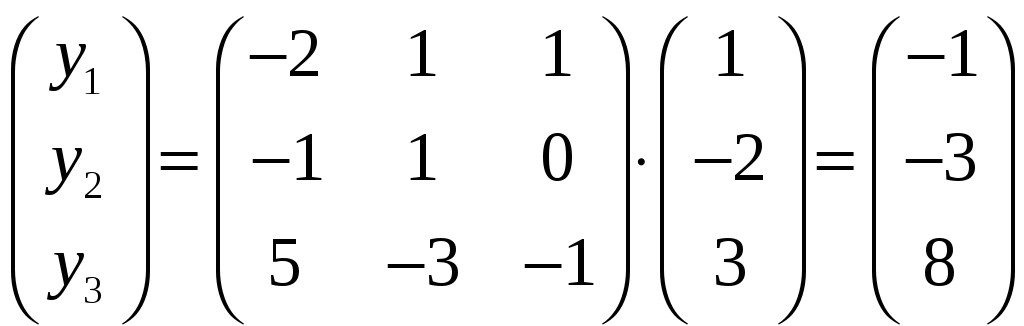 ,
,
Откуда
![]() ,
,
то есть
![]() .
.
Пример 5. Найти размерность и базис
линейного подпространства, натянутого
на векторы
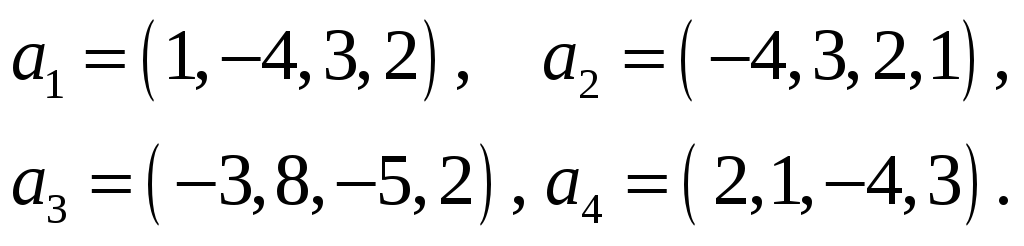
Решение. Базис линейного подпространства
![]()
совпадает с максимальной линейно
независимой подсистемой системы векторов
![]()
(доказать!). Найдем эту подсистему, для
чего составим матрицу, столбцами которой
являются векторы
![]() .
.
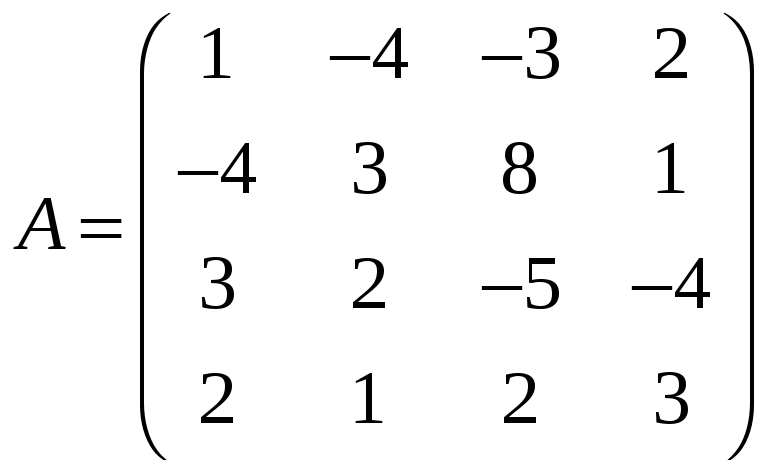 .
.
Найдем базисный минор этой матрицы. Так
как минор второго порядка
![]() ,
,
то рассмотрим минор 3-го порядка, его
окаймляющий
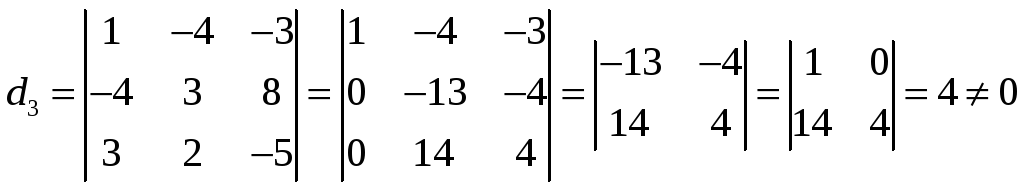 .
.
Теперь рассмотрим минор 4-го порядка,
окаймляющий минор 3-го порядка, отличный
от нуля. Это определитель матрицы
![]() .
.
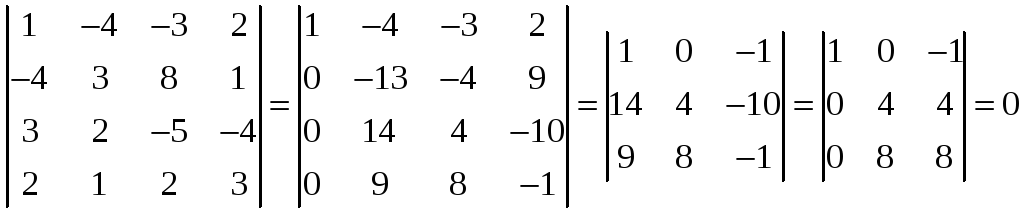 .
.
Он равен нулю. Значит,
![]()
является базисным минором, то есть
минором наибольшего порядка, отличным
от нуля. А тогда
![]()
образуют максимальную линейно-независимую
подсистему системы
![]()
и тем самым
![]()
образуют базис рассматриваемого
подпространства, причем размерность
подпространства равна 3.
Пример 6. Определить размерность и
базис пространства решений однородной
системы линейных уравнений.
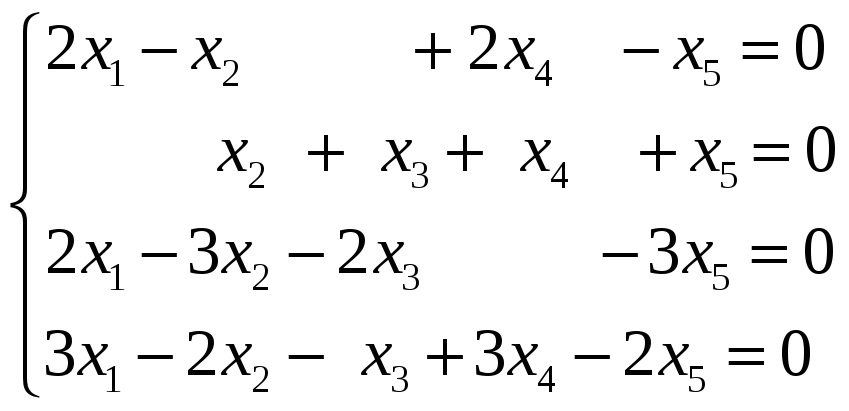
Решение. Множество всех решений
однородной системы линейных уравнений
образует векторное пространство
размерности
![]() ,
,
где
![]()
— число неизвестных системы, а
![]()
— ранг матрицы этой системы. Базис
образует система из любых
![]()
линейно независимых частных решений.
Такая система решений называется
фундаментальной. Находим общее решение
системы методом Гаусса, для чего
составляем матрицу системы:
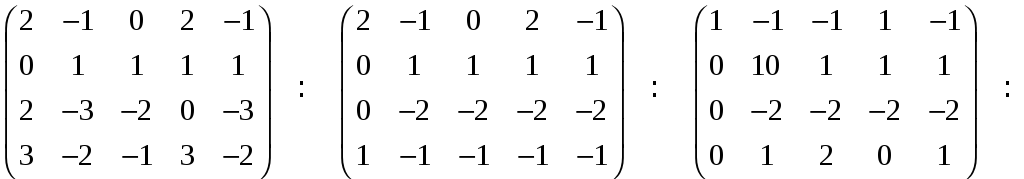
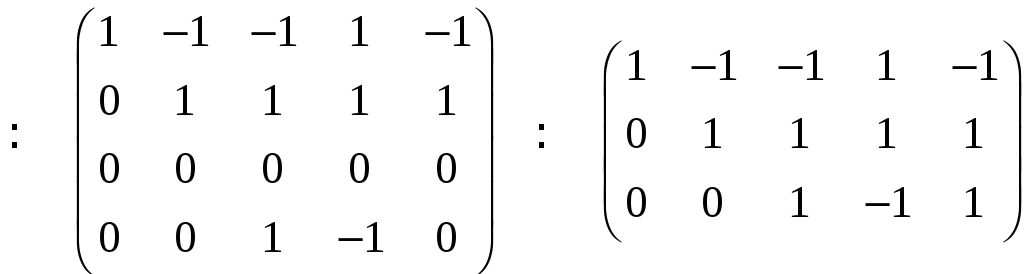 .
.
Ранг матрицы равен трем. Следовательно,
размерность пространства решений равна
2
![]() .
.
Данную систему уравнений заменим
эквивалентной системой:
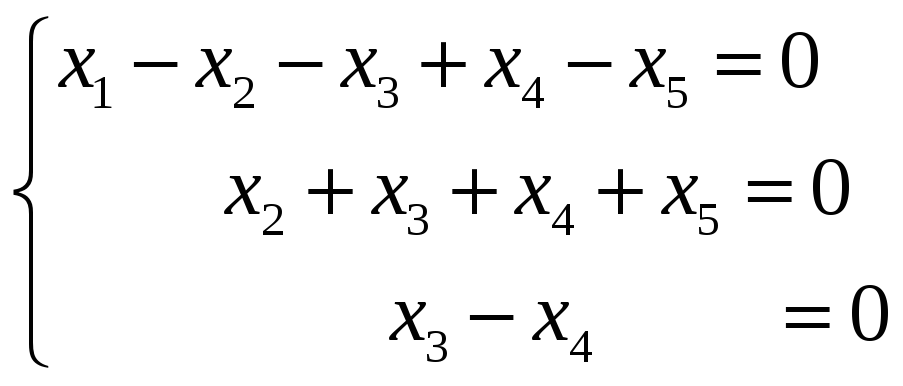
В качестве свободных неизвестных можно
взять
![]() .
.
Тогда
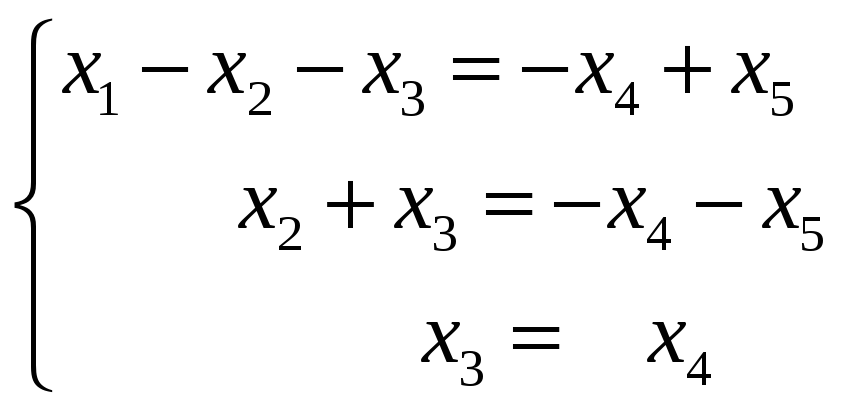
Общее решение системы имеет вид
![]() .
.
Находим два линейно независимых частных
решения. Для их нахождения мы два раза
придаем
![]()
и
![]()
произвольные значения, но так, чтобы
определитель второго порядка, составленный
из этих значений, был отличен от нуля.
Положим
![]() ,
,
а затем
![]()
и найдем
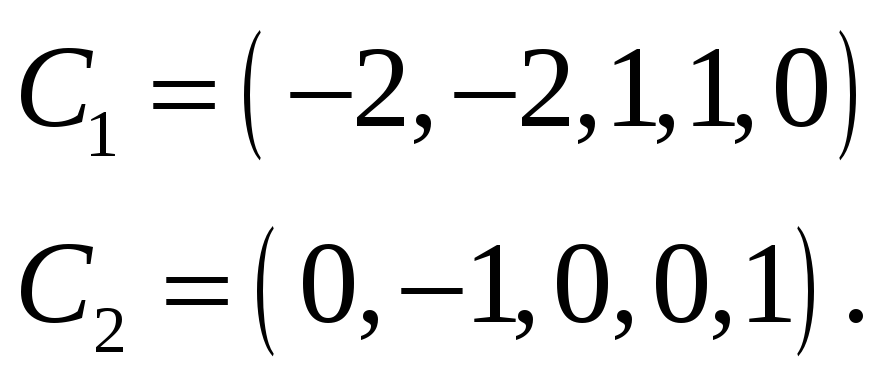
Мы получим один из базисов пространства
решений данной однородной системы
уравнений.
Пример 7. Найти базис и размерность
пересечения подпространств
![]()
и
![]() ,
,
натянутых на системы векторов
![]()
и
![]()
соответственно, если векторы заданы
координатами в некотором базисе
пространства.
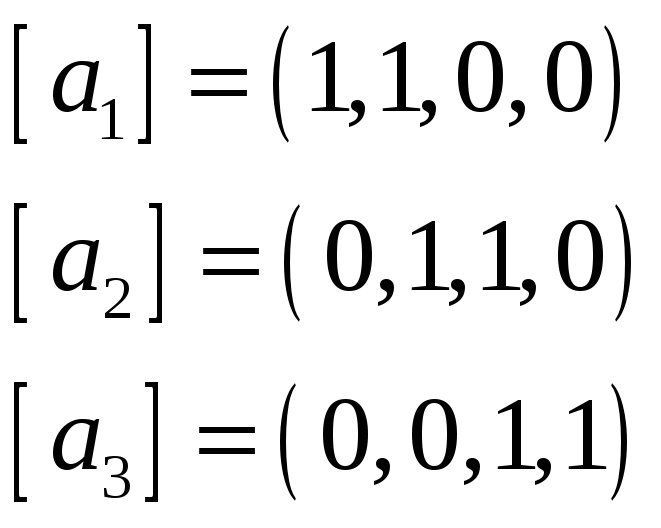
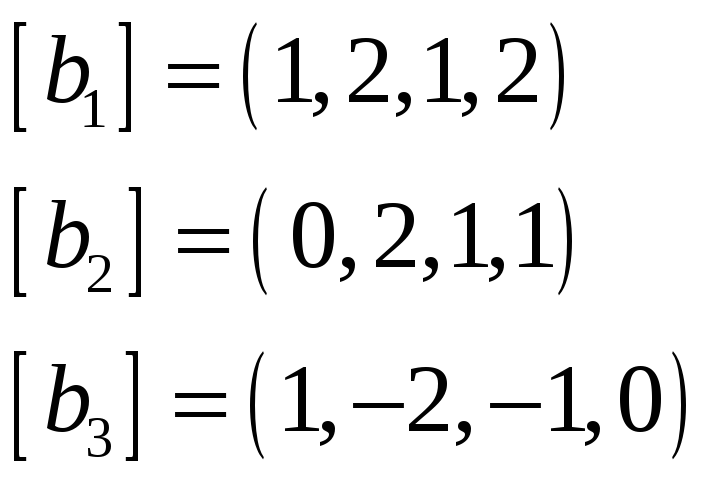
Решение. Вектор
![]()
тогда и только тогда, когда
![]()
линейно выражается через
![]()
и через
![]() .
.
А для этого необходимо и достаточно,
чтобы ранг матрицы
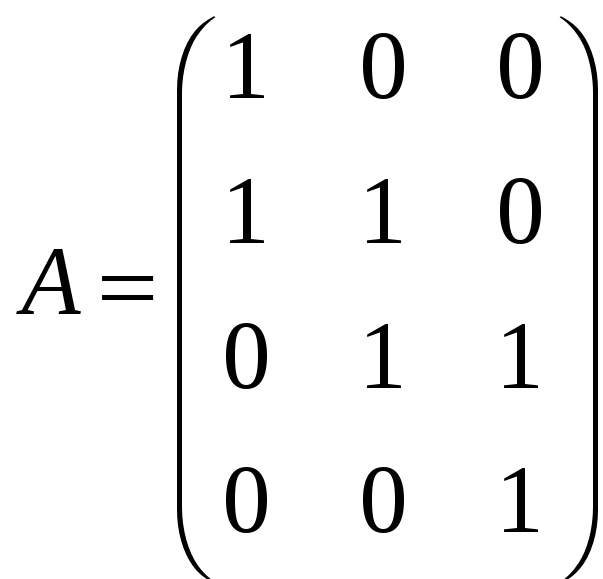
был равен рангу матрицы
![]()
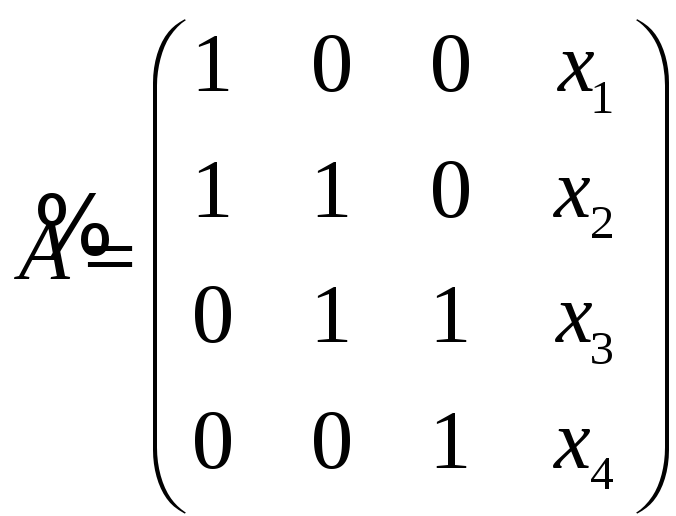
и ранг матрицы
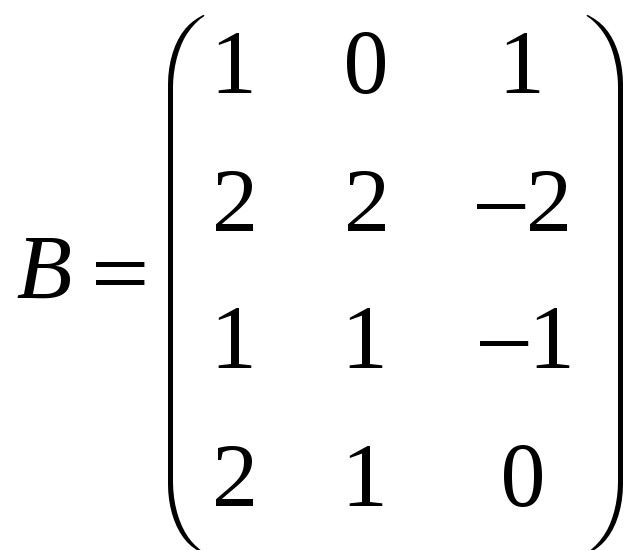
был равен рангу матрицы
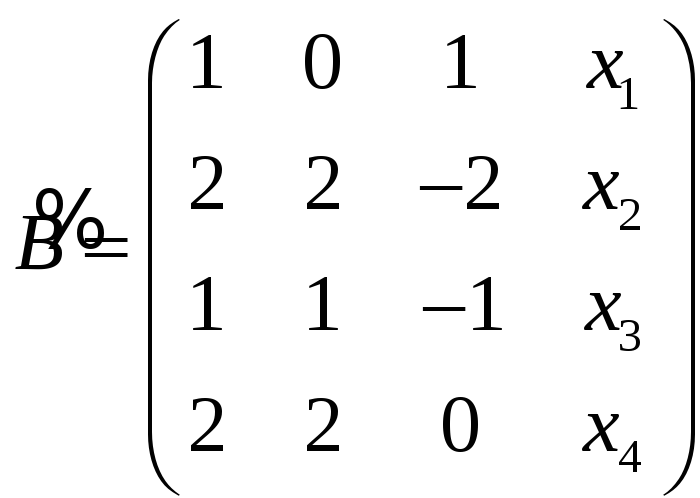 .
.
Выберем базисные миноры
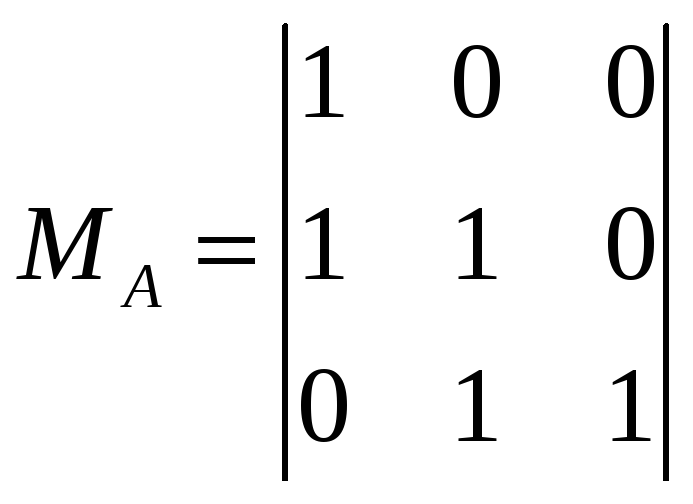
и ![]()
матриц
![]()
и
![]()
соответственно. Для того, чтобы
![]()
и
![]() ,
,
необходимо и достаточно, чтобы
![]()
был базисным минором в
![]() ,
,
а
![]()
— в
![]() .
.
Приравнивая нулю все миноры
![]()
и
![]() ,
,
окаймляющие соответственно
![]()
и
![]() ,
,
содержащие столбец
![]()
и имеющие порядок на единицу выше, чем
![]()
и
![]() ,
,
получим систему линейных уравнений.
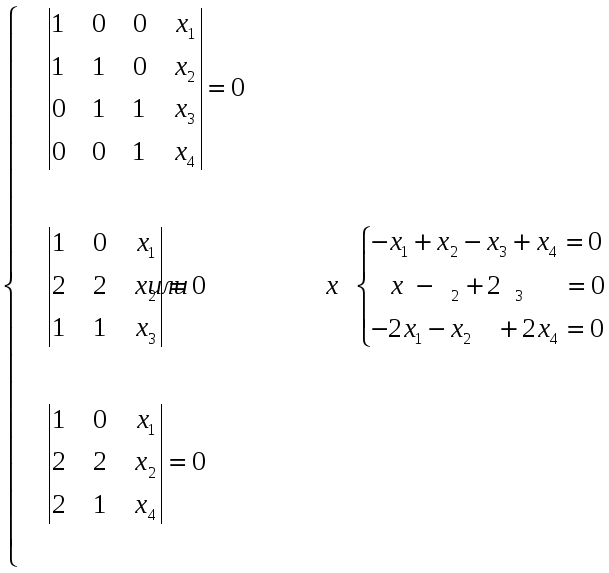
Решаем эту систему методом Гаусса.

![]() .
.
Общее решение имеет вид
![]() .
.
Фундаментальная система состоит из
одного вектора
![]() .
.
Следовательно, вектор
![]()
образует базис подпространства
![]() .
.
Литература: 3 — §17,
18
5 — №№ 608-613, 624-626, 636-650, 652-655, 661-669, 672, 674,
681, 689-695, 702-704, 712-714, 724-727, 1277-1293, 1296-1305,
1309-1311, 1317, 1318, 1320, 1321.
Контрольная работа 2
Найти значение многочлена
![]()
и всех его производных в точке
![]() .
.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
Найти рациональные корни и определить
их кратность.
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]() .
.
12.
![]() .
.
Разложить на неприводимые множители
над полем
![]() .
.
13.
![]() .
.
14.
![]() .
.
15.
![]() .
.
16.
![]() .
.
17.
![]() .
.
18.
![]() .
.
Найти каноническое разложение многочлена
над полем путем отделения кратных
корней.
19.
![]() .
.
20.
![]() .
.
21.
![]() .
.
22.
![]() .
.
23.
![]() .
.
24.
![]() .
.
Найти значение симметрического
многочлена
![]()
на корнях многочлена
![]() .
.
25.
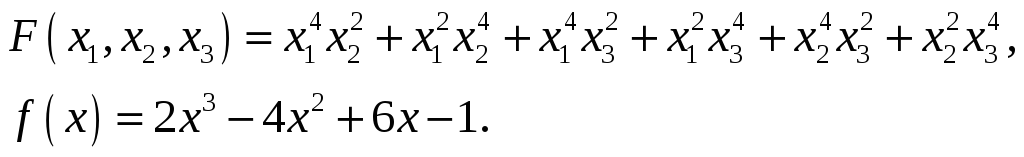
26.
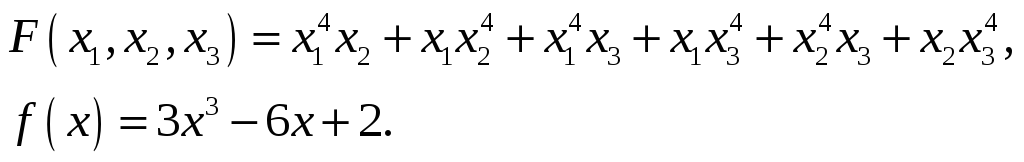
27.
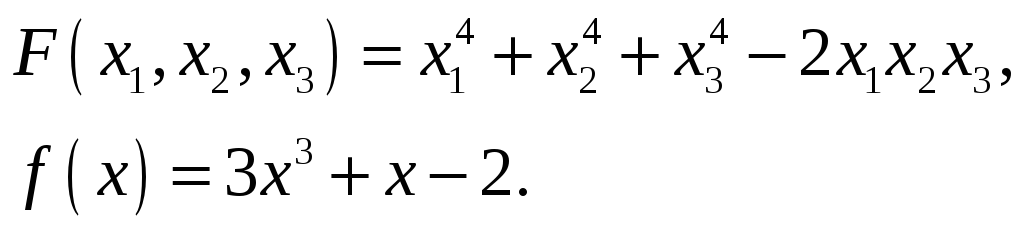
28.
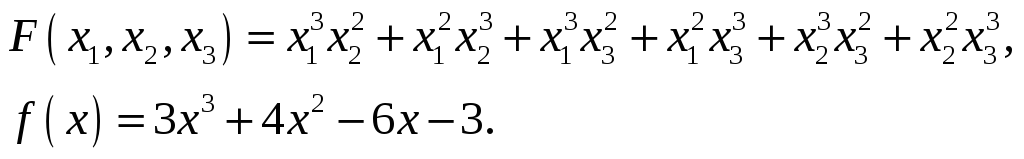
29.
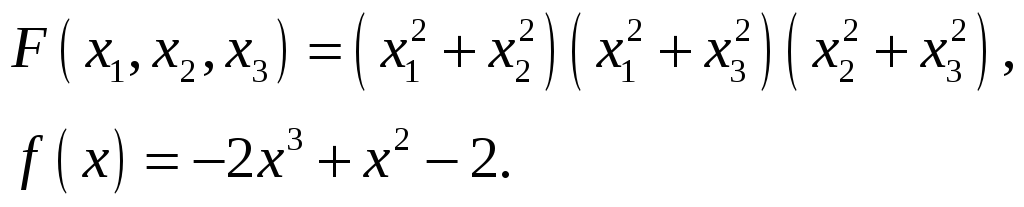
30.
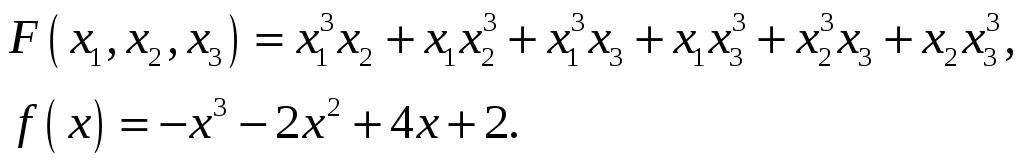
Доказать, что следующее множество
образует векторное пространство над
полем
![]() .
.
Найти его базис и размерность.
31.
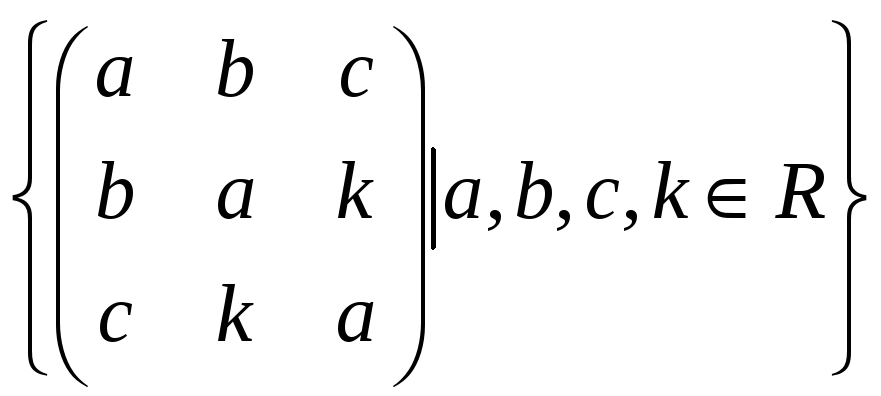 .
.
32.
![]() .
.
33.
![]() .
.
34.
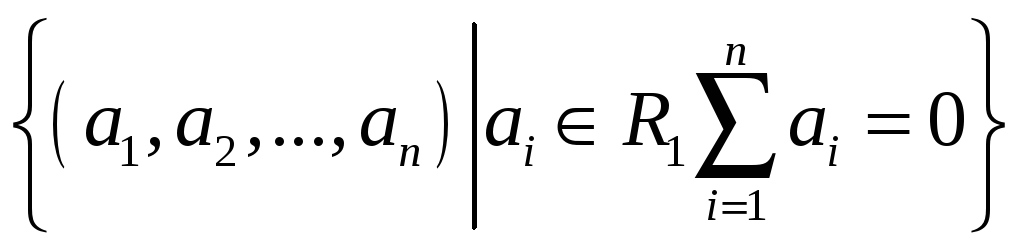 .
.
35.
![]() .
.
36.
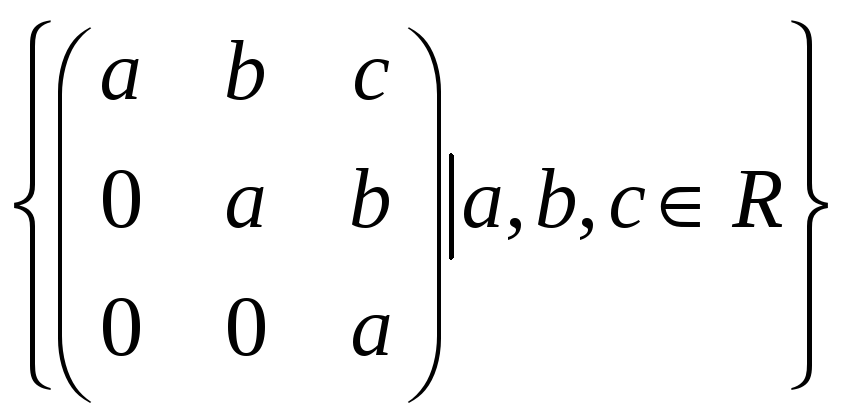 .
.
Выяснить, является ли система векторов
линейно зависимой. Найти коэффициенты
линейной зависимости.
37.
![]()
38.
![]()
39.
![]()
40.
![]()
41.
![]()
42.
![]()
Найти какую-нибудь максимальную
независимую подсистему данной системы
векторов, а остальные векторы выразить
через нее.
43.
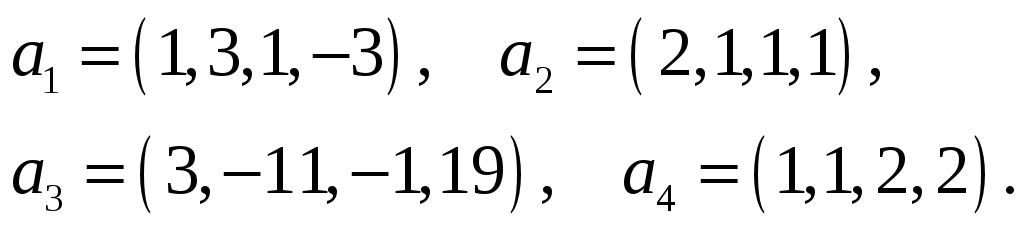
44.
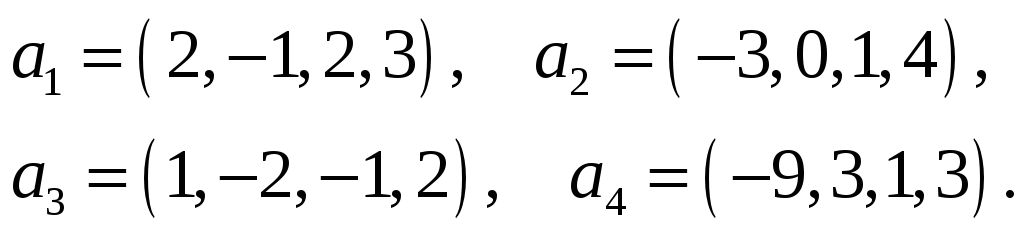
45.
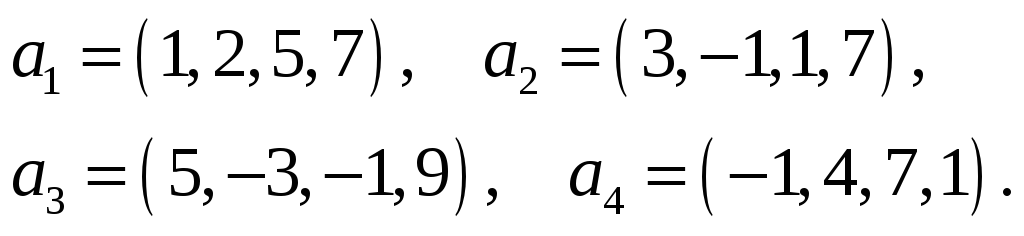
46.
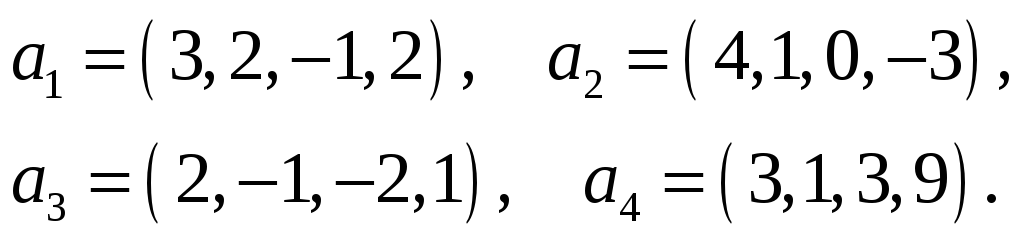
47.
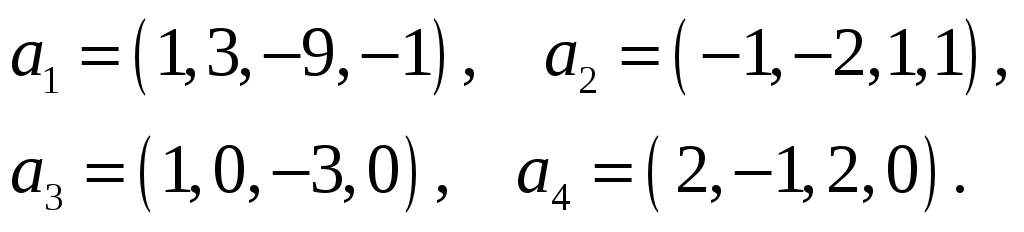
48.
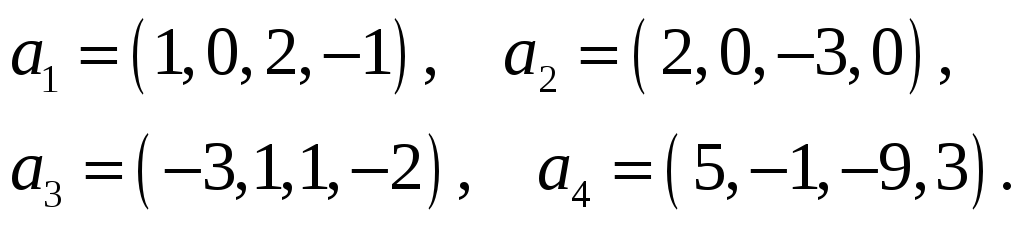
Векторы
![]()
и
![]()
заданы своими координатами в некотором
базисе
![]() .
.
Показать, что векторы
![]()
сами образуют базис, и найти координаты
вектора
![]()
в этом базисе.
49.
![]()
50.
![]()
51.
![]()
52.
![]()
53.
![]()
54.
![]()
Найти размерность и базис пространства
решений однородной системы линейных
уравнений.
55.
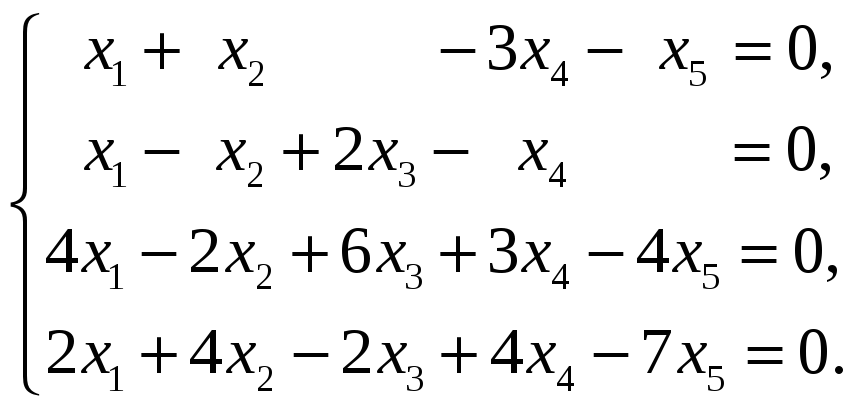 57.
57.
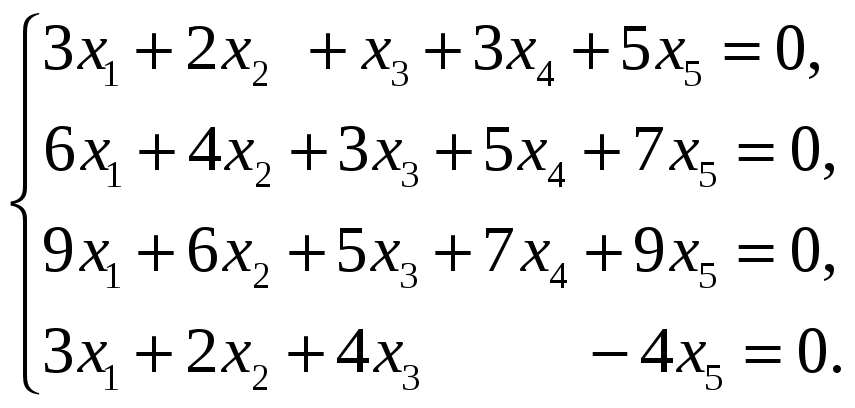
56.
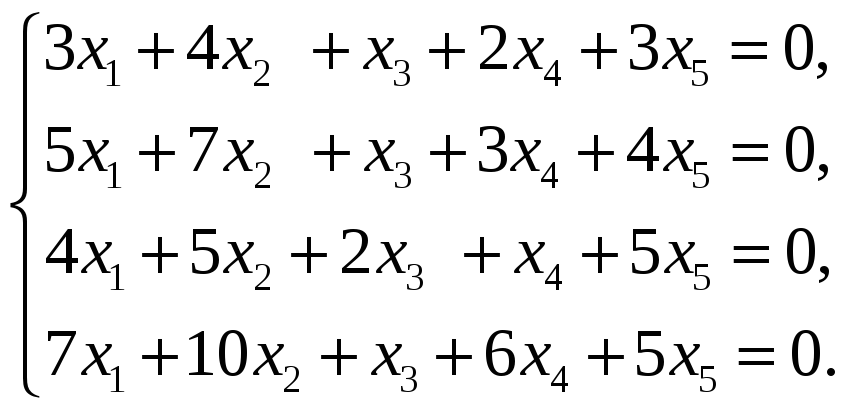 58.
58.
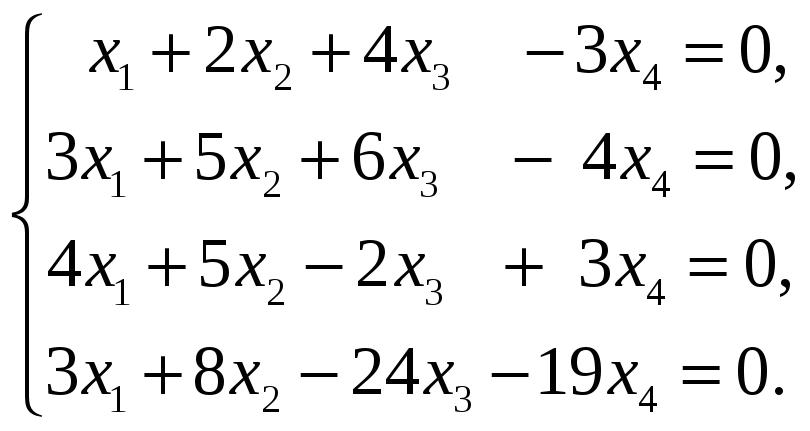
59.
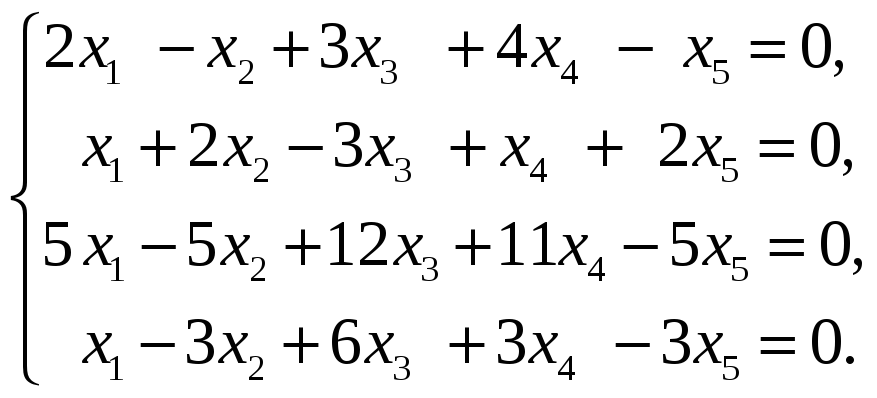 60.
60.
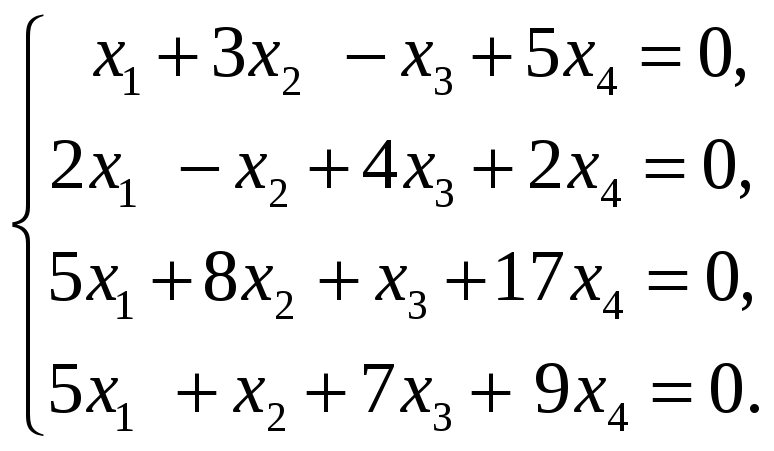
Найти базис пересечения подпространств
![]()
и
![]() ,
,
натянутых на векторы
![]()
и
![]()
соответственно, если все векторы заданы
своими координатами в некотором базисе
пространства.
61. 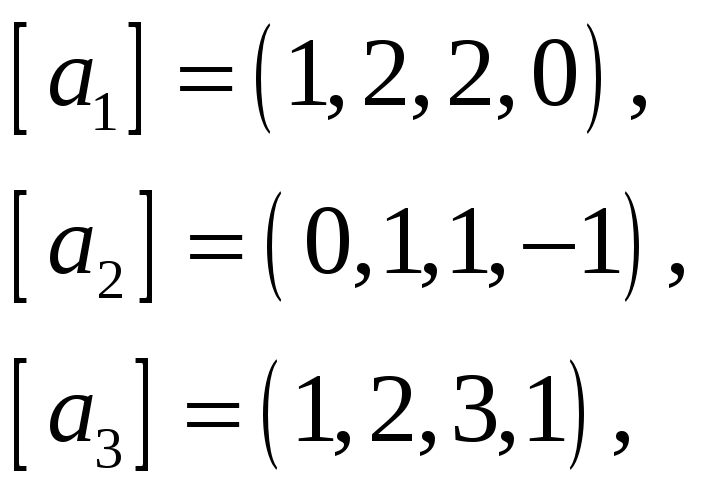
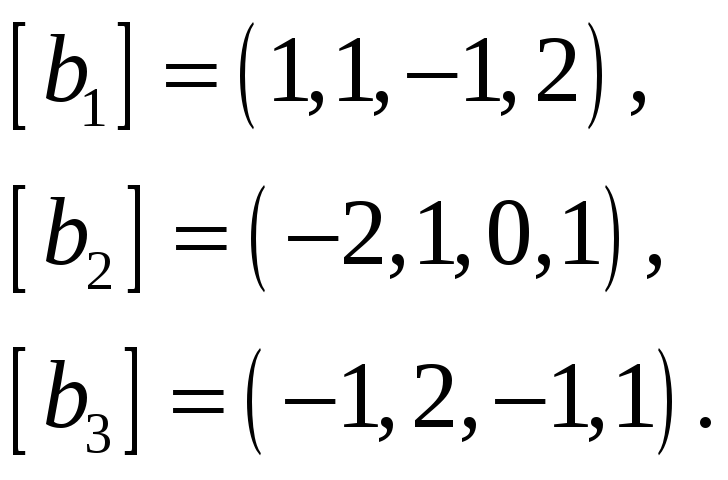
62. 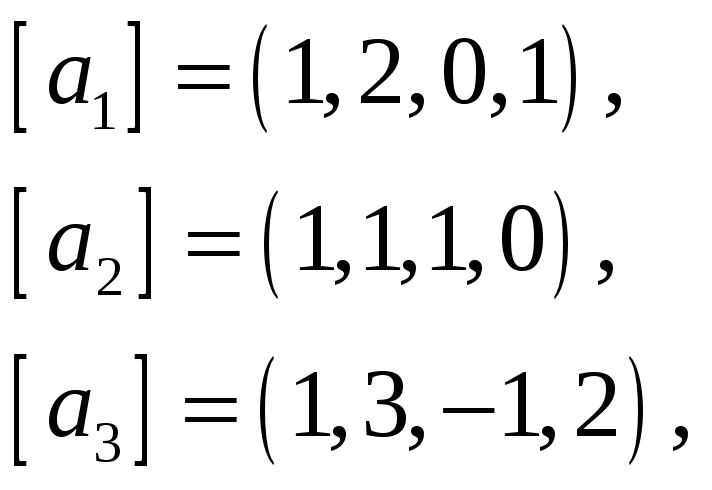
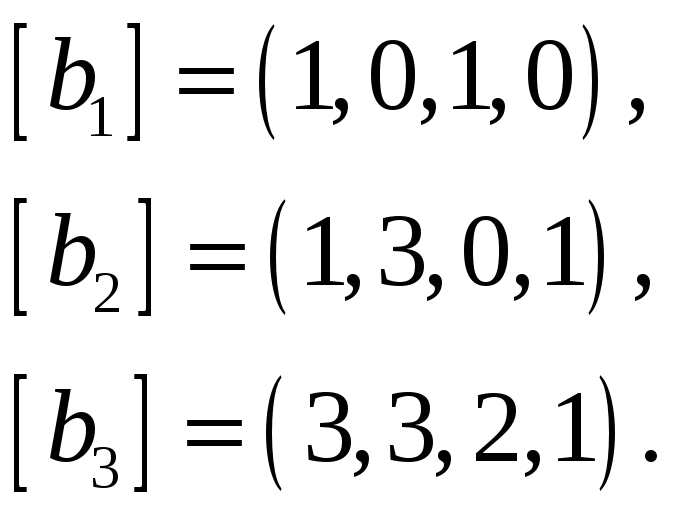
63. 
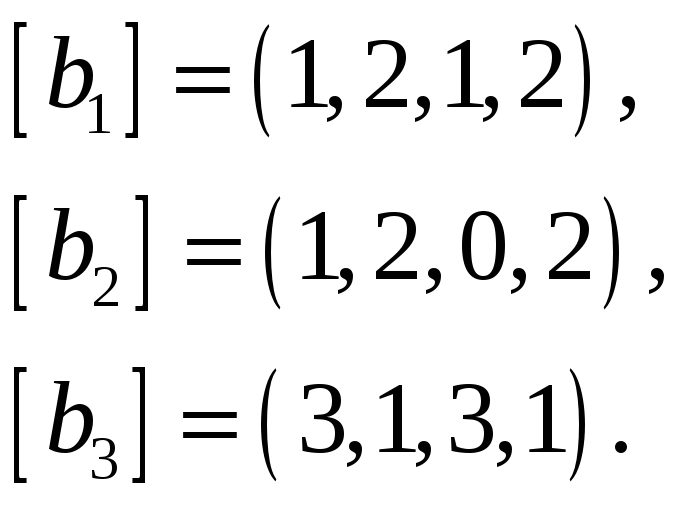
64. 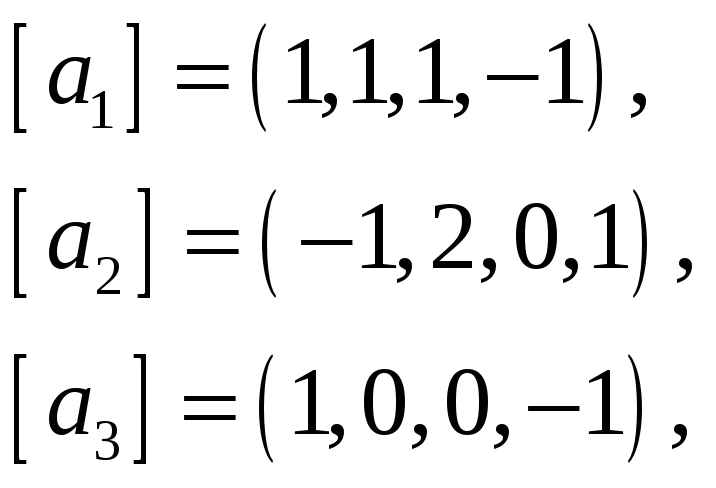
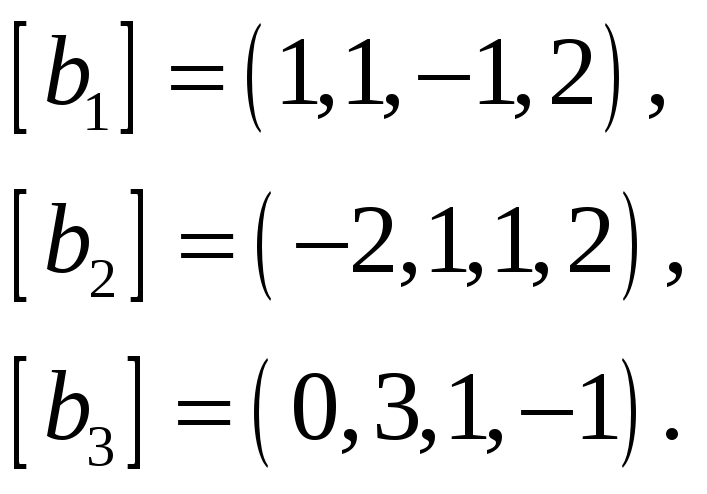
65. 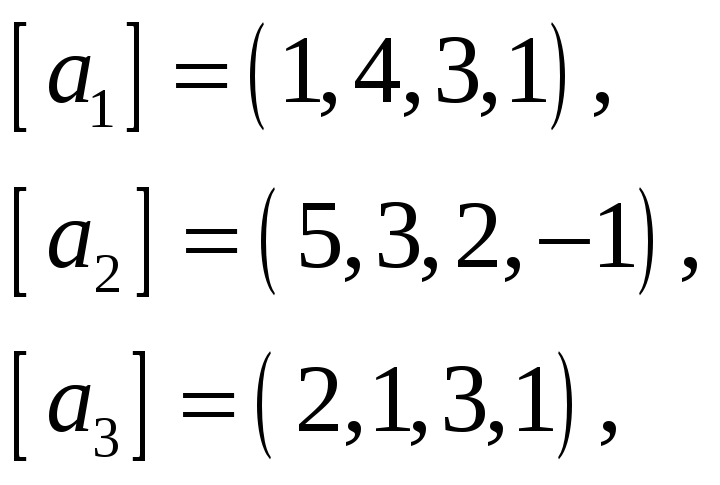
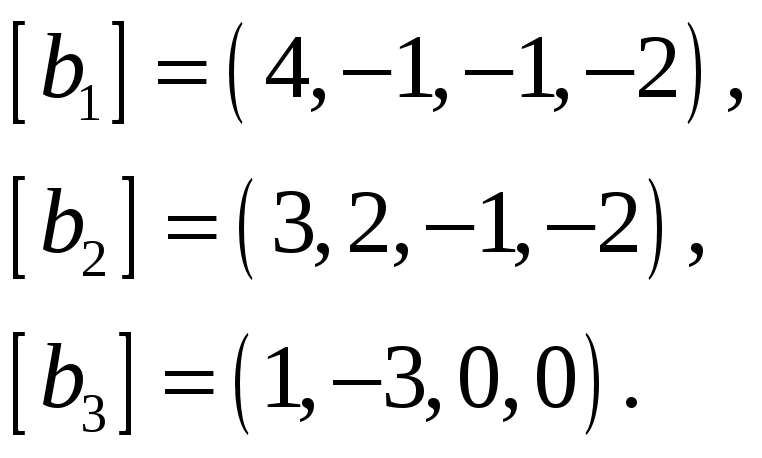
66. 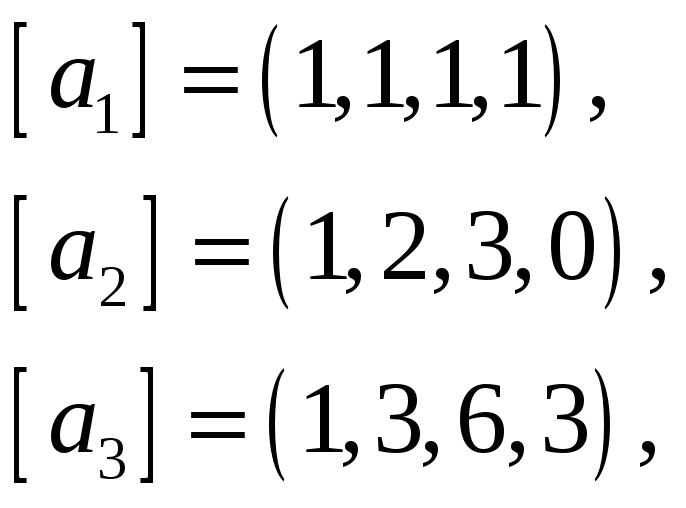
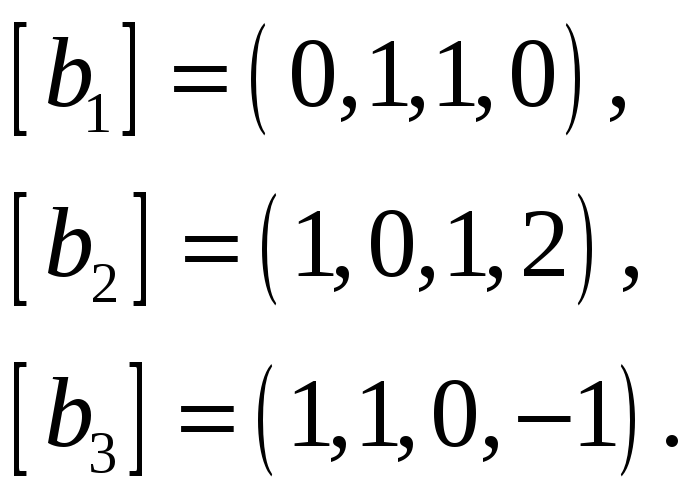
ЛИТЕРАТУРА
-
Курош А.Г. Курс высшей алгебры. 6-е изд.
М., 1971. -
Милованов М.В., Тышкевич Р.И., Феденко
А.С. Алгебра и аналитическая геометрия.
Часть I. Минск, 1984. -
Милованов М.В., Толкачев М.М., Тышкевич
Р.И., Феденко А.С. Алгебра и аналитическая
геометрия. Часть 2. Минск, 1981. -
Фаддеев Д.К., Соминский И.С. Сборник
задач по высшей алгебре. 3- изд. М.: Наука,
1974.
Учебное издание
ЖИГОТА АЛЛА ЭДУАРДОВНА
Методические указания и контрольные
работы
по курсу «Алгебра и теория чисел»
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
У вас система всего из трех векторов. Поэтому можно не заморачиваться общими методами, а решить задачу подбором.
Возьмите первый вектор. Он ненулевой, значит составляет линейно-независимую систему из одного вектора. Присоедините к системе какой-нибудь другой вектор. Наверно любой можно присоединить, чтобы система осталась линейно-независимой. Для двух векторов это проверить особенно легко — они линейно зависимы если и только если они пропорциональны. Остался третий вектор. Попробуйте найти линейную комбинацию первых двух, чтобы получился третий, методом Гаусса. Если у вас это не получится (нет решения) то вы докажете, что третий не зависит от первых двух и его можно присоединить к системе. Если же получится решение, то система останется в количестве двух векторов, но зато вы получите выражение третьего через вектора системы, что и требует задача.
Общий метод, который применяется при больших размерностях и количествах векторов, связан с приведением матрицы к ступенчатому виду. По ссылке Robot это хорошо изложено.
